CrossPlan: systematic planning of genetic crosses to validate mathematical models

Abstract

Motivation

Mathematical models of cellular processes can systematically predict the phenotypes of novel combinations of multi-gene mutations. Searching for informative predictions and prioritizing them for experimental validation is challenging since the number of possible combinations grows exponentially in the number of mutations. Moreover, keeping track of the crosses needed to make new mutants and planning sequences of experiments is unmanageable when the experimenter is deluged by hundreds of potentially informative predictions to test.

Results

We present CrossPlan, a novel methodology for systematically planning genetic crosses to make a set of target mutants from a set of source mutants. We base our approach on a generic experimental workflow used in performing genetic crosses in budding yeast. We prove that the CrossPlan problem is NP-complete. We develop an integer-linear-program (ILP) to maximize the number of target mutants that we can make under certain experimental constraints. We apply our method to a comprehensive mathematical model of the protein regulatory network controlling cell division in budding yeast. We also extend our solution to incorporate other experimental conditions such as a delay factor that decides the availability of a mutant and genetic markers to confirm gene deletions. The experimental flow that underlies our work is quite generic and our ILP-based algorithm is easy to modify. Hence, our framework should be relevant in plant and animal systems as well.

Availability and implementation

CrossPlan code is freely available under GNU General Public Licence v3.0 at https://github.com/Murali-group/crossplan

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Mathematical models of gene and protein regulatory networks are widely used to investigate cellular processes (Le Novere, 2015). A standard approach used in mathematical modeling is to start by constructing the model of a specific cellular process, e.g. the cell cycle, from relevant experimental data. Subsequently, we simulate the model in a new scenario, e.g. a combination of gene knockouts that has not been characterized experimentally. Next, we design and perform an experiment to validate the model’s prediction in this scenario. Finally, we modify or expand the model to reconcile any differences between the prediction and experiment and continue this cycle.

The motivation for this paper is to dramatically scale-up this build-simulate-test cycle. First, we simulate the model to make systematic predictions of the system’s behavior under various perturbations, e.g. all single gene, double gene, triple gene knockouts and so on. Next, we analyze these predictions to select a subset that are likely to be the most informative about the model and the process under study. Finally, we seek to perform the experiments that can test these informative predictions. The last step can be very challenging, since planning experiments to make the genetic mutants to test these predictions becomes unmanageable and daunting, even for more than a dozen or so mutants. Therefore, we focus in this paper on developing new algorithms that can automatically synthesize efficient experimental plans to make the desired mutants.

Previous research has focused mainly on prioritizing the next-best or a small number of experiments, e.g. to distinguish between Boolean network models that fit the available data equally (Atias et al., 2014; Barrett and Palsson, 2006; Ideker et al., 2000; Szczurek et al., 2009; Yeang et al., 2005), to estimate the kinetic parameters of an ordinary differential equation (ODE) model (Bandara et al., 2009; Kreutz and Timmer, 2009; Pauwels et al., 2014) or to resolve model ambiguity (Apgar et al., 2008; Harrington et al., 2012; Kremling et al., 2004; Melykuti et al., 2010).

The problem we are addressing has several unique characteristics that render existing techniques inapplicable. Our primary challenge is that we desire to plan a set of experiments that can test several (hundreds or thousands) promising predictions made by the model. Testing each prediction requires making a multi-gene mutant by performing genetic crosses. Additional challenges arise because we must account for several criteria that are potentially in conflict with each other: (i) there may be many sequences of crosses that can make a mutant, (ii) a strain to be generated may be parental to multiple mutants and (iii) some parental mutants may be known or predicted to be inviable. Further, we need techniques that can operate under cost-effective experimental workflows and efficiently utilize mutant strains that are available in the lab. Therefore, we focus on the novel problem of computationally synthesizing an optimal sequence of experiments to be performed in order to produce multiple mutant strains carrying multi-gene knock-outs of interest.

More specifically, we develop a novel methodology, CrossPlan, to compute a sequence of genetic cross experiments organized into batches such that we can perform the crosses in each batch in parallel. CrossPlan takes as input a source set S of mutants that are available in the lab, a set T of target mutants whose phenotypes we are interested in characterizing experimentally, and the number k of batches (which reflects the experimental budget). The plan computed by CrossPlan maximizes the number of target mutants that can be made from the source set in k batches.

We design an integer-linear program (ILP) that captures all the constraints we have stated earlier and can solve the problem optimally. We apply our method to a comprehensive ODE-based mathematical model of the budding yeast cell cycle (Kraikivski et al., 2015). We use this model to simulate the phenotypes of mutants carrying mutations in up to 4 genes. We analyze the model predictions to identify rescued mutants: a mutant is rescued if the model predicts it to be viable, but there is a strain with one fewer gene deletion is known or predicted to be inviable. We apply CrossPlan to generate experimental designs that can produce the maximum number of rescued mutants starting from single gene mutations.

We also consider two important extensions mandated by experimental requirements. First, we account for a delay factor that decides when a newly synthesized mutant strain is available for subsequent crosses. Second, each gene deletion in a mutant strain carries a marker that we can use to verify that the gene has indeed been deleted in that strain. Our analysis shows that incorporating delays or the requirement that each gene mutation be associated with a unique marker has only a marginal effect on the number of planned mutants. We also suggest other time-efficient ILP formulations that are nearly optimal in terms of the number of target mutants that can be made. The Supplementary Material provides additional insights into our results and a case study where we compare the results of CrossPlan to a manual plan created by an expert yeast geneticist.

2 Materials and methods

In this section, we first describe our experimental methodology (Section 2.1). Next, we define the CrossPlan problem and its variants (Section 2.2). Finally, we design and describe the ILPs that we use to solve these problems (Sections 2.3 and 2.4).

2.1 Experimental workflow

Our strategy for making mutants uses the genetic cross, a standard and widely used technique in budding yeast and several other model organisms (Forsburg, 2001; Page and Grossniklaus, 2002; St Johnston, 2002). In this experiment, we start with two mutants that are already available e.g, aΔB and AbΔ in Fig. 1a) and cross them to produce a new mutant (aΔbΔ in this case). The process of crossing strains, sporulating the heterozygous diploids, performing tetrad dissection (micromanipulation of the four haploid meiotic products from each diploid) and analyzing these tetrads takes about 3 weeks (Fig. 1a).

Fig. 1.

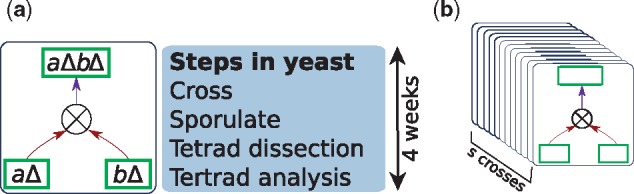
(a) Steps required to genetically cross two mutants to create new mutants. Each genetic cross requires three weeks to complete and (b) a batch of genetic crosses that can be performed in parallel. Each batch takes 3 weeks to complete. Costs of labor and supplies are fixed from one batch to another

We base CrossPlan on a generic experimental workflow in which we perform multiple genetic crosses in parallel in batches. Each batch included s genetic crosses (Fig. 1b). Each cross in a batch involves two viable mutant strains that must have either been made in an earlier batch or are already available to the experimenter (i.e. they are members of source set, S). In this workflow, the experimenter performs all s crosses and characterizes their phenotypes in parallel. In the case of budding yeast, each batch consists of a set of 12 crosses (i.e. s = 12); by sporulating batches of 12 crosses, we can perform tetrad analysis on all cultures before spore viability is reduced. Each batch uses approximately the same resources (supplies and labor). Thus, the number of batches we plan to perform determines the experimental cost.

With some modifications, this workflow can be applied to genetic crosses of other model organisms, for combinatorial siRNA (gene silencing) or CRISPR (genome editing) experiments, or even for testing combinations of bioactive molecules/drugs (Cipriani and Piano, 2011; Shen et al., 2017). For example, for genetic crosses in diploid organisms such as Drosophila melanogaster or mice, we would need to add backcrosses between offspring and parents in order to obtain homozygous mutations (Supplementary Section S1). For combinatorial siRNA, CRISPR or drug experiments, the workflow would be simpler, involving single-step co-introduction of RNAs, expression vectors or drugs to obtain the desired perturbing combinations.

2.2 Problem formulation

We introduce a useful abstraction for organizing mutants and the crosses needed to make them. Let G be a set of genes in an organism. A mutant m contains a combination of mutations (e.g. deletions) in multiple genes. We use G(m) to denote the set of genes mutated in m. The genetic cross graph$\mathcal{G}=(M,X,E)$ is a bipartite directed graph where M is a set of mutant nodes, X is a set of cross nodes and E is a set of edges. Each node in M corresponds to a mutant. Each node in X corresponds to a genetic cross experiment. Each edge e in E is either directed from a node in M to a node in X or vice-versa. More specifically, each node in X has two incoming edges (from nodes in M) and one or more outgoing edges (to other nodes in M). The incoming edges reflect the two mutants involved in a cross, while the outgoing edges reflect all the mutants that are products of the cross. Edges incident on a cross node must satisfy two rules. If there are edges incoming to a cross node x from mutant nodes m₁ and m₂, then

(i) the corresponding mutants must contain distinct single gene deletions, i.e. $G\left(m_1\right)\cap G\left(m_2\right)=\phi$ and

(ii) there is an outgoing edge from x to every mutant in $2^{G\left(m_1\right)\cup G\left(m_2\right)}$, since due to Mendelian inheritance, the cross produces every mutant involving some combination of the genes mutated in m₁ or m₂.

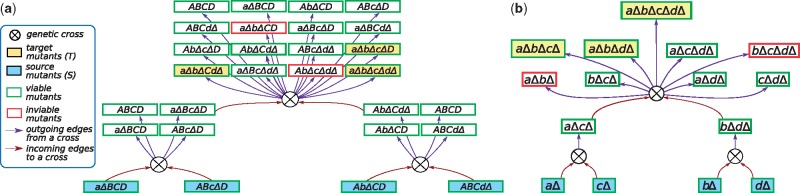
For example, Figure 2a illustrates three genetic crosses. The first cross produces aΔBcΔD from the strains aΔBCD and ABcΔD, while the second cross produces AbΔCdΔ from AbΔCD and ABCdΔ. Each cross also produces the original single mutants and the wild-type strain (shown as ABCD). The third cross combines the double mutants aΔBcΔD and AbΔCdΔ to produce one quadruple mutant aΔbΔcΔdΔ, four triple mutants, six double mutants, four single mutants and the wild type strain. For the sake of clarity and brevity, Figure 2b illustartes a simplified version (used for graphical purposes only) of the same set of crosses as in Figure 2a. In Figure 2b, only the mutated genes are shown for each of the mutants, and the only outgoing edges are from a cross to the new mutants that are produced as a result of that cross. In general, this graph represents all possible ways in which we can make new mutants from previously made mutants. Note that we can construct a mutant using several alternative crosses, which correspond to multiple incoming edges to the corresponding mutant node. Further, we delete from the genetic cross graph any edges that leave mutants that we know are inviable from previous experimental evidence or from model predictions.

Fig. 2.

Illustration of three crosses in a genetic cross graph. Each rectangle is a mutant. Each circle is a genetic cross with two incoming edges (brown) and multiple outgoing edges (purple). (a) The figure illustrates three crosses: aΔBCD with ABcΔD, AbΔCD with ABCdΔ, and aΔBcΔD with AbΔCdΔ. (b) Simplified version of the genetic cross graph (for illustrative purposes only). See the text for more details

Next, we use the terminology of the genetic cross graph to define a batch in the workflow illustrated in Figure 1. A batch is simply a set W of s cross nodes, i.e. $W\subset X$ and $\left|W\right|=s$. We also define the input and output mutant nodes for a batch. The inputs $In\left(W\right)$ to W are the mutant nodes with incoming edges to the cross nodes in W, i.e. $In\left(W\right)=\left\{m\right|(m,w)\in E,w\in W\}$. Informally, we need these mutants in order to perform the crosses in W. Analogously, the outputs $\mathit{Out}\left(W\right)$ of W are the mutant nodes with incoming edges from the cross nodes in W, i.e. $\mathit{Out}\left(W\right)=\left\{m\right|(w,m)\in E,w\in W\}$. Informally, these are the mutants produced by the crosses in W. Figure 3 illustrates the inputs $In\left(W\right)$ and outputs Out(W) to a batch W. Note that the number of mutant nodes in Out(W) may be larger than the number of cross nodes in W since each genetic cross can produce more than one mutant. Moreover, a single mutant in Out(W) may be the product of more than one cross in W. With these definitions, we can now formulate the CrossPlan problem.

Fig. 3.

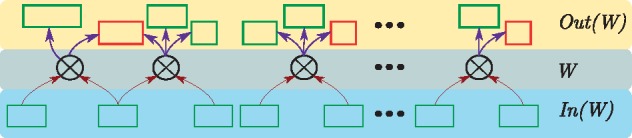
An example of a batch W. The input mutants $In(W)$ are the set of mutants required to perform the crosses in batch W; every mutant in this set is viable (green rectangles). The output mutants Out(W) are the mutants that are produced by performing crosses in the batch; the mutants here may be viable or inviable (red rectangles) (Color version of this figure is available at Bioinformatics online.)

2.2.1 CrossPlan problem

Given the genetic cross graph $\mathcal{G}=(M,X,E)$ , a set $S\subset M$ of source mutants, a set $T\subset M$ of target mutants, the batch size s and the number of batches k, compute k s-batches $\{W_i,1\le i\le k\}$ such that

1. for each $1\le i\le k,\hspace{0.17em}In\left(W_i\right)\subseteq S\cup \left(\underset{1\le j\le i-1}{\cup }Out\right(W_j\left)\right),$ and

2. the size of $T\cap \left(\underset{1\le j\le k}{\cup }Out\right(W_j\left)\right)$ is maximized over all possible sets of k s-batches.

The first condition states that for the set W_i of crosses being performed in batch i, every input in $In\left(W_i\right)$ should be one of the source mutants or have been constructed in one of the earlier batches. The second condition states that the union of the outputs of the k s-batches should contain as many target mutants as possible.

We now define two extensions of CrossPlan. The first problem supports a modification to the experimental workflow where we allow multiple batches to be executed in parallel, e.g. by starting a new batch every week. Hence, the mutants we make in a specific batch will not be available for the very next batch but only after a certain delay. We use a positive integer $d\ge 1$ to model this scenario and require that for every batch i, the mutants made in it are available only for batch i + j, where $j\ge d$.

2.2.2 CrossPlanDelay problem

The definition of CrossPlanDelay is exactly the same as CrossPlan itself with an additional parameter$d\ge 1$and the following modification to the first condition:

(i) for each $1\le i\le k,\hspace{0.17em}In\left(W_i\right)\subseteq S\cup \left(\underset{1\le j\le i-d}{\cup }\mathit{Out}\right(W_j\left)\right)$

When d = 1, this condition is identical to the one for CrossPlan, i.e. a mutant made in a batch is available for use in the next batch.

The second extension is specific to budding yeast and takes into consideration the markers used to verify gene deletions. Each gene deletion construct in a mutant strain must have a unique selectable marker that can confirm the deletion, e.g. aΔ:: kanR represents a deletion of gene A replaced by the kanR G418 resistance gene. Only strains with gene A deleted will grow in the presence of the antibiotic G418, which normally kills budding yeast cells. No two genes participating in a specific cross can share the same marker. We enforce this constraint as follows. Suppose K is the set of possible markers. We associate three sets with a mutant m: the set P(m) of gene-marker pairs in m, the set G(m) of genes mutated in m, and the set $K\left(m\right)$ of markers associated with these genes. We define the genetic cross graph with markers$\mathcal{H}=(M\prime ,X\prime ,E\prime )$ as follows:

1. each node in $M\prime$ is a subset of $G\prime =G\times K$ with the property that $\left|G\right(m\left)\right|=\left|K\right(m\left)\right|$, i.e., each gene in G(m) has a distinct marker,

2. each node in $X\prime$ is a genetic cross,

3. if a cross node in $X\prime$ has two incoming edges from two nodes m and $m\prime$ in $M\prime$, then

(a) both the genes and the markers associated with m₁ and m₂ are disjoint, i.e., $G\left(m_1\right)\cap G\left(m_2\right)=\phi$ and $K\left(m_1\right)\cap K\left(m_2\right)=\phi$, and

(b) the outgoing edges from the cross are to the mutants in $2^{P\left(m_1\right)\cup P\left(m_2\right)}$.

2.2.3 CrossPlanMarkers problem

The definition of CrossPlanMarkers is similar to CrossPlan except we use the genetic cross graph with markers.

2.3 An ILP for CrossPlan

We can prove that CrossPlan is NP-complete (see Supplementary Section S2). Therefore, we solve it using an ILP. An attractive feature of the ILP is that it is easy to state and extend. The ILP contains three sets of variables.

(i) The first set of variables records in which batch we perform a particular genetic cross experiment. Specifically, for each cross node $x\in X$, we introduce k 0-1 variables $c_{x,i}$ where $1\le i\le k$. We set $c_{x,i}=1$ iff we perform that cross experiment in batch i.

(ii) The second set of variables records in which batch we make a particular mutant. Specifically, for each mutant $m\in M$, we introduce k + 1 0-1 variables $b_{m,i}$ where $0\le i\le k$. We set $b_{m,i}=1$ iff we make mutant m in batch i. Over the course of several batches of experiments, we may make mutant m multiple times. Hence, $b_{m,i}$ may be set to 1 for multiple values of i.

(iii) The third set of variables records if we make a target mutant m in any batch. For each mutant $m\in T$, we introduce one 0-1 variable a_m, which we set to 1 iff $b_{m,i}=1$ for at least one value of i. We use the variables a_m to define the function we optimize below.

The ILP contains five sets of constraints.

• (i) Source mutants constraints: Since the mutants in the source set S are already available, we can set their (and only their) b values in batch 0 to be unity:

  $$b_{m,0}=\{\begin{array}{l}1,\hspace{0.17em} \text{for} \text{all} m\in S\hfill \\ 0,\hspace{0.17em} \text{for} \text{all} m\notin S\hfill \end{array}$$ (1)

  There are a total of $\left|M\right|$ such constraints, one for every mutant.
• (ii) Batch size constraints: We can perform at most s crosses in any batch.

  $$\sum _{x\in X}{c}_{x,i}\le s,\hspace{0.17em} \text{for} \text{each} 1\le i\le k$$ (2)

  There are a total of k such constraints, one for every batch.
• (iii) Cross input constraints: If we perform a genetic cross x in batch i, then we must have made both the mutants being crossed in x in one of the earlier batches.

  $$\begin{array}{l}{c}_{x,i}\le \sum _{j=0}^{i-1}{b}_{m,j}\hspace{0.17em} \text{for} \text{every}\hspace{0.17em}m \text{such} \text{that} (m,x)\in E,\\ \text{and} \text{for} \text{every} 1\le i\le k\end{array}$$ (3)

  Note that each $c_{x,i}$ variable appears in two cross input constraints, one for each of the mutants that are inputs to cross x, i.e. one constraint for each mutant m such that (m, x) is an edge in E. The value on the right hand size is zero only if the mutant m is not made in any of the batches between 0 and i–1. There are a total of $2k\left|X\right|$ of these constraints, two for every cross in every batch.
• (iv) Mutant input constraints: If we make a mutant m in batch i, then we must also perform at least one of the genetic crosses that produces m in that batch.

  $$b_{m,i}\le \sum _{\stackrel{x\in X}{(x,m)\in E}}{c}_{x,i}, \text{for} \text{every} 1\le i\le k$$ (4)

  Note that (x, m) is an edge in the genetic cross graph iff m is one of the mutants that are the outputs of the cross x. If the right-hand side is zero, then we cannot make mutant m in batch i. There are $k\left|M\right|$ such constraints, one for every mutant in every batch.
• (v) Making target mutant constraints: For a target mutant m, a_m = 1 only if we make m in at least one batch.

  $$a_m\le \sum _{i=0}^k{b}_{m,i}, \text{for} \text{each} m\in T$$ (5)

  There are $\left|T\right|$ such constraints, one for every target mutant.  In total, the ILP contains $\left(k\right|X|+(k+1\left)\right|M|+|T\left|\right)$ variables and $\left(2k\right|X|+(k+1\left)\right|M|+|T|+k)$ constraints.

 Our objective is to maximize the number of target mutants in T that we can make in k s-sized batches. In other words, our objective function is the following:

$$\max \sum _{m\in T}{a}_m$$ (6)

Note that if some $c_{x,i}$ is set to 1 in a solution to this ILP, then it is not necessary that $b_{m,i}$ is set to 1 for every mutant m such that $(x,m)\in E$, i.e. m is a product of x. The solution will set such a $b_{m,i}$ to 1 only if m is ‘on the path’ to some target mutant l for which a_l = 1. Hence, in any solution to this ILP, for each $1\le i\le k$, batch i is given by

$$W_i=\left\{x\right|c_{x,i}=1\}$$

In Supplementary Section S3, we prove that maximizing this objective function under the specified constraints solves the CrossPlan problem correctly.

2.4 Extensions and alternate approaches

In this section, we describe how to solve CrossPlanDelay and CrossPlanMarkers. We also introduce an alternative algorithm.

2.4.1 ILP for CrossPlanDelay

In the CrossPlanDelay problem, we impose the requirement that for every batch i, every cross in that batch can only use mutants made in batches i – j, where $j\ge d$. To solve this problem, we modify Equation (3) in the ILP for CrossPlan as follows:

$$c_{x,i}\le b_{m,0}+\sum _{j=1}^{i-d}{b}_{m,j}\hspace{0.17em} \text{for} \text{every} m \text{such} \text{that}\hspace{0.17em}(m,x)\in E$$ (7)

Note that we can use the mutants in the source set S in any batch irrespective of the value of d.

2.4.2 ILP for CrossPlanMarkers

We simply apply the ILP for CrossPlan to the genetic cross graph with markers.

2.4.3 Planning with limited horizons

Suppose we want to solve CrossPlan for k batches. In the ‘limited horizon’ approach, we select a horizon h < k, solve the ILP for h batches add the mutants made in the solution for h batches to S, solve the ILP for h batches again and repeat this process until we have a obtained a solution for k or more batches. In practice, this approach is likely to be faster but may be sub-optimal since we do not plan all k batches simultaneously.

3 Results

We start by describing how we simulate the dynamical model of the cell cycle and compute target mutants (Section 3.1.1) and how we construct the genetic cross graph (Section 3.1.2). Next, we perform a detailed analysis of CrossPlan results for these data (Section 3.2 and Supplementary Section S4) before discussing CrossPlanDelay (Section 3.3). We also compare the results of CrossPlan and CrossPlanMarkers using their limited horizon counterparts (Section 3.4). In Supplementary Section S5, we discuss a case study where we compare CrossPlan’s results to a manually created plan for 13 target mutants.

3.1 Datasets

3.1.1 Using the ODE model to identify target mutants

We used a dynamic model of the budding yeast cell cycle (Kraikivski et al., 2015) for our analyses. This model addresses the detailed phenotypic properties of more than 250 yeast strains carrying mutations that interfere with the G1–S and/or the Finish transition (metaphase-anaphase-telophase-cell division). The model consists of 59 species (proteins, their modified forms, and complexes) and 60 differential and algebraic equations, involving 133 adjustable parameters (e.g., rate constants and binding constants). These 59 species correspond to 29 unique genes. We simulated this model for mutations in all combinations of up to 4 genes, ignoring combinations that contained redundant pairs of deletions, e.g. two different ways to knock out Cdc14. For each mutant strain, we recorded whether the simulation predicted the phenotype as ‘viable’ or ‘inviable’. A strain is ‘viable’ if simulated cells grow and divide with a stable cell size at division and ‘inviable’ otherwise. We defined a mutant b to be a parent of mutant a if a carried one additional single gene mutation than b. We defined a mutant a to be rescued if a is predicted to be viable but had a parent b that is either experimentally known or predicted by the cell cycle model to be inviable, e.g. cln3Δbck2Δ is inviable and cln3Δbck2Δwhi5Δ is rescued. We noted that a rescued mutant may be redundant. For example, whi5Δ rescues the inviable mutants cln3Δbck2Δ and cln3Δbck2Δpds1Δ. Since pds1Δ is itself a viable strain, the loss of Pds1 is irrelevant to the rescue phenotype. Hence, we considered only non-redundant rescued mutants. Rescued mutants are highly informative because converting an inviable strain to a viable strain usually occurs only by combining mutations in genes that have opposite functions within the same essential biochemical network. Thus, the prediction of new rescue mutants can assist in generating hypotheses about gene function and the architecture of the regulatory network.

Table 1 summarizes our results. Only 20% of all up-to-four gene deletions of the 54 576 mutants we simulated were viable. The percentage of viable combinations decreased with an increase in the number of genes deleted. Of these viable mutants, the number of rescued ones were 3528, of which 700 (nearly 20%) were non-redundant. We designated all non-redundant rescued mutants as the target set T. For the source set S, we used 35 strains that have been studied in the literature carrying mutations in one of the genes in the model. Note that this number is greater than the number of genes in the model, since some genes have been mutated in different ways.

Table 1.

Statistics on simulations

#Mutations	#Mutants	#Viable	#Rescued	#Rescued non-redundant
1	35	26 (74%)	—	—
2	586	285 (49%)	14	14
3	6250	1896 (30%)	344	170
4	47 705	8872 (18%)	3170	516
Total	54 576	11 079 (20%)	3528	700

3.1.2 Constructing the genetic cross graph

To construct the genetic cross graph $\mathcal{G}$ input to the CrossPlan problem, we needed to define the set G of single gene mutations, the set M of mutant nodes, the set X of cross nodes and the input and output edges for each cross in X. We set G to be the set of 35 single gene deletions. Each mutant node in M corresponded to one of the gene mutation combinations we simulated with the cell cycle model (Table 1). For every pair of mutants m₁ and m₂ such that $G\left(m_1\right)$ and $G\left(m_2\right)$ are disjoint, we created a cross node x in X. We added edges from m₁ and from m₂ to x and from x to each of the mutants corresponding to the power set of $G\left(m_1\right)\cup G\left(m_2\right)$.

We further pruned $\mathcal{G}$ as follows: consider the set G(T) of genes that are deleted in at least one target mutant, i.e. $G\left(T\right)={\cup }_{l\in T}G\left(l\right)$. We deleted every mutant m that contained at least one gene not present in G(T). An alternative way of phrasing this step is that we retained a mutant m in T iff (the set of genes mutated in) m was a subset of G(T). We also deleted any cross nodes that were disconnected as a result. After these modifications, $\mathcal{G}$ contained 2064 mutant nodes, 4958 cross nodes and 59 040 edges.

For the CrossPlanMarkers problem, we constructed the genetic cross graph with markers $\mathcal{H}$ as follows. Recall that K is the set of markers. We used a set of four markers (hph, kan, nat and ura). For every mutant $m\in M$ carrying mutations in one gene, we created $\left|K\right|$ copies of m, pairing it with each marker in turn. In general, for every mutant m, we created $\left(\begin{array}{l}\left|K\right|\\ \left|G\right(m\left)\right|\end{array}\right)\left|G\right(m\left)\right|!$ copies of m, one for each of the ways to assign distinct markers to the genes mutated in m. For example, for single gene mutants, we created $\left(\begin{array}{l}\left|K\right|\\ 1\end{array}\right)1!=\left|K\right|$ copies for each mutant, one for each marker. We created cross nodes as we did for $\mathcal{G}$ but with the added condition that the two mutants being crossed should not share any markers. We pruned this graph as described earlier and retained 43 648 mutant nodes, 112 720 cross nodes and 1 383 192 edges.

3.2 Results for CrossPlan

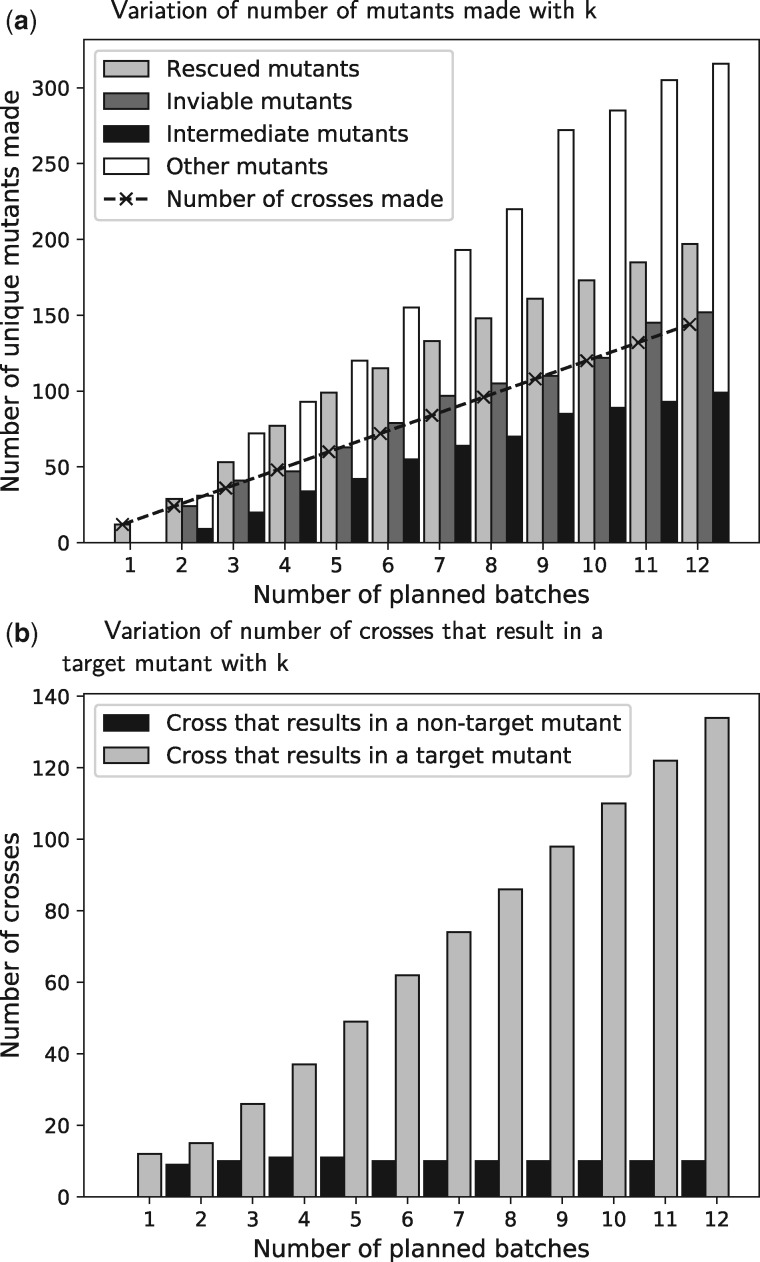
First, we investigated the number of target mutants we could plan with s = 12 (we provided a rationale for this value in Section 2.1) and with different values of k. In the solution for each value of k, we identified four sets of mutants made across all the batches: (i) target mutants, (ii) inviable mutants that are rescued by one of the target mutants made, (iii) (viable) intermediate mutants that we make in order to produce a target mutant and (iv) other mutants that result from the crosses but are not used in any cross in any batch. Note that any cross that produces a target mutant m (which must be viable by our construction of T) will also automatically produce all inviable parents that m rescues. In constructing these sets, we ignored the source mutants in S and counted each other mutant only once.

Figure 4a summarizes these results for $1\le k\le 12$. For every value of k, we succeeded in planning exactly sk crosses (the dashed line in Fig. 4a). When k = 1, we only planned 12 double mutants, all of which rescued inviable single gene deletions. For k > 1, we planned about 1.4 times as many target mutants (light gray bars in Fig. 4a) as the number of crosses. For every value of k, the number of inviable mutants (dark gray bars in Fig. 4a) rescued by the target mutants we planned was almost the same as the number of crosses. We also noted that the number of intermediate mutants (black bars in Fig. 4a) we needed to produce was approximately 0.4 times the number of target mutants. The figure also displays other mutants that we planned (white bars); these mutants result from the planned crosses but are not used to make any other mutants. Figure 2b illustrates why the number of target mutants may be larger the number of crosses: when we cross aΔcΔ with bΔdΔ, we simultaneously produce the target mutants aΔbΔcΔ, aΔbΔdΔ and aΔbΔcΔdΔ.

Fig. 4.

CrossPlan results for different number of batches planned

The trends in Figure 4a suggest that most crosses yield at least one target mutant (e.g. the cross between aΔcΔ and bΔdΔ in Fig. 2b) and very few crosses produce only intermediate mutants (e.g. the cross between aΔ and cΔ in Fig. 2b). To investigate this further, we counted the number of crosses of each type for each value of k. Figure 4b shows that when k = 1, all 12 crosses we plan result in target mutants (light gray bars). In contrast, for $2\le k\le 12$, at most 11 crosses did not yield any target mutants (black bars). For k = 12, we further analyzed each cross in the computed plan. We observed that not only did the majority of crosses produce at least one target mutant, but the entire plan depended on finding an appropriate set of double gene mutants to make in batch one. Complete details of this analysis are in Supplementary Section S4.1.

Finally, we investigated how many more batches we could plan if we started with the CrossPlan solution for k batches. Accordingly, we solved a simpler version of CrossPlan: we solved the ILP for k batches, added all the mutants in the solution to S, set $s=\infty$ (i.e. made the batch size unlimited) and then re-solved the ILP for one batch. Our analysis showed that starting from the CrossPlan solution for 12 batches, we could make as many as 315 additional target mutants simply by crossing pairs of mutants in S, a number enough to occupy 26 batches of size 12. Additional details of this analysis are in Supplementary Section S4.2.

3.3 Results for CrossPlanDelay

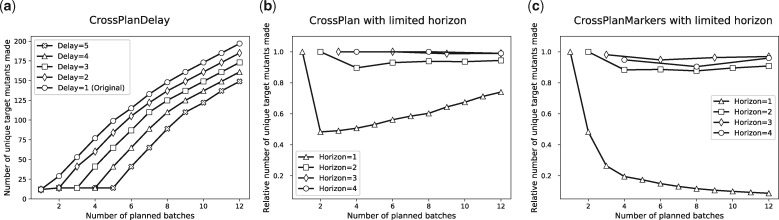
We solved the ILP for CrossPlanDelay for s = 12, the same values of k, i.e. $1\le k\le 12$ and for different values of the delay d. Figure 5a summarizes our results. Here, we compare the number of target mutants planned for different numbers of batches as we varied d from 1 to 5; the plot labeled ‘Original’ corresponds to d = 1. For any value of k, increasing the delay by unity decreased the number of planned target mutants by 12 on average, which is the size of a batch. Even with d = 5, with 12 batches, we could plan 149 target mutants, which is more than 75% of 197 mutants we could plan with d = 1 in the same number of batches. The most striking difference occurred for batches $1\le k\le d$ (nearly horizontal lines in Fig. 5a). There are 14 target mutants in T that are double gene deletions. Since all single gene deletions are present in S, for all values of d, we planned 12 of these double gene deletions in the first batch. When d > 1, we could plan only the last two double gene deletions in the second batch. We had to wait till k > d to plan any other target mutants.

Fig. 5.

Variation with k of (a) number of mutants planned by CrossPlanDelay, (b) the ratio of the number of target mutants planned by the limited horizon strategy and the number planned by CrossPlan and (c) the ratio of the number of target mutants planned by the CrossPlanMarkers with the limited horizon strategy and the number planned by CrossPlan

3.4 CrossPlan and CrossPlanMarkers with limited horizon

We compared the performance of planning experiments for all k batches together with solutions obtained for the limited horizon approach with $1\le h\le 4$. Figure 5b displays the ratio of the total number of unique target mutants we could plan with different horizons with the number planned with an unlimited horizon (i.e. CrossPlan). Clearly, when we plan experiments only for one batch at a time h = 1, we obtain very inefficient solutions. The most striking difference occurs for $k\le 4$. Surprisingly, the best solutions for h > 1 are quite close to the results for CrossPlan, with h = 3, 4 being virtually indistinguishable from CrossPlan.

When we attempted to solve CrossPlanMarkers with $k\ge 5$, we found that ILP sizes were too large, causing the solvers (CPLEX and Gurobi) to use up all the available RAM (32GB). Rather than use a computer with more RAM, we used the limited horizon approach to solve CrossPlanMarkers as well. In Figure 5c, for different values of k, we compare the number of target mutants planned by this version of CrossPlanMarkers to the number planned by CrossPlan (with no limit on the horizon). Remarkably, other than for h = 1, we could plan at least 85% as many target mutants as CrossPlan for all other values of h. However, for h = 3, 4, CrossPlan succeeded in planning more target mutants than CrossPlanMarkers (compare orange and red curves between Fig. 5b and c). The primary reason is that CrossPlan is not constrained by the requirement that each gene in a cross be associated with a unique marker. For example, for k = 3, CrossPlan made 53 target mutants, which was one more than CrossPlanMarkers. Figure 6 illustrates the point with a set of crosses suggested by CrossPlan that require more than four markers or an additional cross.

Fig. 6.

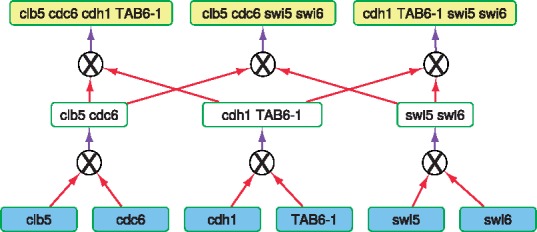
A set of crosses suggested by CrossPlan that require > 4 markers

An advantage of the limited horizon approach is that the sizes of the ILPs are much smaller than for CrossPlan (Table 2). Additionally, the time taken to solve the planning problem with a Limited Horizon is much lower than for CrossPlan. For example, it takes 58 min to solve the ILP for CrossPlan for 12 batches, where as it takes only 24 min to solve three problems with h = 4.

Table 2.

Statistics on ILP sizes and running times for CrossPlan and CrossPlan with Limited Horizon

k	#Variables	#Constraints	Time (in min.)
CrossPlan
1	9744	14 703	0.01
4	30 810	50 646	10.21
12	86 986	146 494	58.34
CrossPlan, h = 4
4	30 810	50 646	10.21
12	30 810	50 646	24.63

4 Discussion

We have introduced the novel problem of efficiently synthesizing experimental plans to produce a desired set of mutant strains. Our methodology uses a generic experimental workflow in which we can make mutants using genetic crosses that are organized into batches. We develop an integer linear program to optimally solve the problem of constructing the largest possible number of target mutants given the batch size and number as inputs. Our results show the effectiveness of our approach. We were easily able to generalize our method to handle natural experimental constraints such as delays and genetic markers.

There are several interesting avenues for future research. The size of the genetic cross graph can be exponential in the maximum number of mutations in a single target mutant. Since CrossPlan took the genetic cross graph as an input, the resulting ILPs were very large, e.g. the ILP for CrossPlanMarkers contained 780 K variables and 11 M constraints. We would like to design more compact ILPs or develop alternative ways of formulating and solving the problem that do not directly use the genetic cross graph. Since the problem is NP-complete, we would also like to ascertain the fixed parameter tractability of the problem, e.g. develop polynomial-time algorithms if k or s is fixed.

We also plan to apply this methodology to other organisms where siRNA or CRISPR-based screens are effective. Our method can also be applied to Boolean models (Steinway et al., 2015) and to other approaches that can predict the phenotypes of combinatorial perturbations (Yu et al., 2016). Ultimately, we seek to complete the entire modeling cycle by performing the experiments that we plan, studying the discrepancies with model predictions and using them to improve and extend the mathematical models themselves.

Funding

Grants from the National Institute of General Medical Sciences of the National Institutes of Health [R01GM095955 to TMM, JP, and JJT] and the National Science Foundation [DBI-1062380 and CCF-1617678 to TMM] supported this work.

Conflict of interest: none declared.