Abstract
Motivation
Current sequencing technologies are able to produce reads orders of magnitude longer than ever possible before. Such long reads have sparked a new interest in de novo genome assembly, which removes reference biases inherent to re-sequencing approaches and allows for a direct characterization of complex genomic variants. However, even with latest algorithmic advances, assembling a mammalian genome from long error-prone reads incurs a significant computational burden and does not preclude occasional misassemblies. Both problems could potentially be mitigated if assembly could commence for each chromosome separately.
Results
To address this, we show how single-cell template strand sequencing (Strand-seq) data can be leveraged for this purpose. We introduce a novel latent variable model and a corresponding Expectation Maximization algorithm, termed SaaRclust, and demonstrates its ability to reliably cluster long reads by chromosome. For each long read, this approach produces a posterior probability distribution over all chromosomes of origin and read directionalities. In this way, it allows to assess the amount of uncertainty inherent to sparse Strand-seq data on the level of individual reads. Among the reads that our algorithm confidently assigns to a chromosome, we observed more than 99% correct assignments on a subset of Pacific Bioscience reads with 30.1× coverage. To our knowledge, SaaRclust is the first approach for the in silico separation of long reads by chromosome prior to assembly.
Availability and implementation
1 Introduction
The ability to accurately reconstruct a person’s genome is a crucial pre-requisite for studies of genetic variation in clinical as well as basic research. In order to capture the full extent of genetic variation of an individual’s genome, there is a shift towards replacing re-sequencing based workflows, which use a reference genome, by de novo assembly of personal genomes. Long read sequencing technologies, such as marketed by Pacific Biosciences (PacBio) and Oxford Nanopore Technologies (ONT), can produce reads of tens of kilobases in length. This allows for much improved genome assemblies in comparison to short read (Illumina) sequencing platforms (Chin et al., 2016; Gordon et al., 2016; Koren et al., 2017; Lin et al., 2016; Myers, 2014). In particular, long reads can resolve many repetitive regions that are inaccessible to short reads, which yields more accurate and contiguous assemblies (Treangen and Salzberg, 2012).
Despite this progress, even contigs (continuously assembled sequences) produced from long-read-based assembly fall short of spanning entire chromosomes. Current assembly workflows therefore rely on an additional scaffolding step that uses orthogonal data to place contigs into their respective chromosomes, for instance through chromatin conformation data (e.g. Hi-C) (Burton et al., 2013). This, however, comes with the disadvantage that mis-assemblies present in the contigs are difficult to detect and correct at this stage of genome assembly (Jiao et al., 2017; Jiao and Schneeberger, 2017). In particular, this applies to chimeric contigs that erroneously join sequences originating from different chromosomes. These errors could be avoided, if the chromosomal origin of each read was known prior to genome assembly.
Such knowledge of chromosomal origin would also entail substantial computational advantages: if reads were sorted by chromosome, genome assembly could then be performed separately per chromosome, which has the potential of saving large amounts of runtime and memory, as well as improving parallelization. This is particularly crucial since assembling third generation sequencing reads is a computationally challenging problem due to high sequencing error rates.
Here, we explore the potential of single-cell template strand sequencing data (Strand-seq, introduced by Falconer et al., 2012) to cluster long reads, such as from the PacBio platform, into their chromosome of origin––and as such enable definite physical assignment of long reads to a chromosome, to considerably facilitate chromosomal scaffolding or de novo assembly. We stress that we aim to cluster long reads in silico, without using a reference genome and before genome assembly.
1.1 Strand-seq
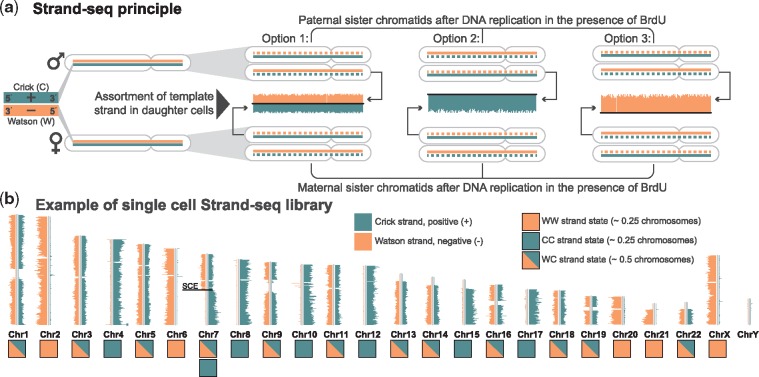
To date, Strand-seq has been successfully applied to answer several biological questions including inversion detection (Sanders et al., 2016), haplotype phasing (Porubský et al., 2016, 2017) and mapping sister chromatid exchange (SCE) events (Claussin et al., 2017; Falconer et al., 2012; van Wietmarschen et al., 2018). We illustrate the underlying idea in Figure 1. Strand-seq sequences only the template strand used for DNA replication during a single mitotic cell division. In doing so, it preserves the directionality of the template strands, which we refer to as Watson (W) and Crick (C; Fig. 1a, left). That means, each chromosome inherits template strands with one of the three possible strand states (WC, WW, or CC), as shown in Figure 1b. One key feature of Strand-seq data consist in the preservation of strand directionalities. That is, reads stemming from a Watson or Crick strand map in forward or reverse direction to a reference genome, respectively. Therefore, different strand state signatures imply different chromosomes of origin. The only exception to this are occasional SCEs, (Claussin et al., 2017; Falconer et al., 2012; van Wietmarschen et al., 2018), which lead to changes in strand state, as apparent in Chromosome 7 shown in Figure 1b. Because the yield from one single-cell library is usually low, one typically applies Strand-seq to many individual single cells (e.g. 132 single cells for the datasets we use in this study). Each single cell library comes with its own strand state profile, because mitotic cell divisions and segregation happen independently of each other. We use the terms ‘single cell’, ‘library’ and ‘single cell library’, interchangeably in this manuscript.
Fig. 1.
Principle of directional single-cell Strand-seq. (a) Maternal and paternal homologues are composed of one positive template strand (Crick; teal) and a negative template strand (Watson; orange). During DNA replication in the presence of bromodeoxyuridine (BrdU), which is a thymidine analogue, a cell incorporates BrdU into the newly synthesized DNA strands. This results in sister chromatids that contain one original template template strand (solid line) and one newly synthesized, BrdU-incorporated strand (dashed line). One single cell division leads to assortment of paternal and maternal sister chromatids to daughter cells, with three possible combinations of template strands: Option 1 (WC), Option 2 (CC) and Option 3 (WW). Newly formed DNA strands containing BrdU are selectively removed in daughter cells during library preparation, such that only the original template DNA strands are being sequenced. (b) Each chromosome is represented as a vertical ideogram, and the distribution of directional sequencing reads is plotted as horizontal lines along each chromosome, with Watson (W) in orange and Crick (C) in teal. Each chromosome inherits its template strand as either Crick or Watson, which results in three possible states WW, CC or WC. Some chromosome can have a combination of strand states as a results of sister chromatid exchance (SCE) events, as shown in Chromosome 7
Strand-seq technology has also been used to cluster contigs into their original chromosomes, as proposed in BAIT and ContiBAIT tools (Hills et al., 2013; O’Neill et al., 2017). These tools rely on mapping Strand-seq reads first to a contig-stage assembly, and then using the strand states of the contigs to scaffold them into chromosomes (Hills et al., 2018). The major limitation of this approach is that any assembly errors, such as chimeric contigs, result in mixed states that confound the clustering method. Additionally, this method is not designed to work with the extremely sparse data resulting from mapping Strand-seq reads to individual long reads.
1.2 Our contributions
Here, we present a novel Expectation Maximization (EM, Dempster et al., 1977) approach for clustering long sequencing reads into their original chromosomes and implement it in an R package called SaaRclust. It allows us to ‘physically’ separate long reads by chromosome through exploiting data from an easily scalable molecular protocol (i.e. Strand-seq, Falconer et al., 2012). SaaRclust is the first tool for computationally clustering individual sequencing reads by chromosome without relying on a reference genome. We emphasize that Strand-seq data are extremely sparse and one single-cell library typically yields a genomic coverage on the order of 0.03×. To address this challenge, we developed an EM-based soft clustering technique that is able to aggregate the weak signal inherent to individual single cell libraries. As a result, we obtain a posterior probability distribution over all chromosomes for each long read. We evaluate our approach on real NA12878 data and find the clustering to yield very favourable results: When imposing a cutoff of 0.8 on the posterior probability, we assign 71% of all long reads to a chromosome and those reads that have been assigned are correct in more than 97% of all cases. With a cutoff of 0.99, we still assign 61.1% of all reads while reaching an accuracy of above 99%.
1.3 Idea
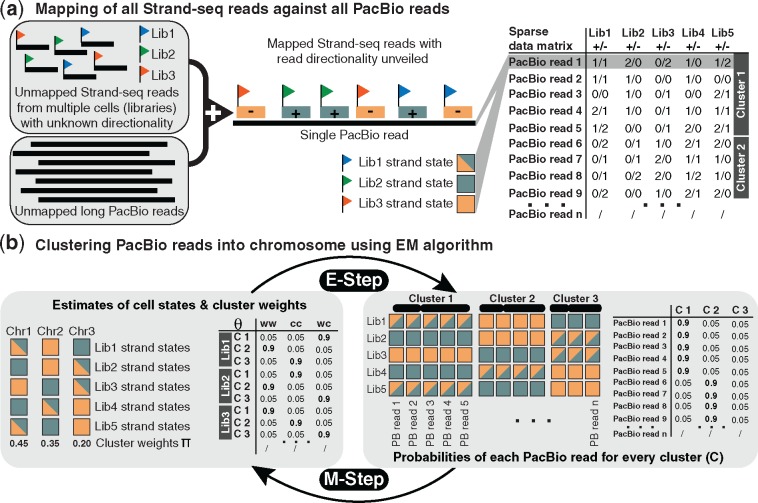
Let us assume we are given a set of long sequencing reads, e.g. PacBio reads. As shown in Figure 2a, we map all Strand-seq reads to all PacBio reads and then count the number of Strand-seq reads from different libraries that are mapped to each PacBio read in either Watson (–) or Crick (+) orientations. This read-to-read mapping does not involve a reference genome. As a central observation, we note that PacBio reads originating from the same chromosome will show the same strand states across the different single cell libraries. Therefore, we can use these directional Strand-seq read counts in order to cluster PacBio reads into their original chromosomes.
Fig. 2.
Overview on algorithmic workflow. (a) After mapping Strand-seq to PacBio reads, their (relative) directionality with respect to the PacBio reads is recorded. That is, for each PacBio read and each Strand-seq single-cell library, the number of Crick (+) and Watson (–) reads is tabulated (right). For example, 2/1 refers to two Crick reads and one Watson read mapped to the corresponding PacBio read in a given row. Note that the data are sparse, with many zero entries in the table. This table is the input to our EM clustering method. (b) Illustration of the main idea of the EM algorithm, which iterates between E-step and M-step. On the left, a table of chromosomal strand states probabilities (Θ) is shown, which contains the current estimates of a certain strand state (i.e. WW, CC, or WC) for each single cell library (Lib 1, Lib 2, Lib 3) and chromosome (C 1, C 2, C 3). On the right, we illustrate that PacBio reads in the same cluster (chromosome) display the same strand signatures (in terms of the Strand-seq reads mapped to them); the table shows, for each PacBio read, the probabilities of stemming from a given chromosome (C 1, C 2, C 3). In the E-step, the current estimates of chromosomal strand states probabilities (Θ) are used to estimate cluster assignments. In the M-step, the current (probabilistic) cluster assignments are used to estimate strand state probabilities
The main idea of the EM algorithm, as shown in Figure 2b, is that the knowledge of single-cell strand states for each chromosome is informative of the chromosomal origin of PacBio reads and vice versa; that is, knowing the true chromosomes of PacBio reads enables us to find the chromosome strand states. This flow of information can be repeated in an iterative manner, starting from an arbitrary initialization, using an EM algorithm. We model the process of sampling Strand-seq read counts from different libraries by a mixture model. Clustering then commences through an EM algorithm that iteratively estimates strand state parameters, cluster weights and read assignments to clusters.
2 Mixture model and the EM algorithm
We consider two clusters per chromosome corresponding to PacBio reads oriented in forward and backward direction, respectively. Let be the number of PacBio reads, single cell libraries and clusters, respectively. We present a full list of notations that we use throughout the paper in Table 1.
Table 1.
Overview of notations
| Notation | Definition |
|---|---|
| The number of Strand-seq reads from single cell j mapped to the n-th PacBio read in Watson direction | |
| The number of Strand-seq reads from single cell j mapped to the n-th PacBio read in Crick direction | |
| T | The set of all possible strand states {WW, WC, CC} |
| The state of single cell j in cluster k | |
| The probability that single cell j has state t in cluster k | |
| πk | The probability that a PacBio read comes from cluster k |
| A binary random variable showing whether PacBio read n comes from cluster k | |
| The set of all integers between 1 and a |
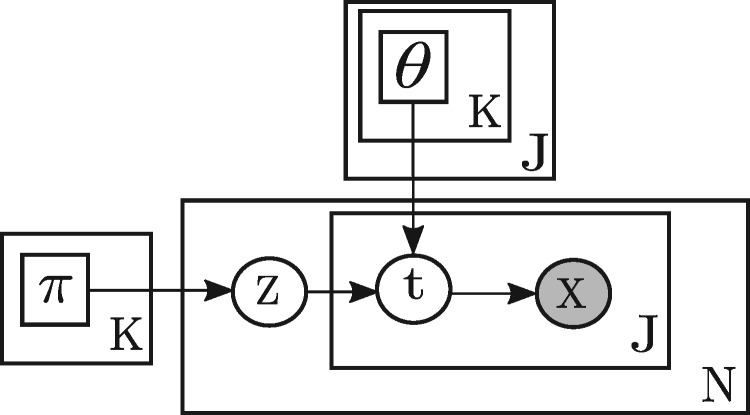
We model the number of Watson and Crick Strand-seq reads mapped to PacBio reads by a mixture model, shown in plate notation in Figure 3. The component weights of the mixture model are , which are the probabilities of sampling PacBio reads from different clusters. In the following, θk,j,t denotes the probability that single cell j has state t in cluster k. One should note that a single cell may have more than one state in a cluster because of SCE events (Fig. 1b, Chromosome 7). To sum up, there are two sets of parameters in the mixture model: cluster weights and strand state parameters Θ, which have the following constraints based on their definitions:
| (1) |
Fig. 3.
SaaRclust’s mixture model expressed in plate notation. πk denotes the weight (relative size) of cluster k. denotes a discrete probability distribution over three different strand states of single cell j in cluster k. Zn and are the chosen cluster and the chosen strand state of single cell j for PacBio read n, respectively. is a pair of Watson and Crick Strand-seq read counts of single cell j for PacBio read n
According to Figure 3, for the n-th PacBio, a cluster Zn is first chosen based on the discrete distribution Π. Then, based on the chosen cluster, strand states for all single cells are generated based on the strand state probabilities θk in the chosen cluster k = Zn. At the end, given the strand states, a random matrix Xn of size containing pairs of Watson and Crick read counts for each single cell is generated by a binomial distribution. More precisely, the likelihood of observing a Watson and Crick read count, given a certain strand state t is computed as follows:
| (2) |
where is the total number of Strand-seq reads from library j mapped to read n (and therefore , which we consider to be a constant) and pt is the probability of having a Watson read from a single cell with state t is defined as follows:
In the above definition, α is the fraction of background reads (reads in the opposite direction of the strand state) in WW or CC strand states, which is considered as a constant parameter in our model. In the rest of the manuscript, we abbreviate as . The likelihood of the mixture model parameters given the observed Strand-seq read counts for all PacBio reads can be then computed as follows:
| (3) |
The maximum likelihood problem is maximizing the objective function (log-likelihood function) in the above formula. This maximization problem does not have a closed form solution, therefore we use the EM algorithm for solving this problem, which has been shown to converge to a local optimum (Wu, 1983). In order to have a simple form complete-data log-likelihood function (likelihood of the mixture model parameters given both hidden and observed random variables), we define the hidden random variables of the EM algorithm as follows: for every , we define a hidden binary random variable which is equal to 1 if and only if PacBio read n belongs to cluster k and stems from a locus where the single cell j has strand state t. Based on this definition, there are some constraints on the hidden random variables: for every , there is only one cluster (where that PacBio read belongs to) such that the following conditions hold.
| (4) |
The complete-data log-likelihood function is computed as follows:
| (5) |
The EM algorithm iterates over the two following steps (Dempster et al., 1977):
| (6) |
Let denote the expectation of the hidden random variable given the observed data and the model parameters at the mth iteration. This expectation can be computed as follows:
| (7) |
Based on the Equations (3)–(7), the objective function of the EM algorithm can be written as
| (8) |
Maximizing the objective function in Equation (8) by Lagrange multipliers corresponding to the constraints in Equation (1) leads to the following update rules for the parameters:
| (9) |
| (10) |
After estimating parameters of the mixture model, the cluster assignment probabilities can be computed as follows:
| (11) |
where denotes a binary random variable showing whether the nth PacBio read is from cluster k, as defined in Table 1.
2.1 Initializing EM parameters
For initializing the EM parameters, we use a combination of k-means and hierarchical clustering. First, we run the k-means algorithm with a number of clusters that is higher than the target number of 46 clusters for a female human genome. Note that the number of clusters in k-means is a user parameter, and we set it to a higher number in order to avoid missing small clusters. We use the J-dimensional feature vector to encode PacBio read n. Once we have run k-means on these input vectors, we compute the single cell strand states with maximum likelihood for each cluster. Note that in this step, we use the simplifying assumption that there is no combination of strand states (resulting from SCEs) in any pair of single cell and chromosome, which makes these maximum likelihood computations straightforward. Lastly, using these single cell strand states as a feature vector for each cluster, we merge similar clusters to obtain the desired number of clusters based on agglomerative hierarchical clustering. At the end, we use the final clusters with their maximum likelihood single-cell strand states to initialize the EM parameters. More precisely, we set the π parameters to the relative sizes of the formed clusters, and we initialize , for each cluster k and single cell j, as follows:
where is the estimated strand state in cluster k and single cell j.
2.2 Pairing clusters with the same chromosome
There are two clusters per chromosome corresponding to the PacBio reads having forward or backward direction, respectively. The directionality of mapped Strand-seq reads is exactly the opposite in a pair of clusters corresponding to PacBio reads in forward or backward direction on a chromosome. As a result, WC strand states are similar in the aforementioned pair of clusters, but WW and CC strand states are the opposite over all single cells. Based on this relation between the strand states for the clusters coming from the same chromosome, we defined a distance measure d over all pairs of clusters as follows:
| (12) |
To convert this distance measure to a similarity measure, we subtracted each computed pairwise distance from the maximum of all pairwise distances. We then used the maximum matching algorithm to find the pairs of clusters with the maximum similarities.
3 Experimental setup
We evaluated the performance of SaaRclust on the human female individual NA12878. The fastq files of 132 Strand-seq libraries for this individual are publicly available at the European Nucleotide Archive (http://www.ebi.ac.uk/ena) under accession number PRJEB14185. Additionally, aligned reads in BAM format for all Strand-seq libraries used in this study are available at Zenodo (doi: 10.5281/zenodo.1203703). PacBio reads are available from the Sequence Reads Archive (https://www.ncbi.nlm.nih.gov/sra/) under accession number SRX1837675 (We thank Tina Graves and Rick Wilson for making this dataset available). For our study, we used the corresponding BAM file made available by PacBio (https://downloads.pacbcloud.com/public/dataset/na12878/hg38.NA12878-WashU.bam). We extracted all reads from this BAM file, including unmapped ones, without applying any filters, to ensure that the reads correspond to the raw data. We reverse complemented each read mapped in reverse orientation such that all reads reflect the original direction present in raw reads. We stored the original genome mapping location as well as the mapping directionality for evaluation purposes, but did not use this information in any other way. In case of Strand-seq reads, we exported only the first mates of each read pair into fastq files. We decided not to use the second mates since the Minimap tool (Li, 2016), the aligner we used in our analysis, does not handle paired-end alignment. Out of all extracted PacBio reads, those of length at least 10 kb were exported as a fasta file to be used for the clustering. Since all reads in the original BAM files were sorted according to the genomic position, we have randomly shuffled Strand-seq and PacBio reads before exporting them into a fastq or fasta file, respectively.
3.1 Mapping strand-seq reads to PacBio reads
Mapping of short Strand-seq reads to the long PacBio reads was done using the Minimap tool (Li, 2016). To allow parallel processing, we split PacBio reads into equally sized chunks of 50 000 reads per chunk. Minimap alignment was then performed on multiple chunks in parallel. We explored different parameter settings for minimap alignment, and we set the optimum parameter setting as follows: –t 8 (number of threads), –w 1 (minimizer window size, 1 means all k-mers are considered for high sensitivity), –k 15 (k-mer size), –L 50 (minimum number of matching bases per alignment) and –f 0.05 (fraction of repetitive minimizers to be removed).
The total number of PacBio reads for individual NA12878 was 20.7M, out of which 5.8% were unmapped. After filtering them based on the minimum length of 10 kb, we processed 10.8 M PacBio reads, which were split in 217 chunks in total. By using Minimap, we obtained 9.1 M PacBio reads with at least one Strand-seq read mapped to them.
3.2 Performance metrics
Original chromosomes and directionality of PacBio reads based on their mapping to the reference genome were used as a ground truth for accuracy assessment of our method. In the evaluation process, we used only the set of PacBio reads for which a ground truth was available, that is, those reads mapped to one of the autosomes or Chromosome X in the original BAM file. Note that the clustering proceeded on all reads, including unmapped ones, but the assignment of those unmapped reads cannot be evaluated.
To evaluate clustering accuracy, we first divided PacBio reads with respect to their true known chromosome and directionality. For each cluster, we determined a “true” chromosome and directionality based on the origin of the majority of PacBio reads in that cluster. Given this assignment, we computed the fraction of PacBio reads that were correctly assigned to a cluster corresponding to their original chromosome and orientation. Such evaluation was used for hard as well as for EM soft clustering. In case of EM soft clustering, we assign each PacBio read to the cluster with highest posterior probability.
3.3 Hard clustering settings
For hard clustering, we selected a set of 50 000 PacBio reads that were represented in at least 35 Strand-seq libraries, i.e. the PacBio reads that have Strand-seq reads mapped to them from at least 35 different Strand-seq libraries. Such strict filtering criteria proved favorable to obtain good cluster centres using hard clustering.
To do hard clustering, we used k-means on the aforementioned subset of PacBio reads, with 54 clusters, 100 random initializations and 10 iterations for each initialization. After k-means, we performed hierarchical clustering to merge the resulting clusters into 47 clusters, based on the estimated single cell strand states in the clusters. Note that we observed that the PacBio reads coming from repetitive genomic regions tend to form an extra (false) cluster. This extra cluster was estimated being WC in almost all libraries (which is unlikely to reflect a true cell state based on the random distribution of strand states). For this reason, we set the number of clusters to 47 instead of 46, which would be an expected number of clusters for a female human used in this study.
3.4 Soft (EM) clustering settings
PacBio reads with an abnormally high numbers of Strand-seq reads mapped to them might adversely affect the performance of the EM algorithm in estimating the model parameters. Those reads are likely to originate from the complex repetitive regions of the genome and therefore do not have a clean Strand-seq strand state signal. We therefore removed PacBio reads that are among the top 95% quantile based on the coverage of Strand-seq reads mapped to them.
We ran our EM algorithm on each chunk of Minimap alignments independently based on the initialization of parameters resulting from hard clustering. The number of EM iterations was set to 50 in each chunk, and the α parameter was set to 0.01.
3.5 Runtime and convergence of the EM algorithm
We measured running times of different steps of our pipeline. The runtime for the alignment of Strand-seq reads to PacBio reads amounted to 414.3 CPU hours, and the runtimes for hard and soft clusterings were 0.87 and 400.5 CPU hours, respectively.
To confirm convergence of the algorithm, we also ran the EM algorithm with 100 iterations in 10 chunks of PacBio reads, and we obtained almost the same clustering accuracy as the default number of 50 iterations in those chunks. For example, we observed that in the 100 iterations experiment, there are 78.76% of PacBio reads with the maximum cluster assignment probability of at least 0.5, among which 92.75% were correctly clustered. The two aforementioned percentages for 50 iterations are 78.72% and 92.7%, respectively, which are almost identical to the results of 100 iterations. This observation indicates that the EM algorithm has sufficiently converged after 50 iterations.
4 Results
4.1 Quality control
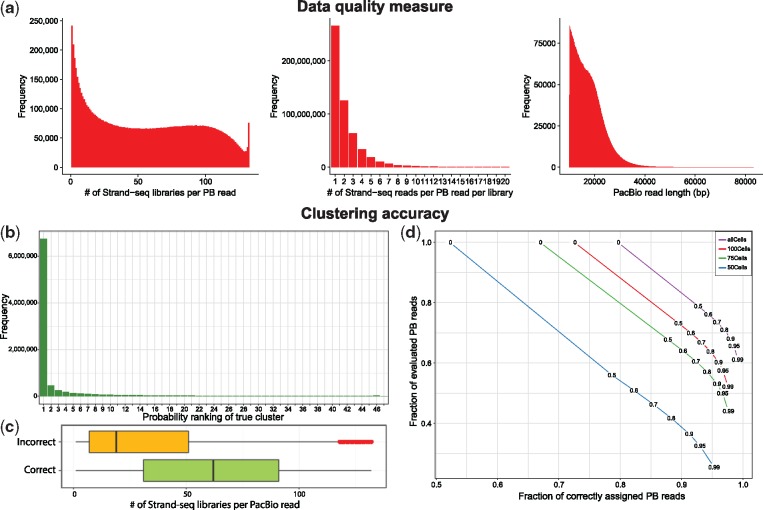
To evaluate the overall performance of aligning Strand-seq reads to PacBio reads, we looked at a number of data quality measures shown in Figure 4a. The leftmost histogram shows how many different Strand-seq libraries are represented per PacBio read. This metric highly depends on the number of Strand-seq libraries as well as the stringency of the mapping step. We observe that the majority of PacBio reads is covered by less then 25 (out of 132) single cell libraries. The peak on the right stems from reads in repetitive contexts which we remove in a pre-processing step (Section 3.4). The middle histogram represents the number of Strand-seq reads per PacBio read per Strand-seq library. Note that we removed the zero read counts from this statistics. That is, this historgram only shows cases in which at least one read from a Strand-seq library mapped to a given PacBio read. This plot reveals that only in a minority of cases there are two or more reads from a single Strand-seq library that cover the same PacBio read. These two histograms highlight the overall sparsity of the data, where each PacBio read is covered by only a handful of Strand-seq reads from a few libraries. This data sparsity is explained by observing the limited PacBio read length (Fig. 4a, right) and the fact that Strand-seq is a single cell sequencing technique with a limited coverage per library.
Fig. 4.
(a) Data quality measures representing unfiltered data after mapping of Strand-seq read to PacBio reads. Clustering accuracy is reported after filtering out 5% of PacBio reads with the highest Strand-seq read coverage. (b) Distribution of PacBio reads based on the ranks of their true clusters sorted by probabilities (the cluster with the highest probability for any given PacBio read has rank 1 etc.) (c) Distribution of the amount of Strand-seq libraries being represented per PacBio read as a function of a given PacBio read being assigned to a correct or incorrect cluster (chromosome and directionality). (d) The accuracy for various probability thresholds (0, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95 and 0.9) among PacBio reads represented in at least five Strand-seq libraries. Each curve represents a different number of Strand-seq libraries used (132, 100, 75, 50)
4.2 Clustering accuracy
For each PacBio read, we sorted the clusters in decreasing order based on their soft clustering probabilities. We then computed the rank of the true cluster in this sorted list for every PacBio read. The histogram in Figure 4b shows the distribution of these ranks across PacBio reads. For the majority (74.6%) of PacBio reads, the true cluster appeared at rank 1, meaning that the cluster with the highest probability was the true (correct) cluster. This means that such reads can be correctly clustered if we choose only the cluster with the highest probability. Besides that, there was a noticeable amount (11.5%) of PacBio reads with ranks 2–5, highlighting the benefits of soft clustering: In such a way, some PacBio reads can be assigned to a small list of clusters with a true one among them, even though there is an ambiguity with respect to the cluster assignment. These results are in line with the fact that some PacBio reads have a low Strand-seq coverage and true clusters might not be well distinguishable from the others.
To see how confidently we can assign each PacBio read to the chromosome with the highest probability, we computed the differences between the highest and second highest probability for all PacBio reads and observed that it was larger than 0.95 in 65.2% and smaller than 0.05 in 13% of all cases. This indicates that for the majority of PacBio reads, the difference is quite pronounced, whereas only a minority shows an ambiguous signal (those with sparse Strand-seq coverage), which is in line with the statistics displayed in Figure 4b.
Next, we sought to investigate the main determinants of a PacBio read being assigned to a correct cluster (chromosome). We assigned each PacBio read to the cluster with the highest probability. We evaluated each cluster assignment as correct or incorrect by comparison to the known original chromosome of each PacBio read. Subsequently, we investigated the distribution of the number of Strand-seq libraries being represented per PacBio read in the set of correctly and incorrectly clustered PacBio reads, respectively, as shown in Figure 4c. It is evident that there is a clear difference between the number of Strand-seq libraries represented in these two groups of PacBio reads, with median values of 62 and 19 for correctly and incorrectly assigned PacBio reads, respectively. The low number of represented Strand-seq libraries in the incorrectly clustered PacBio reads meets our expectation that finding the true cluster is difficult when the data are too sparse. However, according to Figure 4b, the true cluster for these sparse data usually lies among the top clusters. The red points in the yellow box plot show the outliers that likely correspond to PacBio reads falling in repetitive regions of the genome and hence are receiving a lot of Strand-seq reads. Moreover, PacBio reads coming from repetitive regions of the genome are prone to have mis-mapped Strand-seq reads what might violate observed strand states.
To further evaluate the accuracy of our clustering algorithm, we filtered out all PacBio reads that are represented in less than five Strand-seq libraries, which leads to a set of remaining reads with an average genome coverage of 48.9×. Among those selected PacBio reads, we computed the clustering accuracy using a set of probability thresholds (0, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95 and 0.99). In other words, we only evaluated PacBio reads whose maximum cluster probability was above the respective threshold (Fig. 4d). Additionally, results for using varying numbers of Strand-seq libraries are represented as different curves, confirming the importance of including a large number of Strand-seq libraries. For all curves, there is a clear trade-off between the fraction of assigned reads and the clustering accuracy. That is, the more stringently we filter, the higher the accuracy, which confirms that the posterior probabilities indeed capture the degree of certainty about the assignment of a read to a chromosome. For instance, we were able to reach very high clustering accuracy (97.0%) corresponding to the probability threshold 0.8, while retaining 71.0% of PacBio reads. This amount of PacBio reads was sufficient to cover the human genome with 34.8× coverage. With a threshold of 0.99, we attain an accuracy of more than 99% while still retaining 61.1% of all reads and reaching a genome coverage of 30.1× (rightmost dot in top curve in Fig. 4d).
4.3 Hard clustering-based versus random initialization
To assess the merits of our initialization procedure based on hard clustering, we replaced it by random initialization and compared the results. We ran the EM algorithm for the same number of iterations (50) and observed markedly worse performance for random initalizations: When assigning each PacBio read to the cluster with maximum probability, we obtained an accuracy of 9.6% using random initialiation as opposed to an accuracy of 79.6% when using the hard-clustering initialization (leftmost data point in top curve of Fig. 4d). This experiment shows that the hard clustering step, which is orders of magnitude faster than the EM procedure (Section 3.5), drastically improves the final results.
4.4 De novo assembly on clustered PacBio reads
Lastly, we have tested the performance of de novo assembly on clustered PacBio reads. We selected all PacBio reads that were represented in at least five single-cell libraries and that were assigned to Chromosome 1 with a probability of 0.5 and higher. This yields 489 203 of PacBio reads, corresponding to 35× coverage of Chromosome 1. Recall that the outcome of SaaRclust is two clusters, one contains PacBio reads in forward and the other contains PacBio reads in reverse direction. We have reverse complemented all PacBio reads assigned to reverse directionality cluster. In this way, we have synchronized directionality of all Pacbio reads belonging to Chromosome 1. The resulting reads were used as input to the Canu assembler (Koren et al., 2017) with parameters correctedErrorRate = 0.1 and minOverlapLength = 200. These settings resulted in 460 contigs for Chromosome 1 with an N50 length of 1.05 Mbp as reported by Assemblytics (Nattestad and Schatz, 2016).
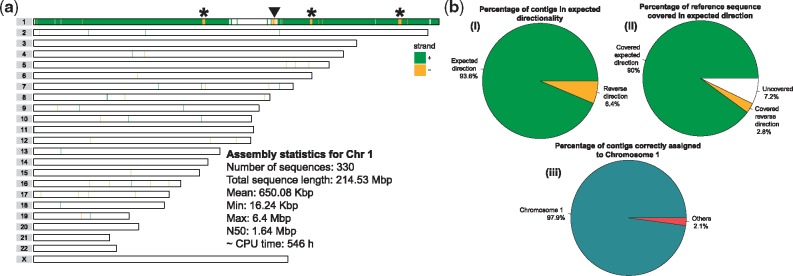
Next, we explored whether the contiguity can be further improved by including more reads. To this end, we also included reads where Chromosome 1 was among the top clusters with probabilities markedly higher than the rest of them, based on detecting a peak in the differences between pairs of consecutive probabilities (after sorting by probability). With this approach, we have increased the number of PacBio reads assigned to Chromosome 1 to 667 346, corresponding to 47× coverage of Chromosome 1. We have repeated the assembly (using the same Canu parameters) with this new read set and obtained a more contiguous assembly consisting of 330 contigs (N50 = 1.64 Mbp) that cover 92.7% of Chromosome 1 after mapping them to the reference genome (Fig. 5a and b). Interestingly, since all contigs are expected to be of the same directionality, any change in directionality might be an indication of structural variation. Based on this assumption we have been able to confirm a large inversion on Chromosome 1 previously reported by Sanders et al. (2016) (Fig. 5a, arrowhead). However, we observed other regions of switched directionality that do not correspond to known inversions (Fig. 5a, asterisks). Overall, the de novo assembly of pre-clustered PacBio reads provided highly specific contigs of which the vast majority (98%) was localized on the expected genomic chromosome (Fig. 5b, iii). Moreover, almost all (93.6%) assembled contigs were mapped back to the reference sequence in forward directionality covering 90% of Chromosome 1 (Fig. 5b, i, ii).
Fig. 5.
(a) An ideogram showing genomic locations of contigs assembled from PacBio reads assigned to Chromosome 1 by SaaRclust. Horizontal lines represent individual chromosomes and vertical lines (green and yellow) depicts genomic location and directionality (’+’: green, ’–’: yellow) of contigs mapped against referenge genome assembly. Black arrowhead points to a switch in contig directionality overlapping with known inversion. Asterisks points to directionality switches not presented as inversion before. Text inset presents various assembly statistics. CPU time is reported for the whole de novo assembly pipeline including read correction, read trimming and assembly using Canu. (b) Statistics of Chromosome 1 assembly (i) Reports how many contigs were mapped in expected directionality to the reference genome. (ii) Shows total percentage of Chromosome 1 covered by contigs with both expected and reversed directionality. White chunk represents uncovered portions of Chromosome 1. (iii) Illustrates specifity at which assembled contigs map to Chromosome 1
5 Discussion
We presented a latent variable model and a corresponding EM algorithm to leverage single-cell Strand-seq data for clustering long sequencing reads by chromosomal origin and directionality. We implemented this algorithm in an R package, called SaaRclust and tested it on the female human genome NA12878. SaaRclust exhibits a high accuracy even though the input data are extremely sparse and the read mapping process is complicated by the high error rates of PacBio sequencing. It is the first tool able to cluster long reads by chromosome. This constitutes a major improvement compared to BAIT (Hills et al., 2013) and ContiBAIT, (O’Neill et al., 2017), which can perform clustering at the level of contigs, but are not designed to work with sparse read-level data.
We observed that the reliability of assigning a given PacBio read to a chromosome strongly depends on the Strand-seq coverage it received. In case of ambiguity, however, the true chromosome was among the top five clusters in most of these cases. The reliability of our clustering is further corroborated by the quality of the resulting de novo assembly of Chromosome 1, which achieved a high N50 value as well as high specificity of assembled contigs to Chromosome 1. Most likely, optimization of assembly parameters will bring further improvements in both accuracy and contiguity of assembled genomes using our approach and we plan to thoroughly test this on whole genomes in the future. Modifying existing assemblers to take advantage of the facts that the input reads have synchronized directionality and come with probabilities for chromsomal assignments is another promising direction we plan to explore.
As third generation sequencing technologies advance further, reads are anticipated to become even longer. We expect a major boost in the performance of SaaRclust on longer reads, such as from the ONT platform. Beyond that, our single cell sub-sampling analysis shows that increasing the number of single cell Strand-seq libraries enhances the clustering accuracy significantly, and saturation has not yet been reached. Given the comparatively low cost for Strand-seq, increasing the number of libraries would be possible while still keeping the costs of Strand-seq significantly below those of long read sequencing. We also plan to explore the utility of pooling Strand-seq libraries from different samples for clustering, for instance using the libraries for nine samples produced by the Human Genome Structural Variation Consortium (Chaisson et al., 2017).
We hypothesize that PacBio reads with poor clustering accuracy despite sufficient coverage are originating from repeat regions in the genome. Such ambiguities can be accounted for by extending our model, and we plan to explore the potential of our approach for resolving segmental duplications in the future.
Here, we have focused on developing the necessary methodology and have benchmarked its performance. There is a wealth of applications of our framework that we aim to address in the future. Genomes comprising complex structural variation are interesting cases for future studies since these variants are difficult to resolve with extant methods. Beyond human genomes, we envision our method to be of high utility for the assembly of plant genomes, which can be very large. Furthermore, clustering by chromosome is a prerequisite for using Strand-seq capabilities for whole-chromosome haplotype phasing. The present work might hence allow lifting our work on reference-based phasing (Porubskỳ et al., 2016, 2017) to de novo assembly settings.
Funding
Funding for this research project was provided to EEE, JOK and TM from the NIH, grant U41HG007497. EEE is an investigator of the Howard Hughes Medical Institute.
Conflict of Interest: none declared.
References
- Burton J.N. et al. (2013) Chromosome-scale scaffolding of de novo genome assemblies based on chromatin interactions. Nat. Biotechnol., 31, 1119–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaisson M.J.P. et al. (2017) Multi-platform discovery of haplotype-resolved structural variation in human genomes. bioRxiv, 193144. [DOI] [PMC free article] [PubMed]
- Chin C.-S. et al. (2016) Phased diploid genome assembly with single-molecule real-time sequencing. Nat. Methods, 13, 1050–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claussin C. et al. (2017) Genome-wide mapping of sister chromatid exchange events in single yeast cells using strand-seq. Elife, 6, e30560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A.P. et al. (1977) Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.), 39, 1–38. [Google Scholar]
- Falconer E. et al. (2012) DNA template strand sequencing of single-cells maps genomic rearrangements at high resolution. Nat. Methods, 9, 1107–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon D. et al. (2016) Long-read sequence assembly of the gorilla genome. Science, 352, aae0344.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hills M. et al. (2013) Bait: organizing genomes and mapping rearrangements in single cells. Genome Med., 5, 82.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hills M. et al. (2018) Construction of whole genomes from scaffolds using single cell strand-seq data. bioRxiv, 271510. [DOI] [PMC free article] [PubMed]
- Jiao W.-B., Schneeberger K. (2017) The impact of third generation genomic technologies on plant genome assembly. Curr. Opin. Plant Biol., 36, 64–70. [DOI] [PubMed] [Google Scholar]
- Jiao W.-B. et al. (2017) Improving and correcting the contiguity of long-read genome assemblies of three plant species using optical mapping and chromosome conformation capture data. Genome Res., 27, 778–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koren S. et al. (2017) Canu: scalable and accurate long-read assembly via adaptive k-mer weighting and repeat separation. Genome Res., 27, 722–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2016) Minimap and miniasm: fast mapping and de novo assembly for noisy long sequences. Bioinformatics, 32, 2103–2110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Y. et al. (2016) Assembly of long error-prone reads using de Bruijn graphs. Proc. Natl. Acad. Sci., 113, E8396–E8405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers G. (2014) Efficient local alignment discovery amongst noisy long reads In: International Workshop on Algorithms in Bioinformatics. Springer, Berlin, Heidelberg, pp. 52–67. [Google Scholar]
- Nattestad M., Schatz M.C. (2016) Assemblytics: a web analytics tool for the detection of variants from an assembly. Bioinformatics, 32, 3021–3023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Neill K. et al. (2017) Assembling draft genomes using contiBAIT. Bioinformatics, 33, 2737–2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porubský D. et al. (2016) Direct chromosome-length haplotyping by single-cell sequencing. Genome Res., 26, 1565–1574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porubskỳ D. et al. (2017) Dense and accurate whole-chromosome haplotyping of individual genomes. bioRxiv, 126136. [DOI] [PMC free article] [PubMed]
- Sanders A.D. et al. (2016) Characterizing polymorphic inversions in human genomes by single-cell sequencing. Genome Res., 26, 1575–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treangen T.J., Salzberg S.L. (2012) Repetitive dna and next-generation sequencing: computational challenges and solutions. Nat. Rev. Genet., 13, 36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wietmarschen N. et al. (2018) BLM helicase suppresses recombination at g-quadruplex motifs in transcribed genes. Nat. Commun., 9, 271.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C.J. (1983) On the convergence properties of the EM algorithm. Ann. Stat., 11, 95–103. [Google Scholar]