Learning with multiple pairwise kernels for drug bioactivity prediction

Abstract

Motivation

Many inference problems in bioinformatics, including drug bioactivity prediction, can be formulated as pairwise learning problems, in which one is interested in making predictions for pairs of objects, e.g. drugs and their targets. Kernel-based approaches have emerged as powerful tools for solving problems of that kind, and especially multiple kernel learning (MKL) offers promising benefits as it enables integrating various types of complex biomedical information sources in the form of kernels, along with learning their importance for the prediction task. However, the immense size of pairwise kernel spaces remains a major bottleneck, making the existing MKL algorithms computationally infeasible even for small number of input pairs.

Results

We introduce pairwiseMKL, the first method for time- and memory-efficient learning with multiple pairwise kernels. pairwiseMKL first determines the mixture weights of the input pairwise kernels, and then learns the pairwise prediction function. Both steps are performed efficiently without explicit computation of the massive pairwise matrices, therefore making the method applicable to solving large pairwise learning problems. We demonstrate the performance of pairwiseMKL in two related tasks of quantitative drug bioactivity prediction using up to 167 995 bioactivity measurements and 3120 pairwise kernels: (i) prediction of anticancer efficacy of drug compounds across a large panel of cancer cell lines; and (ii) prediction of target profiles of anticancer compounds across their kinome-wide target spaces. We show that pairwiseMKL provides accurate predictions using sparse solutions in terms of selected kernels, and therefore it automatically identifies also data sources relevant for the prediction problem.

Availability and implementation

Code is available at https://github.com/aalto-ics-kepaco.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In the recent years, several high-throughput anticancer drug screening efforts have been conducted (Barretina et al., 2012; Smirnov et al., 2018; Yang et al., 2012), providing bioactivity measurements that allow for the identification of compounds that show increased efficacy in specific human cancer types or individual cell lines, therefore guiding both the precision medicine efforts as well as drug repurposing applications. However, chemical compounds execute their action through modulating typically multiple molecules, with proteins being the most common molecular targets, and ultimately both the efficacy and toxicity of the treatment are a consequence of those complex molecular interactions. Hence, elucidating drug’s mode of action (MoA), including both on- and off-targets, is critical for the development of effective and safe therapies.

The increased availability of drug bioactivity data for cell lines (Smirnov et al., 2018) and protein targets (Merget et al., 2017), together with the comprehensive characteristics of drug compounds, proteins and cell lines, has enabled construction of supervised machine learning models, which offer cost-effective means for fast, systematic and large-scale pre-screening of chemical compounds and their potential targets for further experimental verification, with the aim of accelerating and de-risking the drug discovery process (Ali et al., 2017; Azuaje, 2017; Cheng et al., 2012; Cichonska et al., 2015). Under the general framework of drug bioactivity prediction, two related machine learning tasks are identified: (i) prediction of anticancer drug responses and (ii) prediction of drug–protein interactions, both of which can be tackled through similar machine learning techniques. In particular, kernel-based approaches have emerged as powerful tools in computational drug discovery (Cichonska et al., 2017; Marcou et al., 2016; Pahikkala et al., 2015).

Both the drug response in cancer cell line prediction and drug–protein interaction prediction are representative examples of pairwise learning problems, where the goal is to build predictive model for pairs of objects. Classical kernel-based methods for pairwise learning rely merely on a single pairwise kernel. However, such approaches are unlikely to be optimal in applications where a growing variety of biological and molecular data sources are available, including chemical and protein structures, pharmacophore patterns, gene expression signatures, methylation profiles as well as genomic variants found in cell lines. In fact, the advantage of integrating different data types for the multi-level analysis has been highlighted in the recent studies (Ebrahim et al., 2016; Elefsinioti et al., 2016). Multiple kernel learning (MKL) methods, which search for an optimal combination of several kernels, hence enabling the use of different information sources simultaneously and learning their importance for the prediction task, have therefore received significant attention in bioinformatics (Brouard et al., 2016; Kludas et al., 2016; Shen et al., 2014), especially in drug bioactivity inference (Ammad-ud-din et al., 2016; Costello et al., 2014; Nascimento et al., 2016).

However, the existing MKL methods do not scale up to the massive size of pairwise kernels, in terms of both processing and memory requirements, making the kernel weights optimization and model training computationally infeasible even for small numbers of input pairs, such as drugs and cell lines or drugs and protein targets. The recently introduced KronRLS-MKL algorithm for pairwise learning of drug–protein interactions interleaves the optimization of the pairwise prediction function parameters with the kernel weights optimization (Nascimento et al., 2016). However, it finds two sets of kernel weights, separately for drug kernels and protein kernels instead of pairwise kernels, and therefore it does not fully exploit the information contained in the pairwise space.

Here, we propose pairwiseMKL, to our knowledge, the first method for time- and memory-efficient learning with multiple pairwise kernels, implementing both efficient pairwise kernel weights optimization and pairwise model training. In the first phase, the algorithm determines a convex combination of input pairwise kernels by maximizing the centered alignment (i.e. matrix similarity measure) between the final combined kernel and the ideal kernel derived from the label values (response kernel); in the second phase, the pairwise prediction function is learned. Both steps are performed without explicit construction of the massive pairwise matrices (Fig. 1). We demonstrate the performance of pairwiseMKL in two important subtasks of quantitative drug bioactivity prediction. In case of drug response in cancer cell line prediction subtask, we used the bioactivity data from 15 376 drug–cell line pairs from the Genomics of Drug Sensitivity in Cancer (GDSC) project (Yang et al., 2012). We encoded similarities between the drug compounds and cell lines using kernels constructed based on various types of molecular fingerprints, gene expression profiles, methylation patterns, copy number data and genetic variants, resulting in 120 pairwise kernels (10 drug kernels × 12 cell line kernels). In the larger subtask of drug–protein binding affinity prediction, we used the recently published bioactivities from 167 995 drug–protein pairs (Merget et al., 2017) and constructed 3120 pairwise kernels (10 drug kernels × 312 protein kernels) based on molecular fingerprints, protein sequences and gene ontology annotations. We show that pairwiseMKL is very well-suited for solving large pairwise learning problems, it outperforms KronRLS-MKL in terms of both memory requirements and predictive power, and, unlike KronRLS-MKL, it (i) allows for missing values in the label matrix and (ii) finds a sparse combination of input pairwise kernels, thus enabling automatic identification of data sources most relevant for the prediction task. Moreover, since pairwiseMKL scales up to large number of pairwise kernels, tuning of the kernel hyperparameters can be easily incorporated into the kernel weights optimization process.

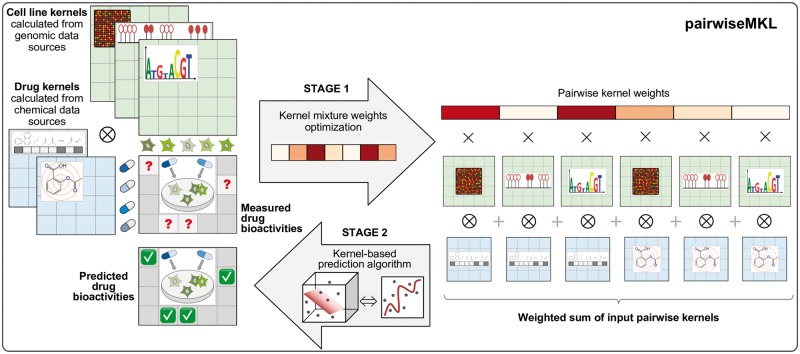
Fig. 1.

Schematic figure showing an overview of pairwiseMKL method for learning with multiple pairwise kernels, using the drug response in cancer cell line prediction as an example. First, two drug kernels and three cell line kernels are calculated from available chemical and genomic data sources, respectively. The resulting matrices associate all drugs and all cell lines, and therefore a kernel can be considered as a similarity measure. Since we are interested in learning bioactivities of pairs of input objects, here drug–cell line pairs, pairwise kernels relating all drug–cell line pairs are needed, and they are calculated as Kronecker products (⊗) of drug kernels and cell line kernels (2 drug kernels × 3 cell line kernels = 6 pairwise kernels). In the first learning stage, pairwise kernel mixture weights are determined (Section 2.2.1), and then a weighted combination of pairwise kernels is used for anticancer drug response prediction with a regularized least-squares pairwise regression model (Section 2.2.2). Importantly, pairwiseMKL performs those two steps efficiently by avoiding explicit construction of any massive pairwise matrices, and therefore it is very well-suited for solving large pairwise learning problems

In summary, this article makes the following contributions.

• We implement a highly efficient centered kernel alignment procedure to avoid explicit computation of multiple huge pairwise matrices in the selection of mixture weights of input pairwise kernels. To achieve this, we propose a novel Kronecker decomposition of the centering operator for the pairwise kernel.

• We introduce a Gaussian response kernel which is more suitable for the kernel alignment in a regression setting than a standard linear response kernel.

• We introduce a method for training a regularized least-squares model with multiple pairwise kernels by exploiting the structure of the weighted sum of Kronecker products. We therefore avoid explicit construction of any massive pairwise matrices also in the second stage of learning pairwise prediction function.

• We show how to effectively utilize the whole exome sequencing data to calculate informative real-valued genetic mutation profile feature vectors for cancer cell lines, instead of binary mutation status vectors commonly used in drug response prediction models.

• pairwiseMKL provides a general approach to MKL in pairwise spaces, and therefore it is widely applicable also outside the drug bioactivity inference problems. Our implementation is freely available.

2 Materials and methods

This section is organized as follows. First, Section 2.1 explains a general approach to two-stage multiple pairwise kernel regression which forms the basis for our pairwiseMKL method described in Section 2.2. We demonstrate the performance of pairwiseMKL in the two tasks of (i) anticancer drug potential prediction and (ii) drug–protein binding affinity prediction, but we selected the former as an example to explain the methodology. Finally, Section 2.3 introduces the data and kernels we used in our experiments.

2.1 Multiple pairwise kernel regression

In supervised pairwise learning of anticancer drug potential, training data appears in the form $({\mathbf{x}}_{\mathbf{d}},{\mathbf{x}}_{\mathbf{c}},y)$, where $({\mathbf{x}}_{\mathbf{d}},{\mathbf{x}}_{\mathbf{c}})$ denotes a feature representation of a pair of input objects, drug ${\mathbf{x}}_{\mathbf{d}}\in {\mathcal{X}}_{\mathcal{D}}$ and cancer cell line ${\mathbf{x}}_{\mathbf{c}}\in {\mathcal{X}}_{\mathcal{C}}$ (e.g. molecular fingerprint vector and gene expression profile, respectively), and $y\in ℝ$ is its associated response value (also called the label), i.e. a measurement of sensitivity of cell line ${\mathbf{x}}_{\mathbf{c}}$ to drug ${\mathbf{x}}_{\mathbf{d}}$. Given $N\le n_d\times n_c$ training instances, they can be represented as matrices ${\mathbf{X}}_{\mathbf{d}}\in {ℝ}^{n_d\times t_d},\hspace{0.17em}{\mathbf{X}}_{\mathbf{c}}\in {ℝ}^{n_c\times t_c}$ and label vector $\mathbf{y}\in {ℝ}^N$, where n_d denotes the number of drugs, n_c the number of cell lines, t_d and t_c the number of drug and cell line features, respectively.

The aim is to find a pairwise prediction function f that models the relationship between $({\mathbf{X}}_{\mathbf{d}},{\mathbf{X}}_{\mathbf{c}})$ and $\mathbf{y}$; f can later be used to predict sensitivity measurements for drug–cell line pairs outside the training space. The assumption is that structurally similar drugs show similar effects in cell lines having common genomic backgrounds. We apply kernels to encode the similarities between input objects, such as drugs or cell lines. Kernels offer the advantage of increasing the power of classical linear learning algorithms by providing a computationally efficient approach for projecting input objects into a new feature space with very high or even infinite number of dimensions. A linear model in this implicit feature space corresponds to a non-linear model in the original space (Shawe-Taylor and Cristianini, 2004). Formally, a kernel is a positive semidefinite (PSD) function that for all ${\mathbf{x}}_{\mathbf{d}},\mathbf{x}{\prime }_{\mathbf{d}}\in {\mathcal{X}}_{\mathcal{D}}$ satisfies $k_d({\mathbf{x}}_{\mathbf{d}},\mathbf{x}{\prime }_{\mathbf{d}})=\langle \mathit{\varphi }\left({\mathbf{x}}_{\mathbf{d}}\right),\mathit{\varphi }\left(\mathbf{x}{\prime }_{\mathbf{d}}\right)\rangle$, where $\mathit{\varphi }$ denotes a mapping from the input space ${\mathcal{X}}_{\mathcal{D}}$ to a high-dimensional inner product feature space $H_{\mathcal{D}}$, i.e. $\mathit{\varphi }:{\mathbf{x}}_{\mathbf{d}}\in {\mathcal{X}}_{\mathcal{D}}\to \mathit{\varphi }\left({\mathbf{x}}_{\mathbf{d}}\right)\in H_{\mathcal{D}}$ (the same holds for cell line kernel k_c). It is, however, possible to avoid explicit computation of the mapping $\mathit{\varphi }$ and define the kernel directly in terms of the original input features, such as gene expression profiles, by replacing the inner product $\langle ·,·\rangle$ with an appropriately chosen kernel function (so-called kernel trick), e.g. the Gaussian kernel (Shawe-Taylor and Cristianini, 2004).

Kernels can be easily employed for pairwise learning by constructing a pairwise kernel matrix $\mathbf{K}\in {ℝ}^{N\times N}$ relating all drug–cell line pairs. Specifically, $\mathbf{K}$ is calculated as a Kronecker product of drug kernel ${\mathbf{K}}_{\mathbf{d}}\in {ℝ}^{n_d\times n_d}$ (computed from, e.g. drug fingerprints) and cell line kernel ${\mathbf{K}}_{\mathbf{c}}\in {ℝ}^{n_c\times n_c}$ (computed from, e.g. gene expression), forming a block matrix with all possible products of entries of ${\mathbf{K}}_{\mathbf{d}}$ and ${\mathbf{K}}_{\mathbf{c}}$:

$$K=K_d\otimes K_c=\left(\begin{array}{cccc}{k}_d(x_d{}_1,x_d{}_1)K_c& k_d(x_d{}_1,x_d{}_2)K_c& \cdots & k_d(x_d{}_1,x_d{}_{n_d})K_c\\ k_d(x_d{}_2,x_d{}_1)K_c& k_d(x_d{}_2,x_d{}_2)K_c& \cdots & k_d(x_d{}_2,x_d{}_{n_d})K_c\\ ⋮& ⋮& \ddots & ⋮\\ k_d(x_d{}_{n_d},x_d{}_1)K_c& k_d(x_d{}_{n_d},x_d{}_2)K_c& \cdots & k_d(x_d{}_{n_d},x_d{}_{n_d})K_c\end{array}\right).$$ (1)

Then, the prediction function for a test pair (${\mathbf{x}}_{\mathbf{d}},{\mathbf{x}}_{\mathbf{c}}$) is expressed as

$$\begin{array}{c}f(x_d,x_c)={\displaystyle \sum _{l=1}^N{\alpha }_l}k\left(\right(x_d{}_l,x_c{}_l),(x_d,x_c\left)\right)={\mathit{\alpha }}^{T}k,\end{array}$$ (2)

where $\mathbf{k}$ is a column vector with kernel values between each training drug–cell line pair ($x_d{}_l,x_c{}_l$) and test pair (${\mathbf{x}}_{\mathbf{d}},{\mathbf{x}}_{\mathbf{c}}$) for which the prediction is made, and $\mathit{\alpha }=({\alpha }_1,\dots ,{\alpha }_N)$ denotes a vector of model parameters to be obtained by the learning algorithm through minimizing a certain objective function. In kernel ridge regression (KRR, Saunders et al., 1998), the objective function is defined in terms of total squared loss along with L2-norm regularizer, and the solution for $\mathit{\alpha }$ is found by solving the following system of linear equations:

$$\begin{array}{c}(\mathbf{K}+\lambda \mathbf{I})\mathit{\alpha }=\mathbf{y},\end{array}$$ (3)

where λ indicates a regularization hyperparameter controlling the balance between training error and model complexity $(\lambda >0)$, and $\mathbf{I}$ is the N × N identity matrix.

Due to the wide availability of different chemical and genomic data sources, both drugs and cell lines can be represented with multiple kernel matrices ${\mathbf{K}}_{\mathbf{d}}^{\left(1\right)},\dots ,{\mathbf{K}}_{\mathbf{d}}^{\left(p_d\right)}$ and ${\mathbf{K}}_{\mathbf{c}}^{\left(1\right)},\dots ,{\mathbf{K}}_{\mathbf{c}}^{\left(p_c\right)}$, therefore forming $P=p_d\times p_c$ pairwise kernels ${\mathbf{K}}^{\left(1\right)},\dots ,{\mathbf{K}}^{\left(P\right)}$ (Kronecker products of all pairs of drug kernels and cell line kernels). The goal of two-stage multiple pairwise KRR is to first find the combination of P pairwise kernels

$$\begin{array}{c}{\mathbf{K}}_{\mathit{\mu }}=\sum _{i=1}^P{\mu }_i{\mathbf{K}}^{\left(i\right)},\end{array}$$ (4)

and then use ${\mathbf{K}}_{\mathit{\mu }}$ instead of $\mathbf{K}$ in Equation (3) to learn the pairwise prediction function.

2.1.1 Centered kernel alignment

The observation that a similarity between the centered input kernel ${\mathbf{K}}^{\left(i\right)}$ and a linear kernel derived from the labels ${\mathbf{K}}_{\mathbf{y}}=\mathbf{y}{\mathbf{y}}^T$ (response kernel) correlates with the performance of ${\mathbf{K}}^{\left(i\right)}$ in a given prediction task, has inspired a design of the centered kernel alignment-based MKL approach (Cortes et al., 2012). Both ${\mathbf{K}}^{\left(i\right)}$ and ${\mathbf{K}}_{\mathbf{y}}$ measure similarities between drug–cell line pairs. However, ${\mathbf{K}}_{\mathbf{y}}$ can be considered as a ground-truth as it is calculated from the bioactivities which we aim to predict, and hence the ideal input kernel would capture the same information about the similarities of drug–cell line pairs as the response kernel ${\mathbf{K}}_{\mathbf{y}}$. The idea is to first learn a linear mixture of centered input kernels that is maximally aligned to the response kernel, and then use the learned mixture kernel as the input kernel for learning a prediction function.

Centering a kernel $\mathbf{K}$ corresponds to centering its associated feature mapping $\mathit{\varphi }$, and it is performed by $\widehat{\mathbf{K}}=\mathbf{C}\mathbf{K}\mathbf{C}$, where $\mathbf{C}\in {ℝ}^{N\times N}$ is an idempotent ($\mathbf{C}=\mathbf{C}\mathbf{C}$) centering operator of the form $[\mathbf{I}-\frac{11^T}{N}]$, $\mathbf{I}$ indicates N × N identity matrix, and $1$ is a vector of N components, all equal to 1 (Cortes et al., 2012). Centered kernel alignment measures the similarity between two kernels $\widehat{\mathbf{K}}$ and $\widehat{\mathbf{K}}\prime$:

$$A(\widehat{\mathbf{K}},\widehat{\mathbf{K}}\prime )=\frac{{\langle \widehat{\mathbf{K}},\widehat{\mathbf{K}}\prime \rangle }_F}{\sqrt{{\langle \widehat{\mathbf{K}},\widehat{\mathbf{K}}\rangle }_F{\langle \widehat{\mathbf{K}}\prime ,\widehat{\mathbf{K}}\prime \rangle }_F}}=\frac{{\langle \widehat{\mathbf{K}},\widehat{\mathbf{K}}\prime \rangle }_F}{\left|\right|\widehat{\mathbf{K}}\left|{|}_F\right||\widehat{\mathbf{K}}\prime |{|}_F}.$$ (5)

Above, ${\langle ·,·\rangle }_F$ denotes a Frobenius inner product, $\left|\right|·|{|}_F$ is a Frobenius norm and A can be viewed as the cosine of the angle, correlation, defined between two matrices. Kernel mixture weights $\mathit{\mu }=({\mu }_1,\dots ,{\mu }_P)$ are determined by maximizing the centered alignment between the final combined kernel ${\mathbf{K}}_{\mathit{\mu }}$ and the response kernel ${\mathbf{K}}_{\mathbf{y}}$ (Cortes et al., 2012):

$$\begin{array}{l}\underset{\mathit{\mu }}{\max }\hspace{0.17em}A({\widehat{K}}_{\mathit{\mu }},{\widehat{K}}_y)=\underset{\mathit{\mu }}{\max }\frac{{\langle {\widehat{K}}_{\mathit{\mu }},K_y\rangle }_F}{\left|\right|{\widehat{K}}_{\text{μ}}|{|}_F},\hfill \\ \text{subject to: }\left|\right|\mathit{\mu }|{|}_2=1, \mathit{\mu }\ge 0.\hfill \end{array}$$ (6)

In (6), $\left|\right|{\widehat{\mathbf{K}}}_{\mathbf{y}}|{|}_F$ is omitted because it does not depend on $\mathit{\mu }$, and ${\langle {\widehat{\mathbf{K}}}_{\mathit{\mu }},{\widehat{\mathbf{K}}}_{\mathbf{y}}\rangle }_F={\langle {\widehat{\mathbf{K}}}_{\mathit{\mu }},{\mathbf{K}}_{\mathbf{y}}\rangle }_F$ through the properties of centering. The optimization problem (6) can be solved via:

$$\underset{\mathbf{v}\ge 0}{\min }{v}^{T}Mv-2v^{T}a,$$ (7)

with the vector $\mathbf{a}$ and the symmetric matrix $\mathbf{M}$ defined by:

$${\left(\mathbf{a}\right)}_i={\langle {\widehat{\mathbf{K}}}^{\left(i\right)},{\mathbf{K}}_{\mathbf{y}}\rangle }_F,i=1,\dots ,P,$$ (8)

$${\left(\mathbf{M}\right)}_{ij}={\langle {\widehat{\mathbf{K}}}^{\left(i\right)},{\widehat{\mathbf{K}}}^{\left(j\right)}\rangle }_F,i,j=1,\dots ,P.$$ (9)

Optimal kernel weights are given by ${\mathit{\mu }}^{*}={\mathbf{v}}^{*}/\left|\right|{\mathbf{v}}^{*}\left|\right|$, where ${\mathbf{v}}^{*}$ is the solution to (7). Then, the combined kernel ${\mathbf{K}}_{\mathit{\mu }}$ is calculated with Equation (4) and used to train a kernel-based prediction algorithm (Cortes et al., 2012).

Such centered kernel alignment-based strategy has proved to have a good predictive performance (Brouard et al., 2016; Cortes et al., 2012; Kludas et al., 2016; Shen et al., 2014), but it is not applicable to most of the pairwise learning problems because the size of pairwise kernel matrices, ${\mathbf{K}}^{\left(1\right)},\dots ,{\mathbf{K}}^{\left(P\right)}$, grows very quickly with the number of drugs and cell lines (Supplementary Fig. S1) making the mixture weights optimization procedure computationally intractable even for small number of inputs (Table 1).

Table 1.

Memory and time needed for a naïve MKL approach explicitly computing pairwise kernels (Section 2.1) and pairwiseMKL (Section 2.2), depending on the number of drugs and cell lines used in the drug bioactivity prediction experiment

Number of drugs	Number of cell lines	Memory (GB)		Time (h)
		Naïve approach	pairwiseMKL	Naïve approach	pairwiseMKL
50	50	9.810	0.001	2.976	0.003
60	60	20.290	0.001	7.797	0.005
70	70	37.750	0.043	17.678	0.057
80	80	64.000	0.044	37.691	0.069
90	90	103.180	0.046	77.408	0.087
100	100	156.890	0.048	145.312	0.106
110	110	229.670	0.050	>168.000a	0.118
120	120	>256.000b	0.053	≫168.000	0.123

Note: A single round of 10-fold CV was run using different-sized subsets of the data on anticancer drug responses (described in Section 2.3.1) with 10 drug kernels and 12 cell line kernels. Regularization hyperparameter λ was set to 0.1 in both methods.

^aProgram did not complete within 7 days (168 h).

^bProgram did not run given 256 GB of memory.

For instance, given 10 kernels for 100 drugs and 10 kernels for 100 cell lines ($P=10\times 10=100$, $N=100\times 100=10\hspace{0.17em}000$ assuming that bioactivities of all combinations of drugs and cell lines are known), the computation of the matrix $\mathbf{M}$ requires $\frac{(P+1)P}{2}=5 050$ evaluations of Frobenius products between pairwise kernels composed of 100 million entries each, and additional 100 evaluations to calculate vector a (the number of evaluations increases when applying a cross validation). Given 200 drugs and 200 cell lines, the size of a single pairwise kernel grows to 1.6 billion entries taking roughly 12 GB memory. For comparison, in case of a more standard learning problem, such as drug response prediction in a single cancer cell line using drug features only, there would be 200 drugs as inputs instead of drug–cell line pairs, and the resulting kernel matrix would be composed of 40 000 elements taking 0.32 MB memory.

2.2 pairwiseMKL

2.2.1 Stage 1: optimization of pairwise kernel weights

In this work, we devise an efficient procedure for optimizing kernel weights in pairwise learning setting. Specifically, we exploit the known identity

$$\langle {\mathbf{K}}_{\mathbf{d}}\otimes {\mathbf{K}}_{\mathbf{c}},\mathbf{K}{\prime }_{\mathbf{d}}\otimes \mathbf{K}{\prime }_{\mathbf{c}}\rangle =\langle {\mathbf{K}}_{\mathbf{d}},\mathbf{K}{\prime }_{\mathbf{d}}\rangle \langle {\mathbf{K}}_{\mathbf{c}},\mathbf{K}{\prime }_{\mathbf{c}}\rangle$$ (10)

to avoid explicit computation of the massive Kronecker product matrices in Equations (8) and (9). The main difficulty comes from the centering of the pairwise kernel; in particular, the fact that one cannot obtain a centered pairwise kernel $\widehat{\mathbf{K}}$ simply by computing the Kronecker product of centered drug kernel ${\widehat{\mathbf{K}}}_{\mathbf{d}}$ and cell line kernel ${\widehat{\mathbf{K}}}_{\mathbf{c}}$, i.e. $\widehat{\mathbf{K}}\ne {\widehat{\mathbf{K}}}_{\mathbf{d}}\otimes {\widehat{\mathbf{K}}}_{\mathbf{c}}$.

In order to address this limitation, we introduce here a new, highly efficient Kronecker decomposition of the centering operator for the pairwise kernel:

$$\begin{array}{c}\mathbf{C}=\sum _{q=1}^2{\mathbf{Q}}_{\mathbf{d}}^{\left(q\right)}\otimes {\mathbf{Q}}_{\mathbf{c}}^{\left(q\right)},\end{array}$$ (11)

where $Q_d{}^{\left(q\right)}\in {ℝ}^{n_d\times n_d}$ and $Q_c{}^{\left(q\right)}\in {ℝ}^{n_c\times n_c}$ are the factors of C. Exploiting the structure of C allows us to compute the factors efficiently by solving the singular value problem for a matrix of size 2 × 2 only, regardless of how large N is (the detailed procedure is provided in Supplementary Material).

Decomposition (11) allows us to greatly simplify the calculation of the matrix M and vector a needed in the kernel mixture weights optimization by (7):

$$\begin{array}{l}{\left(M\right)}_{ij}={\langle {\widehat{K}}^{\left(i\right)},{\widehat{K}}^{\left(j\right)}\rangle }_F=\text{tr}\left(C{K}^{\left(i\right)}CC{K}^{\left(j\right)}C\right)\hfill \\ ={\displaystyle \sum _{q=1}^2{\displaystyle \sum _{r=1}^2 }}\text{tr}\left(Q_d^{\left(q\right)}{K}_d^{\left(i\right)}{Q}_d^{\left(r\right)}{K}_d^{\left(j\right)}\right)\text{tr}\left(Q_c^{\left(q\right)}{K}_c^{\left(i\right)}{Q}_c^{\left(r\right)}{K}_c^{\left(j\right)}\right),\hfill \end{array}$$ (12)

with $\text{tr}(·)$ denoting a trace of a matrix (a full derivation is given in Supplementary Material). Hence, the inner product in the massive pairwise space (N × N) is reduced to a sum of inner products in the original much smaller spaces of drugs ($n_d\times n_d$) and cell lines ($n_c\times n_c$). The computation of the elements of a is simplified to the inner product between two vectors by first exploiting the block structure of the Kronecker product matrix through the identity $(\mathbf{A}\otimes \mathbf{B})\text{vec}\left(\mathbf{D}\right)=\text{vec}\left(\mathbf{B}\mathbf{D}{\mathbf{A}}^T\right)$:

$$\begin{array}{c}{\langle {\mathbf{K}}^{\left(i\right)},{\mathbf{K}}_{\mathbf{y}}\rangle }_F={\langle \left({\mathbf{K}}_{\mathbf{d}}^{\left(i\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(i\right)}\right), \mathbf{y}{\mathbf{y}}^T\rangle }_F\\ =\langle \mathbf{y}, \left({\mathbf{K}}_{\mathbf{d}}^{\left(i\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(i\right)}\right)\mathbf{y}\rangle \\ =\langle \mathbf{y}, \text{vec} \left({\mathbf{K}}_{\mathbf{c}}^{\left(i\right)}\mathbf{Y}{\mathbf{K}}_{\mathbf{d}}^{\left(i\right)}\right)\rangle ,\end{array}$$ (13)

and then accounting for the centering:

$$\begin{array}{l}{\left(a\right)}_i={\langle {\widehat{K}}^{\left(i\right)},K_y\rangle }_F=\langle y, h\rangle ,\hfill \\ h={\displaystyle \sum _{q=1}^2{\displaystyle \sum _{r=1}^2\text{vec}}}\left(\left(Q_c^{\left(q\right)}{K}_c^{\left(i\right)}{Q}_c^{\left(r\right)}\right)Y\left(Q_d^{\left(q\right)}{K}_d^{\left(i\right)}{Q}_d^{\left(r\right)}\right)\right),\hfill \end{array}$$ (14)

where $\mathbf{Y}\in {ℝ}^{n_c\times n_d}$ is the label matrix (if $N<n_c\times n_d$, missing values in Y are imputed with column (drug) averages to calculate a), and $\text{vec}(·)$ is the vectorization operator which arranges the columns of a matrix into a vector, $\text{vec}\left(\mathbf{Y}\right)=\mathbf{y}$.

Gaussian response kernel

The standard linear response kernel $\mathbf{y}{\mathbf{y}}^T$ used in Equations (13) and (14) is well-suited for measuring similarities between labels in classification tasks, where $y\in \{-1,+1\}$, but not regression, where $y\in ℝ$. pairwiseMKL therefore employs a Gaussian response kernel, a gold standard for measuring similarities between real numbers (Shawe-Taylor and Cristianini, 2004). In particular, we first represent each label value $y_i,i=1,\dots ,N,$ with a feature vector of length S which is a histogram corresponding to a probability density function of all the labels y, centered at y_i, and stored as row vector in the matrix $\Psi \in {ℝ}^{N\times S}$. Then, the Gaussian response kernel compares the feature vectors of all pairs of labels by calculating a sum of S inner products:

$$\begin{array}{c}{\mathbf{K}}_{\mathbf{y}}=\sum _{s=1}^S{\mathit{\psi }}^{\left(s\right)}{\mathit{\psi }}^{\left(s\right)T},\end{array}$$ (15)

where ${\mathit{\psi }}^{\left(s\right)}\in {ℝ}^N$ is a column vector of $\Psi$.

By replacing the linear response kernel $\mathbf{y}{\mathbf{y}}^T$ in Equations (13) and (14) with the Gaussian response kernel defined in Equation (15), vector a in regression setting is calculated as a sum of S inner products between two vectors:

$$\begin{array}{l}{\left(a\right)}_i={\langle {\widehat{K}}^{\left(i\right)},K_y\rangle }_F={\displaystyle \sum _{s=1}^S\langle {\mathit{\psi }}^{\left(s\right)}, w\rangle },\hfill \\ w={\displaystyle \sum _{q=1}^2{\displaystyle \sum _{r=1}^2\text{vec}}}\left(\left(Q_c^{\left(q\right)}{K}_c^{\left(i\right)}{Q}_c^{\left(r\right)}\right)Z\left(Q_d^{\left(q\right)}{K}_d^{\left(i\right)}{Q}_d^{\left(r\right)}\right)\right),\hfill \end{array}$$ (16)

where $\mathbf{Z}\in {ℝ}^{n_c\times n_d}$, $\text{vec}\left(\mathbf{Z}\right)={\mathit{\psi }}^{\left(s\right)}$ [$\mathbf{Z}$ is analogous to Y in Equations (13) and (14)]. We used S = 100 in our experiments.

Taken together, pairwiseMKL determines pairwise kernel mixture weights $\mathit{\mu }$ efficiently through (7) with the matrix M and vector a constructed by (12) and (16), respectively, without explicit calculation of massive pairwise matrices.

2.2.2 Stage 2: pairwise model training

Given pairwise kernel weights $\mathit{\mu }$, Equation (3) of pairwise KRR has the following form:

$$\left({\mu }_1{\mathbf{K}}_{\mathbf{d}}^{\left(1\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(1\right)}+,\dots ,+{\mu }_P{\mathbf{K}}_{\mathbf{d}}^{\left(P\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(P\right)}+\lambda \mathbf{I}\right)\mathit{\alpha }=\mathbf{y}.$$ (17)

Since the bioactivities of all combinations of drugs and cell lines might not be known, meaning that there might be missing values in the label matrix $\mathbf{Y}\in {ℝ}^{n_c\times n_d}$, $\text{vec}\left(\mathbf{Y}\right)=\mathbf{y}$, we further get

$$\begin{array}{c}\mathbf{U}\mathit{\alpha }=\mathbf{y},\\ \mathbf{U}=\mathbf{B}\left({\mu }_1{\mathbf{K}}_{\mathbf{d}}^{\left(1\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(1\right)}+,\dots ,+{\mu }_P{\mathbf{K}}_{\mathbf{d}}^{\left(P\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(P\right)}+\lambda \mathbf{I}\right){\mathbf{B}}^T,\end{array}$$ (18)

where B is an indexing matrix denoting the correspondences between the rows and columns of the kernel matrix and the elements of the vector $\mathit{\alpha }$: ${\mathbf{B}}_{i\ell }=1$ denotes that the coefficient α_i corresponds to the $\ell$th row/column in the kernel matrix. Training the model, i.e. finding the parameters $\mathit{\alpha }$ of the pairwise prediction function, is equivalent to solving the above system of linear equations (18). We solve the system with the conjugate gradient (CG) approach that iteratively improves the result by carrying out matrix-vector products between U and $\mathit{\alpha }$, which in general requires a number of iterations proportional to the number of data. However, in practise one usually obtains as good or even better predictive performance with only a few iterations. Restricting the number of iterations acts as an additional regularization mechanism known in the literature as early stopping (Engl et al, 1996).

We further accelerate the matrix-vector product $\mathbf{U}\mathit{\alpha }$ by taking advantage of the structural properties of the matrix U. In (Airola and Pahikkala, 2017), we introduced the generalized vec-trick algorithm that carries out matrix–vector multiplications between a principal submatrix of a Kronecker product of type $\mathbf{B}\left({\mathbf{K}}_{\mathbf{d}}^{\left(1\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(1\right)}\right){\mathbf{B}}^T$ and a vector $\mathit{\alpha }$ in $O(N{n}_d+N{n}_c)$ time, without explicit calculation of pairwise kernel matrices. Here, we extend the algorithm to work with sums of multiple pairwise kernels, i.e. to solve the system of equations (18). In particular, the matrix U is a sum of P submatrices of type $\mathbf{B}\left({\mathbf{K}}_{\mathbf{d}}^{\left(1\right)}\otimes {\mathbf{K}}_{\mathbf{c}}^{\left(1\right)}\right){\mathbf{B}}^T$, and hence each iteration of CG is carried out in $O(PN{n}_d+PN{n}_c)$ time (see Supplementary Material for pseudocode and more details).

In summary, our pairwiseMKL avoids explicit computation of any pairwise matrices in both stages of finding pairwise kernel weights and pairwise model training, which makes the method suitable for solving problems in large pairwise spaces, such as in case of drug bioactivity prediction (Table 1).

2.3 Dataset

2.3.1 Drug bioactivity data

Drug responses in cancer cell lines

In order to test our framework, we used anticancer drug response data from GDSC project initiated by Wellcome Trust Sanger Institute (release June 2014, Yang et al., 2012). Our dataset consists of 124 drugs and 124 human cancer cell lines, for which complete $124\times 124=15 376$ drug sensitivity measurements are available in the form of ln(IC₅₀) values in nanomolars (Ammad-ud-din et al., 2016).

Drug–protein binding affinities

In the second task of drug–protein binding affinity prediction, we used a comprehensive kinome-wide drug–target interaction map generated by Merget et al. (2017) from publicly available data sources, and further updated with the bioactivities from version 22 of ChEMBL database by Sorgenfrei et al. (2017). Since the original interaction map is extremely sparse, we selected drugs with at least 1% of measured bioactivity values across the kinase panel, and also kinases with kinase domain and ATP binding pocket amino acid sub-sequences available in PROSITE (Sigrist et al., 2013), resulting in 2967 drugs, 226 protein kinases, and 167 995 binding affinities between them in the form of −log₁₀(IC₅₀) values in molars.

We computed drug kernels, cell line kernels and protein kernels as described in the following sections and summarized in Figure 2c.

Fig. 2.

Pairwise kernel mixture weights obtained with pairwiseMKL and KronRLS-MKL (average across 10 outer CV folds) in the task of (a) drug response in cancer cell line prediction and (b) drug–protein binding affinity prediction (note: KronRLS-MKL did not execute with 1 TB memory); only the weights different from 0 are shown. KronRLS-MKL finds separate weights for drug kernels and cell line (protein) kernels instead of pairwise kernels. Numbers at the end of kernel names indicate the kernel hyperparameter values, in particular (i) kernel width hyperparameter in case of Gaussian kernels (e.g. Kc-cn-146 with ${\sigma }_c=146$), and (ii) maximum sub-string length L, σ₁ controlling for the shifting contribution term and σ₂ controlling for the amino acid similarity term in case of GS kernels (e.g. Kp-GS-atp-5-4-4 with $L=5,{\sigma }_1={\sigma }_2=4$, see Section 2.3.2 for details). (c) Summary of drug, cell line and protein kernels used in this work for the two prediction problems.

2.3.2 Kernels

Drug kernels

For drug compounds, we computed Tanimoto kernels using 10 different molecular fingerprints (Fig. 2c), i.e. binary vectors representing the presence or absence of different substructures in the molecule, obtained with rcdk R package (Guha, 2007): $k_d({\mathbf{x}}_{\mathbf{d}},\mathbf{x}{\prime }_{\mathbf{d}})=$$H_{x_d,x{\prime }_d}/(H_{x_d}+H_{x{\prime }_d}-H_{x_d,x{\prime }_d}),$ where $H_{x_d}$ is the number of 1-bits in the drug’s fingerprint ${\mathbf{x}}_{\mathbf{d}}$, and $H_{x_d,x{\prime }_d}$ indicates the number of 1-bits common to fingerprints of two drug molecules ${\mathbf{x}}_{\mathbf{d}}$ and $\mathbf{x}{\prime }_{\mathbf{d}}$ under comparison. The above Tanimoto similarity measure is a valid PSD kernel function (Gower, 1971).

Cell line kernels

For cell lines, we calculated Gaussian kernels $k_c({\mathbf{x}}_{\mathbf{c}},\mathbf{x}{\prime }_{\mathbf{c}})=$$=\text{exp}\hspace{0.17em}\left(-\left|\right|{\mathbf{x}}_{\mathbf{c}}-\mathbf{x}{\prime }_{\mathbf{c}}|{|}^2/2{\sigma }_c^2\right)$, where ${\mathbf{x}}_{\mathbf{c}}$ and $\mathbf{x}{\prime }_{\mathbf{c}}$ denote feature representation of two cell lines in the form of (i) gene expression signature, (ii) methylation pattern, (iii) copy number variation or (iv) somatic mutation profile (details given in Figure 2c and Supplementary Material); σ_c indicates a kernel width hyperparameter. We derived real-valued mutation profile feature vectors, instead of employing commonly used binary mutation indicators. In particular, each element $x_{c_i},\hspace{0.17em}i=1,\dots ,M$, corresponds to one of M mutations. If a cell line represented by ${\mathbf{x}}_{\mathbf{c}}$ has a negative ith mutation status, then $x_{c_i}=0$; otherwise, $x_{c_i}$ indicates a negative logarithm of the proportion of all cell lines with positive mutation status. This way, $x_{c_i}$ is high for a mutation specific to a cell line represented by ${\mathbf{x}}_{\mathbf{c}}$, giving more importance to such genetic variant.

Protein kernels

For proteins, we computed Gaussian kernels based on real-valued gene ontology (GO) annotation profiles, as well as Smith–Waterman (SW) kernels and generic string (GS) kernels based on three types of amino acid sequences: (i) full kinase sequences, (ii) kinase domain sub-sequences and (iii) ATP binding pocket sub-sequences (Fig. 2c).

Gaussian GO-based kernels were calculated separately for molecular function, biological process and cellular component domains as $k_p({\mathbf{x}}_{\mathbf{p}},\mathbf{x}{\prime }_{\mathbf{p}})=$$\text{exp}\hspace{0.17em}\left(-\left|\right|{\mathbf{x}}_{\mathbf{p}}-\mathbf{x}{\prime }_{\mathbf{p}}|{|}^2/2{\sigma }_p^2\right)$, where ${\mathbf{x}}_{\mathbf{p}}$ and $\mathbf{x}{\prime }_{\mathbf{p}}$ denote GO profiles of two protein kinases. Each element of the GO profile feature vector, $x_{p_i},\hspace{0.17em}i=1,\dots ,G$, corresponds to one of G GO terms from a given domain. If a kinase represented by ${\mathbf{x}}_{\mathbf{p}}$ is not annotated with term i, then $x_{p_i}=0$; otherwise, $x_{p_i}$ indicates a negative logarithm of the proportion of all proteins annotated with term i.

SW kernel measures similarity between amino acid sequences ${\mathbf{x}}_{\mathbf{p}}$ and $\mathbf{x}{\prime }_{\mathbf{p}}$ using normalized SW alignment score SW (Smith and Waterman, 1981): $k_p({\mathbf{x}}_{\mathbf{p}},\mathbf{x}{\prime }_{\mathbf{p}})=\text{SW}({\mathbf{x}}_{\mathbf{p}},\mathbf{x}{\prime }_{\mathbf{p}})/\sqrt{\text{SW}({\mathbf{x}}_{\mathbf{p}},{\mathbf{x}}_{\mathbf{p}})\text{SW}(\mathbf{x}{\prime }_{\mathbf{p}},\mathbf{x}{\prime }_{\mathbf{p}})}$. Although SW kernel is commonly used in drug–protein interaction prediction, it is not a valid PSD kernel function, and hence we examined all obtained matrices. The matrix corresponding to ATP binding pocket sub-sequences was not PSD, and therefore, we shrunk its off-diagonal entries until we reached the PSD property (126 shrinkage iterations with the shrinkage factor of 0.999 were needed for the matrix to become PSD). There are other ways of finding the nearest PSD matrix, e.g. by setting negative eigenvalues to 0, but we selected shrinkage since it smoothly modifies the whole spectrum of eigenvalues.

Finally, GS kernel compares each sub-string of ${\mathbf{x}}_{\mathbf{p}}$ of size $l\le L$ with each sub-string of $\mathbf{x}{\prime }_{\mathbf{p}}$ having the same length: $k_p({\mathbf{x}}_{\mathbf{p}},\mathbf{x}{\prime }_{\mathbf{p}})={\sum }_{l=1}^L{\sum }_{i=0}^{\left|{\mathbf{x}}_{\mathbf{p}}\right|-l}{\sum }_{j=0}^{\left|\mathbf{x}{\prime }_{\mathbf{p}}\right|-l}\hspace{0.17em}\text{exp}\hspace{0.17em}(-\frac{{(i-j)}^2}{2{\sigma }_1^{\mathrm{2}}})\text{exp}\hspace{0.17em}\left(-\frac{\left|\right|{\mathit{\xi }}^l-{\mathit{\xi }}^{\prime l}|{|}^2}{2{\sigma }_2^{\mathrm{2}}}\right)$, where vector ${\mathit{\xi }}^l$ contains properties of l amino acids included in the sub-string under comparison (Giguère et al., 2013). Each comparison results in a score that depends on the shifting contribution term (difference in the position of two sub-strings in ${\mathbf{x}}_{\mathbf{p}}$ and $\mathbf{x}{\prime }_{\mathbf{p}}$) controlled by σ₁, and the similarity of amino acids included in two sub-strings, controlled by σ₂. We used BLOSUM 50 matrix as amino acid descriptors in the GS kernel and in the SW sequence alignments.

We computed each Gaussian kernel with three different values of kernel width hyperparameter, determined by calculating pairwise distances between all data points, and then selecting 0.1, 0.5 and 0.9 quantiles. In case of each GS kernel, we selected the potential values for its three hyperparameters $L=\{5,10,15,20\},\hspace{0.17em}{\sigma }_1=\{0.1,1,2,3,4\}$ and ${\sigma }_2=\{0.1,1,2,3,4\}$ by ensuring that the resulting kernel matrices have a spectrum of different histograms of kernel values.

3 Results

To demonstrate the efficacy of pairwiseMKL for learning with multiple pairwise kernels, we tested the method in two related regression tasks of (i) prediction of anticancer efficacy of drug compounds and (ii) prediction of target profiles of anticancer drug compounds. In particular, we carried out a nested 10-fold cross validation (CV; 10 outer folds, 3 inner folds) using 15 376 drug responses in cancer cell lines and 167 995 drug–protein binding affinities, as well as chemical and genomic information sources in the form of kernels. We constructed a total of 120 pairwise drug–cell line kernels from 10 drug kernels and 12 cell line kernels, and 3120 pairwise drug–protein kernels from 10 drug kernels and 312 protein kernels (Fig. 2c).

We compared the performance of pairwiseMKL against the recently introduced algorithm for pairwise learning with multiple kernels KronRLS-MKL (Nascimento et al., 2016). Both are regularized least-squares models, but pairwiseMKL first determines the kernel weights, and then optimizes the model parameters, whereas KronRLS-MKL interleaves the optimization of the model parameters with the optimization of kernel weights. Although KronRLS-MKL was originally used for classification only, it is a regression algorithm in its core, and with few modifications to the implementation (see Supplementary Material), we applied it here to quantitative drug bioactivity prediction. We used the same CV folds for both methods to ensure their fair comparison. We also conducted elastic net regression with standard feature vectors instead of kernels (see Supplementary Material).

Unlike pairwiseMKL, KronRLS-MKL assumes that bioactivities of all combinations of drugs and cell lines (proteins) are known, i.e. it does not allow for missing values in the label matrix storing drug–cell line (drug–protein) bioactivities. Therefore, in the experiments with KronRLS-MKL, we mean-imputed the originally missing bioactivities, as well as bioactivities corresponding to drug–cell line (drug–protein) pairs in the test folds. We assessed the predictive power of the methods with root mean squared error (RMSE), Pearson correlation and F1 score between original and predicted bioactivity values.

We tuned the regularization hyperparameter λ of pairwiseMKL and regularization hyperparameters λ and σ of KronRLS-MKL within the nested CV from the set $\{{10}^{-5},{10}^{-4},\dots ,{10}^0\}$. Instead of tuning the kernel hyperparameters in this standard way, we constructed several kernels with different carefully selected hyperparameter values (see Section 2.3.2 for details).

3.1 Drug response in cancer cell line prediction

In the task of anticancer drug response prediction with 120 pairwise kernels, pairwiseMKL provided accurate predictions, especially for those drug–cell line pairs with more training data points (Fig. 3a). It outperformed KronRLS-MKL in terms of predictive power, running time and memory usage (Table 2 and Supplementary Fig. S2). In particular, pairwiseMKL was almost 6 times faster and used 68-times less memory. Even though both pairwiseMKL and KronRLS-MKL achieved high Pearson correlation of 0.858 and 0.849, respectively, the accuracy of predictions from KronRLS-MKL decreased gradually when going away from the mean value to the tails of the response distribution (Supplementary Fig. S2), as indicated by 13% increase in RMSE and 40% decrease in F1 score when comparing to pairwiseMKL (Table 2). These extreme responses are often the most important cases to predict in practice, as they correspond to sensitivity or resistance of cancer cells to a particular drug treatment.

Fig. 3.

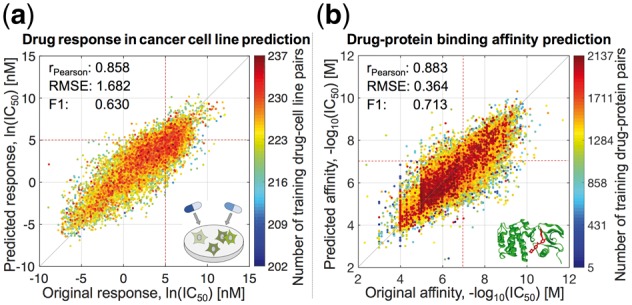
Prediction performance of pairwiseMKL in the tasks of (a) drug response in cancer cell line prediction and (b) drug–protein binding affinity prediction. Scatter plots between original and predicted bioactivity values across (a) 15 376 drug–cell line pairs and (b) 167 995 drug–protein pairs. Performance measures were averaged over 10 outer CV folds. F1 score was calculated using the threshold of (a) ln(IC₅₀) = 5 nM, (b) −log₁₀(IC₅₀) = 7 M, both corresponding to low drug concentration of roughly 100 nM, i.e. relatively stringent potency threshold (red dotted lines). Color coding indicates the number of training data points, i.e. drug–cell line (respectively drug–protein) pairs including the same drug or cell line (drug or protein) as the test data point.

Table 2.

Prediction performance, memory usage and running time of pairwiseMKL and KronRLS-MKL methods in the task of drug response in cancer cell line prediction.

Anticancer drug response prediction	RMSE	rPearson	F1 score	Memory (GB)	Time (h)
pairwiseMKL	1.682	0.858	0.630	0.057	1.45
KronRLS-MKL	1.899	0.849	0.378	3.890	8.42

Performance measures were averaged over 10 outer CV folds. F1 score was calculated using the threshold of ln(IC₅₀) = 5 nM.

Importantly, pairwiseMKL returned a sparse combination of only 11 out of 120 input pairwise kernels, whereas all kernel weights from KronRLS-MKL are nearly uniformly distributed (Fig. 2a). The final model generated by pairwiseMKL is much simpler due to fewer active kernels, and can therefore inform about the predictive power of different chemical and genomic data sources. Figure 2a shows that the pairwise kernel calculated using gene expression in cancer cell lines and molecular fingerprint defined by Klekota and Roth (2008) carries the greatest weight in the model. Klekota-Roth fingerprint is the longest among the considered ones, consisting of 4860 bits representing different substructures in the chemical compound, and gene expression profiles have previously been reported as most predictive of anticancer drug efficacy (Costello et al., 2014). Other fingerprints identified by pairwiseMKL as relevant for drug response inference include information on Estate substructures (Hall and Kier, 1995), connectivity and shortest paths between compound’s atoms. Among the cell line kernels, the ones calculated using genetic mutation and methylation patterns, in addition to gene expression, paired with the above-mentioned fingerprint-based drug kernels, were selected for the construction of the optimal pairwise kernel. Those information sources can therefore be considered as complementing each other. The copy number variation data did not prove effective in the prediction of anticancer drug responses.

3.2 Drug–protein binding affinity prediction

In the larger experiment of prediction of target profiles of almost 3000 anticancer drug compounds, pairwiseMKL achieved again high predictive performance (Pearson correlation of 0.883, RMSE of 0.364, F1 score of 0.713; Fig. 3b). Notably, our method constructed the final model using only 8 out of 3120 pairwise kernels (Fig. 2b). KronRLS-MKL did not execute given 1 TB memory, whereas pairwiseMKL required just a fraction of that memory (2.21 GB).

pairwiseMKL assigned the highest weights to two pairwise kernels build upon amino acid sub-sequences of ATP binding pockets, together with either shortest path fingerprints or extended connectivity fingerprints. A relatively high weight was given also to the pairwise kernel constructed from Klekota-Roth fingerprints and sub-sequences of kinase domains. In fact, kinase domain sequences include short sequences of ATP binding pockets, and capture also their neighboring context. In all of the above selected pairwise kernels, protein sequences were compared using GS kernel. Our results therefore suggest that ATP binding pockets are more informative than full amino acid sequences, and that GS kernel is more powerful in capturing similarities between amino acid sequences than a commonly used protein kernel based on SW amino acid sequence alignments, at least for the prediction of drug interactions with protein kinases investigated. Finally, gene ontology profiles of proteins, in particular those from biological process and cellular component domains, provided also a modest contribution to the optimal pairwise kernel used for drug–protein binding affinity prediction (Fig. 2b).

3.3 Kernel hyperparameters tuning

Our results demonstrate that pairwiseMKL provides also a useful tool for tuning the kernel hyperparameters. In particular, we constructed each kernel with different hyperparameter values from a carefully chosen range (see Section 2.3.2 for details), and the algorithm then selected the optimal hyperparameters by assigning non-zero mixture weights to corresponding kernels (Fig. 2). Notably, pairwiseMKL always picked a single value for the Gaussian kernel width hyperparameter, σ_c in case of cell line kernels and σ_p in case of protein kernels. This is well-represented in Figure 2a where, for each cell line data source, the weights are different from zero only in one of the three rows of the heatmap. Furthermore, pairwiseMKL selected also only a single out of 100 combinations of three values of the hyperparameters (L,σ₁,σ₂) for the GS kernel (Fig. 2b).

4 Discussion

The enormous size of the chemical universe, estimated to consist of up to 10²⁴ molecules displaying good pharmacological properties (Reymond and Awale, 2012), makes the experimental bioactivity profiling of the full drug-like compound space infeasible in practice, and therefore calls for efficient in silico approaches that could aid various stages of drug development process and identification of optimal therapeutic strategies (Azuaje, 2017; Cheng et al., 2012; Cichonska et al., 2015). Especially kernel-based methods have proved good performance in many applications, including inference of drug responses in cancer cell lines (Costello et al., 2014) and elucidation of drug MoA through drug–protein binding affinity predictions (Cichonska et al., 2017). Pairwise learning is a natural approach for solving such problems involving pairs of objects, and the benefits from integrating multiple chemical and genomic information sources into clinically actionable prediction models are well-reported in the recent literature (Cheng and Zhao, 2014; Costello et al., 2014; Ebrahim et al., 2016).

To tackle the computational limitations of the current MKL approaches, we introduced here pairwiseMKL, a new framework for time- and memory-efficient learning with multiple pairwise kernels. pairwiseMKL is well-suited for massive pairwise spaces, owing to our novel, highly efficient formulation of Kronecker decomposition of the centering operator for the pairwise kernel, and a fast method for training a regularized least-squares model with a weighted combination of multiple kernels. To illustrate our approach, we applied pairwiseMKL to two important problems in computational drug discovery: (i) the inference of anticancer potential of drug compounds and (ii) the inference of drug–protein interactions using up to 167 995 bioactivities and 3120 kernels.

pairwiseMKL integrates heterogeneous data types into a single model which is a sparse combination of input kernels, thus allowing to characterize the predictive power of different information sources and data representations by analyzing learned kernel mixture weights. For instance, our results demonstrate that among the genomic views, gene expression, followed by genetic mutation and methylation patterns contributed mostly to the final pairwise kernel adopted for anticancer drug response prediction (Fig. 2a). Although methylation plays an essential role in the regulation of gene expression, typically repressing the gene transcription, the association between these two processes remains incompletely understood (Wagner et al., 2014). Therefore, it can be hypothesized that these genomic and epigenetic information levels are indeed complementing each other in the task of drug response modeling.

In case of prediction of target profiles of anticancer drugs, we observed the highest contribution to the final pairwise model from Tanimoto drug kernels, coupled with GS protein kernels applied to ATP binding pockets (Fig. 2b). This could be explained by the fact that majority of anticancer drugs, including those considered in this work, are kinase inhibitors designed to bind to ATP binding pockets of protein kinases, and therefore constructing kernels from short sequences of these pockets is more meaningful in the context of drug-kinase binding affinity prediction compared to using full protein sequences. Moreover, GS kernel is more advanced than the commonly used SW kernel as it compares protein sequences including properties of amino acids. GS kernel also enables to match short sub-sequences of two proteins even if their positions in the input sequences differ notably. In both prediction problems, pairwiseMKL was able to tune kernel hyperparameters by selecting a single kernel out of several kernels with different hyperparameter values (Fig. 2). It has been noted by Cortes et al. (2012) in the context of ALIGNF algorithm that sparse kernel weight vector is a consequence of the constraint $\mathit{\mu }\ge 0$ in the kernel alignment maximization (Equation 6). This has been observed empirically in other works as well (e.g. Brouard et al., 2016; Shen et al., 2014). In particular, it appears that pairwiseMKL and ALIGNF, given a set of closely related kernels, such as those calculated using the same data source and kernel function but different hyperparameters, tend to select a representative kernel for the group to the optimized kernel mixture.

We compared the performance of pairwiseMKL to recently introduced method for pairwise learning with multiple kernels KronRLS-MKL. pairwiseMKL outperformed KronRLS-MKL in terms of predictive power, running time and memory usage (Table 2 and Supplementary Fig. S2). Unlike pairwiseMKL, KronRLS-MKL does not consider optimizing pairwise kernel weights, i.e. it finds separate weights for drug kernels and cell line (protein) kernels (Fig. 2a), and therefore it does not fully exploit the information contained in the pairwise space. The reduced predictive performance of KronRLS-MKL can be also attributed to the fact that it does not allow for any missing values in the label matrix storing bioactivities between drugs and cell lines (proteins), which need to be imputed as a pre-processing step and included in the model training. KronRLS-MKL has two regularization hyperparameters that need to be tuned, hence lengthening the training time. Furthermore, determining the parameters of the pairwise prediction function involves a computation of large matrices, which requires significant amount of memory that grows quickly with the number of drugs and cell lines (proteins). Finally, KronRLS-MKL applies L2 regularization on the kernel weights, thus not enforcing sparse kernel selection. In fact, KronRLS-MKL returned a nearly uniform combination of input kernels, not allowing for the interpretation of the predictive power of different data sources.

We tested pairwiseMKL using CV on the level of drug–cell line (drug–protein) pairs which corresponds to evaluating the performance of the method in the task of filling experimental gaps in bioactivity profiling studies. However, pairwiseMKL could also be applied, e.g. to the inference of anticancer potential of a new candidate drug compound or prediction of sensitivity of a new cell line to a set of drugs. We plan to tackle these important problems in the future work.

In this work, we put an emphasis on the regression task, since drug bioactivity measurements have a real-valued nature, but we also implemented an analogous method for solving the classification problems with support vector machine. Other potential applications of our efficient Kronecker decomposition of the centering operator for the pairwise kernel include methods which involve kernel centering in the pairwise space, such as pairwise kernel PCA. Finally, even though we focused here on the problems of anticancer drug response prediction and drug–target interaction prediction, pairwiseMKL has wide applications outside this field, such as in the inference of protein–protein interactions, binding affinities between proteins and peptides or mRNAs and miRNAs.