A graph-based approach to diploid genome assembly

Abstract

Motivation

Constructing high-quality haplotype-resolved de novo assemblies of diploid genomes is important for revealing the full extent of structural variation and its role in health and disease. Current assembly approaches often collapse the two sequences into one haploid consensus sequence and, therefore, fail to capture the diploid nature of the organism under study. Thus, building an assembler capable of producing accurate and complete diploid assemblies, while being resource-efficient with respect to sequencing costs, is a key challenge to be addressed by the bioinformatics community.

Results

We present a novel graph-based approach to diploid assembly, which combines accurate Illumina data and long-read Pacific Biosciences (PacBio) data. We demonstrate the effectiveness of our method on a pseudo-diploid yeast genome and show that we require as little as 50× coverage Illumina data and 10× PacBio data to generate accurate and complete assemblies. Additionally, we show that our approach has the ability to detect and phase structural variants.

Availability and implementation

https://github.com/whatshap/whatshap

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

There are two homologous copies of every chromosome, one from each parent, in human and other diploid eukaryotic genomes. Determining the two genome sequences of those organisms per chromosome is important in order to correctly understand allele-specific expression and compound heterozygosity, and in order to carry out many analyses in the genetics of common diseases and in population genetics (Glusman et al., 2014; Tewhey et al., 2011). Furthermore, separate determination of the two haplotype sequences can in principle avoid genotyping errors in complex regions of the genome caused by simplistic models that treat variants at nearby sites as being independent.

The process of assembling two distinct genome sequences from sequencing reads in a haplotype-aware manner is known as diploid or haplotype-aware genome assembly and the assembled sequences are known as ‘haplotigs’. However, next generation sequencing (NGS) reads are generally of short length and contain errors; therefore, solving the diploid genome assembly problem is fundamentally challenging. Additional challenges inherent in the genome assembly problem include dealing with short and long genomic repeats, handling general rearrangements present in the genome, and scaling efficiently with input size, genome size and hardware availability.

Over the last decade, the development of various NGS technologies has impacted the assembly problem. In theory, the problem of de novo assembly—computing the consensus of two or more sequences—is NP-hard, when the problem is modeled either with string graphs or with de Bruijn graphs (Medvedev et al., 2007). In the past decades, a multitude of heuristic approaches to haploid de novo assembly have been proposed (Idury and Waterman, 1995; Myers, 1995, 2005; Nagarajan and Pop, 2009, 2013; Pevzner et al., 2001; Sović et al., 2013).

However, even with Sanger (reads of the order of 800–1000 base pairs) and Illumina sequencing, which deliver short reads with low error rates, assembly of heterozygous diploid genomes has been a difficult problem (Levy et al., 2007; Vinson et al., 2005). In practice, there are several short-read assemblers based on Illumina data for heterozygous genomes (Bankevich et al., 2012; Li, 2015b; Kajitani et al., 2014; Pryszcz and Gabaldón, 2016; Simpson and Durbin, 2012). The assemblies that they produce are accurate, but contain gaps and are composed of relatively short contigs and scaffolds. Third generation sequencing technologies such as methods available from Pacific Biosciences (PacBio) and Oxford Nanopore Technologies (ONT) deliver much longer reads, but with high error rates. There are now several long-read assemblers (Berlin et al., 2015; Chin et al., 2013; Hunt et al., 2015; Koren et al., 2017; Lin et al., 2016; Vaser et al., 2017; Xiao et al., 2016) that use these long-read data for de novo assembly. The assemblies that are delivered from these assemblers are more contiguous, with longer contigs and scaffolds. Finally, there are hybrid assemblers that take advantage of long-read data (with its high error rate) and short-read data (with its low error rate) (Antipov et al., 2016; Bashir et al., 2012; Zimin et al., 2017) and attempt to combine the best aspects of both. These hybrid assemblers have the potential to deliver highly accurate, repeat-resolved assemblies.

However, across the short, long and hybrid categories, most assemblers require collapsing the two genome sequences of a diploid sample into a single haploid ‘consensus’ sequence (or primary contig). The consensus sequence is obtained by merging the distinct alleles at regions of heterozygosity into a single allele, and therefore losing a lot of information. The resulting haploid de novo assembly does not represent the true characteristics of the diploid input genome.

Current approaches to reconstruct diploid genomes usually rely on collapsing assembly graphs to haploid contigs in intermediate steps (contig-based assembly) (Chin et al., 2016; Mostovoy et al., 2016; Pendleton et al., 2015; Seo et al., 2016), or on using a reference genome to partition the reads by haplotype (reference-guided assembly) (Chaisson et al., 2017b; Glusman et al., 2014; Martin et al., 2016). In both types of approaches, the reads are first aligned (either to the reference genome or the contigs). Second, variants such as SNVs are called based on the aligned reads. Finally, the detected variants are phased using long reads from either the same or a different sequencing technology. Because these methods represent the genome with haploid sequences in some processing steps, we refer to them as linear approaches.

For both reference-guided and contig-based assembly, this third step—solving the phasing problem—has been formulated as the minimum error correction (MEC) optimization problem (Cilibrasi et al., 2007; Lippert et al., 2002). The reviews by Rhee et al. (2016) and Klau and Marschall (2017) provide introductions to this formulation. There are several disadvantages to reference-guided assembly; for example, the reads are initially aligned to the reference genome and therefore the process contains reference bias. Also, this approach can fail to detect sequences or large structural variants (SVs) that are unique to the genome being assembled.

However, there are also several reasons why the set of sequences/contigs produced by contig-based assembly is not ideal. First, the contigs produced by haploid assemblers ignore the heterozygous variants in complex regions, opting instead to break contiguity to express even moderate complexity. Second, the contigs do not capture end-to-end information in the genome; the ordering or relationships between contigs are critical in order to generate end-to-end chromosomal-length assemblies.

One example of a newer diploid assembly method is Weisenfeld et al. (2017), where 10× genomics-linked read data is used to determine the actual diploid genome sequence. Their approach is based on de Bruijn graphs and applies a series of graph simplifications, where simple bubbles are detected and phased by using (short) reads that stem from the same (long) input molecule, which is determined through barcoding. There is also a recent study by Chin et al. (2016), who follow a linear phasing approach to generate diploid assemblies (haplotigs) for diploid genomes by using PacBio reads.

1.1 Contributions

We propose a graph-based approach for generating haplotype-aware assemblies of single individuals. Our contribution is two-fold. First, we propose a hybrid approach, integrating accurate Illumina and long PacBio reads in order to generate diploid assemblies. The Illumina reads are used to generate an assembly graph that serves as a backbone for subsequent PacBio-based steps. Second, we generalize the diploid assembly problem to encompass constructing the diploid assembly directly from the underlying assembly graph and thereby avoid ‘flattening’ the assemblies to linear sequences at any time. The two haplotype sequences can be seen as two paths over the regions of heterozygosity in the assembly graph.

Phasing using an assembly graph has several advantages over linear approaches. In particular, it allows us to represent and phase heterozygous SVs, which are represented by bubbles in the assembly graph. A bubble is defined as a set of disjoint paths that share the same start and end nodes. Figure 1 illustrates how such bubbles can represent both small variants (which we define as SNVs and indels up to 50 base pairs in length) and larger SVs. Handling small variants and SVs in a unified way facilitates phasing larger blocks because haplotype reconstruction is not disrupted by SVs. Figure 2 illustrates this conceptual advantage. The figure shows four SNVs separated by two large SVs, and six reads spanning these variants. Out of those reads, the two reads r₃ and r₄ span the two SVs, but do not cover any of the two SNVs. Conversely, the reads which cover the SNVs on either side do not cover the SVs. In this case, Falcon Unzip generates a primary contig that spans from one end to the other, but generates incomplete and fragmented haplotigs (phased primary contigs in the language of Falcon Unzip) covering only the SNVs. In contrast, our graph-based approach attempts to phase across all types of variation, including SVs.

Fig. 1.

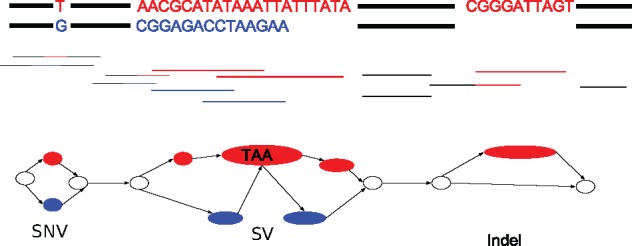
Based on reads (middle) from the two sequences (top), the bubbles in the graph (bottom) show three different heterozygous variants; the first one is an SNV, the second one is an SV, and the third one is an indel

Fig. 2.

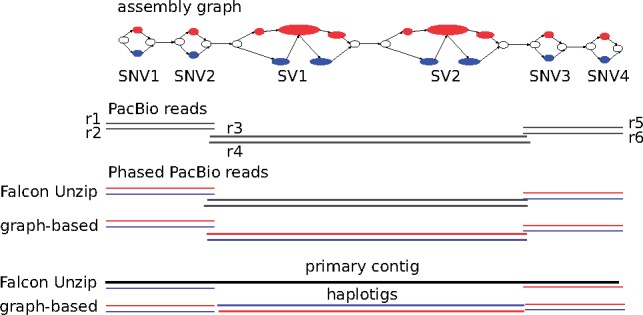
Input: an assembly graph (top) (consisting of four SNVs and two SVs) and the PacBio reads $r_1,r_2,r_3,r_4,r_5,r_6$ (gray). Output: the phased reads (colored in blue and red) and haplotigs (bottom) using Falcon Unzip and our approach. Our graph-based approach also phases the central region. Contrarily, Falcon Unzip does not phase it, and so the region does not contribute to the total haplotig size

We demonstrate the feasibility of our approach by performing a haplotype-aware de novo assembly of a whole pseudo-diploid yeast (SK1 + Y12) genome. We show that we generate more accurate and more contiguous phased diploid genomes compared to Falcon Unzip. Through empirical testing with different input coverage levels, we demonstrate that we require only 50× short-read coverage and as little as 10× long-read coverage data to generate diploid assemblies. This illustrates that our hybrid strategy is a cost-effective way of generating haplotype-resolved assemblies. Finally, we show that we successfully detect and phase large SVs.

2 Diploid assembly pipeline

Our assembly workflow uses short read (e.g. Illumina) and long read (e.g. PacBio) data in combination, as illustrated in Figure 3. We describe the details of this process below.

Fig. 3.

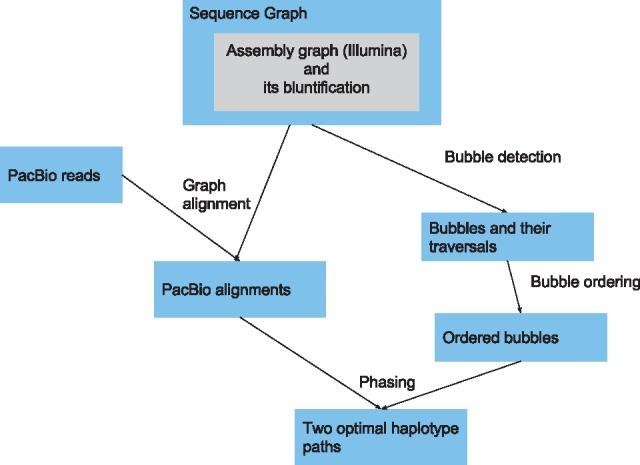
Overview of the diploid assembly pipeline

2.1 Sequence graph

Our first step is to construct a sequence graph using short read data with a low error rate, as provided by the Illumina platform.

Definition 1 (Sequence graph). We define a sequence graph $G_s(N_s,E_s)$ as a bidirected graph, consisting of a set of nodes N_s and a set of edges E_s. The nodes n_i are sequences over an alphabet $\mathcal{A}=\{A,C,G,T\}$. For each node $n_i\in N_s$, its reverse-complement is denoted by $n{\prime }_i$. An edge $e_{i\prime j}$ connects the nodes $n{\prime }_i$ to n_j. Nodes may be traversed in either the forward or reverse direction, with the sequence being reverse-complemented in the reverse direction.

In words, edges represent adjacencies between the sequences of the nodes they connect. Thus, the graph implicitly encodes longer sequences as the concatenated sequences of the nodes along walks through the graph.

To illustrate this, we consider an example sequence graph G_s in Figure 4. It consists of a node set $N_s=\{1,1\prime ,2,2\prime ,3,3\prime ,\dots \}$ and an edge set $E_s=\{1\to 2,1\to 3\prime \dots \}$.

Fig. 4.

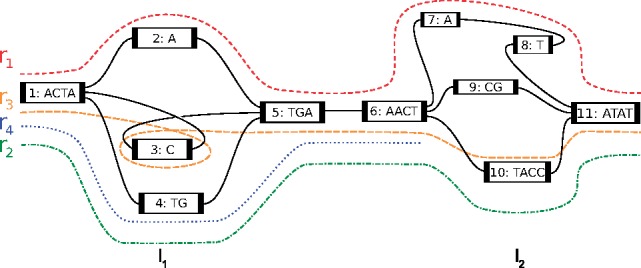
For a subgraph of G_s, the example shows two bubbles l₁ and l₂, and their corresponding alleles. Reads $r_1,r_2,r_3,r_4$ traverse these bubbles

To generate the sequence graph G_s, we first employ SPAdes (Bankevich et al., 2012), which constructs and simplifies a de Bruijn graph, and we subsequently remove the overlaps between the nodes in the resulting graph in a process we call bluntification, explained in the Supplementary Material.

2.2 Bubble detection in sequence graphs

To account for heterozygosity in a diploid genome, we perform bubble detection. The notion of bubble we use is closely based on the ultrabubble concept as defined by Paten et al. (2017). Briefly, bubbles have the following properties:

• Two-node-connectivity. A bubble is bounded by fixed start and end nodes. Removing both the start and end nodes disconnects the bubble from the rest of the graph. Note that a bubble can be viewed in either orientation. If the graph is traversed in one direction, and a bubble is encountered that starts at a node n_i and ends at a node $n{\prime }_j$, then that bubble can also be described as the bubble with start node n_j and end node $n{\prime }_i$, as it would be encountered when traversing the graph in the opposite direction.

• Directed acyclicity. A bubble is directed and acyclic.

• Directionality. All paths through the bubble flow from start to end.

• Minimality. No vertex in the bubble other than the start node n_i (with proper orientation) forms a pair with the end node $n{\prime }_j$ (with proper orientation) that satisfies the above properties. Similarly, no vertex in the bubble other than $n{\prime }_j$ forms such a pair with n_i.

A bubble can represent a potential sequencing error or genetic variation within a set of homologous molecules. We represent bubbles as collections of alternative paths.

Definition 2 (Path). We define path a_i as a linear ordering of nodes $a_i=n_1,\dots n_m$.

A bubble is a collection of paths with the same start and end node and can be defined as follows:

Definition 3 (Bubble). Formally, a bubble is represented as a collection of allele paths $l_k=\{a_1,a_2\dots \}$ where

$a_1=(n_1,n_2,\dots n_m),a_2=(n_1,n_3\dots n_m)$ and so on.

For example, Figure 4 shows a set of two bubbles $L=\{l_1,l_2\}$, and the set of allele paths for the bubble l₂ is $\{a_1,a_2,a_3\}$, where $a_1=(6,7,8\prime ,11),\hspace{0.17em}{a}_2=(6,9,11),\hspace{0.17em}{a}_3=(6,10,11)$.

2.3 PacBio alignments

For phasing bubbles, we consider long reads from third generation sequence technologies such as PacBio. We align these long reads to the sequence graph G_s to generate paths through the graph. We perform graph alignment using a banded version of the algorithm described by Rautiainen and Marschall (2017), which is a generalization of semi-global alignment to sequence-to-graph alignment (https://github.com/maickrau/GraphAligner).

There are several advantages of aligning PacBio reads to graphs instead of to a reference genome or contigs. SNPs often occur near larger variants such as insertions and deletions. SNPs are thus often missed in these regions when reads contain large mismatches with respect to the linear sequences they are aligned against. Graph alignment allows the alignment of reads to variants appropriate to each read’s phase, and to other types of complex events.

Definition 4 (Alignment). We define a set of read alignments as $R=\{r_1,r_2,\dots ,r_j\}$, where each read alignment r_j is given by a path of oriented nodes in graph G_s, written $r_j=(n_1,\dots ,n_m)$.

For example, in Figure 4, $R=\{r_1,r_2,r_3,r_4\}$ and the read alignment path r₁ can be written as $r_1=(1,2,5,6,7,8\prime ,11)$

2.4 Bubble ordering

The next stage of our algorithm is to obtain an ordering of the bubbles $L=(l_1,l_2,\dots l_k)$, which we refer to as a bubble chain. For example, in Figure 4, $L=(l_1,l_2)$ is a bubble chain. A general sequence graph G_s is cyclic, due to different types of repeats present in the genome that create both short and long cycles. Ordering bubbles in such a graph is closely related to resolving repeats, which is a challenging problem. In this study, we rely on the Canu algorithm (Koren et al., 2017) to provide a bubble ordering by aligning Canu-generated contigs to our sequence graph. Furthermore, we detect repetitive bubbles—that is, bubbles that would need to be traversed more than once in a final assembly—based on the depth of coverage of aligned PacBio reads, and remove such bubbles. We deem a bubble repetitive if the number of PacBio reads aligned to its starting node is greater than a coverage threshold specified by the user over the genome. For example, given a 30× ($=c$) dataset and a repeat that occurs 20 ($=r$) times in the genome, then the coverage at the bubble on average is 600 ($=r·c$).

2.5 Graph-based phasing

Given a sequence graph G_s, ordered bubbles L, and PacBio alignments R, the goal is to reconstruct two haplotype sequences $\{h_0,h_1\}$, called haplotigs, along each chain of bubbles.

Definition 5 (Haplotype path). Formally, a pair of haplotype paths (h₀, h₁) can be defined as two paths through a bubble chain in the sequence graph and denoted as:

$$\begin{array}{c}{h}_0=(n_s,n_2,\dots n_e)\\ h_1=(n_s,n_3,\dots n_e)\end{array}$$

where h₀ and h₁ may differ at the heterozygous regions defined by bubbles, and n_s and n_e are the start and end of the bubble chain.

The two genome sequences can be seen as two walks through the bubbles L in the sequence graph G_s that are consistent with the PacBio alignments R. In maximum likelihood terminology, the goal is to find the most likely haplotype paths given the alignment paths traversing through the bubbles. For example, in Figure 4, given bubbles (l₁, l₂) and PacBio alignments $R=\{r_1,r_2,r_3,r_4\}$, the goal is to find two maximum likelihood haplotype paths $\{h_0,h_1\}$ such that each PacBio alignment is assigned to one of the haplotypes.

For a linear chain of bubbles L, the task of finding these two haplotype paths is equivalent to picking one allele path per haplotype for each bubble. To this end, we note that an alignment path r_j for a given read can be viewed as a sequence of allele paths traversed in consecutive bubbles. We represent this association of reads to allele paths in the form of a bubble matrix$\mathcal{F}\in {\{0,1,\dots m,-\}}^{\left|R\right|\times \left|L\right|}$, where $\left|R\right|$ is the number of reads, $\left|L\right|$ is the number of bubbles along a chromosome, and $m={\max }_k\left|l_k\right|$ is the maximum number of paths (or alleles) in any bubble $l_k\in L$. The entry $\mathcal{F}(j,k)\in \{0,1,\dots m,-\}$ represents the allele path index in bubble l_k that read r_j is aligned to, where a value of ‘–’ indicates that the read does not cover the bubble. In Figure 4, note that the read alignment path r₄ does not cover all the nodes in any of the allele paths in l₂ and hence we set the corresponding value $\mathcal{F}(4,2)$ to ‘–’. As a result, this read covers only one bubble, which renders it uninformative for phasing, and we do not consider it further. The remaining phasing-informative reads in Figure 4 are represented as:

$$\mathcal{F}=\begin{array}{ccc}& \hspace{1em}\begin{array}{ccc}\hfill & l_1\hfill & l_2\hfill \end{array}& \\ & \begin{array}{c}{r}_1\hfill \\ r_2\hfill \\ r_3\hfill \end{array}\left(\begin{array}{cc}0\hfill & 0\hfill \\ 2\hfill & 2\hfill \\ 1\hfill & 2\hfill \end{array}\right)& \end{array}$$ (1)

Corresponding to $\mathcal{F}$, we have a weight matrix $\mathcal{W}\in W^{\left|R\right|\times \left|L\right|\times m}$. Each entry in $\mathcal{W}(j,k)$ is a tuple storing a weight for each allele, which can for instance reflect ‘phred-scaled’ (i.e. $-10\hspace{0.17em}\text{log}\hspace{0.17em}\left(p\right)$) probabilities that the read supports a given allele. The weight of ‘0’ at the i-th entry in the tuple $\mathcal{W}(j,k)$ encodes that the read r_j is aligned to allele path index i in bubble l_k. The remaining non-zero values in tuple $\mathcal{W}(j,k)$ store the confidence scores of switching the aligned read r_j to other alleles in bubble l_k.

For example, the corresponding weight matrix $\mathcal{W}(j,k)$ for $\mathcal{F}$ (1) is given by:

$$\mathcal{W}=\begin{array}{ccc}& \hspace{1em}\begin{array}{ccccc}{l}_1\hfill & \hfill & \hfill & \hfill & l_2\hfill \end{array}& \\ & \begin{array}{c}{r}_1\hfill \\ r_2\hfill \\ r_3\hfill \end{array}\left(\begin{array}{cc}[0,q_1,q_2]\hfill & [0,q_3,q_4]\hfill \\ [q_9,q_8,0]\hfill & [q_{11},q_5,0]\hfill \\ [q_{10},0,q_7]\hfill & [q_5,q_6,0]\hfill \end{array}\right)& \end{array}$$ (2)

where the entry $\mathcal{W}(1,1)$ value $[0,q_1,q_2]$ means that the read r₀ is aligned to allele a₀ at bubble l₁. Additionally, the cost of flipping it to other alleles is q₁ for a₁ and q₂ for a₂.

We are now ready to present the problem formulation. The main insight is that solving phasing for bubble chains is similar to solving the phasing problem for multi-allelic SNVs in reference-based haplotype reconstruction. Therefore, we build on the previous formulation of the MEC problem (Lancia et al., 2001) and its weighted version (wMEC) (Lippert et al., 2002; Patterson et al., 2014) and further adapt it to work on a subgraph consisting of a chain of bubbles, defining the Minimum Error Correction for graphs (gMEC) problem.

Problem 1 (wMEC for bubble chains (gMEC)). Assume we are given a bubble chain $L=(l_1,\dots ,l_{\left|L\right|})$ and a set R of aligned reads r_j that pass through these bubbles, with $\mathcal{F}(j,k)$ indicating the index of the allele in bubble l_k that the alignment of read r_j passes through, or ‘–’ if it does not pass through l_k, and that $\mathcal{W}(j,k,i)$ is the cost of flipping $\mathcal{F}(j,k)$ to new value i. We want to find two paths through L, each of which consists of a sequence of allele indices specifying which allele the path takes in each bubble l_k, and then to flip entries of $\mathcal{F}$ such that each row is equal to one of the paths for all non-dash entries while the incurred costs are minimized.

Note that the wMEC problem constitutes a special case of gMEC, where the input graph is a chain of bi-allelic bubbles. Next, we describe how to solve gMEC via dynamic programming (DP).

In the WhatsHap algorithm (Patterson et al., 2014), wMEC is solved in an exact manner for bi-allelic variants using a dynamic programing approach. It runs in $\mathcal{O}(2^c·|L\left|\right)$ time, where $\left|L\right|$ is the number of variants to be phased and c is the maximum physical coverage. The basic idea is to proceed column-wise from left to right over a set of active reads. Each read remains active from its first non-dash position to its last non-dash position in $\mathcal{F}$. In column k, we denote the set of active reads as A(k), particularly, $c={\max }_k\left\{\right|A\left(k\right)\left|\right\}$. The algorithm now considers all bipartitions of A(k), that is, all pairs $B=(P,Q)$ of disjoint sets P and Q such that $P\cup Q=A\left(k\right)$. We fill a DP table column wise and for each column k of $\mathcal{F}$, we fill a DP table column $C(k,·)$ with $2^{\left|A\right(k\left)\right|}$ entries corresponding to these bipartitions of A(k). Each entry C(k, B) is equal to the cost of solving wMEC on the partial matrix consisting of columns 1 to k of $\mathcal{F}$ such that the bipartition of the full read set $A\left(1\right)\cup \dots \cup A\left(k\right)$extends B according to the below definition.

Definition 6 (Bipartition extension). For a given set A and a subset$A\prime \subset A$, a bipartition$B=(P,Q)$of A is said to extend a bipartition$B\prime =(P\prime ,Q\prime )$of$A\prime$if$P\prime \subset P$and$Q\prime \subset Q$.

Once all entries of the DP table have been computed, the minimum of the last column ${\min }_B\left\{C\right(\left|L\right|,B\left)\right\}$ indicates the optimal wMEC cost and the optimal bipartition can be obtained by backtracing. We refer the reader to Patterson et al. (2014) for a more detailed explanation of this algorithm.

Solving gMEC for bubble chains

The basic idea is to now extend the dynamic program to consider all possible path-pairs through each bubble. In the bi-allelic case, we have only two paths in every bubble and, therefore, there is only one pair of distinct paths. In the multi-allelic case, we consider all possible path pairs in each bubble. The goal is to find an optimal pair of paths from the sequence graph G_s. Analogously to the WhatsHap algorithm for wMEC, we proceed from left to right using dynamic programming.

To explain the dynamic programming algorithm that we use, consider a toy example with the weight matrix (2):

$$\mathcal{W}=\begin{array}{ccc}& \hspace{1em}\begin{array}{ccccc}\hfill & l_1\hfill & \hfill & \hfill & \hspace{1em}{l}_2\hfill \end{array}& \\ & \begin{array}{c}{r}_1\hfill \\ r_2\hfill \\ r_3\hfill \end{array}\left(\begin{array}{cc}[0,10,5]\hfill & [0,5,8]\hfill \\ [7,6,0]\hfill & [5,2,0]\hfill \\ [2,0,4]\hfill & [4,3,0]\hfill \end{array}\right)& \end{array}$$ (3)

DP cell initialization

Along similar lines as Patterson et al. (2014), we first compute the local cost incurred by bipartition $B=(R,S)$ in column k, denoted ${\Delta }_C(k,B)$, and later combine it with the corresponding costs incurred in previous columns. The cost $W_{k,R}^i$ of flipping all entries in a read set R to an allele index $i\in \{0,1,\dots |l_k\left|\right\}$ is given by

$$W_{k,R}^i=\sum _{j\in R}\left[\right[\mathcal{F}(j,k)\ne i\left]\right]·\mathcal{W}(j,k,i),$$

In the same manner, we can compute costs $W_{k,S}^i$ for read set S to an allele index i.

To compute the cost incurred by a bipartition in a particular column k, we minimize over all possible pairs of alleles in bubble l_k. There are $\left(\begin{array}{c}\left|l_k\right|\\ 2\end{array}\right)$ such pairs. So given the corresponding column vectors $\mathcal{F}\left(k\right)$ and $\mathcal{W}\left(k\right)$ of the bubble matrix and of the weight matrix, respectively, and the bipartition $B=(R,S)$ of active reads A(k), the cost ${\Delta }_C(k,B)$ is computed by minimizing over all pairs of alleles $A=\left\{\right(x,y)\in l_k\times l_k|x\ne y,x<y\}$:

$${\Delta }_C(k,B)=\underset{(p_0,p_1)\in A}{\min }\left\{\min \{W_{k,S}^{p_0}+W_{k,R}^{p_1},W_{k,S}^{p_1}+W_{k,R}^{p_0}\}\right\},$$ (4)

where the outer minimization considers all allele pairs and the inner minimization considers the two possibilities of assigning those two alleles to the two haplotypes.

DP column initialization

We initialize the first DP column by setting $C(1,B):={\Delta }_C(1,B)$ for all possible bipartitions B. We enumerate all bipartitions in Gray code order, as done previously in Patterson et al. (2014). This ensures that only one read is moved from one set to another in each step, facilitating constant time updates of the values $W_{k,S}^i$.

For a bubble matrix (1) and its corresponding weight matrix (3), the DP column cell for bipartition $B=(R,S)$ is given by

$$\begin{array}{c}{\Delta }_C(k,(R,S\left)\right)=\min \{W_{k,R}^0+W_{k,S}^1,W_{k,R}^1+W_{k,S}^2,\\ W_{k,R}^0+W_{k,S}^2,W_{k,R}^1+W_{k,S}^0,\\ W_{k,R}^2+W_{k,S}^1,W_{k,R}^2+W_{k,S}^0\}\end{array}$$

Now, plugging values from (3) into the above equation for different bipartitions, ${\Delta }_C(1,.)$ can be filled as follows:

$$\begin{array}{cc}{\Delta }_C(1,\hfill & \left(\right\{r_1,r_2,r_3\},\varnothing ))=\hfill \\ \hfill & \text{min}\{9+0,16+0,9+0,16+0,9+0,9+0\}=9\hfill \end{array}$$

Similarly, we can compute ${\Delta }_C(1,.)$ for other bipartitions $\left(\right\{r_1,r_2\},\{r_3\left\}\right),$$\left(\right\{r_1,r_3\},\{r_2\left\}\right),(\varnothing ,\{r_1,r_2,r_3\left\}\right),\left(\right\{r_3\},\{r_1,r_2\left\}\right),\left(\right\{r_2\},\{r_1,r_3\left\}\right).$

Algorithm 1 .

DP COLUMN INITIALIZATION

Input: Set A(1) of reads covering bubble l₁.

Output: $C(1,.)$

forall bipartitions B of column kdo

 Compute ${\Delta }_C(k,B)$ using Equation 4 and store in C(1, B).

end

Due to the use of the Gray code order, we can perform this operation for one DP column in $\mathcal{O}(\left(\begin{array}{c}\left|l_k\right|\\ 2\end{array}\right)·2^{\left|A\right(k\left)\right|})$ time.

DP column recurrence

Note that C(k, B) is the cost of an optimal solution of Problem 1 for input matrices restricted to the first k columns under the additional constraint that the solution’s bipartition of the full read set extends B. Since column k lists all bipartitions, the optimal solution to the input matrix consisting of the first k columns would be given by the minimum in that column. To compute entries in column $C(k+1,·)$, we add up local costs incurred in column k + 1 and costs from the previous column (see Algorithm 2). To adhere to the semantics of $C(k+1,B)$ described above, only entries in column k whose bipartitions are compatible with B are to be considered as possible ‘predecessors’ of $C(k+1,B)$.

Definition 7 (Bipartition compatibility). For bipartitions$B=(P,Q)$of A and$B\prime =(P\prime ,Q\prime )$of$A\prime$, B and$B\prime$are compatible if$P\cap A\cap A\prime =P\prime \cap A\cap A\prime$and$Q\cap A\cap A\prime =Q\prime \cap A\cap A\prime$, denoted by$B\simeq B\prime$

For example, consider the second column from (1) and (3). Let us compute $C(2,.)$ for different bipartitions using recurrence in Algorithm 2:

$$\begin{array}{c}C(2,(\{r_1,r_2,r_3\},\varnothing \left)\right)=\min \{9+0,10+0,9+0,10+0,8+0,8+0\}\\ +\min \left\{C\right(1,\left(\right\{r_1,r_2,r_3\},\varnothing )\}=8+9=17\end{array}$$

To fill DP column $C(2,.)$, we can analogously compute this for the remaining bipartitions $\left(\right\{r_1,r_2\},\{r_3\left\}\right)$, $\left(\right\{r_1,r_3\},\{r_2\left\}\right),\hspace{0.17em}(\varnothing ,\{r_1,r_2,r_3\left\}\right),\hspace{0.17em}\left(\right\{r_3\},\{r_1,r_2\left\}\right)$, and $\left(\right\{r_2\},\{r_1,r_3\left\}\right)$.

Algorithm 2 .

DP TABLE

Input: $C(1,.)$ for all bipartitions of bubble k.

Output: $C(k,.)$ for all the columns k up to the last column $\left|L\right|$

for all columns $k\in \{2\dots |L\left|\right\}$ do

 forall bipartitions$B\in \mathcal{B}(A(k))$do

  Compute ${\Delta }_C(k,B)$ using Equation 4.

  Combine it with cost from column k – 1 to obtain cost for column k:

  

$$C(k,B)={\Delta }_C(k,B)+\underset{B\prime \in \mathcal{B}(A(k-1)):B\simeq B\prime }{\min }C(k-1,B\prime )$$

 end

 where $\mathcal{B}(A(k))$ denotes the set of all bipartitions of A(k).

end

Backtracing

We can backtrace from the last column $C\left(\right|L|,·)$ to compute an optimal bipartition $B=(R,S)$ of all input reads. Given this bipartition, we obtain minimum-cost haplotypes as follows: Let $B_k=(R_k,S_k)$ with $R_k=R\cap A\left(k\right)$ and $S_k=S\cap A\left(k\right)$ be the induced bipartition in column k. We then set

$$\begin{array}{l}{h}_0\left(k\right)=a_i\text{\hspace{1em}with }i:=\underset{i\prime \in \{0,1,\dots |l_k\left|\right\}}{\text{argmin}}{W}_{k,R_k}^{i^{\prime }},\\ h_1\left(k\right)=a_j\text{\hspace{1em}with }j:=\underset{j\prime \in \{0,1,\dots |l_k\left|\right\}}{\text{argmin}}{W}_{k,S_k}^{j^{\prime }},\end{array}$$

where a_i and a_j refer to the corresponding allele paths of bubble k (see Definition 2).

Time complexity

Computing one DP column takes $\mathcal{O}((\begin{array}{c}m\\ 2\end{array})·2^{\left|A\right(k\left)\right|})$ time, and the total running time is $\mathcal{O}((\begin{array}{c}m\\ 2\end{array})·2^{\left|A\right(k\left)\right|}·|L\left|\right)$ for $\left|L\right|$ bubbles, where m is the maximum number of alleles in any bubble from L. Running time is independent of read-length and, therefore, the algorithm is suitable for the increased read lengths available from upcoming sequencing technologies.

2.6 Generation of final assemblies

To generate final assemblies, for every connected component in the base sequence graph G_s, we traverse along the haplotype paths (h₀, h₁) running through that component. For the nodes in each path, we concatenate together the nodes’ sequences from the base sequence graph G_s (in either in their forward or reverse-complement orientations, as specified by the path) in order to generate the final haplotig sequences.

3 Datasets and experimental setup

To evaluate the performance of our method, we consider the real data available from two haploid yeast strains SK1 and Y12 (Yue et al., 2017), which we combine to generate a pseudo-diploid yeast. Both the SK1 and Y12 yeast strains are deeply sequenced using Illumina and PacBio sequencing. The Illumina dataset is sequenced to an average coverage of 469× with 151 bp paired end reads. We randomly downsample the dataset to a lower average coverage of 50×. The PacBio data is sequenced to an average coverage of 334× with an average read length of 4510 bp. For coverage analysis, we randomly downsample the PacBio reads to obtain datasets of different coverages $10\times ,\hspace{0.17em}20\times$ and $30\times$ with their average read-lengths of 4482, 4501 and 4516 bp respectively.

3.1 Pipeline implementation

3.1.1. Sequence graph

The first step in our pipeline is to perform error correction on the Illumina data by using BFC (Li, 2015a), which, in our experience, retains heterozygosities well for diploid genomes. BFC is used with default parameters and provided with a genome size of 12.16 Mbp. The second step is to generate a sequence graph that includes heterozygosity information. To construct such a graph, we first construct the assembly graph by using a modified version of SPAdes v3.10.1 (Bankevich et al., 2012). We modify the original SPAdes to skip the bubble removal step and retain the heterozygosity information in the graph, and run it with default parameters plus the ––only-assembler option. It uses the short Illumina reads to generate a De Bruijn-based assembly graph without any error correction. We then convert the assembly graph to a bluntified sequence graph using VG (Garrison et al., 2017). After graph simplification, the resulting sequence graph has 158 567 nodes and 190 767 edges.

3.1.2. Bubble detection

In the next stage, we use VG’s snarl decomposition algorithm (Paten et al., 2017) to detect the regions of heterozygosity, or snarls, in the sequence graph. This results in 29 071 bubbles.

3.1.3. PacBio alignments

After bubble detection, we align different coverage levels (10×, 20× and 30×) of long read PacBio data to the generated sequence graph using GraphAligner (https://github.com/maickrau/GraphAligner). This resulted in 21 868, 43 459 and 73 129 PacBio alignments for input coverages of $10\times ,\hspace{0.17em}20\times$ and $30\times$, respectively.

3.1.4. Bubble ordering

To obtain an ordering of bubbles, we perform de novo assembly using Canu v1.5 (Koren et al., 2017) on each PacBio dataset. As suggested by Giordano et al. (2017), we use Canu v1.5 with the following parameter values: corMhapSensitivity = high,corMinCoverage = 2,correctedErrorRate = 0.10,minOverlapLength = 499,corMaxEvidenceErate = 0.3. Next, we align these Canu contigs to the sequence graph to obtain the bubble ordering, which we define as the sequence of bubbles encountered by each aligned contig. Note that we use Canu solely for bubble ordering. In this paper, we restrict ourselves to phasing bubbles only in unique, non-repetitive regions. We detect repetitive bubbles based on the coverage depth of the PacBio alignments and remove them from downstream analyses. The coverage depth threshold used is 1.67 times the average coverage. This results in 148, 80 and 71 bubble chains, and 26 576, 27 556 and 27 741 bubbles, at coverages of $10\times ,\hspace{0.17em}20\times$ and $30\times$ respectively.

3.1.5. Graph-based phasing

For each of the coverage conditions, we take as input the ordered bubbles, the long-read PacBio alignments and the sequence graph, and solve the gMEC problem by assuming constant weights in the weight matrix $\mathcal{W}$. The optimal bipartition is computed via backtracing and the final haplotigs are generated by concatenating the node labels of the two optimal paths. These steps have been implemented in our WhatsHap software as a subcommand phasegraph.

3.2 Running Falcon Unzip

The main goal of this study is to measure the performance of phasing using a graph-based approach, and, in particular, the quality of haplotypes at heterozygous sites achievable by using this method with low coverage PacBio data. Therefore, we compared our graph-based approach to the state-of-the-art contig based phasing method Falcon Unzip, which also generates diploid assemblies.

The Falcon Unzip (Chin et al., 2016) algorithm first constructs a string graph composed of ‘haploid consensus’ contigs, with bubbles representing SV sites between homologous loci. Sequenced reads are then phased and separated for each haplotype on the basis of heterozygous positions. Phased reads are finally used to assemble the backbone sequence (primary contigs) and the alternative haplotype sequences (haplotigs). The combination of primary contigs and haplotigs constitutes the final diploid assembly, which includes phasing information dividing single-nucleotide polymorphisms and SVs between the two haplotypes.

We ran Falcon Unzip using the parameters given in the official parameter guide (http://pb-falcon.readthedocs.io/en/latest/parameters.html). We tried to run Falcon Unzip for lower coverages of 10× and 20×, but it did not generate output in these cases (and we assume it is not designed for such low coverages). Therefore, we only ran Falcon Unzip for 30× PacBio coverage. Primary contigs and haplotigs were polished using the Quiver algorithm and corrected for SNPs and indels using Illumina data via Pilon, with the parameters ‘–diploid’ and ‘–fixall’ (Walker et al., 2014).

3.3 Assembly performance assessment

To evaluate the accuracy of the predicted haplotypes, we align reference assemblies of the two yeast strains SK1 and Y12 (Yue et al., 2017) to the sequence graph. We emphasize that these reference assemblies are only used for evaluation purposes and are not a part of our assembly pipeline. We use the following performance measures for the evaluation of diploid assemblies:

3.3.1. Phasing error rate

Over the yeast genome, we compare the different diploid assemblies with the ground truth haploid genomes of SK1 and Y12. As with the reference assemblies, we align the haplotigs produced by Falcon Unzip to our sequence graph. For each phased bubble chain, the predicted haplotype is expressed as a mosaic of the two true haplotypes, minimizing the number of switches. This minimum then gives the number of switch errors. The phasing error rate is defined as the number of switch errors divided by the number of phased bubbles. Figure 5 illustrates this calculation for a toy example. The top panel shows the true references aligned to the sequence graph. At the bottom, predicted haplotypes (from Falcon Unzip or our graph-based approach) are aligned to the graph. Comparing the true and predicted haplotypes, we see one switch between SV1 and SV2, which means that the switch error count is one. The number of phase connections between consecutive bubbles is five and the resulting switch error rate for this example is 1/5.

Fig. 5.

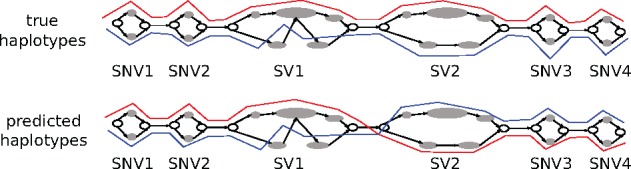
For a subgraph of G_s, this example shows the true (top) and predicted (bottom) versions of two haplotype alignments (red and blue) through a series of bubbles. When comparing the correspondingly-colored lines between the two versions, we see one switch between SV1 and SV2: the prediction contains one switch error. Six bubbles have been phased, for a total of five phase connections between consecutive bubbles. Therefore, the phasing error rate is 1/5

3.3.2. Average percent identity

We consider the best assignment of each haplotig to either of the two true references, obtained by aligning the haplotig to the references. For each whole diploid assembly, we compute the average of the best-alignment percent identities over all haplotigs.

3.3.3. Assembly contiguity

We assess the contiguity of the assemblies by computing the N50 of haplotig size.

3.3.4. Assembly completeness

We consider two assembly completeness statistics: first, the total length of haplotigs assembled by each method, and second, the total number of unphased contigs.

4 Results

In this section, we present the results of our analysis of the diploid assemblies generated by our method and by Falcon Unzip on the datasets described above.

4.1 Coverage analysis

To discover a cost-effective method for assembling a diploid genome, we consider PacBio datasets that vary in terms of coverage—specifically, 10×, 20× and 30× coverage are considered. One of the primary aims of our study is to compare two approaches—the graph-based approach we implemented and the contig-based phasing done by Falcon Unzip. In doing so, we quantify the agreement between the diploid assemblies generated by both methods and the true references. Table 1 shows the assembly performance statistics for both of these methods. In order to assess the accuracy of the competing diploid assemblies, we compute the phasing error rate and the average percent identity at different PacBio coverages. For the graph-based approach, we observe that as we increase the long read coverage from 10× to 30×, the average identity of haplotigs increases from 99.5% to 99.8% and the phasing error rate decreases from 2.5% to 0.7%. In contrast, Falcon Unzip produces haplotigs with an average identity of 99.4% and phasing error rate of 3.8% at 30× coverage. Overall, comparing the agreement between the graph-based approach (at 10× coverage) and Falcon Unzip (at 30× coverage) to the true references, our graph-based approach delivers better haplotigs with respect to all measures reported in Table 1. We believe that one reason for this is that we use an Illumina-based graph as a backbone. Furthermore, optimally solving the gMEC formulation of the phasing problem most likely contributes to generating accurate haplotigs. Overall, our analysis supports the conclusion that our approach delivers accurate haplotype sequences even at a long read coverage as low as 10×.

Table 1.

Comparison of two phasing methods, Falcon Unzip and our graph-based approach, at different PacBio coverage levels

Statistics	PacBio coverage	Graph-based approach	Falcon Unzip
Diploid assemblies quality
Average identity (%)	10×	99.50	—
	20×	99.61	—
	30×	99.80	99.4
Phasing error rate (%)	10×	2.5	—
	20×	1.5	—
	30×	0.7	3.8
Contiguity
N50 haplotig size (bp)	10×	40k	—
	20×	42k	—
	30×	43k	32k
Completeness
Haplotig size (Mbp)	10×	20.7	—
	20×	21.1	—
	30×	23.9	16.6
# Unphased contigs	10×	2	—
	20×	2	—
	30×	2	77

Note: For computing the ‘haplotig N50’, we only consider those portions of a contig for which two haplotypes are available, i.e. those regions where Falcon reports both a primary contig and an alternative haplotig. For ‘haplotig size’, we sum the length of contigs on both haplotypes (‘primary contigs’ plus ‘haplotigs’ in terms of Falcon’s output), so the target size is twice the genome size (24.3 Mbp in case of yeast).

To analyse the effect of different coverages of the Illumina short-read datasets on the quality of our haplotigs, we went back to the original, high coverage Illumina dataset (which we had been downsampled to 50× coverage) and downsampled it to 100× coverage, i.e. twice the amount of reads used above. We observed that increasing the coverage did not have a drastic effect on the quality of haplotigs. The average phasing identity rose to 99.81% and the total haplotig size was 23.9 Mbp, which is virtually identical to the results for 50× as reported in Table 1.

With an increase in average PacBio coverage from 10× to 30×, the haplotype contiguity achievable by using our approach improves from 40 kbp to 43 kbp. By way of comparison, Falcon Unzip delivers haplotigs with a N50 length of 32 kbp at the same coverage level. This highlights the fact that our approach generates more contiguous haplotypes compared to Falcon Unzip. In terms of haplotype completeness, our approach yields diploid assemblies of length 20.7, 21.1 and 23.9 Mbp at average PacBio coverages of 10×, 20× and 30×, respectively. At coverage 30×, Falcon Unzip delivers a total assembly size of 16.6 Mbp, while the total length of both haplotypes of the pseudo-diploid yeast genome is 24.3 Mbp. Our approach therefore delivers more complete haplotypes at a long-read coverage of 10× compared to Falcon Unzip at a coverage of 30×. There are 2 haplotigs that are not phased by our approach; this is due to the lack of heterozygosity over those regions. In comparison there are 77 (out of 123) contigs that are not phased by Falcon Unzip. In summary, our graph-based approach delivers complete and contiguous haplotype sequences even at a relatively low coverage of 10×.

4.2 Bubble characterization

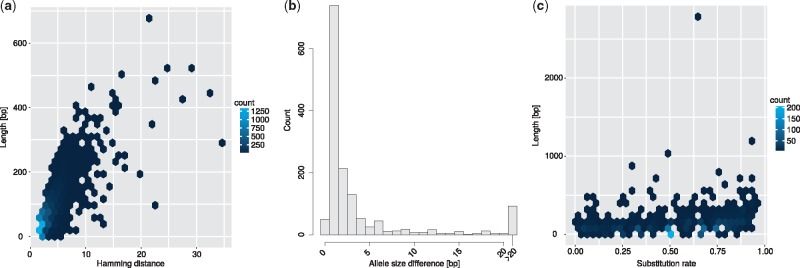
We attempted to characterize the nature of the heterozygous genomic variation encoded in the phased bubbles. There are 25 033 bi-allelic bubbles phased by our approach when using 30× coverage PacBio data. Of these bubbles, there are 15 293 for which both allele sequences have a length of at most 1 bp, out of which 15 258 are single base pair substitutions (SNVs) and 35 are 1 bp indels. The remaining 9 740 bubbles either encode two or more small variants or more complex differences. To differentiate these cases, we computed an alignment between the two allele paths and refer to those bubbles for which the alignment contains only substitutions but no indels as ‘pure substitutions’. Figure 6a shows the joint distribution of length and (Hamming) distance for these pure substitution bubbles. This analysis reveals, on the one hand, that many longer pure substitions have a low distance and hence encode multiple SNVs and, on the other hand, that there also exists a population of more complex substitutions. For the 1 489 bubbles not classified as pure substitutions, which we refer to as ‘mixed bubbles’, Figure 6b shows the absolute length difference between the two alleles. While this difference is small for most bubbles, there are 93 bubbles with a length difference of 21 bp or more. To further elucidate the nature of the sequence differences, Figure 6c presents the joint distribution of length of the longer allele and substitition rate, which is defined as the fraction of substitutions among all edit operations done to align the two sequences. That is, a pure insertion or deletion has a substitution rate of 0.

Fig. 6.

Structural variation analysis of phased bubbles from our graph-based approach. (a) Joint distribution of allele length and Hamming distance, for pure substitutions. (b) Distribution of size difference between the two alleles, for mixed bubbles and indels. Pure substitutions always have a size difference of 0, and are not included in the figure. (c) Joint distribution of the length of the longer allele and the substitution rate, for mixed bubbles. With a higher substitution rate, the bubble has more substitutions, and with a lower rate more indels

5 Discussion

The Falcon Unzip method (Chin et al., 2016) is based purely on PacBio reads which exhibit a high error rate; it is therefore not suitable for lower coverages. By using (costly) high coverage PacBio data, Falcon Unzip can generate good quality assemblies with an average haplotig identity of up to 99.99% (Chin et al., 2016). However, it follows a conservative approach for phasing genomic variants. As sketched in Figure 2, Falcon Unzip generates long primary contigs, but tends to phase them only partially.

To address the above problems, we have created a novel graph-based approach to diploid genome assembly that combines different sequencing technologies. By using one technology producing shorter, more accurate reads, and a second technology delivering long reads, we produce accurate, complete and contiguous haplotypes. Our method provides a cost-effective way of generating high quality diploid assemblies. By performing phasing directly in the space of sequence graphs—without flattening them into contigs in intermediate steps—we can phase large SVs, which is not possible using linear approaches. We have tested our approach using real data, in the form of a pseudo-diploid yeast genome, and we have shown that we deliver accurate and complete haplotigs. Furthermore, we have shown that we can detect and phase SVs.

In this study, our main focus was on phasing unique regions of the genome. As a next step, we plan to develop techniques for phasing repetitive regions as well. Resolving repeats and polyploid phasing are closely related problems, as pointed out by Chaisson et al. (2017a). Therefore, we will aim to solve heterozygous variants and repeats in a joint phasing framework, in order to obtain even more contiguous diploid genome assemblies that include both types of features. That would also remove the need to run an external assembler (Canu) for bubble ordering. Finally, our framework allows, in principle, for incorporating additional data from other sequencing technologies, such as chromatin conformation capture (Burton et al., 2013), linked read sequencing (Weisenfeld et al., 2017), and single-cell template strand sequencing (Strand-seq; Porubský et al., 2016). In previous studies on reference-based haplotyping, we have shown such integrative approaches to be very powerful for reconstructing chromosome-scale haplotypes (Chaisson et al., 2017b; Porubsky et al., 2017); we believe similar results can be obtained for de novo diploid genome assemblies.