Discriminating early- and late-stage cancers using multiple kernel learning on gene sets

Abstract

Motivation

Identifying molecular mechanisms that drive cancers from early to late stages is highly important to develop new preventive and therapeutic strategies. Standard machine learning algorithms could be used to discriminate early- and late-stage cancers from each other using their genomic characterizations. Even though these algorithms would get satisfactory predictive performance, their knowledge extraction capability would be quite restricted due to highly correlated nature of genomic data. That is why we need algorithms that can also extract relevant information about these biological mechanisms using our prior knowledge about pathways/gene sets.

Results

In this study, we addressed the problem of separating early- and late-stage cancers from each other using their gene expression profiles. We proposed to use a multiple kernel learning (MKL) formulation that makes use of pathways/gene sets (i) to obtain satisfactory/improved predictive performance and (ii) to identify biological mechanisms that might have an effect in cancer progression. We extensively compared our proposed MKL on gene sets algorithm against two standard machine learning algorithms, namely, random forests and support vector machines, on 20 diseases from the Cancer Genome Atlas cohorts for two different sets of experiments. Our method obtained statistically significantly better or comparable predictive performance on most of the datasets using significantly fewer gene expression features. We also showed that our algorithm was able to extract meaningful and disease-specific information that gives clues about the progression mechanism.

Availability and implementation

Our implementations of support vector machine and multiple kernel learning algorithms in R are available at https://github.com/mehmetgonen/gsbc together with the scripts that replicate the reported experiments.

1 Introduction

With the increasing availability of genomic characterizations for tumour biopsies taken from patients, machine learning algorithms such as support vector machines (SVMs; Cortes and Vapnik, 1995) and random forests (RFs; Breiman, 2001) have been applied to different prediction tasks related to diagnosis, prognosis and treatment of cancer. These algorithms obtained very high predictive performance in several applications. However, the most important aspect of such automated systems should be extracting relevant and meaningful knowledge from data, which is quite difficult to achieve in very high-dimensional and correlated datasets such as genomic measurements, for follow-up studies.

Understanding cancer formation and progression from early to late stages is quite important since preventing and treating cancer at early stages is much easier. We studied the problem of discriminating early- and late-stage cancers from each other using their gene expression profiles. This problem has been addressed in several previous studies (Broët et al., 2006; Jagga and Gupta, 2014; Bhalla et al., 2017).

Broët et al. (2006) tried to identify gene expression features that separate early stages from late stages using a statistical score-based approach on microarray data. Similarly, Jagga and Gupta (2014) and Bhalla et al. (2017) developed correlation-based and threshold-based algorithms, respectively, to pick individual genes that separate early-stage patients from late-stage patients for just a single disease (i.e. kidney renal clear cell carcinoma), where they evaluated the quality of gene expression features they picked by training standard machine learning algorithms such as SVMs and RFs on them. This kind of scoring/thresholding metrics might identify predictive gene expression signatures with a limited number of features, but their interpretation is quite difficult due to high-dimensional and correlated input data. In this high-dimensional regime, machine learning algorithms might select different biomarkers as predictive when they use different subsets of the same patient cohort for a given prediction task (Ein-Dor et al., 2005, 2006).

Instead of identifying a list of gene expression features first and then feeding this feature subset into a machine learning algorithm, we proposed to combine these two steps together with the prior knowledge about pathways/gene sets into a unified model. By coupling these parts, we identified relevant biological processes and learned a classifier only on the selected pathways/gene sets at the same time for a given classification task. To this aim, we used the multiple kernel learning (MKL) methodology (Gönen and Alpaydın, 2011), which was developed to combine multiple feature representations (i.e. views) or multiple similarity measures (i.e. kernels) in the framework of SVMs. We created multiple views that correspond to input pathways/gene sets from gene expression profiles, calculated kernel matrices on these views and combined these kernels in a weighted sum rule for our classifier to effectively discard some of them.

Our contributions are three-fold: (i) We formulated an MKL algorithm on gene sets to identify relevant biological processes and to learn a classification model conjointly. (ii) We tested the performance of our proposed algorithm on the problem of separating early- and late-stage cancers from each other using their gene expression profiles, to the best of our knowledge, on the largest number of diseases. (iii) We then showed that our algorithm was able to extract meaningful and disease-specific information for the mechanism of cancer progression.

2 Materials

In this study, we used several cancer cohorts from The Cancer Genome Atlas (TCGA) project to understand differences between early- and late-stage cancers. The cohorts we used in our experiments are publicly available at https://portal.gdc.cancer.gov.

2.1 RNA-Seq measurements

TCGA project reported RNA-Seq measurements of 33 cohorts over more than 10 000 tumours and pre-processed these measurements to have a unified RNA-Seq pipeline. For each cohort, we downloaded HTSeq-FPKM files of all primary tumours from the most recent freeze (i.e. Data Release 10-December 21, 2017), leading to 9911 files in total. We decided not to include metastatic tumours reported since their underlying biology would be very different than primary tumours.

2.2 Pathological stage information

TCGA project also provided clinical annotations for cancer patients whose tumours were profiled. Since we were interested in separating early- and late-stage cancers from each other, we checked pathologic_stage annotation for each patient from the most recent freeze (i.e. Data Release 10-December 21, 2017), and there were 6958 patients with this information.

2.3 Dataset construction

To be able to train a predictor for the pathological stage of a primary tumour from its gene expression profile, we need both data sources to be available during training. We extracted primary tumours with available HTSeq-FPKM file and pathologic_stage annotation for each cohort. We first considered primary tumours with Stage I annotation as early-stage (i.e. localized cancers) and the remaining tumours with Stage II, III or IV annotations as late-stage cancers (i.e. regional or distant spreads). Primary tumours annotated with Stage X (i.e. 12 tumours in BRCA) or IS (i.e. 46 tumours in TGCT) were not included in our analyses even if they have their gene expression profiles available. After this step, we only included cohorts with at least 20 tumours both from early- and late-stage categories in our final dataset list. Table 1 gives the list of 15 datasets that were used in our first set of experiments, namely, E1, together with details about the number of samples in early- and late-stage cancers. The total number of primary tumours included is 5547, and dataset sizes vary between 65 (i.e. KICH) and 1067 (i.e. BRCA). The percentage of early-stage tumours varies between 5.79% (i.e. 25/432 in HNSC) and 67.90% (i.e. 55/81 in TGCT). We then considered an alternative labelling of early- and late-stage cancers by assigning primary tumours annotated with Stage I or II to early-stage (i.e. localized cancers and regional spreads) and primary tumours annotated with Stage III or IV to late-stage (i.e. distant spreads). In this case, when we only included cohorts with at least 20 tumours both from early- and late-stage categories, we obtained 18 datasets at the end. Table 1 also gives the list of 18 datasets that were used in our second set of experiments, namely, E2, together with details about the number of samples in early- and late-stage cancers. The total number of primary tumours included is 6038, where the percentage of early-stage tumours varies between 21.99% (i.e. 95/432 in HNSC) and 81.69% (i.e. 406/497 in LUSC).

Table 1.

Summary of 20 TCGA cohorts that we used in our two sets of experiments, namely, E1 and E2

Cohort	Disease name	Stage I	Stage II	Stage III	Stage IV	Early (E1)	Late (E1)	Total (E1)	Early (E2)	Late (E2)	Total (E2)
ACC	Adrenocortical carcinoma	9	37	16	15	—	—	—	46	31	77
BLCA	Bladder urothelial carcinoma	2	130	140	134	—	—	—	132	274	406
BRCA	Breast invasive carcinoma	181	619	247	20	181	886	1067	800	267	1067
COAD	Colon adenocarcinoma	75	176	128	64	75	368	443	251	192	443
ESCA	Esophageal carcinoma	16	69	49	8	16	126	142	85	57	142
HNSC	Head and neck squamous cell carcinoma	25	70	78	259	25	407	429	95	337	429
KICH	Kidney chromophobe	20	25	14	6	20	45	65	45	20	65
KIRC	Kidney renal clear cell carcinoma	265	57	123	82	265	262	527	322	205	527
KIRP	Kidney renal papillary cell carcinoma	172	21	51	15	172	87	259	193	66	259
LIHC	Liver hepatocellular carcinoma	171	86	85	5	171	176	347	257	90	347
LUAD	Lung adenocarcinoma	274	121	84	26	274	231	505	395	110	505
LUSC	Lung squamous cell carcinoma	244	162	84	7	244	253	497	406	91	497
MESO	Mesothelioma	10	16	44	16	—	—	—	26	60	86
PAAD	Pancreatic adenocarcinoma	21	146	3	4	21	153	174	—	—	—
READ	Rectum adenocarcinoma	30	51	51	24	30	126	156	81	75	156
SKCM	Skin cutaneous melanoma	2	66	27	3	—	—	—	68	30	98
STAD	Stomach adenocarcinoma	53	111	150	38	53	299	352	164	188	352
TGCT	Testicular germ cell tumours	55	12	14	0	55	26	81	—	—	—
THCA	Thyroid carcinoma	281	52	112	55	281	219	500	333	167	500
UVM	Uveal melanoma	0	39	36	4	—	—	—	39	40	79
					Total	1883	3664	5547	3738	2300	6038

Note: For each cohort, we report TCGA cohort code, disease name and number of samples in each stage together with details about the numbers of early-stage, late-stage and total samples in experiments E1 and E2. We included 5547 and 6038 patients in total for our two sets of experiments E1 and E2, respectively.

2.4 Gene set database

In addition to predicting the stage of a tumour, we would like to understand the biological mechanisms that differentiate early- and late-stage cancers from each other. For this aim, we can, for example, use pathways and/or gene sets defined in the literature. These collections provide information about groups of genes that have dependencies or similarities in their functions. We extracted the Hallmark gene sets from the Molecular Signatures Database where each gene set conveys a specific biological state or process and displays coherent expression in cancers (Liberzon et al., 2015). This collection includes 50 gene sets, and their sizes vary between 32 and 200.

3 Methods

We addressed the problem of predicting pathological stages (i.e. separating early- and late-stage cancers from each other) of primary tumours at the diagnosis using their gene expression profiles in machine learning algorithms. This problem can be formulated as a binary classification task and can be solved with standard classification methods such as RFs (Breiman, 2001) and SVMs (Cortes and Vapnik, 1995). However, predictive accuracy is not sufficient to draw insights about the differentiation between early- and late-stage cancers. To this aim, we also need knowledge extraction capability within the classification algorithm. It is known that gene-level molecular signatures extracted from gene expression data are not robust when we have limited training data (Ein-Dor et al., 2005, 2006). Due to highly correlated nature of gene expression data, we might obtain different molecular signatures from different subsets of the same training set. Instead, we can integrate our prior knowledge about genes into the model in the form of pathway/gene sets and identify molecular signatures at this level.

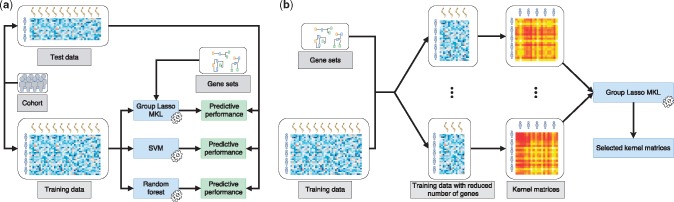
Figure 1 shows the overall evaluation framework we developed in this study. On 15 and 18 datasets we constructed out of 20 TCGA cohorts (Table 1), we compared three machine learning algorithms, namely, RFs, SVMs and MKL on gene sets. RFs and SVMs use gene expression profiles of tumours to predict their pathological stages (Fig. 1a). However, in addition to gene expression profiles, MKL also uses a pathway/gene set database and extracts additional knowledge about the differences between early- and late-stage cancers in the form of gene sets by discarding some of them in the final classifier (Fig. 1b).

Fig. 1.

Overview of the evaluation framework we developed for predicting pathological stages of primary tumours from their gene expression profiles. (a) Unbiased performance evaluation of three machine learning algorithms, namely, RFs, SVMs and MKL on gene sets, for the classification task using the same sets of samples during training and testing. Predictive performances were measured using the AUROC. (b) Integrating pathways/gene sets into the classification algorithm, where we calculate a kernel matrix using the expression features of genes that are included in each pathway/gene set during training or testing

3.1 Problem formulation

We formulated the pathological stage prediction task as a binary classification problem defined on the gene expression data, denoted as $\mathcal{X}$, and the phenotype (i.e. early-stage versus late-stage), denoted as $\mathcal{Y}$. We arbitrarily called early-stage tumours as positive class and late-stage tumours as negative class. For a given cohort, we represented the training dataset as ${\{({\mathit{x}}_i,y_i)\}}_{i=1}^N$, where N is the number of primary tumours, ${\mathit{x}}_i$ is the gene expression profile of tumour i and $y_i\in \{-1,+1\}$ is the class label of tumour i. This classification problem can be represented as learning a discriminant function from gene expression profiles to phenotype, i.e. $f:\mathcal{X}\to \mathcal{Y}$. After learning the discriminant function, we can make predictions for out-of-sample (i.e. unseen during training) tumours.

3.2 Random forests

By combining multiple weak decision trees using an ensemble strategy, we can obtain more robust classification algorithms known as RFs (Breiman, 2001). RFs were chosen as the baseline algorithm since they were frequently used in the literature to predict disease phenotypes from genomic measurements (Díaz-Uriarte and Alvares de Andrés, 2006; Pang et al., 2006; Statnikov et al., 2008; Nam et al., 2009). Although they were reported to be very accurate classifiers in terms of predictive performance in several applications, their knowledge extraction capability is quite restricted. Decision tree models in RFs are usually constructed on randomly selected bootstrap samples, which make knowledge extraction very sensitive to this bootstrapping step.

3.3 Support vector machines

SVMs formulate the binary classification problem as a convex quadratic optimization model (Cortes and Vapnik, 1995). We give the mathematical details of SVMs since our MKL on gene sets algorithm, which we will describe next, is based on SVMs. The optimization problem of binary classification SVMs can be written as

$$\begin{array}{cc}\text{minimize}\hspace{0.17em}\hfill & \frac{1}{2}{\mathit{w}}^{\mathrm{\top }}\mathit{w}+C\sum _{i=1}^N{\xi }_i\hfill \\ \text{with} \text{respect} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & \mathit{w}\in {ℝ}^D,\hspace{0.17em}\hspace{0.17em}\mathit{\xi }\in {ℝ}^N,\hspace{0.17em}\hspace{0.17em}b\in ℝ\hfill \\ \text{subject} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & y_i({\mathit{w}}^{\mathrm{\top }}{\mathit{x}}_i+b)\ge 1-{\xi }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i\hfill \\ \hfill & {\xi }_i\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,\hfill \end{array}$$

where $\mathit{w}$ is the set of weights assigned to features, C is a positive regularization parameter, $\mathit{\xi }$ is the set of slack variables, D is the number of input features (e.g. the number of genes in gene expression profiles) and b is the intercept parameter. Instead of solving this primal optimization problem, we usually solve the corresponding dual optimization problem (i) to reduce the number of decision variables and (ii) to be able to integrate kernel functions into the model, leading to non-linear models. We first write the Lagrangian function as

$$\begin{array}{l}\mathcal{L}=\frac{1}{2}{\mathit{w}}^{\mathrm{\top }}\mathit{w}+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i\left(y_i({\mathit{w}}^{\mathrm{\top }}{\mathit{x}}_i+b)-1+{\xi }_i\right)-\sum _{i=1}^N{\beta }_i{\xi }_i,\end{array}$$

and take derivatives with respect to the decision variables of the primal problem to find the following:

$$\begin{array}{c}\frac{\partial \mathcal{L}}{\partial \mathit{w}}=0\Rightarrow \mathit{w}=\sum _{i=1}^N{\alpha }_i{y}_i{\mathit{x}}_i\\ \frac{\partial \mathcal{L}}{\partial b}=0\Rightarrow \sum _{i=1}^N{\alpha }_i{y}_i=0\\ \frac{\partial \mathcal{L}}{\partial {\xi }_i}=0\Rightarrow C={\alpha }_i+{\beta }_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i.\end{array}$$

We then plug these back into the Lagrangian function to find the objective value of the dual problem, which can be written as

$$\begin{array}{cc}\text{minimize}\hspace{0.17em}\hfill & -\sum _{i=1}^N{\alpha }_i+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathit{x}}_i^{\mathrm{\top }}{\mathit{x}}_j\hfill \\ \text{with} \text{respect} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & \mathit{\alpha }\in {ℝ}^N\hfill \\ \text{subject} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & \sum _{i=1}^N{\alpha }_i{y}_i=0\hfill \\ \hfill & C\ge {\alpha }_i\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall i,\hfill \end{array}$$ (1)

where we have N decision variables instead of $(D+N+1)$ decision variables, and we now can replace ${\mathit{x}}_i^{\mathrm{\top }}{\mathit{x}}_j$ term with a kernel function $k({\mathit{x}}_i,{\mathit{x}}_j)$ to obtain non-linear models.

3.4 MKL on gene sets

The predictive performance of SVMs is highly dependent on the kernel function used. The standard approach is to select the best kernel function among a set of candidates using a cross-validation strategy. However, instead of selecting a single kernel function, using a weighted combination of input kernels might give better predictive performance, which is known as MKL (Gönen and Alpaydın, 2011). MKL algorithms might combine different kernels calculated on the same input representation or combine kernels calculated on different input representations (i.e. multi-view learning). In bioinformatics applications, the same data points can be represented with different measurements (e.g. gene expression, methylation and copy number measurements from the same set of tumours). Instead of combining predictive models trained on each representation (i.e. late integration) or concatenating these input representations into a joint one before learning (i.e. early integration), we can calculate kernel matrices on each representation and learn how to combine them in the predictive algorithm during inference (i.e. intermediate integration).

In this study, we were interested in identifying biological mechanisms that differentiate early- and late-stage cancers from each other. To this aim, we created a separate kernel matrix for each gene set and combined them using an MKL algorithm (Fig. 1b), namely, group Lasso MKL, which can be used to find a sparse combination (i.e. mostly zero kernel weights due to ${\ell }_1$-norm) of the input kernels (Xu et al., 2010). The gene sets that correspond to kernel matrices with non-zero weights might be related to the differentiation between early- and late-stage cancers.

Group Lasso MKL solves the following optimization problem to find the kernel weights and other model parameters simultaneously.

$$\begin{array}{cc}\text{minimize}\hspace{0.17em}\hfill & J\left(\mathit{\eta }\right)\hfill \\ \text{with} \text{respect} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & \mathit{\eta }\in {ℝ}^P\hfill \\ \text{subject} \text{to}\hspace{0.17em}\hspace{0.17em}\hfill & \sum _{m=1}^P{\eta }_m=1\hfill \\ \hfill & {\eta }_m\ge 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall m,\hfill \end{array}$$ (2)

where $\mathit{\eta }$ is the set of kernel weights, P is the number of input kernels and $J\left(\mathit{\eta }\right)$ corresponds to the optimization problem in Equation (1) with a modified objective function, which replaces $k({\mathit{x}}_i,{\mathit{x}}_j)={\mathit{x}}_i^{\mathrm{\top }}{\mathit{x}}_j$ term with ${\sum }_{m=1}^P{\eta }_m{k}_m({\mathit{x}}_i,{\mathit{x}}_j)$. The only equality constraint in Equation (2), which is also known as the unit simplex constraint, is equivalent to enforcing ${\ell }_1$-norm on the kernel weights and leads to a sparse solution.

The optimization problem in Equation (2) cannot be solved globally with respect to $\mathit{\alpha }$ and $\mathit{\eta }$ since the outer minimization problem is convex with respect to $\mathit{\eta }$ and the inner minimization problem is convex with respect to $\mathit{\alpha }$, but the overall problem is not jointly convex with respect to $\mathit{\alpha }$ and $\mathit{\eta }$. That is why we use an alternating optimization strategy to optimise them in an iterative manner. We first start the algorithm by setting the kernel weights to uniform values (i.e. ${\eta }_m^{\left(1\right)}=1/P$). At each iteration t, we solve the inner optimization problem (i.e. a standard SVM model) using the current kernel weights ${\mathit{\eta }}^{\left(t\right)}$ to find the support vector coefficients ${\mathit{\alpha }}^{\left(t\right)}$. We can then find the kernel weights of the next iteration ${\mathit{\eta }}^{(t+1)}$ using the following closed-form update equation:

$${\eta }_m^{(t+1)}=\frac{{\eta }_m^{\left(t\right)}\sqrt{\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i^{\left(t\right)}{\alpha }_j^{\left(t\right)}{y}_i{y}_j{k}_m({\mathit{x}}_i,{\mathit{x}}_j)}}{\sum _{o=1}^P{\eta }_o^{\left(t\right)}\sqrt{\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i^{\left(t\right)}{\alpha }_j^{\left(t\right)}{y}_i{y}_j{k}_o({\mathit{x}}_i,{\mathit{x}}_j)}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall m,$$

where the superscripts $(t+1)$ and (t) show the next and current iterations.

4 Results

To test the predictive performance of MKL on gene sets algorithm, we performed two sets of experiments E1 and E2 on 15 and 18 datasets that we constructed from TCGA cohorts for two alternative labelling strategies (Table 1) by comparing against two baseline algorithms, namely, RFs and SVMs. We compared against RFs since they were frequently used in phenotype prediction tasks of several bioinformatics applications. We compared against SVMs since MKL on gene sets algorithm is mainly based on SVMs, and we wanted to see the effect of integrating pathway/gene set information into the classification algorithm.

4.1 Experimental settings

For each dataset, we picked 80% of the tumours as the training set, and we used the remaining 20% as the test set. While doing so, we tried to keep the negative and positive class ratios in training and test sets almost equal (i.e. stratification). The training set was normalized to have zero mean and unit standard deviation, and the test set was then normalized using the mean and the standard deviation of the original training set. We repeated this procedure 100 times to obtain more robust results and reported the final results over these 100 replications. In each replication, the hyper-parameters for RFs, SVMs and MKL on gene sets were selected using a 4-fold inner cross-validation on the training set.

For RFs, we used randomForestSRC R package version 2.5.1 (Ishwaran and Kogalur, 2017). We picked the number of trees to grow parameter ntree from the set $\{500,1000,\dots ,2500\}$ using the 4-fold inner cross-validation strategy described.

For SVMs and MKL on gene sets, we used our own implementations in R, which uses MOSEK version 8.1.0.34 to solve quadratic optimization problems (MOSEK ApS, 2017). To calculate a similarity measure between gene expression profiles of tumours, we used the Gaussian kernel as

$$k_{\mathcal{G}}({\mathit{x}}_i,{\mathit{x}}_j)=\text{exp}\hspace{0.17em}\left(-\frac{{({\mathit{x}}_i-{\mathit{x}}_j)}^{\mathrm{\top }}({\mathit{x}}_i-{\mathit{x}}_j)}{2{\sigma }^2}\right),$$

where we picked the kernel width parameter σ as the mean of pairwise Euclidean distances between training instances. We selected the regularization parameter C using the 4-fold inner cross-validation strategy described from the set $\{{10}^{-4},{10}^{-3},\dots ,{10}^{+5}\}$.

For MKL on gene sets, we performed 200 iterations to guarantee the convergence since the algorithm usually converges in tens of iterations. Note that the Gaussian kernel functions were calculated on subsets of gene expression profiles by looking at the genes included in the corresponding gene sets, and the kernel width parameters were selected accordingly.

To compare the predictive performances of three algorithms, we used area under the receiver operating characteristic curve (AUROC). AUROC is used to summarize the receiver operating characteristic curve, which is a curve of true positives as a function of false positives while the threshold to predict class labels changes. Larger AUROC values correspond to better predictive performance.

4.2 Predictive performance comparison on TCGA datasets

On 15 datasets for the first set of experiments E1, we compared three machine learning algorithms, namely, RF, SVM and MKL on the Hallmark gene sets (MKL[H]), in terms of their predictive performances.

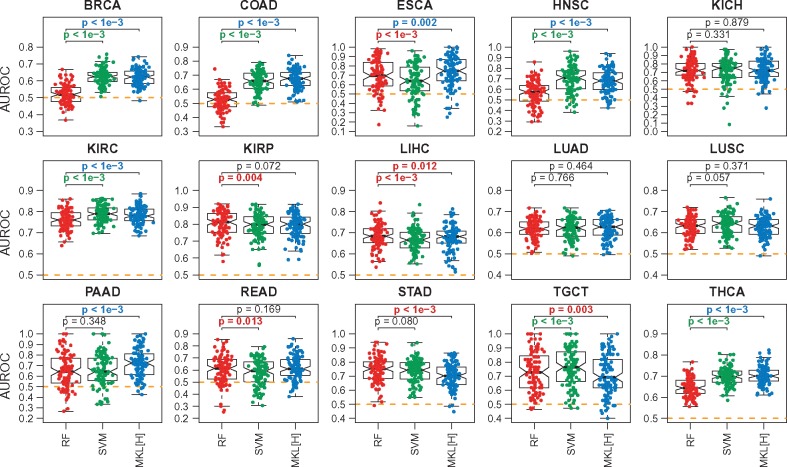
Figure 2 shows the predictive performances of RF, SVM and MKL[H] on each cohort separately. We see that the median performances of all three algorithms are better than the baseline performance (i.e. 0.5 AUROC value shown as dashed lines) on all datasets, which indicates that gene expression profiles carry meaningful information about pathological stages.

Fig. 2.

Predictive performances of RF, SVM and MKL on the Hallmark gene sets (MKL[H]) on 15 datasets constructed from TCGA cohorts for the first set of experiments E1. The box-and-whisker plots compare the AUROC values of the algorithms over 100 replications. SVM and MKL[H] are compared against RF using a two-tailed paired t-test to check whether there is a significant difference between their performances. For P-value results, red: RF is better; green: SVM is better; blue: MKL[H] is better; black: no difference. The orange dashed lines show the baseline performance level (i.e. AUROC = 0.5)

When we compare the performances of RF and SVM, we see that SVM obtained significantly better results on 6 out of 15 datasets (i.e. BRCA, COAD, HNSC, KIRC, TGCT and THCA), whereas RF was significantly better on four of them (i.e. ESCA, KIRP, LIHC and READ). Although RF is also a non-linear model, the non-linearity brought by the Gaussian kernel makes SVM a better algorithm for this highly complex classification problem. SVM improved the predictive performance by 10.44% on BRCA, 13.56% on COAD, 13.36% on HNSC and 5.12% on THCA, whereas the largest performance drop was 5.51% on ESCA.

When we compare the performances of RF and MKL[H], we see that MKL[H] obtained significantly better results on 7 out of 15 datasets (i.e. BRCA, COAD, ESCA, HNSC, KIRC, PAAD and THCA), whereas RF was significantly better on three of them (i.e. LIHC, STAD and TGCT). We see that principled combination of gene set information in the form of kernel functions increased the predictive performance even though MKL[H] used a small portion of the gene expression profiles. To be more specific, RF and SVM were using 19 814 gene expression features, whereas MKL[H] was using only 4357 (i.e. less than one-fourth) gene expression features for the genes included in the Hallmark gene sets. MKL[H] improved the predictive performance by 10.00% on BRCA, 14.89% on COAD, 4.30% on ESCA, 11.43% on HNSC, 7.59% on PAAD and 5.50% on THCA, whereas the largest performance drop was 4.35% on STAD.

Note that SVM also outperformed RF in this set of experiments, but MKL[H] used significantly fewer gene expression features (i.e. even less than 4357 input features) by discarding uninformative gene sets from the machine learning model and allowed us to identify informative ones for classification.

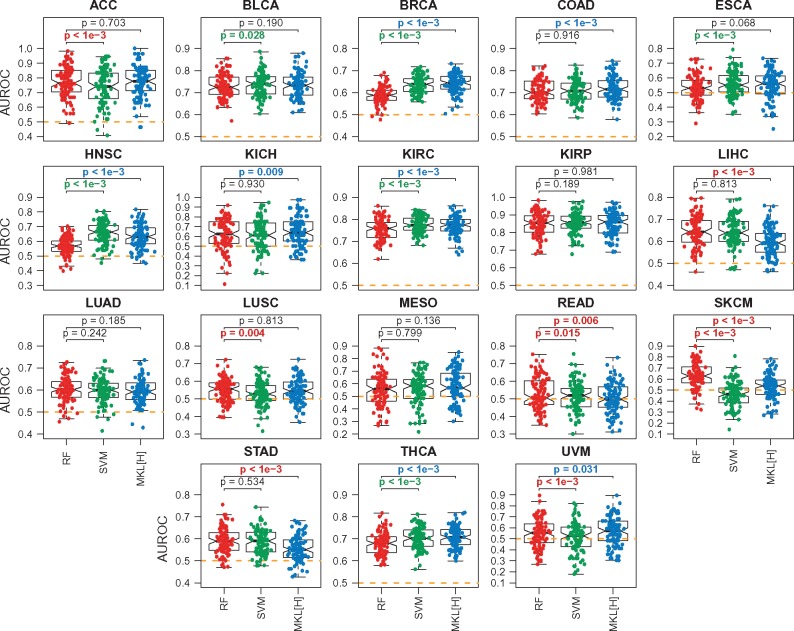
Figure 3 shows the predictive performances of RF, SVM and MKL[H] for the second set of experiments E2 (i.e. Stage I or II versus Stage III or IV). We see that the ordering of the algorithms with respect to their predictive performances stays the same (i.e. RF < SVM < MKL[H]).

Fig. 3.

Predictive performances of RF, SVM and MKL on the Hallmark gene sets (MKL[H]) on 18 datasets constructed from TCGA cohorts for the second set of experiments E2. The box-and-whisker plots compare the AUROC values of the algorithms over 100 replications. SVM and MKL[H] are compared against RF using a two-tailed paired t-test to check whether there is a significant difference between their performances. For P-value results, red: RF is better; green: SVM is better; blue: MKL[H] is better; black: no difference. The orange dashed lines show the baseline performance level (i.e. AUROC = 0.5)

4.3 Biological mechanisms identified by MKL

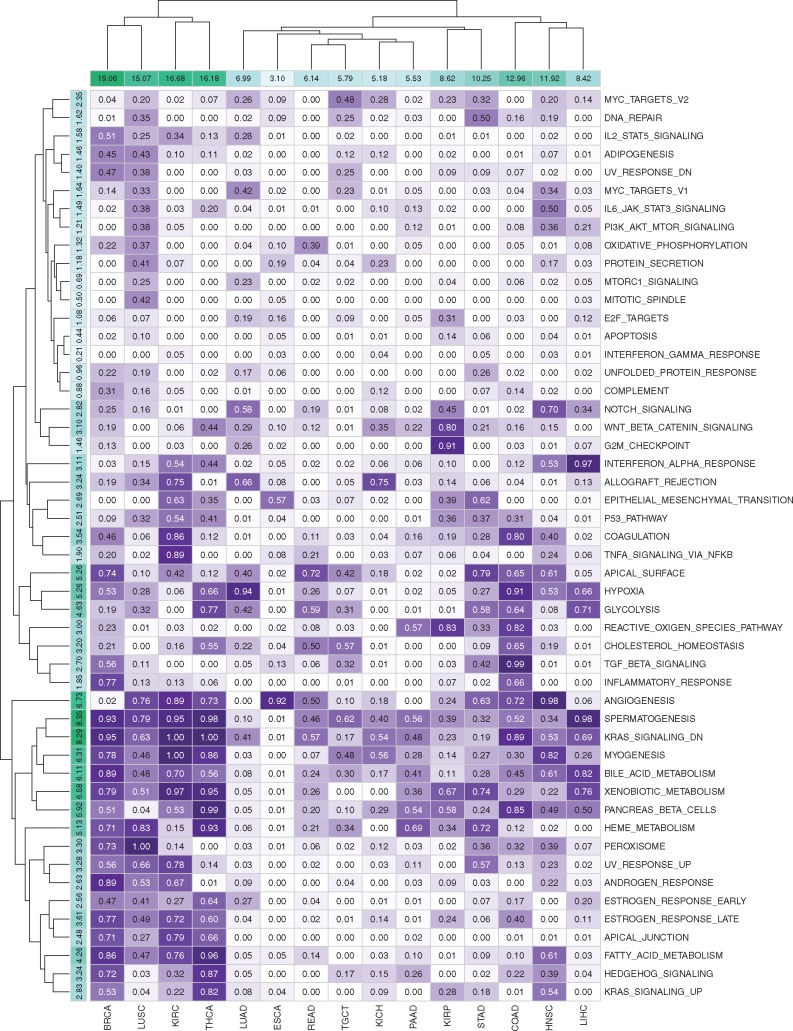
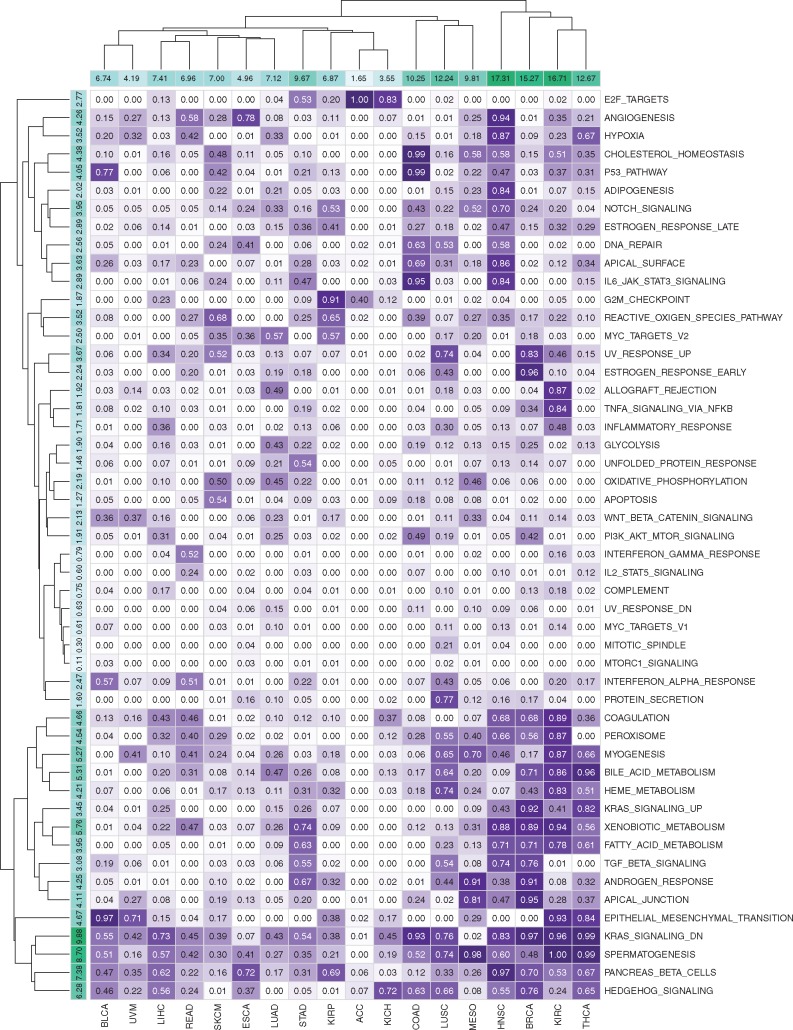
To illustrate the biological relevance of our MKL[H] algorithm, we analysed its ability to identify relevant gene sets based on the kernel weights inferred during training. For each dataset and gene set pair, we counted the number of replications in which the corresponding kernel weight is non-zero (i.e. the number of replications where ${\eta }_m\ne 0$ was satisfied). Figure 4 shows the selection frequencies of 50 gene sets in the Hallmark collection for 15 datasets in the first set of experiments E1.

Fig. 4.

Selection frequencies of 50 gene sets in the Hallmark collection for 15 datasets in the first set of experiments E1. Rows and columns are clustered using hierarchical clustering with Euclidean distance and complete linkage functions. Column sums of selection frequencies are reported to identify datasets that use higher number of gene sets on the average. Row sums of selection frequencies are reported to identify frequently selected gene sets across different datasets

By looking at the column sums of the selection frequencies, we see that discriminating early- and late-stage cancers from each other is much more difficult in some disease types. For example, in BRCA, KIRC, LUSC and THCA datasets, MKL[H] used more than 15 out of 50 gene sets on the average. However, in some disease types such as ESCA and PAAD, MKL[H] used very few gene sets (less than 6 out of 50 gene set on the average) and even improved the predictive performance significantly compared to RF and SVM algorithms.

When we look at the row sums of the selection frequencies, we see that some gene sets were selected heavily across different datasets. For example, ANGIOGENESIS, KRAS_SIGNALING_DN, MYOGENESIS and SPERMATOGENESIS gene sets were used in more than 6 out of 15 datasets on the average, which were reported to be related to the cancer formation in early stages (Bergers and Benjamin, 2003). Similarly, four metabolism-related gene sets, namely, BILE_ACID_METABOLISM, HEME_METABOLISM, PANCREAS_BETA_CELLS and XENOBIOTIC_METABOLISM were used more than 5 out of 15 datasets on the average. For diseases associated with the tissues that are known to be directly related to metabolism such as KIRC (kidney), LIHC (liver), PAAD (pancreas) and THCA (thyroid gland), MKL[H] picked these metabolism-related gene sets with very high frequencies. Gene sets that have quite important roles in epithelial cells, namely, APICAL_SURFACE and HYPOXIA, were selected for more than 5 out of 15 datasets on the average. These two gene sets were picked with very high frequencies in BRCA (breast), COAD (colon), LUAD (lung) and STAD (stomach) whose tissues are known to contain many epithelial cells. We also see that MKL[H] did not pick gene sets that were expected to be irrelevant for discriminating early- and late-stage cancers from each other. For example, cell cycle related gene sets such as DNA_REPAIR, E2F_TARGETS, G2M_CHECKPOINT, MYC_TARGETS_V1, MYC_TARGETS_V2 and MTORC1_SIGNALING were selected with very low frequencies across 15 datasets.

Figure 5 gives the selection frequencies of 50 gene sets in the Hallmark collection for 18 datasets in the second set of experiments E2, where we can make similar observations about selected gene sets.

Fig. 5.

Selection frequencies of 50 gene sets in the Hallmark collection for 18 datasets in the second set of experiments E2. Rows and columns are clustered using hierarchical clustering with Euclidean distance and complete linkage functions. Column sums of selection frequencies are reported to identify datasets that use higher number of gene sets on the average. Row sums of selection frequencies are reported to identify frequently selected gene sets across different datasets

5 Conclusions

With the advancements in molecular characterization technologies, it has become a standard practice to profile tumour biopsies of cancer patients. These tumour profiles have been extensively used in efforts of understanding molecular mechanisms of cancer formation and progression. For example, if we can successfully determine the molecular mechanisms of progression from early to late stages, we can make use of this information to develop new preventive or therapeutic strategies to stop or slow down this progression. Here, we addressed the problem of discriminating early- and late-stage cancers from each other using their gene expression profiles.

We developed a computational framework (Fig. 1) to evaluate the predictive performances of machine learning algorithms on 20 diseases from TCGA collection (Table 1) on this classification task for two different sets of experiments. We compared two well-used baseline algorithms, namely, RFs and SVMs, against our proposed MKL on gene sets algorithm, which is able to integrate prior knowledge about pathways/gene sets into the model and to extract relative importances of the input gene sets in addition to learning a classification model. The main contribution of our proposed approach comes from performing classification and gene set selection using ${\ell }_1$-norm regularization conjointly in a unified formulation. By doing so, we can eliminate some gene sets (i.e. noisy or irrelevant gene sets) from the classification model during training instead of using whole gene expression profiles, which leads to more robust and accurate classifiers.

To demonstrate the predictive performance of our proposed algorithm, we performed two sets of experiments on 15 and 18 datasets constructed from TCGA cohorts. We see that MKL on gene sets was able to get higher predictive performance on the average than baseline methods (Figs. 2 and 3) using significantly fewer (around one-fourth or fewer) gene expression features. To demonstrate the biological relevance of gene set selection by our proposed algorithm, we reported the selection frequencies of gene sets for each dataset (Figs. 4 and 5). We see that frequently selected gene sets in several cohorts were supported by the existing literature. We also note that the gene sets that were not expected to be related to differentiation between early- and late-stage cancers were not selected with high frequencies by our algorithm.

We envision two main extensions of our work in the future. We first will develop an MKL algorithm that assigns the same kernel weights to gene sets across different datasets by training them conjointly (i.e. multi-task learning). In this study, we trained a separate MKL model for each dataset, which makes their kernel weight assignments independent from each other (i.e. single-task learning). By modelling disease types that are known to have similar mechanisms together, we can increase the sample size during inference, leading to more robust classifiers. We will then develop another multi-task learning algorithm that will take all available datasets and conjointly perform (i) clustering of datasets, (ii) making shared kernel weight assignments to each cluster and (iii) learning a separate classifier for each dataset. By doing so, we will be able to identify disease types that have similar mechanisms for the given phenotype.