The Kappa platform for rule-based modeling

Abstract

Motivation

We present an overview of the Kappa platform, an integrated suite of analysis and visualization techniques for building and interactively exploring rule-based models. The main components of the platform are the Kappa Simulator, the Kappa Static Analyzer and the Kappa Story Extractor. In addition to these components, we describe the Kappa User Interface, which includes a range of interactive visualization tools for rule-based models needed to make sense of the complexity of biological systems. We argue that, in this approach, modeling is akin to programming and can likewise benefit from an integrated development environment. Our platform is a step in this direction.

Results

We discuss details about the computation and rendering of static, dynamic, and causal views of a model, which include the contact map (CM), snaphots at different resolutions, the dynamic influence network (DIN) and causal compression. We provide use cases illustrating how these concepts generate insight. Specifically, we show how the CM and snapshots provide information about systems capable of polymerization, such as Wnt signaling. A well-understood model of the KaiABC oscillator, translated into Kappa from the literature, is deployed to demonstrate the DIN and its use in understanding systems dynamics. Finally, we discuss how pathways might be discovered or recovered from a rule-based model by means of causal compression, as exemplified for early events in EGF signaling.

Availability and implementation

The Kappa platform is available via the project website at kappalanguage.org. All components of the platform are open source and freely available through the authors’ code repositories.

1 Introduction

Statistical analysis and visualization efforts have become indispensable for interpreting and navigating the swell of data produced by rapid advances in high-throughput methods at the single-cell level. The abundance of mRNA transcripts, the localization of proteins and their post-translational modifications are data taken to reflect the state of a biological system. The overwhelming effort at analysis and visualization to date has been directed at data originating from such sweeping surveys of system state.

Meanwhile, detailed mechanistic studies are elucidating the structural and post-translational requirements on protein regions, domains and residues that enable specific interactions. These data do not directly pertain to system state, but to the processes that generate system state. The many interactions inferred from biochemical, biophysical and structural deep drills have been combined into static networks. Surveying the properties of such networks, while useful, offers limited insight, since the significance of any one interaction is determined by the dynamic behavior of all interactions that co-occur in a given situation. Likewise, static depictions of pathways are narratives that might serve to organize data, yet pathways do not exist as physical circuits like road networks do; rather, at any moment, pathways emerge from and are maintained by the many concurrent and changing interactions between the molecular agents that populate a system.

Mechanistic models are needed for understanding systems dynamics and making interventions into cellular processes more deliberate. Yet, such models are often viewed with suspicion, because much of the mechanistic detail is missing, either for lack of knowledge or the need to curtail complexity (or both). The utility of mechanistic models appears further diminished by statistical models that can yield prediction without concomitant understanding. Another issue is the perception that mechanistic models, because difficult to build, are rarely kept in sync with a rapidly evolving knowledge base. These are not arguments against the need for mechanistic models in interpreting interaction data. Rather, these arguments articulate the need for mechanistic models that are scalable, easy to update and fork and based on a formal foundation conducive to computer-aided reasoning. In this contribution, we lay out our ideas and their implementation in support of this vision.

2 The rule-based approach

Technology for making, running and analyzing large dynamic models, though in its infancy, is progressing significantly (Bachman and Sorger, 2011; Cohen, 2015; Gyori et al., 2017; Loew and Schaff, 2001). One powerful component are rule-based languages, such as Kappa (Danos et al., 2007a) and BioNetGen (Faeder et al., 2009; Harris et al., 2016) for molecular biology and Mød (Andersen et al., 2016) for organic chemistry.

Common to rule-based languages are entities with a structure represented as a graph and rules that are graph-rewrite directives (Fig. 1a and b). The point of a rule is to distinguish between the transformation of a structure fragment and the reaction instance resulting from it in the context of specific entities. This distinction is a key organizing principle in chemistry (Fig. 1a). Since a particular interaction between proteins often appears to depend on some but not all aspects of their state, rule-based languages adapt the chemical perspective to molecular systems biology by viewing proteins as higher-order atoms and non-covalent associations between proteins as higher-order molecules (Fig. 1b).

Fig. 1.

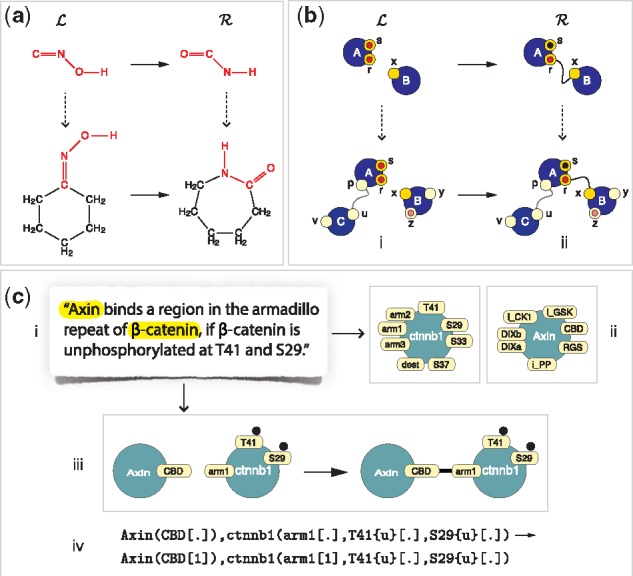
The concept of a rule. Panel (a): In chemistry, a rule of transformation specifies a fragment of structure $\mathcal{L}$ and its modification $\mathcal{R}$. A reaction instance occurs when one or more molecules jointly contain (left dotted arrow) the fragment $\mathcal{L}$, yielding one or more products in which the corresponding occurrence of $\mathcal{L}$ has been replaced by $\mathcal{R}$. Panel (b): Rule-based languages transpose the idea of chemistry to interactions among agents (blue nodes), seen in analogy to atoms and complexes of connected agents, seen in analogy to molecules. Agents have sites (instead of valences) that can carry state (here indicated as black and red disks), upon which interactions depend. This gives rise to the concept of a site graph, in which an agent-node (or node for short) is connected to its site-nodes (or sites for short), shown as directly attached. Importantly, sites, not nodes, anchor edges and a site can anchor at most one edge. Interactions can change the state and connectivity of agents. The embedding of a site graph, such as $\mathcal{L}$, into a target graph, such as i, is a natural extension of a sub-graph isomorphism (see also Fig. 2). Sites and states not mentioned in $\mathcal{L}$ are ignored. Given a transformation rule $\mathcal{L}\to \mathcal{R}$, an embedding of $\mathcal{L}$ into a target graph permits the matching sub-graph to be replaced with $\mathcal{R}$. Panel (c): In rule-based languages for molecular biology agents stand for proteins and sites for their interaction capabilities, without, however, representing the underlying physical features and processes enabling them. A hypothesis or an assertion in the literature (i) typically mentions proteins whose agent abstraction (ii) involves several sites, collectively referred to as the agent’s interface. The interface (ii) appropriate for a particular model can be assembled manually or automatically by scanning bioinformatic databases. The assertion (i) is converted, manually or with computer-assisted reading, into a rule rendered graphically (iii) or textually (iv). Since a rule mentions only the sites and states necessary for a transformation, it is subject to revision as knowledge evolves. Sufficiency is often not within purview of experimental techniques, as not all biochemical aspects of an interaction can be observed

A rule-based language sets a specific level of granularity at which rules ‘axiomatize’ interactions. For example, a rule of chemical transformation, as in Figure 1a, only exposes the net result of underlying electronic rearrangements, which are governed in turn by ‘arrow (or electron) pushing’ rules (Kermack and Robinson, 1922) at a lower level of abstraction. Although not explicitly represented, these processes are not ignored, as they inform what a rule should say. Likewise, rules of protein interaction, Figure 1b and c, are based on structural considerations, bioinformatic sequence analysis and biochemical mechanisms reported in the literature (or hypothesized by the modeler). Yet, a rule does not expose these lower-level aspects, but summarizes their overall effect in terms of pre- and post-conditions on protein state.

2.1 Agents, patterns, embeddings and activity

At the heart of languages like Kappa and BioNetGen lies the agent abstraction, Figure 1c, which conceptualizes a protein as an agent with an interface of sites that represent distinct interaction capabilities, such as binding and post-translational modification (Fig. 1c). Through their sites, agents can connect into site graphs (Fig. 1). A site graph that exhibits the full interface and state of all its agents represents a molecular species. A rule $r:{\mathcal{L}}_r\to {\mathcal{R}}_r$ involves two site graphs, ${\mathcal{L}}_r$ and ${\mathcal{R}}_r$, which usually mention some but not all sites of their agents. ${\mathcal{L}}_r$ and ${\mathcal{R}}_r$ are therefore patterns, not molecular species (Fig. 1).

The state of a system is itself a graph consisting of a (large) ensemble of disconnected site graphs, each representing one instance of a molecular species. We call such an ensemble a mixture (as in reaction mixture) and denote it by $\mathcal{M}$. A rule r is applied to a mixture $\mathcal{M}$ by embedding${\mathcal{L}}_r$ into $\mathcal{M}$, which means a match in $\mathcal{M}$ of all agent types, site names and states (including binding states) mentioned in ${\mathcal{L}}_r$. A rule is executed by replacing the part of the mixture matched to ${\mathcal{L}}_r$ with ${\mathcal{R}}_r$ (Fig. 2).

Fig. 2.

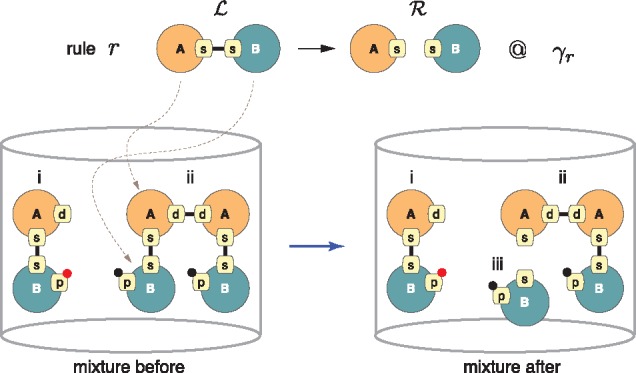
Rule application. Rule r asserts a simple mechanism in which the dissociation of agents of type A from those of B at their respective sites s (the name of a site has no formal meaning and is local to an agent) is independent of the state at all other sites. The bottom left depicts a simple mixture $\mathcal{M}$ of two molecular species, i and ii, each present in a single instance. Agents of type A and B have more sites than are mentioned in the rule; black and red dots indicate a post-translational modification (phosphorylation status, say). $\mathcal{L}$ has three possible embeddings in $\mathcal{M}$. An embedding is a sub-graph isomorphism respecting the type of agents and the state (including connectivity) of sites mentioned. The propensity of r to fire in $\mathcal{M}$ is therefore $3{\gamma }_r$, as each embedding is equally likely to be chosen. Species ii allows for two possible embeddings and will react twice as fast than species i. After application of r, the mixture has changed and a new molecular species iii has appeared

A model is a collection of rules with an initial mixture. The stochastic behavior of a model is explored using continuous time Monte–Carlo (Boutillier et al., 2017a; Danos et al., 2007b; Gillespie, 2007; Sneddon et al., 2011) or CTMC for short. For this purpose, a rule r is assigned a constant, γ_r, which is the instantaneous probability rate that the rule triggers on any given embedding of ${\mathcal{L}}_r$ in $\mathcal{M}$ (Fig. 2). The activity α_r of a rule r (i.e. its propensity to fire) depends on the total number of embeddings of ${\mathcal{L}}_r$ in $\mathcal{M}$ (mass action), denoted by $\left|\right[{\mathcal{L}}_r,\mathcal{M}\left]\right|$, and is given by ${\alpha }_r={\gamma }_r\left|\right[{\mathcal{L}}_r,\mathcal{M}\left]\right|/{\sigma }_r$, where σ_r is the number of symmetries of ${\mathcal{L}}_r$ preserved by r. The term $\left|\right[{\mathcal{L}}_r,\mathcal{M}\left]\right|/{\sigma }_r$ is the number of physical configurations that are distinguishable with respect to the mechanism expressed in r. The activity α_r is the stochastic rule-based analog of the flux through a reaction in standard chemical kinetics. If a reaction event occurs at time t, then the probability that r is applied to one of its embeddings is given by its relative activity ${\alpha }_r/\sum _s{\alpha }_s$.

Even when the set of all reachable molecular species and their reactions can be deduced from a given collection of rules, the size of the resulting network is often too large to be handled explicitly. Importantly, translating rules into kinetic differential equations based on an explicit reaction network would miss the point of rule-based approaches entirely. Rules provide compactness, transparency and a handle on combinatorial complexity; and, perhaps most significantly, systems of rules constitute a more appropriate level for causal analysis than reaction networks, because reasoning at the level of rules avoids contamination with context that defines a reaction but is irrelevant to the application of the underlying rule (Figs 1b and 2).

2.2 Syntax

From here on our discussion refers specifically to the Kappa framework (https://kappalanguage.org). Graphs are the proper formal objects in this framework, but we need a textual notation for convenience. The binding state of a site s is specified in square brackets: s[.] indicates that s is free (unbound), whereas s[n] (n a non-negative integer) is bound to the unique other site in the same expression whose binding state is also n. Thus, A(x[2]), B(y[2]) asserts that agent A is bound at x to agent B at y. Given an agent type with two binding sites, A(x, y), a simple rule might be, bnd: A(x[.]), A(y[.]) → A(x[1]), A(y[1]). This rule yields ‘head-to-tail’ polymerization, because it is matched by any two asymmetric ends (sites x and y). Rule bnd, therefore, generates linear polymers and rings of any size, limited only by the available pool of agents of type A. A site z can also have an internal state, expressed as a string between curly braces. The internal state is typically used to specify a post-translational modification. Thus, C(z{p}[.]) denotes an agent of type C whose site z is in state p (phosphorylated, say) and unbound. When writing patterns, such as observables or rules, states not mentioned do not constrain their matchings into the mixture (‘don’t care, don’t write’). For example, C(z{p}) is matched by any instance of C phosphorylated at z regardless of its binding state. An extensive manual (Boutillier et al., 2017b) provides many details beyond the present scope.

3 Materials and methods

3.1 Kappa software agents

The main Kappa ecology consists of several software agents that communicate through an ad hoc JSON-based protocol and expose high-level functionalities through both a Python API and an HTTP REST service. At present these are: The Kappa Simulator (KaSim), the Kappa Static Analyzer (KaSA) and the Kappa Story Extractor (KaSTOR). A Python client enables scripting to tailor work flows and is available as the kappy package in pip. Modeling in a rule-based language is much like writing large and complex programs, which necessitates an integrated development environment. To integrate the new Kappa web services, we developed a browser-based User Interface (UI), which also comes packaged as a self-contained application for the Windows OS, Mac OS and Ubuntu. This effort raised several challenges pertaining to visualization and analysis that we address below.

The KaSim is an implementation of CTMC designed for rule-based models with particular emphasis on scalability in typical usage regimes (Danos et al., 2007b). A recent optimization targets a costly step in the CTMC core loop (Boutillier et al., 2017a). After a rule has been applied to the mixture, rule activities (Section 2.1) must be updated by identifying all embeddings that were gained or lost (Fig. 2) and likewise for updating counts of user-defined observables. The optimization consists in the initial construction of a model-dependent data structure by virtue of which no pattern—whether the left side of a rule, a user-defined observable, or any sub-pattern of these—is ever scanned twice for the same embedding into the mixture. For example, if two left sides ${\mathcal{L}}_r$ and ${\mathcal{L}}_s$ have a common sub-pattern, any match to that sub-pattern is shared during the attempt at extending the match to ${\mathcal{L}}_r$ and ${\mathcal{L}}_s$.

KaSim is interactive, allowing a simulation to be paused and resumed at any time. A versatile intervention language can be used for defining perturbations, such as altering rate constants and adding/removing agents interactively or at time points set in the input file. The intervention language supports queries about the state of the system and requests for data dumps, such as snapshots of the mixture and rule influence matrices (Section 3.3).

Simulation is the main tool for studying the dynamical behavior of a rule-based model. However, some properties of a model can be determined by direct inspection and manipulation of the rules without execution. Such properties are static in the sense of being time-independent, yet they relate to behavior because they demarcate its envelope. For example, a static property is the reachability of a specific molecular species, i.e. an answer to the question whether a given species (or pattern) can in principle be produced by the joint operation of the rules. Another static property is the impossibility of a rule to ever fire because its $\mathcal{L}$-pattern can never be matched (Section 3.2). Further properties are the existence of invariants, such as between states at two sites of the same agent (i.e. assertions of the kind ‘whenever site s is phosphorylated, site p is bound to agent D’). The firing of a rule r could create a configuration that partially satisfies the ${\mathcal{L}}_s$ of another rule s, thus potentially contributing to an increase in the activity of s. Similarly, r might compete with s for instances, thus potentially decreasing the activity of s. Such potential influence (positive, negative, or none) is also a static property. In Section 3.3, we look at the actual influence that rules have on each other, which is a dynamic property. Static properties are especially helpful in debugging a model, as they can quickly pinpoint discrepancies between expected and actual behavior. The KaSA supports all these analyses. It relies heavily on a technique called ‘abstract interpretation’, described in Section 3.2.

A third tool is the KaSTOR which aims at providing insights into how an event of interest (EOI) occurred in a particular event trace obtained by simulation of a model. The underlying concepts offer a distinctive perspective on (mechanistic) causality in molecular systems. We outline their implementation in Section 3.4.

3.2 Static analysis and abstract interpretation

The formal analysis of graph-rewrite systems relies heavily on elucidating the relationships between graph-morphisms, for which category theory provides a powerful framework. Yet, in practice, computing an exact answer to problems like enumerating the set of reachable species is not feasible, because of numbers beyond imagination. Static analysis algorithms written for Kappa achieve practical utility by deploying an approach known as abstract interpretation (Cousot and Cousot, 1977), wherein the given rules are made more abstract in the sense of systematically discarding specific information. The reachability problem is then approached within the set of abstract rules, where it can be handled faster at the price of an overapproximated rather than exact solution.

Central to the abstract interpretation technique in Kappa is the concept of a local view. The local view of an agent A that occurs in a site graph $\mathcal{G}$ consists of A itself, its sites and their state as mentioned in $\mathcal{G}$, alongside information about which sites of A are bound to which site of which agent type, i.e. without including the bound agent and any additional information about it. For example, in Figure 3, the local view of the first agent (labelled ‘1’) of type A is given by ii, which consists of A, site d bound to site d of another agent of type A (but without including that agent, hence the dotted outline) and site s bound to site s of an agent of type B. We can think of such linkage information as a bond ‘stub’, expressed syntactically as A(s[s.B], d[d.A]). The local view of the other A-agent (labelled ‘2’) is the same. Thus, the complex i yield a set of three distinct local views {ii, iii, iv}. This step is called abstraction, denoted by $\lambda (·)$. Continuing the example, we can stitch the local views back together using the information in the bond ‘stubs’. Doing this in all possible ways yields the set of four complexes shown in Figure 3. This step is called concretization. Clearly, the abstraction step for agent A loses information about the phosphorylation state of the B bound to it. The concretization step reconstructs the original complex, but also others—an overapproximation. We apply this idea to the left sides ${\mathcal{L}}_r$ and right sides ${\mathcal{R}}_r$ of each rule r in a model. In this way, ${\mathcal{L}}_r\to {\mathcal{R}}_r$ is replaced by an abstract version $\lambda \left({\mathcal{L}}_r\right)\to \lambda \left({\mathcal{R}}_r\right)$ cast entirely in terms of local views. It turns out that the fixed point obtained from the forward closure of abstract rules always exists and is finite (even for systems capable of generating infinitely many species). It can be further shown that stitching together these local views in all admissible ways yields a superset of the true reachable molecular species (Danos et al., 2008). Because of overapproximation, a species $\mathcal{Q}$ in the superset obtained from abstraction may not be reachable with the original rules. However, if $\mathcal{Q}$ is not in the superset, it cannot be reached by the original rules either: A no is a no, and a yes is a maybe. The most recent version of KaSA generalizes local views to more flexibly compromise between accuracy, efficiency and expressivity (Feret and Lý, 2018).

Fig. 3.

Abstract interpretation. Complex (i) is ‘exploded’ into its local views (ii), (iii) and (iv) by an abstraction process λ described in the main text. The concretization process γ stitches the local views back into complexes, reproducing the original, but also others, reflecting the fact that information was abstracted away. Reachability via local views is a fast overapproximation, enabling useful real-time analysis that would otherwise be prohibitive

This technique makes reachability analysis fast enough to permit computing, thus visualizing, contact maps (CMs; Section 4.1) and rule influence maps in real-time as a user updates a model. This in turn makes abstract reachability useful in debugging a model, which is a process that furthers understanding.

As a simple example of KaSA’s operation consider the following minimal model snippet. (Rate constants are ignored by static analysis; they only serve the purpose of getting the model past the parser).

%init: 1 E ()

%init: 1 R()

’r1’ E(x[.]) , R (x[.]) - > E(x[1]) , R (x[1]) @0

’r2’ E(x[1]) , R (x[1] , c [.]) -> E(x[.]) , R (x[.] , c [.]) @0

’r3’ R(x[_] , c [.]) , R (x[_] , c [.]) - > R(x[_] , c [1]) , R (x[_] , c [1]) @0

’r4’ R(c[1] , c r[.] , n [.]) , R (c[1] , c r[.] , n [.]) ->

R(c[.] , c r[.] , n [.]) , R (c[.] , c r[.] , n [.]) @0

’r5’ R(c[1] , c r[.] , n [.]) , R (c[1] , c r[.] , n [.]) ->

R(c[1] , c r[2] , n [.]) , R (c[1] , c r[.] , n [2]) @0

’r6’ R(cr[1]) , R (n[1]) - > R(cr[.]) , R (n[.]) @0

’q1’ R(x[.] , c [.] , c r[_] , n [_]) - > R(x[.] , c [.] , c r[_] , n [_]) @0

’q2’ R(c[1] , c r[2]) , R (c[1]) , R (n[2]) ->

R(c[1] , c r[2]) , R (c[1]) , R (n[2]) @0

This snippet is a simplified version of reversible receptor/ligand binding (‘r1’,‘r2’), receptor dimerization (‘r3’,‘r4’) and internal crosslinking (‘r5’,‘r6’). (The underscore denotes a bound state without caring about the type of binding partner.) To query the static analyzer about the reachability of patterns of interest, we defined two identity rules, ‘q1’ and ‘q2’ (in which ${\mathcal{L}}_{\mathrm{q}\{\mathrm{1},\mathrm{2}\}}={\mathcal{R}}_{\mathrm{q}\{\mathrm{1},\mathrm{2}\}}$), to exploit KaSA’s detection of dead rules. Dead rules are rules that cannot fire because their left side pattern is unreachable. As soon as ‘q1’ and (or) ‘q2’ are added to ‘r1’–‘r6’ in the UI editor, KaSA flags them as unreachable. For ‘q1’ this means that a receptor cannot be cross-linked unless it is bound to ligand (but no single rule explicitly states that); for ‘q2’ this means that the bonds at sites c and cr of a receptor must both engage the same second receptor, i.e. no receptor triples. KaSA came to this conclusion by automatic abstract interpretation. The analysis made use of the initialization statements (‘init’) for ligand E and receptor R. (Static analysis only cares whether the initial copy number is non-zero.) If we remove the first statement, KaSA responds in real-time by flagging all rules as unreachable—because of the absence of ligand. This can be useful to ensure that the initial condition of complex models covers the intended agent types. The command line version of KaSA provides many additional analyses that are not yet exposed in the software agent.

3.3 The dynamic influence network

The dynamic influence network (DIN) is a construct for tracking the way rules influence each other over time. Its visualization is discussed in Section 4.3.

A rule r fires with a probability proportional to its activity α_r (Section 2.1). When r fires, it alters the state of the mixture $\mathcal{M}$, which can affect the activity of rule s by generating or destroying matchings to ${\mathcal{L}}_s$ in $\mathcal{M}$. Fix a time interval $[t,t+\tau ]$ and let i index the events that occur in that interval. The ith event causes a transition from state ${\mathcal{M}}_i$ (before the event) to ${\mathcal{M}}_{i+1}$ (after the event). If the ith event is due to the firing of r, its contribution to the relative change in the activity of s, denoted by $\Delta I_{r,s}\left(i\right)$, is given by

$$\Delta I_{r,s}\left(i\right)=\{\begin{array}{cc}\frac{{\alpha }_s(i+1)-{\alpha }_s\left(i\right)}{{\alpha }_s\left(i\right)}\hfill & \text{if} i\hspace{0.17em}\text{is} \text{due} \text{to} r \text{and} {\alpha }_{\mathrm{s}}\left(i\right)\ne 0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (1)

We aggregate these contributions during the interval $[t,t+\tau ]$ and divide by the number n_r of r-events to obtain the average influence of r on s during that interval:

$${\overline{\Delta I}}_{r,s}(t,\tau )=\frac{1}{n_r}\sum _{i \text{in} [t,t+\tau ]}\Delta I_{r,s}\left(i\right),$$ (2)

with the events i occurring in $[t,t+\tau ]$. We refer to the matrix Equation (2) as the DIN. The nodes of the DIN are rules and an edge between r and s has weight ${\overline{\Delta I}}_{r,s}(t,\tau )$.

3.4 Causal lineages and compression

KaSim can output the whole sequence of events generated by a simulation. This is called a trace. The traces of models we work with comprise routinely many millions of events. A persistent challenge is to extract an explanation of how an EOI specified by the user actually occurred in a particular run.

Given a trace τ, i.e. a sequence of events $\tau =e_1{e}_2\cdots e_n$ to an EOI ($\text{EOI}\equiv e_n$), we first identify which events were on the path to the EOI and in which causal order, as the temporal sequence of events may not always be relevant in stochastic systems with concurrency. Two temporally adjacent events $e_1{e}_2$ are concurrent if they can occur in any order—$e_1{e}_2$ or $e_2{e}_1$—while having the same effect, otherwise there is a relation of precedence between them. For e₁ to precede e₂ means that the rule underlying e₁ contributes to satisfying a condition required by the left-hand side of the rule underlying e₂. The naive approach we take here is to view causality as the opposite of concurrency, i.e. a relation of precedence. Not all precedence is causal, however. Suppose a kinase can phosphorylate a substrate and, independently, the substrate can be degraded. Whenever phosphorylation is observed, it must precede degradation, but, given our assumption, we cannot say that phosphorylation caused degradation.

We now wish to identify the events in τ that were involved in bringing about the EOI while revealing their precedence relations. Figure 4 illustrates the method by means of a simple example. Assume the EOI is the production of a free phosphorylated substrate in the following Michaelis–Menten type of model:

Fig. 4.

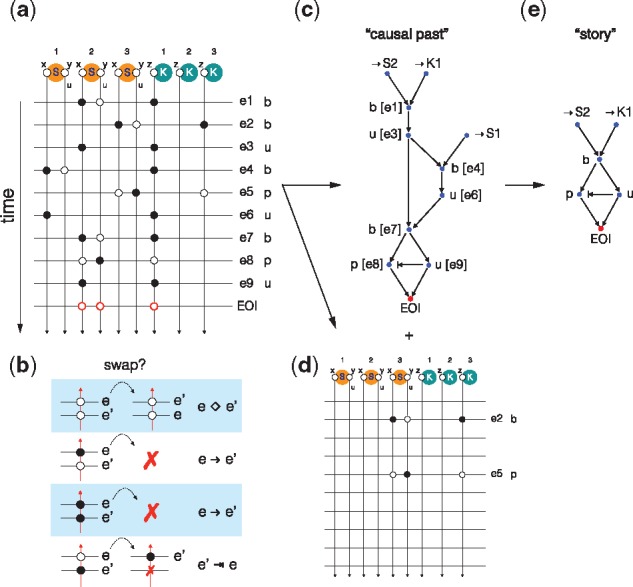
Causal analysis of event traces. Panel (a): The representation of a trace in terms of ‘worldlines’ that record the modifications and tests at each site for each event in the trace. Panel (b): Schematic of allowed moves and annotations emitted when swapping the order of adjacent events for a particular wordline (i.e. site in the model). See text for details. Panel (c): The causal past of the EOI reconstructed from the trace representation in panel (a) following the instructions in panel (b). Panel (d): The events that had no bearing on the EOI. Panel (e): Minimization of the causal past shown in panel (c) by eliminating cycles that return to an equivalent system state from the point of view of the EOI

’b’ K(z[.]) , S (x[.] , y {u}) - > K(z[1]) , S (x[1] , y {u})

’u’ K(z[1]) , S (x[1]) - > K(z[.]) , S (x[.])

’p’ K(z[1]) , S (x[1] , y {u}) - > K(z[1]) , S (x[1] , y {p})

’*’ S(x[.] , y {p}) - > S(x[.] , y {p})

Since causality is a relation between events, the identity rule ‘*’ serves to transform our query into an event. Suppose a particular mixture contains three substrate agents S and two kinase agents K and that a simulation happened to produce the trace $\tau =bbubpuppu*$, where each event is labeled by the rule that produced it and contains information about which agent identifiers matched the rule. KaSTOR, the causal analysis software agent, attaches to every site of every agent instance in the mixture a thread and records whether an event only tested the state of a site or whether it also modified it. In typical Kappa rules, a modification also implies a test. This results in the representation depicted in Figure 4a, where threads run vertically and events horizontally with markings—black filled circles if the thread was modified, white if it was only tested. To reconstruct the causal past of ’*’, we slide its tests backward in time following the instructions shown in Figure 4b. Consider an event e followed by event $e\prime$ and ask for every site involved in$e\prime$ whether the test or modification of that site could have occurred before e. If this is the case, slide that test or modification backwards in time past e and repeat that question against the event that occurred prior to e, etc. A test of the state at a particular site in event $e\prime$ can always slide past a test (or absence thereof) for the same site in event e, as it will not invalidate the occurrence of e. A test associated with event $e\prime$ cannot slide past a modification associated with event e, or $e\prime$ could not have occurred. This generates a causal arrow from e to $e\prime$. A modification cannot slide past a modification for the same reason. Lastly, a modification can slide past a test, but this is a case of non-causal precedence discussed above and is annotated by adding a ‘prevention arrow’ from $e\prime$ to e.

This procedure, applied to our trace, will discard any events that had no bearing on the EOI (Fig. 4d), while producing a directed acyclic graph representing the precedence structure of its causal past (Fig. 4c). Figure 4c reads: S₂ binds K₁, then they dissociate, then K₁ binds S₁, then they dissociate; then K₁ rebinds S₂, then K₁ phosphorylates S₂ and precedes (non-causally) the dissociation of K₁ from S₂, thus causing the EOI. The problem is that events in the causal past of an EOI often violate necessity. In our example, the detour through S₁, although it occurred, was not necessary, since event e₇ could have happened instead of e₁ yielding the same result. One way to isolate necessity is to search, within the causal past reconstructed by the previous procedure, for a minimal sub-set of events that can produce the EOI (Danos et al., 2012). We call this minimization causal compression. KaSTOR automatically translates a causal past into a propositional formula in which each event is associated with a Boolean variable whose value determines whether the event is kept or discarded. Each scenario has implications for which other events must be retained or discarded to ensure that the EOI obtains. KaSTOR then seeks the smallest number of propositional variables that, when set to true (keep), satisfy the formula. This is done with KaSTOR’s own SAT solver tailored to the structure of this problem. The result is the compressed causal past of Figure 4e, which we call a story. A more realistic case of causal compression is touched upon in Section 4.4 and Figure 8.

Fig. 8.

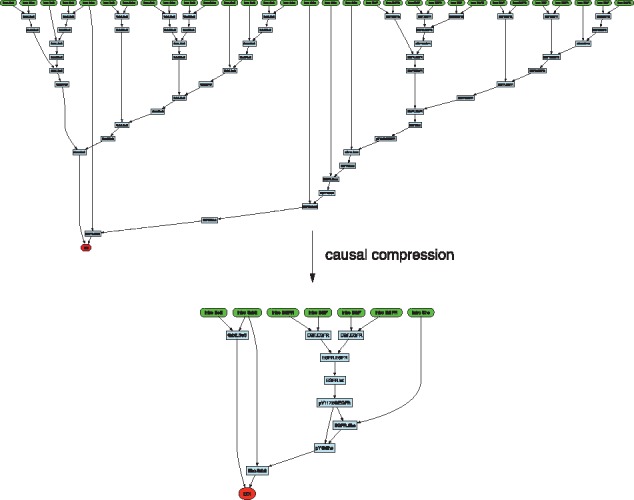
Causal compression in early EGF signaling. The concepts of Figure 4 are illustrated in the case of Sos recruitment

4 Results

The Kappa UI is a suite of interactive visualization tools, integrating various services in the Kappa ecology. Here, we provide details about the Kappa CM, the snapshots tool, the DIN visualization (DIN-Viz) and our initial efforts in visualizing stories created with KaSTOR.

A range of projects introduce techniques for visualizing protein–protein interaction networks in support of analysis (Murray et al., 2017). Kohn et al. (2006) introduce a technique that visualizes regulatory networks, but is not rule-based in the sense defined here. Chylek et al. (2011) provide guidelines for visualizing and annotating rule-based models extending the notion of CM (Danos et al., 2007a). Smith et al. (2012) develop the RuleBender framework for editing and exploring rule-based systems. This is taken further by Sekar et al. (2017), in particular by grouping and merging rules into a more compact diagrammatic representation. Dang et al. (2015) present a visualization technique that uses animation to highlight causal relationships within pathways, and Paduano and Forbes (2015) explore interactive methods to visualize common patterns in biological networks.

4.1 Visualization: the CM

The CM of a model is a generalized site graph in which every agent type occurs exactly once and every site exhibits all bonds and states that are possible according to the rules. The CM is generated automatically. For smaller to moderately sized models, its construction and visualization are updated in real-time while a user is writing rules in the UI text editor. The CM allows a user to quickly check visually whether a molecular species is admissible in principle. The static analyzer KaSA can constrain the CM based on abstract reachability, as outlined in Section 3.2. The most immediate utility of such visualization is in debugging. For example, a missing arc, where a modeler expected to see one, might indicate an omitted, mistyped, or unreachable rule.

Figure 5a depicts the CM of a large model as rendered in the UI. By inspection of the CM one can deduce the existence of proper cycles. A cycle is a path in the CM that starts at an agent type, visits other agent types by following bonds and returns to the original type. A proper cycle is a cycle in which the departure site at any agent differs from the landing site. A proper cycle indicates the potential for polymerization, which is a significant property as it implies an infinite set of possible molecular species. The enumeration of proper cycles in larger CMs, such as in Figure 5, requires computational assistance provided by KaSA.

Fig. 5.

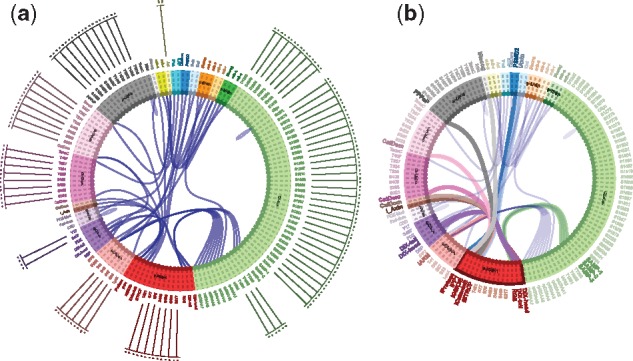
The CM. Agent types are shown as arcs of a circle; a site is depicted as a dotted line at a right angle to its agent arc with binding interactions on the inside and a listing of possible state values on the outside. Panel (a): The CM of a prototype Wnt signaling model with 1440 rules and 19 agent types. It took KaSA about 18 s to generate this CM based on abstract reachability. Panel (b): The same CM as in (a) but with states toggled off and the mouse over Axin (red), highlighting its interconnections with other agent types of the model

Scalable visualization is a challenge. In this instance, we partially address scalability through interactivity by providing a zooming feature and the automatic toggling of detail (information resolution) along with selective emphasis as the user hovers with the mouse over elements of the CM. In Figure 5b, for example, the mouse hovers over Axin, highlighting its binding partners in the model.

4.2 Visualization: snapshots

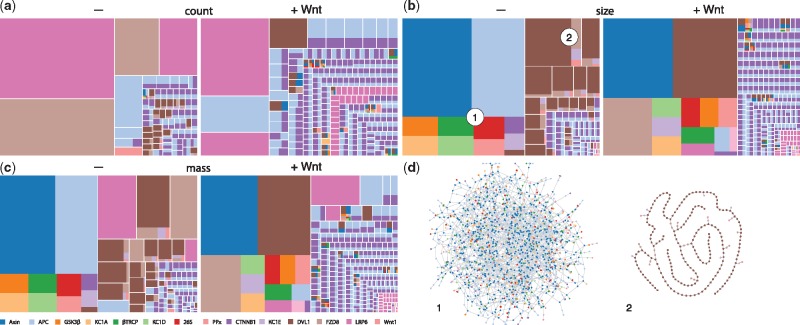
Simulations are often discussed in terms of time series tracking the abundance of molecular species. On their own, such time series are less useful when dealing with combinatorial models, because it is impractical to track all possible molecular species and it is often unclear which of them are salient. This is where visualizing snapshots of the system state at different levels of resolution is useful. A snapshot is a view of the mixture, i.e. the state of the system, at a given time. Presently, snapshots have three levels of resolution, two of which are currently available through the UI. The first level is a ‘patchwork’ (treemap) rendering of the mixture and comes in three views (Fig. 6a–c): count, size and mass. In all views, the term patch refers to a rectangle separated from others by white space. A patch represents a molecular species, but visualizes it only in terms of agent composition, akin to a sum formula in chemistry. The relative abundance of an agent type within a species is shown as a monochromatic rectangle within the patch. Two monochromatic patches of the same color show up separately if the underlying species differ in size (e.g. monomer versus n-mer) or are equal in size but differ in the state of at least one agent. These distinctions are made explicit by clicking on the patch, which opens the next higher level of resolution—connectivity—for that species (Fig. 6d). All three views at the first level contain the same number of patches, but the area of a patch depends on the view. In the count view, the area reflects the relative abundance of the molecular species represented by the patch; in the size view it reflects the size of the species, i.e. the number of connected agents and in the mass view the area is determined by count times size. The differences between these views are particularly notable in systems with polymerization, such as a model of canonical Wnt signaling whose CM is shown in Figure 5. In this system, several scaffold proteins can form a polymeric structure, either alone or in interaction with each other (Fiedler et al., 2011).

Fig. 6.

Snapshots. Panels (a), (b), (c): The patchwork diagrams depict three views of the system state at the resolution of agent composition. See text for details. The diagrams refer to the Wnt model with CM shown in Figure 5. For each view the snapshot was taken at steady state prior and after Wnt addition. Panel (d): The next higher level of snapshot resolution exhibits agent connectivity for a patch clicked by the user. The connectivities shown pertain to the two complexes indicated in the size view

We illustrate the patchwork view by comparing the state of the system before (–) to that after (+) Wnt addition. In both cases the most frequent components in the count view are homogenous, mainly protomers or dimers of scaffolds like Dvl, APC and LRP6. The size view, however, is dominated by a large composite polymer—so large that it also dominates the mass view. Prior to Wnt addition, the polymer has the composition of a so-called ‘destruction complex’, which targets β-catenin (CTNNB1) for degradation. The before/after comparison in the size view yields the following observations. (i) The largest complex has increased in size. (ii) The largest complex has changed composition, gaining a large mass of Dvl (dark brown), previously spread across a variety of separate entities. (iii) The rest of the mixture has become far more fragmented by a greater diversity of smaller species. (iv) The diversity of LRP6 (dark pink) states has increased—prior to Wnt we recognize a few patches in the lower right corner of the size view, while there are many more monochromatic LRP6 patches after Wnt addition. This is more conspicuous in the count view. (v) Proteins that were associated with Dvl prior to Wnt addition (especially Fzd) have now been pulled into the giant component, representing the migration of the destruction complex machinery to the membrane where it interacts with trans-membrane proteins, such as Fzd and CK1d. (vi) The giant component from the pre-Wnt state has lost a large amount of APC, which is now found in isolated association with β-catenin. (vii) Complexes with a composition of more than four agent types are more frequent. Prior to Wnt addition, the only complex with more than four agent types was the destruction aggregate, whereas afterwards the giant component increased in compositional diversity and so did species not connected to it.

Such observations are drawn more readily from patchwork diagrams than time series, especially if it is unclear what to look for at the outset. Patchwork diagrams lay out an overall view of a suitably coarse-grained system state and seem especially conducive for qualitative comparisons. The observations made here, regardless of their biological significance, also illustrate the complexity of phenomena that can arise with a mere dozen agent types—a complexity that would be difficult to capture without a rule-based platform with an integrated visualization environment.

A higher level of informational resolution is accessed when clicking on patches to reveal the connectivity structure of the underlying molecular species, as shown for the pre-Wnt case in Figure 6d. The polymeric cross-linked structure dominating the pre-Wnt regime is shown on the left of that panel, alongside with the second largest structure, revealing a completely segregated aggregate of Dvl. At this resolution, the structures do not exhibit (internal) state and site information, which would not be cognitively scalable. The next level of resolution consists in revealing detailed (local) state information in a split view for any agent that the user hovers over in the connectivity view. An interactively accessible resolution hierarchy increases the effectiveness of the patchwork view.

4.3 Visualization: the DIN

KaSim can be directed to compute influence matrices ${\overline{\Delta I}}_{r,s}(t,\tau )$, Equation (2), aggregated over user-specified time intervals $[t,t+\tau ]$. Typically, τ and increments in t are chosen so as to create overlapping intervals for smoothness. A time series of such matrices can be uploaded to the DIN visualization server (DIN-Viz) (https://github.com/CreativeCodingLab/DynamicInfluenceNetworks), where the DIN is presented as a node-link diagram, leveraging a force-directed layout to position related nodes and clusters near to each other. The nodes represent the rules and the links convey the influence of rules on each other, color-coded with red (green) signifying a negative (positive) influence. This visualization enables the topological analysis of rule-fluxes in a KaSim simulation at the chosen time step scale. By mapping the magnitude of influence to the link strength, highly mutually influential rules are closely grouped together visually. This provides insight as to which rules might (temporarily) conspire in producing a pathway.

In order to further facilitate the analysis of these highly related rules, we perform a clustering operation on the network based on the influence between rules to generate groups with a high inner influence, based on a user-selected threshold. The absolute value of influence between rules, determines the attractive link forces in the network. DIN-Viz maps the number of firings of a rule (during $[t,t+\tau ]$) to the node size, and the influence of one rule on another to the link width. We indicate the directionality of a link and the sign of the influence by using directional color gradients. Figure 7 uses yellow-to-red for negative and yellow-to-green for positive; colorblind-safe colormaps are also available.

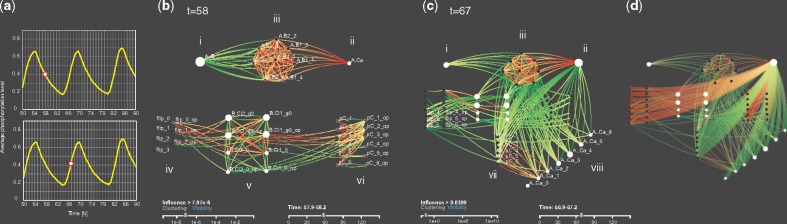
Fig. 7.

DIN and DIN-Viz. Panel (a): System level activity of the KaiABC oscillator. The ordinate is the overall fractional phosphorylation in the system, defined as ${\sum }_{i=1}^{n}i[C(i)]/(n{\sum }_{i=1}^n[C(i)])$, where $[C(i)]$ is the abundance of KaiC proteins whose p-level is i; here n = 6. Panels (b) and (c): DIN snapshots at the cycle phases indicated by the dots in panel (a). Panel (d): An interactive feature of the DIN-Viz highlights the targets of the influences originating from a rule when the user selects it

Details-on-demand are available for each link, showing the source and target, as well as the exact influence value; similarly, hovering over a rule (node) shows the rule name, the amount of self-influence and the rule’s top incoming and outgoing influences. The user may also choose to make visible the names of the rules as labels, either for all rules, or for interactively selected rules.

To represent the dynamism of the system, animation is used to update the influence between the rules, which in turn updates the edge weights, node sizes and cluster definitions. A time slider controls the current time step, enabling the user to move through time or jump to a particular time step. Standard playback controls animate the simulation so that the user can observe changes in the DIN over time.

Although force-directed layouts mitigate visual clutter in node-link diagrams, dense networks can still be difficult to make sense of—an issue that is exacerbated when representing large datasets. DIN-Viz enables the user to manually create a layout of nodes or entire clusters through relocating and ‘pinning’ them to specified locations. This reorganization reduces clutter, but also helps users to distribute rules and clusters in a way that is cohesive with their thought process during exploratory analysis. When pinned, the spatial positioning and grouping of selected rules and clusters is preserved over the course of the entire animation, over-riding the normal layout behavior.

While the mathematically defined clusters capture groups of rules that influence one another, there may be rules which are related through their behavior but lack a strong influence with one another. To solve this problem, we implement a ‘painting’ interaction. The user can provide a color marking to nodes to indicate that they are grouped together, and then insert them into an existing or newly created cluster. These categorical groupings, similar to the spatial groupings achieved through pinning, aid in the logical organization of rules during analysis by the user.

As a use case we analyze a rule-based model of the autonomous KaiABC circadian oscillator in the cyanobacterium Synechococcus elongatus. We forgo a detailed description of the molecular biology and of the Kappa model, which closely follows the literature (van Zon et al., 2007), in favor of a broader outline illustrating the reasoning enabled by the DIN and its visualization.

The KaiABC system consists of three proteins, A, B and C. C can be phosphorylated and dephosphorylated at multiple sites, thereby assuming distinct phosphorylation levels (p-levels for brevity). It also can switch between two conformational states, A and I. At low p-levels C prefers the A-state. The probability of a flip from A to I increases with increasing p-level. When C is in the A-state, it binds A with an affinity that decreases rapidly with increasing p-level. Upon binding A, C gets locked into the A-state, which promotes phosphorylation. As the p-level increases, A dissociates from C, allowing it to flip into the I-state, which favors dephosphorylation. This process results in a p-level oscillation of individual C molecules. Since these oscillations are not coordinated, no p-level oscillations will occur at the macroscopic level of the C-population. Co-ordination between C proteins is achieved by B, which binds C in the I-form. Once bound, B locks C into the I-form, facilitating dephosphorylation. Crucially, once bound to C, B also binds A with an affinity that is maximal at intermediate p-levels of C. By sequestering A in a mechanism that depends on C molecules that are late in the cycle, B holds back the phosphorylation of C molecules that are ahead in the cycle, statistically synchronizing the individual cycles and resulting in oscillations at the macroscopic population level (van Zon et al., 2007), as seen in Figure 7a.

Panels 7b and 7c summarize the insights from the animated DIN by focusing on two snapshots taken at the midpoints of the downward and upward leg of the macroscopic phosphorylation cycle (Fig. 7a). A detailed account of the animation and its interpretation is provided elsewhere (Forbes et al., 2018). The point to note here is the drastic difference in the influence structure of the system between the two time points. This difference characterizes the synchronization mechanism described above. The structure in the upper part of the influence network consists of three groups of activity. Group (i) is a single rule responsible for dissociating A from B; group (ii), also a single rule, is responsible for the binding of A to C in the A-state and group (iii) is a family of rules that control the binding of A to B at various p-levels of the C agent to which B is bound. At t = 58, the structure (i, ii, iii) is disconnected from the lower part of the DIN, which consists of several rule families that control state flipping of C (group iv), binding of B to C (v) and background phosphorylation and dephosphorylation (vi). The structure (i, ii, iii) shows that A agents, once liberated from B, tend to be reabsorbed by available B-C complexes, rather than binding to C-agents in the A-state. This situation puts the breaks on those C-agents that are ready to initiate the upward leg in their cycle. Once the lagging C-cohort has caught up, A becomes again available to bind C and facilitate its phosphorylation. This in turn raises the activity of rule families (vii) and (viii), which control various mechanisms of the dissociation of A from C. Families (vii) and (viii) were absent from the DIN at t = 58. In the thick of this new phase, t = 67, most A agents that dissociate from C can rebind other C agents in the A-state, resulting in the feeder stream from groups (vii) and (viii) toward (ii). In other words, group (iii), no longer captures free A agents. The structure (i, ii, iii) is effectively a systemic break pedal. It is pressed in the downward phase and released in the upward phase. This organizational switch is clearly recognizable and interpretable in the DIN-viz animation.

4.4 Causal analysis

As a proof-of-concept for causal compression of traces (Section 3.4), we consider a small rule-based model capturing early events in EGF signaling. The model consists of agents representing ligand EGF, receptor EGFR, Shc, Grb2, Sos and rules that capture well-known mechanisms of interaction between these proteins. The EOI is the recruitment of Sos. A typical run involves about 30 000 agents and generates traces of 0.5 M events with many occurrences of the EOI. The causal past of the first EOI in one of these traces is shown in Figure 8 and was obtained with the procedure described in Section 3.4. The subsequent causal compression with KaSA’s SAT solver succeeds in removing the many cyclical event sequences that return the system to equivalent states with respect to the EOI. The outcome is a compact interpretable and formal pathway fragment. In this case, the compressed story describes EGF binding, subsequent receptor dimerization and autophosphorylation, which is a pre-condition for the recruitment of Shc and its phosphorylation. Independent of the EGF-induced lineage, Sos binds Grb, which, again independently, binds the Shc that was phosphorylated along the EGF lineage. The two binding events, which can happen in any order, come together in completing the recruitment of Sos.

This story pertains only to one particular EOI in one particular trace. Other EOI instances and traces might compress to other stories. One challenge, therefore, is the aggregation of story statistics over long traces or large samples of short traces to determine the most salient pathways to the EOI. Rule-based modeling gathers mechanistic information about local interactions without preconceptions as to what constitutes a pathway; rather, pathways emerge dynamically from these interactions and our automated approach detects them.

5 Conclusion

In situations not vitiated by complexity, an assumed understanding of some key aspect of a system typically precedes modeling. In the case of complex interaction networks, however, an initial understanding at the systems level may not be readily available even with reasonable knowledge of local interactions. This leads to an inversion—from understanding precedes modeling to modeling precedes understanding—that significantly alters the character of models and the practice of modeling. The traditional criteria that establish a good model—insight, elegance, conciseness, conceptual fertility—are no longer available right away. Rather, a good model should be a data structure that constitutes a transparent, editable, formal and executable representation of the facts it rests upon. This is a prescription for replacing a world we don’t understand with a model we don’t understand but that is easier to analyze and experiment with. The challenge is to develop mathematical techniques and a sound software infrastructure for analyzing, visualizing, manipulating, simplifying—in short, reasoning with—models that are like empirical objects.

We see two major challenges that rule-based approaches need to address. The first consists in developing formal and computational techniques for constructing explanations. The glimpse on causality in Sections 3.4 and 4.4 is just a beginning. Second, languages like Kappa and BioNetGen are not knowledge representations. Tying modeling to knowledge representation requires a structured staging area designed to formally organize the abstraction process leading from biochemically rich and grounded descriptions to logical, ungrounded, but executable expressions (Basso-Blandin et al., 2016; Harmer et al., 2017). Modeling occurs, to a large extent, at that intermediate staging level. In addressing challenges like these, there will be ample need for innovative visualization.

Funding

This work was sponsored by the Defense Advanced Research Projects Agency (DARPA) Big Mechanism Program and the US Army Research Office under grant numbers W911NF-14-1-0367 and W911NF-14-1-0395.

Conflict of Interest: none declared.