Abstract
Motivation
A large number of newly sequenced proteins are generated by the next-generation sequencing technologies and the biochemical function assignment of the proteins is an important task. However, biological experiments are too expensive to characterize such a large number of protein sequences, thus protein function prediction is primarily done by computational modeling methods, such as profile Hidden Markov Model (pHMM) and k-mer based methods. Nevertheless, existing methods have some limitations; k-mer based methods are not accurate enough to assign protein functions and pHMM is not fast enough to handle large number of protein sequences from numerous genome projects. Therefore, a more accurate and faster protein function prediction method is needed.
Results
In this paper, we introduce DeepFam, an alignment-free method that can extract functional information directly from sequences without the need of multiple sequence alignments. In extensive experiments using the Clusters of Orthologous Groups (COGs) and G protein-coupled receptor (GPCR) dataset, DeepFam achieved better performance in terms of accuracy and runtime for predicting functions of proteins compared to the state-of-the-art methods, both alignment-free and alignment-based methods. Additionally, we showed that DeepFam has a power of capturing conserved regions to model protein families. In fact, DeepFam was able to detect conserved regions documented in the Prosite database while predicting functions of proteins. Our deep learning method will be useful in characterizing functions of the ever increasing protein sequences.
Availability and implementation
Codes are available at https://bhi-kimlab.github.io/DeepFam.
1 Introduction
Protein sequences from genome projects have been growing rapidly over the decades. However, biological experiments are too expensive to characterize functions of the exponentially increasing protein sequences. Thus, a majority of protein sequences are yet to be characterized for their functional roles. A practical and standard approach is to infer the function of a protein by comparing to well-annotated protein sequences. Comparing evolutionary related sequences requires resolving technical problems such as how to compare and score amino acids, i.e. scoring scheme, and how to determine an optimal alignment of two protein sequences. These issues have been successfully integrated into a single computational framework of probabilistic modeling (Durbin et al., 1998). The most widely adopted method to compare two protein sequences is Smith-Waterman algorithm (Smith and Waterman, 1981) that computes an optimal local alignment using the dynamic programming technique. However, comparing two distantly related proteins cannot be done effectively by the local sequence alignment. Distantly related proteins can be effectively identified by using protein families because a query sequence may share similar features with some of proteins in the family or would be related to member sequences in a transitive manner. Thus, computational techniques to model multiple protein sequences of similar biochemical functions have been developed over several decades.
1.1 Modeling protein families
Computational methods for modeling protein families can be grouped into two categories: alignment-based and alignment-free protein family modeling methods.
1.1.1 Alignment-based protein family modeling
Comparing multiple sequences needs a computational scheme. The most widely used technique for comparing multiple sequences is the alignment based method. A correct alignment of multiple sequences of similar function is not only useful for modeling protein families but also for determining functions of uncharacterized proteins. Unlike pairwise sequence alignment methods, the computational complexity of aligning multiple sequences increases exponentially to the number of sequences and it is actually known as an NP-Complete problem (Wang and Jiang, 1994). Thus, heuristic and approximation algorithms, such as ClustalW (Thompson et al., 1994), Omega (Sievers et al., 2014) and MUSCLE (Edgar, 2004), are widely used to compute an alignment of multiple sequences. A multiple sequence alignment itself provides valuable information on sequence conservation but needs additional computation algorithms to extract and model conserved regions. For example, manually determining conserved regions in a multiple sequence alignment is not always possible and often incorrect, thus there are tools to compute conserved regions in an multiple sequence alignment, e.g. ARCS (Song et al., 2006). Modeling protein families from multiple sequence alignment also requires sophisticated methods. A major challenge is to deal with insertions and deletions of amino acids in multiple sequence alignment. These computational challenges are nicely handled by using profile Hidden Markov Model (pHMM) (Eddy, 1998) that uses position-specific modeling of columns and modeling of indels by defining explicit insertion and deletion states. pHMM is the most accurate modeling technique and is used by the widely used protein family database, PFam (Bateman et al., 2004).
1.1.2 Alignment-free protein family modeling
The alignment-based methods, though successful, have several limitations which will be discussed in the next section. Thus, there have been significant efforts to develop alignment-free family modeling methods. A major issue of the alignment-free method is a feature vectorization, how to convert raw sequence into numerical feature vector. The most successful approach is to use k-mers, k amino acids, as features and uses all possible k-mers as a feature vector (Vinga and Almeida, 2003). In some cases including remote homology detection, alignment-free methods show better performance than alignment-based methods (Lingner and Meinicke, 2006; Strope and Moriyama, 2007).
1.1.3 Limitations of the current protein modeling methods
As aforementioned, alignment-based methods are useful but have some issues. First, the alignment-based protein family modeling requires a correct alignment of multiple sequences but it is hard to compute the multiple sequence alignment correctly. There are two major reasons that make multiple sequence alignment difficult; computing optimal multiple sequence alignment is a NP-hard problem and methods to score more than two amino acids correctly are not available (i.e. no scoring matrices for multiple amino acids). Thus, existing multiple sequence algorithms are heuristics. Another issue is that the multiple sequence alignment is a global alignment algorithm. However, there are many cases that the same domain is repeated multiple times and different domains appear inconsistently in each of the multiple sequences. Specifically, sequences can have recombined conserved regions by rearrangements, inversion, transposition and translocation without loss of the biochemical function (Vinga and Almeida, 2003). In this case, a global alignment is not possible and, even if possible, much of information is lost while aligning sequences globally.
Alignment-free methods also have critical limitations. First, although using k-mers may be able to handle arbitrary numbers of domains, k-mer approaches lose the order information in biological sequences. Biological sequences cannot be in a random order even though there are few exceptions like domain shuffling, and this is why sequence alignment methods have been used for a long time in the biology community. Second, k-mer approaches require exact matches but it is well known that different amino acids can share biochemical properties, which is modeled as a substitution matrix like BLOSUM(Henikoff and Henikoff, 1992). This is a critical issue since the k-mer approaches do not utilize the biological information of sequences. Lastly, there is no guideline for determining the length of k when using k-mer approaches. This can be easily understood in terms of sensitivity and specificity. The shorter k is, the sensitivity of a k-mer gets better but the specificity becomes worse exponentially. The longer k is, the specificity of a k-mer becomes gets better but the sensitivity gets worse dramatically. This is an unresolved machine learning problem. In general, k-mer based approaches are good to speed sequence alignment by using k-mers as anchors for sequence alignment but they are not successful in modeling protein families. In a recent article (Zielezinski et al., 2017), advantages and disadvantages of the alignment free methods are extensively discussed. In general, alignment-based methods perform better than alignment-free methods, which is why the current protein family databases are predominantly constructed by using alignment-based methods including Pfam (Bateman et al., 2004) and TIGRFAM (Haft et al., 2003).
1.2 Motivation and our approach
As we discussed in the previous section, both alignment-based and alignment-free methods for modeling protein families have limitations. Thus, a new approach to model protein families is needed. We leveraged the recent success in the deep learning community (Alipanahi et al., 2015) to develop a novel method for modeling protein families. Introduced in this paper is DeepFam, a deep learning based alignment-free method for modeling sets of protein sequences or protein families. The predictive power of our model is measured by performing cross validation tests on how good the protein family membership assignments of test sequences or protein function predictions can be made. Thus, in this article, we will use terminologies such as ‘modeling protein families’ and ‘protein function prediction’ in this context. Later in this article, we will show that the protein function prediction is done by detecting motifs, functional or characterizing subsequences, which we interpret that DeepFam is able to extract functional information from a protein sequence.
DeepFam has several merits. First, DeepFam directly generates feature vectors from a raw sequence without requiring a multiple sequence alignment. Second, DeepFam can model arbitrary subsequences in a position-specific and a stochastic manner by using convolution units, functioning similarly as position-specific scoring matrix used in alignment-based methods. Third, DeepFam solves the issue of determining length of a single unit subsequence by using variable-size convolution unit and by using a fully-connected neural network, combining nearby short captured conserved regions. Lastly, DeepFam is an end-to-end model, which extracts features and makes a prediction simultaneously.
2 Materials and methods
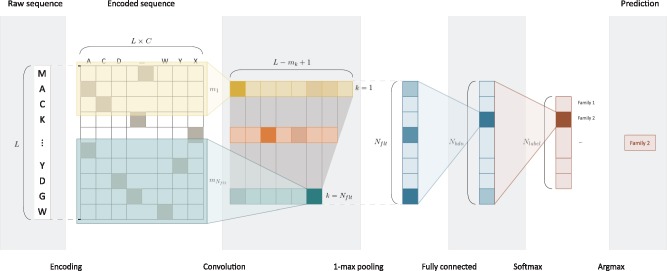
In this section, we describe DeepFam and other existing methods that were used as baselines for performance comparison. DeepFam is an alignment-free protein family prediction model, taking a raw protein sequence as input and inferring family of the protein as output. From the sequence, DeepFam first calculates the existence score of conserved regions by using convolution layer and 1-max pooling layer. The hidden units have the power of detecting conserved regions since the hidden units that are activated frequently for proteins of the same family indicate which k-mers are frequently used for the family. DeepFam has an additional dense layer (fully-connected layer) to extract longer or high-order features from the existences of conserved regions. A feature vector is generated as the output of the dense layer and the multinomial logistic regression computes probabilities of being the member of the each family from the feature vector. The architecture of DeepFam is illustrated in Figure 1. The detail of how the model works and how to train the model is described in Section 2.1 (Table 1).
Fig. 1.
The overview of DeepFam model. It is a feedforward convolution neural network whose last layer represents the probabilities of each family. convolution layer and 1-max pooling layer calculate a score (activation) of the existence of a conserved regions. The next layer is fully-connected neural network which can detect longer or complex sites. In order to infer the probability of each family, the last layer is designed as softmax layer (multinomial logistic regression), generally used for multi-class classification
Table 1.
Notations of variables
| L | Maximum length among all sequences |
| charset | {A, C, D, E, F, G, H, I, K, L, M, N, P, Q, R, S, T, V, W, Y, X} |
| C | Size of charset = 21 |
| N data | Number of sequences |
| Nlabel | Number of families |
| labelset | Set of families |
| Nflt | Number of convolution units |
| Nhdn | Number of hidden units on fully connected layer |
| mk | Length of kth convolution kernel |
2.1 DeepFam
2.1.1 Encoding
To process sequences in a batch, we made the length of all training and test sequences the same by inserting zero padding at the end of the shorter sequences. The raw dataset is the set of pairs of a protein sequence and a family label where . To encode data into numerical values, we applied one-hot encoding to the label and also apply similar approach to the sequence defined as
| (1) |
| (2) |
where and . This encoding follows IUPAC amino acid code notation. As a result of preprocessing, pairs of the sequences and family labels are transformed into pairs of encoded sequence array and label array .
2.1.2 Convolution layer
Convolution layer is the first layer of our model, directly connected to the encoded input layer. Convolution layer converts an encoded protein sequence into the vector of features from sequence. Convolution is operated by windowing each convolution unit over the encoded input sequence. Therefore, for the encoded sequence array of length L, the output size of the convolution layer is reduced to for each mk length unit, and the activation value is defined as
| (3) |
where hk is array and Wk is array for . ReLU activation function is used, defined as
| (4) |
2.1.3 1-Max pooling layer and dropout
There are several pooling strategies for convolution neural network such as max pooling and average pooling (Boureau et al., 2010). To focus on the existence of conserved regions, we used 1-max pooling which takes one maximum activated value among neurons, approaching similarly as DeepBind did (Alipanahi et al., 2015).
| (5) |
Dropout (Srivastava et al., 2014) stochastically removes some neurons at training time and has power of regularization. We adopt dropout after the 1-max pooling layer to prevent overfitting and to train robust features.
2.1.4 Dense layer and softmax layer
To combine features from sequence and to extract high-order features, we employ additional dense hidden layer whose length is Nhdn and weight is array. The output value of this layer is calculated as
| (6) |
where . A softmax layer is connected with a dense layer whose weight matrix is . The softmax layer is used to calculate probability over each family class, defined as
| (7) |
| (8) |
where .
2.1.5 Training
The loss function for the DeepFam model is calculated as cross-entropy with L2 regularization on last layer, defined as
| (9) |
We adopt commonly used techniques for learning a deep feedforward network. First, since all the training data cannot be loaded in the memory and calculating the gradients of all the training data is too slow, we use the mini-batch gradient descent technique, a general optimization technique for training deep neural network. Another technique is the batch normalization (Ioffe and Szegedy, 2015) that accelerates stochastic optimization and has a power of regularization by reducing internal covariate shift. For all layers having activation function such as the convolution layer and the dense layer, batch normalization is adopted before calculating activations. For example, activation of the fully connected layer (Y) is calculated as from input X without batch normalization, while the activation is calculated as with batch normalization. The third technique is Xavier initialization (Glorot and Bengio, 2010) that helps activation to propagate well through the network by initializing weights between adjacent layers, considering the number of both side of neurons. For an optimization algorithm, we use Adam optimization (Kingma and Ba, 2015) which is the state-of-art gradient descent optimization algorithm that works well for sparse gradient. Adam computes different and adaptive learning rates for each parameter by utilizing previous gradients and squared gradients which can alleviate the problem of local optima with stochastic gradient descent. The optimization terminates after training 20 epochs of the train dataset.
2.1.6 Hyperparameters
There are several hyperparameters including the number and the length of convolution kernels, the number of perceptrons in the fully connected layer, a coefficient of regularization, dropout rate, learning rate and batch size. Since there are too many hyperparameters, it is not possible to search optimal values for all parameters exhaustively. Thus, we set the widely used default settings for most of the parameters that are known to perform well in practice. However, the number and the length of convolution units and the number of hidden units in a fully connected layer were parameters specific to DeepFam, so we chose the parameter setting by considering all combinations of candidate parameters. The lengths of the convolution units that we considered were (8 different sizes) and the number of convolution units of each length were tested among , so the total number of all convolution units were respectively. For the number of hidden units in the fully connected layer, we tested with settings of {1000, 1500, 2000}. For each of possible 12 models with settings of and , we chose the best performing model in a one of the cross validation set. The other hyperparametes were set as follows: coefficient of regularization (λ) , dropout rate , learning rate , batch size .
2.2 Existing protein modeling methods used for performance comparison
In this section, we provide a detailed explanation on the three existing protein modeling methods, profile Hidden Markov Model, k-mer based logistic regression and the Provec-based logistic regression. These methods were used to compare classification performances against DeepFam.
2.2.1 Profile Hidden Markov Models
For the alignment-based algorithm, we built profile Hidden Markov Models (pHMM), the state of the art modeling technique for protein families. To build the model, we first used MUSCLE to generate Nlabel multiple sequence alignments. Then we used HMMER to construct pHMM model. For each of Nlabel alignments, we used hmmbulid to build Hidden Markov Model of each family. From individual family models, we concatenated them into a single file and compressed them into single Hidden Markov Model database, indexed with hmmpress. For each test protein, hmmscan generated candidate family assignments of the sequence and the most probable family of which has smallest E-value that represents the significance of a sequence matched to the family model was selected as output. We used MUSCLE v3.8 and HMMER v3.1 with default options. For some sequences, HMMER was not able to assign family label since no E-value was generated from any of the family models. We treated these cases as incorrect predictions.
2.2.2 K-mer based logistic regression
For a benchmark of alignment-free algorithms, we implemented a k-mer based logistic regression model in Tensorflow (Abadi et al., 2016). For preprocessing, raw sequence with length l was split into words considering the overlaps, defined as . For all bag of the k-mers (base is 26 because the FASTA format allows 26 amino acid characters), the frequency of each word was calculated as
| (10) |
| (11) |
A vector of k-mer frequencies was given as input to the multinomial logistic regression model. The loss function was defined as cross entropy of target labels and predictions with small L2-regularization () to prevent overfitting. The other settings including optimization and the size of mini-batch were same as in DeepFam.
2.2.3 Protvec based logistic regression
We used another k-mer based model, adopting Protvec (Asgari and Mofrad, 2015). Protvec converts 3-mers into 100 numerical values that reflect spatial closeness of 3-mers. Implementation of Protvec is available at the archive, referenced in original publication. For preprocessing, raw sequence with length l was split into l – 2 words considering overlaps defined as . With Protvec embedding defined as a function , S was transformed to . The feature vector was calculated by sum of all the embedded 3-mers, the same method as Protvec did in the original publication. Therefore, an input feature vector is defined as . The cross entropy with small L2-regularization () was used as loss function as same as the k-mer based logistic regression model. The other settings were the same as in DeepFam.
2.3 Datasets
For a fair comparison, we chose protein family databases that were not built by any of four methods to be evaluated. For example, PFam (Bateman et al., 2004), one of the most famous database, is excluded because PFam is based on profile Hidden Markov Model. Two datasets, consisting of Clusters of Orthologous Groups of proteins (COG) database and G Protein-Coupled Receptor (GPCR) dataset, were used to compare performance of models. Recently, COG expanded the database using PSSM generated from the 2003 version of COG. Thus, the alignment based method has some advantage over the non-alignment based methods in the experiment using COG. Later, we will show that the two datasets are independent and have different characteristics, which make our experiments more comprehensive.
2.3.1 Clusters of orthologous groups of proteins dataset
Clusters of Orthologous Groups of proteins (COGs) database is one of the most widely used functional annotation databases. COG database has been available to the public since 1997 and the latest version is published in 2014 (Galperin et al., 2015). Protein family assignment was done by utilizing pairwise sequence comparisons in the whole genome context, genome-wide bidirectional best hits (BBH) and then a requirement of forming a triangle of BBHs in three genomes. Use of the genome context information in a triangular way was effective in recognizing distant homologs (Galperin et al., 2015). The functional curation of the clusters was done manually to make the annotation of COG database more reliable. Each COG family contains different number of proteins (from 1 to 10 632) while the proteins vary in its sequence length (from 21 to 29 202). In order to formulate a multi-class classification problem, we discarded proteins which were assigned to more than one family, resulting in 1 674 176 proteins from 4659 families. We filtered out long sequences that were longer than 1000 amino acids because lengths of protein sequences varied considerably but most of the sequences are shorter than 1000 amino acids. As a result, only 1.3% of sequences were filtered out, resulting in 1 652 408 proteins from 4655 families. The number of proteins belongs to each family is highly biased, thus we discarded some families that did not satisfy certain thresholds. For extensive experiments, we tested with three thresholds for the minimum number of sequences, 100, 250 and 500, resulting in 1 565 976 proteins with 2892 families, 1 389 595 proteins with 1796 proteins and 1 129 428 proteins with 1074 families, respectively. We denoted these datasets as COG-100-2892, COG-250-1796 and COG-500-1074.
2.3.2 G protein-coupled receptor dataset
The G protein-coupled receptor (GPCR) is a well studied protein superfamily that consists of diverse proteins with seven highly conserved transmembrane segments (Davies et al., 2007). To categorize divergent proteins, the GPCR proteins are hierarchically annotated. We used one of the biggest GPCR dataset, GDS (Davies et al., 2007). The authors of Davies et al. (2007) did GPCR family prediction experiments with 8222 protein sequences belonging to 5 families, 38 sub-families and 86 sub-subfamilies.
3 Experiments and results
For label and prediction , the overall accuracy is calculated as below,
| (12) |
where I is an indicator function defined in Equation (11).
We compared the predictive power of the methods using the COG dataset and GPCR dataset. All three methods described in Section 2.2 were trained with the same data that were used to train DeepFam. The profile Hidden Markov Model, 3-mer based logistic regression model and ProtVec-based logistic regression model are denoted as pHMM, 3-mer LR and ProtVec LR, respectively.
The experiments were performed with a GeForce GTX 980 GPU machine and Intel Xeon CPU E7-4850 v4 @ 2.10 GHz CPU machine having 128 cores and 504 G RAM. DeepFam, 3-mer LR and ProtVec LR were trained and tested on a GPU machine for most of the experiments except for comparing execution time. The other experiments including training and testing pHMM were done on the CPU machine. All methods were tested on CPU machine when measuring execution time for fair comparison.
3.1 Evaluation of clusters of orthologous groups prediction
The accuracy of the methods was measured in a 3-fold cross-validation experiment using the COG dataset. The proteins of each family were equally split into three folds while preserving the ratio of the families. Before evaluating the DeepFam model, we explored different combinations of hyperparameters and determined a DeepFam model as described in Section 2.1.
Figure 2 presents the error rate of each hyperparameter combination in one of the validation set. With the number of hidden units fixed, DeepFam predicted family labels more accurately as the number of convolution units increased. Likewise, with the number of convolution units fixed, DeepFam predicted better as the number of hidden units increased. However, if the number of the convolution units were not enough, specifically when the number is 800 or 1200, the model with the large number of hidden units showed worse performance.
Fig. 2.
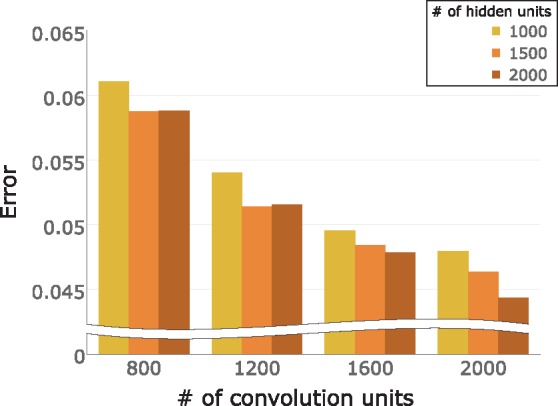
The error rates of DeepFam models with different hyperparameter combinations. The error rate is calculated as , which means that the lower the error is, the better the hyperparameter setting is
DeepFam showed the best accuracy for the COG-500-1074 and COG-250-1796 datasets but showed slightly worse accuracy for the COG-100-2892 dataset than pHMM. In general, pHMM performed second best (Table 2). This is no surprise since it is widely accepted that pHMM is the most accurate protein function modeling method. The k-mer based approach and the Protvec based approach did not perform well which shows the limitation of the existing alignment-free methods.
Table 2.
Prediction accuracy (%) comparison of COG dataset
| Dataset | COG-500-1074 | COG-250-1796 | COG-100-2892 |
|---|---|---|---|
| DeepFam | 95.40 | 94.08 | 91.40 |
| pHMM | 91.75 | 91.78 | 91.67 |
| 3-mer LR | 85.59 | 81.15 | 75.44 |
| Protvec LR | 47.34 | 41.76 | 37.05 |
Bold indicates the best performance for each dataset.
As the number of families increased, accuracies of most methods tended to decrease, which is the current research topic in machine learning community, known as the high multi-class problem (Gupta et al., 2014). The most important issue is how sensitive the modeling method is to the number of classes to be determined. The accuracy of 3-mer LR and Protvec LR dropped almost 10% as the number of families increased from 1074 (COG-500-1074 dataset) to 2892 (COG-100-2892 dataset). The performance of DeepFam, though it is an alignment free method, decreased only 4%. As expected, the alignment-based method, pHMM, was most stable to the number of families.
3.2 Evaluation of G protein-coupled receptor family prediction
We also evaluated the modeling methods in another 10-fold cross-validation experiment. Because of the capacity limitation of the GPU machine that we used, it was not possible to train DeepFam for 284 sequences whose lengths were longer than 1000 amino acids. To overcome this issue, a 10-fold cross validation experiment was designed in a special way that DeepFam was in a disadvantageous situation. The long 284 sequences were first excluded for training, but later appended to the test set of each cross validation. This 10-fold cross validation experiment penalized DeepFam since long sequences were never seen in any training set but always included in test sets.
To evaluate the performance for hierarchical classes, we first trained 86 sub-subfamily level models. From the sub-subfamily prediction, we evaluated sub-family and family level prediction in a bottom-up approach, following up the hierarchy of GPCR labels. For example, the ‘BLT2’ sub-subfamily is treated as ‘Leuko’ in family level and treated as ‘class A’ in family level. We compared 14 modeling methods that included a majority of machine learning methods while 10 machine learning algorithm results were copied from Davies et al. (2007). DeepFam achieved the best accuracy at all levels as shown in Table 3 while pHMM performed the second best. Prediction accuracies of all methods decreased as the level became deeper, which showed similar results with COG experiment.
Table 3.
Prediction accuracy (%) comparison of GPCR dataset in each level
| Method | Family | Sub-family | Sub-subfamily |
|---|---|---|---|
| DeepFam | 97.17 | 86.82 | 81.17 |
| pHMM | 95.77 | 85.39 | 78.50 |
| 3-mer LR | 95.59 | 83.51 | 77.06 |
| Protvec LR | 88.58 | 74.98 | 67.32 |
| Selective top-down* | 95.87 | 80.77 | 69.98 |
| Naive Bayes* | 77.29 | 52.60 | 36.66 |
| Bayesian network* | 85.24 | 64.27 | 50.69 |
| SMO* | 80.21 | 56.67 | 35.96 |
| Nearest Neighbour* | 95.87 | 78.68 | 69.40 |
| PART* | 93.27 | 78.73 | 65.68 |
| J48* | 92.93 | 77.49 | 64.30 |
| Naive Bayesian Tree* | 93.07 | 76.92 | 64.78 |
| AIRS2* | 91.98 | 74.58 | 62.68 |
| Conjunctive Rules* | 76.19 | 49.93 | 16.49 |
Note: Results marked with *are extended from Davies et al. (2007).
Bold indicates the best performance for each dataset.
3.3 Evaluation of execution time over the number of families
We also measured the execution time of the methods, i.e. the elapsed time to get the results from query sequences, which is one of the important issues for a real-world problem when a large number of sequences should be processed. We analyzed the execution time in two aspects; the absolute execution time and the scalability to the number of the families. The absolute execution time was measured in a setting of a fixed number of sequences and a fixed number of families. Scalability was evaluated how much more time each method required for prediction as the number of protein families increased. We used pre-trained models from the COG prediction experiment, described in Section 3.1. A separate model was trained for each dataset, COG-500-1074, COG-250 1796 and COG-100-2892. We measured the execution time by averaging 5 independent trials, each of them were measured with randomly selected 1000 sequences. The experiment was done on a CPU machine with multi-threading. DeepFam, 3-mer LR and Protvec LR could utilize all CPU cores as Tensorflow uses all possible computing resources without additional implementation. pHMM also could use multiple cores by omitting ‘–cpu’ options of HMMER as described in the HMMER documentation.
The result in Figure 3 shows that DeepFam is slower than simple alignment-free methods but much faster than pHMM. For scalability, all the alignment-free methods were not affected much by the number of families while pHMM took significantly more time as the number of families increased. Note that DeepFam, unlike the other alignment free methods, achieved the scalability without sacrifice of predictive power.
Fig. 3.
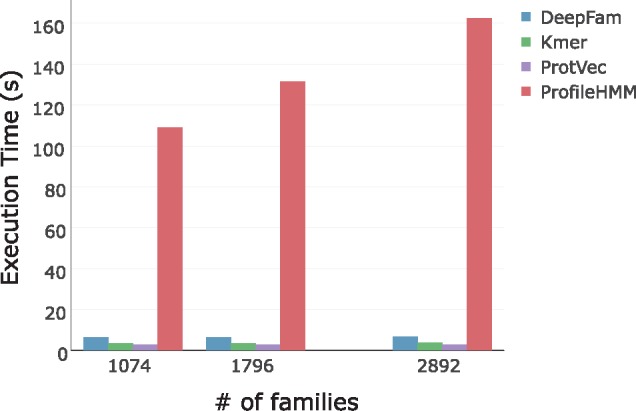
The average elapsed time of five trials to predict families of 1000 protein sequences for each method. Three independent models were built for each method, which were trained to predict one of 1074, 1796 and 2892 families by using COG-500-1074, COG-250 1796 and COG-100-2892 dataset respectively
3.4 Interpreting the performance of the DeepFam model
In the experiments with two large datasets of different characteristics, DeepFam had better predictive power than existing methods. We looked at why DeepFam performed well and we found that the high accuracy of DeepFam came from the power of capturing conserved regions. With a pre-trained DeepFam model, we visually inspected some of convolution units that were activated for a specific family and verified the captured regions were highly conserved in the family. Furthermore, we found that the conserved regions captured at the convolutional units were functionally related to the family.
The experiment was done as follows. We selected a family COG0517 in the COG database and PS51371 in the Prosite database (Sigrist et al., 2012), both annotated as ‘CBS domain’. To visualize convolution units activated for a specific family, we utilized the similar approach as used in DeepBind. We trained additional DeepFam model with COG-500-1074 dataset, using 90% of dataset to train the model and using rest 10% to monitor overfitting. While feeding the sequences that belonged to the family to trained DeepFam, we gathered all sub-sequences that have positive activation on each convolution unit. We filtered out infrequently activated convolution units that were activated in less than 70% of total sequences. Top 30 highly activated convolution units were selected as the convolution units that were most related to the family. For each of 30 convolution units, WebLogo software (Crooks et al., 2004) was used to generate logo images of the corresponding sub-sequences from convolution unit.
To determine conserved regions of COG0517 family, we utilized one of the widely used software MEME (Bailey et al., 2009) that predicts ungapped motifs in a set of sequences. We sampled 500 sequences from COG0517 sequences because of the input size limitation of MEME. We ran MEME with ‘-nmotifs 30 -maxw 36 -minw 8’ options to make motifs detected by MEME to be comparable to the conserved regions determined by DeepFam. For comparison and discussion, we selected 2 top ranked motifs, each of them denoted as MEME-1 and MEME-2.
From logos generated by DeepFam, we could identify two convolution units corresponding to two MEME motifs, MEME-1 and MEME-2. We denoted two convolution units as COG-DF-1552 and COG-DF-921 because the logos are generated from convolution unit of indices 1552 and 921 with sequences belonging to COG0517. The logos are shown in Figure 4; the first logo was generated from MEME and the second logo was generated from DeepFam with COG0517 sequences for both Figure 4a and b. This result shows that DeepFam has a power of detecting conserved regions or motifs related to the family.
Fig. 4.
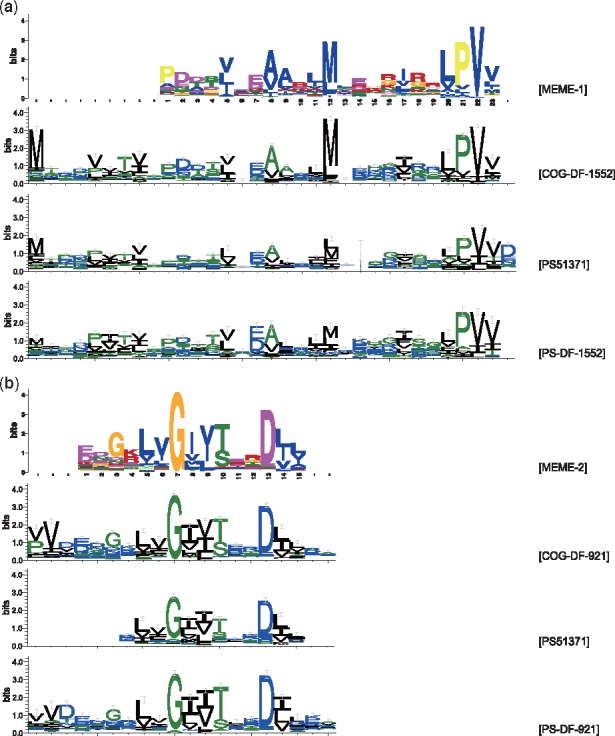
Visualizing MEME motifs, convolution units responsive to COG0517 sequences, PS51371 motifs and convolution units responsive to PS51371 sequences. (a) depicts the highest rank MEME motif and corresponding logos and (b) depicts the second highest rank MEME motif and corresponding logos. Only selected conserved regions are shown for PS51371 motifs because raw PS51371 logo is too long and has too many unconserved regions as PS51371 logo is generated from multiple sequence alignment
Additionally, we found that captured regions were functional family related regions, not a common repeat. To confirm this finding, we generated logos from another sequences that were independent to COG database but whose functional annotation were also ‘CBS domain’. Prosite provides a profile of domain with UniProtKB/Swiss-Prot (Apweiler et al., 2004) protein sequences that are matched to the profile. We downloaded the multiple sequence alignment of PS51371 and generated logo with WebLogo. Unlike other logos we generated, logo from PS51371 had gaps because it was generated from the multiple sequence alignment. As the whole length was too long to depict, PS51371 logos in Figure 4 (third logos) were modified to show un-gapped conserved regions only.
The last logos in Figure 4, prefixed with PS-DF, were generated from DeepFam that were pre-trained with COG sequences but examined by 329 Prosite sequences. We downloaded 366 Prosite sequences with annotation of PS51371 pattern signatures. To make sure that all sequences were never seen to DeepFam, we removed 34 sequences that were also existed in the COG database and further removed 3 sequences whose lengths were over 1000 amino acids. As shown in Figure 4, DeepFam was also able to catch subsequences corresponding to the documented PS51371 pattern signatures that are annotated as a motif for COG0517 but seen at the time of training. This experiment shows that DeepFam has a power of capturing conserved regions related to the protein family.
4 Discussion
We presented DeepFam, a deep learning based alignment-free protein family modeling method. When the number of proteins in the family is sufficient for training, DeepFam achieves better prediction accuracy than the state-of-the-art methods while preserving the advantage of alignment-free methods, i.e. fast runtime. DeepFam has several desirable characteristics. First, DeepFam is more accurate than both existing alignment-based and alignment-free methods in extensive experiments with the COG dataset and the GPCR dataset. DeepFam is an alignment-free method and it is scalable without sacrificing the modeling power. In addition, we showed that DeepFam can detect conserved subsequences while classifying query sequences. Since a huge number of protein sequences are generated from many genome projects, a fast and accurate protein family modeling method is very important. Thus, we believe that DeepFam will be very useful in this regard.
There are several issues that are left as the future work. First, like the k-mer-based approach, a convolutional neural network approach encounters a problem of choosing the optimal length of convolution units. To alleviate this problem, we used different convolution units varying 8–36. A fully connected layer in DeepFam is used to aggregate information captured by multiple distinct filters. This approach worked well in our experiments even with small number of the layers but could be improved with other methods. One possible alternative is to utilize Google inception modules that showed an excellent performance in the ILSVRC 2014 competition (Szegedy et al., 2015) by making the model deeper without explosion of model parameters. Second, different pooling strategies need to be explored. For example, use of k-max pooling showed a good performance for modeling sentences (Kalchbrenner et al., 2014). Use of k-max pooling increases the model complexity, thus it should be tested extensively. Third, unlike COG database, most of the protein family databases, such as GPCR database, hierarchically classify a protein at multiple levels. We simply predicted multiple levels separately in our experiment. By adopting the hierarchical classification or multi-task algorithm in deep learning, DeepFam model may be extended to predict family of protein at multiple levels. Finally, changing the model to the multi-label problem would be more useful because some proteins have more than one function. Datasets that we used in our experiments, though they are representative protein databases, have few proteins of multiple functions, thus DeepFam and the state of the art pHMM achieved very good accuracies. However, to characterize proteins of multiple functions, a new study is necessary.
Funding
This work was supported by Collaborative Genome Program for Fostering New Post-Genome industry through the National Research Foundation of Korea (NRF) funded by the Ministry of Science ICT and Future Planning [NRF-2014M3C9A3063541], Next-Generation Information Computing Development Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT (No. NRF-2017M3C4A7065887) and Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIP) [B0717-16-0098, Development of homomorphic encryption for DNA analysis and biometry authentication].
Conflict of Interest: none declared.
References
- Abadi M. et al. (2016) TensorFlow: A System for Large-scale Machine Learning. In: Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation (OSDI-16), pp. 265–283.
- Alipanahi B. et al. (2015) Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat. Biotechnol., 33, 831–838. [DOI] [PubMed] [Google Scholar]
- Apweiler R. et al. (2004) UniProt: the universal protein knowledgebase. Nucleic Acids Res., 32, D115–D119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asgari E., Mofrad M.R. (2015) Continuous distributed representation of biological sequences for deep proteomics and genomics. PloS One, 10, e0141287.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey T.L. et al. (2009) MEME SUITE: tools for motif discovery and searching. Nucleic Acids Res., 37(suppl. 2), W202–W208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bateman A. et al. (2004) The Pfam protein families database. Nucleic Acids Res., 32, D138–D141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boureau Y.-L. et al. (2010) A theoretical analysis of feature pooling in visual recognition. In: Proceedings of the 27th international conference on machine learning (ICML-10), pp. 111–118.
- Crooks G.E. et al. (2004) WebLogo: a sequence logo generator. Genome Res., 14, 1188–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies M.N. et al. (2007) On the hierarchical classification of G protein-coupled receptors. Bioinformatics, 23, 3113–3118. [DOI] [PubMed] [Google Scholar]
- Durbin R. et al. (1998) Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids. Cambridge, UK: Cambridge University Press. [Google Scholar]
- Eddy S.R. (1998) Profile hidden Markov models. Bioinformatics, 14, 755–763. [DOI] [PubMed] [Google Scholar]
- Edgar R.C. (2004) MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res., 32, 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galperin M.Y. et al. (2015) Expanded microbial genome coverage and improved protein family annotation in the COG database. Nucleic Acids Res., 43, D261–D269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glorot X., Bengio Y. (2010) Understanding the difficulty of training deep feedforward neural networks. In: Proceedings of the thirteenth international conference on artificial intelligence and statistics (AISTATS 2010), vol. 9, pp. 249–256.
- Gupta M.R. et al. (2014) Training highly multiclass classifiers. J. Mach. Learn. Res., 15, 1461–1492. [Google Scholar]
- Haft D.H. et al. (2003) The TIGRFAMs database of protein families. Nucleic Acids Res., 31, 371–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S., Henikoff J.G. (1992) Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA, 89, 10915–10919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioffe S., Szegedy C. (2015) Batch normalization: Accelerating deep network training by reducing internal covariate shift. In: Proceedings of the 32nd International Conference on Machine Learning (ICML-15), pp. 48–456.
- Kalchbrenner N. et al. (2014) A convolutional neural network for modelling sentences. In: Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics (ACL-2014), pp. 655–665.
- Kingma D., Ba J. (2015) Adam: a method for stochastic optimization. In: Proceedings of the 3rd International Conference on Learning Representations (ICLR-15), arXiv preprint arXiv: 1412.6980.
- Lingner T., Meinicke P. (2006) Remote homology detection based on oligomer distances. Bioinformatics, 22, 2224–2231. [DOI] [PubMed] [Google Scholar]
- Sievers F. et al. (2014) Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega. Mol. Syst. Biol., 7, 539.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigrist C.J. et al. (2012) New and continuing developments at PROSITE. Nucleic Acids Res., 41, D344–D347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith T.F., Waterman M.S. (1981) Identification of common molecular subsequences. J. Mol. Biol., 147, 195–197. [DOI] [PubMed] [Google Scholar]
- Song B. et al. (2006) ARCS: an aggregated related column scoring scheme for aligned sequences. Bioinformatics, 22, 2326–2332. [DOI] [PubMed] [Google Scholar]
- Srivastava N. et al. (2014) Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res., 15, 1929–1958. [Google Scholar]
- Strope P.K., Moriyama E.N. (2007) Simple alignment-free methods for protein classification: a case study from G-protein-coupled receptors. Genomics, 89, 602–612. [DOI] [PubMed] [Google Scholar]
- Szegedy C. et al. (2015) Going deeper with convolutions. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1–9.
- Thompson J.D. et al. (1994) CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res., 22, 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinga S., Almeida J. (2003) Alignment-free sequence comparison—a review. Bioinformatics, 19, 513–523. [DOI] [PubMed] [Google Scholar]
- Wang L., Jiang T. (1994) On the complexity of multiple sequence alignment. J. Comput. Biol., 1, 337–348. [DOI] [PubMed] [Google Scholar]
- Zielezinski A. et al. (2017) Alignment-free sequence comparison: benefits, applications, and tools. Genome Biol., 18, 186.. [DOI] [PMC free article] [PubMed] [Google Scholar]