An evolutionary model motivated by physicochemical properties of amino acids reveals variation among proteins

Abstract

Motivation

The relative rates of amino acid interchanges over evolutionary time are likely to vary among proteins. Variation in those rates has the potential to reveal information about constraints on proteins. However, the most straightforward model that could be used to estimate relative rates of amino acid substitution is parameter-rich and it is therefore impractical to use for this purpose.

Results

A six-parameter model of amino acid substitution that incorporates information about the physicochemical properties of amino acids was developed. It showed that amino acid side chain volume, polarity and aromaticity have major impacts on protein evolution. It also revealed variation among proteins in the relative importance of those properties. The same general approach can be used to improve the fit of empirical models such as the commonly used PAM and LG models.

Availability and implementation

Perl code and test data are available from https://github.com/ebraun68/sixparam.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Many studies have examined the role of models in phylogenetic estimation using maximum likelihood (ML). Most studies have focused on tree topology (e.g. Hoff et al., 2016), but the estimates of model parameters also have the potential to provide biological insights. For example, early studies revealed a bias toward transition (rather than transversion) substitutions (Yang, 1994) and later studies examined neighboring-nucleotide effects (Hwang and Green, 2004) and strand asymmetries (Polak and Arndt, 2008). The ratio of non-synonymous to synonymous substitutions in coding regions (called K_A/K_S or d_N/d_S) is the most common use of a model parameter for inference in molecular evolution; the K_A/K_S ratio can be estimated using models of codon evolution (Yang, 1998; Yang and Nielsen, 2002). Codon models are used in many studies, sometimes at the whole-genome scale (e.g. Weber et al., 2014; Zhang et al., 2014). In contrast to models that use nucleotide multiple sequence alignments (MSAs), either coding or non-coding, there is a relative paucity of methods to conduct similar analyses of protein MSAs. In principle, the ratio of ‘radical’ to ‘conservative’ amino acid substitutions (K_R/K_C) could be used in a manner similar to the K_A/K_S ratio (Hanada et al., 2007; Hanada et al., 2009; Smith, 2003; Zhang, 2000), although the K_R/K_C ratio is harder to interpret than the K_A/K_S ratio.

There are two challenges associated with using ML methods to understand patterns of protein evolution. First, there are many ways to define radical versus conservative amino acid substitutions (Hanada et al., 2007), unlike non-synonymous versus synonymous substitutions, which can be defined unambiguously. Second, estimates of the K_R/K_C ratio will ultimately reflect the estimates of parameters in the instantaneous rate matrix (IRM), or Q matrix, which describes amino acid evolution for specific proteins. However, amino acid models have an IRM with a much larger number of free parameters than models of nucleotide sequence evolution. If we assume time reversibility the IRM, which is used to calculate the likelihood, can be is the product of a symmetric rate matrix (R) reflecting the ‘exchangeability’ for specific pairs of character states (i.e. nucleotides, codons or amino acids) and a diagonal matrix (Π) with the equilibrium frequencies of each state (Swofford et al., 1996). The general time reversible model of nucleotide evolution (GTR₄) has eight free parameters (five for R and three for Π), so the variance of the parameter estimates will be acceptable if they are estimated using typical nucleotide MSAs. The analogous amino acid model (GTR₂₀) has 208 free parameters (189 for R and 19 for Π). Individual proteins are often fairly short (e.g. 280–600 amino acids; Tiessen et al., 2012) so typical protein MSAs are unlikely to provide enough information to generate accurate estimates of that many free parameters.

This raises the question of how a codon model can be implemented in a practical manner. After all, GTR₆₁ is the analogous codon model (assuming the universal code); that model has a very large number of free parameters (1829 for R and 60 for Π). However, the dimension of codon models can be reduced using an IRM where all elements that require multiple simultaneous substitutions are set to zero and the remaining elements are assigned values based on a single transition–transversion ratio and K_A/K_S ratio (the κ and ω parameters, respectively, in the study by Yang, 1998). This dimension reduction actually reveals valuable biological information because estimates of K_A/K_S are easier to interpret than the collection of values in the IRM. An analogous approach for models of amino acid evolution would be useful.

Most phylogenetic studies that use proteins eschew estimation of the R matrix parameters using a fixed R matrix generated using a training set of protein MSAs. This approach was pioneered by Kishino et al. (1990), who used Dayhoff et al. (1978) PAM matrix as the R matrix, and it solves the problem of parameter estimation as long as the training set is large enough. Subsequent studies have used other R matrices (Table 1). Although these ‘empirical models’ with fixed R matrices may be useful for phylogenetics they cannot provide insights into the process of protein evolution. For example, Keane et al. (2006) reported that rtREV is the best-fitting model for 33% of archaeal, 21% of proteobacterial and 4% of vertebrate proteins MSAs. However, rtREV was trained using retroviral pol proteins (Dimmic et al., 2002) so it is unclear why diverse archaeal proteins would fit rtREV better than the more general models trained on a diverse set of proteins. This observation raises a fundamental question: does identifying the best-fitting model provide any useful information about specific proteins? That question can only be answered in the negative if we focus on empirical models.

Table 1.

Empirical models of protein sequence evolution

Model	Training data	References
General models:
JTT	—	Jones et al. (1992)
LG	—	Le and Gascuel (2008)
PAM (Dayhoff)	—	Dayhoff et al. (1978)
PMB	—	Veerassamy et al. (2003)
VT	—	Müller and Vingron (2000)
WAG	—	Whelan and Goldman (2001)
Specialized models:
HIVb	HIV (eight proteins)	Nickle et al. (2007)
rtREV	retroelement pol	Dimmic et al. (2002)

Note: ‘—’ indicates that many protein MSAs were used for training. Many different methods were used to estimate R matrix parameters. Only a selected subset of specialized models is shown; many specialized models were trained using viral data (e.g. FLU) or organelle-encoded proteins (e.g. mtREV24 and cpREV).

A lower dimensional model of protein evolution with parameters that have a clear biological interpretation would allow us to examine the ways that patterns of evolution differ among proteins. Simply using the K_R/K_C ratio described above is unlikely to solve this problem, since there are many ways to divide amino acid substitutions into radical versus conservative subsets (Fig. 1). This reflects the fact that there are likely to be many axes in ‘selection space’ (e.g. one for selection against radical changes in amino acid side chain size, a second related to radical changes in side chain polarity and so forth). The complexity of amino acid properties (Fig. 1) suggests that it would be better to eschew simply classifying amino acids interchanges as radical or conservative and devise a parameter that can capture different degrees of ‘radicalness’ (e.g. the selection against a large-to-tiny interchange is likely to be stronger than selection against a large-to-small substitution). Finally, information about the relative rates at which different non-synonymous mutations enter populations is also likely to be important (Yampolsky and Stoltzfus, 2005). I propose a six-parameter model, with two parameters related to mutational input and four parameters that capture the physicochemical properties of amino acids (to address the impact of selection against radical substitutions). Thus, the model only has one more R matrix parameter than the GTR₄ model (although it does have 19 equilibrium frequency parameters). It is likely to be possible to estimate these parameters from typical protein MSAs. The biological interpretability of these parameters should allow us to ask about general patterns across all proteins and to assess the degree to which different proteins exhibit distinct patterns of evolution. The proposed model is used to examine several datasets to explore those general patterns and the variation among proteins in their patterns of sequence evolution.

Fig. 1.

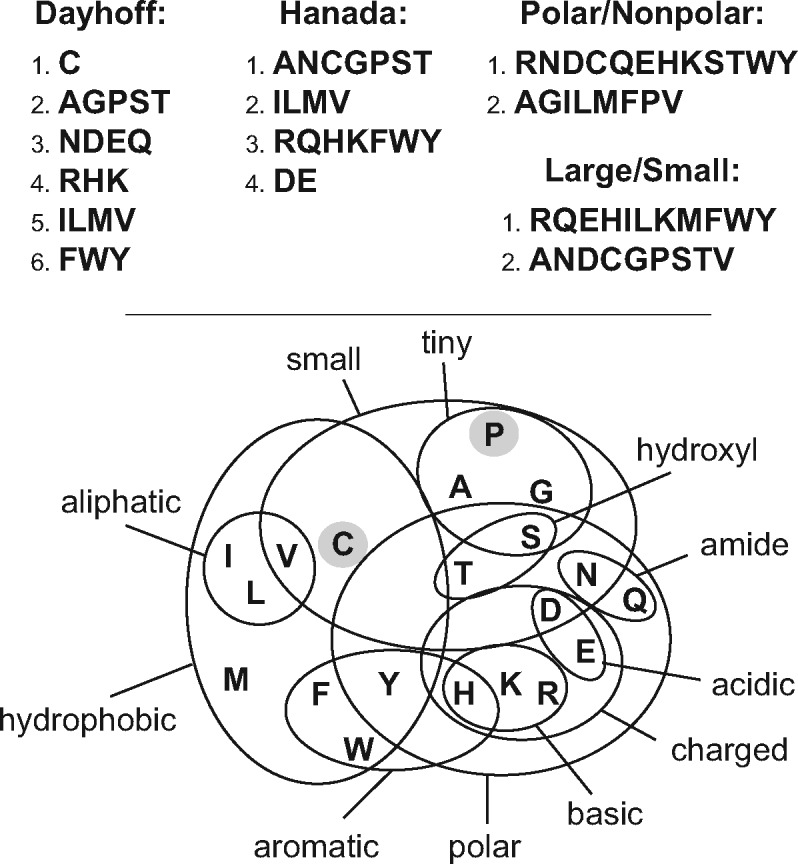
Dividing amino acid interchanges into radical and conservative is difficult. Amino acids can be divided into many different groups; radical changes are those between groups whereas conservative changes are within groups. Dayhoff et al. (1978) groups reflect patterns in their PAM matrix and their physicochemical properties. Hanada et al. (2007) groups maximized the correlation between K_R/K_C and K_A/K_S for mammalian proteins. Many studies (e.g. Weber et al., 2014) calculate K_R/K_C using a simple polar-nonpolar and/or large-small categorization. However, changes in many amino acid properties (i.e. any interchanges that cross lines in the diagram) can be radical, at least in some contexts. In fact, certain amino acids (C and P, shaded) have unique properties and any substitution involving them might be radical. Thus, radical versus conservative changes should be viewed as a matter of degrees rather than absolutes

2 Materials and methods

This section focuses on generating the R matrix; readers are referred to various reviews (Felsenstein, 2004; Swofford et al., 1996; Warnow, 2018; Yang, 2006) for general information about likelihood calculations in phylogenetics. The models proposed here populate an R matrix using the general approach shown as follows:

$$r_{ij}=K_{ij}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\phi }_1{\mathrm{\Delta }}_{ij}^1\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\phi }_2{\mathrm{\Delta }}_{ij}^2\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\phi }_3{\mathrm{\Delta }}_{ij}^3\right)\dots$$ (1)

where r_ij are R matrix elements, φ are weighting parameters and K_ij is a constant. The weighting parameters are estimated by ML (see below). Δ_ij are the absolute value of the difference between amino acids i and j in some property (e.g. polarity) divided by the maximum absolute value for all possible differences between pairs of amino acids. Thus, Δ_ij are fixed numbers between zero and one for any specific property and pair of amino acids (see Supplementary File S1). Equation (1) has the property that setting any φ value to zero yields a sub-model in which the amino acid property related to that φ parameter has no impact on the model. The amino acid properties examined here were side chain volume (V), polarity (P), composition (C) and aromaticity (A). The first three are from the work by Grantham (1974) and the fourth is from work by Xia and Li (1998). The general approach shown in Equation (1) can be rewritten in a more specific manner as

$${\mathrm{ }r}_{ij}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-V{\mathrm{\Delta }}_{ij}^V\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-P{\mathrm{\Delta }}_{ij}^P\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-C{\mathrm{\Delta }}_{ij}^C\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-A{\mathrm{\Delta }}_{ij}^A\right)$$ (2)

where the letters are the φ parameters for the properties studied hare and all K_ij are set to one. There are 16 models based on Equation (2), ranging from the simplest model, where V = P=C = A = 0, to the most complex where all parameters are free to vary. The simplest model is actually an F81-like (Felsenstein, 1981) model for proteins.

Equation (2) models [hereafter, eq2 models] only capture the impact of selection (hereafter, V, P, C and A are called selective parameters). Mutational input was modeled by incorporating the structure of the genetic code, using ‘gencode’ (G) and transversion (T) parameters. The full model is shown as

$$r_{ij}=\mathrm{e}\mathrm{x}\mathrm{p}\left(-V{\mathrm{\Delta }}_{ij}^V\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-P{\mathrm{\Delta }}_{ij}^P\right)\dots N_{ij}^{-G}\mathrm{e}\mathrm{x}\mathrm{p}\left(-T{\mathrm{\Delta }}_{ij}^T\right)$$ (3)

N_ij is the minimum number of nucleotide substitutions necessary for an interchange of amino acids i and j and ${\mathrm{\Delta }}_{ij}^T$ is one if at least one of those substitutions is a transversion and zero otherwise. Gencode is dealt with in a different way than the other parameters, but it has the same behavior as the other parameters (i.e. G = 0 means the number of substitutions necessary for the interchange does not have an impact on the model). There are 64 potential eq3 sub-models. However, the 16 sub-models where T is free to vary but G = 0 will penalize a single transversion more than simultaneous changes to multiple nucleotide so they were not considered. Thus, 48 eq3 models (16 of which are eq2 models) were examined. The models are named based on the free parameters.

Although the eq2 and eq3 models can reveal the amino acid properties that contribute the most to the patterns of evolution for a specific protein they cannot be used to examine the ways that available empirical models fail to capture those processes. However, it is possible to modify Equation (2) to include information from an empirical model:

$${\mathrm{ }r}_{ij}=K_{ij}^{EMP}\mathrm{e}\mathrm{x}\mathrm{p}\left(-V{\mathrm{\Delta }}_{ij}^V\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-P{\mathrm{\Delta }}_{ij}^P\right)\dots N_{ij}^{-G}\mathrm{e}\mathrm{x}\mathrm{p}\left(-T{\mathrm{\Delta }}_{ij}^T\right)$$ (4)

where $K_{ij}^{EMP}$is the relevant R matrix element from an empirical model (e.g. those listed in Table 1). The eq4 models can be used to establish which properties an empirical model fails to capture for specific protein.

These parameters were optimized using a perl program that calls IQ-TREE v. 1.5.5 (Nguyen et al., 2015) to perform the likelihood calculations. Briefly, IQ-TREE was called and used to optimize the amino acid frequency parameters and Γ-distribution shape parameter (α); this study only considered +F + Γ models. Then α and the amino acid frequencies were fixed and the eq3 or eq4 model parameters (V, P, C, A, G and T) were optimized. A simple one-dimensional optimization was performed for each parameter in succession. The optimization began by determining whether adding or subtracting a fixed value (δ) to the focal parameter improves the likelihood. If φ+δ or φ−δ had a higher likelihood than the starting φ value, then δ was added (or subtracted) until the likelihood was maximized. After optimizing all free parameters δ was reduced and another round of optimization was conducted. After δ value reached a minimum (0.00001), the α and amino acid frequencies were re-optimized using the R matrix generated using the estimated parameter values. This procedure was repeated until the likelihood failed to change any further.

The best-fitting model was identified using the corrected Akaike information criterion (AIC_c; Hurvich and Tsai, 1989), using the number of aligned sites in the protein MSA as the sample size. Empirical models were identified in IQ-TREE using the settings ‘-m TESTONLY -mfreq FO -mrate G -merit AICc’; this finds the best fitting model from a set of 18 candidate models (all models in Table 1 and eight additional specialized models). The eq4 models used $K_{ij}^{EMP}$from the best-fitting empirical model identified using IQ-TREE.

3 Results and discussion

This study had the following four major goals: (i) to establish which parameters are necessary to fit eq3 models to protein MSAs; (ii) to determine whether the eq3 parameter estimates differ among proteins; (iii) to compare the fit of eq3 models to empirical models; and (iv) to examine whether the fit of empirical models can be improved using the eq4 models. To accomplish these goals, we examined proteins from yeasts (Rokas and Carroll, 2005), vertebrates (Chen et al., 2015) and birds (Jarvis et al., 2014). The specific proteins were chosen arbitrarily and only the MSAs judged free of homology errors by Springer and Gatesy (2018) were chosen from birds. Individual gene trees can differ from the species tree (Maddison, 1997) and the true species tree is unknown (it is especially uncertain for birds; Reddy, et al., 2017), so we optimized the model parameters on the ML tree generated using the best-fitting empirical model. To complement the analyses of individual genes I used eight concatenated datasets from Wolf et al. (2004). Each Wolf et al. (2004) dataset was limited to proteins with a specific function, so the potential of the eq3 and eq4 models to highlight differences among classes of proteins could be assessed. All datasets and trees are available in Supplementary File S2.

3.1 The most important parameters vary among proteins

All single-parameter eq3 models resulted in substantial likelihood increases relative to the F81-like model. Polarity (P) was the selective parameter that increased per site ΔlnL the most; the median ΔlnL/site for eq3 models with P as the only free parameter increased by 0.8359 for vertebrates, 0.5845 for yeasts and 0.2788 for birds. The estimate of the P parameter was also larger on average than the other selective parameters (Table 2). The least important selective parameters based on those criteria were composition (C) for the vertebrates and yeasts and aromaticity (A) for birds. Gencode (G), the primary mutational input parameter, was very important; the median ΔlnL/site increased by 1.054 for vertebrates, 0.5102 for yeasts and 0.3352 for birds. Estimates of G were especially high in birds (Table 2). Indeed, adding the G parameter resulted in a larger likelihood increase than any other parameter for birds and vertebrates and the second largest (after P) for the yeasts.

Table 2.

Parameter estimates for single parameter eq3 models

Dataset	Sites	V	P	C	A	G	G + T
Yeasts:
Flc2p	494	4.86	4.87	3.33	2.73	3.25	3.05/0.65
Ptc1p	217	4.43	5.72	2.50	2.85	3.61	3.53/0.27
Rfc2p	296	4.69	4.79	3.22	3.71	3.07	2.90/0.54
Ung1p	185	3.71	4.39	1.99	3.22	2.08	1.89/0.48
Tkl1p	629	4.69	4.33	2.64	3.08	2.50	2.42/0.26
Mean		4.48	4.82	2.74	3.12	2.90	2.76/0.44
Birds:
APC (54)	2862	3.51	4.88	2.57	3.76	7.14	6.56/1.03
GFPT1 (15)	700	2.60	4.21	3.43	2.07	3.88	3.70/0.42
HMBS (76)	353	3.54	4.16	3.12	1.53	5.52	5.25/1.09
IFGN1 (78)	845	3.34	4.75	3.12	1.53	7.07	7.21/1.06
PCNX (79)	2359	3.31	4.31	2.52	3.01	5.33	4.89/0.96
Mean		3.26	4.46	3.05	2.55	5.79	5.52/0.91
Vertebrates:
AQR	1020	4.07	4.43	2.94	3.64	4.72	4.59/0.73
COX10	490	3.13	4.06	2.57	4.15	4.70	4.54/0.69
EDC4	761	4.22	5.43	2.80	4.02	4.52	4.43/0.58
GPATCH1	515	3.52	4.74	3.01	3.92	4.12	3.97/0.67
VPS54	347	3.94	4.91	2.40	4.37	4.52	4.24/0.77
Mean		3.78	4.71	2.74	4.02	4.52	4.36/0.69

Parameter estimates are rounded to the nearest 0.01. Estimates of the T parameter were only obtained in combination with G; those parameter estimates are listed in the order G/T. Bird gene numbers are from the study by Jarvis et al. (2015). Complete output of the parameter optimization program is available in Supplementary File S3.

Single-parameter eq3 models provide information analogous the commonly used K_R/K_C and K_A/K_S ratios. Unlike the K_A/K_S ratio (ω), there is no obvious expected value of the K_R/K_C ratio. Assuming synonymous sites evolve at the neutral rate (which may not be true; Chamary et al., 2006; Lawrie et al., 2013) K_A/K_S = 1 provides evidence of neutral evolution. In contrast, K_R/K_C only allows the exploration of differences among proteins (or lineages). The single parameter eq3 models provide similar information while eschewing a simplistic radical versus conservative classification of interchanges.

The number of free parameters in the best-fitting eq3 models for each of the 15 test datasets ranged from two to six (Table 3 and Supplementary File S3); the more parameter-rich (i.e. five- or six-parameter) models had the best fit for most datasets. However, the same patterns revealed in single-parameter eq3 analyses were also evident in the best-fitting models. C had the least impact on the likelihood in the single parameter analyses and C was not included the best-fitting model for 10 of the 15 proteins. In fact, C was not included in the best-fitting model for any yeast protein. P and G had the largest impact on the likelihood in single-parameter analyses and both of those parameters were included in the best-fitting models for the test datasets. However, the parameter estimates obtained using more parameter-rich models tended to be much lower than those obtained using the single-parameter models. This appeared to reflect interactions among the parameters. C presented an interesting case since it was negative for the vertebrate VPS54 dataset. This can happen when certain amino acid interchanges that might be viewed as radical based on composition alone were actually overly penalized by the other parameters (i.e. their instantaneous rate is too low).

Table 3.

Parameter estimates and ΔlnL/site for the best-fitting eq3 models

Dataset	V	P	C	A	G	T	ΔlnL	Best EMP
Yeasts:
Flc2p	2.13	3.24	—	1.97	1.59	0.63	0.9621	LG (−0.2062)
Ptc1p	1.91	4.08	—	1.47	2.48	—	0.8091	LG (−0.1132)
Rfc2p	2.27	3.63	—	2.55	1.50	0.56	0.8790	LG (−0.1692)
Ung1p	1.85	3.51	—	2.66	0.72	0.35	0.7615	rtREV (−0.1217)
Tkl1p	2.65	2.91	—	1.71	1.08	0.24	0.6869	LG (−0.2438)
Mean	2.16	3.48	0.00	2.07	1.47	0.35
Birds:
APC	—	2.66	0.55	2.72	5.95	0.89	0.7518	HIVb (−0.0002)
GFPT1	—	2.91	—	—	3.36	—	0.0862	JTT (−0.0183)
HMBS	1.71	2.00	—	—	4.71	0.93	0.7319	JTT (−0.0006)
IFGN1	0.55	2.40	0.55	1.53	6.46	0.83	2.9576	HIVb (−0.0667)
PCNX	0.91	2.08	0.66	1.78	4.14	0.86	0.2512	HIVb (−0.0039)
Mean	0.63	2.41	0.35	1.21	4.92	0.70
Vertebrates:
AQR	1.33	2.56	—	2.54	3.67	0.57	0.8500	JTT (−0.1015)
COX10	—	2.48	—	3.04	3.73	0.53	1.9200	JTT (−0.1689)
EDC4	0.85	3.32	—	3.13	3.36	0.57	1.8728	JTT (−0.1061)
GPATCH1	0.76	2.55	0.75	2.45	3.12	0.48	2.2052	JTT (−0.2815)
VPS54	0.88	3.15	−0.89	3.13	3.46	0.72	1.2291	JTT (−0.0804)
Mean	0.76	2.81	−0.03	2.86	3.47	0.57

Note: ‘—’ indicates parameters that were not in the best-fitting eq3 model (based on the AIC_c). Any parameters absent from the best-fitting model were assumed to be zero when the mean was calculated. Parameter estimates are rounded to the nearest 0.01. ΔlnL is the likelihood difference per site (ΔlnL/site) relative to the F81-like model. ΔlnL/site is rounded to the nearest 0.0001. The best-fitting empirical model (‘Best EMP’) is followed by the ΔlnL/site relative to the best-fitting eq3 model. Complete output of the parameter optimization program is available in Supplementary File S3.

The best-fitting empirical models differed among proteins in the test datasets. LG had the best fit for most of the yeast proteins (the exception had the best fit to rtREV), whereas JTT was the best-fitting model for all of the vertebrate proteins. The avian proteins were split between HIVb (three proteins) and JTT (two proteins). The likelihood of the best-fitting empirical model was higher than the best-fitting eq3 model in all cases, although the best eq3 model had a likelihood that of the best empirical model for two avian proteins. In fact, adding the V parameter to analyses of APC actually resulted in a slightly higher likelihood than that of the best-fitting empirical model (lnL = −23308.4891 for the full VPCAGT model and lnL = −23308.9690 for the HIVb model; ΔlnL = 0.4799). However, the estimate of V was quite low (V = 0.23) when the VPCAGT model was used to analyze APC; that is why the V parameter was not included in the best-fitting eq3 model for that protein. The V parameter was also absent from the best-fitting eq3 model for one other avian protein and one vertebrate protein. Regardless, eq3 parameter estimates for proteins with the same best-fitting empirical model were often very different. This suggests that eq3 models can reveal patterns of evolution for different proteins; simply identifying the best-fitting empirical model cannot reveal that information.

3.2 The fit of empirical models can be improved

Although the six-parameter models result in substantial likelihood improvements relative to a simple F81-like model, they did not fit the data for any protein MSA and the best-fitting empirical model (with the exception of APC). The raises two questions. First, can the fit of empirical models be improved? Second, which aspects of the evolutionary process do empirical models fail to capture? Using eq4 to adjust the best-fitting empirical model resulted in improvements (based on the AIC_c) in all but one case (GFPT1; Table 4). Parameter estimates for the eq4 models were much lower than those obtained using eq3 models (compare Tables 3 and 4); this was expected since the ‘starting point’ for the models (i.e. the empirical model) was presumably much better than the F81-like model. However, the parameters that played a role in best-fitting eq4 model differed among proteins, emphasizing the fact that the ‘one size fits all’ nature of empirical models is inappropriate.

Table 4.

Parameter estimates for eq4 models using the best-fitting empirical model

Dataset	V	P	C	A	G	T	Best EMP
Yeasts:
Flc2p	—	—	—	—	0.60	—	LG (0.0098)
Ptc1p	—	1.03	—	—	1.00	−0.44	LG (0.0550)
Rfc2p	1.34	—	—	—	—	—	LG (0.0164)
Ung1p	—	1.06	−1.06	1.13	—	—	rtREV (0.0464)
Tkl1p	0.92	—	—	—	—	—	LG (0.0086)
Mean	0.45	0.42	−0.21	0.23	0.32	−0.09
Birds:
APC	−0.26	0.97	−0.63	1.38	1.55	0.25	HIVb (0.0251)
GFPT1	—	—	—	—	—	—	JTT (—)
HMBS	—	—	—	—	2.57	0.56	JTT (0.0834)
IFGN1	0.35	0.40	—	−0.28	2.76	—	HIVb (0.0381)
PCNX	—	0.45	—	0.80	—	—	HIVb (0.0027)
Mean	0.02	0.36	−0.13	0.38	1.18	0.16
Vertebrates:
AQR	0.56	—	—	0.85	1.47	—	JTT (0.0452)
COX10	−0.56	—	—	1.11	1.56	—	JTT (0.0961)
EDC4	—	1.01	—	1.71	1.11	0.20	JTT (0.1488)
GPATCH1	—	—	0.63	0.52	0.92	—	JTT (0.0605)
VPS54	—	0.86	−1.22	1.54	1.16	0.30	JTT (0.0858)
Mean	0.00	0.38	−0.12	1.15	1.25	0.10	LG (−0.2062)

Note: ‘—’ indicates parameters that were not in the best-fitting (based on the AIC_c) eq4 model. In all cases, the best-fitting empirical model was used as the ‘base model’ that provided the K_ij values in eq3. Any parameters not present in the best-fitting model were assumed to be zero for calculating the mean. Parameter estimates are rounded to the nearest 0.01. The best-fitting empirical model is followed by the ΔlnL per site relative to that model (‘—’ indicates the empirical model was not improved using eq4). Complete output of the parameter optimization program is available in Supplementary File S3.

3.3 Parameter estimates for concatenated datasets of functionally related proteins

Empirical models obtained ultimately correspond to fixed R matrix values estimated using large training sets. From a conceptual standpoint, the simplest way to estimate those parameters would be optimize the GTR₂₀ model given a diverse set of functionally unrelated proteins. In practice, many empirical models used less computationally demanding approximate methods for parameter estimation. However, the general point is that R matrix values for empirical models should be close to the average GTR₂₀ model parameters for many different proteins. Thus, one might expect parameter estimates for concatenated datasets to converge on some average value that is as close as possible to the empirical model parameters. However, this might not be true for concatenated datasets that comprise functionally related proteins.

Most concatenated datasets used in phylogenomics (e.g. Chen et al., 2015; Jarvis et al., 2014; Rokas and Carroll, 2005) comprise diverse and functionally-unrelated proteins. An early phylogenomic study (Wolf et al., 2004) represents an exception to this; that study analyzed eight separate six-taxon concatenated datasets, each of which comprises functionally related proteins. The six focal taxa for Wolf et al. (2004) are three animals (a vertebrate, an insect and a nematode), two fungi (fission yeast and budding yeast) and a plant. There are two plausible trees for those taxa: (i) Ecdysozoa (an insect + nematode clade) and (ii) Coelomata (an insect + vertebrate clade); these trees are available in Supplementary File S2. Wolf et al. (2004) supported Coelomata but later phylogenomic studies with larger taxon samples have strongly supported Ecdysozoa (e.g. Dunn et al., 2008; Hejnol et al., 2009). Thus, Wolf et al. (2004) data provide an opportunity to ask two questions. First, do parameter estimates for functionally related sets of proteins differ, like those for individual proteins? Second, do analyses using the proposed models support the Ecdysozoa tree? To do this the likelihood given the best-fitting models (empirical, eq3, and eq4) was calculated using both plausible topologies (Ecdysozoa and Coelomata).

The eq3 parameter estimates for the concatenated datasets did show variation, albeit less than for individual proteins (compare Tables 3 and 5). The C and A parameter estimates were especially variable. All Wolf et al. (2004) datasets had the same best-fitting eq3 model (VPCAGT) and empirical model (LG). LG always had a better fit than the VPCAGT model. However, it was always possible to improve model fit relative to the LG model using eq4 (Table 5). The V and G parameters were included in every eq4 model, although the estimates of G were always negative, suggesting LG overcorrects for the impact of the genetic code on these data.

Table 5.

Parameter estimates for concatenated datasets

Dataset	Sites	V	P	C	A	G	T
Eq3 models:
Chaperonins	3970	2.68	3.87	−0.20	1.86	0.74	0.19
Clathrin	2138	2.11	3.62	−0.25	3.06	0.68	0.39
DNA polymerase	1782	2.19	2.99	0.53	2.15	1.03	0.16
DNA replication	2284	2.36	3.10	0.47	2.08	0.98	0.15
Proteasome	2474	2.43	3.18	0.21	2.44	0.76	0.18
Ribosomal proteins	11 586	2.23	2.92	0.29	2.28	0.62	0.10
RNA polymerase	3274	2.26	2.97	0.29	1.96	0.86	0.27
Translation factors	2045	2.13	3.21	0.32	2.36	0.80	0.21
Mean		2.30	3.23	0.21	2.27	0.81	0.21
Eq4 models:
Chaperonins	3970	1.10	0.88	−0.55	—	−0.44	−0.18
Clathrin	2138	0.49	0.74	−0.65	1.11	−0.54	—
DNA polymerase	1782	0.68	—	—	0.24	−0.24	−0.21
DNA replication	2284	0.89	—	—	—	−0.21	−0.21
Proteasome	2474	0.84	0.27	—	0.51	−0.47	−0.19
Ribosomal proteins	11 586	0.73	−0.23	—	0.45	−0.34	−0.55
RNA polymerase	3274	0.54	—	—	0.25	−0.31	−0.11
Translation factors	2045	0.44	—	—	0.42	−0.33	−0.20
Mean		0.71	0.21	−0.15	0.37	−0.38	−0.18

All parameter estimates reflect the Ecdysozoa tree. ‘—’ indicates parameters that were not in the best-fitting eq4 model (based on the AIC_c). Any parameters not present in the best-fitting model were assumed to be zero for calculating the mean. Parameter estimates are rounded to the nearest 0.01. The empirical model used for the eq4 models was always LG. ‘DNA replication’ refers to DNA replication licensing factors, i.e. the MCM family. Complete output of the parameter optimization program is available in Supplementary File S4.

Parameter estimates in Table 5 were calculated using the Ecdysozoa topology but analyses using the Coelomata topology resulted in similar values (Supplementary File S4). Wolf et al. (2004) found that different datasets supported different trees, with three (proteasome subunits, ribosomal proteins and RNA polymerase) supporting Ecdysozoa and the other five datasets supporting Coelomata. Analyses using LG, eq3 and eq4 also revealed conflict; four datasets (chaperonins and the same datasets as Wolf et al., 2004) supported Ecdysozoa and the other four supported Coelomata. Although that result was equivocal, the Ecdysozoa tree had the highest overall likelihood in all analyses, consistent with the results of studies with more taxa (e.g. Dunn et al., 2008; Hejnol et al., 2009). The overall likelihood is the sum of the likelihoods of for eight of the concatenated MSAs given a specific tree; this is the likelihood given a model where each of the eight MSAs has distinct parameters and distinct branch lengths. Surprisingly, the likelihood difference (ΔlnL) favoring Ecdysozoa was actually larger for eq3 than for eq4 (ΔlnL = 44.9233 for eq3; ΔlnL = 33.5569 for eq4), despite the better fit (based on AIC_c) of the eq4 models. However, the relationship between model and topology was complex; the overall ΔlnL favoring Ecdysozoa was smallest for LG (ΔlnL = 29.3364) and largest for the F81-like model (ΔlnL = 60.1499). Moreover, one additional dataset (clathrin) supported Ecdysozoa when the F81-like model was used (see Supporting File 4 for details). Despite these complexities the fact that the eq4 models resulted in a modest increase in the likelihood difference relative to LG should be viewed as encouraging. Broader surveys will be necessary to explore the potential of these models for estimating phylogenetic tree topologies.

3.4 General patterns and variation among proteins

A general framework for models of protein evolution that can be used to explore general patterns of protein evolution and variation among proteins was proposed (eq1). Specific versions of that general model that focused amino acid physicochemical properties (eq2, eq3 and eq4) emphasized the important roles of side chain volume (V), polarity (P), aromaticity (A) and the structure of the genetic code (G) in determining relative rates of amino acid interchanges. The role of polarity, volume, and the genetic code in determining rates of amino acid interchanges has long been appreciated, but a role for aromaticity independent of volume might be viewed as surprising since aromaticity and volume are correlated (Pearson’s r = 0.716). Composition (C) had less impact on protein evolution. That could reflect way composition is calculated; composition has a modest correlation with the other parameters (the maximum is with aromaticity; r = -0.474) if all amino acids are considered, but it is strongly correlated with polarity (r = 0.809) if cysteine is excluded (the composition-polarity correlation is r = 0.37 when cysteine is included). Thus, C could reflect two distinct aspects of protein evolution (polarity and the special nature of cysteine). This may explain why negative estimates of the C parameter emerged in some analyses using eq3 (Tables 3 and 5). It also suggests that it may be desirable to abandon the C parameter in favor of other properties. Regardless of the details of the amino acid properties used for analyses, it is clear that the patterns of evolution vary among proteins in ways that cannot be examined using empirical models. The models proposed here can reveal that variation and highlight the best amino acid properties to examine in future studies.

The goal of this study was to develop an amino acid model that could reveal the ways that patterns of molecular evolution vary among proteins. The eq3 models include six parameters, four of which reflect selection against radical amino acid substitutions. This could make the eq3 models testable in a way that empirical models (e.g., Table 1) are not. For example, if analyses of a specific protein using eq3 results in a high estimate of V that protein is likely to be more sensitive to volume changing substitutions than another protein associated with a lower estimate of V. Thus, eq3 could be tested by mutagenesis experiments (e.g. using methods similar to the work by Georgelis et al., 2007). The fact that K_R/K_C and effective population size appear to be negatively correlated (Hughes and Friedman, 2009; Weber et al., 2014) could permit another test of eq3. The correlation probably reflects the higher efficiency of selection in organisms with large population sizes (Akashi et al., 2012). Since the eq3 model parameters are analogous to K_R/K_C they should exhibit the same correlation. However, eq3 also of highlights the properties of amino acids that contribute to the radical versus conservative nature of substitutions in different proteins. Overall, eq3 provides a novel tool to explore the differences among proteins.

Eq4 models provide different information than the eq3 models. Specifically, eq4 reveals the ways that empirical models fail to capture specific patterns of amino acid substitution. The results shown in Tables 4 and 5 reflect the use of eq4 with the best-fitting empirical model; they do not show the degree to which other empirical models might be improved. Testing the full set of empirical models in Table 1 revealed three cases (APC, IFGN1 and PCNX) where eq4 with a suboptimal ‘base model’ performed better than eq4 with the best-fitting empirical model (Supplementary File S5). In all three cases, combining eq4 and the JTT model resulted in a better likelihood than eq4 with the HIVb model; the estimate of the G parameter was much larger for the JTT + VPCAGT model than for the HIVb + VPCAGT model for all three proteins (Supplementary File S5). The parameter estimates that can be obtained using the eq4 models (Supplementary Files S5 and S6) provide an interesting way to examine the ways each empirical model fails to capture the patterns of amino acid substitution for individual proteins.

This study did not address variation among sites in patterns of sequence evolution or the impact of these models on the estimation of tree topology. Many studies have revealed variation among sites within proteins in their evolutionary rate (Echave et al., 2016); substantial variation in the pattern of evolution is also likely to exist. These models do not address that variation (except to the extent that the Γ distribution captures variation in rates for all models examined here). However, it would be straightforward to extend eq3 or eq4 to a mixture model where one or more of the parameters are drawn from a prior distribution (e.g. a Γ distribution or a uniform distribution); the mean and variance of that distribution could be estimated by ML. Likewise, the potential for the proposed models to improve tree topology estimation is unclear, although the fact that eq4 improves the fit of empirical models makes it reasonable to speculate that it could be useful. However, other analytical approaches should also be considered in studies focused on tree estimation (e.g. site heterogeneous CAT models; Lartillot and Philippe, 2004; Le, et al., 2008). However, information analogous to the K_R/K_C ratio cannot be obtained from analyses using standard empirical models (or the CAT models). Ultimately, the value of the proposed models is their potential to reveal differences among proteins in their patterns of evolution and to identify the characteristics of amino acids that contribute to protein evolution.