Convolutional neural networks for classification of alignments of non-coding RNA sequences

Abstract

Motivation

The convolutional neural network (CNN) has been applied to the classification problem of DNA sequences, with the additional purpose of motif discovery. The training of CNNs with distributed representations of four nucleotides has successfully derived position weight matrices on the learned kernels that corresponded to sequence motifs such as protein-binding sites.

Results

We propose a novel application of CNNs to classification of pairwise alignments of sequences for accurate clustering of sequences and show the benefits of the CNN method of inputting pairwise alignments for clustering of non-coding RNA (ncRNA) sequences and for motif discovery. Classification of a pairwise alignment of two sequences into positive and negative classes corresponds to the clustering of the input sequences. After we combined the distributed representation of RNA nucleotides with the secondary-structure information specific to ncRNAs and furthermore with mapping profiles of next-generation sequence reads, the training of CNNs for classification of alignments of RNA sequences yielded accurate clustering in terms of ncRNA families and outperformed the existing clustering methods for ncRNA sequences. Several interesting sequence motifs and secondary-structure motifs known for the snoRNA family and specific to microRNA and tRNA families were identified.

Availability and implementation

The source code of our CNN software in the deep-learning framework Chainer is available at http://www.dna.bio.keio.ac.jp/cnn/, and the dataset used for performance evaluation in this work is available at the same URL.

1 Introduction

A couple of pioneering studies (Alipanahi et al., 2015; Zhou and Troyanskaya, 2015), followed by several studies (Kelley et al., 2016; Lanchantin et al., 2016; Zeng et al., 2016), have come up with the idea that a convolutional neural network (CNN) can be applied to extraction of a sequence motif specifically conserved among target sequences. A motif is a sequence pattern that occurs repeatedly in a set of target sequences and is usually represented as a position weight matrix that describes the score (probability) of each nucleotide at each position in the conserved pattern. If one-hot coding representation of four DNA nucleotides is employed, then a kernel (filter) with a one-dimensional convolution operation applied temporally over a sequence can be considered a position weight matrix for representing a motif. The kernels are learned by training CNNs on positive and negative samples of sequences such as those obtained in experiments on chromatin immunoprecipitation with high-throughput sequencing (ChIP-seq) (Zeng et al., 2016). Here, a ‘one-dimensional’ convolution operation for sequences is interpreted as scanning the input sequence only in one direction along the sequence with a kernel of the same width (dimension) as that of the distributed representation of input (see Fig. 1). Of note, the motifs are acquired by a gradient descent during the training of CNNs, while the existing well-known motif identification methods such as MEME (Bailey et al., 1994) use a more computationally expensive calculation such as Gibbs sampling.

Fig. 1.

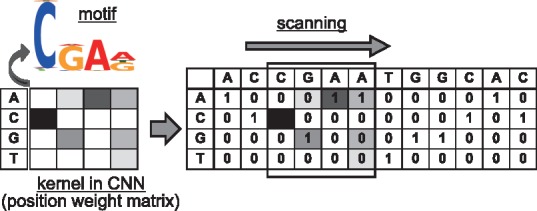
One-hot coding representation of four DNA nucleotides, a kernel (filter) with a one-dimensional convolution operation that is considered a position weight matrix for representing a motif

On the other hand, a sequence motif may sometimes contain insertions and deletions among conserved sequences. Nonetheless, the existing motif discovery methods involving one-dimensional CNNs cannot deal with such insertions and deletions in the motifs. To accommodate such operations, we need alignments as input to the one-dimensional CNNs. An alignment calculation for a pair of biological sequences such as DNA, RNA and protein sequences is a fundamental and robust method of sequence analysis (Durbin et al., 1998). The pairwise alignment of biological sequences is achieved according to insertions, deletions and match operations so that the two sequences are aligned at the same column length. The first major aim of this study is to identify a motif in pairwise alignments of sequences with gaps, called an alignment motif, by applying the one-dimensional CNN to the input of pairwise alignments.

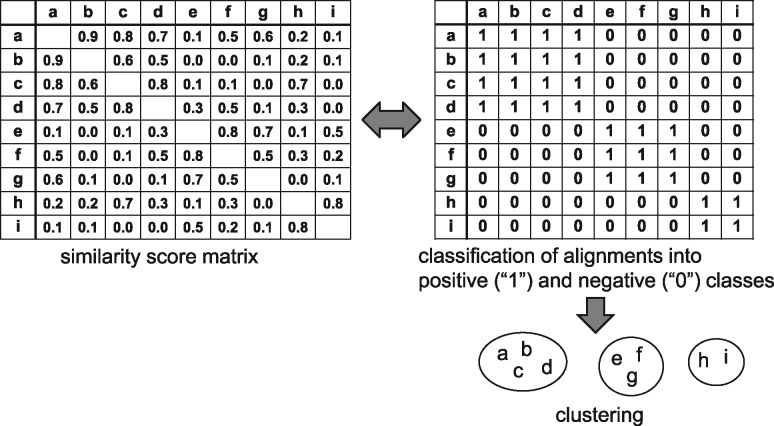
The similarity score of an alignment is calculated in accordance with the predefined scores for insertions, deletions and matches, and the similarity scores between two sequences in the alignment are next used for clustering the input sequences into several groups of similar sequences. After calculation of the similarity score matrix for all pairs of the input sequences, some clustering algorithm such as agglomerative hierarchical clustering or k-means clustering is applied to obtain a set of clusters composed of similar sequences. Nevertheless, there is a limitation to the clustering of a set of sequences based only on this scalar value of similarity. The second major aim of this study is to improve the clustering accuracy by identifying alignment motifs and by classifying pairwise alignments into two classes, positive and negative, via training the one-dimensional CNNs in a supervised learning manner (Fig. 2). Here, a pair of sequences in the pairwise alignment is defined as a positive class if the pair belongs to the same family (true cluster) and as negative if the pair does not belong to the same family. If we regard the matrix (shown on the right-hand side of Fig. 2) that contains the positive-class label ‘1’ and the negative label ‘0’ for all pairs of non-coding RNA (ncRNA) sequences as an adjacency matrix for graph representation, then each complete subgraph (that is, fully connected subgraph, called a clique) corresponds to a cluster. Thus, the classification of a pairwise alignment of two sequences into positive and negative classes and the extraction of cliques in the derived graph can be regarded as exact clustering of the input sequences.

Fig. 2.

Classification of pairwise alignments of two sequences. (Left) A score matrix consisting of scores on similarity between every pair of sequences. (Right) A matrix (called a classification matrix) consisting of classification to the positive-class label ‘1’ and to the negative label ‘0’ for all pairs of sequences. Clustering is yielded from the classification matrix

In this study, we developed a novel method, called CNNclust, for applying one-dimensional CNNs to classification of pairwise alignments of ncRNA sequences. Furthermore, we combined the distributed representation of RNA nucleotides with the secondary-structure information specific to ncRNAs and with mapping profiles of next-generation sequence reads. One of the advantages of applying a one-dimensional convolution operation in CNNs to the analysis of biological sequences is that multiple types of molecular information such as primary sequences and secondary structures can be easily integrated, and the effective features that combine these multiple datasets can be automatically discovered by representation learning (Bengio et al., 2013). When applied to ncRNAs, the representation learned on a kernel is a motif of sequences and secondary structures. We demonstrated that training of one-dimensional CNNs with input of pairwise alignments outperforms the existing clustering methods for ncRNA sequences and succeeds in the discovery of several sequence motifs and secondary-structure motifs known for the small nucleolar RNA (snoRNA) family and specific to microRNA (miRNA) and transfer RNA (tRNA) families.

2 Materials and methods

2.1 Distributed representations of nucleotides, secondary structure and an alignment column

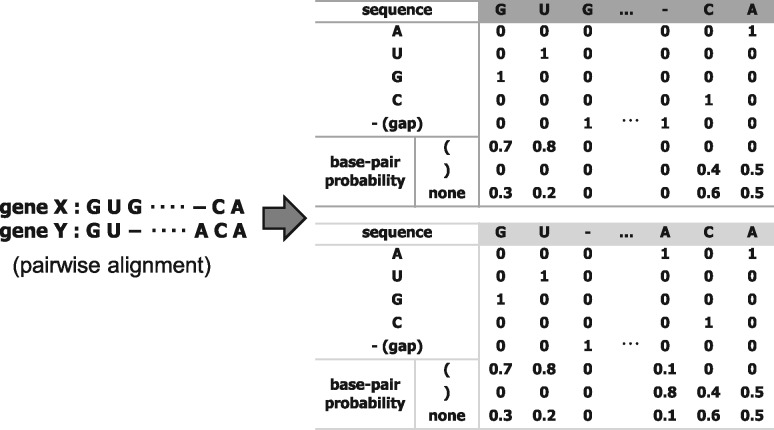
The input to our one-dimensional CNNs is a distributed representation of a pairwise alignment with gaps of two sequences. Each column in the pairwise alignment is represented by a pair of one-hot codings of four nucleotides ‘A’, ‘C’, ‘G’ and ‘U’ and the gap symbol ‘-’, that is, a five-dimensional vector (1, 0, 0, 0, 0), (0, 1, 0, 0, 0), (0, 0, 1, 0, 0), (0, 0, 0, 1, 0) and (0, 0, 0, 0, 1), respectively, as shown in Figure 3.

Fig. 3.

Distributed representations for a pairwise alignment: a pair of one-hot codes of four nucleotides of RNA and the gap symbol and a three-dimensional vector for representing secondary-structure information specific to ncRNAs. The parentheses ‘(’ and ‘)’ represent the left side of a base pair and the right side of a base pair, respectively (This dot-bracket notation is a convenient way of representing secondary structure originally used in the Vienna RNA package (Hofacker, 2003).)

Another distributed representation for RNA (DNA) sequences is the word2vec method (Mikolov et al., 2013) to convert subsequences into n-dimensional vectors; word2vec is a technique for converting words into vectors that are mainly used in the field of natural language processing. A couple of studies (Asgari and Mofrad, 2015; Ng, 2017) using word2vec for biological sequence analysis were reported. In the case of RNA (DNA) sequences, each k-mer (that is, RNA subsequence of length k) is considered a word and converted into a vector by word2vec. Learning of word2vec was carried out via the dataset prepared for performance experiments. There are two types of word2vec models: continuous bag-of-words and skip-gram. For this study, a skip-gram was selected. The dimension size of the feature vector of word2vec was set to 12, and the other hyperparameters were left at default values. The size of the k-mer as input to word2vec was examined at following three values: 3, 4 and 5.

In addition, a three-dimensional vector for representing secondary-structure information specific to ncRNAs is added as shown in Figure 3. The folding of an ncRNA into a functional molecule is governed by the formation of the standard Watson-Crick base pairs A–U and C–G, and such base pairs constitute secondary structures of ncRNAs. The base-pairing probability p_ij that the ith and jth nucleotides in an RNA sequence form a base pair can be calculated by the McCaskill algorithm (McCaskill, 1990), and subsequently, for each position i, we categorize the base-pairing probabilities into three kinds of sums: left-side base-pairing probability $p_i^{\text{left}}=\sum _{j>i}{p}_{ij}$ that a pair is formed with one of the downstream nucleotides, right-side base-pairing probability $p_i^{\text{right}}=\sum _{j<i}{p}_{ji}$ that a pair is formed with one of the upstream nucleotides, and unpaired probability $p_i^{\text{unpaired}}=1-(p_i^{\text{lef}t}+p_i^{\text{right}})$ that the nucleotide is unpaired. Therefore, the three-dimensional vector for representing secondary-structure information in column i consists of left-side base-pairing probability $p_i^{\text{left}}$, right-side base-pairing probability $P_i^{\text{right}}$ and unpaired probability $p_i^{\text{unpaired}}$.

2.2 CNN architecture

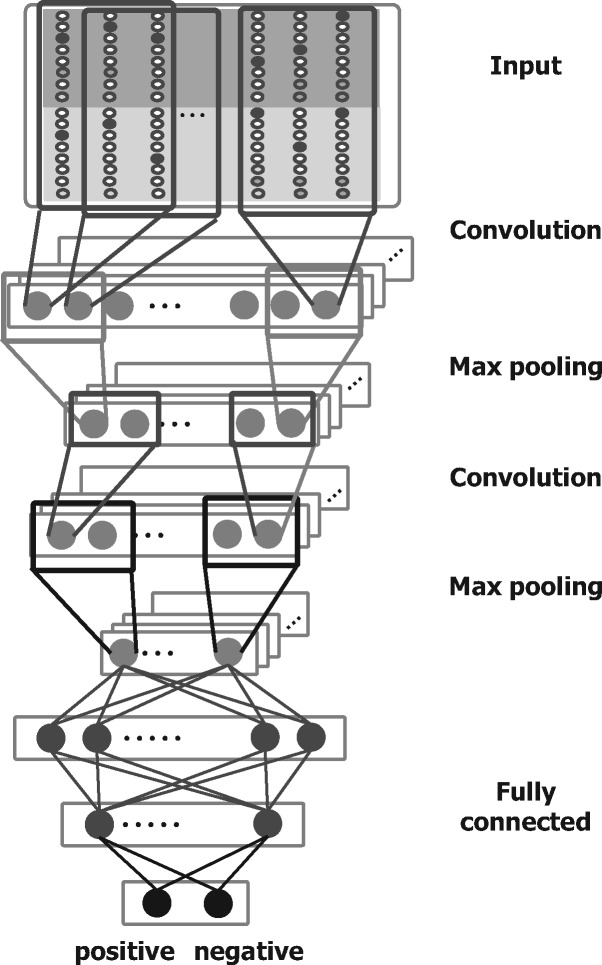
The model of a CNN used in this study consists of a three-layer fully connected network with one hidden layer following two convolution layers and two pooling layers as illustrated in Figure 4. The output of each unit in the convolution layer is the result of a convolution operation by each kernel. In the pooling layer, max pooling is carried out to output the maximum value across the whole input sequence. In this study, we used local max pooling, which yields the maximum value from each small subregion in the whole input sequence. During learning the CNN, six hyperparameters (convolution kernel size, the number of kernels, pooling size, the number of units in the hidden layer and the learning algorithm) were tuned. The ranges within which each hyperparameter was tuned are listed in Table 1. Batch normalization was conducted with a minibatch of size 128, and Dropout was employed for prevention of overfitting. The CNNs were implemented by means of the Chain class of Chainer (Tokui et al., 2015).

Fig. 4.

CNN architecture for the input of pairwise alignments

Table 1.

The list of hyperparameters in CNNs to be tuned

Hyperparameter	Range
Kernel size for convolution	3, 7, 15, 20, 30, 40, 50
Number of kernels (in two convolution layers)	6:13, 13:26, 19:38, 32:64, 45:90, 64:128, 128:256
Pooling method	Max pooling, average pooling,
Pooling in second layer	Global max pooling, local max pooling
Number of units in hidden layer (ratio to input layer)	1/3, 1/2, 2/3, 3/4, 1
Learning algorithm	Adam, AdaGrad, AdaDelta, Momentum SGD

2.3 Generating clusters from CNN predictions for pairs of ncRNAs

After the classification of pairwise alignments is obtained for all pairs of ncRNA sequences, finally, the clustering procedure is necessary to generate a set of clusters. A matrix called classification matrix (shown on the right-hand side of Fig. 2) that contains the positive-class label ‘1’ and the negative label ‘0’ for all pairs of ncRNA sequences can be regarded as an adjacency matrix for graph representation. Theoretically, each complete maximal subgraph extracted from the entire graph represented by the adjacency matrix corresponds to a cluster including similar ncRNA sequences, and hence extraction of every complete subgraph corresponds to the clustering operation. Although several algorithms for finding maximal cliques have been proposed, we chose a rather simple method of clustering the classification matrix of size N × N for finding almost complete maximal subgraphs (pseudo cliques), where N is the number of ncRNA sequences in the test dataset. We applied the k-means clustering algorithm to clustering rows of the classification matrix by regarding each row of an N-dimensional vector as a cluster indicator.

2.4 CNNs with alignment of read mapping profiles

Another useful piece of information about an ncRNA sequence is the transcript information on the ncRNA sequence.

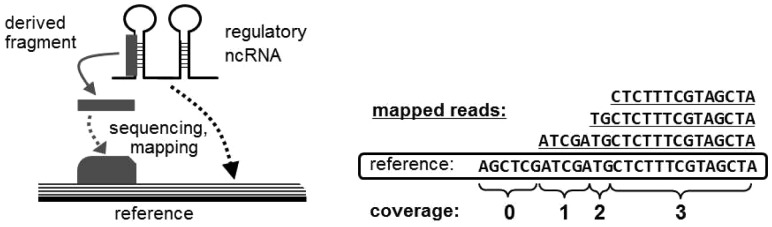
Deep sequencing of transcripts of regulatory ncRNA sequences generates footprints of post-transcriptional processes (Chen and Heard, 2013 ). After sequence reads are obtained, the short reads are mapped onto a reference genome and specific mapping patterns in the ncRNA sequences can be detected, which are called read mapping profiles (Tsuchiya et al., 2016). These patterns reflect the maturation processes that produce shorter RNA sequences called derived RNAs (Fig. 5 (left)). For example, the so-called tRNA-derived RNA fragments are derived from processing at the $5\prime$ or $3\prime$-end of mature or precursor tRNAs (Lee et al., 2009). These sequences constitute a class of short RNAs that are the second most abundant type of RNA after miRNAs.

Fig. 5.

(Left) Schematic illustration of a derived RNA fragment and the mapping pattern obtained from sequencing. (Right) The read coverage calculation from the mapped reads

To incorporate a read mapping profile into the distributed representation for the input of CNNs, the distributed representation of the read mapping profile is coded as follows. A set of sequence reads generated by high-throughput RNA sequencing (RNA-seq) data for ncRNAs is mapped onto the reference genome with standard mapping tools such as BWA (Li and Durbin, 2009). The read coverage, i.e. the number (count) of mapped reads, at each position in an annotated ncRNA region is calculated from the output of the mapping tool [see Fig. 5 (right)]. Normalized read coverage c_i at each position i in the ncRNA sequence is quantized to a 10-dimensional vector where each dimension represents a real-value interval. This 10-dimensional vector is combined with the distributed representation of the ncRNA sequence and secondary structure.

2.5 Comparison with CNNs involving input of a single sequence

To demonstrate a possible advantageous effect of the input of pairwise alignments to CNNs, the conventional method involving one-dimensional CNNs with input of a single sequence is compared with our method in the solution of the family prediction problem. This conventional method is exactly the same as the existing one-dimensional CNN method for classification of sequences (Kelley et al., 2016).

In this setting, the input to one-dimensional CNNs is the distributed representation of a single sequence, and the label of each sequence in the training data is positive if the sequence belongs to the target family and negative if it does not. Thus, the one-dimensional CNNs with input of single sequences classify the input sequences into two classes: positive and negative. In our experiments on clustering ncRNA sequences in multiple families, the multitask (multilabel) learning is applied using one-dimensional CNNs with the same (multiple) number of output nodes as the number of ncRNA families.

2.6 Datasets and accuracy evaluation

In this section, details of the dataset tested in performance analysis are described. The sequence data of an ncRNA provided by Ensembl is integration of the sequence data of ncRNA present in multiple databases such as Rfam and HUGO Gene Nomenclature Committee (HGNC) databases (RNA family databases). Because the sequence data on tRNA are not included in the data provided by Ensembl, they were retrieved from the Genomic tRNA Database (GtRNAdb). We are testing nine ncRNA families in performance analysis, and the number of genes for each family included in the dataset is shown in Table 2.

Table 2.

The number of ncRNA genes per family included in the sequence dataset of ncRNA

snRNA	snoRNA C/D	snoRNA H/ACA	scaRNA	miRNA	YRNA	Vault RNA	5S rRNA	tRNA
2053	322	160	56	1890	831	11	29	631

For 10-fold cross-validation experiments, six families—snRNA, snoRNA C/D box, snoRNA H/ACA box, miRNA, YRNA and tRNA—shown in Table 2 were used. One hundred ncRNA genes were randomly chosen from each of the six families. Ninety genes among the 100 chosen in each family are employed for training data, and the remaining 10 genes are used for test data. The cross-validation process is then repeated 10 times. Every pair of ncRNA sequences in the training data is labeled as a positive class if two sequences of the pair belong to the same RNA family and as a negative class if the two sequences belong to two different families. Every pair of ncRNA sequences in the test data is then labeled in the same manner.

In addition to the 10-fold cross-validation experiment, as a more difficult task and for the more practical purpose of finding new ncRNA families, the ncRNA families for generating the training data were chosen to be different from the ones for the test data. This experiment, called unknown-family validation, may evaluate the capacity of our one-dimensional CNN method for accurate clustering of ncRNA sequences of unknown families that do not exist in the training data.

The performance of each method was evaluated as follows. For classification accuracy, given the prediction of one-dimensional CNN for a pair of ncRNA sequences in the test data, the prediction is defined as true positive (TP) if the pair is labeled as the positive class and the prediction is positive. In the same manner, false positives (FPs), true negatives (TNs) and false negatives (FNs) are defined if the pair is labeled as the negative class, but the prediction is positive, the pair is labeled as the negative class and the prediction is negative, or the pair is labeled as the positive class but the prediction is negative, respectively.

For clustering accuracy, given the set of clusters generated by a clustering method for ncRNA sequences in the test data, a pair of ncRNA sequences is defined as TP if the pair is labeled as the positive class and both sequences of the pair are included in the same resultant cluster. In the same manner, FPs, TNs and FNs are defined if the pair is labeled as the negative class, but both sequences of the pair are included in the same resultant cluster, the pair is labeled as the negative class and the two sequences are included in different resultant clusters, or the pair is labeled as the positive class, but the two sequences are included in different resultant clusters, respectively.

On the basis of the above definitions of TP, FP, TN and FN, we apply two measures, Accuracy and F-value calculated as follows:

$$\text{Accuracy}=\frac{\#\text{TP}+\#\text{TN}}{\#\text{TP}+\#\text{FP}+\#\text{TN}+\#\text{FN}}$$

$$\text{Precision}=\frac{\#\text{\#TP}}{\#\text{TP}+\#\text{\#FP}}$$

$$\text{Recall}=\frac{\#\text{\#TP}}{\#\text{\#TP}+\#\text{\#FN}}$$

$$F-\text{value}=\frac{2\text{Recall}*\text{Precision}}{\text{Recall}+\text{Precision}}$$

where $\#\text{\#TP},\hspace{0.17em}\#\text{\#FP},\hspace{0.17em}\#\text{\#TN}$ and $\#FN$ represent the numbers of TPs, FPs, TNs and FNs, respectively.

3 Results

3.1 Performance on classification of pairwise alignments of ncRNA sequences

A pairwise alignment input to the one-dimensional CNN was generated by two software packages: DAFS (Sato et al., 2012) for the simultaneous aligning and folding of ncRNA sequences that incorporates secondary structures, and Clustal Omega (Sievers et al., 2014) for pairwise alignment based only on primary-sequence information. Although Clustal Omega generates a sequence alignment with gaps, DAFS generates a sequence alignment and predicted secondary structure specific to ncRNA that is called structural alignment. We will see the effects of the two types of input alignment on the prediction accuracy of CNNs.

The prediction accuracy of the one-dimensional CNN in the classification of pairwise alignments among different types of alignments and different distributed representations is summarized in Table 3 for the 10-fold cross-validation.

Table 3.

Performance on classification accuracy of one-dimensional CNNs

Method	Accuracy	F-value
CNN with DAFS (word2vec)	0.980	0.931
CNN with DAFS (one-hot coding)	0.971	0.901
CNN with DAFS (only secondary structure)	0.943	0.803
CNN with Clustal Omega (one-hot coding)	0.958	0.850

Note: ‘CNN with DAFS (word2vec)’ represents one-dimensional CNN with input of DAFS alignments and word2vec distributed representation, ‘CNN with DAFS (one-hot coding)’ denotes the one with input of DAFS alignments and one-hot coding distributed representation, ‘CNN with DAFS (only secondary structure)’ represents the one with input of only secondary structure information, and ‘CNN with Clustal Omega (one-hot coding)’ denotes the one with input of Clustal-Omega alignments and one-hot coding distributed representation.

The CNN with input of DAFS pairwise structural alignment and of the word2vec distributed representation yielded the best and almost perfect predictions in terms of both Accuracy and F-value. Between the two different distributed representations, word2vec showed better performance than one-hot coding. Between the two types of alignment, the DAFS structural alignment showed better performance than did the Clustal-Omega sequence alignment. On the other hand, the input of only secondary-structure information was not enough to obtain an accurate prediction.

3.2 Performance on clustering of ncRNA sequences

We compared the performance on clustering accuracy of our one-dimensional CNN with three existing clustering methods for ncRNA sequences: RNAclust (Engelhardt et al., 2010), Ensembleclust (Saito et al., 2011) and spectral clustering based on the DAFS structural alignment score. Although DAFS is a program that performs pairwise alignment, we conducted spectral clustering by regarding the alignment score as a metric of similarity of two ncRNAs. Likewise, because Ensembleclust calculates similarity between two ncRNAs, spectral clustering was applied to perform clustering based on similarity.

The comparison of clustering accuracy rates is summarized in Table 4. For the unknown-family validation, we examined two cases for the training data: when three families—snoRNA H/ACA box, miRNA and YRNA—are used, and when six families—snoRNA H/ACA box, miRNA, YRNA, scaRNA, vault RNA and 5S rRNA—are employed for the training data. For the test data, three families—snRNA, snoRNA C/D box and tRNA—were chosen.

Table 4.

Performance comparison on clustering accuracy for ncRNA families

Method	Accuracy	F-value
10-fold CV
CNN with DAFS (word2vec)	0.957	0.868
CNN with DAFS (one-hot coding)	0.939	0.824
CNN with DAFS (only secondary structure)	0.910	0.731
CNN with Clustal Omega (one-hot coding)	0.927	0.784
RNAclust	0.890	0.580
Ensembleclust	0.887	0.654
Spectral clustering based on DAFS	0.855	0.554
Unknown family
CNN with DAFS (word2vec, six families)	0.752	0.646
CNN with DAFS (word2vec, three families)	0.717	0.586
CNN with DAFS (one-hot coding)	0.685	0.560
RNAclust	0.707	0.208
Ensembleclust	0.711	0.650
Spectral clustering based on DAFS	0.664	0.588

In 10-fold cross-validation, the CNN-based methods outperformed three existing methods on both Accuracy and F-value and in particular yielded a significantly superior F-value than the existing methods did. In the unknown-family validation, the CNN-based method involving six families as training showed the highest Accuracy, higher than that of the CNN-based method involving three families. F-values were comparable between Ensembleclust and the CNN-based method based on six families.

3.3 Performance on the input sequences with flanking regions

In practical situations, we know neither the exact boundaries of the coding regions of unannotated ncRNAs nor transcripts mapped to the reference genome. To simulate such situations, we concatenated sequences 5 bp in length with both ends of ncRNA sequences and named them the ‘plus flanking regions’ dataset (Saito et al., 2011). The 5-bp-long sequences were extracted from the upstream and downstream regions adjacent to the annotated ncRNAs in the reference genome sequence. The flanking regions were concatenated with 25% of the ncRNA sequences in the test dataset. The result is presented in Table 5.

Table 5.

Clustering accuracy on the ‘plus flanking regions’ dataset

Method	Accuracy	F-value
10-fold CV
CNN with DAFS (word2vec)	0.945	0.834
RNAclust	0.900	0.616
Ensembleclust	0.867	0.592
Unknown family
CNN with DAFS (word2vec, six families)	0.700	0.573
RNAclust	0.697	0.157
Ensembleclust	0.695	0.598

Accuracy levels and F-values of three methods slightly decreased for the ‘plus flanking regions’ dataset except for 10-fold cross-validation of RNAclust. This result indicated that the effect of the ‘plus flanking regions’ was limited for all clustering methods.

3.4 Comparison with the input of a single sequence

The prediction accuracy of the CNN with input of pairwise alignments was compared with the prediction accuracy of the conventional CNN with input of a single sequence to elucidate possible advantages of the input of pairwise alignments to CNNs. The result is presented in Table 6. The CNN with input of a single sequence involved the distributed representation of one-hot coding and secondary structures.

Table 6.

Performance comparison with one-dimensional CNNs with input of a single sequence

Method	Accuracy	F-value
CNN with input of single sequence	0.913	0.734
CNN with DAFS alignment	0.939	0.824

The CNN with input of a DAFS pairwise alignment gave better predictions than did the CNN with input of a single sequence in terms of both Accuracy and F-value, thereby proving the advantage and usefulness of inputting pairwise alignments.

3.5 Performance with additional information, i.e. transcriptome data

First, we generated a sequence-read dataset in an RNA-seq experiment for LNCaP cells, that is, an androgen-sensitive human prostate adenocarcinoma cell line. The small RNAs extracted from cultured LNCaP cells were sequenced on the next-generation sequencer MiSeq (Illumina) with a sequence-read length of 295 bp, which enabled generation of complete sequences of most small-RNA families. A total of 33.3 million (M) sequence reads with a length of 295 bp for small ncRNAs was generated. After quality filtering, 29.1 M reads were mapped onto the human reference genome GRCh38 by means of BWA. From the output in BAM format, normalized read mapping profiles for ncRNAs in families snRNA, snoRNA C/D box, snoRNA H/ACA box, miRNA and tRNA were obtained. Because the number of expressed ncRNAs was insufficient in the family YRNA, this family was eliminated from the following analysis.

A pairwise alignment for a pair of read mapping profiles of ncRNAs with primary sequences and secondary structures was calculated in software called SHARAKU developed in our previous work (Tsuchiya et al., 2016). When read mapping profiles for a pair of ncRNAs are obtained, SHARAKU fundamentally aligns two read mapping profiles by inserting gaps so that the sum of the differences of coverages at all positions between the two profiles is minimized. Simultaneously, SHARAKU takes information on the sequence and secondary structures of RNAs into account when aligning read mapping profiles via integration with DAFS.

The result is presented in Table 7. CNN with input of a SHARAKU pairwise alignment of sequences, secondary structures and read mapping profiles showed slightly better accuracy than did the one with a DAFS structural alignment. Thus, the additional information, i.e. read mapping profiles, helped to improve the clustering performance for ncRNA families.

Table 7.

Performance comparison on clustering accuracy by means of read mapping profiles as additional information

Method	Accuracy	F-value
CNN with SHARAKU (one-hot coding)	0.907	0.815
CNN with DAFS (one-hot coding)	0.903	0.811
Spectral clustering based on SHARAKU	0.747	0.516

Note: ‘CNN with SHARAKU (one-hot coding)’ represents one-dimensional CNN with input of SHARAKU alignments of sequences, secondary structures and read mapping profiles with one-hot coding; ‘spectral clustering based on SHARAKU’ represents spectral clustering based on the SHARAKU alignment score.

4 Discussion

The clustering accuracy of CNNclust can be ranked in the following ascending order: Clustal Omega sequence alignment and DAFS structural alignment involving distributed representation of one-hot coding and structural alignment involving word2vec distributed representation. Furthermore, in 10-fold cross-validation, CNNclust outperformed three existing methods on both Accuracy and F-value. Because RNAclust, Ensembleclust and the spectral clustering algorithm are unsupervised methods, they do not require training data for clustering the test data. In this sense, CNNclust utilizes more information for clustering the test data in a supervised manner, and hence the conditions for these supervised and unsupervised methods are not equivalent for the performance comparison. On the other hand, when advanced information about the target domain such as the training data is available, the supervised method can show significantly higher performance than the unsupervised method can. In unknown-family validation, the CNNclust based on six families as training data showed the highest Accuracy: higher than that of the CNNclust using three families. This result implies that more ncRNA families were available as the training data, and more accurate clustering of ncRNA sequences of unknown families was achieved by CNNclust.

The additional information, i.e. read mapping profiles, helped to improve the clustering performance for ncRNA families. This finding indicates that the read mapping profile representing post-transcriptional processes such as splicing is also useful information to capture some characteristic of each ncRNA family for the family classification. For example, a read mapping pattern depicted in Figure 6a may present the expression of a mature miRNA processed at the $3\prime$-end from pre-miRNA and (b) may present $5\prime$-end processing in tRNA.

Fig. 6.

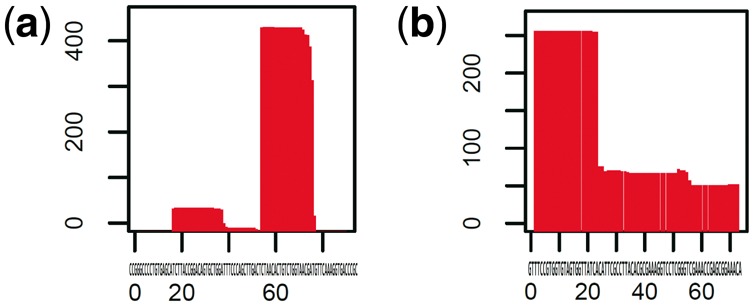
Two examples of read mapping patterns observed in our RNA-seq experiment for LNCaP. (a) A read mapping pattern observed in miRNA (MIR200A) and (b) a read mapping pattern observed in tRNA (tRNA-Val-TAC). The X-axis denotes the position (loci) of an ncRNA gene and the Y-axis indicates the count of mapped reads

Several interesting sequence motifs and secondary-structure motifs known for the snoRNA family and specific to miRNA and tRNA families were identified. The sequence motif depicted in Figure 7a is the typical motif ‘UUCGA’ found in the T-loop of tRNA (Laslett and Canback, 2004), and the motif is concretely presented in tRNA-Arg-CCT as illustrated in Figure 7b. The motif ‘UUCGA’ with a secondary-structure motif of three base pairs ‘G–C’ is highlighted in Figure 7b. The motif depicted in Figure 7c is the typical motif ‘ACA’ present in the snoRNA H/ACA box; and the motif presented in Figure 7d is the typical motif ‘CUGA’ present in the snoRNA C/D box (Ganot et al., 1997; Samarsky et al., 1998). Besides, a secondary-structure motif representing the stacking regions often present in tRNA and miRNA was found as shown in Figure 7e. A motif containing some gaps was also identified as shown in Figure 7f. Thus, the motif identification in pairwise alignments by training CNNs may be considered the construction of an iterative multiple alignments from pairwise alignments. Note that those motifs were extracted from the learned kernels in CNN with input of DAFS alignments and one-hot coding distributed representation.

Fig. 7.

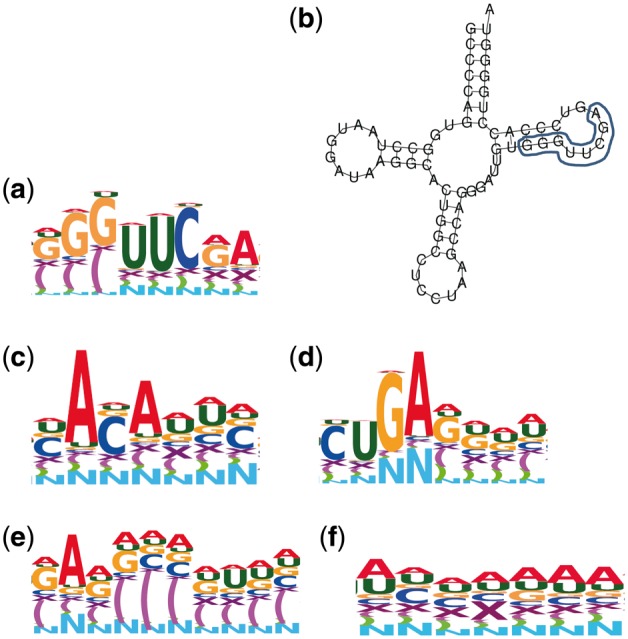
The identified sequence motifs and secondary-structure motifs of snoRNA, miRNA, and tRNA families. ‘X’ in the sequence Logo represents a gap, the parentheses ‘(’ and ‘)’ represent secondary structure and ‘N’ denotes ‘unpaired’

In this study, we dealt only with annotated ncRNAs. Nevertheless, CNNclust can also be applied to the clustering of novel and unannotated regions by employing tools such as blockbuster (Langenberger et al., 2009) to determine the expressed block regions in the reference genome from RNA-seq reads. As shown in the experiment involving the ‘plus flanking regions’ dataset, CNNclust can tolerate ambiguous boundaries of unannotated ncRNA transcripts in clustering performance. Another important issue that we have not addressed is the computational complexity of clustering algorithms. The alignment-free approach such as GraphClust (Heyne et al., 2012) and RNAscClust (Miladi et al., 2017) was proposed to accelerate the clustering task of ncRNA sequences. The alignment-free method avoids the computationally heavy alignment process and is applied to clustering very large sets of ncRNA sequences while keeping the comparable accuracy. The basic idea of CNNclust could be extended to the alignment-free approach to gain the practically fast computational time. These issues will be addressed in our future work.

5 Conclusion

With the aim of applying a one-dimensional CNN to accurate clustering of ncRNA sequences in a supervised learning manner, we developed a new CNN-based method for classification of pairwise alignments of ncRNA sequences. Two types of distributed representation, word2vec and one-hot coding, were combined with the secondary-structure information specific to ncRNAs and furthermore with mapping profiles of next-generation sequence reads. As a result, the training of one-dimensional CNNs for classification of alignments of ncRNA sequences outperformed three existing clustering methods in terms of clustering ncRNA sequences and the conventional one-dimensional CNN with input of a single sequence for the family prediction. Furthermore, several sequence motifs and secondary-structure motifs known for the snoRNA family and specific to miRNA and tRNA families were identified.

Our one-dimensional CNN method with input of pairwise alignments is general enough to be applicable to not only ncRNA sequences but also other biological sequences such as DNA and proteins with the aim of finding conserved domains.

Funding

This work was supported by a Grant-in-Aid for Scientific Research in Innovative Areas [no. 221S0002] from the Ministry of Education, Culture, Sports, Science and Technology of Japan (MEXT), by a Grant-in-Aid for Scientific Research (A) (KAKENHI) [no. 23241066] from the Japan Society for the Promotion of Science (JSPS) and by another JSPS KAKENHI grant [no. 16H06279]. This work was also funded by a MEXT-supported Program for the Strategic Research Foundation at Private Universities.

Conflict of Interest: none declared.