SIMPLE: Sparse Interaction Model over Peaks of moLEcules for fast, interpretable metabolite identification from tandem mass spectra

Abstract

Motivation

Recent success in metabolite identification from tandem mass spectra has been led by machine learning, which has two stages: mapping mass spectra to molecular fingerprint vectors and then retrieving candidate molecules from the database. In the first stage, i.e. fingerprint prediction, spectrum peaks are features and considering their interactions would be reasonable for more accurate identification of unknown metabolites. Existing approaches of fingerprint prediction are based on only individual peaks in the spectra, without explicitly considering the peak interactions. Also the current cutting-edge method is based on kernels, which are computationally heavy and difficult to interpret.

Results

We propose two learning models that allow to incorporate peak interactions for fingerprint prediction. First, we extend the state-of-the-art kernel learning method by developing kernels for peak interactions to combine with kernels for peaks through multiple kernel learning (MKL). Second, we formulate a sparse interaction model for metabolite peaks, which we call SIMPLE, which is computationally light and interpretable for fingerprint prediction. The formulation of SIMPLE is convex and guarantees global optimization, for which we develop an alternating direction method of multipliers (ADMM) algorithm. Experiments using the MassBank dataset show that both models achieved comparative prediction accuracy with the current top-performance kernel method. Furthermore SIMPLE clearly revealed individual peaks and peak interactions which contribute to enhancing the performance of fingerprint prediction.

Availability and implementation

The code will be accessed through http://mamitsukalab.org/tools/SIMPLE/.

1 Introduction

Metabolites are small molecules which are used in, or created by, chemical reactions occurring in living organisms (Wishart, 2007). They play a lot of important functions such as energy transport, signaling, building block of cells and inhibition/catalysis. Understanding biochemical characteristics of metabolites is an essential and important part of metabolomics to enlarge the knowledge of biological systems. It is also key to development of many applications and areas such as biotechnology, biomedicine or pharmaceutical sciences. Mass Spectrometry is a common technique in analytical chemistry (de Hoffmann and Stroobant, 2007) for metabolite identification. A mass spectrometer analyses a chemical sample by fragmenting it and measuring the mass-to-charge ratios (m/z) of its fragments. The resulting mass spectrum (MS) or tandem mass spectrum (MS/MS) is represented by a graph with m/z on the x-axis and the relative abundance of ions with m/z values on the y-axis (Fig. 1). Another common representation of mass spectrum is a list of peaks, each defined by its m/z and intensity value (top-right corner of Fig. 1).

Fig. 1.

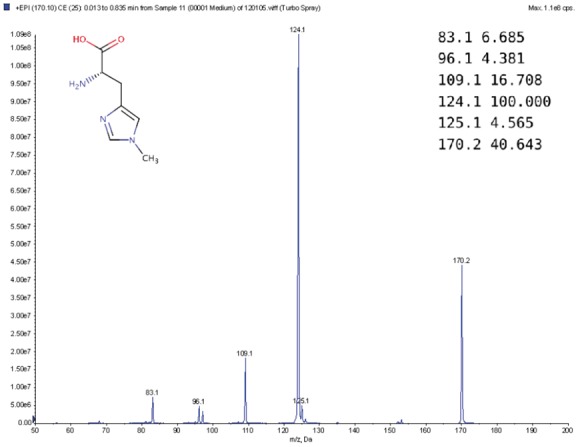
Example MS spectrum from Human Metabolome Database (Wishart et al., 2012) for 1-Methylhistidine (HMBD00001), with its corresponding chemical structure (top-left) and peak list (top-right)

Many methods have been proposed for metabolite identification. A traditional approach is to compare a query MS or MS/MS spectrum of unknown compound against a database of a number of reference MS or MS/MS spectra (Scheubert et al., 2013). The candidate molecules from the database are ranked based on the similarity, and the query spectrum and the best matched candidates are returned. However, the main disadvantage of this approach is that the reference database often contains only a small fraction of molecules in reality, leading to unreliable matching results if the molecule of the query spectrum is not in the database. Consequently, to mitigate the insufficiency of the reference databases, alternative approaches for metabolite identification are devised to deal with unavailable measured reference spectra. In general, we can divide computational methods for metabolite identification into the following three categories: i) searching in spectral libraries; ii) in silico fragmentation; iii) machine learning (ML).

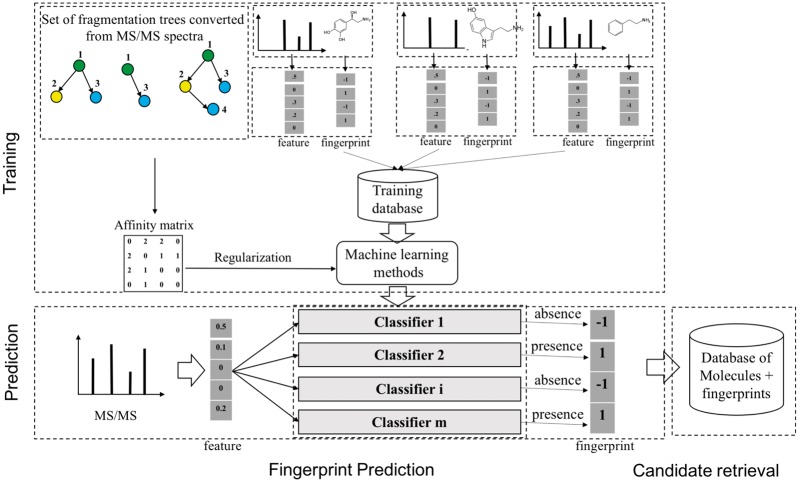
We focus on the ML approach, where the common scheme is, given a set of MS/MS spectra, to learn a map from a MS/MS spectrum to a molecule (Fig. 2). This has two steps: i) fingerprint prediction: predict a fingerprint with supervised ML, and ii) candidate retrieval: use the predicted fingerprint to query the database. Our particular focus is the first step, which predicts the fingerprint that is a binary (or rarely real-valued) vector, indicating the presence (or absence) of certain substructure. This step has been tackled by many ML methods, including linear discriminative analysis (LDA) (Imre et al., 2008) and decision tree (Hummel et al., 2010). A notable method is FingerID (Heinonen et al., 2012), which used support vector machine (SVM) with kernels for pairs of mass spectra, including integral mass kernel and probability product kernel (PPK) (Jebara et al., 2004).

Fig. 2.

A general scheme to identify unknown metabolites based on molecular fingerprint vectors. There are two main stages: 1) fingerprint prediction: learning a mapping from a molecule to the corresponding binary molecular fingerprint vector by classification methods, given a set of MS/MS spectra and fingerprints; 2) candidate retrieval: using the predicted fingerprints to retrieve candidate molecules from the databases of known metabolites. Note that the step of constructing an affinity matrix is optional and is used in L-SIMPLE only

We point out three drawbacks of the existing ML approaches: i) all methods are based on the information from individual peaks in spectra, without explicitly considering peak interactions, which leads to the limitation of predictive performance. ii) There is an interesting (not ML-based) software, which outputs, given a spectrum, a so-called fragmentation tree (FT) (Böcker and Rasche, 2008; Rasche et al., 2011). In a FT, possible fragments corresponding to peaks in spectrum are shown as node labels, where parent–child relationships in this tree are inclusive relations of fragments in chemical structure. FT is indeed interesting, but this software of converting a given spectrum into a FT is very slow. CSI: FingerID (Dührkop et al., 2015; Shen et al., 2014) used both mass spectra and FTs as input, thinking that structural information of chemical compounds can be captured by FTs. Indeed using FTs might be similar to considering peak interactions. However if FTs are used as input features, spectrum must be converted into a FT not only in training and but also in prediction, which needs a heavy computational load. iii) The size/length of a fingerprint is not short, while the number of peaks is usually small, meaning that most elements of a fingerprint vector are zero. So the training data is very sparse, while sparse models have not been considered yet. In addition, sparse models are advantageous in that their results are easily interpretable.

Motivated by these drawbacks, we address the following two problems: i) incorporation of peak interactions into the learning model to improve the predictive performance; ii) introduction of sparsity into the models for interpretation. For the above i), we propose a kernel for peak interactions and combine this kernel with other kernels through multiple kernel learning (MKL). For the above both i) and ii), we propose a sparse, interpretable model, which we call Sparse Interaction Model over Peaks of moLEcules (SIMPLE). Additionally, we also propose a FT-induced Laplacian regularization to make SIMPLE more robust. We note that in SIMPLE, FTs are used for regularization only and not for input, by which we do not need FTs for prediction, meaning that computationally SIMPLE is much lighter for prediction than (Shen et al., 2014). We formulate the model as a convex optimization problem, for which we develop an alternating direction method of multipliers (ADMM) algorithm.

We evaluated our two proposed models by using real data obtained from the MassBank dataset (Horai et al., 2010), which was used in (Shen et al., 2014). We found that incorporation of peak interactions can significantly improve the prediction accuracy of not using interactions, resulting in comparable performance with the current top method. Furthermore, SIMPLE could show the interpretability of results, i.e. peaks and peak interactions which contribute to high predictive performance.

2 Related work

In Figure 2, the standard data preprocessing converts spectra into high-dimensional feature vectors by dividing m/z range into bins and taking accumulated intensity within each bin as a feature value. However the width of bins is hard to determine. In fact, wide bins can cause noise, and narrow bins can induce alignment errors due to mass error. One idea to overcome this issue is using a kernel, say probability product kernel (PPK; Jebara et al., 2004), which can be computed directly from mass spectra. PPK treats each peak in a spectrum as a two-dimensional Gaussian distribution and a spectrum as a uniform mixture of these distributions. Then, kernel between two spectra is computed by all-against-all matching between the component Gaussians. The detail is in Section 3.1.1.

Also we briefly explain the current cutting-edge ML method by MKL, CSI: FingerID (Dührkop et al., 2015; Shen et al., 2014), where the input is both MS/MS spectra and FTs. Motivation behind this method is to use structural information, which might be captured by FTs. So they use numerous kernels for FTs to capture any information of FTs, ranging from simple ones, such as node kernels: node binary (NB), node intensity (NI) and edge kernels: loss binary (LB), loss count (LC), loss intensity (LI) to more complex one like common path counting (CPC) which is one of path based kernels. Subsequently, these kernels are combined by MKL methods, such as centered alignment (Gönen and Alpaydin, 2011), quadratic combination and $l_p-$norm regularized combination (Kloft et al., 2011). The combined kernel is then used in learning the final model for fingerprint prediction.

We again emphasize that these methods consider mainly only peaks in MS/MS spectra without explicitly taking peak interactions into account. Also kernels using FTs have the limitation of processing MS/MS spectra, particularly for prediction, due to the need of computationally heavy conversion of spectra into FTs. More importantly, kernels are difficult to interpret and deal with sparse data, such as MS/MS spectra, where each spectrum (fingerprint vector) has only a few number of peaks (nonzeros).

3 Materials and methods

3.1 Kernel method

We develop kernel for peak interactions and combine this kernel with PPK (kernel for peaks) (Heinonen et al., 2012) through the framework of MKL.

3.1.1. Preliminary: kernel for peaks

MS/MS spectra have peak information, i.e. m/z and intensity. The problem is that peaks are not correctly aligned each other, due to measurement errors in mass spectrometry devices (alignment error). To overcome this problem, PPK (Jebara et al., 2004) was developed to calculate the similarity between two spectra. The idea is that a peak can be considered as a two-dimensional Gaussian distribution and the spectrum is a uniform mixture of peaks (or distributions). The kernel between two spectra is computed by all-against-all matching between the Gaussians.

More specifically, given a mass spectrum S, being a list of peaks, i.e. $\left\{\right(m_1,I_1),(m_2,I_2),\dots ,(m_{N_{\mathbf{S}}},I_{N_{\mathbf{S}}}\left)\right\}$. The kth peak of the spectrum S is represented by a Gaussian distribution p_k centered around the peak measurement $(m_k,I_k)$ and with covariance shared with all peaks: $\Sigma =\text{diag}({\sigma }_m^2,{\sigma }_I^2)$, where ${\sigma }_m^2$ and ${\sigma }_I^2$ are the variances for the mass and intensity, respectively. Hence, the spectrum S can be represented as a uniform mixture of the peaks contained in it, i.e. $p\left(\mathbf{S}\right)=\frac{1}{N_{\mathbf{S}}}{\sum }_{k=1}^{N_S}{p}_k$. Likewise, another spectrum ${\mathbf{S}}^{\prime }$ is also represented by a mixture of distributions q_l, $l=1,2,3,\mathrm{..},N_{{\mathbf{S}}^{\prime }}$ and $p\left({\mathbf{S}}^{\prime }\right)=\frac{1}{N_{{\mathbf{S}}^{\prime }}}{\sum }_{l=1}^{N_{{\mathbf{S}}^{\prime }}}{q}_l$.

With definitions above, the kernel for peaks, ${\mathbf{K}}_{peak}$, between two spectra S and ${\mathbf{S}}^{\prime }$ is given by:

$${\mathbf{K}}_{peak}(\mathbf{S},{\mathbf{S}}^{\prime })={\int }_{{\mathbb{R}}^2}{p}_{\mathbf{S}}\left(x\right)q_{{\mathbf{S}}^{\prime }}\left(x\right)dx$$ (1)

$$=\frac{1}{N_{\mathbf{S}}{N}_{{\mathbf{S}}^{\prime }}}\sum _{1\le i\le N_{\mathbf{S}}1\le j\le N_{{\mathbf{S}}^{\prime }}}\mathbf{K}(p_i,q_j)$$ (2)

where $\mathbf{K}(p,q)$ is the PPK between two component Gaussian distributions p and q, computed by (3).

$$\mathbf{K}(p,q)=\frac{1}{4\pi {\sigma }_m{\sigma }_I}\text{exp}(-0.5(\frac{{({\mu }_p^m-{\mu }_q^m)}^2}{{\sigma }_m}+\frac{{({\mu }_p^I-{\mu }_q^I)}^2}{{\sigma }_I}\left)\right)$$ (3)

where ${\mu }_p^m$ and ${\mu }_p^I$ denote the mass and intensity values of the peaks corresponding to p.

3.1.2. Kernel for peak interactions

Being rather straight-forward, kernel for peak interactions between two spectra S and ${\mathbf{S}}^{\prime }$ can be defined as follows:

$${\mathbf{K}}_{interaction}(\mathbf{S},{\mathbf{S}}^{\prime })=\sum _{\begin{array}{c}1\le i\le j\le N_{\mathbf{S}}1\le k\le l\le N_{{\mathbf{S}}^{\prime }}\end{array}}\mathbf{K}(p_i,q_k)*\mathbf{K}(p_j,q_l),$$ (4)

where K is the function defined by (3).

Note that ${\mathbf{K}}_{interaction}$ also can overcome the alignment error problem by taking advantage of ${\mathbf{K}}_{peak}$. Intuitively, ${\mathbf{K}}_{peak}$ can be considered as a probabilistic version of the number of common peaks. Similarly ${\mathbf{K}}_{interaction}$ can be considered as a probabilistic version of the number of common edges or interactions between two spectra.

3.1.3. Combining kernels for peaks and peak interactions

We combine kernels for peaks and peak interactions by using a regular approach: Multiple Kernel Learning (MKL; Gönen and Alpaydin, 2011), which can combine kernels from different sources. We use three approaches: the first is the uniform combination of the kernels (UNIMKL: the weights for kernels are equal), which can produce good results for prediction in many practical applications. The second and third are two different MKL algorithms: centered alignment (ALIGN) and alignment maximization algorithm (ALIGNF) (Cortes et al., 2012).

These algorithms have the same setting. Given a set of kernels $\{{\mathbf{K}}_j\in {\mathbb{R}}^{n\times n},j=1,\mathrm{..},m\}$, computed from n data points and representing different sources of information. The vector $\mathbf{y}={\{-1,1\}}^n$ corresponds to the output or labels of data points. The aim of MKL is to seek a combination of these kernels, as defined by:

$${\mathbf{K}}_{\alpha }=\sum _{j=1}^m{\alpha }_j{\mathbf{K}}_j$$ (5)

A popular approach to MKL, which is called two-stage MKL, separate kernel learning from prediction learning. In the first stage, the combined kernel is learned through the use of an objective function, such as centered alignment that measures the similarity of two kernels over the training dataset. For the purposes of MKL, alignment is often measured between the combined kernel in (5) and the target kernel ${\mathbf{K}}_y=\mathbf{y}{\mathbf{y}}^T$. Subsequently, the learned combined kernel is used in the second stage with kernel based classifiers such as relevance vector machine (RVM) used in (Burden and Winkler, 2015) or SVM used in our experiments.

Formally, the centered kernel of a given kernel $\mathbf{K}\in {\mathbb{R}}^{n\times n}$ is defined by:

$${\mathbf{K}}_c=[\mathbf{I}-\frac{\mathbf{e}{\mathbf{e}}^T}{n}]\mathbf{K}[I-\frac{\mathbf{e}{\mathbf{e}}^T}{n}]$$ (6)

where I is the identity matrix and e is the vector with all ones.

The centered alignment between two kernels K and ${\mathbf{K}}^{\prime }$ is defined by:

$$\rho (\mathbf{K},{\mathbf{K}}^{\prime })=\frac{<{\mathbf{K}}_c,{\mathbf{K}}_c^{\prime }>}{\left|\right|{\mathbf{K}}_c\left|{|}_F\right|\left|{\mathbf{K}}_c\right|{|}_F}$$ (7)

$$\text{where}<{\mathbf{K}}_c,{\mathbf{K}}_c^{\prime }> =\text{trace}\left({\mathbf{K}}_c^T{\mathbf{K}}_c^{\prime }\right) \text{and} \left|\right|{\mathbf{K}}_c|{|}_F=\sqrt{\text{trace}\left({\mathbf{K}}_c^T{\mathbf{K}}_c\right)}$$ (8)

Cortes et al. (2012) proposed two MKL algorithms: i) a simple centered alignment algorithm (ALIGN), which assigns alignment scores computed in (7) to combination weights in (5), i.e. ${\alpha }_j=\rho ({\mathbf{K}}_j,{\mathbf{K}}_{\mathbf{Y}}),\hspace{0.17em}j=1,2,3,\dots ,m$. and ii) the alignment maximum algorithm (ALIGNF) seeks the weights α by maximizing the alignment scores between the combined kernels ${\mathbf{K}}_{\alpha }$ and target kernel ${\mathbf{K}}_y$, resulting in the objective function:

$${\alpha }^{*}=\underset{{}_{\alpha }}{\text{argmax}}\frac{<K_{\alpha },K_y>}{\left|\right|K_{\alpha }|{|}_F}$$ (9)

$$\text{subject} \text{to} \left|\right|\alpha \left|\right|=1 , \alpha \ge 0$$ (10)

In our experiments, we conducted comparative experiments by using these algorithm for combining kernels for peaks and interactions.

3.2 Sparse Interaction Model over Peaks of moLEcules (SIMPLE)

Kernel-based methods are difficult to deal with sparse data and lack of interpretation. Thus we present a more interpretable, fast, sparse learning: Sparse Interaction Model over Peaks of moLEcules (SIMPLE), to incorporate peak interactions explicitly. We first preprocess each MS/MS spectrum to generate a feature vector: we divide m/z range into bins and taking accumulated peak intensities in a bin as a feature value to obtain high dimensional vector for each spectrum. These feature vectors are normalized such that all feature values are in [0, 1].

3.2.1. Prediction model

Given a MS/MS spectrum, represented by a feature vector, $\mathbf{x}={[x_1,x_2,\dots ,x_d]}^T\in {\mathbb{R}}^d$, we formulate the model for individual peaks and peak interactions as follows:

$$f(\mathbf{x};w,W)=b+\sum _{i=1}^d{w}_i{x}_i+\sum _{i=1}^d\sum _{j=1}^d{W}_{ij}{x}_i{x}_j$$ (11)

$$=b+w^T\mathbf{x}+{\mathbf{x}}^{T}W\mathbf{x}$$ (12)

where $b\in \mathbb{R},\hspace{0.17em}w\in {\mathbb{R}}^d$ and $W\in {\mathbb{R}}^{d\times d}$. The prediction function consists of a bias b and two terms: main effect term parameterized by the weight vector w and interaction term parameterized by the weight matrix W. Their roles are different. While the former capture information about the peaks, the latter captures information about peak interactions. Since our task is classification which predicts the presence or absence of properties in fingerprint vector, the output of the model can be computed by $y\left(\mathbf{x}\right)=\text{sign}\left(f\right(\mathbf{x};w,W\left)\right)\in \{-1,1\}$.

In order to predict a binary vector of fingerprint, we predict one response variable (hereafter a property or a task) at each time with a separate classifier. Let consider a property and give a set of n training input/output pairs ${\left\{\right({\mathbf{x}}_i,{\mathbf{y}}_i\left)\right\}}_{i=1}^n$, where ${\mathbf{x}}_i\in {\mathbb{R}}^d$ represent the ith spectrum and ${\mathbf{y}}_i\in \{-1,1\}$ indicates the presence (+1) or absence (-1) of the property. We can learn the parameters by minimizing the following optimization function:

$$\begin{array}{ll}\underset{{}_{b,w,W}}{\min }\hfill & {\displaystyle \sum _{i=1}^{n}l}(y_i,f(x_i;w,W\left)\right)+\mathcal{R}\left(w\right)+\mathcal{R}\left(W\right)\hfill \end{array}$$ (13)

where $l(\mathbf{y},\widehat{\mathbf{y}})$ is the hinge loss function and computed by $l(\mathbf{y},\widehat{\mathbf{y}})={(1-\mathbf{y},\widehat{\mathbf{y}})}_{+}$, in which the operator ${\left(z\right)}_{+}$ denotes $\text{max}(0,z)$. $\mathcal{R}\left(w\right)$ and $\mathcal{R}\left(W\right)$ are the regularization terms for vector w and matrix W, respectively.

Our purpose is to seek a model which is accurate as well as interpretable. Different from SVM using $l_2$-norm regularizer, $\mathcal{R}\left(w\right)=\alpha \left|\right|w|{|}_2^{\mathrm{2}}$, our model uses sparsity-induced regularizer (Tibshirani, 1994), $\mathcal{R}\left(w\right)=\alpha \left|\right|w|{|}_1$ to yield sparse solution and interpretation. As for interaction term, it is natural to impose low-rankness on matrix W due to the existence of groups of peaks interacting with each other. Thus, we propose to use trace norm, similar to (Blondel et al., 2015), i.e. $\mathcal{R}\left(W\right)=\beta \left|\right|W|{|}_{*}$. Furthermore, due to the symmetry of matrix W, we also impose the positive semidefiniteness on matrix W, i.e. $W\hspace{0.17em}\succcurlyeq \hspace{0.17em}0$. Therefore, putting all above things together, the objective function of SIMPLE becomes:

$$\begin{array}{ll}\underset{{}_{b,w,W}}{\min }\hfill & {\displaystyle \sum _{i=1}^{n}l}(y_i,f(x_i;w,W\left)\right)+\alpha \left|\right|w|{|}_1+\beta |\left|W\right|{|}_{*}\hfill \\ \text{subject\hspace{0.17em}to}\hfill & W\hspace{0.17em}\mathrm{\succcurlyeq }\hspace{0.17em}0\hfill \end{array}$$ (14)

where α and β are hyperparameters to control the sparsity of w and low-rankness of W, respectively. Note that (15) is the convex function which guarantees to find the global optimal solution.

3.2.2. Fragmentation trees (FTs) as prior information

As the number of interactions is large, it would be a good idea to regularize (14) with background knowledge. We propose to regularize the interaction matrix W by FTs of the spectra. However, there are two questions to deal with: i) How to represent the structural information from FTs; ii) how to incorporate them into the convex objective function (14) while preserving its convexity to guarantee the global optimal solutions.

To answer the first question, our idea is to construct an affinity (adjacency) matrix A for all peaks in the spectra. Concretely, each spectrum is converted into a FT by algorithms in (Rasche et al., 2011). Our assumption is that, the frequency of an interaction present in the fragmentation trees reflects how strongly the corresponding features are interacting with each other. From that, we calculate the co-occurrence of all peak pairs in the trees to construct the affinity matrix (Fig. 3).

Fig. 3.

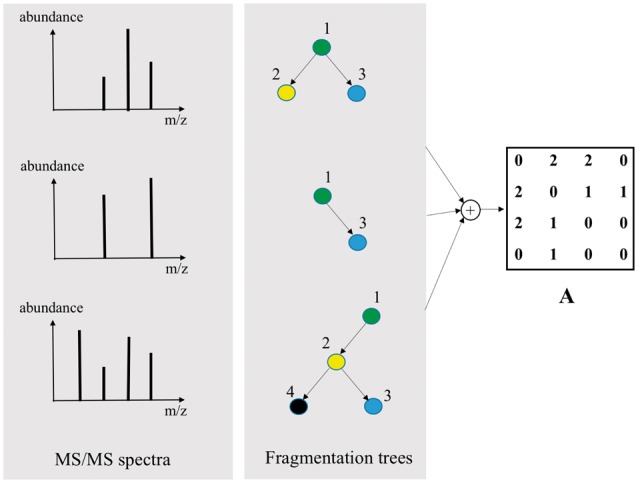
Illustration of constructing affinity matrix A from the set of fragmentation trees. The constructed matrix A is used as prior information for regularizing interaction matrix W

To answer the second question, we impose the constraint of being positive semidefinite on interaction matrix W. By this, W can be decomposed into the low rank matrix, i.e. $W=V{V}^T$ where $V\in {\mathbb{R}}^{nxk},\hspace{0.17em}k=\text{rank}\left(W\right)$. Thus, the interaction term in the prediction function (12) can be rewritten as following:

$${\mathbf{x}}^{T}W\mathbf{x}=\sum _{i,j=1}^d\left(v_i^T{v}_j\right){\mathbf{x}}_i{\mathbf{x}}_j,$$

where v_i and v_j are the ith and jth bins of spectrum x and correspond to representation of ith and jth features in the space ${\mathbb{R}}^k$.

We assume that if ith and jth peaks are strongly interacting with each other, then their representation in the vector space should be close, i.e. $\left|\right|v_i-v_j|{|}_2$ should be small. From this observation, we include the following term, Laplacian smoothness, into the objective function (14):

$$\mathcal{R}\left(V\right)=\sum _{i,j=1}^d{A}_{ij}\left|\right|v_i-v_j|{|}_2^{\mathrm{2}}$$ (15)

$$=\text{trace}\left(V^{T}LV\right)$$ (16)

$$=\text{trace}\left(V{V}^{T}L\right)=\text{trace}\left(WL\right)$$ (17)

where $L=D-A$, D is the degree matrix of A, i.e. $D_{ii}={\sum }_{j=1}^n{A}_{ij},i=1,\mathrm{..},n$

Thus, we can formulate the following optimization problem, which we call L-SIMPLE:

$$\begin{array}{ll}\underset{{}_{b,w,W}}{\min }\hfill & {\displaystyle \sum _{i=1}^{n}l}(y_i,f_i)+\alpha \left|\right|w|{|}_1+\beta |\left|W\right|{|}_{*}+\gamma \text{trace}\left(WL\right),\hfill \\ \text{subject to}\hfill & W\mathrm{\succcurlyeq }0\hfill \end{array}$$ (18)

where ${\mathbf{f}}_i=f({\mathbf{x}}_i;w,W)$, γ is an additional hyperparameter to control Laplacian smoothness of the objective function (18). It is noteworthy that, our derived formulation is still convex due to convexity of regularization terms, thus, the solution of (18) is guaranteed to be the global optimal. Below we will present an optimization method for efficiently solving (18).

3.2.3. Optimization: ADMM algorithm

Equation (18) is convex and guaranteed that the algorithm converges to the global optimal solution. However, it is challenging to solve this problem directly, because terms are nondifferentiable. Our optimization method is based on alternating direction method of multipliers (ADMM). Due to the nondifferentiability of the hinge loss, we introduce the auxiliary variable C, where $\mathbf{C}={(C_1,C_2,\dots ,C_n)}^T$ and $C_i=1-{\mathbf{y}}_i{\mathbf{f}}_i$, then (18) can be reformulated into the following equivalent constrained problem:

$$\begin{array}{lll}\underset{{}_{b,w,W,C}}{\min }\hfill & \hfill & {\displaystyle \sum _{i=1}^n{\left(C_i\right)}_{+}}+\alpha \left|\right|w|{|}_1+\beta |\left|W\right|{|}_{*}+\gamma \text{trace}\left(WL\right)\hfill \\ \text{subject to }\hfill & \hfill & C=1-YF\text{ and }W\mathrm{\succcurlyeq }0\hfill \end{array}$$ (19)

where $\mathbf{F}={[{\mathbf{f}}_1,{\mathbf{f}}_2,\dots ,{\mathbf{f}}_n]}^T$.

The augmented Lagrange function of (19) is defined by:

$$\begin{array}{cc}\mathcal{L}(w_0,w,W,\mathbf{C},\mathbf{u})\hfill & =\sum _{i=1}^n{\left(C_i\right)}_{+}+\alpha \left|\right|w|{|}_1+\beta |\left|W\right|{|}_{*}+\gamma \text{trace}\left(WL\right)\hfill \\ \hfill & +{\mathbf{u}}^T(1-\mathbf{Y}\mathbf{F}-\mathbf{C})+\frac{1}{2}\left|\right|1-\mathbf{Y}\mathbf{F}-\mathbf{C}|{|}_2^{\mathrm{2}}\hfill \end{array}$$ (20)

where $\mathbf{u}={[u_1,u_2,\dots ,u_n]}^T$ is a dual variable corresponding to the constraint $\mathbf{C}=1-\mathbf{Y}\mathbf{F}$. Note that the constraint $W\mathrm{\succcurlyeq }0$ is not included in (20) because this property will be imposed automatically on W after each iteration of updating W, as explained in the Appendix section. We solve the problem of finding the saddle point $(b^{*},w^{*},W^{*},{\mathbf{C}}^{*},{\mathbf{u}}^{*})$ of the augmented Lagrangian function (20) through an iterative algorithm between the primal and the dual optimization as follows:

$$\{\begin{array}{cc}{b}^{t+1},w^{t+1}\hfill & ={\text{argmin}}_{b,w}\hspace{0.17em}\mathcal{L}(b,w,W^t,{\mathbf{C}}^t,{\mathbf{u}}^t)\hfill \\ W^{t+1}\hfill & ={\text{argmin}}_W\hspace{0.17em}\mathcal{L}(b^{t+1},w^{t+1},W,{\mathbf{C}}^t,{\mathbf{u}}^t)\hfill \\ {\mathbf{C}}^{t+1}\hfill & ={\text{argmin}}_{\mathbf{C}}\hspace{0.17em}\mathcal{L}(b^{t+1},w^{t+1},W^{t+1},\mathbf{C},{\mathbf{u}}^t)\hfill \\ {\mathbf{u}}^{t+1}\hfill & ={\mathbf{u}}^t+1-\mathbf{Y}{\mathbf{F}}^{t+1}-{\mathbf{C}}^{t+1}\hfill \end{array}$$ (21)

where the first three steps update the primal variables based on the current estimate of the dual variable ${\mathbf{u}}^t$ and the final step updates the dual variable based on the current estimate of the primal variables. Note that the efficiency of ADMM for solving (20) depends on whether the subproblems in (21) can be solved quickly. Algorithm 1 summarizes the ADMM steps for solving the optimization problem (20). To avoid confusion, the detailed derivation of the update rules for subproblems of (21) are in Appendix.

3.3 Model summary

We here summarize the advantageous features of (L-)SIMPLE:

1. Peak interactions: SIMPLE has, in its formulation, the term for peak interactions explicitly, which has not been considered by existing methods, particularly kernel-based methods.

2. Sparse interpretability: MS spectra are with many zeros and sparse data. We formulate SIMPLE as a sparse model, by which peaks or peak interactions which contribute to improve the predictive performance can be checked and found easily.

3. Convex formulation: our formulation keeps SIMPLE (L-SIMPLE) a convex model, which guarantees to find the global optimum. We have developed an alternating direction method of multipliers (ADMM) algorithm, to realize the detection of the global optimum.

4. No fragmentation trees in prediction: L-SIMPLE uses fragmentation trees for regularization in training, and they are not inputs, meaning that we do not need fragmentation trees in prediction, which can avoid heavy computational cost of generating fragmentation trees from spectrum.

4 Experimental evaluation

Our focus is to incorporate peak interactions of mass spectra into fingerprint prediction, and to build sparse models for model interpretability, and so we conducted experiments to answer the following two questions:

• (Q1): Can peak interactions due to sets of correlated peaks in spectra be used to predict fingerprint vectors more accurately?

• (Q2): For the purpose of interpretation, how to identify a smaller subset of predictors (i.e. peaks or peak interactions) that exhibit the strongest effects on fingerprints?

4.1 Data, preprocessing and evaluation measures

MassBank (Horai et al., 2010) was used. We used the same dataset with 402 compounds as (Shen et al., 2014), and followed the same preprocessing steps as in (Shen et al., 2014): for each compound, peaks recorded from different energies were merged for each MS/MS spectra. Then, spectra were normalized such that the sum of intensities is up to 100%. In terms of the output for the learning models, molecular fingerprints, which are binary vectors of 528 bits in total, were generated using OpenBabel (O’Boyle et al., 2011). Fingerprints have a high class imbalance, i.e. mostly +1 or reverse. Thus we only trained models for predicting fingerprints in which the majority class occupies less than 90% of instances.

We used micro-average accuracy, F1 score to evaluate the performance of different methods, computed by taking the average of accuracies and F1 scores over all tasks.

Algorithm 1 .

ADMM algorithm for optimizing the objective function (19).

1: Inputs:

    A set of MS/MS spectra $\mathbf{X}={[{\mathbf{x}}_1^T,{\mathbf{x}}_2^T,\dots ,{\mathbf{x}}_n^T]}^T$ and associated output $\mathbf{Y}={[y_1,y_2,\dots ,y_n]}^T$. Laplacian L (only for L-SIMPLE).

2: Outputs:

    weight vector w and interaction matrix W.

3: Initialize:

    $b\leftarrow 0,w\leftarrow \mathbf{0},\hspace{0.17em}W\leftarrow \mathbf{0},\hspace{0.17em}\mathbf{C}\leftarrow \mathbf{0},\hspace{0.17em}\mathbf{u}\leftarrow \mathbf{0}$

4: while not converged do

5:   1. Fix W, C, u and update b, w

6:   Precompute ${\widehat{\mathbf{F}}}_1\leftarrow \mathbf{Y}(\mathbf{1}-\mathbf{C}+\mathbf{u})-\text{diag}\left(\mathbf{X}W{\mathbf{X}}^T\right)$

7:   while not converged do

$$\{\begin{array}{c}\mathbf{z}\leftarrow w-\rho {\mathbf{X}}^T(\mathbf{X}w+b-{\widehat{\mathbf{F}}}_1)\hfill \\ w\leftarrow {\mathcal{S}}_{\alpha }\left(z\right)\hfill \\ b\leftarrow \frac{1}{n}\text{sum}({\widehat{\mathbf{F}}}_1-\mathbf{X}w)\hfill \end{array}$$

8:   end while

9:   2: Fix b, w, C, u and update W

10:   precompute ${\widehat{\mathbf{F}}}_2\leftarrow \mathbf{Y}(1-\mathbf{C}+\mathbf{u})-b-\mathbf{X}w$

11:   while not converged do

$$\{\begin{array}{c}\mathbf{R}\leftarrow \text{diag}\left(\mathbf{X}W{\mathbf{X}}^T\right)-{\widehat{\mathbf{F}}}_2\hfill \\ {\Delta }_W\mathcal{L}\leftarrow {\mathbf{X}}^T\mathbf{R}\mathbf{X}\hfill \\ \mathbf{Z}\leftarrow W-\rho ({\Delta }_W\mathbf{L}+\gamma L)\hfill \\ \mathbf{U},\mathbf{E}\leftarrow \mathbf{E}\mathbf{V}\mathbf{D}\left(\mathbf{Z}\right)\hfill \\ \widehat{\mathbf{E}}\leftarrow {\mathcal{S}}_{\beta }\left(\mathbf{E}\right)\hfill \\ W\leftarrow \mathbf{U}\widehat{\mathbf{E}}{\mathbf{U}}^T\hfill \end{array}$$

12:   end while

13:   3: Update C

14:   $\mathbf{F}=b+\mathbf{X}w+\text{diag}\mathbf{X}W{\mathbf{X}}^T,\hspace{0.17em}\mathbf{C}\leftarrow {\mathcal{T}}_1(1-\mathbf{Y}\mathbf{F}+\mathbf{u})$

15:   4: Update the dual variable u

16:   $\mathbf{u}\leftarrow \mathbf{u}+\mathbf{1}-\mathbf{Y}\mathbf{F}-\mathbf{C}$

17: end while

4.2 Benefit of incorporating interaction

We show the benefit of incorporating peak interactions using kernel methods described in Section 3.1. The MKL algorithms, i.e. UNIMKL, ALIGN and ALIGNF, were used to combine two kernels, ${\mathbf{K}}_{peak}$ and ${\mathbf{K}}_{interaction}$ (we call their results ComUNIMKL, ComALIGN, ComALIGNF, respectively) and compared with PPK, which has only kernel for peaks. The combined kernels were coupled with SVM to predict the fingerprint properties. Each property was separately trained by a classifier. Five-fold cross-validation was conducted to seek suitable margin parameter C where $C\in \{2^{-3},2^{-2},\dots ,2^{\mathrm{6}},2^{\mathrm{7}}\}$.

Table 1 shows the results, in which the micro-average accuracy and F1 score of combined kernels were higher than PPK. This shows that incorporating peak interactions can improve the performance on predicting molecular fingerprint properties. Additionally, the performance of ALIGNF algorithm was slightly better than the rest.

Table 1.

Micro-average performance of kernels: PPK (Heinonen et al., 2012) is used to compute ${\mathbf{K}}_{peak}$

Method	Acc (%)	F1-score (%)
PPK	75.74 (±8.13)	60.59 (±13.75)
ComUNIMKL	78.41 (±6.82)	65.05 (±12.16)
ComALIGN	78.57 (±6.24)	65.34 (±11.99)
ComALIGNF	79.03 (±7.89)	65.67 (±13.02)

Note: ComUNIMKL, ALIGN, ALIGNF are combinations of ${\mathbf{K}}_{peak}$ and ${\mathbf{K}}_{interaction}$ by algorithms UNIMKL, ALIGN, ALIGNF, respectively.

4.3 Benefit of (L-)SIMPLE, sparse interaction models

Since kernel methods in Section 3.1 are unable to provide sparse solutions for interpretability, we examined (L-)SIMPLE to gain insight into the models to predict fingerprints. (L-)SIMPLE needs to construct feature vectors from MS/MS spectra: we divided m/z range into 500 bins and took accumulated peak intensities in a bin as a feature value to obtain high dimensional vector for each spectrum. These feature vectors were normalized such that all feature values are in [0, 1]. (L-)SIMPLE was trained by ADMM (see algorithm 1) with all variables initialized at zero. The algorithm was iterated until the relative difference in training errors fell below 0.0001 or the number of iterations reaches 100. Five-fold cross-validation was used to evaluate the generalization of the learning machines. Specifically, parameters α, β and γ, for controlling sparsity, low-rankness and Laplacian smoothness were chosen from the lists: {1, 2, 3}, $\{2,3,4,5\}$ and $\{0.1,0.5,1.0\}$, respectively.

Also, to evaluate the effects of adding the Laplacian smoothness term into the objective function, we compared the accuracy and F1 score over tasks by performing five-fold cross-validation. Table 2 shows the accuracy and F1 score obtained for the first ten tasks (Note that we used only tasks in which the majority class occupies less than 90% of instances). The micro-average over all tasks is also displayed at the bottom. We can see that Laplacian regularization worked to make SIMPLE more robust, resulting in better predictive performance of L-SIMPLE.

Table 2.

Performance comparison between SIMPLE and L-SIMPLE

Task Id/Name	SIMPLE		L-SIMPLE
	Acc (%)	F1 (%)	Acc (%)	F1 (%)
3 (Aldehyde)	71.16	69.24	73.14	70.75
27 (Hydroxy)	91.24	95.19	90.29	94.82
29 (Primary alcohol)	79.36	53.74	79.85	53.98
30 (Secondary alcohol)	80.35	54.18	81.84	56.17
37 (Ether)	80.35	71.39	80.61	72.03
38 (Dialkyl etherEther)	82.35	70.98	82.6	71.16
45 (Aryl)	83.83	81.67	83.34	82.16
50 (Carboxylic acid)	69.38	62.00	69.65	62.15
56 (Primary Carbon)	73.12	40.42	73.88	44.46
57 (Secondary Carbon)	71.88	67.15	72.39	67.28
60 (Alkene)	81.35	23.49	84.08	27.75
Avg ± Std	78.33 ± 6.05	66.69 ± 13.03	78.86 ± 5.87	67.59 ± 12.35

We further compared (L-)SIMPLE with various kernel, namely PPK, NB, NI, LB, LC, LI, CPC and their combination, which we call ComFT, all from (Shen et al., 2014). While these kernels (except for PPK) are all computed from the fragmentation trees, in which the cost for converting MS/MS spectra to these trees is heavy and time-consuming, our method uses peaks from spectra only and is efficiently computable in prediction.

Table 3 shows the results of accuracy, F1 scores and computation time for prediction by all compared methods. The prediction time (in milliseconds) was averaged over all spectrum in the dataset. The first four methods including PPK achieved around the accuracy of 75%, which is clearly worse than the other methods, which achieved around 78–80% and are very comparable each other. In fact ComFT, the current cutting-edge MKL-based method, performed best in both accuracy and F1 score, while the second best was not clear (NB by accuracy and L-SIMPLE by F1 score). On the other had, about computation time, FT-based methods, i.e. from LB to ComFT, were clearly slower than the others, because they need convert spectra into FTs. In fact ComFT needed more than 1500 ms, which is more than 300 times slower than that of (L-)SIMPLE, which just spent only less than 5 ms. This is a sizable difference when we have to process a huge amount of spectra produced by the current high-throughput MS/MS. We stress that the performance difference between (L-)SIMPLE and ComFT was very slight and statistically insignificant, while (L-)SIMPLE was exceedingly faster than ComFT.

Table 3.

Micro-average performance and computation time (for prediction) of kernel-based methods in Shen et al. (2014) and proposed methods in this paper

Method	Acc	F1 score	Run. time
	(%)	(%)	(ms)
PPK (Peaks)	75.74 (±6.72)	60.59 (±14.54)	52.37
LB (Loss binary)	76.63 (±7.03)	61.64 (±15.48)	1501.02
LC (Loss count)	75.33 (±5.4)	61.25 (±13.99)	1501.02
LI (Loss intensity)	74.54 (±8.49)	58.46 (±16.01)	1501.02
NB (Node binary)	79.11 (±5.02)	67.34 (±11.75)	1501.09
NI (Node intensity)	78.41 (±4.99)	66.87 (±12.11)	1501.01
CPC (Common path count)	79.02 (±7.4)	67.55 (±12.93)	1501.11
ComFT (combining all above)	80.98 (±6.05)	69.04 (±11.98)	1559.20
ComALIGNF (Proposed: MKL)	79.03 (±7.89)	65.67 (±13.02)	471.71
SIMPLE (Proposed)	78.33 (±6.05)	66.70 (±13.03)	4.57
L-SIMPLE (Proposed)	78.86 (±5.87)	67.59 (±12.35)	4.32

4.4 Model interpretation

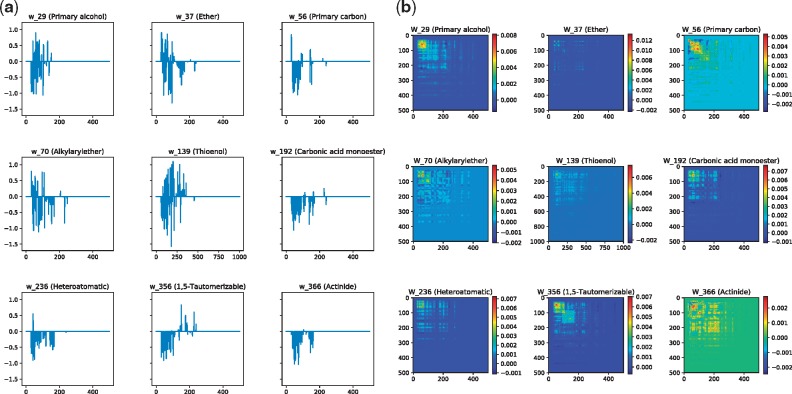
One advantage of sparse learning models over kernel based methods is interpretation. For illustration purposes, Figure 4 shows the weights of main effect terms (w) and the interaction weight matrix (W) obtained by L-SIMPLE for nine fingerprint properties (or tasks): 29, 37, 56, 70, 139, 192, 236, 356 and 370 (these are randomly selected for investigation). As observed, the weight of main effect and interaction terms were different between properties, suggesting that different properties are strongly affected by different subsets of a few peaks in spectra.

Fig. 4.

(a) Weight vectors (w) of the main effect terms and (b) smooth heat map of weight matrices (W) of the interaction terms learned by L-SIMPLE for properties or tasks: 29 (Primary alcohol), 37 (Ether), 56 (Primary Carbon), 70 (Alkylarylether), 139 (Thioenol), 192 (Carbonic acid monoester), 236 (Heteroaromatic), 356 (1,5-Tautomerizable) and 366 (Actinide)

Table 4 shows case studies to illustrate the effects of peak interactions. We consider four interaction pairs frequently present in these tasks. w₁ and w₂ denote the weights for peaks and W₁₂ denotes the weight for their interactions. We can raise the following three interesting findings:

Table 4.

Case studies of weight vector w and interaction matrix W learned by L-SIMPLE over a set of randomly selected tasks

Tasks/Name	(42, 85)			(42, 163)			(85, 227)			(130, 201)
	w1	w2	W12	w1	w2	W12	w1	w2	W12	w1	w2	W12
29 (Primary Alcohol)	0.0	0.0	0.0016	−0.0545	0.0	0.0442	−0.4085	−0.0545	0.0765	−0.4085	0.0	0.0218
37 (Ether)	0.0	0.0	0.0120	0.0260	0.0	0.0471	0.0	0.0260	0.1264	0.0	0.0	0.3389
56 (Primary Carbon)	0.0	0.0	0.0271	−0.5657	0.0	0.0047	−0.9833	−0.5657	0.0271	−0.9833	0.0	0.0104
70 (Alkylarylether)	0.0	0.0	0.0159	0.0	0.0	0.0551	−0.1238	0.0	0.0972	−0.1238	0.0	0.0265
139 (Thioenol)	0.1575	0.3939	0.0	−0.2308	−0.4094	0.0	−0.3589	−0.2308	0.0	−0.3589	−0.1126	0.0
192 (Carbonic acid monoester)	−0.1542	0.0	0.0	0.0	0.0	0.0	−0.6945	0.0	0.0	−0.6945	0.0	0.0
236 (Heteroaromatic)	0.0	0.0	0.0107	0.0	0.2499	0.0537	−0.3069	0.0	0.1062	−0.3069	0.1401	0.0201
356 (1,5-Tautomerizable)	0.0	0.0	0.0170	0.0	0.0	0.0301	0.5539	0.0	0.0607	0.5539	0.0	0.0107
366 (Actinide)	0.0	0.0	0.0245	−0.1891	0.6065	0.0282	−0.5373	−0.1891	0.0399	−0.5373	0.0	0.0153

Note: w₁ and w₂ denote weights corresponding two mass positions and W denotes the weight of their interactions. Four pairs of mass positions which are frequently present in these tasks, including (42, 85), (42, 163), (85, 227) and (130, 201) are shown.

1. Either w₁ or w₂ (or both) can be zero but the interaction weights are often nonzero: For example, W₁₂ of interaction (42, 85) are mostly nonzero, while w₁ and w₂ are both zero with respect to tasks 29, 37, 56, 70. This means that individual peaks are not good predictive descriptors of properties, while their interactions are. Thus this result clearly shows the importance of considering peak interactions in fingerprint prediction.

2. Despite of negative impacts of individual peaks, their interactions can be positive: For example, interaction (85, 227) with respect to tasks 29, 56 and 366. This means that while individual peaks indicate the absence of a property, the interactions of two peaks mean the presence of the property.

3. Interaction of peaks can be zero, indicating these peaks are independent of each other even if their corresponding weights are nonzeros: For example, interaction (42, 85) with respect to task 139.

They are just part of numerous findings, but even these examples show a fact that even individual peaks are not good indicators of some fingerprints, their interactions with others may significantly contribute to the prediction. This again confirms the importance of peak interactions for fingerprint prediction.

5 Discussion and conclusion

The goal of this work is to propose machine learning models which are able to incorporate peak interactions for fingerprint prediction. Our experiments showed that peak interactions are definitely useful to improve fingerprint prediction, along with discriminative information about peaks.

Our first model is based on kernel learning, defining two kernels, one for peaks and the other for peak interactions, which are combined through MKL. Again we note that Shen et al. (2014) used fragmentation trees for prior structural information of spectral, and converting spectra into fragmentation trees is definitely computationally expensive. On the other hand, our model of kernel learning uses only peaks in the spectrum as input for prediction, indicating that our model is much more efficient. Kernel learning does not have to construct feature vectors for spectra, and instead this is done implicitly by kernels defined, which can avoid any error caused when generating feature vectors. However, a big issue of kernel learning is interpretability. That is, it is difficult for kernel learning to figure out which subset of peaks or peak interactions exhibit the strongest effects on fingerprint prediction, despite that clearly each property depends on a very few number of mass positions in each given spectrum.

Our sparse interaction models, (L-)SIMPLE, have a number of advantages, which are summarized in Section 3.3: (L-)SIMPLE is formulated as a sparse, convex optimization model, which can capture peak interactions and also give interpretable solutions. We emphasize that next generation fingerprint prediction needs a ML model, which should learn, from huge but sparse spectra, peaks as well as peak interactions comprehensibly and predict fingerprints against again huge spectra highly efficiently. (L-)SIMPLE would be a reasonable solution for this situation.

Funding

This work was partially supported by MEXT KAKENHI Grant Number 16H02868, Grant Number JPMJAC1503 ACCEL JST, FiDiPro Tekes (currently Business Finland) and AIPSE Academy of Finland.

Conflict of Interest: none declared.

Appendix

We will derive the updating rules of ADMM for steps in (21).

A1. ADMM for updating b and w

The subproblem for optimizing b, w in (21) is equivalent to

$$\begin{array}{lll}{b}^{t+1},w^{t+1}\hfill & =\underset{{}_{b,w}}{\text{argmin}}\hfill & \mathcal{L}(b,w,W^t,C^t,u^t)\hfill \\ \hfill & =\underset{{}_{b,w}}{\text{argmin}}\hfill & \alpha \left|\right|w|{|}_1+\frac{1}{\mathrm{2}}||1-Y{F}^t-C+u|{|}_2^{\mathrm{2}}\hfill \\ \hfill & =\underset{{}_{b,w}}{\text{argmin}}\hfill & \alpha \left|\right|w|{|}_1+\frac{1}{\mathrm{2}}||Xw+b1-{\widehat{F}}_1|{|}_2^{\mathrm{2}}\hfill \end{array}$$ (22)

where ${\widehat{\mathbf{F}}}_1=\mathbf{Y}(1-\mathbf{C}+\mathbf{u})-\text{diag}\left(\mathbf{X}W{\mathbf{X}}^T\right)$. We denote the operator $\text{diag}(.)$ to produce a vector composed of diagonal elements of given square matrix.

In fact, solving (22) can be done easily with proximal gradient descent through alternately updating estimate of w and b as follows:

$$\begin{array}{c}\{\begin{array}{cc}{\mathbf{z}}^{k+1}\hfill & =w^k-{\delta }_w{\mathbf{X}}^T(\mathbf{X}{w}^k+b^k-{\widehat{\mathbf{F}}}_1)\hfill \\ w^{k+1}\hfill & ={\mathcal{S}}_{\alpha }\left({\mathbf{z}}^{k+1}\right)\hfill \\ b^{k+1}\hfill & =\frac{1}{n}\text{sum}({\widehat{\mathbf{F}}}_1-\mathbf{X}{w}^{k+1})\hfill \end{array}\hfill \end{array}$$ (23)

where δ_w is the learning rate for the proximal gradient updates and set to 0.01 in our experiments, k is the index of inner loop for optimizing b, w, ${\mathcal{S}}_{\lambda }\left(t\right)$ is the element-wise soft-thresholding operator, defined by:

$${\mathcal{S}}_{\lambda }\left(t\right)=\text{sign}\left(t\right)\text{max}(0,|t|-\lambda )$$ (24)

A2. ADMM for updating W

The subproblem of optimizing W in (22) is equivalent to:

$$\begin{array}{l}{W}^{t+1}=\underset{{}_W}{\text{argmin}}\mathcal{L}(b^{t+1},w^{t+1},W,C^t,u^t)\hfill \\ =\underset{{}_W}{\text{argmin}}\beta \left|\right|W|{|}_{*}+\gamma \text{trace}(WL)\hfill \\ +\frac{1}{\mathrm{2}}\left|\right|1-Y{F}^t-C^t+u^t|{|}_2^{\mathrm{2}}\hfill \\ =\underset{{}_W}{\text{argmin}}\beta \left|\right|W|{|}_{*}+\gamma \text{trace}(WL)\hfill \\ +\frac{1}{\mathrm{2}}\left|\right|\text{diag}\left(XW{X}^T\right)-{\widehat{F}}_2|{|}_2^{\mathrm{2}}\hfill \end{array}$$ (25)

where ${\widehat{\mathbf{F}}}_2=\mathbf{Y}(1-\mathbf{C}+\mathbf{u})-b1-\mathbf{X}w$. It is obvious that the objective function (25) split in two components: $\gamma \text{trace}\left(WL\right)+\frac{1}{2}\left|\right|\text{diag}\left(\mathbf{X}W{\mathbf{X}}^T\right)-{\widehat{\mathbf{F}}}_2|{|}_2^{\mathrm{2}}$, which is convex, differentiable and $\beta \left|\right|W|{|}_{*}$, which is also convex with inexpensive proximal operator. It is known that the solution of (25) is given by the matrix shrinkage operation which corresponds to a singular value decomposition (SVD) [see, e.g. Cai et al. (2010) and Ma et al. (2011) for more details]. Hence, proximal gradient descent for updating W again is given as follows:

$$\{\begin{array}{cc}{\mathbf{R}}^{k+1}\hfill & =\text{diag}\left(\mathbf{X}{W}^k{\mathbf{X}}^T\right)-{\widehat{\mathbf{F}}}_2\hfill \\ {\Delta }_W\mathcal{L}\hfill & =\gamma L+{\mathbf{X}}^T{\mathbf{R}}^{k+1}\mathbf{X}\hfill \\ {\mathbf{Z}}^{k+1}\hfill & =W^k-{\delta }_W{\Delta }_W\mathcal{L}\hfill \\ {\mathbf{U}}^{k+1},{\mathbf{E}}^{k+1}\hfill & =\mathbf{E}\mathbf{V}\mathbf{D}\left({\mathbf{Z}}^{k+1}\right)\hfill \\ {\widehat{\mathbf{E}}}^{k+1}\hfill & ={\mathcal{S}}_{\beta }\left({\mathbf{E}}^{k+1}\right)\hfill \\ W^{k+1}\hfill & ={\mathbf{U}}^{k+1}{\widehat{\mathbf{E}}}^{k+1}{\mathbf{U}}^{k+1}\hfill \end{array}$$ (26)

where ${\Delta }_W\mathcal{L}$ is the derivative of the differentiable component of (26) with respect to W, δ_W is the learning rate for the proximal gradient updates and set to 0.05 in our experiments, k is the index of inner loop for optimizing W. U and E are columns of eigenvectors and diagonal matrix of eigenvalues obtained by applying eigendecomposition (EVD) to Z, by which we can guarantee the semidefiniteness of weight matrix W after each iteration.

A3. ADMM for updating C

For the subproblem of optimizing C in (22), it is equivalent to

$$\begin{array}{ll}{C}^{t+1}\hfill & =\underset{{}_C}{\text{argmin}} \mathcal{L}(b^{t+1},w^{t+1},W^{t+1},C,u^t)\hfill \\ \hfill & =\underset{{}_C}{\text{argmin}}{\displaystyle \sum _{i=1}^n{\left(C_i\right)}_{+}}+\frac{1}{\mathrm{2}}\left|\right|1-Y{F}^{t+1}+u^t-C|{|}^2\hfill \end{array}$$ (27)

In order to solve (27), we use the following proposition in (Watanabe et al., 2014):

Proposition 1: the solution ${\mathcal{T}}_{\lambda }\left(t\right)={\text{argmin}}_{x\in \mathbb{R}}\lambda {\left(x\right)}_{+}+\frac{1}{2}{(x-t)}^2$ has the following form:

$${\mathcal{T}}_{\lambda }\left(t\right)=\{\begin{array}{cc}t-\lambda \hfill & \text{if} t \ge \lambda \hfill \\ 0\hfill & \text{if} 0\le t\le \lambda \hfill \\ t\hfill & \text{if} t <0\hfill \end{array}$$ (28)

Note that components of C are independent of each other in (27). By applying Proposition 1 in element-wise, we can derive the update for C in the following closed form solution:

$$\begin{array}{c}{\mathbf{C}}^{t+1}={\mathcal{T}}_1(1-\mathbf{Y}{\mathbf{F}}^{t+1}+{\mathbf{u}}^t)\hfill \end{array}$$ (29)