aliFreeFold: an alignment-free approach to predict secondary structure from homologous RNA sequences

Abstract

Motivation

Predicting the conserved secondary structure of homologous ribonucleic acid (RNA) sequences is crucial for understanding RNA functions. However, fast and accurate RNA structure prediction is challenging, especially when the number and the divergence of homologous RNA increases. To address this challenge, we propose aliFreeFold, based on a novel alignment-free approach which computes a representative structure from a set of homologous RNA sequences using sub-optimal secondary structures generated for each sequence. It is based on a vector representation of sub-optimal structures capturing structure conservation signals by weighting structural motifs according to their conservation across the sub-optimal structures.

Results

We demonstrate that aliFreeFold provides a good balance between speed and accuracy regarding predictions of representative structures for sets of homologous RNA compared to traditional methods based on sequence and structure alignment. We show that aliFreeFold is capable of uncovering conserved structural features fastly and effectively thanks to its weighting scheme that gives more (resp. less) importance to common (resp. uncommon) structural motifs. The weighting scheme is also shown to be capable of capturing conservation signal as the number of homologous RNA increases. These results demonstrate the ability of aliFreefold to efficiently and accurately provide interesting structural representatives of RNA families.

Availability and implementation

aliFreeFold was implemented in C++. Source code and Linux binary are freely available at https://github.com/UdeS-CoBIUS/aliFreeFold.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The folding structure of non-coding ribonucleic acid (RNA) is crucial for their functions. Indeed, the role of many non-coding RNA such as transfer RNA, ribosomal RNA or RibonucleaseP RNA is intrinsically related to their conformations. For instance, the typical cloverleaf shape of transfer RNA secondary structure is required for carrying amino acids to the ribosome for the translation mechanism. Accurately predicting RNA secondary structure is a challenge and it is essential for subsequent RNA functional analyses.

Single-sequence and comparative approaches have been devised for predicting RNA secondary structures from a single RNA sequence or a set of homologous RNA sequences. Regarding single-sequence approaches, several methods have been developed to compute a structure satisfying a given criterion of optimality. The most popular criterion is the free-energy minimization hypothesizing that the functional structure of an RNA is the most stable one i.e. the structure with minimum free energy (MFE). RNAfold (Lorenz et al., 2011), UNAFold (Markham and Zuker, 2008) and RNAstructure (Bellaousov et al., 2013) are popular methods based of the latter criterion. A major shortcoming of single-sequence approaches is their limited accuracy. In fact, they are able to retrieve only on average 60–70% of the true base pairs, decreasing to 40% for long sequences (Doshi et al., 2004; Mathews et al., 1999). The incomplete energy model and the ignorance of tertiary interactions and protein stabilizing the structure are the main causes explaining the limited accuracy of single-sequence approaches. Compared to the latter, comparative approaches have been shown to yield structures with improved accuracy (Puton et al., 2013).

Comparative approaches compute the consensus secondary structure common to a set of homologous RNA sequences, making use of the structure conservation among the sequences. It has been shown that the best performing approaches for RNA secondary structure prediction are comparative approaches (Puton et al., 2013) such as CentroidAlifold (Hamada et al., 2011), MXSCARNA (Tabei et al., 2008), RNAalifold (Lorenz et al., 2011) and TurboFold II (Tan et al., 2017). The conservation of base pairs associated with compensatory mutations is a strong signal of structural conservation that is exploited by comparative approaches. This explains the superiority of the latter over single-sequence approaches.

Comparative methods can be categorized into two classes. First, there are the methods that treat the sequence and structure information separately usually by aligning then folding sequences. Second, there are the methods that integrate in the folding prediction process, the sequence and structure information by aligning and folding sequence simultaneously. The first class of methods derives consensus structures from precomputed multiple alignments of homologous sequences like for RNAalifold (Lorenz et al., 2011) and CentroidAlifold (Hamada et al., 2011). The prediction accuracy of these approaches is constrained by the accuracy of multiple sequence alignment algorithms which starts to drop significantly when sequences are dissimilar i.e. have less than 60% percentage of sequence identity (PID; Bremges et al., 2010; Gardner et al., 2005). The second class of methods bypasses this limit because they simultaneously align and fold RNA sequences. These methods originated from the well-principled approach originally developed by Sankoff (Sankoff, 1985) are based on the idea that the consensus structure must optimize at the same time the scores of the sequence and structure alignments of homologous RNA. However, this approach is time-consuming in practice as it is associated with an exponential time complexity, i.e. $O\left(n^6\right)$, for a pair of sequences of length n. Heuristics have been developed to make the Sankoff approach more practical leading to methods such as DynAlign (Fu et al., 2014), Foldalign (Havgaard et al., 2007), LocarNA (Will et al., 2007), RAF (Do et al., 2008), SPARSE (Will et al., 2015) or MXSCARNA (Tabei et al., 2008).

While approaches that simultaneously align and fold sequences perform generally better at lower PID than approaches aligning then folding sequences, the former are typically slower than the latter. Therefore, there is room for the development of fast methods yielding accurate results regardless of the PID. In this direction, alignment-free approaches, such as RNAcast (Reeder and Giegerich, 1991), are promising since their complexity are usually linear in the number of sequences and provide framework to predict RNA secondary structures. RNAcast explores the set of abstract shapes of sequences in order to find a representative shape. An abstract shape is a coarse-grained representation of structures such that, for instance, a structure ((.((.)).)) is represented by the abstract shape [[]] comprising only two stems. One limitation of RNAcast is that there is no guarantee of finding a representative shape and this depends on the number of generated shapes to explore. A solution for this limitation is to consider sub-optimal structures. Regarding sub-optimal structures, it has been shown that, for a sequence having less than 800 nucleotides, there is always, within the first 25 sub-optimal structures, an ideal sub-optimal structure having on average 80% common base pairs with the curated one (Zuker et al., 1991). Moreover, another study showed that finding an appropriate structural template from sub-optimal structures allows to capture RNA homology even in divergent species (Pánek et al., 2011). In fact, they explored sub-optimal structures of 6S RNA from divergent species and found a structural template having common features with most 6S while exhibiting known functional property of this family. Consequently, exploring sub-optimal structures of homologous sequences and particularly the first 25, can lead to the discovery of an accurate representative structure associated with functional properties of RNA. However, effectively and efficiently computing the representative structure is challenging since it requires to define an appropriate way to calculate the representative capturing conserved structural features across sub-optimal secondary structures. Note that the RNAspa method (Horesh et al., 2007), which can be considered as a fold-then-align approach has been developed to predict secondary structures by exploring the similarity of generated sub-optimal structures. However, it still includes a structure alignment procedure to make the prediction.

To address the challenge of finding a representative structure from a set of sub-optimal structures of homologous sequences, we propose a novel alignment-free approach named aliFreeFold. The main idea of aliFreeFold is to weight structural features of sub-optimal structures according to their conservation across the sub-optimal structures. In this respect, aliFreeFold computes a weighted n-motifs representation such that each sub-optimal structure is represented by a vector of n-motifs occurring in the structure. A n-motif is a set of adjacent elementary motifs such as hairpin, stem, bulge, internal or multiple loops (Glouzon et al., 2017). Each n-motif is weighted according to a conservation index measuring how well the n-motif is conserved across the set of sub-optimal structures. The structure representing the whole set of sub-optimal structures is the structure comprising the most conserved structural features. It is computed as the sub-optimal structure closest to the centroid, i.e. the mean vector, of the weighted n-motif representation. The main contributions of aliFreeFold can be described as follows:

1. It identifies from the set of sub-optimal structures a representative structure close to the functional ones. aliFreeFold finds most of the time a structure having at least 80% correct base pairs.

2. It makes fast and accurate predictions since it relies on an alignment-free approach that is based on a vector representation of sub-optimal structures.

3. It effectively captures increasing structural conservation signals compared to align-and-fold and align-then-fold approaches.

2 Materials and methods

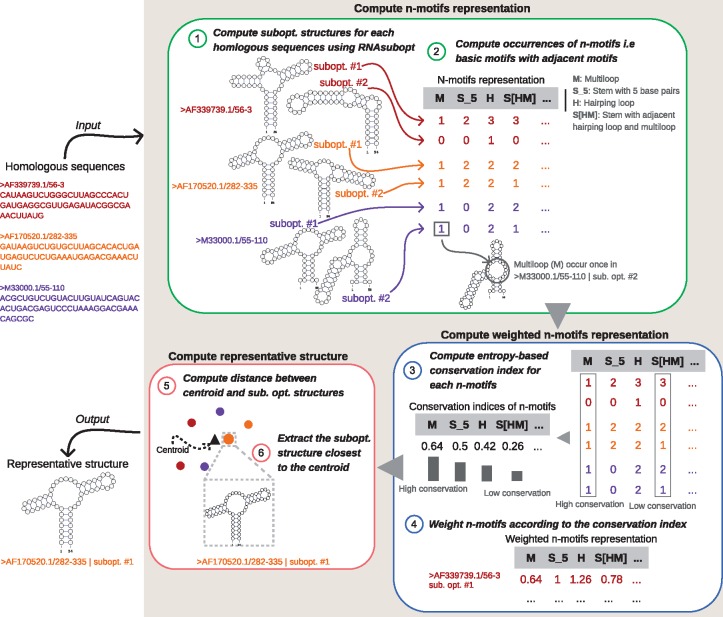
aliFreeFold takes as input a set of unaligned RNA homologous sequences and ouputs a representative structure. It generates the first 25 sub-optimal structures for each sequence using RNAsubopt (Lorenz et al., 2011) as the hypothesis is that the first 25 sub-optimal structures comprise an ideal structure i.e. having on average 80% correct base pair (Zuker et al., 1991). Then aliFreeFold computes a structural motif-based representation of all sub-optimal structures capturing structural features. After that, the motif-based representation is transformed into a weighted motif-based representation using a conservation index. Finally, a representative structure of all sub-optimal structures is derived from the weighted motif-based representation by computing the closest structure to the centroid. Figure 1 presents an outline of aliFreeFold approach considering three sequences where only two sub-optimal structures were generated for each sequence.

Fig. 1.

Outline of AliFreefold approach. AliFreeFold takes as input a set of homologous sequences. It computes the n-motifs representation of the sub-optimal structures of sequences which are generated using RNAsubopt. The weighted n-motifs representation is then computed by weighting n-motifs according to the level of conservation. Finally, the representative structure is derived by extracting the sub-optimal structure closest, in terms of distance, to the centroid of all sub-optimal structures represented by the weighted n-motifs representation

2.1 N-motif representation

aliFreeFold represents each sub-optimal structure of a RNA sequence using the n-motif representation (Glouzon et al., 2017). The latter representation captures structural features of the sub-optimal structures by representing each structure by a vector of occurring n-motifs counts. A n-motif is an elementary RNA structural motif such as multi-loop (M), hairpin loop (H), stem (S), internal loop (I), external loop at 5’ (E5) and 3’ end (E3), bulge (B), pseudoknot (P) with its adjacent motifs. Adjacent motifs are shown in square brackets ‘[]’. For instance, S[HM] denotes a n-motif which is a stem having a hairpin and multi-loop as adjacent motifs. It is important to note that S[HM] and S[HM] represent the same n-motifs since the stem S shares with a multi-loop and a hairpin loop H an adjacency relationships. The n-motif representation also integrates properties of the motifs such as the number of single stranded bases for hairpin loop, external loop and bulge, the symmetry or asymmetry of an internal loop and the number of base pairs for stem and pseudoknot. For example, S_3[H_5B_2] denotes a stem of 3 base pairs having a hairpin and bulge of, respectively, 5 and 2 single-stranded nucleotides as adjacent motifs. A detailed description of n-motifs is provided in (Glouzon et al., 2017).

Formally, for a total number of n sub-optimal structures and m n-motifs, the n-motif representation of sub-optimal structures yields a n × m matrix $X=\left\{x_{ij}\right\}$, where x_ij is the number of occurrences of the n-motif j in the sub-optimal structure i. For instance, in Figure 1 the n-motif M representing multi-loop occurs once in the sub-optimal structure number 2 from the sequence denoted by ‘>M33000.1/55–100’. The n-motif representation is able to integrate information related to circular RNA by ignoring information related to external loops. aliFreeFold represents the structural features of sub-optimal structures by computing the n-motif representation that is then transformed into a weighted n-motif representation, considering the n-motifs conservation across the sub-optimal structures.

2.2 Weighted n-motif representation

The n-motif representation is transformed into a weighted n-motif representation using a conservation index giving more importance to conserved n-motifs. This index is inspired from the diversity index used in ecology to quantify how many different species, genus or families are present in a population (Hill, 1973; Jost, 2006). The conservation index of a n-motif j, denoted by w_j is defined as an entropy-based function measuring how well a n-motif j is conserved across all sub-optimal structures of all homologous sequences. w_j computation is given by:

$$w_j=\frac{1}{e^{\sum _k{p}_{kj}*\hspace{0.17em}\text{log}\hspace{0.17em}\left(p_{kj}\right)}}$$ (1)

where p_kj is defined as $p_{kj}=\frac{\left|\right\{x_i:x_{ij}=n_{kj}\left\}\right|}{n}$ with $\left|\right\{x_i:x_{ij}=n_{kj}\left\}\right|$ representing the total number of structures having n_kj occurrences of n-motif j. n_kj is defined as a specific number of occurrences of n-motif j. When w_j is high (resp. low) this indicates that the n-motifs is highly (resp. weakly) conserved. For example, in Figure 1, the n-motifs j (Multi-loop M) represented by a vector of occurrences (1, 0, 1, 1, 1, 1) is associated with $n_{.j}=(0,1)$ and is highly conserved since M occurs once in most sub-optimal structures. The computation of w_j leads to a transformed matrix, $X\prime$, defined as: $X\prime =\left\{x{\prime }_{ij}\right\}$ where $x{\prime }_{ij}=x_{ij}*w_j$. This latter matrix represents the weighted n-motif representation of the sub-optimal structures.

2.3 Representative structure

The representative structure is the structure having the most common structural features with the sub-optimal structures of homologous sequences. It is computed as the sub-optimal structure closest, in terms of distance, to the centroid of all the sub-optimal structures represented by the weighted n-motifs representation. The representative structure i is defined as the structure satisfying the following criterion:

$$\underset{i}{\text{arg\hspace{0.17em}min}}d(x{\prime }_i,c)$$ (2)

where $d(x{\prime }_i,c)=\sqrt[]{{\displaystyle {\sum }_{j=0}^m{(x_{ij}^{\prime }-c_j)}^2}}$ is the Euclidean distance between the structure represented by $x{\prime }_i$ and the centroid $c=\frac{1}{n}{\sum }_{i=0}^{n}x{\prime }_i$.

2.4 aliFreeFold time and space complexity

The time and space complexities of aliFreeFold are $O(a{l}^4+nm)$ and $O(a{l}^2+nm)$ where n represents the total number of generated sub-optimal structures for all sequences, a is the number of homologous sequences, m is the number of n-motifs and l is the length of the sequences. $O\left(l^4\right)$ and $O\left(l^2\right)$ are associated to RNAsubopt (Lorenz et al., 2011; Wuchty et al., 1999) time and space complexity whereas O(nm) is the time and space complexity for computing the n-motif based representation and the representative structure. It is important to note that by default $n=25a$ since the ideal structure having on average 80% correct base pairs can be found within the 25 first sub-optimal structures. The main component of aliFreeFold computation is mostly related to the complexity of RNAsubopt with the generation of the sub-optimal structures.

3 Results

3.1 Dataset

aliFreeFold has been evaluated based on a dataset composed of 30 non-coding RNA families (Table 1 and Supplementary Material) from BRALIBASE II (Gardner et al., 2005) and MXSCARNA dataset (Tabei et al., 2008). Each family is composed of a set of homologous sequences with each sequence being associated with a corresponding secondary structure. The latter is obtained by projecting the validated consensus structure of the corresponding family onto the sequence using the ViennaRNA script refold.pl (Lorenz et al., 2011). Families are diverse in terms of the number of homologous sequences, the average PID and the average sequence length respectively ranging from 16 to 98 sequences, from $\approx$58% PID to $\approx$98% PID and from $\approx$48 nt to $\approx$463 nt length. The average PID is defined as the mean ratio of the number of matching nucleotides over the length of the smallest sequence, computed from pairwise aligned sequence using Biostrings R package (Pages et al., 2008).

Table 1.

Statistics of RNA families used in the experimentation

Family	Nb of seq.	Avg. PID	Avg. seq. length
BRALIBASE II (Gardner et al., 2005)
g2intron	70	65.882 ± 8.062	83.129 ± 21.266
rRNA	98	63.347 ± 9.254	117.551 ± 2.483
tRNA	72	58.118 ± 10.699	72.306 ± 2.891
U5	80	70.518 ± 11.145	118.162 ± 4.853
MXSCARNA (Tabei et al., 2008)
RF00002-5-8S_rRNA	46	71.941 ± 9.16	154.065 ± 6.198
RF00003-U1	42	67.681 ± 10.378	158.048 ± 7.73
RF00004-U2	51	72.533 ± 8.144	185 ± 17.233
RF00008-Hammerhead_3	54	73.695 ± 12.659	55.593 ± 6.356
RF00011-RNaseP_bact_b	19	68.409 ± 7.725	391.105 ± 20.08
RF00012-U3	17	67.099 ± 10.473	246.529 ± 48.758
RF00015-U4	25	74.138 ± 10.812	141.4 ± 8.718
RF00017-SRP_euk_arch	49	58.704 ± 9.567	294.49 ± 11.518
RF00019-Y	16	73.112 ± 10.184	94.688 ± 11.898
RF00023-tmRNA	36	60.047 ± 6.007	374.611 ± 22.09
RF00024-Telomerase	24	69.91 ± 9.578	463.125 ± 32.332
RF00025-Telomerase	16	69.203 ± 10.443	168.938 ± 16.027
RF00031-SECIS	49	54.205 ± 8.691	64.592 ± 3.278
RF00037-IRE	37	67.658 ± 17.802	28.757 ± 1.442
RF00045-U17	23	75.837 ± 8.466	214.174 ± 7.088
RF00050-RFN	28	69.952 ± 5.845	150.179 ± 11.845
RF00162-S_box	17	72.446 ± 6.275	128.941 ± 17.594
RF00163-Hammerhead_1	21	98.078 ± 1.195	115.095 ± 5.281
RF00164-s2m	37	78.798 ± 9.912	42.919 ± 0.682
RF00167-Purine	35	62.371 ± 5.52	99.571 ± 0.884
RF00168-Lysine	37	59.646 ± 5.828	179.838 ± 6.56
RF00169-SRP_bact	55	62.417 ± 8.332	95.309 ± 8.613
RF00181-sno_14q_I_II	42	70.603 ± 9.011	73.976 ± 4.027
RF00233-Tymo_tRNA	28	71.698 ± 10.734	82.643 ± 2.87
RF00236-ctRNA_pGA1	17	77.224 ± 12.086	80.294 ± 1.724
RF00436-UnaL2	60	78.47 ± 9.396	54.4 ± 1.861

3.2 Compared methods

We selected seven RNA structure prediction methods RNAspa (Horesh et al., 2007), RNAcast (Reeder and Giegerich, 1991), SPARSE (Will et al., 2015), TurboFold II (Tan et al., 2017), MXSCARNA (Tabei et al., 2008), CentroidAlifold (Hamada et al., 2011) and RNAalifold (Lorenz et al., 2011), for comparison with aliFreeFold, in terms of prediction accuracy and efficiency. TurboFold II, MXSCARNA, CentroidAlifold and RNAalifold were selected since they are among the best performing comparative approaches (Puton et al., 2013). SPARSE was also selected because it was shown to be more efficient and accurate than other methods simultaneously aligning and folding sequences such as RAF (Do et al., 2008) and Locarna (Will et al., 2007). RNAspa was chosen because it uses, as aliFreeFold, sub-optimal structures generated via RNAsubopt combined with a structure alignment procedure to predict structures. It is important to mention that all the performance results for RNAcast are made on the subset of 23 families having less than 182 nt average sequence length because RNAcast ran out of memory above this threshold. All algorithms were run using default parameters, except for RNAcast for which the percent sub-optimality number parameter was increased to enforce prediction in case where no prediction was obtained. It would have been interesting to select approaches such as GraphClust (Heyne et al., 2012) or BlockClust (Videm et al., 2014) using a sub-graph decomposition framework to represent RNA and similar to the n-motif representation. However, it is not possible to include GraphClust and BlockClust in the evaluation procedure because they serve a different purpose, namely clustering of RNA secondary structures, compared to all the other selected approaches that are for structure prediction.

3.3 Evaluation criteria

We evaluated aliFreeFold capability to perform accurate and efficient predictions of RNA secondary structures from homologous sequences regarding four different criteria. First, we measure the ability of the method to extract accurate structural features from a set of sub-optimal structures. Second, we compare the prediction effectiveness of the state-of-the-art RNA structure prediction methods with aliFreeFold. Third, we compare the prediction efficiency of the same set of methods. Fourth, we measure how the effectiveness of the method evolves when the number of homologous sequences increases.

We use the following performance metrics. The positive predictive value (PPV) represents the quantity of the predicted base pairs that are retrieved in the reference structure. The sensitivity (SENS) represents how much of the known base pairs of the reference structure have been found in the predicted one. The Matthew correlation coefficient (MCC) summarizes the SENS and the PPV. SENS and PPV are bounded between [0, 1] where 1(resp. 0) means for PPV that all (resp. none) base pairs in the reference are found in the predicted structures and for SENS that all (resp. none) base pairs in the predicted structures are found in the reference. MCC is bounded between –1 and 1. MCC score of 1 (resp. –1) means that the overall prediction is perfect (resp. wrong). SENS, PPV and MCC are computed as followed:

$$\begin{array}{l}\text{SENSITIVITY=}\frac{\text{TP}}{\text{TP+FN}}\hfill \\ \text{POSITIVE PREDICTIVE VALUE}=\frac{\text{TP}}{\text{TP}+(\text{FP}-\mathrm{ϵ})}\hfill \\ \text{MATTHEW CORRELATION COEFFICIENT}\hfill \\ =\frac{\text{TP}*\text{FN}-(\text{FP}-\mathrm{ϵ})*\text{FN}}{\sqrt[]{(\text{TP}+\text{FP}-\mathrm{ϵ})(\text{TP}+\text{FN})(\text{TN}+\text{FP}-\mathrm{ϵ})(\text{TN}+\text{FN})}}\end{array}$$

where the true positives, the true negatives, the false negatives and the false positives represent, respectively, the number of correctly predicted base pairs, the number of nucleotide pairs correctly identified as not forming base pairs, the number of base pairs in the reference not predicted and the number of wrongly predicted base-pairs. ϵ represents the number of base pairs in the predicted structures that are compatible with base pairs in the reference. A predicted base pair (i, j) is compatible relative to a base pair (k, h) of the reference structure when they are neither inconsistent i.e. there is no (i, k) or (j, h) base pair in the reference, nor contradicting i.e. k < i<h < j and i < k<j < h are not satisfied meaning base pairs are not crossing.

In the first evaluation, the performance of aliFreeFold is assessed regarding its capability to systematically compute a representative structure having at least 80% correct base pairs compared to the validated structure (Table 2). This threshold is derived from a study showing that for a sequence having less than 800 nucleotides, there is always, within the first 25 sub-optimal structures, an ideal sub-optimal structure having on average 80% common base pairs with the validated one (Zuker et al., 1991). We further validate this threshold by evaluating the average percentage of correct base pairs relatives to the increasing number of homologous sequences and considering the first 25 sub-optimal structures for each sequence (Fig. 2). Finally, we evaluate the impact of using a conservation index in order to compute the weights of n-motifs in the weighted n-motif representation and the effect of increasing the number of sub-optimal structures on the prediction quality of aliFreeFold (Fig. 3).

Table 2.

Statistics regarding aliFreeFold and the sub-optimal structures generated by RNAsubopt (Lorenz et al., 2011) on the dataset of 30 families

Proportion of predictions having 80% or more correct bp.	70%
Proportion of predictions having 70% or more correct bp.	76%
Avg. prop. of sub-opt. structures having at least 80% correct bp.	34% ± 26
Avg. percentage of correct bp. of the best sub-optimal structuresa	97% ± 10

^aThe best sub-optimal structure is a structure from a set of sub-optimal structures maximizing the number of correct base pairs.

Fig. 2.

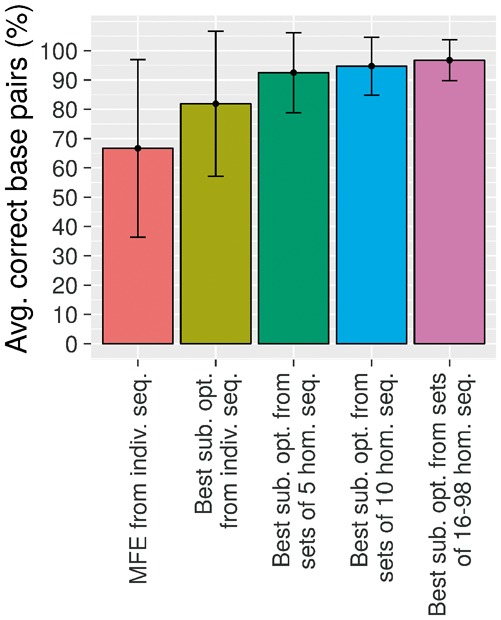
Average percentage of correct base pairs considering MFE structures and best structures of all sub-optimal structures from one (individual sequence), 5, 10 and 16–98 homologous sequences. The best sub-optimal structures are the sub-optimal structures maximizing the average percentage of correct base pairs represented by the PPV

Fig. 3.

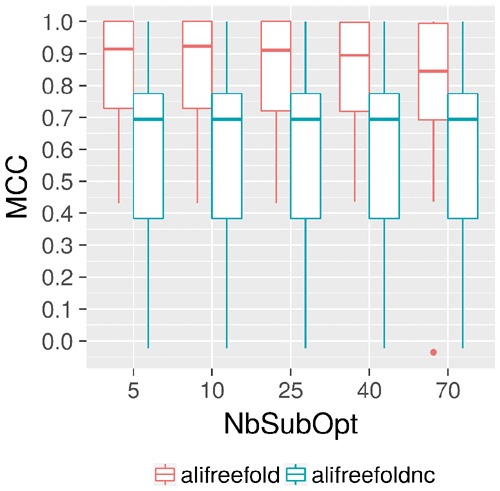
Assessment of the prediction quality of aliFreeFold and aliFreeFold without computing the conservation index (aliFreeFoldnc), while increasing the number of sub-optimal structures (NbSubOpt). Prediction quality is based on the MCC computation. aliFreeFoldnc computation is obtained by adding the parameter ’-c 0’ to aliFreeFold. The number of sub-optimal structures has gradually increased from 5, 10, 25, 40 to 70

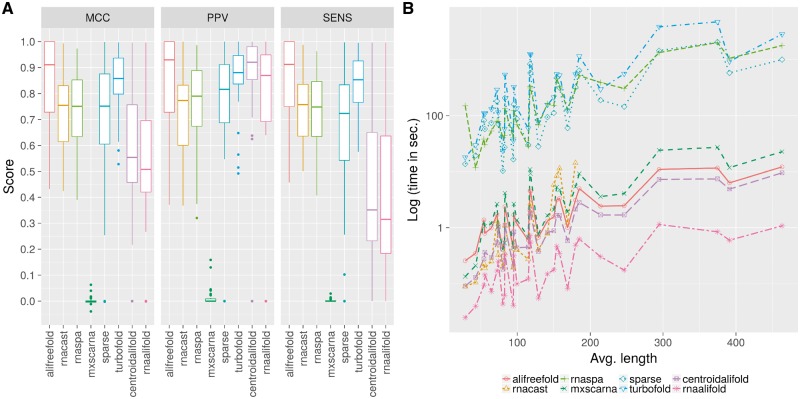
In the second and third evaluations, we compare the accuracy of predicted secondary structures and the efficiency of aliFreeFold, RNAspa (Horesh et al., 2007), RNAcast (Reeder and Giegerich, 1991), SPARSE (Will et al., 2015), TurboFold II (Tan et al., 2017), MXSCARNA (Tabei et al., 2008), CentroidAlifold (Hamada et al., 2011) and RNAalifold (Lorenz et al., 2011; Fig. 3). The accuracy of predictions has been assessed using the MCC, the PPV and SENS (Fig. 4A). In order to evaluate MXSCARNA, SPARSE, CentroidAlifold and RNAalifold it was necessary to refold each sequence based on the computed the consensus structure using the ViennaRNA script refold.pl (Lorenz et al., 2011). The efficiency of each method is evaluated by computing the time required to calculate predictions on a 4-CPU (3.3 GHz) desktop PC with 7.7GB of RAM (Fig. 4B).

Fig. 4.

Prediction accuracy (A) and running time analysis (B) of aliFreeFold, RNAcast, RNAspa, MXSCARNA, SPARSE, TurboFold II, CentroidAlifold and RNAalifold. The prediction accuracy is measured by MCC, PPV and sensitivity on a dataset of 30 RNA families

In the last evaluation, we assess the capacity of the tested methods to improve the prediction quality as the conservation signal increases (Fig. 5). The methods performance is assessed on sets of 5, 10 homologous sequences and on a set of more than 15 homologous sequences. The sets of 5 and 10 homologous sequences come from the sampling without replacement of sequences of each the 30 families. We obtained, respectively, 300 and 150 sets of 5 and 10 homologous sequences. The sets containing more than 15 homologous sequences are the 30 sets of homologous sequences defining the families.

Fig. 5.

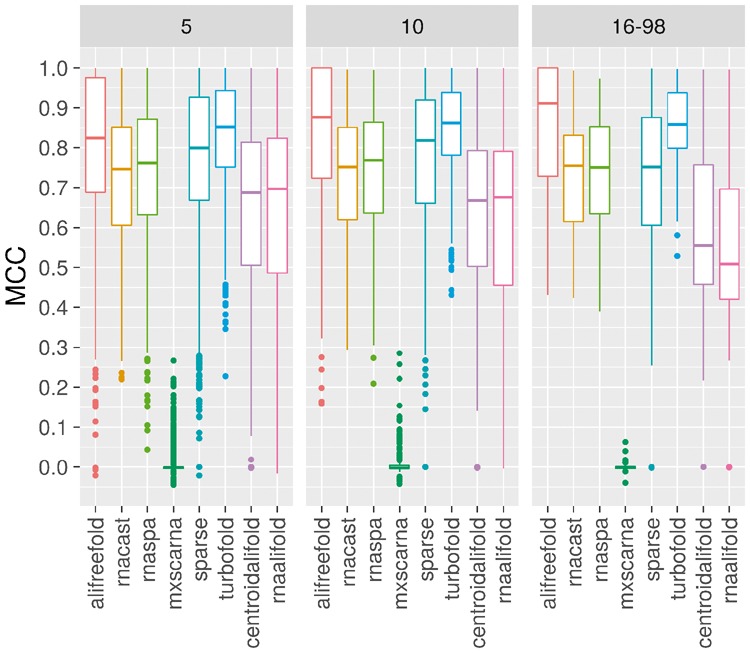
Evolution of the prediction accuracy of aliFreeFold, RNAcast, RNAspa, MXSCARNA, SPARSE, TurboFold II, CentroidAlifold and RNAalifold as the conservation signal increases. The increasing of structure conservation signals is achieved by successively increasing the number of sequences from 5, 10 to more than 15 in the sets of homologous sequences

3.4 Assessment of prediction quality

The prediction quality of all the tested methods is reported using the MCC, the PPV and the SENS considering all pairs composed of the predicted and the validated structures for each sequence of each set of homologous RNA (Kalvari et al., 2018). PPV, SENS and MCC represent, respectively, the proportion of correctly predicted base pairs, the proportion of the retrieved true base pairs and a summary score of PPV and SENS. They are computed using compare_ct.pl script (Gardner and Giegerich, 2004). Note that MCC, PPV and SENS scores are averaged for each set of homologous sequences regarding all methods except aliFreeFold. In fact, we report aliFreeFold MCC, SENS and PPV between the representative structure and the validated structure of the corresponding sequence since it outputs one representative sequence and structure for each set of homologous sequences.

4 Discussion

4.1 Capacity of aliFreeFold to find accurate sub-optimal structures

We found that aliFreeFold is able to find most of the time an ideal sub-optimal structure, i.e. a structure having, on average, 80% or more correct base pairs, as compared to the validated structure. In fact, aliFreeFold finds an ideal sub-optimal structure in 70% of the 30 families of our dataset, despite that we have on average only a third (34.1% ± 26.2%) of the sub-optimal structures having 80% or more correct base pairs for each family (Table 2). The proportion of ideal structures predicted increases from 70% to 76% for ideal structures having on average 70% or more correct base pairs. This shows that aliFreeFold can detect relevant conservation signals thanks to its conservation index.

While aliFreeFold is capable of detecting conservation signals, there is room for improvement. In fact, the best sub-optimal structure, i.e. the sub-optimal structure maximizing the number of correct base pairs, has on average 97% ± 10% of correct base pairs for the first 25 sub-optimal structures of more than 15 homologous sequences (Table 2). It is important to note that having an increasing number of homologous sequences is beneficial for predictions. Indeed, we observe that the average percentage of correct base pairs of the best sub-optimal structures increases from $\approx$80% to $\approx$97% as the number of homologous sequence grows from 1 to more than 15 sequences (Fig. 2). In addition, it seems better to consider sub-optimal structures rather than the MFE structure because the best sub-optimal structures considering individual sequences have a higher percentage of correct base pairs compared to the MFE structures. The latter observation confirms an analysis of a previous study showing that an ideal structure having on average 80% correct base pair can be found in the first 25 sub-optimal structures (Zuker et al., 1991).

The conservation index is crucial for the performance of aliFreeFold. Indeed, computing the predictions without the conservation index used to weight n-motifs in the method, leads to a significant drop in prediction quality illustrated by low MCC scores compared to aliFreeFold scores (Fig. 3). Furthermore, increasing the number of sub-optimal structures does not benefit to aliFreeFold performance because the median MCC scores tends to decrease when we reach 70 sub-optimal structures per sequences on our dataset of 30 RNA families (Fig. 3). This indicates that adding more sub-optimal structures have a negative impact on the computed conservation index. Since the conservation signal is more related to the number of homologous sequences compared to the number of sub-optimal structures, increasing the number of sub-optimal structures has a possible effect of adding noise to the conservation signals making the computation of the conservation index more challenging. While aliFreeFold is able to find a suitable representative, it is important to compare its prediction quality and efficiency against other alternatives approaches to see whether aliFreeFold captures conserved structural features in a more effective and efficient manner.

4.2 Performance analysis

The performance of alignment-free approaches i.e. aliFreeFold and RNAcast shows that aliFreeFold is a good alternative to RNAcast since it is more effective and reliable than RNAcast. In fact, aliFreeFold yields structures of better quality than RNAcast. This is illustrated by the higher MCC, PPV and SENS scores of aliFreeFold than the scores of RNAcast (Fig. 4A). Theses results indicate that aliFreeFold finds more correct base pairs compared to RNAcast. Furthermore, aliFreeFold is reliable since it guaranties to find a representative structure. This is not the case for RNAcast because it runs out of memory for sets of sequences having more than $\approx$180 nt average length. In some cases, the percent sub-optimality number has been increased to enforce the structure prediction. It is important to note that aliFreeFold is as fast as RNAcast because there is not much difference between the two in terms of running time (Fig. 4B). Thus, aliFreeFold presents a valuable alternative to RNAcast as a sequence alignment-free approach to compute the best template structure. While the comparison of aliFreeFold and RNA cast is essential because they are both sequence alignment-free approach, it is also important to compare aliFreeFold with the fold-then-align approach RNAspa, the align-and-fold approaches, MXSCARNA, SPARSE, TURBOFOLD II and the align-then-fold approaches CentroidAlifold and RNAalifold. The majority of these methods have been shown to be among the best comparative approaches (Puton et al., 2013).

Considering the global quality of prediction, we observe that aliFreeFold and align-and-fold methods such as TurboFold II yield the overall best results (Fig. 4A) compared to all other approaches i.e. RNAspa, RNAcast, SPARSE, MXSCARNA, CentroidAlifold and RNAalifold. In fact, aliFreeFold and TurboFold II yield the highest MCC scores among all methods. The difference in terms of MCC scores of aliFreeFold and TurboFold II compared to the other approaches, is mostly explained by the fact that both approaches maintain a high precision (high PPV) and a high sensitivity (high SENS) whereas the others usually yield a lower sensitivity. The high sensitivity of aliFreeFold and TurboFold II indicates that they recover most of the true base pairs of the validated structures compared to the other approaches. It also shows, on one hand, that aliFreeFold conservation index is as effective as the procedure of the align-and-fold approach to capture structure conservation signals. On the other hand, it illustrates that it is possible to obtain high quality prediction by only focusing on structural information since aliFreeFold compute conservation index based solely on sub-optimal structure analysis ignoring sequence information.

There is a performance advantage at considering structural information at an early step of the prediction process. In fact, we observe that majority of the approaches integrating structural information at an early prediction step yield a higher sensitivity compared to align-then-fold approaches such as CentroidAlifold and RNAalifold which use structural information in the last step of the prediction (Fig. 4A). Indeed, the latter approaches consider sequence and structure information as independent, treating one information after another by aligning sequences, then folding them using structure conservation signals detected from alignment. This can lead to miss true base pairs because on one hand sequence alignment is primarily meant to uncover sequence conservation and not structure conservation. On the other hand, potential errors during the sequence alignment process can be propagated to the folding process adding noise to structure conservation signals. Those points are supported by the fact that the accuracy of align-then-fold approaches is largely dependent upon the quality of the computed alignment and sequence similarity (Bremges et al., 2010; Gardner et al., 2005). Considering MXSCARNA, it yields surprisingly the worst results whereas it considers simultaneously both sequence and structure information to compute structural prediction. It is probably due to the coarse-grained approach of MXSCARNA seeking to align blocks of stems rather than base pairs.

4.3 Efficiency analysis

While RNAalifold appears as the fastest approach, aliFreeFold is among the fastest one since it has a running time close to CentroidAlifold, MXSCARNA, RNAcast and RNAalifold (Fig. 4B). aliFreeFold is fast because it is an alignment-free approach, relying on a weighted vector representation of sub-optimal structures to compute the representative one. Alignment-free approaches usually exhibit a lower time complexity compared to alignment-based approaches (Vinga, 2014). Indeed, here we observed than RNAcast and aliFreeFold are among the fastest ones. Moreover, aliFreeFold only requires the first 25 sub-optimal structures for each homologous RNA since it has been shown that a structure having on average 80% correct base pairs is always found in the first 25 sub-optimal structures (Zuker et al., 1991). While TurboFold II and aliFreeFold yield comparable accuracy for the prediction, TurboFold II is among the slowest one because it is time-consuming to compute the predictions by simultaneously aligning sequence and structure rather than aligning then folding sequence, or using an alignment-free framework for prediction. While MXSCARNA is considered as an align-and-fold approach, it is fast because it aligns blocks of nucleotides representing stems and not individual pairs on nucleotides as SPARSE and TurboFold II do. It is important to note that the average length of the sequences has a higher impact on the running time analysis than the number of homologous sequences in the families. Indeed, there is a statistically significant high correlation between the running time and the average sequence length (Table 3). No statistically significant correlation has been observed between the number of sequences per family and the running time of the methods, except for SPARSE and RNAalifold.

Table 3.

Spearman correlation of methods running times (Run time) against average sequence length (Avg. seq. len.) and number of homologous sequences (Nb. hom. seq.)

	Run time versus Avg. seq. len.	Run time versus Nb. hom. seq.
aliFreefold	0.76a	0.31
RNAspa	0.819a	0.082
MXSCARNA	0.773a	0.301
SPARSE	0.71a	0.393a
RNAcast	0.821a	0.243
TurboFold II	0.748a	0.328
CentroidAlifold	0.845a	0.155
RNAalifoldP	0.709a	0.37a

Note: Correlation is computed relative to the running time of aliFreefold, RNAcast, RNAspa, SPARSE, TurboFold II, MXSCARNA, CentroidAlifold and RNAalifold over the dataset of 30 families.

^aCorrelation statistically significant using a two-sided t-test.

4.4 Impact of increasing the structure conservation signal

As the structure conservation signal increases, the quality of aliFreeFold predictions improves. The capacity to improve the prediction quality when the structure conservation signal increases is crucial since the number of non-coding RNA families increases in diversity and in the number of sequences as for the RFAM database (Kalvari et al., 2018). As the number of homologous sequences increases from 5 to more than 15, the structural conservation signal becomes stronger (Fig. 5) leading to an improvement of aliFreeFold prediction. The conservation index used by aliFreeFold takes advantage of the fact that the increasing structural conservation signal indicates less variability and therefore more conserved structural features. As the structural features appear more and more conserved their computed weight increase accordingly. However, the other approaches are less sensitive to the increasing of the number of homologous sequences per family since we do not observe any significant improvement of the MCC scores (Fig. 5). In some cases, the prediction quality decreases, for instance for CentroidAlifold and RNAalifold. This could be explained by the fact that increasing the number of homologous sequences reduces the quality of the sequence alignment, in the cases where the added sequences are divergent.

5 Conclusion

A new approach, called aliFreeFold, has been devised to find the representative structure of a set of sub-optimal structures from homologous RNA sequences. It constitutes a novel and alternative way to predict RNA secondary structures from a set of homologous sequences. Contrary to current approaches usually based on alignment of sequences and/or structures, it computes a vector representation of structures helping to extract the representative structures containing conserved structural features. This approach yields fast and accurate predictions of RNA secondary structures.

While aliFreeFold has advantages in terms of prediction accuracy and speed, it yields a representative structure for a set of homologous sequences and not a structure for each sequence. Future extensions of the method will include the computation of structures for each homologous sequence. It is possible to find the optimal projection or match of the representative structure to each homologous sequence. The optimal match could be defined as the sub-optimal structure of the sequence minimizing the distance to the representative structure, or a secondary structure maximizing an alignment score between the sequence and the representative structure. This procedure can also be extended to obtain multiple sequence and structure alignment by computing a multiple alignment guided by the representative structure.

The results of aliFreeFold suggest that, by using an appropriate weighting function, one can get insight into the conserved structural features of a set of homologous RNA. However, aliFreeFold somehow misses important information since in some cases a better structure having on average more than 90% correct base pairs is not retrieved by aliFreeFold. Future works will explore four different ways to improve aliFreeFold. The first improvement is to use softwares supporting pseudoknots such as vs_subopt (Dawson et al., 2014) instead of RNAsubopt to compute the sub-optimal structures. It will allow aliFreeFold to find a more appropriate representative structure in cases where pseudoknots are well conserved such as in RNaseP family (Brown et al., 1996; Harris et al., 2001). The second improvement consists in computing the representative structures based on statistical sampling of the Boltzmann ensemble of secondary structures. This can help computing a more precise conservation index since the statistical sampling of the Boltzman ensemble yields information about the diversity of possible secondary structure conformations (Chan et al., 2005; Ding et al., 2005). The third way to improve aliFreeFold would be to learn the weighting function from the data in a supervised manner. We hypothesize that learning a weighting function can offer better generalization over the data and consequently increases the percentage of correct base pairs in the predicted structure. Finally, a fourth improvement will be to extend aliFreeFold in order to account for sequence motif such as k-mers to represent RNA sequence and structure. We hypothesize that combining sequence and structure motifs in the model will allow to retrieve more accurate representative structures.