Improving genomics-based predictions for precision medicine through active elicitation of expert knowledge

Abstract

Motivation

Precision medicine requires the ability to predict the efficacies of different treatments for a given individual using high-dimensional genomic measurements. However, identifying predictive features remains a challenge when the sample size is small. Incorporating expert knowledge offers a promising approach to improve predictions, but collecting such knowledge is laborious if the number of candidate features is very large.

Results

We introduce a probabilistic framework to incorporate expert feedback about the impact of genomic measurements on the outcome of interest and present a novel approach to collect the feedback efficiently, based on Bayesian experimental design. The new approach outperformed other recent alternatives in two medical applications: prediction of metabolic traits and prediction of sensitivity of cancer cells to different drugs, both using genomic features as predictors. Furthermore, the intelligent approach to collect feedback reduced the workload of the expert to approximately 11%, compared to a baseline approach.

Availability and implementation

Source code implementing the introduced computational methods is freely available at https://github.com/AaltoPML/knowledge-elicitation-for-precision-medicine.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

An urgent challenge in computational biology is how to bring machine learning and statistical models closer to clinical practitioners. Toward resolving this, we study human-in-the-loop prediction, in which a medical expert interacts with a machine learning model with the goal to improve predictions for genomics-based precision medicine. In precision medicine, large-scale screening and sequencing produce thousands of genomic and molecular features for each individual, which can then be used for predicting a phenotype of interest, such as quantitative drug sensitivity scores (DSS) of cancer cells. What makes the task particularly difficult is that the sample sizes may be extremely small, possibly dozens of individuals only, or even fewer, for example, in the case of rare cancers. Statistical methods exist for learning predictive features and models in omics-based data analysis tasks and are in principle applicable across similar tasks. Commonly applied methods include multivariate analysis of variance (Garnett et al., 2012) and sparse regression models, such as lasso and elastic net (Garnett et al., 2012; Jang et al., 2014). Kernel methods enable finding more complex nonlinear combinations of the features (Ammad-ud din et al., 2016; Costello et al., 2014). However, the scarcity of data poses a serious challenge for accurate prediction with any of these techniques.

One solution to the problem of small sample size is to measure more data, using, for example, active learning to design next clinical trials (Deng et al., 2011; Minsker et al., 2016). This, however, is often not viable due to costs, risks or the rarity of the disease. Statistical means to alleviate the problem include multitask learning to share strength between related outputs (Ammad-ud din et al., 2016; Yuan et al., 2016), and the use of biological prior knowledge available in data bases. For instance, knowledge about cancer pathways has been used as side information for prediction (Ammad-ud din et al., 2016; Costello et al., 2014), for feature selection (De Niz et al., 2016; Jang et al., 2015) or to modify regularization of a model (Sokolov et al., 2016). Another method, complementary to these methods, is to collect prior knowledge directly from an expert. Such prior elicitation techniques (O’Hagan et al., 2006) have been used for constructing prior distributions for Bayesian data analysis that take into account expert knowledge and hence can restrict the range of parameters in predictive models (Afrabandpey et al., 2017; Garthwaite et al., 2013; Garthwaite and Dickey, 1988; Kadane et al., 1980).

The field of precision medicine poses a major challenge for eliciting prior knowledge directly from medical experts, namely the huge number of possible genomic features that the expert needs to provide feedback on. Consequently, in practice elicitation is only possible if the effort required from the expert can be minimized. The key insight in this paper is that interactive and sequential learning can help by carefully deciding what to ask from the expert. It has earlier been used in different types of tasks, for clustering (Balcan and Blum, 2008; Lu and Leen, 2007), Bayesian network learning (Cano et al., 2011) and visualization (House et al., 2015). We have applied it recently also to prediction using linear regression in our preliminary work (Daee et al., 2017; Micallef et al., 2017; Soare et al., 2016). However, these methods are not immediately applicable to precision medicine due to many open questions, in particular (1) how to most effectively personalize predictions for a specific patient, (2) which of the different ways of collecting feedback interactively are the most efficient, (3) what kind of feedback most efficiently improves prediction accuracy and (4) how to handle the multi-task problem arising in multi-output settings.

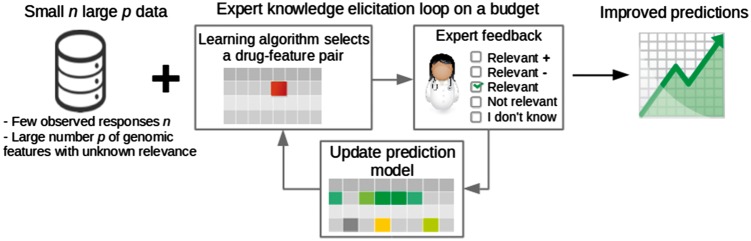
In this paper, we carefully address these challenges in the context of prediction of multivariate quantitative traits from genomic features. In particular, we (i) introduce a new targeted sequential expert knowledge elicitation approach, (ii) compare it to non-targeted and baseline sequential elicitation methods, (iii) introduce and compare two kinds of feedback for precision medicine tasks and (iv) formulate and evaluate the approaches in multivariate precision medicine tasks with real medical datasets. In order to do this, we introduce a joint probabilistic model for the prediction and for the expert feedback; in detail, we use a sparse linear regression model that extends the textual-data model of Daee et al. (2017). The expert feedback is here extended to include information about the direction of a putative effect, in addition to indicating whether or not a particular effect is at all relevant in a given prediction problem. We then formulate two sequential methods for collecting expert feedback in the precision medicine task. The first targets improving personalized predictions for a single individual, while the second averages predictions over all individuals. Both aim at minimizing the effort required from the expert (Fig. 1).

Fig. 1.

Overview. Predictions in small-sample-size problems are improved by asking experts in an elicitation loop. The system presents questions for the expert sequentially to maximize performance with a minimal number of questions, i.e. on a budget. The expert answers the questions by indicating whether a feature is relevant in predicting quantitative traits, such as cancer cell’s sensitivity to a drug. The expert can also indicate in which direction the effect is likely to be

Our main methodological innovation, in addition to the important technical extensions of including directional feedback and tailoring the sequential elicitation to the multi-task precision medicine problem, is in introducing a new targeted or personalized sequential knowledge elicitation approach, where the queries to the expert are chosen to be the most informative for predicting the phenotype of a new, previously unseen patient. The methods are evaluated empirically in this paper; our main experimental contribution is assessing the feasibility of expert knowledge elicitation for precision medicine. Our experiments consist of two parts. First, we apply the proposed methods in a realistic simulated expert setting. In particular, we show that simulated expert feedback based on a published meta-analytic genome-wide association study improves prediction of metabolite concentrations from single nucleotide polymorphisms (SNPs) and that the sequential elicitation can reap the benefit with a small number of queries to the expert. Second, and more importantly, we demonstrate the clinical potential of the proposed approach in the difficult task of predicting drug sensitivity of ex vivo blood cancer cells from patients, with feedback from domain experts.

2 Models and algorithms

In this section, we describe the proposed models and algorithms for sequential expert knowledge elicitation. First, we describe a sparse linear regression model that is used to learn the relationship between the features (here, genomic features) and the multivariate quantitative traits (metabolite concentrations or drug sensitivities) and which takes into account the elicited expert knowledge. Then we introduce the two elicitation methods developed for prediction tasks in precision medicine.

2.1 Prediction model

2.1.1 Sparse Bayesian linear regression

Sparse linear regression is used to predict the quantitative traits based on the genomic features. Let $y_{n,d}$ be the value of the dth trait for nth patient, and ${\mathit{x}}_n\in {ℝ}^M$ be the vector of the individual’s M genomic features. We assume that the trait depends linearly on the genomic features:

$$y_{n,d}\sim \mathrm{N}({\mathit{w}}_d^{\mathrm{\top }}{\mathit{x}}_n,{\sigma }_d^2),$$

where the ${\mathit{w}}_d\in {ℝ}^M$ are the regression weights and ${\sigma }_d^2$ is the residual variance. In practice only a small number of features are expected to have any effect on the trait, and we encode this assumption using a sparsity-inducing spike-and-slab prior (George and McCulloch, 1993; Mitchell and Beauchamp, 1988) on the weights:

$$w_{d,m}\sim {\gamma }_{d,m}\mathrm{N}(0,{\tau }_{d,m}^2)+(1-{\gamma }_{d,m}){\delta }_0,$$

where ${\gamma }_{d,m}$ is a binary variable indicating whether the mth feature is relevant (i.e. $w_{d,m}$ drawn from a zero-mean Gaussian prior with variance ${\tau }_{d,m}^2$) or not ($w_{d,m}$ is set to zero via the Dirac delta spike δ₀) when predicting for the dth trait. The prior probability of relevance ρ_d controls the expected sparsity of the model via the prior

$${\gamma }_{d,m}\sim \text{Bernoulli}({\rho }_d).$$

The model is completed with the hyperpriors

$$\begin{array}{c}{\sigma }_d^{-2}\sim \text{Gamma}({\alpha }_{\sigma },{\beta }_{\sigma }),\\ {\rho }_d\sim \text{Beta}({\alpha }_{\rho },{\beta }_{\rho }),\\ {\tau }_{d,m}\sim \hspace{0.17em}\text{Log}-\mathrm{N}(\mu ,{\omega }^2).\end{array}$$

Settings for the values of the hyperparameters are discussed within the details of the experiments (Sections 3.1.1 and 3.2.1).

Given the observed trait values $\mathit{Y}\in {ℝ}^{N\times D}$ for N patients and D traits and the genomic features $\mathit{X}\in {ℝ}^{N\times M}$, the posterior distribution of the model parameters $\mathit{\theta }=(\mathit{w},\mathit{\gamma },\mathit{\rho },{\mathit{\tau }}^2,{\mathit{\sigma }}^2)$ is computed via the Bayes theorem as follows:

$$p(\mathit{\theta }|\mathit{Y},\mathit{X})=\frac{p(\mathit{Y}|\mathit{X},\mathit{w},{\mathit{\sigma }}^{\mathbf{2}})p(\mathit{w}|\mathit{\gamma },{\mathit{\tau }}^{\mathbf{2}})p(\mathit{\gamma }|\mathit{\rho })p(\mathit{\rho })p({\mathit{\tau }}^2)p({\mathit{\sigma }}^{\mathbf{2}})}{p(\mathit{Y}|\mathit{X})}.$$

The posterior distribution of w together with the observation model is then used to compute the predictive distribution of the traits $\tilde{y}={[{\tilde{y}}_1,\dots ,{\tilde{y}}_D]}^{\mathrm{\top }}$ for a new individual $\tilde{x}$:

$$p(\tilde{y}|\mathit{Y},\mathit{X},\tilde{x})=\int p(\tilde{y}|\tilde{x},\mathit{w},{\mathit{\sigma }}^{\mathbf{2}})p(\mathit{\theta }|\mathit{Y},\mathit{X})d\mathit{\theta }.$$ (1)

2.1.2 Incorporating expert feedback

We assume that an expert has provided feedback about the relevance of some genomic features, for example, using elicitation techniques described in the next section, corresponding to the expert’s opinion of whether or not the features should be included into the model when predicting a certain trait. In addition, we assume that for some of the relevant features the expert has also indicated her expectation about the direction of the effect. These types of feedback are assumed to be available for some or all of the feature-trait pairs in the dataset, and they are treated as additional data when learning the parameters of the spike-and-slab regression model. The relevance feedback has been used in Daee et al. (2017) for univariate prediction in textual data, which we extend by including directional feedback (Micallef et al., 2017) in the multi-output scenario.

Technically, the expert knowledge is incorporated into the model via feedback observation models. The relevance feedback $f_{d,m}^{rel}\in \{0,1\}$, where 0 denotes not relevant, 1 relevant, of feature m for trait d follows:

$$f_{d,m}^{rel}\sim {\gamma }_{d,m}\text{Bernoulli}({\pi }_d^{rel})+(1-{\gamma }_{d,m})\text{Bernoulli}(1-{\pi }_d^{rel}),$$

where ${\pi }_d^{rel}$ is the probability of the expert being correct. For example, when the mth feature for trait d is relevant in the regression model (i.e. ${\gamma }_{d,m}=1$), the expert would a priori be assumed to say $f_{d,m}^{rel}=1$ with probability ${\pi }_d^{rel}$. In the model learning (i.e. calculating the posterior distribution in Equation (2) below), once the expert has provided the feedback based on his or her knowledge, ${\pi }_d^{rel}$ effectively controls how strongly the model will change to reflect the feedback.

The directional feedback $f_{d,m}^{dir}\in \{0,1\}$, where 0 denotes negative weight and 1 positive, follows:

$$f_{d,m}^{dir}\sim I(w_{d,m}\ge 0)\text{Bernoulli}({\pi }_d^{dir})+I(w_{d,m}<0)\text{Bernoulli}(1-{\pi }_d^{dir}),$$

where I(C) = 1 when the condition C holds and 0 otherwise, and ${\pi }_d^{\text{dir}}$ is again the probability of the expert being correct. For example, when the weight $w_{d,m}$ is positive, the expert would a priori be assumed to say $f_{d,m}^{\text{dir}}=1$ with probability ${\pi }_d^{dir}$. To simplify the model, we assume ${\pi }_d={\pi }_d^{\text{dir}}={\pi }_d^{\text{rel}}$ and set a prior on π_d as

$${\pi }_d\sim \text{Beta}({\alpha }_{\pi },{\beta }_{\pi }).$$

Given the data Y and X and a set of observed feedbacks F encoding the expert knowledge, the posterior distribution is computed as follows:

$$\begin{array}{l}p(\mathit{\theta }|\mathcal{D})=\frac{p(\mathit{Y}|\mathit{X},\mathit{w},{\mathit{\sigma }}^2)p(\mathit{w}|\mathit{\gamma },{\mathit{\tau }}^2)p(\mathit{\gamma }|\mathit{\rho })p(\mathit{\rho })p({\mathit{\tau }}^2)p({\mathit{\sigma }}^2)}{p(\mathit{Y},\mathit{F}|\mathit{X})}\\ \times \hspace{0.17em}p(\mathit{F}|\mathit{\gamma },\mathit{w},\mathit{\pi })p(\mathit{\pi }),\end{array}$$ (2)

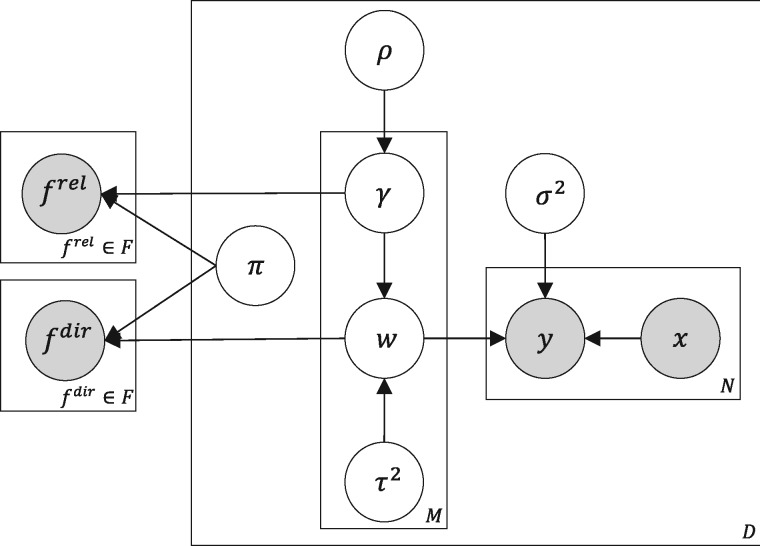
where $\mathcal{D}=(\mathit{Y},\mathit{X},\mathit{F})$ and $\mathit{\theta }$ now includes also $\mathit{\pi }$. The predictive distribution follows from Equation (1). Figure 2 shows the plate diagram of the model.

Fig. 2.

Plate notation of the quantitative trait prediction model (right) and feedback observations (left) as introduced in Section 2.1. The feedbacks f ^rel and f ^dir are sequentially queried from the expert based on an expert knowledge elicitation method

The computation of the posterior distribution is analytically intractable. We use the expectation propagation algorithm (Minka and Lafferty, 2002) to compute an efficient approximation. In particular, the posterior approximation for the weights w is a multivariate Gaussian distribution and the predictive distribution for ${\tilde{y}}_d$ is also approximated as a Gaussian (Daee et al., 2017; Hernández-Lobato et al., 2015). The mean of the predictive distribution is used as the point prediction in the experimental evaluations in Section 3.

2.2 Expert knowledge elicitation methods

The purpose of expert knowledge elicitation algorithms is to sequentially select queries to the expert, such that the effort from the expert is maximally beneficial for prediction. In univariate outcome prediction, an algorithm needs to select the next feature for an expert to provide feedback on. In the present multi-output setting, the elicitation algorithm needs to select both the output and the feature to be shown to the user in the next query. Based on preliminary experiments, we focus on sequential experimental design methods, which produced the best results for multi-output settings [Based on preliminary experiments in the multi-output setting (not shown), a Bandit model approach (Micallef et al., 2017) was not better than the sequential experimental design approach by Daee et al. (2017)]. We next describe two new sequential experimental design methods and a baseline approach that will be compared in the results.

2.2.1 Sequential experimental design

We introduce a sequential experimental design approach to select the next (trait, feature) pair candidate, extending the work by Daee et al. (2017). Specifically, at each iteration t, we find the pair for which the feedback from the expert is expected to have the maximal influence on the prediction. The amount of information in the expert feedback is measured by the Kullback–Leibler divergence (KL) between the predictive distributions before and after observing the feedback. As the feedback value itself is unobserved before the actual query, an expectation over the predictive distributions of the two types of feedback is computed in finding the (trait, feature) pair $(d^{*},m^{*})$ with the highest expected information gain:

$$(d^{*},m^{*})=\underset{(d,m)\notin {\mathit{F}}_{t-1}}{\text{arg}\hspace{0.17em}\text{max}}{\mathbb{E}}_{{\tilde{f}}_{d,m}^{\mathrm{rel}},{\tilde{f}}_{d,m}^{\mathrm{dir}}|{\mathcal{D}}_{t-1}}[\sum _{n=1}^N{u}_{n,d,m,t}],$$ (3)

where $u_{n,d,m,t}=\text{KL}[p({\tilde{y}}_d|{\mathit{x}}_n,{\mathcal{D}}_{t-1},{\tilde{f}}_{d,m}^{\text{rel}},{\tilde{f}}_{d,m}^{\text{dir}})\left|\right|p({\tilde{y}}_d|{\mathit{x}}_n,{\mathcal{D}}_{t-1})],{\mathcal{D}}_{t-1}=(\mathit{Y},\mathit{X},{\mathit{F}}_{t-1}),\hspace{0.17em}\mathit{Y}\in {ℝ}^{N\times D}$ are the observed trait values for N individuals and D traits, $\mathit{X}\in {ℝ}^{N\times M}$ are the genomic features, and ${\mathit{F}}_{t-1}$ is the set of feedbacks given before the current query iteration. The $u_{n,d,m,t}$ term measures the impact the feedback on feature m would have on the predictive distribution of trait d of the nth individual. The summation in n runs over the training data, and hence the criterion (3) selects the next query assuming that the individuals for whom predictions are made are similar to the training set (unlike the targeted criterion presented in the next section). Once the query $(d^{*},m^{*})$ is selected and presented to the expert, the provided feedback is added to the set ${\mathit{F}}_{t-1}$ to produce ${\mathit{F}}_t$. Queries where the expert is not able to provide an answer do not affect the prediction model but are added to the set so as not to be repeated.

Using the approximate posterior distribution, the posterior predictive distribution of the relevance and directional feedback, $p({\tilde{f}}_{d,m}^{\text{rel}},{\tilde{f}}_{d,m}^{\text{dir}}|{\mathcal{D}}_{t-1})=p({\tilde{f}}_{d,m}^{\text{rel}}|{\mathcal{D}}_{t-1})p({\tilde{f}}_{d,m}^{\text{dir}}|{\mathcal{D}}_{t-1})$, follows a product of Bernoulli distributions. The approximate posterior predictive distribution of ${\tilde{y}}_d$ follows a Gaussian distribution, which makes the KL divergence calculation simple. However, to make inference efficient enough for online use, we approximate the posterior with partial expectation propagation updates (Daee et al., 2017; Seeger, 2008).

2.2.2 Targeted sequential experimental design

We define a new, targeted version of the sequential experimental design by computing the utility for a single new target sample instead of summing over the training dataset samples. The motivation is to try to improve the prediction specifically for the current target individual rather than overall.

For this, we maximize the following information gain:

$$\begin{array}{c}(d^{*},m^{*})=\underset{(d,m)\notin {\mathit{F}}_{t-1}}{\text{arg}\hspace{0.17em}\text{max}}{\mathbb{E}}_{{\tilde{f}}_{d,m}^{\mathrm{rel}},{\tilde{f}}_{d,m}^{\mathrm{dir}}|{\mathcal{D}}_{t-1}}\left[{\tilde{u}}_{d,m,t}\right] \text{where}\\ \hspace{0.5em}{\tilde{u}}_{d,m,t}=\text{KL}[p({\tilde{y}}_d|\tilde{x},{\mathcal{D}}_{t-1},{\tilde{f}}_{d,m}^{\mathrm{rel}},{\tilde{f}}_{d,m}^{\mathrm{dir}})\hspace{0.17em}\left|\right|\hspace{0.17em}p\left({\tilde{y}}_d\right|\tilde{x},{\mathcal{D}}_{t-1}\left)\right],\end{array}$$

where $\tilde{x}$ are the genomic features of the new, previously unseen individual. This is identical to the previous except for evaluating the information gain only at the target individual’s $\tilde{x}$.

2.2.3 Random sequential sampling

As a baseline, we use uniform random sampling for the next query from the set of (trait, feature) pairs that have not yet been queried.

3 Experiments

The proposed methods are evaluated first in metabolite concentration prediction from genomic data with simulated expert feedback and then applied to real expert feedback in multiple myeloma drug sensitivity prediction. In both cases, we first compare the predictive accuracy with and without expert feedback and then assess the performance of the sequential elicitation methods.

3.1 Metabolite concentration prediction from genomic data—simulated expert feedback

We performed a simulation study of predicting the concentrations of four standard lipid profile metabolites [high-density lipoprotein cholesterol (HDL-C); low-density lipoprotein cholesterol (LDL-C); total serum cholesterol (TC); serum triglycerides (TG)] using genotype data as predictors. Both the genotypes and the metabolites were real observations, and also the feedback was simulated using real Genome-wide association study (GWAS) meta-analysis results. This setup emulates prior elicitation from a knowledgeable geneticist, who provides feedback about the relevance of different SNPs on predicting different metabolites and on the directions of the putative effects.

3.1.1 Experimental methods

The dataset comes from the Finnish FINRISK07 (DILGOM07 subset) study that sampled a random set of adults in Finland to participate in a study on general health of Finnish population (Borodulin et al., 2015). We included unrelated individuals for whom genotype data and the four metabolite concentrations (measured using NMR spectroscopy) existed (Kettunen et al., 2016; Marttinen et al., 2014). The total number of individuals was 3918. Standard quality control was applied to the genotype data (SNP missingness rate < 0:05, minor allele frequency > 0:01, imputation quality (info) > 0:3, and HWE > 10⁻⁶. Pairs of related individuals, as defined by pi-hat statistic > 0:2, were pruned out by removing one of them. The number of individuals after this is 3918).

We used the results of a GWAS meta-analysis of 24 925 individuals (Kettunen et al., 2016) to generate the feedback and to prune the number of SNPs for consideration. The meta-analysis included the same metabolites (among others) measured using the same technology as the target metabolites here. However, the dataset we used was not included in the meta-analysis. The set of SNPs was pruned by prioritizing SNPs that had low P-values in the meta-analysis for at least one of the target metabolites and requiring that the SNPs were at least 0.125cM and 25 kb apart in the genetic map, to select a non-redundant set of SNPs. The final number of included SNPs was 3107.

Feedback was generated from the results of the meta-analysis by taking all SNPs with P-value smaller than $2.3\times {10}^{-9}$ (the significance threshold in the meta-analysis (Kettunen et al., 2016)) as relevant (for each target separately) and those with larger than 0.9 (arbitrary; sensitivity to this is investigated in the result) as irrelevant. Directional feedback was generated for all relevant SNPs by taking the sign of the regression coefficient in the meta-analysis results. This resulted in 13, 46, 39, and 11 SNPs being considered relevant and 1010, 859 620 and 628 SNPs not relevant for HCL-C, LDL-C, TC and TG, respectively. The rest of the SNPs was considered to be of unknown relevance.

The hyperparameters of the prediction model were set as ${\alpha }_{\sigma }=4,\hspace{0.17em}{\beta }_{\sigma }=4,\hspace{0.17em}{\alpha }_{\rho }=2,\hspace{0.17em}{\beta }_{\rho }=98,\hspace{0.17em}\mu =-3.25,\hspace{0.17em}{\omega }^2=\frac{1}{2}$, and ${\alpha }_{\pi }=19,\hspace{0.17em}{\beta }_{\pi }=1$ to reflect relatively vague information on the residual variance (roughly higher than 0.5), a preference for sparse models and small effect sizes that one expects in SNP-based regression, and the a priori quality of the expert knowledge as 19 correct feedbacks out of 20. A sensitivity analysis with regard to the sparsity and effect size parameters is given in the Supplementary Material.

For predictive performance evaluation, the data were divided randomly into a training set of 1000 and a test set of 2918 individuals. The proposed methods are compared against two baselines: constant prediction with the training data mean and elastic net. Elastic net is a state-of-the-art method that includes ridge and lasso regression as special cases [Elastic net is implemented using the glmnet R-package (Friedman et al., 2010) with nested cross-validation for choosing the regularization parameters.]. The concordance index (C-index; the probability of predicting the correct order for a pair of samples; higher is better) (Costello et al., 2014; Harrell, 2015) and the mean squared error (MSE; lower is better), computed on the test set, are used as the performance measures. Bayesian bootstrap (Rubin, 1981) over the predictions is used to evaluate the uncertainty in pairwise model comparisons: in particular, we compute the probability that model M₁ is better than model M₂ as follows $\mathrm{Pr}(M_1\text{isbetterthan}{M}_2)=\frac{1}{B}{\sum }_{b=1}^{B}I(M_1\hspace{0.17em}\text{is}\hspace{0.17em}\text{better}\hspace{0.17em}\text{than}\hspace{0.17em}{M}_2\hspace{0.17em}\text{in}\hspace{0.17em}\text{bootstrapsample}\hspace{0.17em}b)$, where I(C) = 1 if condition C holds and 0 otherwise (Vehtari and Lampinen, 2002).

3.1.2 Simulated sequential elicitation user experiment

We simulated sequential expert knowledge elicitation by iteratively querying (metabolite, feature) pairs for feedback, and answering the queries using the generated feedback. At each iteration, the models were updated and the next query chosen, based on the feedback elicited up to that iteration, and the training data which does not change. We compared the elicitation methods described in Section 2.2.1. The queries for the targeted sequential experimental design approach were generated by running each test sample as a target individual separately. The queries were selected without replacement from the 12 428 possible queries (4 metabolites × 3, 107 SNPs).

3.1.3 Results

Expert knowledge can improve genomics-based prediction accuracy. Table 1 shows the prediction performance averaged over the four target metabolites (see Supplementary Material for target-wise performance measures; same conclusions hold for those as given here for the averaged case). As a side result, the sparse linear model without feedback (SnS no fb) improves over both baselines (data mean and elastic net), with bootstrapped model comparison probabilities for both MSE and C-index greater than 0.99 in favor of it. Next, we established whether the simulated feedback improves the model. Giving all of the feedback (SnS all fb) improves the performance (Table 1), with bootstrapped model comparison probabilities greater than 0.99 in favor of it against all other models.

Table 1.

Performance in metabolite concentration prediction

	Data mean	Elastic net	SnS no fb	SnS all fb	SnS rel. fb
C-index	0.500	0.519	0.540	0.558	0.556
MSE	1.017	1.010	0.999	0.984	0.988
PVE	0.000	0.007	0.018	0.032	0.028

Note: Values are averages over the four target metabolites. Best result on each row has been boldfaced. SnS = spike and slab sparse linear model; fb = feedback; Rel. fb = Only relevance feedback; MSE = mean squared error; PVE = proportion of variance explained.

Although the results show that the predictive models with feedback are confidently better, the absolute improvements in MSE are small. Yet, the amount of explanatory power in GWAS is usually small and especially when learning from small datasets. The meta-analysis results, with a much larger dataset, explained 4–11% of the variance among the four metabolites studied here (note that this is also not predictive power but computed in the same dataset as the association study). Computing the proportion of variance explained (PVE) by the cross-validated predictions, $\text{PVE}=1-\frac{\text{MSE}}{{\text{MSE}}_{\text{datamean}}}$, the improvement is 1.4 percentage points, corresponding to almost doubling ($1.8\times$) the predictive PVE from no feedback to all feedback model (Table 1).

Feedback with the direction of the putative effect is more effective than general relevance feedback. We then examined the effect of the directional feedback compared to using relevance feedback only. Using only the relevance feedback (SnS rel. fb) improves over the no feedback model, but the performance is decreased compared to using both relevance and directional feedback (SnS all fb). We further ran a sensitivity analysis with respect to the amount of not relevant feedback: removing all not relevant feedback had a small deteriorating effect in this dataset, resulting in MSE of 0.986 and PVE of 0.031.

Sequential knowledge elicitation reduces the number of queries required from the expert. The sequential knowledge elicitation performance was then studied. Figure 3 shows the MSE as a function of the number of queried feedbacks for random, experimental design, and targeted experimental design sequential methods. The random method finds hardly any useful queries in 1000 steps. Both experimental design methods improve over this significantly, with the targeted version being preferred overall. The targeted sequential experimental design attains 70% of the performance of the all feedback case in 122 queries (1% of all possible queries) and 80% of the performance in 257 queries (2%). This indicates that most of the benefit from the feedback can be obtained using the experimental design with much less effort from the expert than going through all the possible queries or using random selection would require.

Fig. 3.

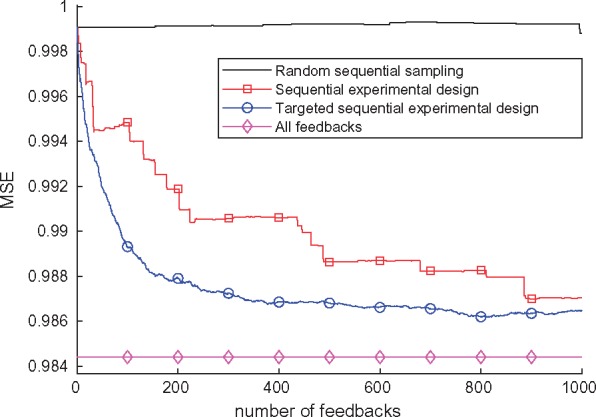
Sequential experimental design performance in metabolite concentration prediction comparing random querying, information gain-based sequential experimental design and its targeted version. First 1000 iterations of feedback are shown and the result with all feedbacks is included for reference. For the targeted sequential experimental design, each individual in the test set was the target separately and the predictions in the resulting feedback sequence were used for that individual. The curve is a mean over all these sequences

3.2 Drug sensitivity prediction for multiple myeloma patients—real expert feedback

To evaluate the proposed methods in a realistic case, we apply them to a dataset of real patients with the blood cancer multiple myeloma and use feedback collected from two well-informed experts to simulate sequential knowledge elicitation. Details of the dataset and the expert feedback collection are presented in the next section, followed by experimental results showing the effectiveness of the methods in practice.

3.2.1 Experimental methods

We used a complete set of measurements on ex vivo drug sensitivities, somatic mutations and karyotype data (cytogenetic markers), generated for a cohort of 44 multiple myeloma patient samples. Drug sensitivities are presented as quantitative DSS as described by Yadav et al. (2014) and were calculated for 308 drugs that have been tested for dose–response in the cancer samples in five different concentrations over a 1000-fold concentration range. Somatic mutations were identified from exome sequencing data and annotated as described earlier by Kontro et al. (2014).

We focus our analysis on 12 targeted drugs, grouped in 4 groups based on their primary targets (BCL-2, glucocorticoid receptors, PI3K/mTOR, and MEK1/2). Also, among the mutations, we focus our analysis on those present in more than one patient. This results in data matrices of 44 × 12 (samples versus drugs), $44\times 2,935$ (samples versus mutations) and 44 × 7 (samples versus cytogenetic markers). In this paper, we ask the experts only about the somatic mutations and cytogenetics markers, which the experts know better and hence need to spend less time on in the experiments. We will extend to molecular features with less well known effects, such as gene expression, in follow-up work.

We use leave-one-out cross-validation (That is, in computing the predictions for each patient, that particular patient is not used in learning the prediction model.) to estimate the performances of the drug sensitivity prediction models, with the C-index (the probability of predicting the correct order for a pair of samples; higher is better) (We note that C-index computed from leave-one-out cross-validation can be biased as it compares predictions for pairs of samples.We do not expect this to favor any particular method.) (Costello et al., 2014; Harrell, 2015) and the MSE (lower is better) as the performance measures. MSE values are given in the normalized DSS units (zero mean, unit variance scaling on training data). Bayesian bootstrap (Rubin, 1981) over the predictions is used to evaluate the uncertainty in pairwise model comparisons (see Section 3.1.1).

The hyperparameters of the prediction model were set as ${\alpha }_{\sigma }=4,\hspace{0.17em}{\beta }_{\sigma }=4,\hspace{0.17em}{\alpha }_{\rho }=1,\hspace{0.17em}{\beta }_{\rho }=2,\hspace{0.17em}\mu =-2.5,\hspace{0.17em}{\omega }^2=\frac{1}{2}$ and ${\alpha }_{\pi }=19,\hspace{0.17em}{\beta }_{\pi }=1$ to reflect our assumptions of relatively vague information on the residual variance (roughly higher than 0.5), a minor preference for sparse models and moderate effect sizes and the a priori quality of the expert knowledge as 19 correct feedbacks out of 20.

3.2.2 Feedback collection

We collected feedback from two well-informed experts of multiple myeloma, using a form containing genes with mutations that have been causally implicated in cancer (Forbes et al., 2015) (155 genes in our data), and seven cytogenetic markers, in total 162 features. The experts were asked to give feedback on the relevance of features and the direction of their effect for predicting the sensitivity to 12 targeted drugs, grouped by the targets (BCL-2, glucocorticoid receptors, PI3K/mTOR and MEK1/2). We note that the experts indicated that the same feedback applies to all drugs in the same drug group. The answer counts by feedback type are summarized in Table 2 for both of the experts. The experts were instructed not to refer to external databases while completing the feedback form, in order to collect their (tacit) prior knowledge on the problem and make the task faster for them.

Table 2.

Feedback type and count, given to the 1944 (drug, feature) pairs by the experts

Answer	SR	DC
Relevant, positive correlation	192	47
Relevant, negative correlation	14	34
Relevant, unknown correlation direction	26	358
Not relevant	13	0
I don’t know	1699	1505
Total	1944	1944

Note: SR = Senior researcher, DC = Doctoral candidate.

3.2.3 Simulated sequential elicitation user experiment

Similar to the metabolite prediction experiment (Section 3.1.2), we simulate sequential expert knowledge elicitation by iteratively querying (drug, feature) pairs for feedback and answering the queries using the pre-collected feedback described in Section 3.2.2. The queries are selected without replacement from the 1944 pairs (12 drugs × 162 genomic features) included in the feedback collection. The rest of the mutation data (2780 mutations) are not queried for feedback, but all 2942 genomic features are included in the prediction model.

3.2.4 Results

Expert knowledge elicitation improves the accuracy of drug sensitivity prediction. Table 3 establishes the baselines by comparing the prediction model we use, the spike-and-slab regression model without expert feedback, to constant prediction of training data mean and elastic net regression (see Supplementary Material for drug-wise performance measures). Elastic net has poor performance with regard to MSE on this dataset, while the spike-and-slab model performs better.

Table 3.

Performance of drug sensitivity prediction without expert feedback

	Data mean	Elastic net	Spike-and-slab
C-index	0.500	0.505	0.577
MSE	1.079	1.153	1.050

Note: Values are averaged over the 12 drugs. Best result on each row has been boldfaced.

The main result is that the complete sets of feedback from both of the experts improves the predictions, as can be seen in Table 4, which compares the spike-and-slab model without feedback to the model incorporating all available expert feedback. The model with feedback from the senior researcher has 4% higher C-index and 2% lower MSE compared to the no feedback model and is confidently better according to the bootstrapped probabilities (0.80 for C-index and 0.97 for MSE).

Table 4.

Predictive performance of spike-and-slab regression with and without expert feedback

	No feedback	Doctoral candidate	Senior researcher
C-index	0.577	0.582	0.597
MSE	1.050	1.040	1.025

Note: Values are averaged over the 12 drugs.

Feedback with the direction of the putative effect is more effective than general relevance feedback. We also assess the importance of the type of the feedback by comparing a spike-and-slab model with relevance only feedback (interpreting potential expert knowledge on the direction only as relevance) to a model with both types of feedback. Table 5 shows that the directional feedback improves the performance markedly, especially in the case of the senior researcher (who gave more directional feedback than the doctoral candidate; see Table 2). The bootstrapped probabilities are 0.79 in the C-index and 0.96 in the MSE in favor of both types of feedback compared to relevance only feedback for the senior researcher and, similarity, 0.50 and 0.85 in the case of doctoral candidate. For the senior researcher, we also tested discarding all ‘not-relevant’ feedback (doctoral candidate didn’t give any): this didn’t have a noticeable effect on the performance (MSE: 1.025).

Table 5.

Performance of drug sensitivity prediction with only relevance feedback and with relevance and directional feedback

	Doctoral candidate		Senior researcher
	Relevance fb	All fb	Relevance fb	All fb
C-index	0.583	0.582	0.578	0.597
MSE	1.048	1.040	1.048	1.025

Note: Values are averaged over the 12 drugs.

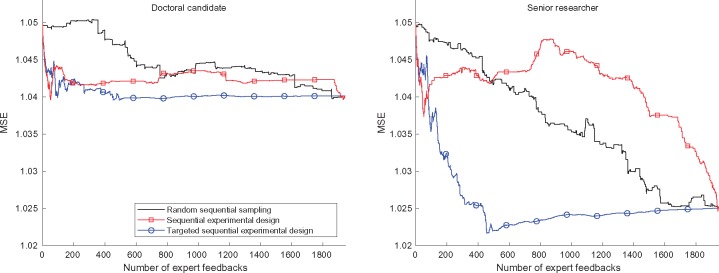
Sequential knowledge elicitation reduces the number of queries required from the expert. In the results presented so far, the experts had evaluated all (drug, feature) pairs and given their answers. We next present the main result, of how much the sequential knowledge elicitation models are able to reduce the impractical workload of the experts to give feedback on all drug-feature-pairs. We compare the effectiveness of the elicitation methods developed in this paper using a simulated user experiment (see Section 3.2.3). The results in Figure 4 show that both methods achieve faster improvement in prediction accuracy than the random selection, as a function of the amount of feedback. With sequential knowledge elicitation, 80% of the final improvement is reached in the first 230 (81) and 1871 (35) feedbacks for the targeted experimental design and non-targeted experimental design methods, respectively, using senior researcher feedback (doctoral candidate feedback). For comparison, 1362 (1619) feedbacks are required for similar accuracy if the queries are chosen randomly. Thus, on average, the targeted sequential experimental design requires only 11% (senior researcher: 17%, doctoral candidate: 5%) of the number of queries compared to random elicitation order, and the sequential experimental design model 70% [SR: 137%, DC: 2% (The improvement, however, is not stable for doctoral candidate for sequential experimental design)], to achieve 80% of the potential improvement.

Fig. 4.

Performance improves faster with the active elicitation methods than with randomly selected feedback queries. The curves show MSEs as a function of the number of iterations for the three query methods, with feedback of the doctoral candidate (left) and senior researcher (right). In each iteration, a (drug, feature) pair is queried from the expert

4 Discussion and conclusion

Our goal was to study open questions in expert knowledge elicitation in the context of precision medicine. In summary, we introduced expert knowledge elicitation methods for and studied their feasibility in the challenging task of prediction in precision medicine. To our knowledge, this kind of approach has not been evaluated previously in precision medicine. Our results show that accumulating expert knowledge with intelligent, experimental design-based algorithms can improve the predictive performance in an efficient manner considering the effort from the expert. This is particularly important as evaluating the queries can be time-consuming for the expert, and involve searching through databases, literature and data (although here, in the real expert experiment, we evaluated the algorithms based on the tacit knowledge of two well-informed experts).

To address the individualized prediction task characteristic to precision medicine, we introduced a targeted sequential expert knowledge elicitation algorithm that sequentially selects queries that will have the greatest effect locally close to the target patient, as opposed to maximizing the effect of feedback globally over the training set of patients. In both of our experiments with real-world medical datasets, with simulated feedback and with real expert feedback, the targeted method performed clearly better than the general experimental design algorithm (and the random sampling based baseline). The developed elicitation algorithms also address the multivariate aspect of predicting for multiple quantitative traits simultaneously, which is particularly important in cases where the predictions are to be used in support of deciding, for example, between multiple alternative treatment strategies.

Our experiments showed that even relatively limited feedback may improve predictions in real-world precision medicine. In general, we expect feedback to be the most useful when the amount of data is limited, making learning of accurate effects challenging. With a lot of data, the prior distributions, and hence the feedback, are expected to have a smaller impact. Also, in extreme cases, it could happen that none of the features has any real influence on the output variable, in which case no model, with feedback or not, will be able to improve beyond the simplest mean prediction; however, such extreme situations seem unrealistic in many real-world precision medicine problems.

Furthermore, we studied the usefulness of different types of feedback. Our elicitation algorithm proceeded by selecting an input–output pair to be evaluated by an expert, and two kinds of feedback were considered: whether the genomic input feature has an effect on the output variable (relevance feedback), and, if it does, what is the direction of the putative effect (directional feedback). Our experiments indicated that including directional feedback improves upon using relevance feedback only and can often be provided without any extra effort by the expert. Nevertheless, the relevance feedback (without direction) is also needed because sometimes specifying the direction may be difficult for the expert. The directional feedback effectively halves the space of values a regression weight can take, and it can be seen as a simple case of general monotonicity constraints found useful in health care related analyses (Riihimäki and Vehtari, 2010). Of the two possible choices of relevance feedback, relevant or not relevant, we found the former much more important. It is also debatable how reliably an expert may deem some genomic feature as not relevant, because scientific studies rarely provide statistical evidence against any effect.

A natural question for future studies is how willing the experts are to use such a system. For example, if the outcome is well predicted in general, the experts may not be willing to invest time in the interaction. This potential future direction also relates to interface design, to convey the meaningfulness of the interaction to the expert. Another future direction would be to extend the model to incorporate feedback from multiple experts, which could be useful by averaging out any incorrect or biased answers a single expert might occasionally provide. Currently, our model has a parameter (π) reflecting the probability that the expert is correct, and in the extension multiple such parameters might be introduced, corresponding to experts of different levels of credibility.

The methods introduced here for precision medicine can be placed into the wider context of augmented intelligence tasks, in which a human expert works together with a machine learning system to achieve a common goal. In specific applications, some of the expert’s knowledge may already be found in databases. Naturally, any reliable and structured information from databases should be built into the predictive model automatically, to save the effort from the expert. However, not all informative data are available in a structured format that could be easily incorporated and, for example, the natural language processing capabilities of machines cannot yet match the quality of human curators. Moreover, expert knowledge elicitation and incorporating data mining-based information are complementary rather than redundant. Active knowledge elicitation could, for example, be used to query an expert about the correctness or reliability of database information. Yet most importantly, the doctors and researchers will anyway be analyzing their data, even if in many cases sophisticated tools incorporating comprehensive prior knowledge will not be available in practice. In these cases not taking the experts’ knowledge and expertise into account would neglect an important data source, when the lack of data may be a significant problem.