Deconvolution and phylogeny inference of structural variations in tumor genomic samples

Abstract

Motivation

Phylogenetic reconstruction of tumor evolution has emerged as a crucial tool for making sense of the complexity of emerging cancer genomic datasets. Despite the growing use of phylogenetics in cancer studies, though, the field has only slowly adapted to many ways that tumor evolution differs from classic species evolution. One crucial question in that regard is how to handle inference of structural variations (SVs), which are a major mechanism of evolution in cancers but have been largely neglected in tumor phylogenetics to date, in part due to the challenges of reliably detecting and typing SVs and interpreting them phylogenetically.

Results

We present a novel method for reconstructing evolutionary trajectories of SVs from bulk whole-genome sequence data via joint deconvolution and phylogenetics, to infer clonal sub-populations and reconstruct their ancestry. We establish a novel likelihood model for joint deconvolution and phylogenetic inference on bulk SV data and formulate an associated optimization algorithm. We demonstrate the approach to be efficient and accurate for realistic scenarios of SV mutation on simulated data. Application to breast cancer genomic data from The Cancer Genome Atlas shows it to be practical and effective at reconstructing features of SV-driven evolution in single tumors.

Availability and implementation

Python source code and associated documentation are available at https://github.com/jaebird123/tusv.

1 Introduction

Genomic methods have provided a wealth of information about mutational landscapes of developing cancers, but have also created a great need for sophisticated computational models to make sense of the resulting data. They have revealed extensive variation patient-to-patient (intertumor heterogeneity) as well as cell-to-cell within single patients (intratumor heterogeneity) (Marusyk and Polyak, 2010) and suggested a far more complex landscape of somatic variations in cancer development than earlier mutational models (Fearon and Vogelstein, 1990; Nowell, 1976) had anticipated. Extracting meaningful biological insight from such data nonetheless remains challenging. Much effort has focused on the difficulty of identifying those variants relevant to tumorigenesis and progression, known as the drivers, from the background noise of the many more chance mutations carried along with a developing tumor despite being functionally irrelevant, known as the passengers (McGranahan et al., 2015). More recently, attention has shifted to understanding what one can learn even from passengers regarding how a particular tumor’s mutational spectrum (Alexandrov and Stratton, 2014) shapes its genome across stages of progression and how that knowledge can predict its future progression and help improve prognosis. These remain substantively unsolved problems that must be better tackled if cancer researchers are to make sense of enormous and ever-growing libraries of genetic variations in cancers.

One key advance in understanding tumor genomic data was the advent of tumor phylogenetics, i.e. the use of phylogenetic inference to reconstruct tumor progression. This field arose from the observation that cancer progression is fundamentally the evolution of clonal cell populations and thus in principle interpretable via algorithms for reconstructing evolutionary trees, i.e. phylogenetics. Tumor phylogenetics itself has greatly evolved, from its initial use in making sense of intertumor heterogeneity via oncogenetic tree models (Desper et al., 1999), through the advent of methods for interpreting variation between distinct tumor regions (Khalique et al., 2009; Maley et al., 2006), between distinct cells in single tumors (Pennington et al., 2007) and ultimately to recent variants that seek to explain whole-genome evolution of numerous single-cells per tumor (Jahn et al., 2016; Ross and Markowetz, 2016; Zafar et al., 2017). Single-cell genomic data is beginning to become available in quantity, though most studies of non-trivial patient populations are still limited to bulk sequence data, providing at best variant frequencies averaged across many single cells. Modern methods for working with such data combine phylogenetic inference with a deconvolution step, in which one infers clonal sub-populations from mixed genomic samples prior to or concurrent with inferring phylogenetic relationships between those sub-populations (Schwartz and Shackney, 2010). Numerous tumor phylogeny methods now work on this basic model of joint deconvolution and phylogenetics, with prominent examples including THeTA (Oesper et al., 2014), Pyclone (Roth et al., 2014), Canopy (Jiang et al., 2016), PhyloWGS (Deshwar et al., 2015), SPRUCE (El-Kebir et al., 2016) and CITUP (Malikic et al., 2015). See (Beerenwinkel et al., 2015; Schwartz and Schäffer, 2017) for recent reviews.

Despite many advances, though, key aspects of the problem of reconstructing tumor evolution from variation data remain unresolved, an important one being the interpretation of structural variations (SVs). SVs, along with the copy number aberrations (CNAs) they frequently induce, are the primary mechanism of phenotypic adaptation in developing cancers (Zack et al., 2013). Most tumor phylogeny methods until recently focused primarily on single nucleotide variations (SNVs) [e.g. (El-Kebir et al., 2015; Popic et al., 2015)]. SNVs are generally abundant and make for computationally simpler analyses than other marker types but omit much of the functional mutation that we often seek to understand with tumor phylogenetics. Some early methods did focus primarily on CNAs for deconvolution (Tolliver et al., 2010) and phylogenetics (Chowdhury et al., 2013; Pennington et al., 2007; Schwarz et al., 2014) and several tools are now available for joint inference of SNVs and CNAs [e.g. (Deshwar et al., 2015; El-Kebir et al., 2016; Jiang et al., 2016)]. There is, to our knowledge, however, no method that handles phylogenetics of SVs more comprehensively. Despite their importance, SVs introduce a number of technical challenges, including difficulty of reliable detection leading to a high expected missing data rate, of reconstructing variants that by their nature are associated with copy number variant regions of the genome, and of interpreting these more complicated event types phylogenetically.

The goal of this paper is to address the lack of methods for tumor deconvolution and phylogenetics of diverse classes of SVs at nucleotide resolution. Specifically, we develop a new method for simultaneously deconvolving inferences of SVs, derived from the Weaver variant caller (Li et al., 2016) and reconstructing the likely evolution of clonal populations via these SV events. The method relies on a novel model extending prior literature on SNV and CNA phylogenetics (El-Kebir et al., 2016) to handle SVs. It depends on a model of joint likelihood of genomic sequence data and clonal phylogenies, which we pose and solve through a combinatorial coordinate descent inference strategy. We demonstrate, on simulated and the Cancer Genome Atlas [TCGA (The Cancer Genome Atlas Network, 2012)] samples that these methods are practical and effective in inferring progression of major clones from bulk whole genome sequence (WGS) data.

2 Materials and methods

2.1 Breakpoint and structural variant definitions

Let chrm: pos denote the position and chromosome for each base pair in a reference genome. For example, 7:501 represents the base pair at position 501 on chromosome 7. We define a breakpoint as any base pair c: i that is found non-adjacent to either base pair c: i–1 or base pair c: i + 1. If base pair c: i was found non-adjacent to base pair c: i–1 we denote the breakpoint as [c: i[as the intact chromatin extends to the right, while if base pair c: i was found non-adjacent to base pair c: i + 1 we denote the breakpoint as]c: i]. We define a structural variant (SV) as a pair of breakpoints found adjacent to one another in the cancer genome but at non-adjacent positions in a reference genome. We call each such pair of breakpoints a mated pair, or mates for short. For example, SV]2:30],[5:10[means that the segment on the reference genome on chromosome 2 at position 30 extending to the left was found next to the segment on the reference genome on chromosome 5 at position 10 in the cancer genome. This is specifically an example of a translocation SV, as the re-arrangement involves different chromosomes.

To relate SVs to CNAs, we assume the reference genome is partitioned into r segments, with breakpoints positioned on the ends of segments excluding ends of chromosomes. (In practice, edges of segments are not always supported by breakpoints as mated breakpoints cannot always be supported with a sufficient number of reads). Each breakpoint is found in exactly one segment. Because of this, we can define both the number of times a mated breakpoint appears in a genome (denoted c_b for the copy number of breakpoint b) and the copy number of the segments containing each breakpoint (denoted γ_b for the copy number of the segment containing breakpoint b). A more in depth example for the appearance and copy number of breakpoints is given in Figure 1.

Fig. 1.

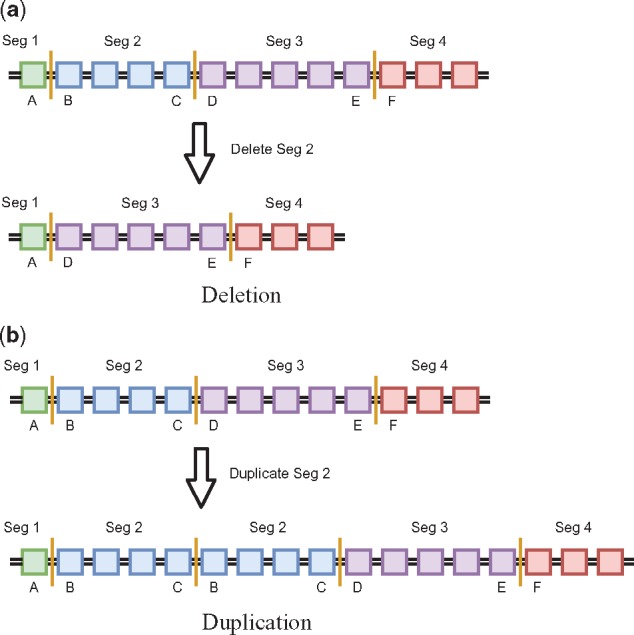
Example genomes before and after segmental deletion and duplication. Top images are the reference genome while bottom images are the genome after deletion/duplication. Each colored box represents a single base pair and base pairs between two vertical orange lines represent segments. The letters below a base pair identify the position of that base pair in the reference genome. Assume this is example holds for any single chromosome labeled z. (a) Shows a deletion of segment 2 (base pairs B through C) producing structural variant ]z: A],[z: D[. The copy number of each of the mated breakpoints ($c_{]\mathtt{z}:\mathtt{A}]}$ and $c_{[\mathtt{z}:\mathtt{D}[}$) and the copy number of each of the segments containing these breakpoints (${\gamma }_{]\mathtt{z}:\mathtt{A}]}$ and ${\gamma }_{[\mathtt{z}:\mathtt{D}[}$) are all 1 ($c_{]\mathtt{z}:\mathtt{A}]}=c_{[\mathtt{z}:\mathtt{D}[}={\gamma }_{]\mathtt{z}:\mathtt{A}]}={\gamma }_{[\mathtt{z}:\mathtt{D}[}=1$). (b) Shows a duplication of segment 2 producing structural variant [z: B[,]z: C]. The copy number of each of the mated breakpoints is 1 ($c_{[\mathtt{z}:\mathtt{B}[}=c_{]\mathtt{z}:\mathtt{C}]}=1$) while the copy number of each of the segments containing breakpoints is 2 (${\gamma }_{[\mathtt{z}:\mathtt{B}[}={\gamma }_{]\mathtt{z}:\mathtt{C}]}=2$)

2.2 Problem statement

Our method takes as input variant calls. We currently assume these calls are of the form produced by Weaver (Li et al., 2016), which calls SVs and CNAs from bulk genomic read data and estimates copy numbers for copy number segments and breakpoints supporting the SVs. Weaver partitions the genome into r segments and infers the mixed copy number of these segments. Weaver reports the copy number of $\ell$ phased breakpoints with sufficient number of reads supporting them, as well as a mapping of mated breakpoints to form SVs. Although Weaver provides additional phase information, we combine homologous chromosomes by summing copy number segments of sister chromatids and assuming SVs initially appear on only one of the chromatids. We use the Weaver output to construct an $m\times (\ell +r)$ mixed copy number matrix F, the m rows of which represent tumor samples and columns of which represent mutations. The first $\ell$ columns correspond to breakpoints and the next r to mixed segmented copy numbers. The variant calls also provide a mapping of breakpoint positions to segments, which we code as an $\ell \times r$ binary matrix Q. We also use information mapping breakpoints to structural variants, encoded as $\ell \times \ell$ binary matrix G. From these inputs, we seek simultaneously to infer an integer copy number matrix C, which describes copy numbers across the genome regions profiled for each inferred clonal cell population; a mixture fraction matrix U, which describes how clonal populations are distributed among tumor samples and a phylogeny T, describing ancestral relationships among the clones. We assume the number of leaves n in the phylogenetic tree containing $N=2n-1$ total nodes (clones) is known. More formally, given

$F\in {ℝ}_{\ge 0}^{m\times (\ell +r)}$	$f_{p,s}$ is mixed copy number of variant s in sample p
$Q\in {\{0,1\}}^{\ell \times r}$	$q_{b,s}$ is 1 iff breakpoint b is in segment s
$G\in {\{0,1\}}^{\ell \times \ell }$	$g_{s,t}$ is 1 iff breakpoints s and t are mated pairs
$n\in \mathbb{N}$	number of leaves in the phylogenetic tree
$c_{max}\in {\mathbb{N}}_{>2}$	maximum allowed sub-clonal copy number for
	breakpoints and segments
${\lambda }_1\in {ℝ}_{\ge 0}$	regularization term to weight total tree cost
${\lambda }_2\in {ℝ}_{\ge 0}$	regularization term to weight breakpoint consistency

where ${\sum }_{s=1}^r{q}_{b,s}=1\hspace{0.17em}\forall \hspace{0.17em}b\in \{1,\dots ,\ell \},{\sum }_{b^{\prime }=1}^{\ell }{g}_{b,b\prime }=1\hspace{0.17em}\forall \hspace{0.17em}b\in \{1,\dots ,\ell \}$, we seek to determine

$C\in {\mathbb{Z}}_{\ge 0}^{N\times (\ell +r)}$ $c_{k,s}$ is the integer copy number of segment or

breakpoint s in clone k

$U\in {[0,1]}^{m\times N}$ $u_{p,k}$ is the cell type k that makes up sample p

$E\in {\{0,1\}}^{N\times N}$   $e_{i,j}$ is 1 iff directed edge (vi, vj) exists in the

inferred phylogeny T

and minimize the objective function

$$\underset{{}_{U,C}}{\min }\left(|F-UC|+{\lambda }_{1}R+{\lambda }_{2}S\right)$$ (1)

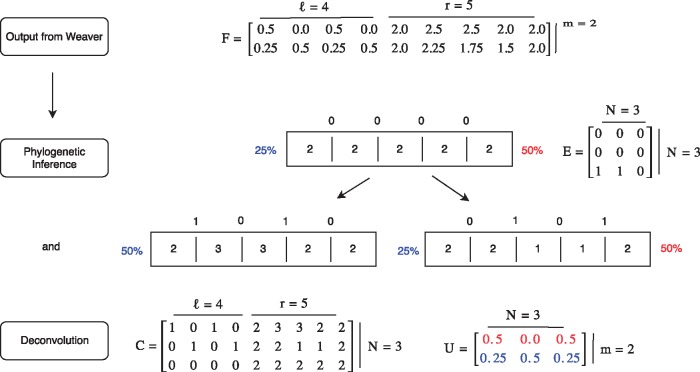
where $|F-UC|$ describes the deviation between true and inferred mixed copy numbers, R is a phylogenetic cost, S is a cost capturing consistency between SVs and copy number segments, and λ₁ and λ₂ are regularization terms (constants). An overview of of the inputs and outputs to this problem including a toy example is given in Figure 2.

Fig. 2.

Illustrative example of the TUSV algorithm. This figure provides an overview of the method and its inputs and outputs using a small artificial example. m = 2 samples are run through Weaver, which produces $\ell =4$ breakpoints (2 SVs) and r = 5 segments. Each breakpoint and segment has an average copy number represented by matrix F. Simultaneous phylogenetic inference and deconvolution yields matrices C, U and E which are visually depicted above as a simple n = 2 leaf phylogeny. Each node is represented by the inferred vector of segment copy numbers and by the inferred copy number for each breakpoint. Segments are represented by adjacent boxes while breakpoints are shown by lines between boxes with inferred copy numbers above those lines. The appearance of breakpoints 1 and 3 along the edge to the left leaf corresponds to the regional duplication of segments 2 and 3 while the appearance of breakpoints 2 and 4 along the edge to the right leaf corresponds to a deletion across segments 2 and 3. In this ideal scenario, $U·C$ exactly equals F

2.3 Coordinate descent algorithm overview

We solve for U, C and T given F, Q and G using coordinate descent (Zaccaria et al., 2017). We write two linear programs: one solving for U given F and C and the other solving for C given U and F. We then iteratively alternate between solving for U and for C while holding the other constant, either until convergence where U and C remain unchanged between iterations, or until a maximum number of iterations is reached. To avoid local minima, we run coordinate descent on multiple random initializations of U. Each row in U is independently randomly uniformly initialized so ${\sum }_{k=1}^N{u}_{p,k}=1$$\forall \hspace{0.17em}p\in \{1,\dots ,m\}$ and samples independently distributed.

2.4 Estimating U

In solving for Equation (1), we define the L1 distance $|F-UC|$ as

$$\begin{array}{cc}{f}_{\Delta ,p,s}\ge f_{p,s}-\sum _{k=1}^N{u}_{p,k}·c_{k,s}\hfill & \forall \hspace{0.17em}p\in \{1,\dots ,m\},\hfill \\ \hfill & s\in \{1,\dots ,\ell +r\}\hfill \end{array}$$ (2)

$$\begin{array}{cc}{f}_{\Delta ,p,s}\ge -f_{p,s}+\sum _{k=1}^N{u}_{p,k}·c_{k,s}\hfill & \forall \hspace{0.17em}p\in \{1,\dots ,m\},\hfill \\ \hfill & s\in \{1,\dots ,\ell +r\}\hfill \end{array}$$ (3)

$$|F-UC|=\sum _{p=1}^m\sum _{s=1}^{\ell +r}{f}_{\Delta ,p,s}$$ (4)

Assume then that F and C are given. To ensure each element $u_{p,k}\in U$ is a percentage of cell type k in sample p and that percentage for a single sample sum to 1, we constrain $u_{p,k}$ so

$$0\le u_{p,k}\le 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}k\in \{1,\dots ,N\}$$ (5)

$$\sum _{k=1}^N{u}_{p,k}=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}p\in \{1,\dots ,m\}$$ (6)

Since the regularization terms in our minimization [Equation (1)] do not depend on U, we can then simply find U to minimize $|F-UC|$ [Equation (4)] given F and C subject to constraints Equations (2), (3), (5) and (6).

2.5 Estimate C

We then estimate C and T given F, U, Q and G.

2.5.1 Binary indicator variables

Any variable x has an associated indicator variable $\overline{x}$ defined as

$$\text{bin}\left(x\right)=\overline{x}=\{\begin{array}{cc}1\hfill & x>0\hfill \\ 0\hfill & x=0\hfill \end{array}$$ (7)

This is used throughout the following sections. To linearly define $\overline{x}$, we introduce temporary variable $y_b\in \{0,1\}$ as the bit representation of x over q bits (Zaccaria et al., 2017). The values of temporary variable y_b only apply to Equations (8) and (9). y_b is then defined by

$$\sum _{b=0}^{\lfloor \hspace{0.17em}{\text{log}}_2{x}_{\text{max}}\rfloor +1}{2}^b·y_b=x$$ (8)

and constrains $\overline{x}$ as

$$0\le y_b\le \overline{x}\le \sum _{a=0}^{\lfloor \hspace{0.17em}{\text{log}}_2{x}_{\text{max}}\rfloor +1}{y}_a\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}b\in \{0,\dots ,\lfloor \hspace{0.17em}{\text{log}}_2{x}_{\text{max}}\rfloor +1\}$$ (9)

so $\overline{x}$ is 0 if all bits b are 0 and 1 if any bit of x is 1. In this way, any integer variable x with a maximum value x_max can be represented in binary form $\overline{x}$. Binary indicator variables are noted with a bar on top $\overline{x}$ or by bin (x).

2.5.2 Phylogenetic constraints

Since the individual rows of C are not independent but instead share a phylogenetic history, we create a tree structure T representing the inferred relationships between rows in C. We define a binary tree T using a N × N directed adjacency matrix E. To impose a tree structure on E, assume the first n clones are leaf nodes and clones n + 1 through $2n-1=N$ are internal nodes, with node N as the root. We constrain element $e_{i,j}$ as follows:

root, incoming edges

$$e_{i,N}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,N\}$$ (10)

non-root, incoming edges

$$\sum _{i=1}^{N-1}{\mathrm{e}}_{i,j}=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}j\in \{1,\dots ,N-1\}$$ (11)

leaves, outgoing edges

$${\mathrm{e}}_{i,j}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,n\},\hspace{0.17em}j\in \{1,\dots ,N\}$$ (12)

internal nodes, outgoing edges

$$\sum _{j=1}^N{\mathrm{e}}_{i,j}=2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{n+1,\dots ,N\}$$ (13)

Equations (10) and (11) ensure the root has no in-edges and all other nodes have exactly one in-edge. Equations (12) and (13) force leaves to have no out-edges and all internal nodes to have exactly two out-edges.

2.5.3 Phylogenetic cost

We next ensure all copy numbers are below some input maximum c_max and force the normal (non-tumor) root node to be diploid (each segment having copy number 2) and free of structural variants (copy number of all breakpoints is 0):

$$c_{k,s}\le c_{\text{max}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}k\in \{1,\dots ,N\},\hspace{0.17em}s\in \{1,\dots ,\ell +r\}$$ (14)

$$c_{N,b}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}b\in \{1,\dots ,\ell \}$$ (15)

$$c_{N,s+\ell }=2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}s\in \{1,\dots ,r\}$$ (16)

We next model a phylogenetic tree cost, using CNAs to estimate evolutionary distance ${\rho }_{i,j}$ across each tree edge $(v_i,v_j)\in E$. We approximate evolutionary distance by the L1 distance between the copy number profiles of an edge’s endpoints $\sum _{s=1}^r|c_{i,s+\ell }-c_{j,s+\ell }|$. While there are more sophisticated models of copy number distance in the literature (Chowdhury et al., 2014; Chowdhury et al., 2015; El-Kebir et al., 2017; Schwarz et al., 2014), we use L1 distance as an approximation as it can be coded and computed efficiently within the ILP framework. To linearly define ${\rho }_{i,j}$ we use temporary variable $x_{i,j,s}\in {\mathbb{N}}^{\mathit{N}\times \mathit{N}\times \mathit{r}}$, defined as the absolute change in copy number of segment s on edge (v_i, v_j). Here, the values of temporary variable $x_{i,j,s}$ only apply to Equation (17) through Equation (20).

$$\begin{array}{c}0\le x_{i,j,s}\le c_{\text{max}}·e_{i,j}\hfill \\ \hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}s\in \{1,\dots ,\ell +r\}\hfill \end{array}$$ (17)

$$\begin{array}{c}{x}_{i,j,s}\ge c_{i,s+\ell }-c_{j,s+\ell }-c_{\text{max}}·(1-e_{i,j})\hfill \\ \hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}s\in \{1,\dots ,\ell +r\}\hfill \end{array}$$ (18)

$$\begin{array}{c}{x}_{i,j,s}\ge -c_{i,s+\ell }+c_{j,s+\ell }-c_{\text{max}}·(1-e_{i,j})\hfill \\ \hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}s\in \{1,\dots ,\ell +r\}\hfill \end{array}$$ (19)

Equation (17) sets the cost to zero for any pair of nodes (v_i, v_j) where v_i is not the parent of v_j, while Equations (18) and (19) set the cost to be the absolute difference between copy number for of end nodes for any edge (v_i, v_j). We then define the cost across edge (v_i, v_j) and total cost of tree as

$${\rho }_{i,j}=\sum _{s=1}^r{x}_{i,j,s}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\}$$ (20)

$$R=\sum _{i=1}^N\sum _{j=1}^N{\rho }_{i,j}$$ (21)

2.5.4 Perfect phylogeny on appearance of breakpoints

We next impose a perfect phylogeny on breakpoints. While the perfect phylogeny assumption is problematic for other variant types, we argue that it is sufficiently unlikely for a base-resolution breakpoint to recur that it can be neglected. Note that violations of the infinite sites model due to allelic loss are handled separately by treating a lost allele as having copy number zero. We therefore impose constraints to force each breakpoint to appear across exactly one edge in T and for mated breakpoints to appear together. Define $W\in {\{0,1\}}^{N\times N\times \ell }$, where each element $w_{i,j,b}$ is 1 if the copy number of breakpoint b goes from 0 to a positive integer across edge (v_i, v_j) and 0 otherwise. To linearly define $w_{i,j,b}$ we define temporary variable $x_{i,j,b}\in \{0,1,2,3\}$ to be

$$x_{i,j,b}=2+{\overline{c}}_{i,b}-{\overline{c}}_{j,b}-e_{i,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}b\in \{1,\dots ,\ell \}$$ (22)

so $x_{i,j,b}$ is 0 iff the copy number of breakpoint b increases from 0 across edge (v_i, v_j). The value of temporary variable $x_{i,j,b}$ only applies to Equations (22) and (23). Using the binary representation ${\overline{x}}_{i,j,b}$ of $x_{i,j,b}$, define $w_{i,j,b}$ and ensure $w_{i,j,b}$ is 1 for a single edge in the tree.

$$w_{i,j,b}=1-{\overline{x}}_{i,j,b}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}b\in \{1,\dots ,\ell \}$$ (23)

$$\sum _{i=1}^N\sum _{j=1}^N{w}_{i,j,b}=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}b\in \{1,\dots ,\ell \}$$ (24)

Using breakpoint mate indicator $g_{s,t}\in \{0,1\}$, where $g_{s,t}$ is 1 iff breakpoints s and t are mates, we force breakpoint indicators to be equal for mates.

$$w_{i,j,s}-w_{i,j,t}\le 1-g_{s,t}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}s,t\in \{1,\dots ,\ell \}$$ (25)

$$-w_{i,j,s}+w_{i,j,t}\le 1-g_{s,t}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hspace{0.17em}s,t\in \{1,\dots ,\ell \}$$ (26)

Note we extend the notation of breakpoint appearance indicator $w_{i,j,b}$ to have $w_{j,b}={\sum }_{i=1}^N{w}_{i,j,b}$ be 1 if breakpoint b appears at node v_j and 0 otherwise.

2.5.5 Ancestry condition for non-disappearing SVs

We next impose the two-state perfect phylogeny ancestry condition as described in (El-Kebir et al., 2015) for the appearance of breakpoints. For any breakpoint s that appears as an ancestor to breakpoint t, the total fraction of cells with breakpoint s must be larger than the fraction with breakpoint t so long as breakpoint s never subsequently disappears. To enforce this, the fraction of cells ${\varphi }_{p,b}$ containing breakpoint b in sample p is defined as

$${\varphi }_{p,b}=\sum _{k=1}^N{u}_{p,k}·{\overline{c}}_{k,b}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}b\in \{1,\dots ,s\}$$ (27)

We then must define a few variables to force ${\varphi }_{p,s}\ge {\varphi }_{p,t}$ if breakpoint s appears before breakpoint t and is never subsequently lost. Let v_i be the ith node in the phylogeny and $v_i\prec v_j$ denote that node v_i is an ancestor of v_j. We first define ancestor variables $a_{i,j}\in \{0,1\}$ as 1 if $v_i\prec v_j$ and 0 otherwise for all $i,j\in \{1,\dots ,N\}$. Linearly define $a_{i,j}$ by

root v_N is ancestor to all nodes

$$a_{N,j}=1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}j\in \{1,\dots ,N-1\}$$ (28)

root v_N has no ancestors

$$a_{i,N}=0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,N\}$$ (29)

any parent is an ancestor

$$a_{i,j}\ge {\mathrm{e}}_{i,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\}$$ (30)

child gets parent’s ancestor profile

$$\begin{array}{cc}{a}_{g,j}\ge {\mathrm{e}}_{i,j}+a_{g,i}-1\hfill & \forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hfill \\ \hfill & g\in \{1,\dots ,i-1,i+1,\dots ,N\}\hfill \end{array}$$ (31)

$$\begin{array}{cc}{a}_{g,j}\le 1-{\mathrm{e}}_{i,j}+a_{g,i}\hfill & \forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hfill \\ \hfill & g\in \{1,\dots ,i-1,i+1,\dots ,N\}\hfill \end{array}$$ (32)

Next, define the number of descendants to node v_i with at least one copy of breakpoint b as $d_{i,b}$ for all $i\in \{1,\dots ,N\},\hspace{0.17em}b\in \{1,\dots ,\ell \}$. To linearly define $d_{i,b}$, define temporary binary variables $x_{i,j,b}\in \{0,1\}$ for Equation (33) through Equation (36) for all $i,j\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$ to be 1 if $a_{i,j}$ and ${\overline{c}}_{j,b}$ and zero otherwise.

$$x_{i,j,b}\ge a_{i,j}+{\overline{c}}_{j,b}-1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (33)

$$x_{i,j,b}\le a_{i,j}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (34)

$$x_{i,j,b}\le {\overline{c}}_{j,b}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i,j\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (35)

$$d_{i,b}=\sum _{j=1}^N{x}_{i,j,b}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (36)

Define temporary binary variables ${\overline{y}}_{i,b}\in \{0,1\}$ for Equation (37) through Equation (39) to be 0 to be zero if all descendants of node v_i contain at least one copy of breakpoint b and 1 otherwise.

$$y_{i,b}=\sum _{j=1}^N{a}_{i,j}-d_{i,b}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (37)

$${\overline{y}}_{i,b}=\text{bin}\left(y_{i,b}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}i\in \{1,\dots ,N\},b\in \{1,\dots ,\ell \}$$ (38)

Define temporary binary variable ${\overline{z}}_{i,j,s,t}\in \{0,1\}$ for Equations (39) and (40) to be 0 only if breakpoint s appears at node v_i, breakpoint t appears at node v_j, node v_i is an ancestor to node v_j and breakpoint s never disappears.

$$\begin{array}{cc}{z}_{i,j,s,t}=3-w_{i,s}-w_{j,t}-a_{i,j}+{\overline{y}}_{i,s}\hfill & \forall \hspace{0.17em}i,j\in \{1,\dots ,N\},\hfill \\ \hfill & s,t\in \{1,\dots ,\ell \}\hfill \end{array}$$ (39)

Finally, apply the condition that the fraction of cells ${\varphi }_{p,s}$ containing breakpoint s in sample p must be larger than the fraction of cells ${\varphi }_{p,t}$ containing breakpoint t in sample p if breakpoint s appears in an ancestor to the node where breakpoint t appears and breakpoint s is never lost in any descendant (no descendant has copy number 0 for breakpoint s).

$$\begin{array}{cc}{\varphi }_{p,s}\ge {\varphi }_{p,t}-1+\sum _{i=1}^N\sum _{j=1}^N\left(1-{\overline{z}}_{i,j,s,t}\right)\hfill & \forall \hspace{0.17em}p\in \{1,\dots ,m\},\hfill \\ \hfill & s,t\in \{1,\dots ,\ell \}\hfill \end{array}$$ (40)

Note that ${\sum }_{i=1}^N{\sum }_{j=1}^N\left(1-{\overline{z}}_{i,j,s,t}\right)$ can only take on values 0 or 1 since breakpoint appearance indicator $w_{i,s}$ and $w_{j,s}$ can only be both 1 at most once across all i, j. This means the condition ${\varphi }_{p,s}\ge {\varphi }_{p,t}$ only holds when breakpoint s appears before breakpoint t and never subsequently disappears. Note the ancestry condition is implied by but weaker than the sum condition described in (El-Kebir et al., 2015), but can similarly be enforced by linear constraints.

2.5.6 Structural variant and segment consistency

Since each breakpoint belongs to exactly one segment, we define the copy number of each segment containing a breakpoint b and constrain it so a breakpoint’s copy number never exceeds that of its containing segment:

$$\begin{array}{cc}{c}_{k,b}\le {\gamma }_{k,b}=\sum _{s=1}^r{q}_{b,s}·c_{k,s+\ell }\hfill & \forall \hspace{0.17em}k\in \{1,\dots ,N\},\hfill \\ \hfill & b\in \{1,\dots ,\ell \}\hfill \end{array}$$ (41)

where input $q_{b,s}\in \{0,1\}$ is 1 if segment s contains breakpoint b. ${\sum }_{s=1}^r{q}_{b,s}=1$ as each breakpoint belongs to a single segment. We similarly define ${\psi }_{p,b}$ directly from the input to be the mixed copy number of the segment containing breakpoint b.

$$\begin{array}{c}{\psi }_{p,b}=\sum _{s=1}^r{q}_{b,s}·f_{p,s+\ell }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}b\in \{1,\dots ,\ell \}\\ {\pi }_{p,b}=\frac{f_{p,b}}{{\psi }_{p,b}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}b\in \{1,\dots ,\ell \}\end{array}$$

Intuitively, the ratio ${\pi }_{p,b}$ of the mixed copy number of a breakpoint to the mixed copy number of the segment containing that breakpoint should be maintained in the integer output as this preserves the difference in mutation types (duplication, deletion). To penalize for discrepencies between the inferred ratio of breakpoint and its segment copy number given ${\pi }_{p,b}$, we incorporate the following quantity into our objective function:

$$\left|{\pi }_{p,b}-\frac{{\sum }_{k=1}^N(u_{p,k}·c_{k,b})}{{\sum }_{k=1}^N(u_{p,k}·{\gamma }_{k,b})}\right|$$

To convert this from a ratio to units of copy numbers, we re-arrange the expression and define S for the final term in the objective function Equation (1) to be

$$\begin{array}{c}{z}_{p,b}\ge {\pi }_{p,b}·\sum _{k=1}^N(u_{p,k}·{\gamma }_{k,b})-\sum _{k=1}^N(u_{p,k}·c_{k,b})\hfill \\ \forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}b\in \{1,\dots ,\ell \}\hfill \end{array}$$ (42)

$$\begin{array}{c}{z}_{p,b}\ge -{\pi }_{p,b}·\sum _{k=1}^N(u_{p,k}·{\gamma }_{k,b})+\sum _{k=1}^N(u_{p,k}·c_{k,b})\hfill \\ \forall \hspace{0.17em}p\in \{1,\dots ,m\},\hspace{0.17em}b\in \{1,\dots ,\ell \}\hfill \end{array}$$ (43)

$$S=\sum _{p=1}^m\sum _{b=1}^{\ell }{z}_{p,b}$$ (44)

In this way, increased emphasis is placed on the relationship between segments and breakpoints. The solution for C and T is found by minimizing Equation (1) subject to constraints Equation (2) through Equation (44).

3 Results

3.1 Simulated data

To validate accuracy of the method on data of known ground truth, we assess accuracy in inference of copy number profiles across clones. For each such test, we generate a copy number matrix C_tru containing breakpoints and segments, mix this matrix with a mixture fraction matrix U_tru to get the mixed copy number matrix ($C_{\text{tru}}\times U_{\text{tru}}\to F$), run our deconvolution algorithm and compare the inferred copy number matrix C_inf with the original true copy number matrix C_tru. We score our result as the L1 distance ($|C_{\text{tru}}-C_{\text{inf}}|$) between copy number matrices after a maximum matching between copy number profiles (for clones).

To generate C_tru, we simulated mutation data varying the expected number of mutations l, number of samples m and number cell types n. For each triplet (l, m, n), five synthetic patients were generated. Reported scores are averaged across those five patients. For each run of the simulation, we generated a binary tree T with n leaves and a random topology. Mutations were assigned so that the expected numbers of mutations across all edges in each tree are equal. We start with a genomic profile for the root (assumed to be a normal diploid cell containing no structural variants) and progressively added a Poisson-distributed number of mutations across each edge down to the leaves. Initially, the root node contains three pairs of homologous chromosomes of the same lengths as human chromosomes 1–3. To generate mutations, a central location is uniformly chosen across all chromosomes, then a mutation size is sampled from an exponential distribution, with expectation equal to the mean structural variant size found across 59 TCGA samples (approximately 5 745 000 base pairs). The mutation type is uniformly randomly selected to be either a tandem duplication, deletion, or inversion. From the generated tree, we obtain a copy number matrix C_tru. We then create a cell type mixture matrix U_tru by uniformly randomly assigning cell type fractions such that the fraction of all cell types in each sample sums to 1. U_tru and C_tru are subsequently multiplied to generate mixed copy number matrix F.

Since there is no method for validating how accurate the choice of regularization terms λ₁ and λ₂ are on real data, we define empirical values for these terms based on each sample and show they perform well on simulated data. We choose regularization terms λ₁ and λ₂ empirically from the data to be ${\lambda }_1=\frac{\ell +r}{\ell }·\frac{m}{N}$ and ${\lambda }_2=\frac{\ell +r}{\ell }$. This allows the maximum error in the $|F-UC|$ term in the minimization, which is $m·(\ell +r)·c_{\text{max}}$, to equal the maximum errors in ${\lambda }_{1}R$ and ${\lambda }_{2}S$ terms, which are $\ell ·N·c_{\text{max}}$ and $\ell ·m·c_{\text{max}}$, respectively. To show these empirical definitions do as well as iteratively choosing the hyperparameters, we test on simulated data generated for n = 3 leaves, m = 3 samples and l = 50 mutations as this produces approximately 100 breakpoints, a value comparable to the average number of breakpoints found in real, TCGA samples. To ensure consistency in scoring, we generate five simulated patients with exactly 99 segments (not 100 since we have an odd number of chromosomes) and report the mean L1 distance between copy number segment matrices across the n = 3 leaves. Figure 3 shows that automatically selecting hyperparameters λ₁ and λ₂ (solid green curve) leads to very good performance relative to that seen across a scan of possible parameter values (dotted blue curve), suggesting the automated parameter inference is effective. Both outperform the algorithm when excluding the regularization terms (dashed red curve), indicating the usefulness of including phylogenetic cost and breakpoint-segment consistency into the model. To further assess the novel value of including the SV phylogeny constraints in our model, we removed all phylogenetic constraints as well as structural variants from our model and found the results to be nearly the same as those when excluding both regularization terms (mean score of 480.6 and 487.0, respectively). This result further demonstrates the value of simultaneous SV phylogenetic inference and deconvolution even when the method is judged solely on deconvolution quality.

Fig. 3.

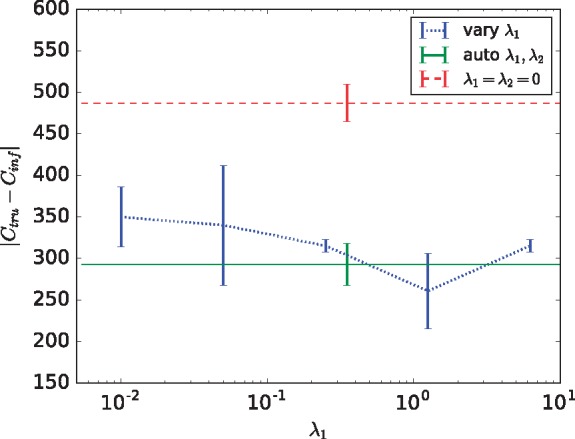
Deconvolution quality on simulated data for varying hyperparameters λ₁ and λ₂. Accuracy is scored by the sum of L1 distances between the true C_tru and inferred C_inf copy number matrices for all segments in each leaf after maximum matching (lower means better performance). The reported score is an average across five simulated datasets each containing 99 segments with standard errors shown as error bars. The dotted blue line is the score when ${\lambda }_2=0$ is held constant and λ₁ varies from 0.01, 0.05, 0.25, 1.25, 6.25 across the x-axis. The solid green line shows the score when hyperparameters are automatically chosen based on the number of SVs and CNAs in the dataset, while the dashed red line shows scores when only the first term in the objective function, corresponding to accuracy of copy number deconvolution, is used

We further evaluated the effectiveness of the methods by their ability to identify the correct phylogenetic trees. We assessed accuracy using Robinson Foulds (RF) distance, which measures the number of bi-partitions differing between two trees on a common set of nodes, between the true and inferred trees for each of the simulated test cases. We found that three of the five inferred trees had identical topology to the true trees (RF distance 0). The remaining two trees differed solely by swapping the root node with one leaf neighbor of the root (RF distance 2). While the trees are too simple and few in number to attach any significance to this result, it does demonstrate that the method is generally accurate at inferring correct or near-correct phylogenies despite some error in deconvolution of the nodes of the trees.

3.2 TCGA data

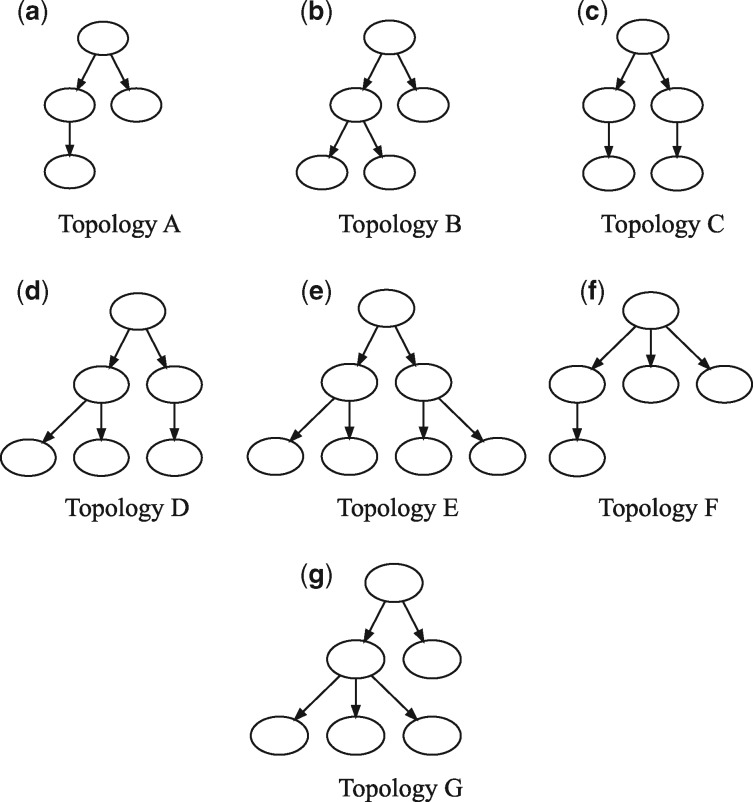
We next apply the methods to a selection of TCGA breast cancer (BRCA) samples (The Cancer Genome Atlas Network, 2012), restricting analysis to a sub-set of 59 samples for which WGS data was available. Of these, 31 ran successfully within a prescribed run time limit of 2 days, while 28 with the highest SV counts timed out before completion or required more memory than was available to us (128 Gb of RAM). Since there is no known ground truth for these samples, we cannot assess their individual accuracies. Nonetheless, they provide some basis for analysis of trends across samples. Space does not permit us to display all observed trees, so for purposes of illustration we classify them into seven observed topologies (A-G), shown in Figure 4, with frequencies of occurrence shown in Figure 5. None of the inferred trees are purely linear, consistent with a model of significant sub-clonal heterogeneity rather than a simple sequential model of clonal progression. Quantitation by several measures of heterogeneity, as shown in Figure 6, likewise suggests a wide diversity among samples. The data is suggestive of a possible clustering into distinct low-diversity and high-diversity sub-clusters, but with substantial overlap between clusters.

Fig. 4.

Tree topologies observed across 31 TCGA BRCA samples, grouped into seven categories (A–G)

Fig. 5.

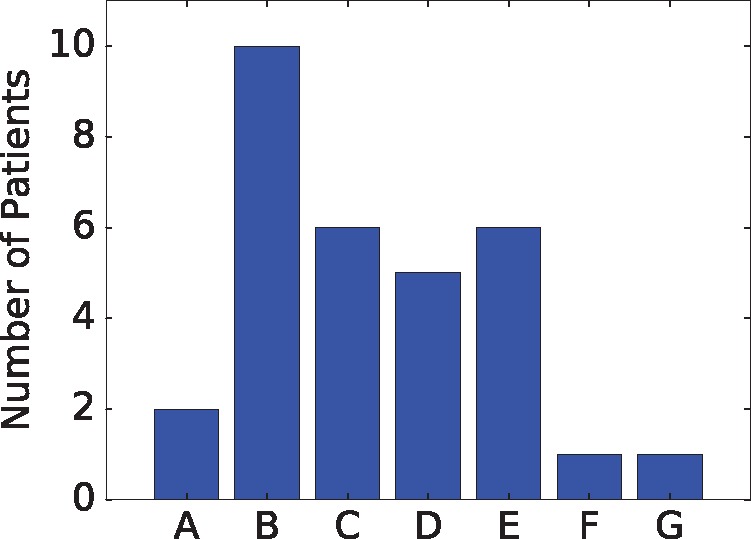
Histogram of occurrences of tree topologies across 31 TCGA BRCA samples

Fig. 6.

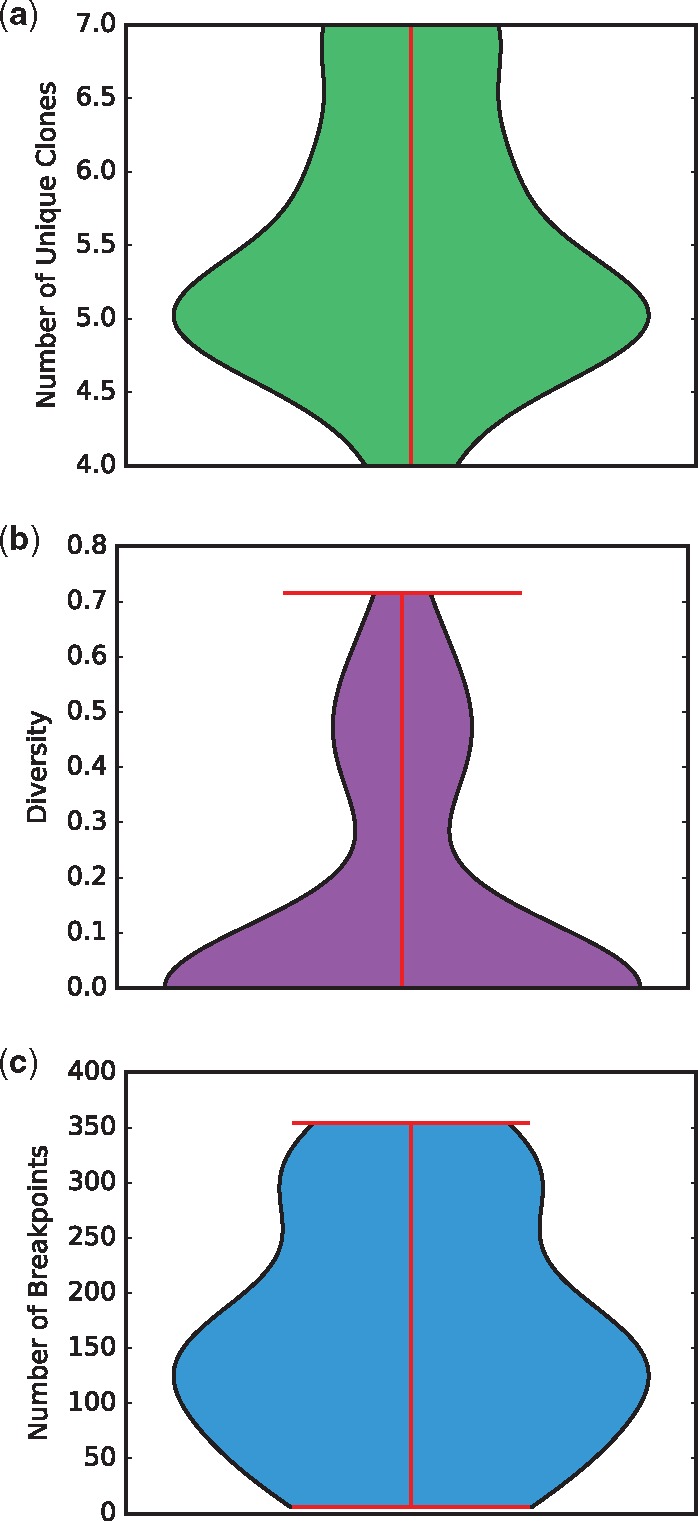
Violin plots quantifying heterogeneity of the 31 TCGA trees. (a) Number of unique clones. (b) Diversity, defined in terms of the clonal frequency vector $u_{p,k}$ as $1-{\sum }_{k=1}^N{u}_{p,k}$. (c) Number of breakpoints

4 Discussion

We have developed a new method for automated joint deconvolution and phylogeny inference of tumor genomic data designed to address the important unsolved problem of describing progression via SVs. We specifically learn a model encompassing CNAs and SVs of major clones, mixture fractions of these clones across samples and a phylogenetic tree relating the clones. We pose the model inference problem to balance the likelihood of sequence read data with respect to copy numbers and observed breakpoints against the evolutionary cost of the phylogenetic tree. We solve the resulting model via a co-ordinate descent algorithm posed as a pair of MILPs. We demonstrate that the method can accurately and efficiently reconstruct clonal populations and phylogenetic histories from simulated tumor data. Application to WGS data from the TCGA shows the method to be effective on real data supportive of a range of tree topologies and complexities.

This work provides a proof-of-concept demonstration of the feasibility of more comprehensively modeling the important role of SVs in tumor evolution, but also suggests a number of avenues for future work. Our methods currently rely on a sometimes costly and potentially sub-optimal model fitting algorithm, and further algorithmic advances might plausibly lead both to greater efficiency and improved solution quality. In particular, there are currently practical limits on the total SV counts the method can handle without excessive run time and memory usage. While most of the TCGA BRCAs considered fell within those limits, a significant minority did not. The method also makes some assumptions about its input data that may not always be satisfied, particularly that base-pair resolution SV breakpoints can be inferred accurately and will form sufficiently rarely that we can assume a perfect phylogeny of SVs. While we argue that this is a sounder assumption for SVs than for SNVs, one might nonetheless anticipate some violations either due to truly recurrent mutation or to errors in breakpoint assignment that might lead to conflation of distinct breakpoints. Extending the model to allow for tolerance of such violations of the SV perfect phylogeny assumption would thus be a good avenue for future work. Furthermore, our work focuses only on the sub-problem of handling SVs (and associated CNAs), and will likely benefit from incorporating other variant types, most notably SNVs but also potentially expression, methylation, or other markers of cell state. In addition, biotechnology for data generation is continuing to advance, with growing numbers of computational methods taking advantage of single-cell sequence or long read technologies that can provide direct single-cell readouts of SNV or CNA data. SV detection is problematic for all current single-cell technologies, and we can anticipate value in combining single-cell methods with bulk deconvolution methods such as ours for SVs. Finally, the present work has focused only on the development of the new technology and its validation. The ultimate value of the work will lie in bringing SV-aware phylogenetics to diverse patient cohorts, to begin to develop a comprehensive understanding of the landscape of SV variation in tumor progression and its implications for patient prognosis and treatment.