SLTCAP: A simple method for calculating the number of ions needed for MD simulation

Abstract

Accurate depiction of electrostatic interactions in molecular dynamics requires the correct number of ions in the simulation box to capture screening effects. However, the number of ions that should be added to the box is seldom given by the bulk salt concentration because a charged biomolecule solute will perturb the local solvent environment. We present a simple method for calculating the number of ions that requires only the total solute charge, solvent volume, and bulk salt concentration as inputs. We show that the most commonly used method for adding salt to a simulation results in an effective salt concentration that is too high. These findings are confirmed using simulations of lysozyme. We have established a web server where these calculations can be readily performed to aid simulation setup.

TOC image

While electrostatic interactions are indisputably an essential contribution to biomolecule interactions,¹ it still remains challenging to model them theoretically. Continuum models, like Poisson-Boltzmann (PB), provide key intuition about salt screening effects, however, such mean field theories cannot handle temporal or spatial fluctuations. Furthermore, the relevant lengthscales for biomolecule interactions are often too small to justify the averaging underlying mean field approaches. Explicit solvent models address precisely these limitations by explicitly representing all charges and allowing mean-field phenomena, like screening, to emerge organically from the microscopic dynamics.

In setting up a simulation, care must be taken in considering the contents of the box. The solvent environment near a solute is perturbed by the presence of the solute and cannot be assumed to be identical to bulk solution. This perturbation comes with significant entropic cost that contributes strongly to the free energy of biomolecule interactions. For example, the reduction in H-bonding partners for water molecules near non-polar surfaces gives rise to the hydrophobic effect.² Similarly, and more to the point of this paper, the presence of charges on the solute distorts the ionic environment surrounding the solute, which results in non-intuitive many-body corrections to the association free energy.^3,4 Therefore, it is important that the solvent composition in the simulation box is representative of the perturbed environment near the solute.

There are two main approaches to computing the number of salt ions that should be added to a simulation (not including grand canonical methods). The first is to simply add enough counterions to achieve a neutral box. Since this method omits coions entirely, it is representative of a salt-free solution where the only counterions present are those that dissociated from the solute. The second is to add enough coion/counterion pairs to achieve the desired solution salt concentration, and then to add enough additional counterions to achieve a neutral box. We refer to this as the Add-then-Neutralize (AN) method. The problem with this approach is that charged solutes are expected to deplete the surrounding environment of coions. Therefore, this method is actually representative of a higher bulk salt concentration than intended.

Here we present a method, Screening Layer Tally by Container Average Potential (SLTCAP), to compute the number of salt ions that should be added to a simulation given an external salt concentration. This method requires no additional information beyond what is needed for AN. To do this we take advantage of the fact the ion fluctuations will be less significant when averaging over the entire simulation box. This allows us to employ a mean field formalism to compute the number of ions. The fluctuations will be restored, at least locally, by the ion dynamics in the final simulation.

Consider a solute of charge Q and volume v_p immersed in a simulation box with volume v_t = v_p + v_w, where v_w is the volume occupied by solvent. We assume that the simulation box is in equilibrium with a large solvent reservoir with a concentration c₀ of symmetric, monovalent salt. Inside the box the ion concentrations are perturbed by interactions with the solute charges. The perturbed concentrations are related to the electrostatic potential, ϕ, by

$$c_{+}(\mathbf{x})=c_0{e}^{-e\varphi (\mathbf{x})/k_{B}T}$$ (1)

$$c_{-}(\mathbf{x})=c_0{e}^{e\varphi (\mathbf{x})/k_{B}T}$$ (2)

The total number of ions in the box can be obtained by integrating over the solvent volume

$$N_{\pm }={\displaystyle {\int }_{v_w}{c}_0{e}^{\mp e\varphi (\mathbf{x})/k_{B}T}}{d}^3\mathbf{x}$$ (3)

where e is the electron charge, k_B is the Boltzmann constant, T is the absolute temperature, and the integral is evaluated over the ion accessible volume. While Eq. (3) is the optimal method for computing the ion numbers, it requires the cumbersome step of finding the potential by solving the PB equation. Although excellent tools exist for this,^5,6 this level of effort is unnecessary given that the important features of ion screening will be captured by the ion dynamics in the simulation. Instead, we employ an approximation in which we replace the spatially dependent potential ϕ(x) with an average potential $\overline{\varphi }$ that is uniform across the simulation box. With this approximation Eq. (3) becomes $N_{\pm }=v_w{c}_0{e}^{\mp e\overline{\varphi }/k_{B}T}$. The value of the average potential can be determined from the charge neutrality condition −Q/e = N₊ − N₋ (the conditions underlying this assumption are discussed below) which yields

$$\frac{e\overline{\varphi }}{k_{B}T}=\text{ArcSinh}\left(\frac{Q}{2e{v}_w{c}_0}\right)$$ (4)

The required ion numbers are then given by

$$N_{\pm }=v_w{c}_0\text{Exp}\left[\mp \text{ArcSinh}\left(\frac{Q}{2e{v}_w{c}_0}\right)\right]$$ (5)

Thus, it is possible to estimate the required ion numbers knowing only the solute charge, solvent volume, and bulk salt concentration.

Figure 1 plots Eq. (5) as a function of the protein charge (solid lines). A key feature is that the box is depleted of coions in addition to being enriched in counterions. This feature is not present in the AN method (dashed lines) which simply adds counterions on top of ion pairs present at bulk concentration. This means that AN results in the simulation of a system that has an effective salt concentration higher than intended. We can estimate the effective concentration generated by the AN method as follows. Assuming that we have a solute with a positive charge Q > 0, the number of ions added to the box under the AN method is

$$\begin{array}{l}{N}_{+}=v_w{c}_0\\ N_{-}=v_w{c}_0+Q\end{array}$$ (6)

The same number of ions can be obtained if the box is in equilibrium with a solution at an effective salt concentration c_eff

$$\begin{array}{l}{N}_{+}=v_w{c}_{\text{eff}}{e}^{-e{\varphi }_{\text{eff}}/k_{B}T}\\ N_{-}=v_w{c}_{\text{eff}}{e}^{e{\varphi }_{\text{eff}}/k_{B}T}\end{array}$$ (7)

where ϕ_eff is the average potential inside the box. Eliminating N₊, N₋, and ϕ_eff from Eq. (7) and Eq. (8), we find that the effective salt concentration is

$$c_{\text{eff}}=c_0\sqrt{1+Q/(e{v}_w{c}_0)}$$ (8)

We see that the key parameter is the ratio of the solute charge Q/e to the number of ions that would be found in the box with an uncharged solute v_wc₀. When this ratio is small, such as when the box is large or the solute charge is small, the difference between AN and SLTCAP is minimal. However, the ratio can be quite large when the system of interest contains highly charged molecules like nucleic acids.

Figure 1.

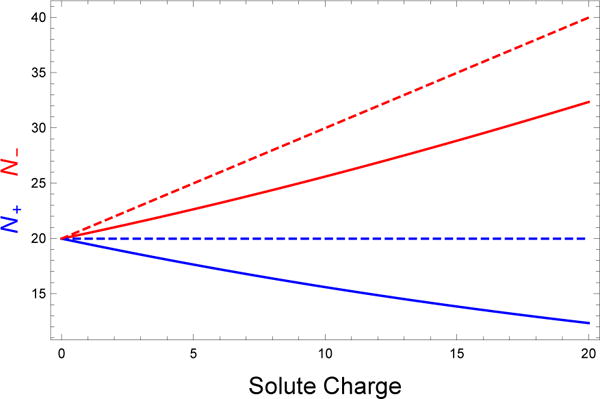
Calculated number of salt ions needed to achieve a bulk concentration of 150 mM in a solvent volume of 221 nm³. The number of coions (cations in this case) required by the AN method (dashed lines) is independent of the solute charge, which is unrealistic because electrostatic repulsion between the solute and coions will deplete the local environment of coions. The SLTCAP method (solid lines) accounts for coion depletion, which also reduces the required number of counterions.

We compared the ion distributions predicted by AN and SLTCAP using simulations of a model protein. Lysozyme (PDB id:1AKI) was simulated at 300 K and 1 bar in the presence of four different NaCl concentrations, 0.15, 0.39, 0.67, and 0.95 M. The MD simulations were performed for 40-60 ns at each salt concentration with the Amber 99SB-ILDN force field,⁷ as implemented in the Gromacs simulation package,⁸ using the Particle Mesh Ewald approach to determine the electrostatic interactions.⁹ The charge on Lysozyme (Q = +8 at pH 7.0) corresponds to the assumption that all the amino acids display standard pKa values. These simulations were conducted in a large ≃ 15 nm simulation box where there are almost 6 Debye lengths between the surface of the protein and the edge of the box at the lowest salt concentration investigated. This setup approximates dilute solution with a large reservoir of ions that can relax around the protein. Ions were added to the box according to the AN method due to the fact that the large reservoir makes the system insensitive to this choice. We then count the number of anions and cations contained within a fictitious box of variable dimension L_box that is centered around the protein. The protein volume (22.2 nm³) was determined by plotting the difference between the system volume and the water volume (N_w times molar volume of TIP3P water) as a function of bulk salt molality followed by an extrapolation to zero salt.

Figure 2 shows the local ion concentrations as a function of distance from the center of the box. Interestingly, we observed large, but highly variable, concentrations of coions at distances less than the lysozyme radius of ∼ 1.6 nm, indicating a short-ranged affinity between the protein and Na⁺ ions. At distances somewhat greater than the molecular radius the system shows a significant depletion of coions and enrichment of counterions. This imbalance signifies the presence of the screening layer. The perturbed concentrations decay back to the bulk concentration with a characteristic distance of the screening length.

Figure 2.

Local ion molality within cubic shells with an edge length L_box and a shell thickness 0.1 nm. For L_box values somewhat larger than the lysozyme radius ~1.6 nm there is an enrichment of counterions (red) and depletion of coions (blue). At distances much greater than the screening length, the ion concentrations are both equal to the bulk concentration. The high concentration of coions at small distances indicates a short-ranged affinity between Na⁺ and the protein.

Figure 3 plots the number of ions contained within the fictitious box as a function of the salt concentration. The solid and dashed lines show the expected number of ions as calculated by SLTCAP and AN, respectively. The simulation data is in good agreement with the SLTCAP simulation and is systematically lower than the AN method. This agreement is despite the fact that the simulation box was prepared using the AN method and the presence of specific cation-protein interactions that are not accounted for by our theory.

Figure 3.

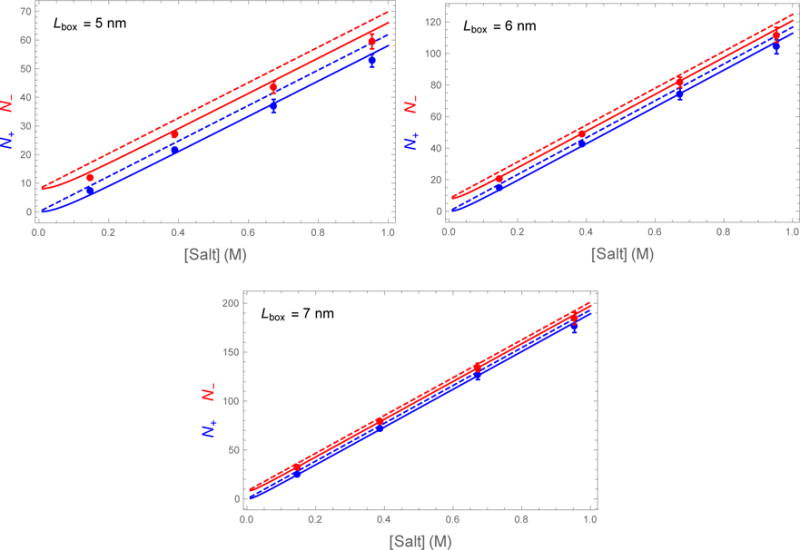
Number of Na⁺ (blue dots) and Cl⁻ (red dots) found within a fictitious box of width L_box centered on a lysozyme molecule of charge Q = +8. The observed number of ions is consistent with the SLTCAP calculation (solid lines) but is systematically lower than the AN method (dashed lines).

Figure 4 plots the number of entrained ions as a function of the fictitious box size. The agreement with SLTCAP is quite good over the plotted range of L_box/2 = 2.5-4.0 nm. For box sizes above ~5.0 nm the number of entrained ions approaches the AN result, which is a consequence of the fact that the simulations were prepared by AN. For smaller box sizes the number of entrained ions dips below the SLTCAP calculation, and even further below the AN method. The deviation is more pronounced at low salt concentration where the fictitious box passes inside the screening layer. In these cases charge neutrality is not enforced, which can be seen by the fact that the simulation values for N₋ and N₊ are closer together than the theoretical values from either SLTCAP or AN (which both enforce neutrality). For these small box sizes our simulations are not a good test of the theory because the large box size of 15 nm mimics dilute solution whereas the overlap of screening layers indicates the onset of the concentrated regime.

Figure 4.

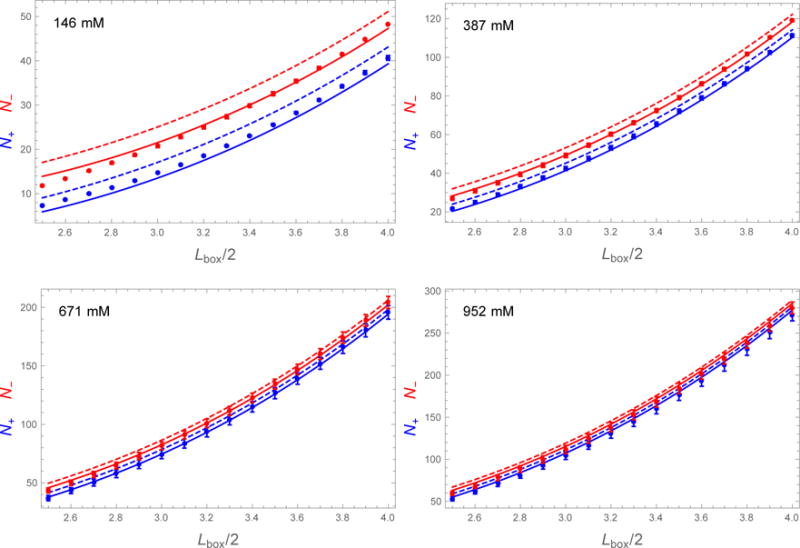
Number of Na⁺ (blue dots) and Cl⁻ (red dots) found within a fictitious box of width L_box centered on a lysozyme molecule of charge Q = +8. The SLTCAP and AN methods are shown in solid and dashed lines, respectively. The simulation data agrees well with the SLTCAP method except for a small amount of cation adsorption to the protein surface and the small and large box effects discussed in the text.

The charge neutrality requirement should be considered in light of the conditions that are intended to be replicated by the simulations. The periodic boundary conditions employed by most simulations effectively produce a system with a protein concentration $v_t^{-1}$. Usually this is much higher than the concentration of the system of interest. However, assuming the enhanced periodicity effects due to the use of PME are small, the absence of direct protein-protein interactions closely corresponds to the infinitely dilute protein solute case provided the solution is allowed to relax back to the bulk state between replicas. This relaxation is not possible for highly charged proteins because there is no place for the coions to escape from the protein environment. The SLT-CAP method allows the simulation to mimic dilute conditions by effectively allowing the ions to exchange with a large buffer reservoir.

When the system of interest is at high concentration, the correct handling of the ionic atmosphere is more complicated. If the solution is formed by dissolving a protein salt, the dissociated counterions from the protein will add to the buffer salt. This is the situation described by the AN method. However, if the system is allowed to exchange with an external buffer, either in a centrifugal concentrator or by dialysis, then SLTCAP becomes the correct description. Of course, the condition of greatest interest is in vivo. While this environment is highly crowded, it is better described by SLTCAP because the heterogenous environment allows for the depletion of coions near a charged solute.

In order to simulate a protein under conditions resembling dilute solution it is necessary that the potential is small near the edges of the box ϕ(x) ≪ k_BT/e ≃ 25 mV. Since the potential decays on a lengthscale set by the Debye screening parameter κ² ≡ 2e²c₀/(εk_BT), this condition can be approximated as $\overline{\varphi }{e}^{-\kappa L_{\text{buff}}}\ll 25\text{mV}$, where L_buff is the distance between the solute and the edge of the box and ε is the permittivity of water. In practice, a few nanometers is usually sufficient for L_buff since κ⁻¹ ≃ 1 nm for 100 mM salt.

We have established a web server that will rapidly perform SLTCAP calculations to facilitate the setup of molecular simulations.¹⁰ The server provides several methods for computing the solvent volume, either directly from the number of water molecules, or by estimating the solute volume using an average protein specific volume of 0.72 cm³/g and subtracting this from the box volume. This estimate of the protein volume will be adequate provided the volume error δv_p is smaller than $c_0^{-1}$. The server then outputs N₊, N₋, and $\overline{\varphi }$. Our hope is that this tool will lead to an improved representation of screening effects in biomolecule simulations.