Modeling Structure and Dynamics of Protein Complexes with SAXS Profiles

Abstract

Small-angle X-ray scattering (SAXS) is an increasingly common and useful technique for structural characterization of molecules in solution. A SAXS experiment determines the scattering intensity of a molecule as a function of spatial frequency, termed SAXS profile. SAXS profiles can be utilized in a variety of molecular modeling applications, such as comparing solution and crystal structures, structural characterization of flexible proteins, assembly of multi-protein complexes, and modeling of missing regions in the high-resolution structure. Here, we describe protocols for modeling atomic structures based on SAXS profiles. The first protocol is for comparing solution and crystal structures including modeling of missing regions and determination of the oligomeric state. The second protocol performs multi-state modeling by finding a set of conformations and their weights that fit the SAXS profile starting from a single-input structure. The third protocol is for protein-protein docking based on the SAXS profile of the complex. We describe the underlying software, followed by demonstrating their application on interleukin 33 (IL33) with its primary receptor ST2 and DNA ligase IV-XRCC4 complex.

1 Introduction

SAXS has become a widely used technique for structural characterization of molecules in solution [1]. A key strength of the technique is that it provides information about conformational and compositional states of the system in solution. Moreover, SAXS profiles can be rapidly collected for a variety of experimental conditions, such as ligand-bound and unbound protein samples, ligand titration series, different temperatures, or pH values [2]. The experiment is performed with ~15 µl of the sample at the concentration of ~1.0 mg/ml. It usually takes only a few minutes on a well-equipped synchrotron beam line [1, 3]. The SAXS profile of a macromolecule, I(q), is computed by subtracting the SAXS profile of the buffer from the SAXS profile of the macromolecule in the buffer. The profile can be converted into an approximate distribution of pairwise atomic distances of the macromolecule (i.e., the pair distribution function) via a Fourier transform. The challenge lies in data interpretation since the profiles provide rotationally, conformationally, and compositionally averaged information about protein solution conformation(s).

Computational approaches for modeling a macromolecular structure based on its SAXS profile can be classified based on the system representation into ab initio and atomic resolution modeling methods [4, 5]. On the one hand, the ab initio methods search for coarse three-dimensional shapes represented by dummy atoms (beads) that fit the experimental profile [6–8]. On the other hand, atomic resolution modeling approaches generally rely on an all atom representation to search for models that fit the computed SAXS profile to the experimental one [9]. Therefore, atomic resolution modeling can be used only if an approximate structure or a comparative model of the studied molecule or its components is available. With the increasing number of structures in the Protein Data Bank (PDB) [10] that can serve as templates for comparative modeling of a large number of sequences [11], we have focused our own efforts on atomic resolution modeling with SAXS profiles [12–17].

SAXS-based atomic modeling can be used in a wide range of applications, such as comparing solution and crystal structures, modeling of a perturbed conformation (e.g., modeling active conformation starting from non-active conformation), structural characterization of flexible proteins, assembly of multi-domain proteins starting from single-domain structures, assembly of multi-protein complexes, fold recognition and comparative modeling, modeling of missing regions in the high-resolution structure, and determination of biologically relevant states from the crystal [18–20]. Several software packages and web servers are available for some of these tasks, including ATSAS [21] and pyDockSAXS [22, 23]. Here, we describe how our tools can be used to facilitate addressing several of these questions (Fig. 1). Specifically, we describe three protocols for modeling atomic structures based on SAXS profiles. The first protocol is for comparing solution and crystal structures including comparative modeling and modeling of missing regions and determination of the oligomeric state. The second protocol is for multi-state modeling (finding a set of conformations and their corresponding weights that fit the data) based on the SAXS profile and single-input structure. The third protocol is for protein-protein docking based on the SAXS profile of the complex. We describe the underlying software, followed by demonstrating their application on interleukin 33 (IL33) with its primary receptor ST2 (BIOISIS ST2ILP) [24] and DNA ligase IV-XRCC4 complex.

Fig. 1.

Overview of the input and output of the three protocols: (a) comparing solution and crystal structures, (b) multi-state modeling, and (c) protein-protein docking

2 Materials

2.1 Software

The following software packages are used in the protocols described below:

1. Integrative Modeling Package (IMP)—a software package that includes SAXS module can be downloaded from http://salilab.org/imp/download.html and is available in binary form for most common machine types and operating systems; alternatively, it can be rebuilt from the source code; either the stable 2.7.0 release of IMP or a recent development version should be used. The code related to the protocols described here is mainly in the saxs, foxs, kinematics, multi_state, and integrative_docking IMP modules.

2. BILBOMD—a web server for multi-state modeling accessible from http://sibyls.als.lbl.gov/bilbomd.

3. PatchDock—a software for protein-protein docking can be downloaded from http://bioinfo3d.cs.tau.ac.il/PatchDock/.

4. MODELLER—a software for comparative modeling of protein structures can be downloaded from https://salilab.org/modeller/download_installation.html.

5. Gnuplot (http://www.gnuplot.info/) is used for plotting by the scripts provided with the examples used here.

The example files and scripts can be downloaded from https://modbase.compbio.ucsf.edu/foxs/mmb_files.zip.

3 Methods

3.1 Comparing Solution and Crystal Structures

Rapid and accurate computation of the SAXS profile of a given atomic structure and its comparison with the experimental profile is a basic component in any SAXS-based atomic modeling. FoXS is a program that is based on the IMP SAXS module that performs this task [13, 16]. The profiles are calculated using the Debye formula [25].

$$I(q)=\sum _{i=1}^N\sum _{j=1}^N{f}_i(q)f_j(q)\frac{\text{sin }\left({\mathit{\text{qd}}}_{\mathit{\text{ij}}}\right)}{{\mathit{\text{qd}}}_{\mathit{\text{ij}}}}$$ (1)

where the intensity, I(q), is a function of the momentum transfer q = (4π sin θ)/λ and where 2θ is the scattering angle and λ is the wavelength of the incident X-ray beam; f_i(q) is the atomic form factor, d_ij is the distance between atoms i and j, and N is the number of atoms in the molecule. In our model, the form factor f_i(q) takes into account the displaced solvent as well as the hydration layer:

$$f_i(q)=f_v(q)-c_1{f}_s(q)+c_2{s}_i{f}_w(q)$$ (2)

where f_v(q) is the atomic form factor in vacuo [26], f_s(q) is the form factor of the dummy atom that represents the displaced solvent [27], s_i is the fraction of solvent accessible surface of the atom i [28], and f_w(q) is the water form factor. The computed profile is fitted to the experimental data with adjustment of the excluded volume (c₁) and hydration layer density (c₂) parameters. The fit score is computed by minimizing the χ function with respect to c, c₁, and c₂:

$$\chi =\sqrt{\frac{1}{S}\sum _{i=1}^s{\left(\frac{I_{\text{exp}}(q_i)-\mathit{\text{cI }}(q_i,c_1,c_2)}{\sigma (q_i)}\right)}^2}$$ (3)

where I_exp(q) and I(q) are the experimental and computed profiles, respectively, σ(q) is the experimental error of the measured profile, S is the number of points in the profile, and c is the scale factor.

3.1.1 Inputs

The input to FoXS is one or more structure files in the PDB format and an experimental SAXS profile. The profile is specified in a text file with three columns: q in Å⁻¹ units, intensity I(q), and error σ(q)

# q           intensity     error
0.185480E−01  0.192175E+03  0.639769E+01
0.191560E−01  0.197885E+03  0.575226E+01
0.197640E−01  0.196492E+03  0.472259E+01

In addition, FoXS has several optional input parameters. Maximal q value determines the range for calculating the profile (default 0.5 Å⁻¹) and is controlled by –q option. The sampling resolution of the profile is controlled by the –s option that sets the number of points in the profile (default 500). The profile will be sampled at the resolution equal to the maximal q value divided by the number of profile points. For example, if the q_max value is 0.5 Å⁻¹ and the user asks for 1000 profile points, the resulting profile will be uniformly sampled at the interval of 0.0005 Å⁻¹. The range of fit parameters (c₁ and c₂) is controlled by --min_c1 (default 0.99), --max_c1 (default 1.05), and --min_c2 (default −2.00), --max_c2 (default 4.00) options. By default hydrogen atoms are considered implicitly, unless -h option is specified. FoXS supports residue-level coarse graining by specifying -r option. This option is recommended only for very big structures where atomic resolution calculation is not feasible. It is also possible to adjust the background of the experimental profile (-b option, disabled by default) and use a constant in profile fitting (-o option, disabled by default). It is possible to write the profile to file before it is summed up using c₁ and c₂ parameters (-p option, disabled by default). This profile file will have six columns with different contributions to the intensity, and it is used in multi-state modeling by MultiFoXS (below). Another useful option is -m, which specifies how to read PDB files with multiple models. By default FoXS reads the first model only (-m 1). Alternatively, each model can be read into a separate structure (-m 2) or all models into a single structure (-m 3). If -g is specified, FoXS will print a script file for display of the fit file in Gnuplot.

3.1.2 Running FoXS

Here, we compare the SAXS profile of the ST2-IL33 complex [24] to the crystal structure (PDB 4kc3) using default program options:

> foxs 4kc3.pdb complex.dat

3.1.3 FoXS Output

The output is the values of χ, c₁, and c₂ for the resulting fit:

4kc3.pdb complex.dat Chi = 3.26 c1 = 1.04 c2 = 4.0

The program also outputs two files: the computed SAXS profile file (4kc3.pdb.dat) and the fit file between the computed profile and the experimental one (4kc3_complex.dat). The format of the computed profile file is identical to the format of the input experimental file: three columns (q, I(q), σ(q)). The fit file contains four columns: q, experimental intensity, computed intensity, and the error of the experimental intensity:

#  q        exp_intensity    model_intensity error
0.01855     192.17500305     183.99343682    6.39769
0.01916     197.88499451     182.93727554    5.75226
0.01976     196.49200439     181.86241725    4.72259

The computed profile does not fit the experimental data within the noise (χ = 3.26). We hypothesized that the several loops and the C-terminal histidine tag that are unresolved in the crystal structure explain the difference (see Note 1).

3.1.4 Running MODELLER to Complete the Structure

We used MODELLER v9.8 [11] to add the missing fragments as follows. Two template structures were used: the ST2-IL33 complex (PDB 4kc3) and the IL33 structure (PDB 2kll). The additional IL33 structure was used since it does not have missing fragments. The corresponding MODELLER alignment file (fill. ali) and the script file (model_mult.py) are provided in the download zipfile. MODELLER v9.8 was run as follows:

> mod9.8 model_mult.py

After the models are generated, each candidate can be fitted to the experimental SAXS profile using FoXS (we repeat Part 2):

> foxs  st2_il33.B999900*.pdb  complex.dat
st2_il33.B99990001.pdb complex.dat Chi=1.88 c1=1.02 c2=4.0
st2_il33.B99990002.pdb complex.dat Chi=1.80 c1=1.03 c2=4.0
st2_il33.B99990003.pdb complex.dat Chi=1.61 c1=1.03 c2=4.0
st2_il33.B99990004.pdb complex.dat Chi=1.64 c1=1.03 c2=4.0
st2_il33.B99990005.pdb complex.dat Chi=1.53 c1=1.03 c2=4.0
st2_il33.B99990006.pdb complex.dat Chi=1.71 c1=1.03 c2=4.0
st2_il33.B99990007.pdb complex.dat Chi=1.85 c1=1.04 c2=3.4
st2_il33.B99990008.pdb complex.dat Chi=1.74 c1=1.03 c2=4.0
st2_il33.B99990009.pdb complex.dat Chi=1.83 c1=1.02 c2=4.0
st2_il33.B99990010.pdb complex.dat Chi=1.57 c1=1.03 c2=4.0

The resulting models have a significantly better fit than the crystal structure (1.5 < χ < 1.9), with the best χ value of 1.5 (Fig. 2a), which is within the experimental noise [29]. The fit plot along with the difference weighted by the error (Fig. 2a, Note 2) was generated from the fit files using plotFit.pl script (available in the zipfile scripts folder) that relies on Gnuplot:

> plotFit.pl 4kc3_complex.dat 2 x-ray
st2_il33.B99990005_complex.dat 3 model

Fig. 2.

Comparing solution and crystal structures: (a) ST2-IL33 complex and (b) ST2. The crystal structure is in red and the models with missing fragments added are in blue

The ST2 chain extracted from the crystal structure of the complex (PDB 4kc3, chain B) does not fit the experimental profile either (Fig. 2b, χ = 7.1). In this case, addition of missing atoms improved the fit only slightly (Fig. 2b, χ = 6.0), in contrast to the ST2-IL33 complex:

> foxs 4kc3B.pdb st2.pdb st2.dat
4kc3B.pdb st2.dat Chi = 7.1 c1 = 1.05 c2 = 4.0
st2.pdb st2.dat Chi = 6.0 c1 = 1.05 c2 = 4.0

We concluded that the ST2 solution structure is different from its crystal structure in complex with IL33. Therefore, we used multi-state modeling to sample the conformational space of ST2 and fit one or more conformations to the SAXS profile.

3.2 Multi-state Modeling

Multi-state modeling protocol addresses conformational heterogeneity in solution by relying on a SAXS profile. The input is a single atomic structure (or a comparative model), a list of flexible residues, and a SAXS profile for the protein. The protocol proceeds in three stages (Fig. 1b).

In the first stage, the conformations of the input structure are generated. We provide two methods for conformational sampling: RRTsample and BILBOMD. RRTsample explores the space of the φ and ψ main-chain dihedral angles of the user-defined flexible residues with a rapidly exploring random trees (RRTs) algorithm [30–33]. Since the sampling uses internal coordinates, the sampled structure cannot contain cycles and can work with linear or tree-like arrangements of rigid bodies. The RRT algorithm samples the conformational space by leveraging an iteratively constructed nearest-neighbor linked tree. This iterative strategy expands the tree toward unexplored regions of the conformational space and significantly improves the efficiency compared to random sampling. In contrast, BILBOMD works in Cartesian coordinates and is not limited to tree-like topologies of the input structure. In BILBOMD molecular dynamics (MD) simulation is used to explore the conformational space. A common strategy is to perform the MD simulation on the linkers between the domains at very high temperature, where the additional kinetic energy prevents the molecule from becoming trapped in a local minimum. The MD simulation or RRT-based sampling provides a pool of atomistic models for SAXS profile calculation and fitting to the experimental profile in the subsequent steps.

In the second stage, a SAXS profile is pre-calculated for each sampled conformation using FoXS. To avoid data overfitting, the method sets a single pair of free parameters (c₁ and c₂) for each multi-state model, rather than using a different pair for each conformation. Therefore, at this stage the different parts contributing to the profile intensity are pre-calculated without summing up using c₁ and c₂ parameters.

In the third stage, best-scoring multi-state models are enumerated using the multi-state scoring function and branch and bound combinatorial optimization. Given N input conformations and their computed SAXS profiles, we look for multi-state models (subsets of conformations and their weights) of size n (n << N), such that the corresponding sum of weighted SAXS profiles fits the experimental SAXS profile. The score of a multi-state model is:

$$\chi =\sqrt{\frac{1}{S}\sum _{i=1}^s{\left(\frac{I_{\text{exp}}(q_i)-c\sum _n{w}_n{I}_n(q_i,c_1,c_2)}{\sigma (q_i)}\right)}^2}$$ (4)

where I_n(q, c₁, c₂) and w_n are the computed profile and the corresponding weight, respectively, for each of the N states in the model; this equation minimizes data overfitting by using a single set of c₁ and c₂ values for all N states. In each “branch” step, we extend K (K = 10,000) best-scoring models of size n to KN models of size n + 1 by addition of each of the N input conformations. In the “bound” step, we select K best-scoring models out of the total KN models for the next iteration. Therefore, generation of K multi-state models of size n + 1 from K multi-state models of size n requires KN SAXS score calculations. This greedy approach avoids the exponential growth in scale of enumeration while still hopefully producing the best-scoring multi-state models.

This protocol is modular and can work with a different method for generating conformations, such as normal mode analysis [34, 35] and KGSrna for RNA molecules [36, 37]. We provide two examples for multi-state modeling protocol: ST2 models are generated with RRT-based sampling using IMP software, and human DNA ligase IV-XRCC4 complex models are generated by BILBOMD web server.

3.2.1 ST2 Multi-state Modeling with IMP

Inputs

The input to the multi-state modeling protocol is a structure file in the PDB format, a text file with the list of flexible residues, and an experimental SAXS profile. Flexible residues list specifies to the RRT-based sampling program which φ and ψ angle to sample. Those residues divide the input protein into rigid bodies and linkers. This list should contain linkers or hinge regions between the rigid protein domains. HingeProt [38] can be used to identify hinges automatically. Flexible loops should not be specified, as the program cannot handle cycles, the current implementation is limited to linear or tree-like topologies. The flexible residues file contains one residue per line, specified as residue index in the PDB file and chain identifier.

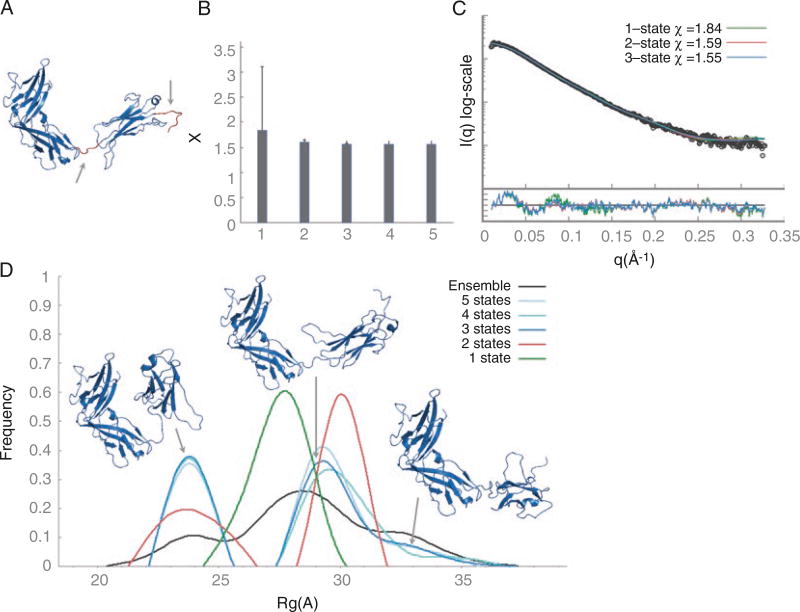
ST2 consists of three immunoglobulin-like domains (D1–D3). Based on the previous studies, we defined the linker between the D2 and D3 domains as flexible, as we did the C-terminal histidine tag (residues 203–208 and 318–327, respectively). The flexible residues (Fig. 3a) are defined using hinges.dat file:

203 B
204 B
...
208 B
318 B
...
327 B

Fig. 3.

ST2 multi-state modeling with IMP. (a) Flexible residues that were sampled by RRTsample are colored red. (b) The lowest χ value for N-state models (N = 1…5). (c) Fits between the experimental profile (black) and the best-scoring one-, two-, and three-state models (green, red, and blue, respectively). (d) R_g distribution of the best-scoring multi-state models

The whole protocol can be ran using runMultiFoXS.pl script as follows:

> runMultiFoXS.pl st2.pdb hinges.dat st2.dat -

Below we provide a step-by-step instruction with the goal to explain to the advanced user the various program options of each step.

Running RRT-Based Sampling

We run the conformational sampling program with the input PDB file and flexible residues file as follows:

> rrt_sample st2.pdb st2.dat –i 100000 –n 10000

The program continues to run until it performs the specified number of iterations (-i, default 100) or until it generates the specified number of conformations (-n, default 100). Here, we ask to generate 10,000 conformations (see Note 3). The program has several optional parameters. When a new node is added to the tree, a collision-free path is generated between the closest tree node and the new node by a linear interpolation between the sampled angles of the two nodes. The conformations of the path are very close to each other; as a result the program saves every tenth conformation by default. This number can be controlled with -p option. When the number of the sampled rotatable angles (degrees of freedom) is high (>30), it might be hard to find moves that allow changing all the degrees of freedom at once. Therefore, the program supports random selection of a smaller number of degrees of freedom to sample in each iteration (-a, default 0 -all degrees of freedom are sampled). When there are more than 15 flexible residues, it is recommended to set this number to 10. The radii scaling parameter is controlled by -s option (0.5 < s < 1.0). The sampling can start only from collision-free conformation. If decreasing the scaling parameter does not help, the structure has to be minimized to remove steric clashes (see Note 4). When sampling multi-chain structure, we often want to maintain the relative position of specific domains from different peptide chains as they are in the input structure by connecting them into a single rigid body. For example, this option is useful when a protein is a dimer where each monomer consists of two domains connected by a flexible linker and the first domain is the one involved in the dimerization, such as ATG7 (PDB 3vh1). In the ATG7 case, we want to maintain the dimerization interface intact and move only the N-terminal domains of each monomer. This is supported by -c option that receives a text file with a pair of residues one from each dimerization domain:

326 A 513 B

This will link two rigid bodies into a single one: the rigid body that residue 326 (chain A) belongs to and the rigid body that residue 513 (chain B) belongs to. Definition of two flexible linkers (between the N-terminal and C-terminal domains of each monomer) and one bridging region (for the dimerization domains) will result in three rigid bodies connected by two linkers (Fig. 4a). The same option also enables to maintain ligands position with respect to a protein by specifying an atom number from a ligand and from a protein. For example, to sample the structure of the calmodulin protein (PDB 1cll) with the calcium atoms, we will connect the four calcium atoms as follows:

1135	166
1136	420
1137	724
1138	1019

where 1135–1138 are the indexes of calcium atoms in the PDB file and 166, 420, 724, and 1019 are the indexes of the oxygen OD1 atoms in the aspartate residues that are closest to the calcium atom (Fig. 4b).

Fig. 4.

Defining rigid bodies for RRTsample. (a) Connecting two domains from two chains into a single rigid body (PDB 3vh1). After the lower domains are connected (rigid body 2), we obtain a linear topology with three rigid bodies connected by two linkers (blue). (b) The calcium atoms (green) in the calmodulin (ODB 1cll) are linked to the protein by creating a connection with one of the oxygen atom of the aspartate

The rrt_sample program writes the conformations into PDB files named nodesX.pdb. By default 100 conformations are written to each PDB file using MODEL/ENDMDL to separate between the conformations. This number can be modified by -m option.

Running SAXS Profile Calculation

Here, we run FoXS to pre-calculate the profiles as explained above (-p option). Since the sampled conformations are models in the PDB format files, we use -m 2 option to read each model into a separate structure:

> foxs -m 2 -p nodes[1–9].pdb nodes10.pdb

This will pre-calculate SAXS profiles for the first 1000 conformations and write them into nodesX_mY.pdb.dat files, where X is the number of the original PDB file and Y is the model number in this file (see Note 5).

Running Multi-state Models Enumeration

We prepare the experimental SAXS profile file (st2.dat) and a file with the names of pre-computed profiles from the previous step:

> ls nodes*.pdb.dat > filenames

and run multi-state enumeration as follows:

> multi_foxs st2.dat filenames --max_c2 4.0

There are several optional parameters accepted by the program. The maximal number of states is set with -s option (default 10). The number of good-scoring multi-state models retained in each “bound” step is set with -k option (default 1000). It is recommended to increase this number to 10,000 for a large number of input profiles (>10,000). The minimal weight for a conformation to be included in the multi-state model is set with -w option (default 5%). Prior to the enumeration of multi-state models, the program clusters the profiles based on similarity as measured by the χ score. The clustering threshold is set with -t option (default 0.3), and it is defined as the percentage of the χ score of the best-scoring conformation. For example, if the best-scoring conformation has a χ score of 2.0 when compared to the experimental profile, the default clustering threshold will be 0.6. We use the error bars from the experimental profile to ensure that the χ values are comparable. The maximal q value to consider in the experimental profile is set by -q option. The range of fit parameters (c₁ and c₂) is controlled by the same options as in FoXS, --min_c1 (default 0.99), --max_c1 (default 1.05), --min_c2 (default −0.5), and --max_c2 (default 2.00) with smaller range for c₂ parameter to avoid data overfitting. In the ST2 example, we increased the default c₂ range because we obtained c₂ value of 4.0 in the fit of the complex structure (Subheading 3.1.4).

Output Analysis

The generated ensembles of multi-state models are written into ensembles_size_X.txt files (X stands for the number of states) that are formatted as follows:

==> ensembles_size_1.txt <==
1 |  1.84 | ×1 1.84 (1.05, 4.00)
    0  | 1.00 (1.00, 1.00) | nodes80_m93.pdb.dat (0.001)
2 |  2.08 | ×1 2.08 (1.05, 4.00)
    1  | 1.00 (1.00, 1.00) | nodes63_m14.pdb.dat (0.001)
3 |  2.19 | ×1 2.19 (1.05, 4.00)
    2  | 1.00 (1.00, 1.00) | nodes72_m54.pdb.dat (0.001)
==> ensembles_size_2.txt <==
1 |  1.59 | ×1 1.59 (1.05, 4.00)
  212  | 0.73 (0.69, 0.08) | nodes81_m36.pdb.dat (0.053)
 1229  | 0.27 (0.29, 0.06) | nodes8_m76.pdb.dat (0.016)
2 |  1.59 | ×1 1.59 (1.05, 4.00)
  212  | 0.71 (0.69, 0.08) | nodes81_m36.pdb.dat (0.053)
 1112  | 0.29 (0.34, 0.05)  | nodes9_m78.pdb.dat (0.015)
==> ensembles_size_3.txt <==
1 |  1.55 | ×1 1.55 (1.05, 4.00)
  637  | 0.49 (0.47, 0.08) | nodes43_m93.pdb.dat (0.417)
 1270  | 0.36 (0.36, 0.04) | nodes98_m82.pdb.dat (0.399)
 1541  | 0.15 (0.16, 0.04) | nodes40_m34.pdb.dat (0.016)
...

The first line is a summary of scores and fit parameters for a multi-state model: the first column is a number/rank of the multi-state model (sorted by score), a χ value for the fit to SAXS profile, and a pair of c₁ and c₂ values (in brackets) that optimize the fit to data are in the third column. In the ST2 example above, the χ values of the best-scoring one-, two-, and three-state models are 1.84, 1.59, and 1.55, respectively. After the model summary line, the file contains information about the states (one line per state). For example, the best-scoring two-state model consists of conformation numbers 212 and 1229, with the weights of 0.73 and 0.27, respectively. The first conformation is model 36 in the nodes81.pdb file, and the second conformation is model 76 in the nodes8.pdb file. The numbers in brackets after the conformation weight are an average and a standard deviation of the weight calculated for this conformation across all good-scoring multi-state models of this size. The number in brackets after the filename is the fraction of good-scoring multi-state models that contain this conformation.

The program also outputs fit files (multi_state_model_X_Y_1. dat, where X is the number of states and Y is the number/rank of the multi-state model) between the weighted sum of profiles of the multi-state models and the experimental SAXS profile for the ten best-scoring models. The fit file is the same as in FoXS and contains four columns: q, experimental intensity, computed intensity, and the error of the experimental intensity.

Selecting the Representative Multi-state Models

Usually, the best explanation of the data is obtained by minimizing the number of conformations that resulted in the data (Occam’s razor principle). Therefore, we are looking at the minimal number of states that enables fitting the data within the noise. However, the program usually produces a large ensemble of multi-state models with the same number of states and equally good scores. The conformations belonging to these multi-state models are generally neither accurate nor precise, but they provide a general shape for representative states. We describe these conformations using more robust structural features, such as radius of gyration (R_g) and maximal distance (D_max). Next, we analyze the distribution of R_g values for the ensemble of good-scoring multi-state models to estimate the number of possible states [39]. The number of peaks in the R_g distribution is a lower-bound estimate on the number of states, and the width of the peak is indicative of the state precision [40].

We generate the R_g distribution as follows. First, we calculate the radius of gyration for all the sampled conformations:

> runRg.pl nodes?.pdb nodes??.pdb nodes???.pdb

Second, we generate the distribution for best-scoring N-state models (N = 1‥0.5) using plotHistograms.pl script:

> plotHistograms.pl 5 100 1.75

where 5 is the maximal number of states to consider, 100 is an ensemble size (the number of top-scoring multi-state models to analyze for each number of states), and 1.75 Å is a bin size in the R_g distribution. The output of the script is the R_g distribution plot (hist.png, Fig. 3d) and the χ values plot (chis.png, Fig. 3b). The χ values plot displays the χ values for the best-scoring N-state model (N = 1..0.5), where the error bar indicates the range of χ values for the top 100 multistate models. We can use plotFit.pl script to generate the fit plot for the top-scoring one-, two-, and three-state model as follows (the output is written to multi_state_model_1_1_1.eps file):

> plotFit.pl multi_state_model_1_1_1.dat 1 1-state
multi_state_model_2_1_1.dat 2 2-state multi_state_mod-
el_3_1_1.dat 3 3-state

For ST2 the χ value improved significantly even for a single-state model (χ = 1.8, Fig. 3b, c) compared to the crystal structure (χ = 6.0, Fig. 2b). The fit is even better with two- or three-state models (χ = 1.6), as expected. To estimate the number of states in solution, we examined the R_g distribution (Fig. 3d). The R_g distribution in the initial pool of 10,000 conformations is almost uniform (black line). The top-scoring one-state models (green line) have R_g in the range of 25–30 Å. The R_g distribution of the two-state models (red line) has two peaks: one corresponding to closed conformations at 21–26.5 Å and the other corresponding to open conformations at 28–32 Å. For three-state models (blue line), the R_g distribution has three peaks: the first peak at 22–25.5 Å overlaps with the closed conformations peak of two-state models, the second peak at 27–31 Å corresponds to open conformations that are similar to the IL33 binding conformation in the crystal structure, and the third low-frequency peak at 32–36 Å represents structures that are more open than the crystal structure. For models with four or five states, we observe three peaks overlapping with the peaks of the three-state models. Therefore, based on multi-state modeling results, we can conclude that ST2 exists in multiple states in solution, corresponding to a wide range of open and closed conformations (see Note 6). Upon IL33 binding, there is a population shift to the IL33 binding conformation.

3.2.2 DNA Ligase IV-XRCC4 Multi-state Modeling with BILBOMD

BILBOMD is a stand-alone web server that performs all the multi-state modeling stages: conformational sampling, SAXS profile calculation, and multi-state models enumeration (Fig. 5). The conformational sampling is based on the minimal molecular dynamics (MD) simulation using CHARMM version 40b [41]. SAXS profile calculation and enumeration of multi-state models use FoXS [16] and MultiFoXS [17] programs, respectively. The entire protocol is fully automated and does not require user interaction.

Fig. 5.

DNA ligase IV-XRCC4 multi-state modeling with BILBOMD. (a) Web server input page. (b) Screenshot of the server interface for rigid bodies definitions (“Create const.inp File” option) for DNA ligase IV-XRCC4 complex, including visualization with circles and lines. (c) The initial model colored as the domain selections in the panel B. Flexible linkers are colored red. (d) R_g vs. D_max plot derived from foxs_rg.out output file with values for top-scoring one-state, two-state, and three-state models. (e) Fits between the experimental profile (black) and the best-scoring one- and two-state models (red and green, respectively). (f) Conformations of the top-scoring two-state model and their corresponding weights

Inputs

BILBOMD web server accepts the following inputs (Fig. 5a):

1. Protein initial model in the PDB format where each peptide chain is uploaded as a separate segment/file.

2. A text file const.inp that defines rigid bodies and the connections of segments to maintain complex architecture.

3. Experimental SAXS profile file in a three-column format as in FoXS.

4. R_g min and R_g max values in Å for restraining the movement extent in the conformational sampling. A maximum of ten parallel simulations will be started in the range defined by these values.

5. Extent of conformational sampling that determines the number of conformers that will be generated for each R_g value.

6. An email address the results will be sent to.

We used BILBOMD web server to model solution state of the multi-protein complex human DNA ligase IV-XRCC4 (LigIV) [42]. LigIV is composed of N-terminal DNA-binding and catalytic domains connected by a long linker (50 residues) to the C-terminal tandem BRCT domain that interacts directly with the coiled-coil stalk domain of XRCC4 [43]. XRCC4 also contains long unfolded C-terminal regions (~120 residues) (Fig. 5c). The initial atomistic model was built by comparative modeling of the LigIV N-terminal consisting of DNA-binding domain (DBD), the nucleotidyltransferase domain (NTD), and OB-fold domain (OBD). Structures of the homologous human DNA ligases I [44] (PDB 1×9n) and III [45] (PDB 3l2p) were used as templates. The N-terminal domains model was connected to the crystal structure of XRCC4-BRCT [43] (PDB 3ii6) via addition of the flexible linker regions in between the catalytic core domains of LigIV and the tandem BRCT domain by MODELLER v9.8 [11]. MODELLER was also used to add the partially unfolded C-terminal regions of XRCC4.

BILBOMD input PDB files are the individual peptide chains of the complex corresponding to three segments. In our case segments 1 and 2 are the two chains of the XRCC4 dimer. Segment 3 is the DNA ligase IV chain containing DBD, NTD, OBD, and BRCT domains. Definition of rigid bodies is required for conformational sampling and can be done by clicking on “Create const.inp File” button on the BILBOMD input page (Fig. 5a). Rigid bodies are defined by selecting a relevant residue range in each segment (Fig. 5b). Residues that do not belong to rigid bodies are defined as the flexible regions for the MD simulations. In the XRCC4-BRCT complex, we would like to maintain the XRCC4 dimer interface and the XRCC4-BRCT interface (the XRCC4-BRCT crystal structure [43], PDB 3ii6) as one rigid body during MD simulation. Therefore, we group residues 1–210 from segments 1 and 2 (the XRCC4 dimer) and residues 611–833 from segment 3 (BRCT domain) into a single rigid body (Fig. 5b, domain 1 box). We also define rigid bodies for DBD, NTD, and OBD domains (Fig. 5b, domains 2–4) and a few shorter fragments in the XRCC4 dimer (Fig. 5b, domains 5–8). The server automatically creates a visualization of the rigid bodies and flexible regions. The rigid bodies are displayed as circles with the circle size proportional to the number of residues, while the flexible regions are shown as lines that connect to the circles (Fig. 5a, b). The definitions are written to the const.inp file:

define fixed1 sele (resid 1:210 .and. segid 1) end
define fixed2 sele (resid 1:210 .and. segid 2) end
define fixed3 sele (resid 611:883 .and. segid 3) end
cons fix sele fixed1 .or. fixed2 .or. fixed3 end
shape desc dock1 rigid sele  (resid 1:219 .and.  segid 3) end
shape desc dock2 rigid sele (resid 226:421 .and. segid 3) end
shape desc dock3 rigid sele (resid 428:574 .and. segid 3) end
shape desc dock4 rigid sele (resid 260:279 .and. segid  1) end
shape desc dock5 rigid sele (resid 260:279 .and. segid 2) end
shape desc dock6 rigid sele (resid 315:331 .and. segid 1) end
shape desc dock7 rigid sele (resid 315:331 .and. segid 2) end
return

where the fixed1, fixed2, and fixed3 define rigid domains of XRCC4 dimer (segid 1 and 2) and BRCT domain in LigIV (segid 3). These domains are connected into a single rigid body by cons fix command for maintaining their position during MD simulation. dock1–3 define the three rigid bodies of DBD, NTD, and OBD in the DNA ligase IV (segid 3). dock4–7 define small rigid regions in XRCC4 C-terminus (segid 1 and 2) (Fig. 5b, c). The user can also upload a revised const.inp file from a previous BILBOMD run.

Once the rigid bodies are defined, we submit additional inputs required by the server: the experimental SAXS profile, R_g min = 30 Å and R_g max = 90 Å values, the extent of the conformational sampling (800 conformations per R_g), and an email address (Fig. 5a).

BILBOMD Run

In the first phase, BILBOMD performs minimization of the entire model to eliminate steric clashes and optimize bond length and angles. This minimization enables to upload input structures with imperfect chain connectivity that may be present due to manual modeling of loops or linkers. In the second phase, the linkers connecting the defined rigid bodies are heated up to 1500 K. In the production phase, a maximum of ten parallel MD simulations are initiated at the various R_g increments within the R_g min and R_g max range (see movie in the ligase folder). One conformer for each simulation (corresponding to a specific R_g) is recorded every 0.5 ps. The length of the simulations is determined by the “Extend of conformational sampling” input parameter with the option to record up to 800 conformers (400 ps) per simulation. The final trajectory files are split into PDB format files with one conformer, out_X_Y_Z.pdb, where X corresponds to the R_g value, Y is a simulation step, and Z is the time in simulation. Next, BILBOMD pre-computes SAXS profiles for all the conformers using FoXS and enumerates multi-state models using MultiFoXS (see Subheading 3.2.1 on ST2 multi-state modeling, Parts 3–5).

BILBOMD Outputs

Top-scoring multi-state models for 1–5 states are delivered by email. Additional output includes foxs_rg.out file with the list of R_g and maximal dimension (D_max) values for all generated models. Plotting R_g vs. D_max values and its comparison to the selected models enables additional visualization and validation of the conformational space of the multi-state models (Fig. 5d).

In the LigIV example, the χ values of the best-scoring one-, two-, and three-state models are 2.15, 1.19, and 1.05, respectively. The best-scoring two-state model consists of conformer 30_1_24500 and 90_4_398500, with the weights of 0.61 and 0.39, respectively. This model has a significantly better fit to the experimental data in comparison to the best-scoring one-state model (Fig. 5e). These two states are derived from the simulation restrained by R_g values of 30 Å and 90 Å and were recorded at the time step 24,500 and 398,500, respectively (Fig. 5f).

3.3 Protein-Protein Docking

While many structures of single-protein components are increasingly available, structural characterization of their complexes remains challenging. Methods for modeling assembly structures from individual components frequently suffer from large errors, due to protein flexibility and inaccurate scoring functions. SAXS profile of the complex can significantly improve the success rate of protein-protein docking [14, 15]. The input to protein-protein docking protocol is the structures of the docked proteins in the PDB format and a SAXS profile of their complex. The protocol proceeds in three stages (Fig. 1c).

In the first stage, the proteins are docked using PatchDock, which is an efficient rigid-docking method that maximizes geometric shape complementarity [46, 47]. Protein flexibility is accounted for by a geometric shape complementarity scoring function, which allows for a small amount of steric clashes at the interface. The configurational sampling precision can be controlled by the resolution of the surface representation (i.e., the minimal distance between surface points used to generate docking models) and clustering parameters (see Note 7).

In the second stage, a SAXS profile is calculated for each docking model and is compared to the experimental SAXS profile using FoXS. It is possible that the complex sample in the SAXS experiment contained a mixture of monomers and complexes. Therefore, the SAXS scoring can optionally rely on a multi-state weighted scoring function (Eq. 4). This option is extremely useful for docking of transient complexes.

In the third stage, combined SAXS and statistical potential (SOAP-PP) [48] scores are calculated. To calculate the combined score, SAXS χ scores and statistical potential scores are normalized with respect to all the docking models. The combined score is the sum of the normalized Z-scores. The normalization of the scores allows us to avoid the use of weights for the terms of the combined score.

3.3.1 Inputs

The input to the protocol is two structure files in the PDB format and an experimental SAXS profile of the complex. Here, we will use the ST2 model with missing residues added (PDB 4kc3), the IL33 NMR structure (PDB 2kll), and the SAXS profile of the ST2-IL33 complex.

3.3.2 Docking

We can run all the steps of the protocol using idock IMP script as follows:

> idock st2.pdb 2kll.pdb --saxs complex.dat --patch_
dock patch_dock_path

The script accepts several optional parameters. The sampling precision of PatchDock (see Note 7) can be controlled by --precision option (1, normal; 2, medium; and 3, high precision). The usage of multi-state scoring function that accounts for monomer contributions is controlled by the --weighted_saxs_score option (default = False). There is a special parameter set for docking antibody-antigen and enzyme-inhibitor complexes (--complex_type AA or EI; see Note 8).

3.3.3 Results

The output file results_saxs_soap.txt is a list of complex models computed via rigid docking sorted by a combined SAXS and statistical potential scores:

# | Score |fil| ZScore| saxs | Zscore| soap     |
Zscore |  Transformation
1 | −5.72  | + | −3.93 | 1.68 | −1.71 | −2765.39 |
−4.006 |  0.69 0.53 −2.03 45.73 −41.86 16.25
2 | −5.61  | + | −3.85 | 1.43 | −1.81 | −2616.54 |
−3.794 |  0.69 0.09 −2.00 43.54 −41.20 16.74
3 | −4.67  | + | −3.21 | 1.55 | −1.76 | −1997.67 |
−2.910 |  −0.98 −0.76 3.10 55.82 −33.84 −4.72
4 | −4.66  | + | −3.20 | 1.39 | −1.83 | −1942.27 |
−2.831 |  0.33 0.31 −1.77 47.94 −42.51 17.87
5 | −4.64  | + | −3.19 | 1.94 | −1.62 | −2076.15 |
−3.022 |  0.52 0.47 −2.09 48.75 −41.56 15.09

Each line corresponds to one docking model; the models are ranked by the total score, best first (second column). The individual SAXS and SOAP-PP score/z-score pairs are also shown (columns 5–6 and 7–8, for SAXS and SOAP-PP, respectively). The last column is a transformation (three rotation angles and a translation vector) that transforms the second protein relative to the first (the first molecule is kept fixed).

To generate the output PDB files, we use PathDock transOutput.pl script that takes as an input the output file and a range of docking models ranks, applies the transformation on the second molecule, and produces complex files. To generate top ten models, we run the script as follows:

> patch_dock_path/transOutput.pl results_saxs_soap.txt
1 10

The ST2-IL33 example illustrates the benefit of docking restrained by a SAXS profile: the model with the best combined SAXS and energy score has a relatively low interface-RMSD from the crystal structure of 3.5 Å (Fig. 6a), while the model ranked as top scoring by the SAXS score alone has a much larger interface-RMSD of 18.2 Å. The model ranked as fourth has even higher accuracy with interface-RMSD of 1.7 Å (Fig. 6b).

Fig. 6.

Protein-protein docking. (a) Superposition (according to ST2) between the top-scoring model (green) and the crystal structure (red). (b) Superposition (according to ST2) between the top fourth scoring model (green) and the crystal structure (red). The fit between the model and the SAXS profile of the complex is below

4 Conclusion

The three protocols presented here facilitate the use of SAXS data in a variety of molecular modeling applications, such as comparing solution and crystal structures, structural characterization of flexible proteins, assembly of multi-protein complexes, and modeling of missing regions in the high-resolution structure. Atomic resolution representation of the modeled system provides strong constraints on possible solutions consistent with SAXS data, thus making SAXS-based modeling helpful for characterizing biomolecular systems. To maximize the accuracy of the predictions, the protocols rely on: (1) scoring functions for fitting multi-state models with single set of fitting parameters to reduce data overfitting, (2) efficient deterministic approach for enumeration of multiple states, and (3) advanced methods for exhaustive sampling of conformations and complexes. The SAXS-based modeling of the ST2-IL33 and DNA ligase IV-XRCC4 complexes provided an illustration of the protocols usage. The protocols are also available as web services [17] from http://salilab.org/foxs, http://salilab.org/multifoxs, http://salilab.org/foxsdock, and http://sibyls.als.lbl.gov/bilbomd.