Characterization of X-ray scattering for various phantoms and clinical breast geometries using breast CT on a dedicated hybrid system

Abstract

OBJECTIVE

The purpose of this study was to utilize a dedicated breast CT system using a 2D beam stop array to physically evaluate the scatter to primary ratios (SPRs) of different geometric phantoms and prospectively acquired clinical patient data.

METHODS

Including clinically unrealizable compositions of 100% glandular and 100% fat, projection images were acquired using three geometrically different phantoms filled with fluids simulating breast tissue. The beam stop array method was used for measuring scatter in projection space, and creating the scatter corrected primary images. 2D SPRs were calculated. Additionally, a new figure of merit, the 3D normalized scatter contribution (NSC) volumes were calculated.

RESULTS

The 2D SPR values (0.52–1.10) were primarily dependent on phantom geometry; a secondary dependence was due to their uniform density; 2D SPRs were low frequency and smoothly varying in the uniformly filled phantoms. SPRs of clinical patient data followed similar trends as phantoms, but with noticeable deviations and high frequency components due to the heterogeneous distribution of glandular tissue. The maximum measured patient 2D SPRs were all <0.6, even for the largest diameter breast. These results demonstrate modest scatter components with changing object geometries and densities; the 3D NSC volumes with higher frequency components help visualize scatter distribution throughout the reconstructed image volumes. Furthermore, the SPRs in the heterogeneous clinical breast cases were underestimated by the equivalent density, uniformly filled phantoms.

CONCLUSIONS

These results provide guidance on the use of uniformly distributed density and differently shaped phantoms when considering simulations. They also clearly demonstrate that results from patients can vary considerably from 2D SPRs of uniformly simulated phantoms.

1. Introduction

Due to the gaining popularity of dedicated breast CT over the past few years, various studies have investigated the effect of scatter radiation in breast imaging with cone beam CT systems [1–12], and various methods have been proposed to reduce as well as correct for signals arising from scatter radiation [13–24]. The purpose of this particular study is to characterize the scatter-to-primary ratios (SPR) for cone beam breast CT for a range of (breast) densities in the typical 2D format [3, 24]. This will be accomplished by examining phantoms and prospectively acquired human clinical cases. A secondary objective was to develop a metric to quantify the effectiveness of the scatter correction method using the 3D data obtained from the full CT scan. For this research, we use the quasi-monochromatic cone beam x-ray CT sub-system of a dual modality dedicated breast SPECT-CT scanner developed in our lab [24–27]. The beam stop array (BSA) method for estimating scatter has been well established [16, 22, 23, 28–30] and is used in this study. In a clinical setting, acquiring a second BSA scan is not feasible due to the extra x-ray exposure to the patients. However, we have previously shown that comparable image quality [24, 28] can be achieved by using only 6 additional BSA projection images, which would translate to <2.5 % additional dose to the patients, and is therefore clinically acceptable in this research.

The material density range used for this study includes very low densities, below the clinically unrealizable extreme of 100% fat, up to the clinically unrealizable extreme of 100% glandular breast compositions. Often in the literature, a single regular geometrical object, usually a cylinder, is used to determine 2D SPRs as a measure of the system performance and object scatter characteristics that need correction [1–3, 7]. However, these simple cylindrical geometries do not adequately represent the intersection of the incident 3D cone beam with the spectrum of complex geometrical shapes posed by various pendant breast geometries, nor the subsequent x-ray interactions modulated by these complex shapes. By starting with two simple geometrical shapes containing varying densities of uniform fluid, and additionally evaluating an anthropomorphically shaped breast phantom, we can better understand the impact of size, shape and density, on scatter correction, and ultimately quantification accuracy in dedicated breast CT. These shapes allow for straightforward and intuitive evaluations of SPR as well as quantitative characterizations of the target volumes with cone beam imaging. Use of the anthropomorphic breast phantom better approximates what would be expected to be encountered clinically. By varying the overall phantom shapes and filled densities, we can characterize the effect that both geometrical degradation factors and object composition will have on the SPR in dedicated cone beam breast CT. The same measurement techniques were used while acquiring clinical data under an IRB approved study. Comparing the human breast SPRs with those phantom results can also corroborate the accuracy of the overall scatter correction technique.

Furthermore, a new metric is introduced in this study, the 3D normalized scatter contribution (NSC), which allows us to visualize and quantify the contribution of scatter to the reconstructed attenuation coefficients in every voxel of a volume. This figure of merit also allows the testing of the uniformity of the employed scatter correction method under different phantom and clinical conditions.

2. Methods

2.1. Object density variation

Various uniform liquid mixtures were used for simulating different breast densities; we have previously shown that mineral oil and distilled water serve as excellent limits on simulated breast tissue in the lab [28, 31]. Uniform materials, such as liquids, will allow interrogation of systematic errors in the acquisition, correction and reconstruction processes that may otherwise be hidden by high frequency data such as in a real human breast. Since nuclear medicine tracer compounds to be used in dual-modality SPECT-CT (or PET-CT) imaging are generally not miscible in oil, we evaluated readily accessible methanol as a water soluble, low density liquid candidate (Table 1). Aqueous mixtures with methanol are also usable for emission radioactive measurements in the breast background when using the SPECT component of our dual-modality dedicated breast imaging system.

Table 1.

Water-Methanol concentrations, calculated densities (g/cm³) and corresponding mass attenuation coefficient values at 36 keV. Glandular and Adipose tissue densities and mass attenuation coefficients reported by and extrapolated from Johns and Yaffe [35]

Water (%)	Methanol (%)	Density (g/cm3)	Scatter Component	Photoelectric Component (cm2/g)	Total Mass Attenuation Coefficient (cm2/g)	Linear Attenuation Coefficient (cm−1)
100	0	1.00	0.218	0.080	0.298	0.298
67	33	0.93	0.217	0.072	0.289	0.269
50	50	0.896	0.217	0.068	0.285	0.256
33	67	0.861	0.216	0.065	0.281	0.242
0	100	0.791	0.216	0.057	0.273	0.216
Glandular Tissue		1.035	–	–	0.291	0.301
Adipose Tissue		0.928	–	–	0.246	0.228

The mean energy of the quasi-monochromatic cone beam used in our system is 36 keV [32]. The attenuation coefficients for water and methanol standards were obtained from the NIST photon cross sections database [33], whereas the values for breast tissue were obtained from previously published data by Johns and Yaffe [34].

Since glandular tissue (ρ = 1.035 g/cm³) has a linear attenuation coefficient of 0.301 cm⁻¹ and fatty tissue (ρ = 0.928 g/cm³) has a linear attenuation coefficient of 0.228 cm⁻¹ at 36 keV, we used water (ρ = 1.00 g/cm³) which has a linear attenuation coefficient of 0.298 cm⁻¹ and methanol (ρ = 0.79 g/cm³) with a linear attenuation coefficient of 0.216 cm⁻¹, as surrogates for simulating a range of attenuation coefficients which include the clinically unrealizable boundaries of 100% glandular and 100% fatty breast tissue (Table 1).

Since methanol and water are easily miscible, varying mixture concentrations of the aqueous fluids can be used to simulate breast densities with varying uniform glandular/fatty compositions (Table 1). The aqueous nature of methanol also makes it easier to clean the phantoms without leaving traces of prior media for subsequent data acquisitions. One caveat is that care must be taken while selecting phantoms for use in experiments since some types of plastic react poorly to prolonged methanol exposure. The use of fluids to simulate various breast density compositions has been proposed in our previous work [36] and more recently validated by other groups [37].

2.2. Phantoms, CT sub-system and BSA

For this study, we utilized two geometric phantoms (cylindrical and conical) as two extreme breast shapes often used in computer simulation modeling, as well as an anthropomorphic breast phantom developed for us [31] (Radiology Support Devices, Newport Beach, CA). This phantom combines features from both geometric phantoms, but is more realistic (Fig. 1). Our previous work has shown that the average breast volume encountered clinically is approximately 740 mL [38]. Therefore, each phantom was filled in turn with 700 mL of varying concentrations of water and methanol to simulate the effective attenuation coefficients and densities spanning a range that includes 100% glandular to below 100% fatty (Table 1). The details of the phantoms used are listed in Table 2. Not only do the geometric phantoms represent a wide range of shapes that are expected to be encountered, but precisely varying the overall filled-volume densities allows us to control both geometric degradative factors in cone beam CT as well as simulated uniform breast composition.

Fig. 1.

Photographs of a suspended cylinder (LEFT), cone (CENTER) and anthropomorphic breast (RIGHT) phantom arrangement near the iso-center of the cone beam CT sub-system.

Table 2.

Compositional details, diameters and heights of phantoms used, after being filled with 700 mL of fluid. Density of the phantom material and linear attenuation coefficients at 36 keV are also provided

Phantom	Diameter (cm)	Wall Thickness (cm)	Height (cm)	Material	Material Density (g/cm3)	Linear Attenuation Coefficient (cm−1)
Cylinder	13	0.1	5.7	Acrylic	1.19	0.302
Cone	3–20	0.3	10	Polyethylene	0.93	0.227
Anthropomorphic Breast	15 (max)	0.05	7	Polyethylene terephthalate	1.38	0.345

Experiments were conducted with the CT sub-system of the dual-modality dedicated breast SPECT-CT scanner [24, 27, 39]. The phantoms were positioned at the iso-center of the cone beam CT imaging system (Fig. 1). The CT component uses a rotating tungsten target x-ray source (model Rad-94, Varian Medical Systems, Salt Lake City, UT) with a 0.4 mm nominal focal spot size and 14^◦ anode angle, irradiating a 25 × 20 cm² FOV CsI(T1)-based amorphous silicon flat panel digital x-ray detector (model Paxscan 2520, Varian Medical Systems, Salt Lake City, UT) with a grid size of 1920 × 1536 pixels and 127 m pixels. A custom-built collimator was attached to the x-ray source to hold the ultra-thick K-edge beam shaping filters to produce a quasi-monochromatic beam [32]. For these studies, a 60 kVp x-ray beam with a 1.25 mAs exposure per projection and a 0.051 cm cerium filter (Z = 58, ρ = 6.77 g/cm³, K-edge = 40.4 keV, Santoku America, Inc., Tolleson, AZ) were used. This filter yielded an energy spectrum that had a mean energy of approximately 36 keV and the full-width at half-maximum of 15%. The source-to-image distance (SID) was 60 cm and source-to-object distance (SOD) was 38 cm resulting in a magnification of 1.57 for an object located at the center of rotation of the system. A total of 360 exposures were acquired over the complete 360-degree azimuthal scan.

Each phantom was suspended into the field-of-view simulating a pendant breast, and projections were collected with and without a beam stop array [24] (BSA). The BSA used was a 9.5 × 9.5 cm² and 5 mm thick acrylic plate that consisted of 130 lead balls, each having 2.0 mm diameters, and spaced 5.0 mm apart on a Cartesian grid. An acrylic plate, with or without beads was placed in front of the collimator (~15 cm from the x-ray source). In our previous work [24, 28], we reported on the method used for scatter correction and the algorithm to determine the scatter distribution using the BSA. That work demonstrated that we could obtain linear attenuation coefficients of a variety of known materials to within 8% [28] of narrow beam NIST attenuation values [33]. 360 BSA projections were acquired over the complete 360-degree azimuthal scan of the phantoms.

2.3. 2D Scatter-to-primary ratio calculations

A 2D scatter distribution for each projection was estimated by cubic spline interpolating the measured average values found behind the shadow of each beam stop within the boundaries of the object. However, an extra row or column of beads just outside the phantom was used in the scatter approximation to account for beads partially inside or outside the boundary of the object, and to get an accurate scatter measurement at the edges. Scatter images, containing only a mask of the object, are subtracted from the original corresponding projections to obtain the final scatter-corrected projections (see ahead to Fig. 2). For this study, we were interested in the 2D scatter distribution within the projection images and its subsequent effect on the 3D reconstructed object volume. Scattered photons deposited outside the phantom do not affect the intrinsic attenuation coefficient values of the object density and therefore do not need to be corrected. Hence, the projections were cropped at the fluid level surface to remove the air gap and disregard any scatter arising above and away from the volume density under consideration. That region corresponds to the anterior chest wall in pendant breast CT which could cause scatter, but would not otherwise be directly irradiated during clinical imaging.

Fig. 2.

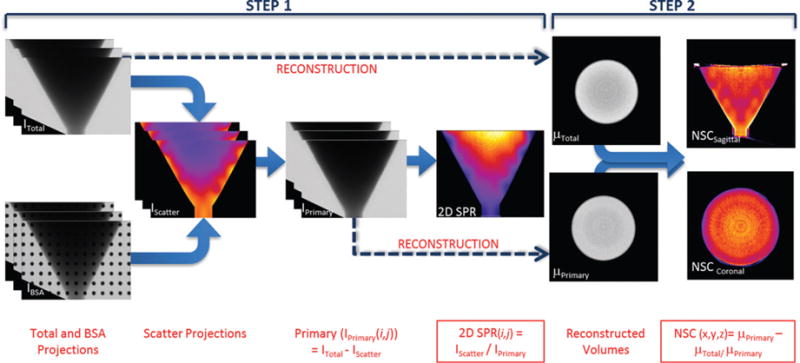
Flowchart showing steps to obtain the 2D SPR and NSC: STEP 1 - Use projections with and without BSA to calculate scatter; STEP 2 - Use projections to reconstruct Total and Primary volumes and then calculate the 3D NSC volume. Note that the wedge seen in the lower left of the projection images in Step 1 is the shadow of the SPECT camera in the dual modality SPECT-CT system.

The Scatter-to-Primary Ratio (SPR) is defined as the ratio of the scatter signal to the primary signal. In projection image space, this can be obtained as follows:

$${\mathrm{I}}_{\text{i,j}}^{\text{Total}}={\mathrm{I}}_{\text{i,j}}^{\text{Scatter}}+{\mathrm{I}}_{\text{i,j}}^{\text{Primary}}$$ (i)

$$2\text{DSPR}(\text{i,j})=\frac{{\mathrm{I}}_{\text{i,j}}^{\text{Scatter}}}{{\mathrm{I}}_{\text{i,j}}^{\text{Primary}}}$$ (ii)

$$2\text{DSPR}(\text{i,j})=\frac{{\mathrm{I}}_{\text{i,j}}^{\text{Scatter}}}{{\mathrm{I}}_{\text{i,j}}^{\text{Total}}{\text{-I}}_{\text{i,j}}^{\text{Scatter}}}$$ (iii)

where, $I_{i,j}^{\mathit{Total}}\to$ the photon intensity of un-corrected ‘total’ projection measured at the (i, j)th detector pixel, $I_{i,j}^{\mathit{Scatter}}\to$ the photon intensity of ‘scatter’ projection image, at (i, j)th detector pixel (from interpolation), $I_{i,j}^{\mathit{Primary}}\to$ the photon intensity of ‘primary’ projection image, at (i, j)th detector pixel obtained from equation (i), and $2DSP{R}_{(i,j)}\to$ the 2D Scatter-to-Primary ratio calculated for the (i, j)th detector pixel.

2.4. Volumetric reconstruction and normalized scatter contribution

Volumetric reconstructions were performed using a ray-driven ordered subsets convex algorithm [40] which provided an estimate of the non-uniform attenuation distribution of the object. Reconstruction parameters were set to 5 iterations, 16 subsets, 350 × 350 × 400 reconstruction grid, and 508 m voxel sizes. The scatter corrected and un-corrected data were individually reconstructed to give us total and primary image volumes (see ahead to Fig. 2). The algorithm reconstructs the photon intensities from the projection images to yield images of total attenuation coefficients.

When an x-ray photon scatters from a point in the target volume and is incident on the detector, all spatial information is lost. In this configuration, there is no physical way to locate the origin of a scattered particle from within the target volume without the use of other techniques, e.g. coded apertures [41, 42] or energy sensitive detectors. For a scattered photon detected at a pixel (i,j) on the detector, the reconstruction algorithm would trace it back along the cone beam, towards the x-ray source, consequently mis-registering the detected scatter photon at a certain voxel (x,y,z) in the center of the volume. This phenomenon is one of the major causes of cupping artifacts in cone beam CT images. Practically, the precise location of the scatter interaction within a volume is of less importance than the effect that the scattered photon would have on the final reconstructed images. By using the 2D scatter estimate from projection image, it is in fact possible to determine this effect of scatter on the reconstructed attenuation coefficients in each voxel. To evaluate this effect, a new metric was developed – the Normalized Scatter Contribution (NSC) – which quantifies the effect of scatter on reconstructed attenuation coefficients. The difference between the individually reconstructed “total” and “primary” image volumes is a 3D voxelized measure of the contribution of scatter to the reconstructed 3D attenuation coefficients. Normalizing this value allows comparison of the effect of scatter contribution on attenuation coefficients, between reconstructed objects of different size, shape and material composition. The NSC metric can be formulated as follows:

$$NS{C}_{(\text{x,y,z})}=\frac{{\mu }_{\mathit{primary}(x,y,z)}-{\mu }_{\mathit{Total}(x,y,z)}}{{\mu }_{\mathit{primary}(x,y,z)}}$$ (iv)

where, μ_{Primary(x,y,z)} and μ_Total(x,y,z) are the reconstructed attenuation coefficients at each (x,y,z) voxel of the primary and total volumes respectively, and NSC_(x,y,z) is the relative contribution of scattered photons to the attenuation coefficients at each (x,y,z) voxel. Using the conical phantom as the example, the flowchart in Fig. 2 shows the individual steps taken to arrive at the final 2D SPR and 3D scatter contribution values.

2.5. SPR and NSC dependence on density

The phantom experiments were performed with 5 different uniform background densities (Table 1). To evaluate the change in scatter to primary ratios and their subsequent effect on reconstructed attenuation coefficients with changing densities, we measured the peak SPR value for the 2D SPR projection images and average NSC for the 3D NSC volumes. The comparative measurements of peak SPR and average NSC were made at a constant 13 cm diameter across all phantom geometries and various uniform fluid densities. Profiles were measured at a 13 cm fixed diameter and fitted with a first order Gaussian curve to measure the peak SPR value. These profile values were plotted against fluid density for each phantom configuration. The average NSC values were measured using a circular ROI on a coronal slice through the volume, and similarly plotted against density.

2.6. Clinical patient studies

As a part of a Duke IRB approved clinical study (IRB pro00026702), patients undergoing diagnostic parathyroid imaging exams at Duke University hospital were approached to take part in our breast imaging study. Between their routine scintigraphy and SPECT scans, seven (7) consented volunteers were scanned using our dual modality SPECT–CT system. Patients were marked with dual modality ^99mTc-soaked nylon bead fiducial markers (5 mm diameter) prior to the scan. 240 CT projections were acquired over 360 degrees followed by 6 equally distributed BSA projections. The 6 additional BSA projection images were performed with the same technique as the CT projection images. Thus, there is <2.5% additional cumulative dose delivered to each patient, since the beads block a portion of the breast in each exposure. Note that the overall dose to each subject is still within 2/3 that of the MQSA limit on dual-view mammography [43, 44]. The complete CT scan and 6 BSA scatter projection measurements took approximately 8 minutes, excluding patient set-up. The CT was immediately followed by a 15-minute SPECT scan using the previously injected clinical dose of ^99mTc-sestamibi, which is part of the volunteers’ routine clinical imaging procedure.

Cubic spline interpolation was performed on the 6 BSA projections to obtain 240 BSA projections corresponding to each projection angle [28]. In phantoms, we have shown that this method is equivalent to collecting BSA measurements at all projection angles for scatter correction. The data were then scatter corrected and the 2D SPR and 3D NSC volumes were calculated using Eqnation (ii) and (iii). Scatter correction using the BSA method requires one major assumption: that the object being scanned does not move between the acquisition of projections with and without BSA. This is very difficult to achieve with human patients undergoing 8-minute-long CT scans. Therefore, the data with major motion artifacts could not be used for accurate SPR measurements. Even retrospective registration yielded inaccurate edge alignment given the 2-dimensional projection magnification and torsion of the breast. In some cases, the subject’s breast size was larger than the projection onto the field of view of the 20 × 25 cm² detector, which yielded a truncated breast. Therefore, only 3 data sets were rendered viable (motion and truncation free) for scatter measurements and SPR calculations.

The scatter corrected data were then reconstructed and segmented based on their attenuation coefficients using a previously published segmentation algorithm [45, 46]. The skin was removed from all breast volumes and a histogram of the attenuation coefficients was plotted. A dual Gaussian function was fitted to the image histogram, and using the minimum point as threshold, the volume was segmented into glandular and adipose tissue components. Density of the breast volume (minus skin) was calculated based on the weighted ratio of tissue percentages and actual density values of glandular (1.035 g/cm³) and adipose tissue (0.928 g/cm³) (Table 3). The peak 2D SPR was also measured, as explained above, and was plotted against density. Comparative peak SPR measurements were made at approximately similar radii, since exact radius measurements were unattainable due to the large variation in subjects’ breast sizes.

Table 3.

Percent glandular & adipose tissue and estimated whole breast densities (g/cm³) for the 3 subjects

	Glandular (%)	Adipose (%)	Density (g/cm3)
Subject 1	52	48	0.981
Subject 2	40	60	0.969
Subject 3	21	79	0.949

3. Results

3.1. 2D Scatter-to-primary ratio

The profiles through 2D SPR images are measured at 4 indicated locations over each projection (Fig. 3). A threshold was applied to all images in order to exclude the values outside the breast. Gradually decreasing towards the edges, SPR values peak centrally in all of these uniform phantoms. Minor irregularities (distortions in the images) are due to spline interpolation around the blocking spheres used in the BSA. Vertical profiles show that SPR values decrease as we move from the chest to the nipple, except in the cylinder case which has a uniform thickness (diameter) along its length.

Fig. 3.

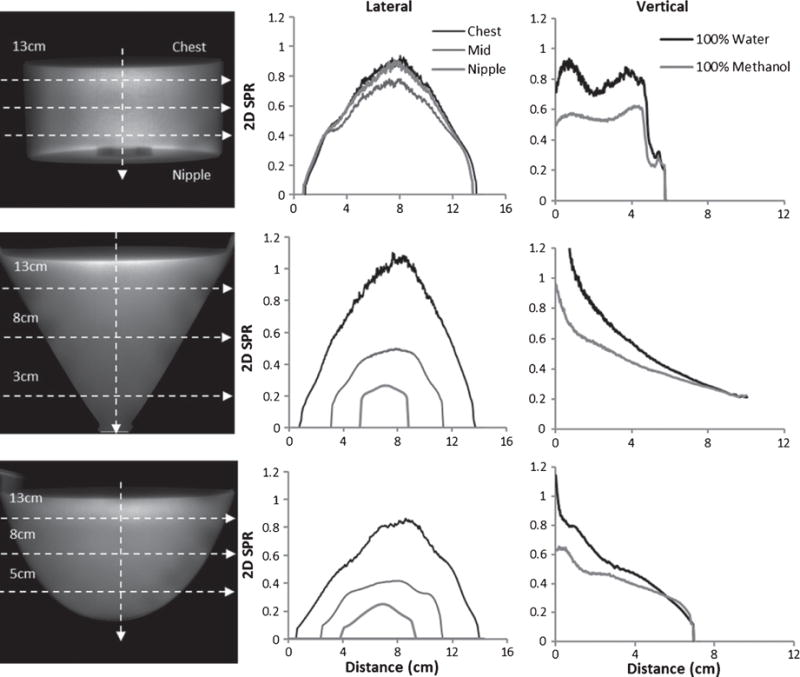
(LEFT COLUMN) Calculated 2D projection SPRs from each 100% water phantom with uniformly spaced horizontal profile locations indicated by dotted lines. Diameters of the phantoms at the profile locations are also indicated. (CENTER COLUMN) Horizontal 2D SPR profiles through the CHEST, MIDDLE and NIPPLE of the 100% water case, and (RIGHT COLUMN) comparison of vertical 2D SPR profiles of 100% Water and 100% Methanol for the (TOP) Cylinder, (MIDDLE) Cone and (BOTTOM) Anthropomorphic Breast phantoms. In these uniformly filled phantoms, SPR values are highest (White) at the center and gradually reduce (gray) laterally; they also decrease with phantom diameter.

The cylinder phantom was a compact disk (CD) storage case which comprised a slight air protrusion into the phantom at the bottom near the “nipple” region. This cylinder was the only symmetric phantom tested, and so it is no surprise that the values at the ends are nearly identical. A comparison of 100% methanol and 100% water-filled phantoms reveals that water yields the higher SPR, irrespective of phantom geometry (Fig. 3), at the widest diameter. While not explicitly illustrated here, the 2D SPR profile results from the other intermediate density phantoms fall uniformly between the methanol and water bounds (see ahead to Fig. 8, left).

Fig. 8.

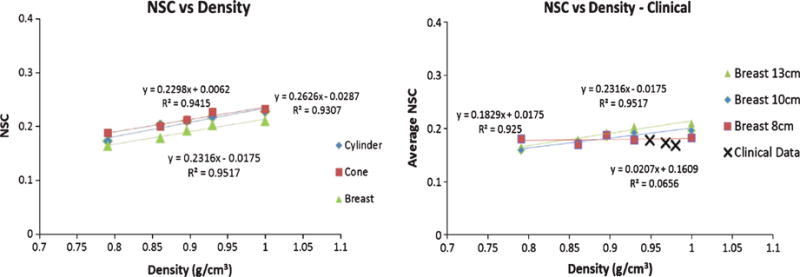
Average NSC vs. Density plots for (LEFT) the three geometric phantoms, and (RIGHT) the three clinical subjects with various breast phantom values as a reference. Abcissa corresponds to the simulated water-methanol densities and calculated patient breast densities. The geometric phantom values were all obtained at a constant diameter of 13 cm. Note that the phantoms contained material densities uniformly distributed in the volumes, but the patient breasts did not.

3.2. Normalized Scatter Contribution (NSC) volumes

The NSC volumes were calculated from Eqn (iii) with the individually reconstructed image volumes. Sagittal slices of the calculated NSC volumes for cylinder, cone and breast phantoms are shown in Fig. 4. The measured profiles clearly show the non-uniformity introduced in the volume due to the scatter correction process. Slightly elevated NSC values can be observed near the nipple region, which corresponds to smaller diameter regions for the cone and breast phantoms; not surprisingly, the uniform diameter cylinder phantom serves as an exception to decreased NSC in the nipple region. The increase in NSC values for smaller diameter slices, near the nipple region, is clearer from the plotted vertical profiles (Fig. 4, right). For the cone phantom, in order to prevent fluid leaks a silicone stopper was used to plug the bottom end of the cone. This stopper may also affect the amount of scatter near the nipple region.

Fig. 4.

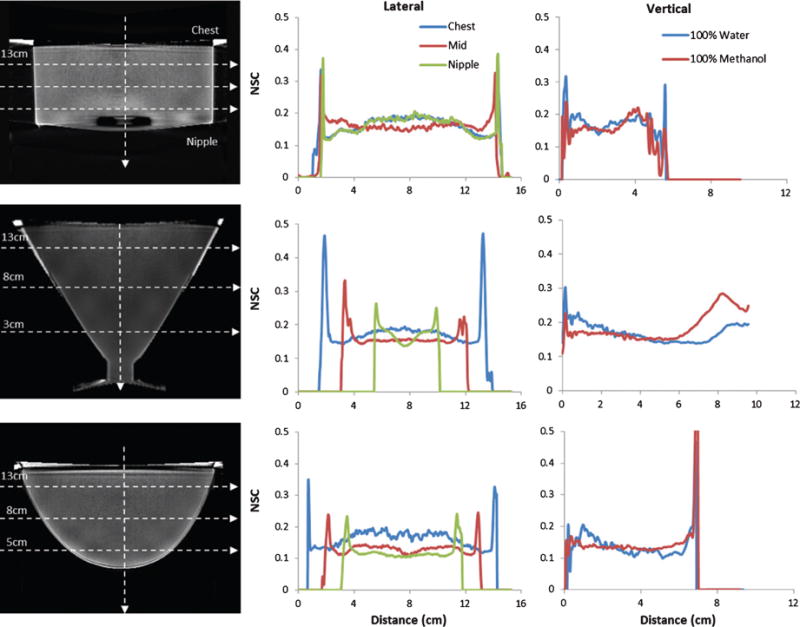
(LEFT COLUMN) Calculated NSC from reconstructions of each 100% water phantom with uniformly spaced horizontal profile locations indicated by dotted lines. Diameters of the phantoms at the profile locations are also indicated. (CENTER COLUMN) Horizontal NSC profiles through the CHEST, MIDDLE and NIPPLE of the 100% water case, and (RIGHT COLUMN) Vertical NSC profiles the of 100% Water case for the (TOP) Cylinder, (MIDDLE) Cone and (BOTTOM) Anthropomorphic Breast phantoms. NSC values decrease with phantom diameter.

As explained earlier, the BSA scatter correction algorithm uses an edge detection process to limit the scatter estimate within the target volume. This edge detection process in some cases results in the mislabeling of a few pixels outside the target volume, as the edge of the phantom. These edge artifacts are evident from Fig. 4 (middle). On reconstruction, this pseudo edge has a very low attenuation coefficient; after performing mathematical operations of equation (iv) for creation of NSC volumes, the difference and ratio of small numbers results in extremely large values at the edges. These spikes are evident from the illustrated line profiles, especially for the cone phantom due to its thicker (5 mm) phantom wall (Fig. 4). This effect is most evident in the clinical data (see ahead to Fig. 6) where edge detection errors are higher around the nipple, resulting in high NSC values around the nipple region.

Fig. 6.

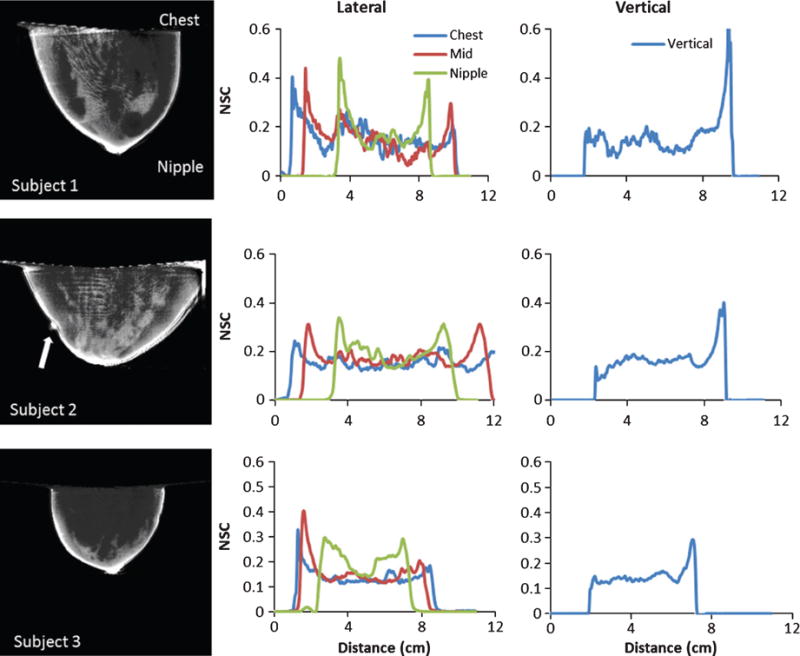
(LEFT COLUMN) Central sagittal slices through calculated NSC volumes for subjects. (CENTER COLUMN) Horizontal NSC profiles through the CHEST, MIDDLE and NIPPLE regions, and (RIGHT COLUMN) vertical NSC profiles measured from the CHEST to NIPPLE. Note that due to the presence of a chest wall, the bright artifact near the chest is absent for the patient data. For Patient 2, the external fiducial marker lateral to the breast is evident (indicated by white arrow).

Some noticeable artifacts in the regions of these slices include: (1) increased intensity at the fluid–air interface (near the top of the image) of the uniform phantoms; most likely due to the continuous presence of tissue (chest wall), this artifact is absent in the clinical data (see ahead to Fig. 8); [2] due to spline interpolation of the BSA beads, high and low intensity ridges near the edges of the phantoms; and [3] also due to the cubic spline interpolation around the BSA beads in the middle of the phantom, smoothly varying concentric patterns (uniformity bands).

3.3. Clinical patient studies

Similar to the uniform phantom studies, the SPR profiles through 2D SPR patient images are measured at 4 indicated locations over each projection (Fig. 5). SPR values peak centrally in all images, and gradually decrease towards the edges. Vertical profiles show that SPR values decrease as we move from the chest to the nipple, which is expected as the amount of breast tissue closer to the chest wall is higher than at the nipple. An asymmetric SPR is also observed throughout the breast, corresponding to the heterogeneous and asymmetrical glandular density distribution in each subject.

Fig. 5.

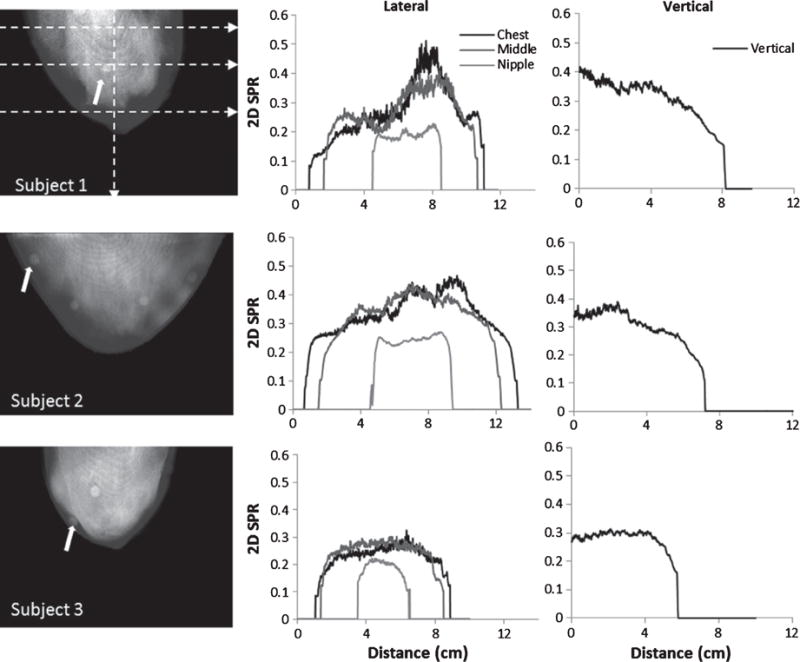
(LEFT COLUMN) Calculated 2D SPRs from projections of each subject’s breast with uniformly spaced horizontal profile locations indicated by dotted lines. Circular regions within the breast boundaries (at arrow tips and elsewhere) are due to the fiducial markers taped to the outside of each patient’s breast. (CENTER COLUMN) Horizontal 2D SPR profiles through the CHEST, MIDDLE and NIPPLE regions, and (RIGHT COLUMN) vertical 2D SPR profiles measured from the CHEST to NIPPLE. SPR values are highest (White) in the most glandular breast regions, and reduce (gray) in regions of more adipose tissue.

The NSC volumes (Fig. 6) were created similarly to the phantom images. Due to the presence of continuous tissue near the chest wall above the breast, the bright artifact seen at the fluid air interface in the phantoms is not visible in any of the patient data. However, low frequency variations within the volume and the dark and light ridges near the edges of the breast are evident. In addition, there are minimal motion artifacts between projection and BSA scans.

3.4. SPR and NSC vs. Density

Based on these SPR measurements for all phantoms and conditions, we illustrate the trend in the measured peak 2D SPR vs. density at a constant diameter of 13 cm in each phantom (Fig. 7). As the image data illustrated earlier (Fig. 3), SPR values for water and methanol form the boundaries of the peak values in the uniform phantoms, and the SPR peaks for all other background concentrations lie within these bounds (Fig. 7). Not surprisingly, the geometry of the phantom seems to affect the peak SPR values, where the more breast-like the phantom, the lower the overall SPR for a given density.

Fig. 7.

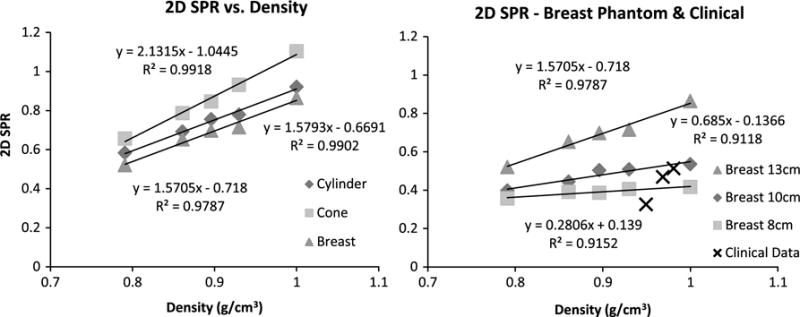
2D Peak SPR vs. Density plots, where the abcissa corresponds to the simulated water-methanol densities and calculated patient breast densities (LEFT). For the three uniformly filled geometric phantoms, these are the overall highest peak values. (RIGHT) Various uniform breast phantom values, measured at the indicated diameters and densities as a reference, are plotted with the peak SPRs of the three clinical subjects.

Figure 7 (right) also shows a comparative plot of peak SPR vs. density for clinical patient data and the breast phantom peak SPRs re-measured at appropriate diameters – 10, 13 and 8 cm for more accurate comparison with subjects 1, 2 and 3, respectively. With only these 3 patients, and the added high variability of the peak SPR within any single profile location due to the non-uniform and heterogeneous density distribution throughout the breast(s) (see Fig. 5), it is hard to draw a conclusion of change in SPR with density in the patient cohort. Otherwise, the plot shows reasonable alignment of patient data with phantom results. Patient SPR values increase with density, however, more samples would be required to obtain suitable error bars.

Average NSC values were measured on coronal slices of the reconstructed volumes, at a fixed 13 cm diameter, and are illustrated in Fig. 8. Results show that the fractional contribution of scatter to attenuation coefficients is between ~15–22% for all phantoms and simulated densities. Based on the fact that uniform 2D SPR varies linearly with density, in addition to object shape and size, the NSC values are expected to depend on the density of the target material. To that effect, the NSC values seem to linearly increase with increasing density (Fig. 8); linear fits reveal an R² of >0.93.

4. Discussion

The measured 2D SPR with different uniform geometries and background densities are consistent with our and others’ previous measurements and simulations. Kwan et al. [1] have explored dependence of SPR on x-ray beam energy and have previously reported peak 2D SPR values of ~0.5 for a 50% glandular – 50% fatty, 14 cm diameter cylindrical uniform phantom using a 60kVp tungsten x-ray spectrum. Chen et al. [2] in their investigation of SPR dependence on breast size and x-ray energy, have also reported values of ~0.8 for a 14 cm diameter simulated breast at the same uniform density and energy using Monte Carlo simulations in GATE. For a comparable cylindrical phantom of 13 cm diameter, filled with 33% methanol – 67% water (similar in attenuation coefficient to the 50-50 glandular-fatty case) we measured peak SPR values of ~0.78, with our quasi-monochromatic 36 keV mean-energy (60 kVp) x-ray spectrum. It is important to note that for the beam stop method, Kwan et al. [1] used a 2.9 mm steel plate and Chen et al. [2] used a 2 mm lead strip to estimate scatter in the center of the phantom volume which corresponded to a few rows of pixels on the detector. Our measurements were made with 2.0 mm diameter lead beads (130 beads embedded in a 5.0 mm acrylic plate), allowing measurements of 3D scatter throughout the 2D projection image. This 2D BSA array permits us to investigate differences in scatter at different locations in the phantoms due to a cone beam x-ray source (Fig. 3). Thus, our systematic measurements of various uniformly filled fluid geometries, with a quasi-monochromatic beam, in addition to estimation of the entire 2D scatter distribution on projection images fundamentally distinguishes this study from past investigations of 2D SPR.

Furthermore, we used a comprehensive set of phantom geometries to measure the SPRs because the intersection of the x-ray CT cone beam source with the 3D object is different in each case. These different geometries potentially give rise to variations in measured SPRs with location throughout the phantoms. The resultant variations are most clearly illustrated in the results where the cone phantom shows higher SPR values than the cylindrical or breast phantom (Figs. 3, 4). To normalize the effect of the different intersections of the cone beam with the object, SPR values are measured in the resultant images at the same object radius irrespective of geometry. However, the height (between nipple and chest wall) at which the 3D x-ray cone beam intersected the different geometrical objects varied somewhat in each case, thereby potentially causing a variation in SPR with measured location. This was unintentional from the measurement set-up point of view. While specific SPR values differ due to differences in geometrical shapes and especially object densities, the 2D SPR trends obtained are consistent: (1) SPR values are peaked in the central regions of uniform objects, and decrease peripherally; this is a low frequency phenomenon seen in [2]; (2) SPR values reduce with decreasing object size; (3) the changing SPRs vary smoothly for all geometrical shapes. Apart from this, the thickness, shape and density of the phantom material also play roles in the SPR distributions. The cone phantom with 5 mm thick polyethylene edge shows higher SPR at the edges than the acrylic cylinder and polyester terephthalate breast phantoms, which only have a ~1 mm edge. Spline interpolation errors, also lead to some distortions in our 2D SPR images, which are otherwise fairly easy to read through. Despite interpolation errors, the BSA scatter correction method reconstructed provides attenuation coefficients within 8% of reported NIST values [30]. Better spline interpolation in the future should eliminate these distortions.

Scatter is a 3D effect such that it affects the imaged object throughout its volume. Therefore, only measuring the 2D SPR for an object is not completely accurate. The scatter propagated to the reconstructed voxels in the 3D space can also be investigated. Monte Carlo simulations are one way of investigating this effect. Otherwise, until now, measurements have not allowed determination of the origin of a scattered photon within a target volume with physical experiments. It is, however, possible to determine the effect of scatter on the reconstructed attenuation coefficients, in each voxel, by using a new metric – the 3D normalized scatter contribution (NSC). We introduce this figure of merit here, which quantifies the effect of scatter on reconstructed attenuation coefficients. Unlike the 2D SPR which has low frequency phenomena [2], this 3D NSC measurement appears to have more high frequency components (Figs. 4 and 6). The NSC metric helps visualize the uniformity of the correction method employed, and as a consequence of the scatter correction, can tease out subsequent artifacts left behind in the scatter-corrected primary volume. These artifacts would otherwise be difficult to discern in a clinical breast due to the presence of a heterogeneously distributed fibroglandularity (Fig. 6), vasculature and other breast components.

The NSC, calculated as the normalized difference between the un-corrected and scatter corrected reconstructions of the target object, shows three dominant features in the scanned phantoms: (1) a bright high-frequency band near the fluid-air interface; this is most likely due to a combination of insufficient cone beam sampling at that edge, and the fact that the interface is insufficiently detected as an edge during the BSA scatter measurement; these two factors yield over estimated scatter there, and subsequently increased SPR values. Additionally, (2) bright and dark sphere-like distortions along the cone and breast phantom edges are seen; this is likely due to the longer diagonal distance between two lead BSA beads on the tapering edges of the phantoms, resulting in discrepancies in the spline interpolation. And finally, (3) a smoothly varying low frequency pattern in the images, due to inaccurate cubic spline interpolation. Vertical profiles measured across the images clearly show artifact (1) in the form of spikes; however, it is important to note that in the clinical data, this artifact is absent due to the presence of continuous tissue (i.e. chest wall) posterior to the breast. Minor motion blur is also present and could detrimentally couple with these other artifacts, though less likely since scatter is predominantly a low frequency phenomenon. These artifacts reveal shortcomings of the employed BSA correction method and demonstrate the need for an additional step to correct for these inaccuracies in the future. Two corrections could include decreased acquisition time, and use of collimated rays [18] instead of blocker beads.

The patient data 2D SPR results generally mimic the phantom results. The data in Fig. 7 show that the peak SPR values obtained from the clinical data align reasonably well with peak SPR values obtained from the breast phantom data measured at similar diameters. However, for the 3 patient data sets, there is an observable dependence of SPR on the distribution of breast tissue glandularity (and other obvious features, such as the fiducial markers) (Fig. 5). Overall, the density distributions in the patients are heterogeneous and not nearly as uniform as the fluid filled phantoms. Thus, there is a larger variability in the non-uniform patient SPRs, indicating that a straightforward patient-to-phantom diameter-and-density comparison cannot be easily be made. Even if we determine the average SPR profile-located breast density (which may be different from the entire breast volume density), the peak patient SPR value will be dominated by the densest part of the tissue, and therefore not be directly comparable to the uniformly dense phantom values.

One caveat of using the BSA method for clinical studies is the assumption that the target volume does not move between the data collection with and without BSA. Although this necessity limits the amount of artifact free data suitable for scatter estimation, it can easily be overcome by reduction in scan times and optimization of the system being used. Current CT scan time for the clinical protocol is ~8 minutes on our system which is primarily due to hardware limitations and implementation of the serial acquisition software. Optimization of the acquisition software has already reduced scan times to ~3 minutes on the current version of the SPECT-CT system [47]. With hardware upgrades and better use of parallel processing capabilities of the acquisition system, the scan time can be further reduced to less than 1 minute. The truncation artifacts resulting from large patient breast sizes and a small FOV detector will potentially be remedied by the use of a large FOV 40 × 30 cm² active area flat panel detector which has already been installed on the system [48]. Therefore, the larger FOV coupled with reduced CT scan times paves the way for the BSA scatter correction method to be more efficiently used clinically.

5. Conclusions

Two-dimensional SPR evaluations were undertaken and compared using various breast CT-appropriate geometrical phantoms containing different uniformly filled densities; there was also SPR evaluation of prospectively acquired clinical breast CT data sets. In addition, a Normalized Scatter Contribution figure of merit was derived which characterizes the scatter contribution to 3D reconstructed volumes after scatter correction. Based on the SPR results from both geometric phantoms and human studies, we conclude that the SPR appears to strongly depend on object geometry, then density (as a surrogate for attenuation coefficients) and density distribution in 3D. Our measured results corroborate previous Monte Carlo assessment [2]. The 2D SPR increases with increasing glandular density in an object, and also with increasing radius; generally higher SPRs are found at the chest wall region of the posterior breast, and lower overall values nearer the nipple. Additionally, with the help of NSC volumes, we derived a method to estimate the scatter in each individual reconstructed voxel and additionally visualized minor, albeit visible inconsistencies due to the BSA scatter correction method introduced into the scatter-corrected volumes. The phantom results characterize the 2D SPR values and the NSC in detail for a broad range of uniform object densities and shapes. The clinical imaging results similarly characterized the changes for different sized breasts and densities, clearly indicating a higher SPR in the more glandular breast regions. Additionally, these systematic phantom results are a step towards providing guidance on how to correct scatter effects when making clinical measurements without actual measured scatter correction, but just using the measured attenuation of the breast itself.