Color opponency: tutorial

Abstract

In dialogue, two color scientists introduce the topic of color opponency, as seen from the viewpoints of color appearance (psychophysics) and measurement of nerve cell responses (physiology). Points of difference as well as points of convergence between these viewpoints are explained. Key experiments from the psychophysical and physiological literature are covered in detail to help readers from these two broad fields understand each other’s work.

Steve: The OSA would like to publish a tutorial chapter on color opponency, and I thought we could do it together, Paul. After all, I am a psychophysicist interested in color appearance, and you are a physiologist interested in how the brain processes color. It’s clear that opponency is an important topic for both of us.

Paul: That sounds like a great idea, Steve, but as you know we see the topic from very different angles. For you, opponency is about the color that various lights appear to humans. But for me, opponency is how nerve cells respond to light of different wavelengths.

Steve: Well then, let’s see how our perspectives compare, and find out where the points of difference lie. After all, opponent-color theory has been controversial since Ewald Hering proposed it in 1874 [1,2]. Hering and another giant of German physiology, Herman von Helmholtz, had fierce disagreements about it, both scientific and philosophical [2]. The controversy continued long after they died, but we now know that each of their theories captures a fundamental aspect of the human visual system. Let’s plow ahead, aiming for an equally happy coexistence of our perspectives, and hopefully within our lifetimes.

Paul: First, please tell me about the controversy.

Steve: Let’s begin with some context. The dominant theory of color vision in the mid-19th century was based on the trichromatic theory of Young (1802) [3,4]. Young’s theory posits three types of photoreceptors that signal the percepts red, green, and blue (or violet). Other hues, according to the Young theory, are mixtures of these three primaries. Young’s theory was championed by Helmholtz [5] in his 1860 edition of the Handbuch der physiologischen Optik (Treatise on Physiological Optics) [6]. Helmholtz was professor of physiology at the University of Heidelberg, and already was renowned for inventing the ophthalmoscope about a decade earlier, so his opinion carried weight. He made extensive and incisive use of Young’s three-receptor theory, so much so that it became known as the Young–Helmholtz trichromatic theory, and was broadly accepted.

Hering was completing his medical training at the University of Leipzig when Helmholtz published his Handbuch. But by 1874, Hering was himself established as professor of physiology at the German-speaking University of Prague. Here, he developed a new theory of color vision. Hering introduced the idea of four unique hues, each of which is a psychological primary perceived as a single pure color. His four unique hues are red, yellow, green, and blue. Unique yellow, for example, is a pure yellow without any tinge of redness toward orange, or of greenness toward lime green. The unique hues are “primary” in the sense that no unique hue can be described as a combination of the others. Orange, for example, cannot be a fifth unique hue because it can be described as a combination of red and yellow.

Paul: That all makes sense to me so far. Where does the opponent idea fit into this psychological scheme?

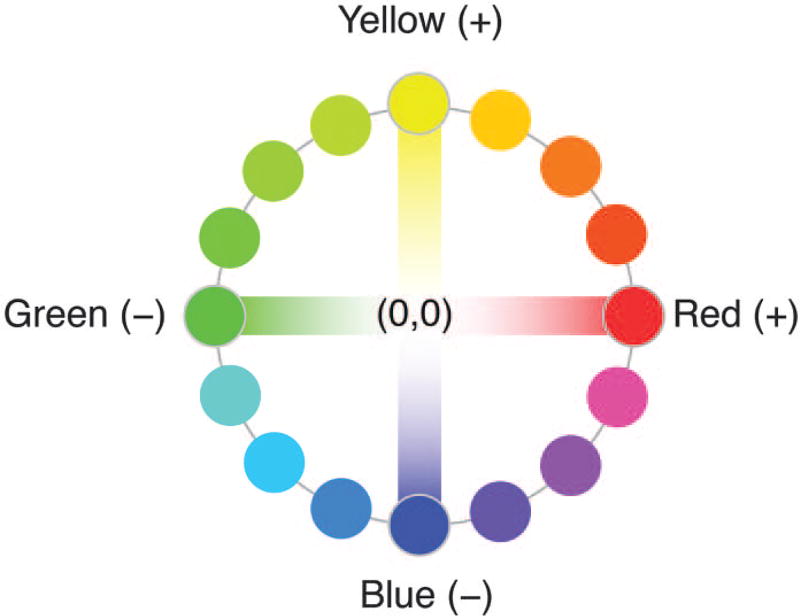
Steve: Try to imagine a hue that has both red and green components. You can’t! No hue in human color perception is both reddish and greenish at the same time. Hering declared red and green to be unique colors represented at the opposite ends of a single axis, as in Fig. 1. In most modern formulations, positive values on the axis are reddish, negative values are greenish, and zero represents a hue that has no redness or greenness at all. Hering also noted that no hue has both yellow and blue components, so he posited a second axis running from unique yellow (positive) to unique blue (negative), with zero for hues that have no yellowness or blueness.

Fig. 1.

Color opponent axes. Hering declared red and green to be opponent colors represented along a single axis. Here, positive values on the axis are reddish, negative values are greenish, and zero represents a hue that has no redness or greenness at all—that is, unique blue, unique yellow, or white. Hering also proposed a second axis running from yellow (positive) to blue (negative), with zero for hues that have no yellowness or blueness (so unique red, unique green, or white). Any hue can be represented by two coordinate values, one on each axis. Orange, for example, has a positive value on both axes; aqua, composed of both greenness and blueness, has a negative value on both axes. White has zero on both axes (no trace of redness, greenness, yellowness, or blueness).

The significance of the two opponent axes is that any hue we see can be represented by two values: one on each axis (Fig. 1). Orange, for example, with its components of both redness and yellowness, has a positive value on both axes; aqua, composed of both greenness and blueness, has a negative value on both axes. White sits at zero on both axes (no trace of redness, greenness, yellowness, or blueness).

Hering’s opponent formulation eliminates the theoretical possibility that a hue can appear both reddish and greenish because hue is represented by a single value on a red–green axis and, of course, no single value on an axis can be both positive (reddish) and negative (greenish) at the same time. The same applies to the yellow–blue axis so no hue can be bluish and yellowish simultaneously.

Paul: So why didn’t Helmholtz accept opponent-color theory? Why should an argument over three versus four primary color sensations be so long-lived and vehement?

Steve: The four “primary” colors of Hering were considered a serious challenge to the three-primary Young–Helmholtz theory, extending even to alternative explanations for after-images and abnormal color vision [7]. Moreover, Helmholtz and Hering found fault with each other’s scientific approach. Helmholtz criticized Hering for being “far too trusting of our ability to distinguish primitive from compound sensations through introspection,” and for his “readiness to explain visual effects by postulating hypothetical neural mechanisms” (Turner, 1993, p. 83) [2]. Hering, on the other hand, “denounced Helmholtz’s approach as too physicalist in orientation, too obsessed with physical models of end-organ function, and too prone to confound physical stimulus with subjective response” or assume a simplistic relation between them (Turner, 1993, p. 82) [2]. Hering wanted to understand color vision in the biological context of living organisms. It is worth noting that modern renditions of some of these ideological differences will come up again as we aim to integrate psychophysical and physiological laboratory measurements.

Paul: I agree with Helmholtz on the value of empirical evidence, but Hering’s protest against slavish reliance on physical models also makes sense to me. In addition to his contributions to color science, Hering produced key early evidence for what we now call homeostatic principles in physiology. With benefit of hindsight, it is easy to recognize the principles of neural excitation and inhibition (at that time poorly understood), which are implicit also in his color opponent axes you described.

But let’s not get ahead of ourselves. Can we first ask whether opponent-color theory has advanced our understanding of the visual system?

Steve: That’s a fair question, Paul, but let’s not presume opponent-color theory and the Young–Helmholtz theory are incompatible alternatives, one of which ultimately will be proved right and the other wrong. Let’s start with some basic psychophysical measurements underpinned by opponent-color theory.

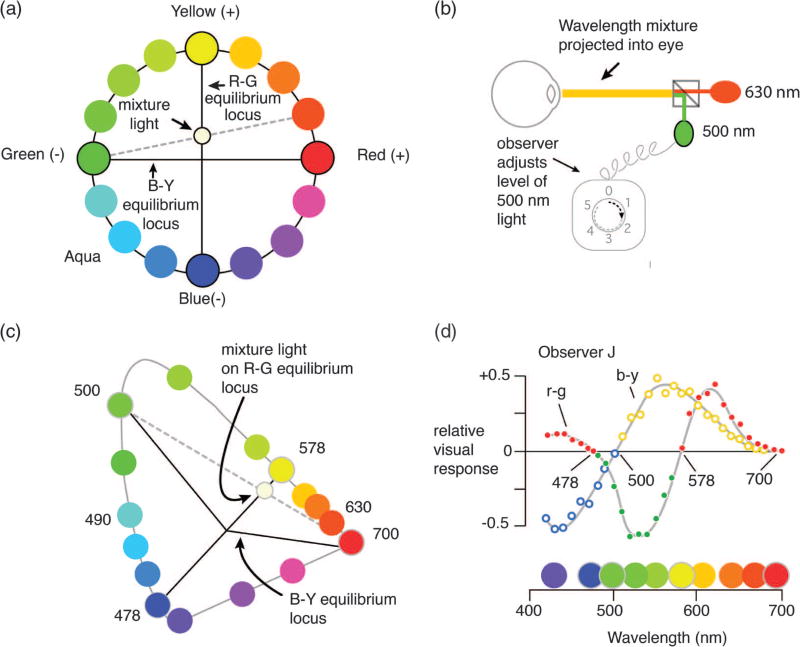
Opponent-color theory holds that every hue is represented by some value on the red–green axis, be it positive (reddish), negative (greenish), or zero (not at all reddish or greenish). Now consider what happens if we combine two hues that are separated by more than 90 deg on our color circle (Fig. 1). Geometry suggests that a line joining these hues must pass through either the R–G equilibrium locus [as in Fig. 2(a)] or through the B–Y equilibrium locus. In a classic study, the wife and husband team Jameson and Hurvich [8] used this logic to map out the red–green and blue–yellow opponent responses in human observers.

Fig. 2.

How to use color mixtures to characterize opponent-color mechanisms. (a) Hues that do not lie on the opponent axes have both red–green and blue–yellow components. In this case, orange has red and yellow components. By adding 500 nm (“green”) to the orange hue its reddish component can be canceled (i.e., bringing the mixture light to the R–G equilibrium locus). (b) Mixing spectral lights. The observer views a mixture of 630 nm plus a greenish-appearing wavelength (here, 500 nm), and adjusts the level of the 500 nm light until the mixture appears neither reddish nor greenish. (c) A representation of the Jameson and Hurvich color cancellation experiment in CIE space. Repeating the chromatic cancellation for wavelengths above 578 nm quantifies the redness in each of these wavelengths. (d) The resulting measurements can be plotted together as a function of all the physical wavelengths in the visible spectrum (see text).

Jameson and Hurvich reasoned that the amount of redness in a reddish-appearing wavelength (say, 630 nm, which appears reddish-orange) could be eliminated by mixing it with a second light which, viewed alone, appears greenish (say, 500 nm). In their experiment, an observer controls the level of a 500 nm light and is instructed to adjust it so the (500 nm + 630 nm) light mixture appears neither reddish nor greenish [Fig. 2(b)]. In terms of opponent-color theory, the observer adjusts the 500 nm level so the resulting mixture has a value of zero on the red–green opponent axis. Percepts like this with no redness or greenness may appear unique yellow, unique blue, or white, and are called red–green equilibrium colors.

Jameson and Hurvich next repeated the cancellation experiment with other reddish-appearing wavelengths throughout the visible spectrum in place of 630 nm. At each of these wavelengths, the level of the 500 nm light was adjusted by the observer so the mixture appeared a red–green equilibrium color. The redness of each wavelength was quantified by the amount of 500 nm light that made the mixture appear neither the least bit reddish nor greenish. This level of 500 nm greenish light is said to cancel the redness in the wavelength, so the technique is called chromatic cancellation.

Paul: But not all wavelengths appear reddish …

Steve: You’re right, of course. In fact, nearly all other wavelengths have a greenish component (the two exceptions are the wavelengths that appear unique yellow or unique blue). The greenness in these wavelengths was measured by finding the level of a reddish light (say, 700 nm) that when mixed with the wavelength again gave a red–green equilibrium color. This level quantified the greenness in each of these wavelengths. The resulting measurements of redness and greenness can be plotted together as a function of all the wavelengths in the visible spectrum [red and green solid symbols, Fig. 2(d)] [9]. These particular measurements are from none other than observer J(ameson).

Jameson and Hurvich went on to measure the yellowness or blueness of each wavelength in a similar way, but now they used a bluish light (say, 475 nm) to cancel yellowness, or a yellowish light (say, 580 nm) to cancel blueness. In other words, the light added to each wavelength (either 475 nm or 580 nm) was adjusted in level so the appearance of the mixture was neither yellowish nor bluish (so the mixture appeared unique green, unique red, or white). These percepts are the yellow–blue equilibrium colors. The yellowness or blueness of each wavelength so measured is shown by the open blue and yellow symbols in Fig. 2(d) [10].

So, this is a classic psychophysical approach to quantify the opponent-color components of any color percept. These experiments do not explain unique hues [11], but they do show that the kinds of opponent interactions envisioned by Hering (he called them assimilative and dissociative processes) are at play in human color vision. Of course, Paul, it is far different from a physiologist’s approach. Can you start by explaining how a physiologist infers an opponent-color process from a nerve cell’s response?

Paul: Measuring opponent-color processing is straightforward for a physiologist, but you first need to know something about how nerve cell recording works. We use a device called a microelectrode to pick up tiny electrical signals that nerve cells emit when they are activated. The signals are called action potentials or spikes because they are very brief: each spike lasts for just 1 or 2 ms. In the visual system, spikes are generated inside the eye (in the retina), and pass down the optic nerve into the brain. We make these measurements in non-human primate species that have trichromatic color vision just as most humans do. When a nerve cell that feeds into the optic nerve is activated, the cell rapidly emits a series of spikes. So, the strategy is to measure the rate of spikes (typically spike impulses per second) while changing the wavelength or intensity of light being delivered to the retina. This establishes a relation between the stimulus (light) and the response (spikes), just as in psychophysics. But physiologists can measure inside the nervous system so don’t need to consider what their subjects perceive.

Steve: Can you tell me how these methods are used to study color opponency?

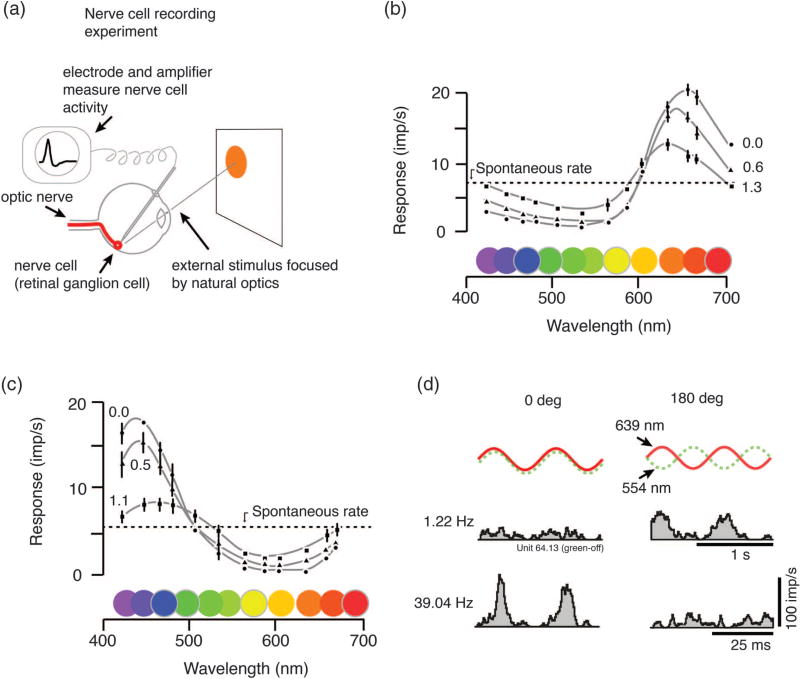
Paul: One way to pick up an opponent-color process in a nerve cell is to record from the cell while we present brief pulses of light, typically less than a second in duration, on a stimulus screen. The image of the external stimulus is focused by the eye’s optics onto the position that excites the recorded cell, as shown in Fig. 3(a). Some results obtained using a similar approach are shown in Figs. 3(b) and 3(c). These are classic measurements made by DeValois et al. [12], and show some of the first recordings of opponent cell responses ever made. Here we see that opponent cells are excited (their spike rate is increased) by some wavelengths, and inhibited by other wavelengths (their spike rate falls below the background or “spontaneous” rate). What’s more, the wavelength selectivity does not depend on the overall stimulus level, as shown by the roughly parallel curves in each of Figs. 3(b) and 3(c). Even better, the responses of different cells are minimal (that is, they are comparable to the spontaneous rate) at points close to a red–green equilibrium wavelength [unique yellow, Fig. 3(b)] or blue–yellow equilibrium wavelength [unique green, Fig. 3(c)]. You must admit, Steve, that these cells seem to have what it takes to serve the red–green and blue–yellow opponent processes proposed by Hering in 1874.

Fig. 3.

Physiological measurement of opponency. (a) Opponency defined by nerve cell recording. The visual system of an anaesthetized monkey responds to brief pulses of light presented on a stimulus screen. The small electrical signals (action potentials) from these cells are picked up by an electrode and amplified. (b) These famous recordings by De Valois and colleagues show responses of single nerve cells in monkey visual system to lights at different wavelengths. Here the opponent process is revealed as the cell is excited by some wavelengths (in this case, long wavelengths) and inhibited by others (that is, the spike rate falls below the maintained rate). Measurements were taken at three steps of brightness attenuation, showing that the opponent characteristic does not depend heavily on brightness. (c) Other cells show blue–yellow opponent property. (d) Opponency can also be measured by responses to a mixture of wavelengths projected into the eye. The frequency of action potentials is measured as a function of time relative to the stimulus modulation. If the response to in-phase modulation (0 deg phase difference, left column) is less than the response to out-of-phase modulation (180 deg phase difference, right column), we know that something in the retina has “subtracted” the neural response to 554 nm (“green”) light from the response to 639 nm (“red”) light (upper histograms). The process can be studied in detail by changing the frequency and phase of light modulation (lower histograms). Panels (b) and (c) modified from [12]. Panel (d) modified from Solomon et al. (2005) [13].

A second approach to identifying opponent processing in nerve cells is to project a mixture of two different wavelengths (for example, a green-appearing 554 nm light and a red-appearing 639 nm). We know that these wavelengths differentially excite the middle-wave sensitive (M) and long-wave sensitive (L) cone photoreceptors [14,15], but the experiment works even without knowing much about the receptors. These two lights are then modulated at the same temporal frequency; critically, the modulation can be either in-phase or out-of-phase. As you can see from the curves at the top of Fig. 3(d), the average intensity of these two waveforms is identical: they differ only in timing [16]. If the number of spikes we measure during in-phase stimulation is smaller than the number measured during out-of-phase stimulation, then we say the nerve cell is color opponent [middle panels, Fig. 3(d)]. In other words when the greenish (554 nm) and reddish (639 nm) lights are in-phase, something in the retina “subtracts” the neural response to the 554 nm light from the response to the 639 nm light. Conversely, these lights combine constructively in the retina when they are presented out-of-phase, and the spike rate of the cell is strongly modulated up and down at the temporal frequency of the stimulus.

Steve: Changing the temporal phase is a clever approach.

Paul: It’s a very simple stimulus, but we can use it to discover quite a lot about the physiology of opponent processing. For example, when the temporal frequency of light modulation is sped up [Fig. 3(d), histograms in lower panels] the cell response changes to show a color non-opponent signature. That is, now the response is strongest when the two wavelengths are in-phase. This result shows that the color opponent response is due to interaction between slow inhibitory and rapid excitatory inputs to the cell [17]. We can also systematically vary the phase of the lights, tracing out cell responses as a function of phase at each frequency. It turns out that responses of some cells match well the sensitivity of human observers viewing the same stimulus [16,18].

Steve: I am convinced that the cell responses show color opponent properties. That’s an important result, but you seem to be assuming that these neurons’ physiological responses mediate the colors we see. That’s not been shown by these experiments. Perhaps instead the cells serve some other visual function such as image segmentation [19,20]. Or a cell might contribute to color perception even though its response alone does not determine the hue one sees [21]. In other words, this cell might be part of an ensemble of neurons that determines color [22]. Of course, Paul, this does not undercut the physiological criterion for opponency that you stated clearly, but it highlights that “color opponency” does not always mean the same thing to physiologists and psychophysicists so we should not aim to equate them directly.

A related point is the critical methodological difference between physiology and perception. In cell recording, inferences are made by varying the stimulus (that is, the independent variable), for example, by changing from in-phase to out-of-phase 554 nm and 639 nm lights. Changes in a cell’s response (the dependent variable) are recorded as the stimulus is varied. If and how the cell’s response determines perception of color usually is not considered. On the other hand, in the Jameson and Hurvich psychophysical experiment the independent variable is again the stimulus but the dependent variable is based on the actual hue one sees [Fig. 2(d)]. Paul, if you hear an echo, it’s a 21st century reverberation from the Hering–Helmholtz controversy. Can’t we at least agree not to label these cells with hue names, which confuses nerve cell responses with color percepts? There are no “red–green” or “blue–yellow” cells. My argument here is a simple extension of Hering’s point from the 19th century applied to neurons: do not confound neural signals with percepts of color (abridged from Turner, 1993, p. 82 [2]).

Paul: I take your point about hue names, Steve, but some physiologists do refer to cone opponent cells in this unsophisticated way; we will need to accept it as a quirk of nomenclature. In any event, aren’t we now just raking over the Hering versus Helmholtz embers? What about some of the hoped-for convergence? After all, physiology and psychophysics aim to understand the same visual system.

Steve: Agreed. So let’s ask whether the same models of opponency that were developed to explain psychophysical measurements can also predict neural properties found in physiological experiments. The answer to that is an emphatic “sometimes.”

Let’s start with your example of a temporally varying mixture of 554 and 639 nm lights. Here the convergence is excellent. You explain the change in response due to altering temporal phase by a difference between the L-cone and M-cone responses; put in a simple equation, neural response N = aL − bM, where L and M are cone responses, and a and b are weights for the relative contribution of each type of cone. A similar model accounts for the psychophysical red–green chromatic cancellation measurements [solid symbols, Fig. 2(d)], which can be modeled by a linear combination of cone responses:

$${(r-g)}_{\lambda }=a{\mathrm{L}}_{\lambda }-b{\mathrm{M}}_{\lambda }+c{\mathrm{S}}_{\lambda }.$$ (1)

Here, (r − g)_λ is the redness or greenness of a given wavelength λ [vertical axis, Fig. 2(d)]; L_λ, M_λ, and S_λ are the L-, M-, and S-cone responses at λ; and weights a, b, and c set the relative contribution of each cone type [23]. For a mixture of 554 and 639 nm, the S-cone term for (r − g)_λ may be dropped because S cones are insensitive to such long wavelengths. Then the psychophysical model is (r − g)_λ = aL_λ − bM_λ, which is identical to the physiological one. Voilà! We have convergence.

Paul: I like it! Let’s try another example.

Steve: Okay, let’s try. The psychophysical opponency model for redness–greenness [Eq. (1)] includes an S-cone contribution at short wavelengths. The redness lobe at wavelengths below 470 nm in Fig. 2(d) is well supported by psychophysical evidence [8,24]. Is there physiological evidence for a neural response in which S- and L-cone signals are combined in antagonism with M-cone responses?

Paul: Hmm, this question is not so easy to answer. To get started, let’s take a trip down the optic nerve, to the place where it connects to the brain. In this brain center (called the lateral geniculate nucleus, or LGN), the color-selective cells have almost identical properties to the retinal cells that feed them. What’s more, the cells are nicely arranged into layers. Some layers contain many +L − M opponent cells (also known to physiologists as red–green cells), and other layers contain many opponent cells with short-wave sensitive (S) cone input (also known as “blue–yellow” cells). This anatomical arrangement makes it easy to sample opponent cells in microelectrode experiments. In fact, De Valois’ experiment shown in Figs. 3(b) and 3(c) was carried out in monkey LGN. Here in the LGN we can say, with some confidence, that the classically reported cells that take a difference between responses from M and L cones do not also combine S-cone signals, contrary to the results from psychophysics; further, opponent cells that include an S-cone input do not line up with the blue–yellow opponent axis from perception.

Steve: But didn’t you argue earlier that these cell responses look a lot like Hering’s red–green and blue–yellow opponent axes?

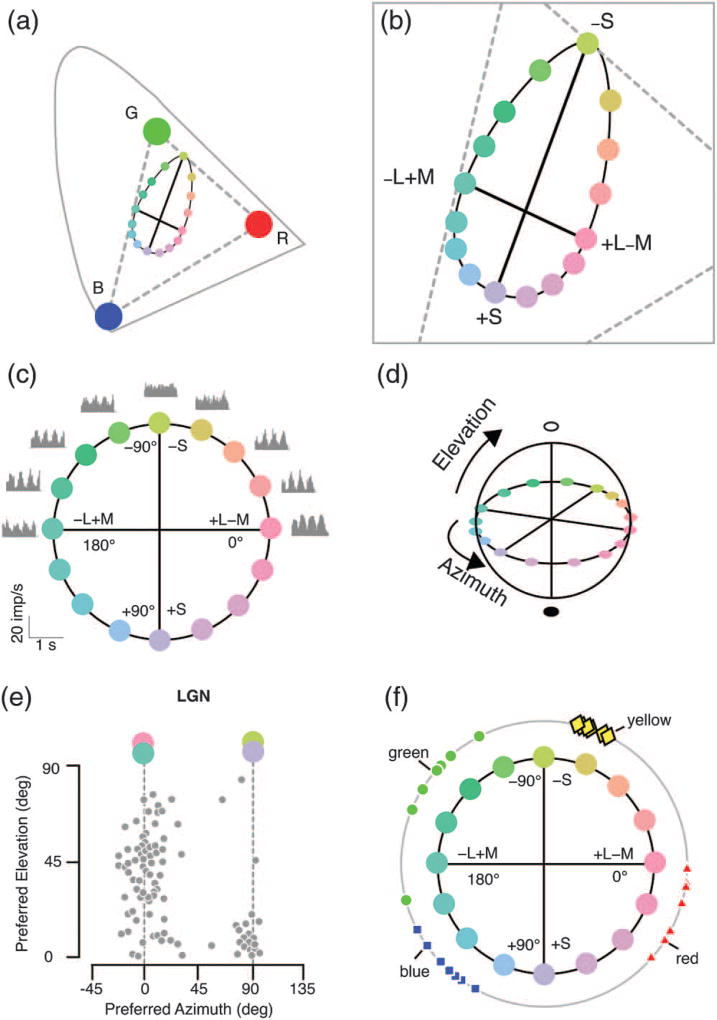
Paul: I said that the cell responses line up close to the Hering opponent axes, but it turns out the match is only approximate. To discover the discrepancy, look at Fig. 4(a). Here you see the coordinate points where red (R), green (G), and blue (B) pixels of a color television monitor are plotted in CIE color space. The gray broken lines joining these points enclose the range (or gamut) of colors that can be produced by the monitor [25]. Now look more closely at an almond-shaped set of points within this gamut [Fig. 4(b)]. In a classic study of sensory physiology, Derrington, Krauskopf, and Lennie (now famously known as DKL) used this set of points to study how S, M, and L cones contribute to opponent responses in monkey LGN. The way they did it might seem complicated at first, but we will see that some very simple and beautiful results came out of these experiments. Allow me to explain!

Fig. 4.

Cone opponency defined physiologically by chromatic cardinal axes in experiments by Derrington and colleagues. (a) Projection of the stimulus set onto the CIE axes. Broken lines show the range of colors that lie within the monitor gamut. (b) Enlarged view of part of this space. Thick solid lines show two cardinal exchange axes producing selective modulation of S cones and out-of-phase modulation of M and L cones at constant luminance. Intermediate modulation directions form an ellipse in this space. (c) Here the space is reformed into a circle with cone excitation azimuth. Gray profiles show response modulation of a single nerve cell along different color modulation directions (four cycles of modulation are shown). Note that the cell is modulated maximally by exchange along the L–M axis (0–180 deg), and shows no modulation (response “null”) along the S-cone axis (90 to −90 deg). (d) A third axis (elevation) is defined by in-phase modulation of S, M, and L cones. (e) Two clusters of cells are present in monkey lateral geniculate nucleus (LGN) with preferred azimuth close to zero (L–M) or 90 (S) deg. The L–M cells prefer a combination of luminance and color exchange (elevations around 45 deg), whereas the S cells prefer near-equiluminant color exchange. (f) Unique hues (outer circle) do not align with the cardinal color axes. The points show unique hue settings made on the circumference of an S versus ML cone space circle by seven observers. Note that the settings do not align with the L–M or S axis. Note also the differences in unique hue position among observers, with little variation in unique yellow but wide variation in position of unique blue, red, and green. Data in panels (c) and (e) redrawn from [40]. Data in panel (f) redrawn from [35].

The points shown in Fig. 4(b) are chosen to lie on an equiluminant plane, that is, they all have the same luminance (roughly speaking, they have equal brightness), but they vary in color. The points are shown, rescaled to form a circle, in Fig. 4(c). The plane enclosed by this circle gives the first two dimensions of DKL’s stimulus space. There are two orthogonal opponent axes in this plane, but they are cone-opponent axes, not Hering color-opponent axes like those in Fig. 1. Exchanging points on the horizontal axis changes the activation levels of L and M cones, but leaves S cones unchanged. Exchanging points on the vertical axis changes the activation level of S cones, but leaves L and M cones unchanged. The third axis in DKL space, labeled elevation, defines in-phase modulation of all three (L, M, and S) cone types, that is, overall light-level modulation [Fig. 4(d)].

Let’s go back now to Fig. 4(c). DKL’s strategy was to exchange points on opposite sides of the equiluminant circle, and measure spike rates in single LGN cells. Here you see spike rate histograms arranged next to the stimulus modulation angle for nine directions in DKL space. Each histogram shows responses accumulated during four stimulus cycles, and you can see four clear peaks in the response histograms for most stimulus modulation directions. The strongest spike rate modulation for this cell is for stimulus modulation along the L–M axis (at zero or 180 deg) [26]. You can also see that for modulation along the S-cone axis (90 deg) the spike rate does not vary; in other words, the stimulus changes but the neural response does not. This result shows that this so-called red–green cell does not receive functional input from S cones, but rather gets its opponent (opposite-sign) input from only L cones and M cones. That’s a beautiful and clear result, don’t you agree?

Steve: I do agree. Still, this particular opponent cell would not account for the redness of short wavelengths because it does not combine S and L cones in antagonism with M cones. What about other cells in the LGN?

Paul: The result in LGN is very clear, as you can see from a scatterplot of cells’ preferred stimulus angle in DKL space [Fig. 4(e), horizontal axis]. One group of cells gets opponent input from L and M cones so prefers modulation near 0 deg azimuth (L–M). By the way, these “red–green” cells also can signal brightness contrast: their preferred elevations in DKL space [Fig. 4(e), vertical axis] are scattered around 45 deg. Four different sub-types within this group of cells can be distinguished by their dominant excitatory cone input (L or M) and the contrast polarity of their preferred stimulus (increment, “on,” or decrement, “off ”): thus, L-on, L-off, M-on, M-off. A second group of cells responds vigorously to modulation along the S-cone line (near 90 deg azimuth) indicating strong functional input from S cones; most of these cells have the +S − (M + L) or so-called “blue-on” receptive field property identified by different methods in other studies [27–30]. Further, the +S − (M + L) cells and the L–M opponent cells turn out to have many distinct properties, and even have distinct evolutionary origins [31–33]—a fascinating topic in its own right. From the point of view of cone opponency one important difference is that +S − (M + L) cells respond only weakly to brightness modulation: their preferred elevation is near 0 deg [Fig. 4(e), vertical axis]. It is clear from these and other results [34] that there is variation around the DKL cardinal axes (the main variation seems to be in strength of S-cone inputs). But the main point is that the cone-opponent cells in LGN do not line up along the red–green or blue–yellow Hering color-opponent axes. The discrepancy is clear in Fig. 4(f), which plots unique hue settings made on the circumference of the DKL space by seven human observers [35].

Steve: So we agree that Hering’s unique hues are not represented in the visual pathway at early processing stages. But let’s not be discouraged. Other perceptual measurements correspond well with the neural responses of LGN cells. Hering was concerned with the appearance of hues, but another psychophysical approach is to measure the threshold for detecting chromatic change. Imagine that the chromaticity of a white circle briefly shifts toward redness [36]. The threshold in the reddish direction is the smallest detectable chromatic shift from white [visualize it as the smallest detectable shift from the center point (0,0) in Fig. 1 along the line toward Red]. Subsequently, separate threshold measurements from white can be made in each of many different color directions (say in the direction toward each of the colored circles in Fig. 1).

In a classic psychophysical study, which in fact predated some of the physiology discussed above, Krauskopf et al. [37] asked how chromatic thresholds are changed by prior adaptation to different chromatic directions. One of their adapting directions was like the out-of-phase red-to-green temporal oscillation shown in the upper-right part of Fig. 3(d). The adapting stimulus was presented for 30 s at 1 Hz, and then chromatic thresholds from white were remeasured in each color direction. The result was that the prior red-to-green adaptation raised the thresholds in the red and green color directions, but thresholds in the S-cone direction changed little if at all. This showed the 1 Hz red-to-green adaptation desensitized one chromatic neural mechanism more than another.

They next posited that two separate mechanisms mediate chromatic thresholds, and went about assessing the specific chromatic tuning of each mechanism. The tuning was inferred by seeking an adapting light in one chromatic direction that did not raise threshold in some other chromatic direction, analogous to the neural null response at 90 deg in Fig. 4(c). This experiment yielded three important results. First, adapting oscillation between unique blue and unique yellow produced threshold increases in all directions; that is, there was no evidence for a neural process tuned to the unique-blue to unique-yellow Hering direction. Second, they found that chromatic adapting oscillation between a light near unique red and a light near unique green did not appreciably raise the chromatic threshold along the pure S-cone axis; also, adapting oscillation along the S-cone axis did not appreciably raise chromatic thresholds on the red–green axis. Finally, adapting oscillation in other chromatic directions raised threshold in all color directions. Thus, they inferred the existence of two independently adaptable chromatic directions, consistent with the preferred azimuth of cells in Fig. 4(e) at 0 and 90 deg, respectively. Other studies have since extended these findings, showing close correspondence between single-cell thresholds and human sensitivity mapped in M–L cone space [38,39]. This is another nice convergence between perception and physiology, wouldn’t you say, Paul?

Paul: Agreed. This is clear psychophysical evidence for cone-opponent axes. And threshold measurements are something that a physiologist is quite familiar with, so this seems a sensible way to link psychophysical and physiological measures of opponency. However, Steve, it’s an inconvenient truth that LGN cells do not exhibit strong response adaptation of the type you just described [34,38,40]. But cortical cells, on the other hand, are renowned for their rapid adaptation to prolonged stimuli [41], and there is some evidence that the cone opponent inputs are leaving their physiological signature in these downstream parts of the brain [42].

Steve: I take your point. In fact, Krauskopf et al. [37] found second-order deviations from the LGN cone-opponent directions, and subsequently identified additional “higher-order” chromatic mechanisms posited to reflect neural activity at the cortical level [43]. Nonetheless, these results drive home that “convergence” of perceptual and physiological opponency does not require correspondence between Hering’s unique hues and neural responses at a particular level of the visual system.

Further, there is another inconvenient truth on the psychophysical side. Perceptual equilibrium colors are not as simple as they seem from idealized versions in Figs. 1 and 2, and Eq. (1). An important complication is that the locus of yellow–blue equilibrium colors (that is, all colors with no yellowness or blueness) is not a straight line in color space. This may seem surprising. How can physically adding two lights, each without a hint of yellowness or blueness when viewed alone, give a yellowish hue? The explanation actually is straightforward and points out an implicit (over)simplification in Eq. (1) and its analogous form for yellowness–blueness:

$${(y-b)}_{\lambda }=d{\mathrm{L}}_{\lambda }+e{\mathrm{M}}_{\lambda }-f{\mathrm{S}}_{\lambda },$$ (2)

where (y − b)_λ is the yellowness or blueness of a given wavelength λ [vertical axis, Fig. 2(d)]; L_λ, M_λ, and S_λ are the L-, M-, and S-cone responses at λ; and weights d, e, and f set the relative contribution from each type of cone. Equations (1) and (2) capture opponency by having both positive and negative contributions from the cone responses on the right side of each equation, but these equations combine the cone responses linearly; that is, the redness–greenness (r − g)_λ and yellowness–blueness (y − b)_λ are simply a weighted sum of the L-, M-, and S-cone responses. Redness–greenness and yellowness–blueness, however, need not be linear. Suppose, for example, that cone response L is raised to a power n, where n ≠ 1 [44]. Then the yellowness–blueness of one light (say #1) that’s perceived to be a yellow–blue equilibrium color when viewed alone is ${(y-b)}_1=0=d{\mathrm{L}}_1^n+e{\mathrm{M}}_1-f{\mathrm{S}}_1$; and for a second light alone (#2) is ${(y-b)}_2=0=d{\mathrm{L}}_2^n+e{\mathrm{M}}_2-f{\mathrm{S}}_2$. Even though each light appears neither yellowish nor bluish when viewed by itself (since (y − b)₁ = (y − b)₂ = 0), a physical admixture of the two lights gives (y − b)₁₊₂ = d(L₁ + L₂)ⁿ + e(M₁ + M₂) − f (S₁ + S₂), which in general will not be zero because d(L₁ + L₂)ⁿ does not equal $(d{\mathrm{L}}_1^n+d{\mathrm{L}}_2^n)$ when n ≠ 1. Nonlinear responses, therefore, predict that the additive mixture of two lights that are each devoid of yellowness or blueness may appear yellowish or bluish. Psychophysical measurements of the locus of yellow–blue equilibrium colors confirm nonlinearity: the locus has an approximate dog-leg shape, as shown in Fig. 2(c). And you can see that a straight line between the chromaticities that appear unique red and unique green, which represents mixtures of the two chromaticities [dashed line in Fig. 2(c)] passes through a point for a light that appears yellowish, not white.

Overall, then, unique hues are important for understanding perceptual color opponency, but they may not be represented neurally by any cell’s preferred stimulus. Instead, for example, unique hues may follow from some minimum of population activity averaged across many cone-opponent cells rather than a particular response from a single cell.

Still, Paul, we know that different regions of the cerebral cortex are specialized to analyze distinct aspects of the visual world. Is there a region of cortex where we might find cells that bring physiology and Hering opponency into correspondence?

Paul: So far we have at best only tantalizing glimpses of how unique hues and color opponent axes might be represented in the cerebral cortex. Some studies suggest specialized cell pathways and cortical centers for extracting object color [45–47]. But it is also clear that for the most part, cortical cells show some degree of selectivity for both shape and color [48–52], so we need to consider how chromatic opponency fits into the cells’ spatial receptive field properties.

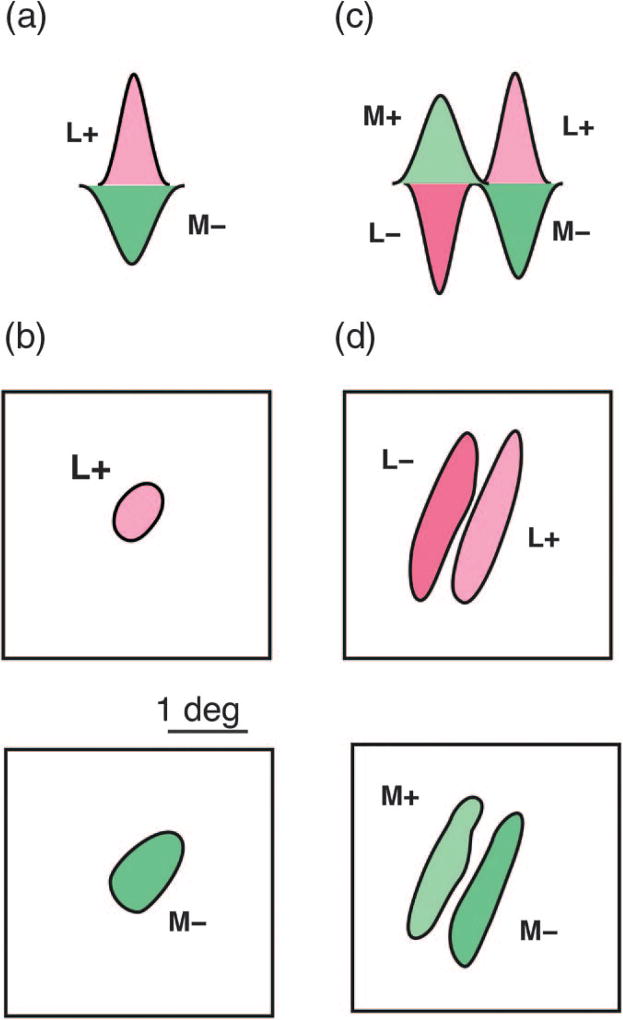
The opponent LGN cells, discussed earlier, project to primary visual cortex (V1), so it is not surprising to find cortical receptive fields with excitatory input from long-wavelength sensitive cones (L+) and inhibitory input from middle-wavelength sensitive cones (M−). But up in the primary visual cortex, most receptive fields are elongated, not round, and this elongation makes them selective for the orientation of edges in the visual world. The receptive field projection of such a single-opponent receptive field [Figs. 5(a) and 5(b)] shows to a first approximation spatially overlapping cone opponent inputs [20,53]. Thus, these cells will be excited by long-wavelength light and inhibited by middle-wavelength light, of any shape or size (provided the stimulus at least fills the receptive field center). This type of cell (called a single-opponent cell) is selective for both wavelength and orientation. Somewhat surprisingly, however, it is not selective for colored edges. For example, suppose the left half of the receptive field were stimulated by middle-wavelength light and the right half by long-wavelength light, creating a sharp green–red edge through the center of the receptive field. The cell’s response to such an edge would be weaker than its response to uniform long-wavelength light covering the whole receptive field.

Fig. 5.

Spatial and chromatic opponent receptive fields. (a) Schematic spatial sensitivity profile of a single-opponent receptive field receiving excitatory input (L+) from long-wave sensitive cones, and inhibitory input (M−) from middle-wave sensitive cones. (b) The receptive field projection of a single-opponent field shows approximately overlapping and circularly symmetric cone-opponent inputs. (c) Schematic spatial sensitivity profile of a double-opponent receptive field. Here the receptive field comprises two opponent sub-regions which are spatially offset. (d) The receptive field projection of a double-opponent field shows complementary, orientation-selective sub-regions which produce both spatial and chromatic selectivity. Modified from [53].

Steve: So a single-opponent receptive field is unable to explain a classic finding from perception: a chromatic surround induces color contrast. For example, a spot of light that looks yellow on a black background takes on a greenish appearance when surrounded by long-wavelength (reddish-appearing) light.

Paul: That’s right. Detecting colored edges requires so-called double-opponent receptive fields, and some cells in V1 indeed do have this kind of property [Fig. 5(c)]. Here the receptive field comprises two opponent sub-regions that are spatially offset [45,50,54,55]. The receptive field projection of this double-opponent field [Fig. 5(d)] shows complementary, orientation-selective sub-regions, which produce both spatial and chromatic opponency [53,56]. The ideal stimulus for this cell would be a chromatic edge like the one mentioned above, say middle-wavelength light toward the left and long-wavelength toward the right, with the edge between them aligned with the two sub-regions. This cell responds to a difference between the +L and −M responses across the edge. Further, unlike a single-opponent receptive field [Fig. 5(a)], a large uniform light of any wavelength causes little or no response from a double-opponent cell.

Steve: This may be clear evidence that color opponent signals are getting combined with signals that can serve other aspects of visual perception, but it seems to be taking us further from neural responses that represent only color percepts.

Paul: It does. And this example is just part of a wide variety of V1 receptive fields. In fact, cells that nicely meet the theoretical requirements of ideal chromatic contrast detectors are exceedingly rare [45,50,54,55]. And it is very hard to imagine that there would be enough cells to cope with all possible combinations of orientation and color contrast.

Steve: What happened to the nice groups of cone-opponent cells in LGN? Do we see the same kinds of functional groupings anywhere else in the cortex?

Paul: I’m sorry to disappoint you, but it seems that opponent signals from the nicely segregated LGN groups are recombined in wide variety of ways, even at early processing stages. Some cortical cells do show high chromatic selectivity [19,50,52,57–59], and some areas of cortex contain cells that are capable of supporting color constancy [46,60], which is another key aspect of human color vision [61–63]. Also, we need to remember that if, as proposed, unique hues are more a property of the environment than of the visual system [11,64], then specific collections of cells with responses aligned to cone-opponent or Hering-opponent axes may not even be needed.

To sum up, then, perceptual and physiological opponency need not converge at the level of individual highly tuned nerve cells. Instead, the convergence may lie in analyzing response minima, or perhaps relative responses among cells forming an ensemble. Experiments to test these possibilities are difficult for a physiologist to tackle: how do you know which cells are forming the ensemble you are looking for? The experiments are also complex because they require parallel nerve cell recordings, but we now have microelectrode array technologies [65,66] that go far beyond the simple wire that I described earlier. With the help of these new tools we might get closer to our hoped-for convergence in our lifetimes.