Cine Cone Beam CT Reconstruction Using Low-Rank Matrix Factorization: Algorithm and a Proof-of-Principle Study

Abstract

Respiration-correlated CBCT, commonly called 4DCBCT, provides respiratory phase-resolved CBCT images. A typical 4DCBCT represents averaged patient images over one breathing cycle and the fourth dimension is actually breathing phase instead of time. In many clinical applications, it is desirable to obtain true 4DCBCT with the fourth dimension being time, i.e., each constituent CBCT image corresponds to an instantaneous projection. Theoretically it is impossible to reconstruct a CBCT image from a single projection. However, if all the constituent CBCT images of a 4DCBCT scan share a lot of redundant information, it might be possible to make a good reconstruction of these images by exploring their sparsity and coherence/redundancy. Though these CBCT images are not completely time resolved, they can exploit both local and global temporal coherence of the patient anatomy automatically and contain much more temporal variation information of the patient geometry than the conventional 4DCBCT. We propose in this work a computational model and algorithms for the reconstruction of this type of semi-time-resolved CBCT, called cine-CBCT, based on low rank approximation that can utilize the underlying temporal coherence both locally and globally, such as slow variation, periodicity or repetition, in those cine-CBCT images.

I. Introduction

When cone beam computed tomography (CBCT) is applied to thorax or upper abdomen regions, motion-induced artifacts, such as blurring or distortion, become a serious problem, because different X-ray projections correspond to different volumetric CBCT images due to patient respiratory motion. To overcome this problem, four-dimensional CBCT (4DCBCT) [1]–[3] has been developed. In such a modality, all X-ray projections are first retrospectively grouped into different respiratory phase bins according to a breathing signal tagged on every projection image. A set of CBCT images are then reconstructed, each at a breathing phase, under the assumption that the projections placed into each bin correspond to the same or similar CBCT image. The number of phase bins is usually empirically chosen by a user based on the consideration of balancing temporal resolution and image quality. On one hand, a high temporal resolution requires a large number of phase bins, which leads to insufficient number of projections available to each phase and hence degraded quality of reconstructed CBCT images. On the other, a small number of phase bins results in low temporal resolution, as well as a relatively large bin width and the associated residual motion artifacts in the reconstructed images. To maintain clinically acceptable temporal resolution and image quality, 4DCBCT acquisition protocols such as slow gantry rotations and multiple gantry rotations have been proposed [3]–[5], and novel reconstruction or image processing techniques have been employed [6]–[9].

Conventional 4DCBCT reconstruction approach reconstructs CBCT images at different phases independent of each other [1]. This straightforward method neglects the temporal correlations of CBCT images at different phases. In contrast, a collaborative reconstruction scheme has been recently proposed [10]–[15]. Among them, [11] and [13] proposed a temporal nonlocal means method to constraint that the reconstructed CBCT images at neighboring phases must contain repetitive anatomical features. The locations of these features are allowed to vary among phases. The work of [10] and [14] first reconstructs an average CBCT image using all projections at all phases and impose a similarity constraint between this average image and the CBCT at each phase. These methods explicitly enforces the similarity among reconstructed CBCT images. Gao et al. [12] utilizes robust PCA techniques for the 4DCBCT reconstruction problem. This method restores a matrix whose columns are the 4DCBCT images at all phases under the assumption that, after a proper transformation, this matrix can be decomposed as the sum of a low-rank matrix corresponding to an almost static background and a sparsematrix corresponding to a moving foreground. The low-rank constraint achieved by minimizing the nuclear norm [16] of the associated matrix implicitly imposes the inter-phase similarity of the background. However, in the context of anatomical motion in thorax or upper abdomen, there is no clear distinction between foreground and background. Besides, as pointed out in [17], the nuclear norm minimization always finds a matrix factorization with mutually orthogonal factors. In this sense, it may have some unfavourable bias on the resulting low-rank matrices.

Although commonly called 4DCBCT, respiration-correlated CBCT [18] is a more accurate name for this imaging technique, since its fourth dimension is actually the respiratory phase rather than time. Clinically, it is more preferable to reconstruct true 4DCBCT with the fourth dimension being time, i.e., one CBCT image is reconstructed based on the corresponding instantaneous projection, if possible. This time-resolved CBCT, called cine-CBCT in this work to avoid confusion, encounters an apparent technical barrier of reconstructing a CBCT image based on only one projection where the information needed for a good reconstruction is severely insufficient. One way to overcome this barrier is to borrow some useful information of a particular patient’s anatomy from prior images. Previously we have tried to utilize prior 4DCT images of the same patient [19], [20]. Particularly, we have built a lung motion model for the patient by performing a principle component analysis (PCA) on the motion vector fields obtained from deformable registration on prior 4DCT images. We discovered that only a few principle components are sufficient to represent the lung motion to a satisfactory degree of accuracy. The reconstruction of a volumetric image based on one acquired X-ray projection is then achieved by finding those PCA coefficients, so that the projection of the corresponding CBCT matches the acquired one. However, this method heavily depends on how similar the current CBCT images are to the prior 4DCT images and how accurately the PCA parameters can be determined using one projection.

In this paper, we will propose another way to overcome this technical barrier without using any prior images. We will show the principle of proof of a computational model and numerical algorithms for cine-CBCT reconstruction based on a low rank assumption of the matrix which includes all cine-CBCT images as its columns. The low rank approximation, which uses a form of matrix factorization, maximally and automatically exploits the temporal coherence of the patient anatomy locally and globally without using any prior knowledges. Moreover, sparsity condition is also enforced under appropriate transforms, i.e., wavelet transform in space, to satisfy desired properties for the sequence of CBCT images. Simulation studies have demonstrated promising results for our method for this challenging problem.

II. Methods and Materials

Assumption

Let us denote a patient CBCT image at time t by x(t), which can be viewed as a point embedded in a high dimensional space R^N with its pixel values being the coordinate, where N is the total number of pixels in each CBCT image. x(t) travels along a smooth trajectory as patient breathes. A cine-CBCT reconstruction problem tries to recover points on this trajectory, each corresponding to a moment at an X-ray projection measurement. The key assumption in our approach is that the trajectory stays piecewisely close to a low dimensional subspace in the very high dimensional embedding space. Equivalently, when we form a matrix U with each column being an CBCT image, the resulting matrix is approximately of low-rank. We believe this assumption is valid due to the fact that body motion is far from a free form motion, which is verified by the fact that only a few principle components are sufficient to represent the lung motion to a satisfactory degree of accuracy as studied in [19], [20]. Based on this assumption, we use a matrix factorization formulation U ≈ LR. The number of columns for the matrix L constraints the rank of approximation. We further impose desired image properties by enforcing sparsity of the tight wavelet frame transform of L. In this matrix factorization formulation both the low rank approximation and the sparse representation in wavelet transform domain reduces the true degree of freedom of U significantly. In all previous approaches mentioned in the Section of Introduction, reduction of degrees of freedom are exploited explicitly or implicitly from redundancy and coherence in space and time as well as sparse representation. In particular, 4DCBCT based on phase binning explicitly used the low rank assumption, i.e., the rank is equal to the number of phases. However, as mentioned before, the number of phases, i.e., the rank, is usually empirically chosen and more importantly coherence in time or among different phases are not explored at all.

Another important practical issue is how well the small number of image basis for the low dimensional subspace and the factorization U ≈ LR can be recovered from the projection data. Intuitively, this requires each basis image or equivalently all cine-CBCT images collectively have a sufficient number of projections covering a sufficiently large scanning angle, which is also required for the construction of a single CBCT image. As shown in experiments in Section IV-C, reconstruction from data using different projections can produce different results for the same ground truth.

A. Model

In this proof-of-principle study, we consider the reconstruction of a 2-D slice of the CBCT to illustrate the principles of the new algorithm. The basic ideas, however, can be easily generalized into 3-D contexts. Let the unknown 2-D image be a function u defined in ℝ². When the X-ray source is placed with angle θ, the projection measured by the imager at location z is

$$f_{\theta }(z)={\mathcal{P}}_{\theta }u(z):={\int }_0^{{\ell }_z}u({\mathit{x}}_{\theta }+s{\mathit{r}}_z)ds$$ (1)

where x_θ ∈ ℝ² is the coordinate of the X-ray source, and r_z ∈ 𝕊² and ℓ_z are respectively the direction and the length of the line connecting the X-ray source and the location z on the imager. The operator ℘ in (1) is also known as Radon transform. If f_θ(z) is sampled with respect to z, the resulting projection data can be written as a vector f_θ ∈ ℝ^M that obeys

$${\mathit{P}}_{\theta }\mathit{u}={\mathit{f}}_{\theta }.$$ (2)

Here P_θ ∈ ℝ^M×N and u ∈ ℝ^N are the discretization of ℘_θ and u in (1) respectively. Suppose that we have T projections where the X-ray source is placed with angels θ₁, θ₂, …, θ_T, respectively. Let P_i and f_i stand for P_θi and f_θi respectively. Then, by putting (2) with different angles together, the CT projection can be written into a system of linear equations

$$\mathit{Pu}=\mathit{f}$$ (3)

where P = [P₁; P₂; …; P_T] ∈ ℝ^MT×N and f = [f₁; f₂; …; f_T] ∈ ℝ^MT. In other words, the CT image reconstruction problem is to recover image u from its partial Radon transform.

In the context of cine-CBCT reconstruction, instead of only one unknown image u as in the CBCT problem, there is a set of unknown images, each associated with a projection, denoted by {u₁, u₂, …, u_T} and the projection condition in (3) may be modified to

$${\mathit{P}}_i{\mathit{u}}_i={\mathit{f}}_i,i=1,2,\dots ,T.$$ (4)

If we write all the unknown images in a matrix form U = [u₁, u₂, …, u_T], (4) can be rewritten into a compact matrix equation

$$\mathcal{P}\mathit{U}=\mathit{F}$$ (5)

where ℘U = [P₁u₁, …, P_Tu_T] and F = [f₁, …, f_T].

With low rank approximation assumption for U as discussed in Section II-A, the number of intrinsic unknowns of (5) are possibly less than the number of measurements, and therefore it is possible to reconstruct T CBCT images in U from T projections. To incorporate the underlying low-rank assumption into the cine-CBCT reconstruction process, we would like to explore matrix factorization based low-rank models in this study. More specifically, we enforce a decomposition form of the unknown matrix U of images as U = LR where L ∈ ℝ^N×K and R ∈ ℝ^K×T for a small integer K. From basic linear algebra knowledge, any matrix U of rank K can be represented in U = LR and conversely, the rank of U is at most K given the factorization form. In our algorithm, the value of K is specified by the user and our method regarding the selection of K will be presented later. We would like to point out that there is another popular approach for imposing the low rank condition that penalizes the nuclear norm of the matrix U, namely the sum of the singular values. Compare these two methods, the latter always finds orthogonal basis because of the involved singular value decomposition process. In contrast, our factorization method does not require this implicit orthogonality and hence attains the advantage of avoiding unfavourable bias on the resulting low-rank matrices [17]. In some sense, the approach of penalizing the nuclear norm of U is like principle component analysis and our approach is like independent component analysis. As a consequence, each of our basis, i.e., each column of L, represents more meaningful images and hence we can enforce some desired image properties on L, such as sparsity under wavelet transform.

This matrix factorization approach also allows for the additional regularizations on L and R, so that U = LR carries desirable physical properties. First, the columns of the matrix L, corresponding to images, can be interpreted as a basis that efficiently represents all the columns of U. Notice that images usually have sparse coefficients under suitable transforms such as wavelet tight frames [21], [22]. Let 𝒟 be such a transform. Since the columns of L are images, we want 𝒟L to be sparse. It is well-known that ℓ₁-norm minimization leads to sparse solutions. Therefore, the ℓ₁-norm ||𝒟L||₁ is penalized. Second, the rows of R are the coefficients of U under the basis L, which reflect the respiratory motion. As the respiratory motion varies and could be irregular sometimes, there is no universal regularization that is suitable for all kinds of respiratory motion. We simply penalize its Frobenius norm ${\Vert \mathit{R}\Vert }_F^2:={\sum }_{i,j}{R}_{ij}^2$ to balance the energy of L and R. By enforcing sparse representation of L in wavelet domain, the intrinsic degrees of freedom are further reduced. Both low rank and sparse conditions can be regarded as some kind of regularization that makes the whole problem less under-determined or ill-posed.

Altogether, we propose to reconstruct the cine-CBCT by solving an optimization problem

$$\underset{\mathit{L},\mathit{R}}{min}\lambda {\Vert \mathcal{D}\mathit{L}\Vert }_1+{\Vert \mathit{R}\Vert }_F^2,\text{s.t.}\mathcal{P}(\mathit{LR})=\mathit{F}.$$ (6)

In practice, (5) is barely satisfied, because there is always unavoidable noise in the measurements F. Moreover, in reality the matrix U is only approximately low-rank and explicitly enforcing a low-rank representation leads to error. For these considerations, we solve

$$\underset{\mathit{L},\mathit{R}}{min}\lambda {\Vert \mathcal{D}\mathit{L}\Vert }_1+{\Vert \mathit{R}\Vert }_F^2,\text{s.t.}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2\le {\sigma }^2$$ (7)

where ||·||_F is the Frobenius norm, namely ${\Vert \mathit{A}\Vert }_F=\sqrt{{\sum }_{i,j}{A}_{i,j}^2}$ for a matrix A. In (7), σ is a parameter to control to what extent the violation of (5) is allowed.

Algorithm

Let us first consider the algorithm for solving (6). We use a split Bregman method [23], [24] (also known as augmented Lagrangian method) to solve this problem. The augmented Lagrangian of (6) is

$$E(\mathit{L},\mathit{R},\mathit{Z})=\lambda {\Vert \mathcal{D}\mathit{L}\Vert }_1+{\Vert \mathit{R}\Vert }_F^2+\langle \mathit{Z},\mathcal{P}(\mathit{LR})-\mathit{F}\rangle +\frac{\mu }{2}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2$$ (8)

where 〈·, ·〉 is the inner product, and Z is Lagrange multipliers. With appropriate fixed Z, an optimal L, R can be found by simply minimizing E(L, R, Z) with respect to (L, R). Therefore, the trick is to determine Z. In the augmented Lagrangian algorithm, we use

$$\{\begin{array}{l}\{\begin{array}{l}\mathit{L}\leftarrow arg{min}_{\mathit{L}}E(\mathit{L},\mathit{R},\mathit{Z})\hfill \\ \mathit{R}\leftarrow arg{min}_{\mathit{R}}E(\mathit{L},\mathit{RZ})\hfill \end{array}\hfill \\ \mathit{Z}\leftarrow \mathit{Z}+(\mathcal{P}(\mathit{LR})-\mathit{F}).\hfill \end{array}$$ (9)

Algorithm 1.

1:	Repeat for sout times. Solve the first subproblem in (9) by performing the following steps for sin times. Update $\mathit{L}\leftarrow arg{min}_{\mathit{L}}\frac{\mu }{2}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}+\mathit{Z}/\mu \Vert }_F^2+\frac{{\mu }_1}{2}{\Vert \mathcal{D}\mathit{L}-\mathit{C}-{\mathit{Z}}_1/{\mu }_1\Vert }_F^2$. Update C ← 𝒯λ/μ1 (𝒟L − Z1/μ1). Update Z1 = Z1 + (C − 𝒟L) Solve the second subproblem in (9) by performing the following steps for sin times. Update $\mathit{R}\leftarrow arg{min}_R\frac{\mu }{2}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}+\mathit{Z}/\mu \Vert }_F^2+\frac{{\mu }_2}{2}{\Vert \mathit{R}-\mathit{B}-{\mathit{Z}}_2/{\mu }_2\Vert }_F^2$. Update B ← (R − Z2/μ2)/(1 + 1/μ2). Update Z2 = Z2 + (B − R).
2:	If ${\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2$ is small enough, then return.
3:	Update Z ← Z + (℘(LR − F).
4:	Goto Step 1.

The two subproblems in (9) are solved by split Bregman algorithm again in a similar fashion to (8) and (9). Let us take the first one as an example. By introducing an auxiliary variable C, the first subproblem in (9) is equivalent to

$$\underset{\mathit{L}}{min}{\Vert \mathit{C}\Vert }_1+\langle \mathit{Z},\mathcal{P}(\mathit{LR})-\mathit{F}\rangle +\frac{\mu }{2}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2\text{subject}\text{to}\mathit{C}=\mathcal{D}\mathit{L}$$ (10)

and the associated augmented Lagrangian is

$$E_1(\mathit{L},\mathit{C},{\mathit{Z}}_1)=\lambda {\Vert \mathit{C}\Vert }_1+\langle \mathit{Z},\mathcal{P}(\mathit{LR})-\mathit{F}\rangle +\frac{\mu }{2}{\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2+\langle {\mathit{Z}}_1,\mathit{C}-\mathcal{D}\mathit{L}\rangle +\frac{{\mu }_1}{2}{\Vert \mathit{C}-\mathcal{D}\mathit{L}\Vert }_F^2.$$

Then, a split Bregman method for solving the first subproblem in (9) is as follows:

$$\{\begin{array}{l}\mathit{L}\leftarrow arg{min}_{\mathit{L}}{E}_1(\mathit{L},\mathit{C},{\mathit{Z}}_1)\hfill \\ \mathit{C}\leftarrow arg{min}_{\mathit{C}}{E}_1(\mathit{L},\mathit{C},{\mathit{Z}}_1)\hfill \\ {\mathit{Z}}_1\leftarrow {\mathit{Z}}_1+(\mathit{C}-\mathcal{D}\mathit{L}).\hfill \end{array}$$ (11)

All steps involved in (11) can be solved easily by either entrywise soft-thresholding (for C) and linear equation solvers (for L), e.g., conjugate gradient method. We use the same method for solving the second subproblem in (9). The full algorithm is summarized in Algorithm 1, where 𝒯 is the soft-thresholding operator defined by [𝒯_α(A)]_ij = sign([A]_ij) · max{|[A]_ij| − α, 0}.

For any true or semi time resolved CBCT reconstruction, both storage and computational cost is a challenge. An important feature of our formulation and computational algorithm is to explore the low rank property. In our numerical computation, the huge matrix is stored and manipulated in a low-rank decomposition form, which can significantly reduce the memory size and computational cost. In particular, the computational cost of Algorithm 1 is mainly on solving linear equations in Step 1(a)(i) and 1(b)(i), where the conjugate gradient (CG) algorithm is employed. For moderately large μ₁/μ and μ₂/μ, the condition number of these linear equations is small, and therefore only a few iterations are necessary for the convergence of the CG algorithm. Consequently, each step in Algorithm 1 can be done in several matrix-vector products. The computational time for the reconstruction of images with 128×128 pixels and 360 projections is typically a few hours, on a computer with Core i7–2600 CPU at 3.40 GHz, 8 GB memory, and MATLAB R2013a.

One complexity of this problem comes from the nonconvexity of the objective function in (6). Since there may exist local minima, we have to make sure our algorithm get a desired solution. Yet, in our numerical experiments, this nonconvexity issue is not found to be a problem for the following two reasons. First of all, our algorithm may find the global minimum of (6). As pointed out in [25], the augmented Lagrangian algorithm attains the global minimum for nonconvex objectives in low-rank factorization form under suitable assumptions. Similar algorithms to ours has been used in, e.g., SDPLR (semi-definite programming via low rank factorization) [26]. Secondly, we have also chosen the initial guess to the iterative algorithm in the Algorithm 1 carefully as following. We first solve a convex minimization problem

$$\underset{\mathit{U}}{min}\frac{1}{2}{\Vert \mathcal{P}\mathit{U}-\mathit{F}\Vert }_F^2+\lambda {\Vert \mathit{U}\Vert }_{\ast }$$ (12)

where ||U||_* is the nuclear norm, i.e., the summation of the singular values of U. The nuclear norm minimization is able to find a lowest-rank solution U_* of (5) within a precision [16]. Then, the initial guess in the Algorithm 1 is chosen to be the best rank-K approximation to U_*. Let U_* = WΣV^T be a singular value decomposition. If the rank of U_* is less than K, we choose L⁽⁰⁾ = WΣ^1/2 and R⁽⁰⁾ = Σ^1/2V^T as the initial guesses. If the rank of U_* exceeds K, we choose ${\mathit{L}}^{(0)}={\mathit{W}}_K{\mathrm{\sum }}_K^{1/2}$ and ${\mathit{R}}^{(0)}={\mathrm{\sum }}_K^{1/2}{\mathit{V}}_K^T$ as the initial guesses, where W_K, V_K are the first K columns of W and V respectively, and Σ_K is the K×K principle submatrix of Σ. By this way, L⁽⁰⁾ R⁽⁰⁾ is the best rank-K approximation of U_*.

As for the problem in (7), we still use the Algorithm 1, but we stop the iteration as soon as ${\Vert \mathcal{P}(\mathit{LR})-\mathit{F}\Vert }_F^2\le {\sigma }^2$. By this way, we can get a quite good approximate solution to (9); see [27] for a detailed discussion. This approach has been previously used and discussed in similar mathematical problems but in other contexts, e.g., [24], [27], [28].

B. Choice of K

One practical issue in our algorithm is the selection of the parameter K to control the matrix rank. In practice, we achieve this goal by the following procedure.

We first set K to be a large enough number, e.g., K = 20, and run our algorithm. Recall that the columns of L forms a basis to represent the images in U. Because of the sufficiently large K value in this trial run, the algorithm is forced to generate a set of K basis vectors containing those good ones for U, as well as the unnecessary bad ones. This is reflected by the fact that some columns of L in the solution make significant contributions to U, while the other columns contribute little. For those unnecessary columns in L, their presence introduces a small but observable amount of signals into the finally reconstructed images in U and compromises its quality. It is therefore desirable to eliminate them from the first place by setting the value of K to be the number of the significant columns. A second reconstruction is then performed with this properly chosen K value.

It remains to determine which columns are significant and which ones are negligible. Since the contribution of the ith column of L to U is L(:, i)R(i, :) any norm of this project reflects the importance of this basis vector L(:, i). The larger norm is, the more significant L(:,i) is. In the experiments, we use the ∞-norm to identify the significance, which is the maximum of row absolute sums of a matrix, or equivalently, the pixel that has the largest absolute sum over time. The column L(:, i) is considered to be negligible, if ||L(:, i)R(i, :)||_∞ is close to zero, and significant otherwise.

C. Experiments

We tested our cine-CBCT reconstruction algorithm on a digital NURBS-based cardiac-torso (NCAT) phantom [29], which generates a patient body in thorax region with detailed anatomical features and a realistic motion pattern. The patient respiratory period is 4 s. The CBCT gantry rotates about the patient at a constant speed for a full rotation in 59 s, in which 360 X-ray projections are acquired. At each X-ray projection acquisition, we compute the NCAT phantom image at the specific time point with a resolution of 128 × 128, and the projection is then computed using a ray-tracing algorithm at the associated projection angle with a detector resolution of 256 bins. The patient breathing period and the gantry rotation period are chosen to be incommensurate deliberately, so that all the 360 patient images are distinct, although some of them visually look close. Some of the underlying true images are shown in Fig. 1. Under this setup, the size of U is 16384 × 360, and the size F of is 256 × 360.

Fig. 1.

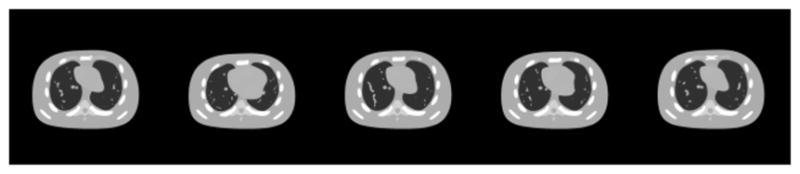
Ground truth cine-CBCT images. From left to right: frame 20, 81, 160, 256, 334. Display window is (−1000,420) HU.

Two experiments are performed in this feasibility study, namely the measured projections F generated from a full-fan and half-fan scan. In each case, we will first present the results for the selection of the parameter K and then the reconstruction results. Apart from visual inspection of the reconstructed cine-CBCT images, we have also quantitatively assessed the restored image quality using relative error as a metric defined by ||LR − U_true||_F/||U_true||_F, where L, R are the outputs of the proposed method, and U_true is the matrix consisting of ground truth NCAT images. Unless specified, the parameters used throughout our experiments are λ = 4000, μ = 1, μ₁ = μ₂ = 10⁵, and s_in = s_out = 10. We stop the algorithm when ||℘(LR) − F||_F/||F||_F ≤ ε and ε is chosen case by case.

III. Experimental Results

A. Full-Fan Scan

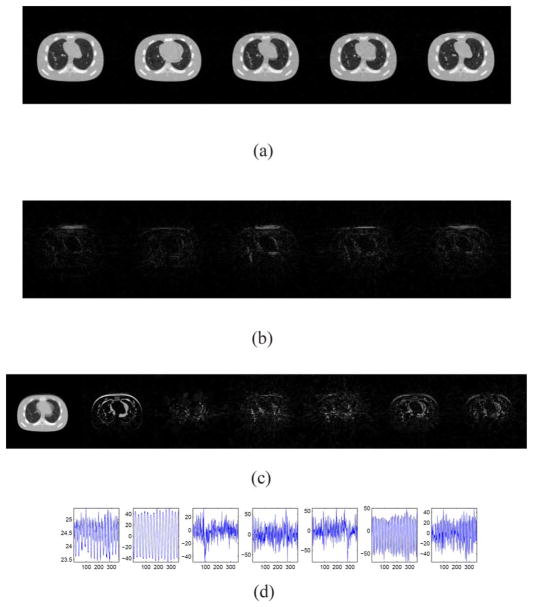
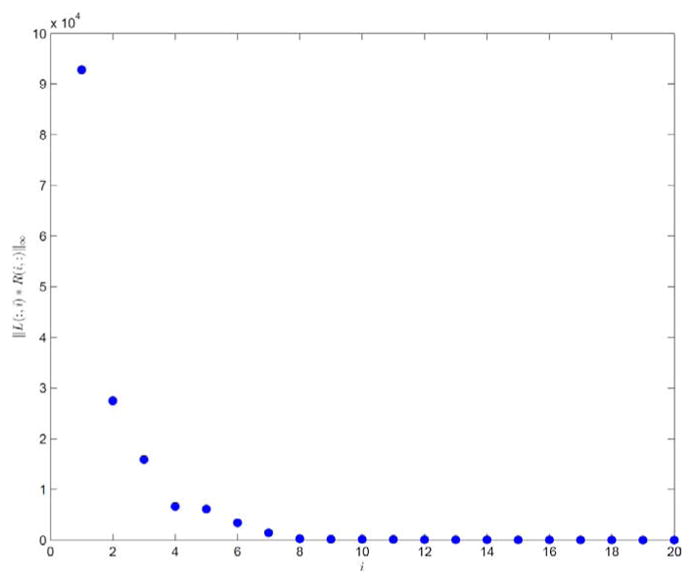
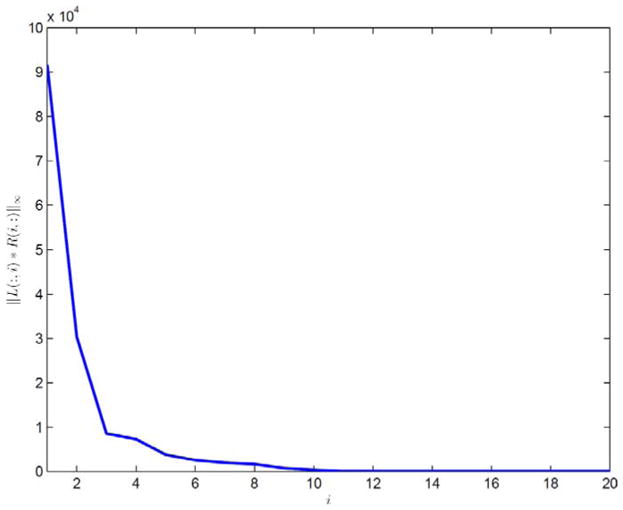
For this case, the plot of ||L(:, i)R(i, :)||_∞ in a descending order as a function of the column index i is first depicted in Fig. 2, with a trial run of K = 20. Clearly, the eighth column and beyond contribute little to the reconstructed images and hence should be removed. As such, K = 7 is selected and the corresponding results are shown in Figs. 3 and 4. Comparing the restored images in Fig. 3 with the corresponding ground truth images in Fig. 1, it is found that our algorithm is able to capture the motions of the anatomy and restore the structures, even those small ones inside the lung. Meanwhile, observable artifacts inside the heart and at its boundary also exist. Quantitatively, the relative error of the restored cine-CBCT images is 3.89%.

Fig. 2.

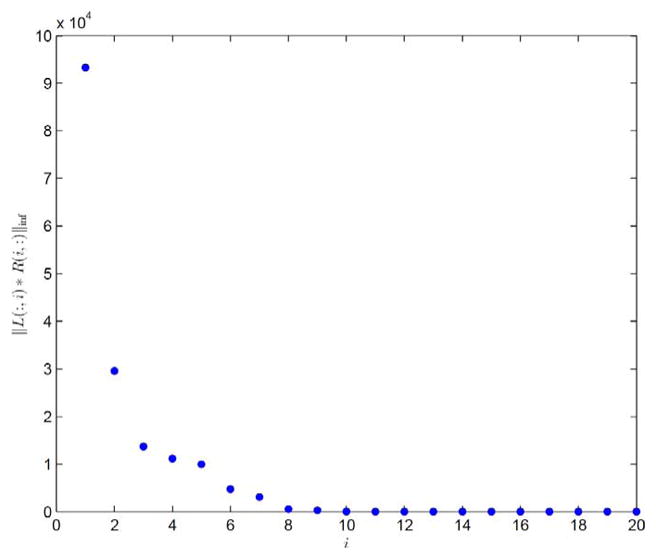
||L(:, i)R(i, :)||_∞ in descending order. Result is produced with K = 20.

Fig. 3.

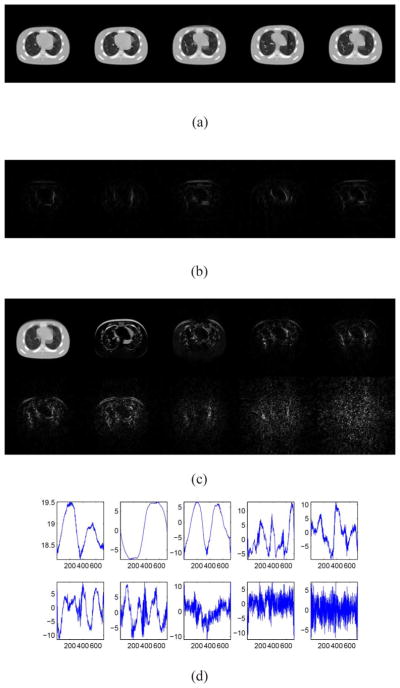
Restored cine-CBCT images from a full-fan scan and the absolute value of the differences to the ground truth. Relative error is 3.89%. From left to right: frame 20, 81, 160, 256, 334. (a) Restored cine-CBCT images. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. Display window is (0,280) HU.

Fig. 4.

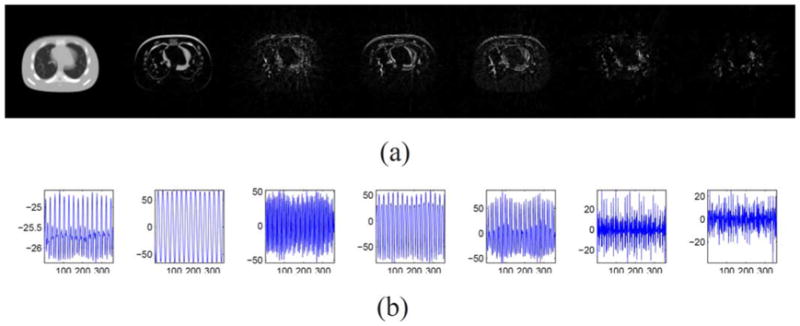
L and R in the cine-CBCT image reconstruction from a full-fan scan. (a) Columns of L. Each column is reshaped into an image. (b) Rows of R.

To further look into the reconstruction results, we plot the columns of L in Fig. 4(a), where each column is reshaped into a 128 × 128 image. These images form the basis to represent all the reconstructed cine-CBCT images. It is observed that the first one is similar to an image averaged over all the cine-CBCT images. Its presence provides an overall structure that is common to all the images in the cine-CBCT. Meanwhile, other basis images represent differences between images of U. We also plot the corresponding coefficients in R in Fig. 4(b), which attain a periodically variation pattern, indicating the patient respiratory motion.

B. Noisy Data From a Full-Fan Scan

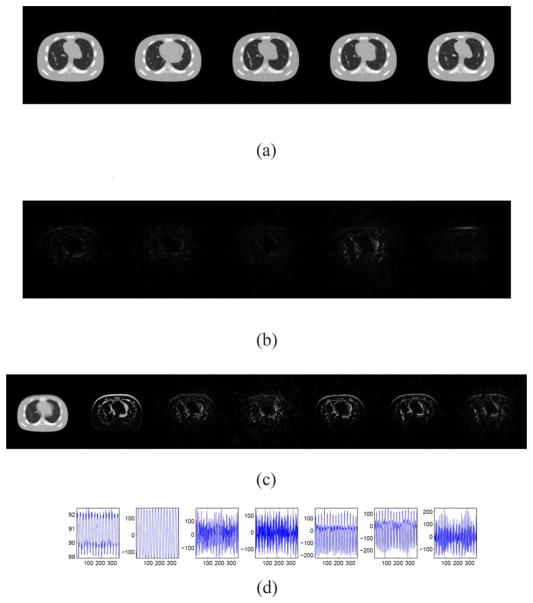
To demonstrate the robustness of our algorithm to noise, we test our algorithm with noisy data. We add noise at 0.5 mAs/projection to the projection data from the full-fan scan in Section III-A. In this case, the parameter K is selected as K = 4 according to Fig. 5. Fig. 6(a) depicts the reconstructed images. The relative error of the restored cine-CBCT images is 6.81%. The columns of L and the rows of R are plotted in Fig. 6(b) and (c), respectively. Again, we see that the columns of L are meaningful basis corresponding to the average image as well as the variations between them, and the rows of R oscillate periodically.

Fig. 5.

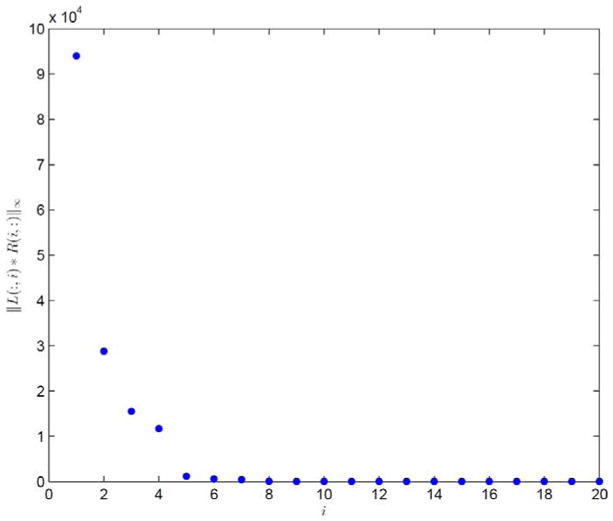
||L(:, i)R(i, :)||_∞ in descending order. Result is produced with K = 20 and noise at 0.5 mAs/projection.

Fig. 6.

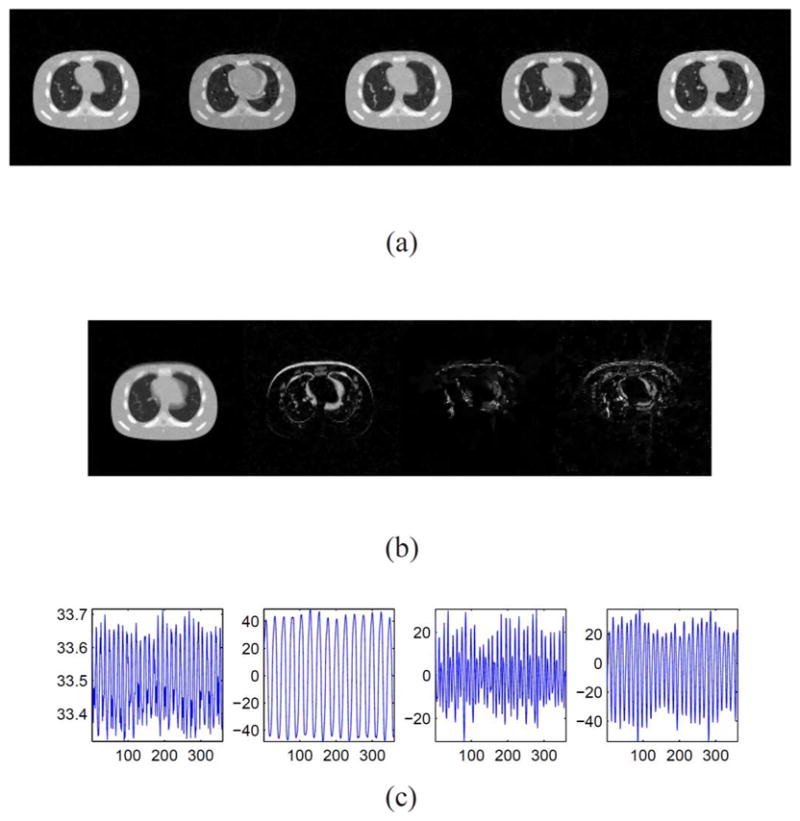
Result of cine-CBCT image reconstruction with noise at 0.5 mAs/projection from a full-fan scan. (a) Restored cine-CBCT image with the relative error 6.81%. From left to right: frame 20, 81, 160, 256, 334. Display window is (−1000,420) HU. (b) Columns of L. Each column is reshaped into an image. (c) Rows of R.

C. Half-Fan Scan

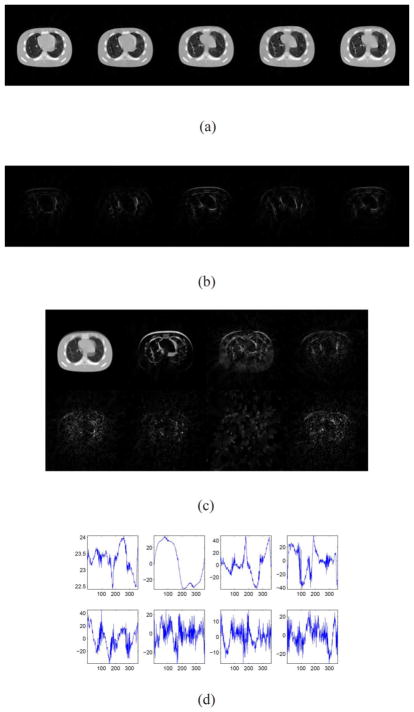
For the case with noiseless data from a half-fan scan, the parameter K is selected as K = 7 according to Fig. 7. In Fig. 8, we plot the reconstructed images, the columns of L, and the rows of R. The relative error of the restored cine-CBCT images is 6.62%, and we see again that the columns of L are meaningful basis corresponding to the average image as well as the variations between them, and the rows of R oscillate periodically.

Fig. 7.

||L(:, i)R(i, :)||_∞ in descending order. Result is produced with K = 20 from a half-fan scan.

Fig. 8.

Result of cine-CBCT image reconstruction from a half-fan scan. (a) Restored cine-CBCT image with the relative error 6.62%. From left to right: frame 20, 81, 160, 256, 334. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. Display window is (0,710) HU. (c) Columns of L. Each column is reshaped into an image. (d) Rows of R.

IV. Validations on Our Model

A. Validation on the Low-Rank Assumption

To demonstrate validity of the low rank assumption, we have conducted a study on a digital NCAT phantom, where typical images of such a phantom are in Fig. 1. A sequence of T images are generated at a transverse slice during a breathing cycle. Each of these images is represented by a vector of length N, where N is the number of pixels in one image. We then form a N × T matrix using these vectors as columns. Singular value decomposition of this matrix is conducted. For a case with T = 100 per breathing cycle, there are in total 100 nonzero singular values (SVs), indicating that the matrix is strictly speaking of full rank. Yet, only the first few SVs dominate, as illustrated in the left panel of Fig. 9. This implies that the matrix is approximately of low rank. In particular, the eight largest SVs accounts for over 97% of the sum of all the SVs. Moreover, this ratio, namely the required number of leading SVs to account over 97% of the sum of all SVs to the total number of SVs (or images), decreases dramatically as the number of images T sampled in a breathing cycle increases, as shown in the right panel of Fig. 9. This simple numerical experiment demonstrates the validity of our assumption to a certain extent and the rest of our reconstruction work is based on this assumption. However, we remark that whether this assumption holds in real clinical cases is subject to further validations.

Fig. 9.

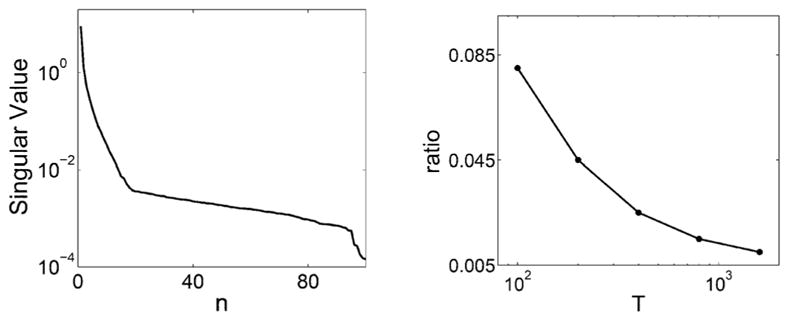
Left: Singular values of a set of 100 NCAT images taken with in one breathing cycle. Right: the ratio of required number of singular values to restore 97% of the NCAT images to the total number of images n_f in a breathing cycle.

B. Exactly Low-Rank Ground Truth

We have also conducted one experiment where the ground truth 4DCT images are indeed forms a low-rank matrix. This experiments show that our model works better for exactly low-rank ground truths than with approximately low-rank ones.

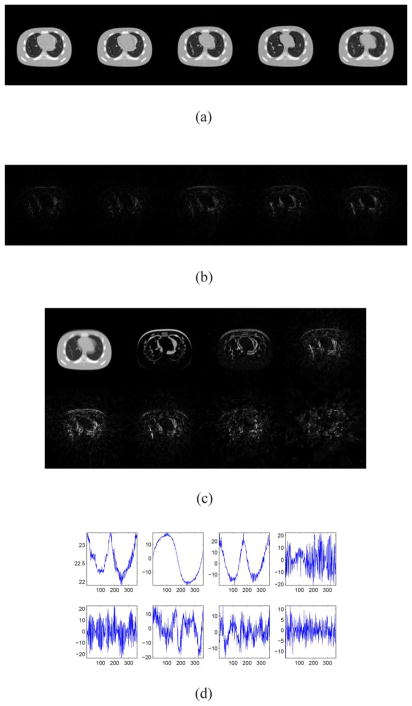
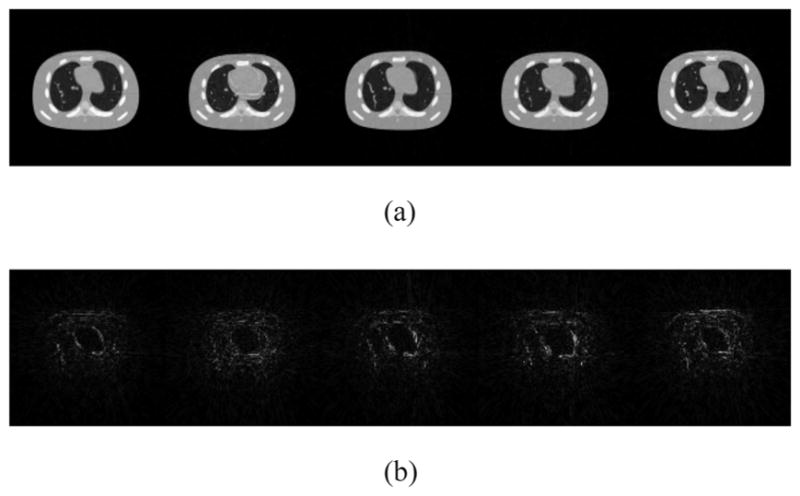
We generate the true images Û₁ by Û₁ = L̂₁R̂₁, where L̂₁ and R̂₁ are from Fig. 4(a) and (b), respectively. By this way, the true cine-CBCT image Û₁ is an approximation to the cine-CBCT image in Section II-E whose respiratory motion is rather regular. Clearly, the rank of Û₁ is 7 and the dimension is 16384 × 360, as L̂₁ consists of 7 basis images of size 128 × 128 and R̂₁ of 7 coefficients of length 360. Then, we restore L and R from F = ℘Û₁ by Algorithm 1. The restored basis images and the ground truth images are compared in Fig. 10. The relative error of the restored cine-CBCT image is 1.35%, which is smaller than that in Section III-A, where the ground truth is not exactly but approximately low-rank. This shows the low-rankness of the ground truth 4DCT images can help reduce the reconstruction error.

Fig. 10.

Result of cine-CBCT image (with exactly rank 7) reconstruction from a full-fan scan. (a) Restored cine-CBCT image with the relative error 1.35%. From left to right: frame 20, 81, 160, 256, 334. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. Display window is (0,280) HU. (c) Columns of L. Each column is reshaped into an image. (d) Rows of R.

C. One Cycle Scan

Our model does not depend on the periodicity of the respiratory motion. To validate this fact, we tested our model on cine-CBCT images generated in one breathe cycle, where no breathe phase is repeated. We use the true cine-CBCT image from the one described in Section II-E with a scanning period 4.1 s and still T = 360, and frames of this true cine-CBCT image are shown in Fig. 11. Therefore, there is only one full cycle of respiratory motion in the true cine-CBCT images. The results are plotted in Figs. 12 and 13. Our method can still give a satisfactory result, and the relative error of the restored cine-CBCT images is 9.78%.

Fig. 11.

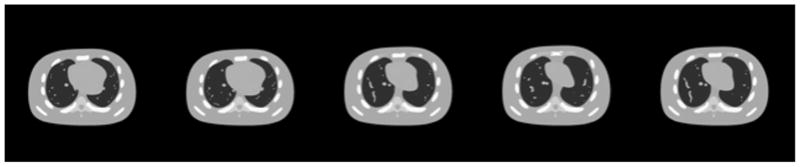
Ground truth cine-CBCT images generating from one breathe cycle. From left to right: frame 50, 120, 190, 260, 330. Display window is (−1000,420) HU.

Fig. 12.

||L(:, i)R(i, :)||_∞ in descending order in Experiment 5. Result is produced with K = 20.

Fig. 13.

Result of cine-CBCT image (one breathe cycle) reconstruction from a full-fan scan. (a) Restored cine-CBCT image with the relative error 9.78%. From left to right: frame 50, 120, 190, 260, 330. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. The display window is (0,1420) HU. (c) Columns of L. Each column is reshaped into an image. (d) Rows of R.

For the one cycle scan, we performed two more experiments to see how the projection operator ℘ affects the quality of the reconstructed images. Firstly, we find that a random permutation on the projection angels could improve the quality of the reconstructed image. This can be seen from the results presented in Fig. 14, and the relative error of the restored cine-CBCT images is 5.39%. The reason is that, when we randomly permute the projection angels, the projection angels for similar images are random, making the reconstruction more accurate and robust especially when using one cycle scan. Secondly, increasing the temporal resolution could improve the quality of reconstructed images. To see this, we use the true cine-CBCT image from the one described in the previous paragraph with a scanning period 4.1 s and T = 720. The results are depicted in Fig. 15. The relative error of the restored cine-CBCT images is 7.42%. This is related to the validation test presented in Section IV-A, i.e., the ration of required number of leading SVs to account over a certain percentage of the sum of all SVs to the total number of SVs (or images), decreases dramatically as the number of images T sampled in a breathing cycle increases, as shown in the right panel of Fig. 9.

Fig. 14.

Result of cine-CBCT image (one breathe cycle) reconstruction from a full-fan scan with randomly permuted projection angels. (a) Restored cine-CBCT image with the relative error 5.39%. From left to right: frame 50, 120, 190, 260, 330. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. The display window is (0,710) HU. (c) Columns of L. Each column is reshaped into an image. (d) Rows of R.

Fig. 15.

Result of cine-CBCT image (one breathe cycle) reconstruction from a full-fan scan with T = 720. (a) Restored cine-CBCT image with the relative error 7.42%. From left to right: frame 100, 240, 380, 520, 660. Display window is (−1000,420) HU. (b) Absolute value of the differences to the ground truth. Display window is (0,1420) HU. (c) Columns of L. Each column is reshaped into an image. (d) Rows of R.

D. High Resolution Images

Since the image video is stored and manipulated in a low-rank decomposition form, our method can reconstruct images with high resolution images. To demonstrate this, we test our algorithm on a high resolution correspondence of the datasets in Section III-A. In particular, we test images with 512 × 512 pixels and 360 projections, and we still use a detector resolution of 256 bins. The results are depicted in Fig. 16. The relative error of the restored cine-CBCT images is 10.11%. The error is larger than that for low-resolution since the linear (5) is more under-determined than the low resolution case.

Fig. 16.

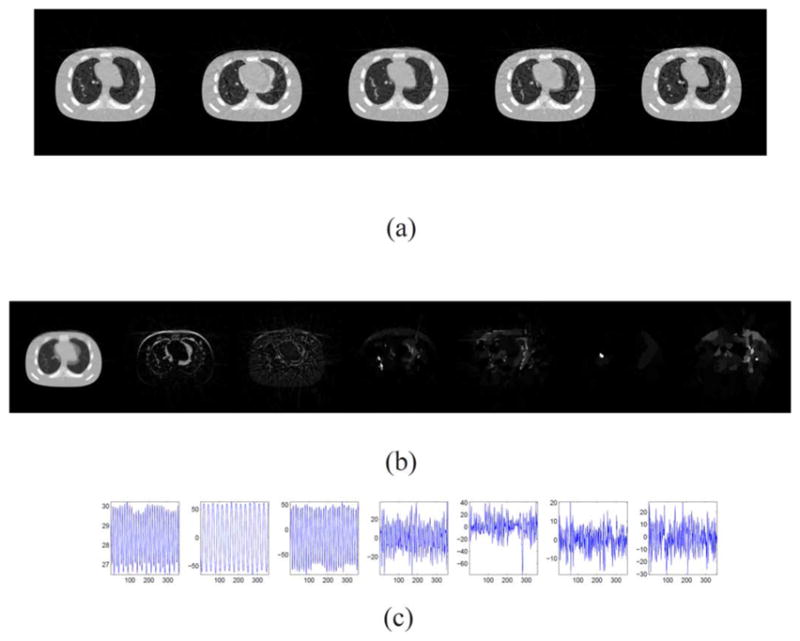
Result of 512 × 512 cine-CBCT image reconstruction from a full-fan scan. (a) Restored cine-CBCT image with the relative error 10.11%. From left to right: frame 20, 81, 160, 256, 334. Display window is (−1000,420) HU. (b) Columns of L. Each column is reshaped into an image. (c) Rows of R.

V. Conclusion and Discussion

In this work, we have proposed an computational algorithm to reconstruct cine-CBCT to provide a set of time-dependent images in the thorax region under the assumption that the matrix formed by all of these images to be reconstructed has a low rank approximation. In contrast to the currently used 4DCBCT, where only respiratory phase-resolved imaging is achieved, the cine-CBCT modality retrieves the instantaneous patient anatomy corresponding to each CBCT projection. Cine-CBCT reconstruction is apparently a challenging problem due to the very limited projection information. Yet, by effectively incorporating the underlying local and global temporal coherence of cine-CBCT images into the reconstruction process, we demonstrate the feasibility of this modality. In particular, the low rank approximation is based on matrix factorization form U = LR for the matrix U whose columns are the images to be reconstructed. The dimension of the matrix L constraints the rank of U and hence maximally and automatically exploits a coherence condition among all the images in cine-CBCT. Simulation studies on an NCAT phantom serve as a very preliminary test to demonstrate the feasibility of our approach, where successive reconstructions have been observed in various experiments.

In addition to the apparent advantage of improved temporal resolution in the cine-CBCT over 4DCBCT, the reconstruction of cine-CBCT is not as demanding regarding the amount of projection data as 4DCBCT, at least based on our simulation studies. Because of the phase binning in 4DCBCT, a certain number of projections are required in each bin to yield a CBCT image for the bin with a satisfactory quality. Hence, it is usually challenging to get a 4DCBCT with only one-minute scan and in practice, protocols of multiple rotations or a slow rotation is utilized. In contrast, the cine-CBCT effectively incorporates the inter-image correlations into the reconstruction and a set of images with visible major anatomical features are obtained even with a super-fast scan protocol corresponding to only a single breathing period, i.e., a 4-s scan if the patient’s breathing period is 4 s, as demonstrated in our studies. Another advantage is that our method can deal with respiratory motion quite well in the sense that irregularity does not affect the construction of the regular images too much as shown in the experiments.

Although the fourth dimension in cine-CBCT is more than breathing phase as in conventional 4DCBCT, we would like to point out that cine-CBCT is not completely time resolved in general. A good cine-CBCT reconstruction is based on two key assumptions. First, all cine-CBCT images can be represented (approximately) by linear combinations of a small number of basis images, meaning certain irregular patient anatomy variation may not be captured by cine-CBCT if they cannot be approximated well by the basis images. Second, all cine-CBCT images collectively correspond to a sufficient number of projections covering a sufficiently large scanning angle, meaning our algorithm will not work if the scanning angle is smaller than that required by the regular CBCT reconstruction. Nor will other methods do since no reconstruction method can recover information beyond the data. That being said, cine-CBCT images reconstructed using our algorithm still contain clinically valuable temporal information and represent a quantum leap from the conventional 4DCBCT images with the same setup and measurements.

Despite the success in this feasibility study, there are a few practical issues as for the clinical applications of cine-CBCT. First of all, the low rank assumption has to be verified using clinical data. Second, only one slice of the patient anatomy is reconstructed in this proof-of-principle study. When cone-beam geometry is considered to reconstruct volumetric CBCT images, although the fundamental principles in our algorithm can be easily applied, one has to address challenges for both storage and computational time for any true or semi-time resolved CBCT reconstruction in clinical practice. Currently, it takes a few hours to reconstruct those images shown in our study with 128 × 128 pixels and 360 projections on a typical computer using MATLAB. For real clinical cases with a cone beam geometry and a high resolution, e.g., voxels, the computation time would be estimated too long under the current computation platform. However, more powerful computational platforms, such as graphics processing unit (GPU) [30], or multi-GPU [31], are expected to greatly accelerate the reconstructions. GPU is essentially a parallel processing platform with a large number of processing cores. For example, in Algorithm 1, the most computation intensive part is computing forward projection ℘ and its transpose ℘^T when solving the least-square problems. For problems of large sizes, these matrices are too large to be stored. But these operations can be greatly accelerated on the GPU platform by splitting the operations according to projection ray-lines, or image voxels [32]. Other computation intensive tasks, such as matrix-matrix or matrix-vector operations, can be easily parallelized to achieve significant speed up. Another challenge is large memory requirement which can not fit into single GPU. In this case, splitting calculations across multiple GPUs will be the solution, at the cost of inter-GPU communications [31]. It will be our future research project to implement the reconstruction algorithm on GPU. Over the years, GPU-based computing has demonstrated the feasibility of greatly accelerating CBCT reconstructions, such that the computation time of a high-resolution 3-D case on GPU is comparable to that for a 2-D case using MATLAB on CPU [33]. It is expected that these advanced approaches can eventually render the computation efficiency to a practically acceptable level.

Moreover, even in the current form, namely reconstructing only a 2-D slice in a time-resolve fashion, our algorithm will still have some important applications and attain advantages over those methods employed in current clinical practice. One context is lung tumor motion management in advanced radiation therapy. At present, this is typically achieved by monitoring external surrogate motion, e.g., chest wall or diaphragm, and inferring tumor motions via a certain motion model. This indirect method suffers from problems such as motion model accuracy and reliability caused by poor internal-external correlations and temporal variations of motion patterns. Measuring motions of makers that are implanted to the lung tumor is another practical way. Yet, the invasive nature makes it less clinically preferred. Compared to these approaches, our method is capable of directly imaging motions, although in a 2-D slice in this initial study due to computational costs. It will hence provide valuable information to facilitate a number tasks in radiotherapy motion managements, e.g., tumor tracking or gated treatment delivery. In addition, because our algorithm does not rely on motion periodicity, its application can be generalized to tumor sites other than lung, such as prostate, which are affected by motions of nearby organs. For these sites, 4DCBCT cannot be applied due to the lack of motion periodicity. With limited correlations between the organ of interest and other surrogates, it is not possible to infer organ motions via surrogate motions. Tracking implanted markers is employed currently if needed. Our method could be another method to retrieve motion information for these sites and therefore help motion managements in this context.

Finally, we would also like to remark that, we propose a new modality of cine-CBCT in this study and a reconstruction algorithm that can be potentially used to achieve it. It is not our claim that the algorithm is practical enough for cine-CBCT reconstruction, as only a 2-D slice is reconstructed in the studies here and 3-D cases are apparently computationally challenging for the moment. However, the problem of interest here is a temporally resolved imaging modality on the cone beam CT hardware system. Hence, the experimental designs in this study have been focused on the CBCT context, such that parameters in the simulation cases, e.g., gantry rotation speed and projection geometry, are set according to those in a CBCT scanner. It is also our study in near future to test the algorithm in real data acquired in a CBCT machine. The X-ray source will be collimated, so that only the central slice projection data will be used for reconstructing only one transverse plane. We also noticed that our algorithm can be applied to cases with a fan-beam projection geometry, i.e., conventional CT. Yet, cine-CT has been already achieved there [34]–[36]. Due to the ultra fast source rotation speed, cine-CT reconstruction is not a difficult problem with modern CT scanners, as enough many projections covering a large angular range can be acquired with in a short time window for a time point. Therefore, we focus our study on a much more challenging context with the current CBCT scanner, which hence leads to the name of cine-CBCT.