Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Feb 13;14(4):1841–1852. doi: 10.1021/acs.jctc.7b01206

Explicit Solvation Matters: Performance of QM/MM Solvation Models in Nucleophilic Addition

Jelle M Boereboom †, Paul Fleurat-Lessard ‡, Rosa E Bulo †,*
PMCID: PMC6023263  PMID: 29438621

Abstract

graphic file with name ct-2017-01206c_0008.jpg

Nucleophilic addition onto a carbonyl moiety is strongly affected by solvent, and correctly simulating this solvent effect is often beyond the capability of single-scale quantum mechanical (QM) models. This work explores multiscale approaches for the description of the reversible and highly solvent-sensitive nucleophilic N|···C=O bond formation in an Me2N–(CH2)3–CH=O molecule. In the first stage of this work, we rigorously compare and test four recent quantum mechanical/molecular mechanical (QM/MM) explicit solvation models, employing a QM description of water molecules in spherical regions around both the oxygen and the nitrogen atom of the solute. The accuracy of the models is benchmarked against a reference QM simulation, focusing on properties of the solvated Me2N–(CH2)3–CH=O molecule in its ring-closed form. In the second stage, we select one of the models (continuous adaptive QM/MM) and use it to obtain a reliable free energy profile for the N|···C bond formation reaction. We find that the dual-sphere approach allows the model to accurately account for solvent reorganization along the entire reaction path. In contrast, a simple microsolvation model cannot adapt to the changing conditions and provides an incorrect description of the reaction process.

1. Introduction

Compared to the gas phase, the mechanism of a chemical reaction in solvent can be strongly affected by the interactions between the solute and the solvent molecules. More than a century ago, the pioneering work of Berthelot1 and Menshutkin2 paved the way for a better understanding of these solvent effects, but despite this and many more advances,3−5 the atomistic details of solvent effects cannot yet be resolved experimentally. In contrast, atomistic aspects of chemical mechanisms can be intimately studied with computer simulations, and recent progress allows solvent inclusion into many molecular models used.6−12 Such an atomistic description of a reaction in solution requires rigorous sampling of all possible configurations of the solvent molecules around the solute. This sampling can be achieved through molecular dynamics (MD) simulations, but as the size of the molecular model increases, the approach becomes very arduous.

The efficiency of MD simulations of large solute–solvent systems can be greatly improved with a multiscale approach. Microsolvation is the simplest multiscale solvation model; it includes explicitly only the solvent molecules in the first solvation shell using a quantum mechanical (QM) description, while the long-range effects are approximated by implicit solvation.13 A more complex model uses the same QM description for the closest solvent molecules but describes the rest of the system explicitly with molecular mechanics (MM). The latter (QM/MM) models have been used since the 1970s and were recognized in 2013 with the Nobel Prize in Chemistry. Originally the systems studied with QM/MM were biomolecular proteins or other relatively rigid systems.14,15 In such applications, the composition of the region of interest does not change over time. Nowadays, there is an increasing interest in extending the application of these QM/MM models to highly diffusive systems (e.g., homogeneous/heterogeneous catalysis and chemistry of solvated systems).16−30 Several QM/MM solvation models have been developed for this purpose, but so far, there has not been one model that clearly outperforms the others.31 In this work, we first benchmark the state of the art in multiscale solvation models and then go on to perform accurate simulations of a class of particularly solvent-sensitive reactions.

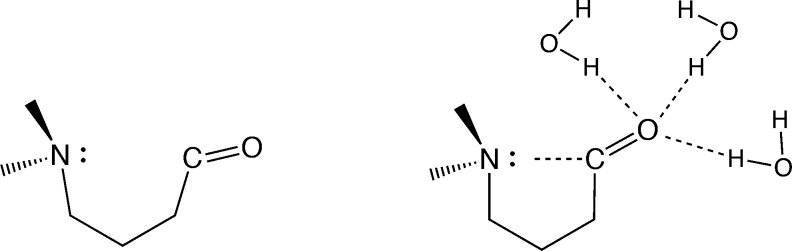
Chemical reactions involving charged intermediates are especially strongly affected by solvent. The intermediates are stabilized in polar protic solvents, while they are destabilized in apolar solvents, often yielding different mechanisms. Acid-catalyzed nucleophilic substitutions, for example, usually proceed through a nucleophilic addition onto the carbonyl moiety followed by the elimination of a different nucleophile in a subsequent step.32 However, a direct SN2 mechanism has also been observed (in polar solvents),33−36 and computations have comfirmed that the latter mechanism benefits from the stabilization of negative charge on the oxygen atom as the nucleophile approaches the carbonyl carbon. Bürgi and Dunitz identified crystal structures featuring a nucleophilic tertiary amino group and a carbonyl moiety separated by remarkably short distances.37 The unusual interaction (Figure 1) has since then been observed in many biological systems (e.g., as a central part of a new class of HIV inhibitors)38,39 and has been exploited in the development of heterogeneous catalysts for the enantioselective hydrogenation of α-functionalized ketones.40,41 But foremost, it can be seen as a transition state analogue in the nucleophilic addition of an amine to a carbonyl moiety. Indeed, the interaction is known to be stable only in the presence of polar protic solvents (Figure 1).42

Figure 1.

Figure 1

Open in a new tab

Lewis structures of the NCO molecule in only implicit solvent (left) and the NCO molecule in implicit solvent and three explicit water molecules (right).

Previous works42,43 have focused on understanding the N|···C=O interaction at the electronic level. It was found that this interaction has a partial dative character (nN → πCO*), but this participation is quite low, less than 0.18 electrons. Instead, a four electron/three center bonding model is more suited. As the N–C distance decreases, the donation of electrons into the N–C bond stems not only from the lone pair of the nitrogen atom but from the C=O bond as well. Overall, the combined effects result in a polarized carbonyl moiety (N|···C+–O–), which explains the observed stabilization by protic solvents; they stabilize the ionic C+–O– bond. One study42 employed a single molecule model system containing both moieties (denoted NCO molecule, Figure 1). Indeed, in this system, the absence of solvent does not yield stable N|···C distances that correspond to a bond. Step-wise introduction of water molecules in the model yields a decreasing N|···C bond length after geometry optimization. This demonstrates the remarkable sensitivity to solvation of this nucleophilic substitution mimic. Calculations of the electronic structure of the NCO molecule in its N–C bonded state, using both microsolvation models and QM/MM electrostatic embedding, revealed that a QM description of only the solute molecule is not sufficient to correctly describe the electronic structure of the weak bond.44 This makes the system ideally suited to benchmark QM/MM solvation models that can deal with diffusion of water molecules in the QM region. Pilmé et al. obtained binding energies for the N|···C+–O– bond,42 using a bimolecular model containing Me3N|···H2CO, only one explicit water molecule and an implicit solvent model. Static electronic structure calculations yielded binding energies of 9 kcal/mol (B3LYP) and 11 kcal/mol (CCSD(T)), which is about twice as strong as an average hydrogen bond in water. In this work, we aim to improve on this result by representing the aqueous solvent at varying levels of accuracy. We use the NCO molecule in Figure 1, which has the advantage that whenever the N|···C distance becomes large the different moieties do not diffuse away from each other.

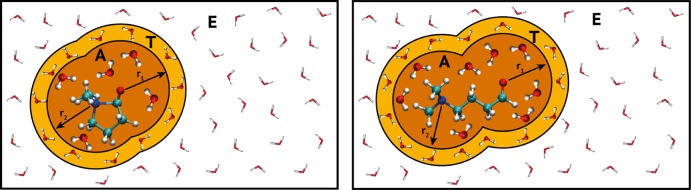
The QM/MM solvation models tested in this work all divide the system into an active (A) region and an environment (E) region. Molecules in the A-region are treated QM, and molecules in the E-region are treated MM. More complex models also define a third region: the transition (T) region. This region separates the A- and E-regions, and molecules inside the T-region have fractional QM character (depending on their distance to the QM center). In Figure 2, a schematic representation of a QM/MM simulation is shown for NCO solvated in water. Note that the A-region is defined by two spheres around the nitrogen and oxygen of the central NCO molecule. The two spheres can overlap or separate depending on the geometry of the system. The dual-sphere adaptive QM/MM scheme was introduced 10 years ago by Heyden et al.18 and constitutes a vast improvement over previous multiscale applications, in which a single large QM sphere needs to encapsulate all reactive chemical entities as well as the surrounding solvent. It is therefore noteworthy that the present work is the first application of the suggested dual-sphere scheme. For each of the two central atoms, the T-region is the volume between two spheres of different radii centered on the same atom (either nitrogen or oxygen of the NCO molecule). We define the E-region as the remaining volume, after exclusion of the A- and T-regions.

Figure 2.

Figure 2

Open in a new tab

Schematic representation of a QM/MM description of the closed state of NCO solvated in water (left) and the open state of NCO solvated in water. The system is partitioned into three regions: A-region [orange], T-region [yellow], and E-region [white] around the central NCO molecule. Ball and stick water molecules are QM, and MM molecules are depicted by thick lines. The QM character of the solvent molecules is determined by their distance to the nitrogen and oxygen of the NCO molecule (r1 and r2).

In summary, we aim to obtain an accurate free energy profile for the revesible intramolecular nucleophilic addition of an amine moiety to a carbonyl group, using multiscale solvation models. After benchmarking several of these models, we select two for the final computation of the reaction free energies (an explicit and an implicit solvation model) and discuss their performance in the simulation of the reaction mechanism. The work is organized as follows: In Section 2, we briefly describe our methodology and list the computational details. In Section 3.1, the different models are benchmarked on the structural features of the bonded (closed) state (Figure 2, left). Finally, in Section 3.2, the best performing explicit solvation model is used to obtain an accurate free energy profile. A comparison is made with a microsolvation model that only includes five explicit water molecules. A summary and conclusion can be found in Section 4.

2. Methodology

In this section, we provide a very brief overview of the multiscale solvation methods used, summarize our computational details, and discuss the relative computational costs of the different solvation models.

2.1. Multiscale Solvation

Simulation of complex systems often requires a multilevel description that treats a region of interest (active or A-region) with a quantum mechanical (QM) method and embeds it in an environment (E) region that is treated in a more approximate way. The approximate description can be a mean field (implicit) solvation method or it can be explicit molecular mechanics (MM). The latter combination of QM and MM (QM/MM) was originally designed for the simulation of biological systems, in which case most challenges arise from the description of covalent bonds across the boundary between the QM and MM zones. The QM/MM description of smaller solvated molecules does not require a boundary placed across covalent bonds. In order to account for solvent diffusion, however, aditional measures are required. Molecules need to be either reassigned to the A- or E-region every single MD time-step, or they need to be constrained to their respective regions. Throughout this work, we refer to the former as adaptive QM/MM models and to the latter as restrictive QM/MM models.

In this work, we employ five different multiscale models that include solvation effects on the NCO solute molecule. Three of them are adaptive QM/MM models: DAS19 (continuous switching between QM and MM in T-region), abrupt19 (instantaneous switch between QM and MM), and buffered-force.20 The latter switches instantaneously between QM and MM, but the molecules in the A-region feel a QM interaction with the molecules in the T- region, whereas molecules in the T-region in turn feel an MM interaction with molecules in the A-region. The fourth model is a restrictive QM/MM model; FIRES21 restricts MM solvent molecules from penetrating the QM region by a quadratic wall that is positioned where the outermost QM solvent molecule is located. The fifth model is not a QM/MM model. It is a simple microsolvation model that uses a continuum description to simulate the interaction with the E-region. It is also a restrictive model, in the sense that five explicit solvent molecules are restricted to a small region near the NCO molecule. A comprehensive overview of all solvation models is provided in the Supporting Information, and for most of the models, more in-depth descriptions are available in refs (45 and 46). In all QM/MM simulations, we deploy a dual-sphere scheme that guarantees QM solvation of both the amine and the carbonyl moiety. We note that this is the first application of the dual-sphere scheme, which was first proposed by Heyden et al.18

2.2. Computational Details

All MD simulations are performed with FlexMD,47 which is distributed with the ADF program package.48,49 FlexMD is a python wrapper around several molecular modeling packages. These packages provide the required QM or MM forces used to propagate the system. The MD propagation is handled by the atomistic simulation environment (ASE).50 In order to accurately describe our NCO model system in the open state (Figure 2, right), we need a cubic box with a minimum dimension of 18 Å. MD simulations of a box with this dimension containing only QM molecules are very costly, but a QM/MM model can simulate significantly larger systems. Our model system is a 30.8 Å cubic box containing the NCO molecule and 913 water molecules. For the QM/MM simulations, we choose an A-region that consists of two QM spheres with a radius of 4.1 Å around the NCO solute molecule (centered on nitrogen and oxygen). In this manner, the two hydrophilic moieties are both solvated by QM water, even when the system is in the open state. For DAS and buffered-force there is also a T-region (or buffer region) with a thickness of 0.9 Å around the A-region spheres, yielding a maximum QM radius of 5.0 Å around the two central atoms. More details on the dual-sphere scheme18 can be found in the Supporting Information. In an average DAS simulation, the dual-sphere approach assigns (on average) 29 water molecules to the QM set of the most demanding DAS QM/MM partition (5.0 Å radius). A single-sphere DAS computation with the same accuracy (with a radius large enough that it would encompass all water molecules within a radius of 5.0 Å around the oxygen and the nitrogen atom when the system is in the open state) assigns 76 water molecules to the QM set of the most demanding partition. More details regarding the relative efficiency of a dual-sphere simulation versus a single-sphere simulation can be found in the Supporting Information.

Our molecular model system was pre-equilibrated with the REAXFF potential51,52 at 1 atm for 20 ps (time step 0.25 fs). The PM6-DH+ functional53 as implemented in the MOPAC program54 was then used for the QM part of the system, whereas the MM part was calculated with REAXFF51,52 as implemented in the ADF program package.48,49 REAXFF was chosen because it reproduces the experimental water-in-water radial distribution function well.31 For the interactions across the periodic boundary, the REAXFF code uses the particle mesh Ewald method.55 We use mechanical embedding for the QM/MM interaction according to the IMOMM scheme.56,57 We selected this scheme to avoid the aggregation of molecules near the QM/MM boundary observed in electrostatic embedding simulations20 and extensively tested its performance for the accurate description of the solvated NCO molecule (see Section 3.1.2). A direct comparison of mechanical embedding with electrostatic embedding can be found in the Supporting Information.

The reference molecular system (fully PM6-DH+) is a 14.2 Å cubic box containing the NCO solute molecule and 87 water molecules. The microsolvation system is nonperiodic and contains five explicit water molecules close to the oxygen atom of the NCO solute molecule. The long-range effects of water are computed with the PCM model13,58 with a dielectric constant of 78.4 in the static calculations and by the COSMO model59 with a dielectric constant of 78.4 in the MD simulations. The five water molecules are restricted near the NCO molecules with a half-harmonic wall placed at 4.1 Å from the NCO oxygen atom. We positioned this wall based on a priori knowledge of the desired water structure. Results on the effect of different cluster sizes and different wall positions on electronic structure, geometries, and free energy differences can be found in the Supporting Information.

To benchmark the solvation models on the description of the closed NCO state (Figure 2, left), we run five different MD simulations with each model (including the reference), all with randomly generated starting velocities and a time step of 0.5 fs. The first 10 ps of each of these 30 simulations is considered equilibration. The subsequent 10 ps of the simulations are used for analysis. All simulations are in the canonical ensemble (NVT) using a Langevin thermostat with a friction of 0.05 au for DAS, FIRES, reference and microsolvation, and a friction of 0.5 au for abrupt and buffered-force to avoid overheating (see Supporting Information).

To analyze the electronic structure of the NCO molecule with different solvation models and different A-region sizes, we compute the Mulliken charges on the oxygen and nitrogen atoms. We use 100 snapshots taken from the equilibrated reference QM simulation and gradually increase the size of two spheres around the two atoms that contain QM water molecules. To assess the affect of geometry on the NCO electronic structure, we also compute the average Mulliken charges from 1000 geometries from simulations equilibrated with the solvation models. The snapshots are separated by time-intervals of 500 fs (QM reference) and 50 fs (solvation models), such that the available 50 ps of trajectory are optimally represented. To analyze the molecular structure of the NCO molecule after equilibration with the different solvation models, we compute the root mean square deviation (ϵRMSD) of the heavy atoms in an average geometry of the NCO molecule from an average QM geometry. The average geometries are computed using 1000 snapshots from the respective simulations.

Reaction free energy profiles are obtained using metadynamics to simulate the rare event of opening and closing the N|···C bond. Background information on metadynamics can be found in the Supporting Information or in several excellent reviews.60,61 In order to keep these metadynamics simulations affordable, we restrict the number of collective variables (CV) to two. As CV for this system we choose (1) the bond distance between the nitrogen of the tertiary amine-group and the carbon of the aldehyde-group and (2) the combination of two dihedral angles (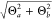Inline graphic) (see Supporting Information) that together describe the twist of the 5-ring. The first CV was chosen because the bond distance between the nitrogen and the carbon of the aldehyde group is the main coordinate that differentiates between the closed and open states of NCO (Figure 2, left and right, respectively). The second CV was chosen to conveniently explore the potential energy surface in the open state and avoid any hysteresis. The Gaussians that form the history dependent bias are deposited every 100 MD steps and have a height of 0.1 kcal/mol. The width of the Gaussians along CV1 is 0.1 Å, and along CV2 the width is 18°. In order to obtain statistically meaningful free energy profiles, we use 10 different metadynamics simulations that all have different starting velocities. Convergence of the result with the number of simulations is quantified by the error of the mean. The typical length of a single metadynamics simulation is around 125 ps (with a time step of 0.5 fs). The metadynamics simulations all start with an equilibrated closed state structure. Based on an examination of different criteria, we determine the Helmholt free energy barrier for the bond breaking reaction for the opening of the N|···C bond from the deposited Gaussians when our simulations reach an N|···C distance of 2.50 Å. We estimate the free energy barrier to correspond to an N|···C distance of 2.25 Å. Since only Gaussians corresponding to a single well are used to compute the barrier height, the exact barrier location cannot be determined. Other choices yield barrier heights that deviate no more than 0.3 kcal/mol within one simulation. To determine the barrier for the backward reaction, we sum the deposited Gaussians when the N|···C distance reaches 2.0 Å after having been completely open (N|···C distance of more than 5.0 Å). The free energy difference between the closed and the open state of the NCO molecule is defined as the difference between the barriers of the forward and the backward reaction.

The geometry optimizations for different microsolvation models are computed with MP2,62,63 PBE-D3,64,65 and PM6-DH+.53 Both the MP2 and PBE-D3 optimizations use a 6-31+G(d,p) basis set66,67 using Gaussian09, revision D.01.68 The geometry optimizations with the PM6-DH+ functional were performed with MOPAC.54

2.3. Simulation Timings

As mentioned above, the complexity of the solvation models differs. The microsolvation model is by far the least time-consuming because it explicitly describes only the NCO molecule and five water molecules. The most efficient adaptive QM/MM models (abrupt and buffered-force) are approximately 30 times more computationally intensive, as can be seen in Table 1. The difference in cost between abrupt and buffered-force is caused by the number of QM solvent molecules, which is larger in the buffered-force model. The cost of FIRES is roughly the same as the cost of the most efficient adaptive QM/MM model. The most time-consuming model is DAS, which calculates forces over on average 15 different QM/MM partitions each time step. When using four parallel CPU cores, it takes around six times longer than abrupt (instead of an optimal factor of 3.75). Note that the different QM/MM force calculations are trivially parallel. With our semiempirical QM description, the individual force calculations are fast, and as a result, the overhead of the master process causes a loss in speedup. With more time-consuming force calculations (e.g., DFT), the scaling is linear with the number of cores. For all other models we use one core per simulation.

Table 1. Relative Timings Compared to Abrupt Model of PM6-DH+/REAXFF Simulations of Periodic Box Containing One Me2N–(CH2)3–CH=O Molecule and 913 Water Moleculesa.

  Relative timing per step
Microsolvation 0.03
DASa 6.34
Abrupt 1
Buffered-force 1.12
FIRES 1.10
Open in a new tab
a

These simulations are run in parallel on four cores, whereas all other simulations are run in serial.

3. Results and Discussion

In Section 3.1, we first test the accuracy of our QM description (PM6-DH+) of the NCO molecule. We then benchmark the five different multiscale solvation models described in Section 2 based on the properties of the NCO molecule in the solvent-sensitive closed state (Figure 1, right). In Section 3.2, we use the best explicit solvation model to compute an accurate free energy profile of the reversible nucleophilic addition of the amine to the carbonyl (N|···C+–O–). We compare the results with those from a microsolvation model, and we show that long-range interactions with explicit water molecules are needed to obtain a reliable free energy profile.

3.1. Structure of Closed State

As mentioned in the Introduction, solvation is crucial for the stability of the closed state of the NCO molecule (Figure 1, right) since the ionic C+–O– entity needs to be stabilized by solvation. In Section 3.1.1, we review the solvent sensitivity of the NCO molecule and test how well the solvated system is described at different levels of QM theory. In Section 3.1.2, we benchmark the multiscale solvation models on a range of properties of the closed state.

3.1.1. Test of QM Description

Using simple microsolvation models, we examine the effect of implicit and explicit solvations on the N–C bond at different levels of theory: Møller–Plesset perturbation theory to the second order (MP2), Density Functional Theory with the PBE-D3 functional, and the semiempirical PM6 functional with dispersion corrections (PM6-DH+). Without any solvation, the optimized N–C distances with MP2 (2.66 Å), PM6-DH+ (2.77 Å), and PBE-D3 (2.48 Å) do not correspond to a chemical bond (Table 2). As expected, the introduction of explicit water reduces the N|···C distance considerably (Figure 1). The PCM model for implicit solvation also stabilizes the N|···C bond, especially when the number of explicit water molecules equals zero or one. For all levels of theory, the optimized N|···C bond length converges (to roughly 1.6 Å) with three explicit water molecules in a PCM environment. Note that the implicit solvent model has a bigger effect with MP2 and PM6-DH+ than it does with PBE-D3.

Table 2. Effect of Implicit and Explicit Water on N|···CO Distance for Different Levels of Theory: MP2, DFT with PBE-D3 Functional, and Semiempirical PM6-DH+ Functionala.
  gas phase
 with PCM
n H2O MP2 (Å) PM6-DH+ (Å) PBE-D3 (Å) MP2 (Å) PM6-DH+ (Å) PBE-D3 (Å)
0 2.66 2.77 2.48 1.71 1.64 2.06
1 2.50 1.72 2.30 1.65 1.63 1.79
3 1.64 1.65 1.98 1.59 1.61 1.65
4 1.64 1.67 1.73 1.59 1.61 1.65
Open in a new tab
a

We use the MP2, PBE-D3, and PM6-DH+ distances (in bold) with four explicit water and PCM as a reference here.

The different levels of theory do not greatly affect the spatial distribution of the coordinated water molecules. In all cases, the first three water molecules are directly hydrogen bonded to the solute oxygen, and the fourth water molecule forms a bridge between two of them. The average deviation ⟨ϵRMSD⟩ of all H2O (plus the C=O) coordinates from the reference MP2 coordinates is not large (PM6-DH+: 0.34 Å, PBE-D3:0.47 Å). Comparison of the geometries of the NCO molecule itself shows that in all cases the N|···C distance computed with PM6-DH+ is closer to the MP2 result than the distance computed with PBE-D3 (Table 2). Upon microsolvation (nH2O = 4, PCM), PM6-DH+ reproduces both the N–C and C=O bonds very well (Table 3), with very small root mean square deviations (N–C: 0.009 Å, C=O: 0.003 Å) compared to PBE-D3 (N–C: 0.028 Å, C=O: 0.004 Å). The deviation of the ring geometry, however, is considerably larger (PM6-DH+: 0.152, PBE-D3:0.025).

Table 3. Root Mean Square Deviation Values (ϵRMSD) of NCO Geometry Optimized in Presence of Four H2O and PCMa.
  ϵRMSD (Å)
  N|···C C=O backbone
PM6-DH+ 0.009 0.003 0.152
PBE-D3 0.028 0.004 0.026
Open in a new tab
a

Left: Heavy atoms. Middle: Only the two atoms in the N–C bond. Right: Only the two atoms in the C=O bond.

The potential energy barriers for the N–C bond breaking reaction computed with PBE-D3 and PM6-DH+ also deviate from the MP2 reference value. Using the same molecular model as above (nH2O = 4, PCM), we find that the PBE-D3 barrier is lower than the MP2 reference (MP2:12.4 kcal/mol, PBE-D3:8.5 kcal/mol), while the PM6-DH+ barrier is higher than the MP2 reference with approximately the same amount (PM6-DH+: 16.5 kcal/mol). More information on the potential energy barriers can be found in the Supporting Information. Overall, the performances of PBE-D3 and PM6-DH+ are similar, and we can use the efficient PM6-DH+ description for the lengthy simulations in this work. The data in Table 2 was used to guide the construction of the microsolvation model used in the remainder of this study (nH2O = 5, PCM).

3.1.2. Benchmark Solvation Models

Now that we established that the PM6-DH+ functional can be used to describe the N|···C interaction, we assess the performance of the five different solvation models discussed in Section 2 (four explicit solvation and one microsolvation model). The assessment is based on three criteria: (i) the electronic structure of the NCO molecule, (ii) the local molecular structure near the NCO molecule, and (iii) the global structure of the solvent.

Electronic Structure

To address the effect of a finite-size QM region on the electronic structure of the solute, we compute the Mulliken charges on the oxygen and the nitrogen atom (qO and qN, respectively) for NCO–water clusters with an increasing number of water molecules around the two atoms (Figure 3). The gas phase charges (thick lines, round markers) represent the electronic structure in mechanical embedding simulations. The PCM charges (thin line, square markers) represent the electronic structure in microsolvation simulations. In both cases the charges converge to the reference QM value (black line). In the case of the gas-phase clusters, the charges converge slowly with cluster size. If we define a convergence criterion of 0.01e (which is very small with respect to the standard deviation of 0.03e), then the error of the charge on the oxygen atom (ΔqO) is smaller than this criterion only for clusters of 19 water molecules or more. The PCM charges of the same clusters converge to the QM result much faster (ΔqO = −0.01e with only three water molecules), which supports our selected microsolvation model of five explicit water molecules.

Figure 3.

Figure 3

Open in a new tab

Convergence of the Mulliken charges on the oxygen and nitrogen atom of the NCO molecule with increasing size of the water cluster. The charges are averaged over 100 geometries extracted from the fully QM simulation. The large dots represent atomic charges in 1000 structures from a simulation equilibrated in each solvation model, and the vertical lines represent the corresponding average number of QM water molecules.

With increasing gas-phase cluster size, the charge on the oxygen atom becomes more negative, while at the same time the charge on the nitrogen atoms becomes more positive. This suggests that more charge is transferred from the nitrogen atom to the oxygen atom as the cluster grows. We thus (carefully) propose that the bond between the oxygen and the nitrogen atom increases in strength as the number of water molecules increases. Interestingly, in implicit solvent very small clusters overestimate the negative charge on the oxygen atom, as well (mostly) as the positive charge on the nitrogen atom. We propose that small microsolvated clusters transfer too many electrons from N to O and therefore overestimate the bond strength.

In Figure 3, vertical lines represent the average number of QM water molecules after equilibration with the different solvation models. Based on the convergence behavior of the gas phase and PCM charges, only buffered-force and microsolvation include an adequate number of water molecules (buffered-force: nw = 21, ΔqO < 0.01e), while the QM regions of the other models appear to be too small. However, we are interested in the description of the electron density during an MD simulation: This involves equilibration of the clusters with the respective solvation models and alters the geometries and the charges. The geometry changes generated by the microsolvation model amplify the already present overestimation of the charge transfer from N to O (ΔqO = −0.02e). Surprisingly, the buffered-force geometries invoke an even stronger deviation but in the opposite direction (ΔqO = +0.03e). The charges obtained with the three remaining QM/MM models exhibit more modest effects of the geometry change, coincidentally bringing them closer to the reference value. The charges produced with the DAS model reflect the reference charges extremely well, with the error well below the convergence criterion (ΔqO < 0.01e).

Geometry of the NCO Molecule

We also benchmark the equilibrated geometry of our model system in the closed state with respect to a reference simulation that treats all molecules QM. The average N|···C and C=O distances in the NCO molecule for the five different solvation models are extracted from the simulations (Table 4, left side), together with the standard deviations. The first thing to note is a correlation between the N|···C and the C=O distances (see Supporting Information), meaning that the stronger (shorter) the N|···C bond is, the weaker (longer) the C=O bond becomes. All the models yield average N|···C distances that correspond to a bonded N|···C pair and C=O distances that are about 8 to 9.5% longer than a typical C=O bond (e.g., acetaldehyde: 1.22 Å). That means that the CO bond is more polarized, and the negatively charged oxygen atom needs to be stabilized by the solvent.42 The average distances are a bit larger than our reference results with the static model (1.61 Å) due to anharmonic thermal bond elongation. The abrupt solvation model yields the largest deviation of the N|···C bond (1.66 Å versus 1.64 Å). In our setup, this model has a smaller effective QM region than DAS and buffered-force, and we expect that it is the lack of electrostatic interaction with a second solvation shell that slightly destabilizes the N|···C bond. The microsolvation model yields a slightly shorter N–C bond (1.63 Å) than the reference and a slightly longer C=O bond (1.34 Å). This result is in agreement with our earlier observation that microsolvation appears to overestimate the strength of the bond. The root mean square deviations (ϵRMSD) of all the heavy atoms in the NCO molecule from the reference (Table 4, center) strikingly yield very small values with abrupt and FIRES (0.04 Å), while the accuracies of the remaining three models are comparable (0.13 Å). Taking into account the N–C distances, the C=O distances, and the ϵRMSD values, FIRES yields the best NCO molecular structure out of all the models. DAS and buffered-force provide high accuracy particularly in the N|···C=O region. The abrupt model appears to underestimate the N–C interaction, and the microsolvation model may overestimate the strength of this bond.

Table 4. N|···C and C=O Distances (with standard deviation) in NCO Molecule (left), Root Mean Square Deviation (ϵRMSD) of Average Geometry of Backbone Atoms from Average Reference Structure (center), and Average Number of Hydrogen Bonds toward Oxygen of Aldehyde Group with Standard Deviation (right) for Different Solvation Models Studied in This Work.
  N|···C distance (Å) C=O distance (Å) ϵRMSD (Å) Average number of hydrogen bonds
Reference 1.64 ± 0.05 1.33 ± 0.03 0 2.76 ± 0.43
DAS 1.64 ± 0.05 1.33 ± 0.03 0.13 2.95 ± 0.47
Abrupt 1.66 ± 0.05 1.32 ± 0.03 0.04 3.07 ± 0.56
Buffered-force 1.63 ± 0.05 1.33 ± 0.03 0.13 3.13 ± 0.68
FIRES 1.64 ± 0.05 1.32 ± 0.03 0.04 2.75 ± 0.70
Microsolvation 1.63 ± 0.05 1.34 ± 0.03 0.12 3.01 ± 0.41
Open in a new tab
Local Solvent Structure

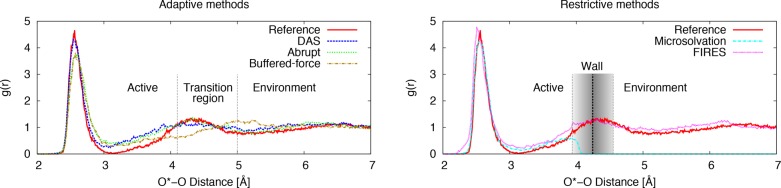
The first solvation shell contributes approximately three hydrogen bonds to the oxygen of the NCO molecule (Table 4, right), but there is quite some fluctuation between the models. Interestingly, these subtleties in the short-range solvation around the NCO molecule do not appear to affect the average N|···C bond length. Abrupt and buffered-force yield structures with slightly more hydrogen bonds directed toward the C=O oxygen than the other models. In Figure 4, the radial distribution g(r) of oxygen atoms of water (O) around the oxygen of the NCO molecule (O*) is depicted. On the left, the results for the three adaptive QM/MM models are shown, and the positions of the active, transition, and environment region are indicated. The first solvation shell computed with abrupt and buffered-force models is less sharp than that of the DAS model. The latter is in almost perfect agreement with the reference. This agreement can be related to the Langevin friction term, which can be relaxed when using the DAS model. The friction terms in abrupt and buffered-force are 1 order of magnitude larger to correct for the local heating near the QM/MM boundary. In order to keep a Boltzmann distribution of the velocities during a simulation, the Langevin thermostat counteracts the imposed friction with a proportional stochastic term. This stochastic part of the thermostat causes more randomized geometries, hence broadening the first solvation shell. The FIRES model can also afford a small friction constant, and indeed, the first peak in the g(r) obtained with the FIRES model (Figure 4, right) is nearly as accurate as the DAS result. The first solvation shell in the g(r) obtained with the microsolvation model also matches quite well with that of the reference. It should be noted that this agreement is highly sensitive to the position of the wall, which was selected based on a priori knowledge of the solvent structure. Combining all results from Table 4 and Figure 4, the DAS and FIRES solvation models describe the first solvation shell very accurately.

Figure 4.

Figure 4

Open in a new tab

Radial distribution function (g(r)) from the oxygen of the NCO molecule to the oxygens atoms of the water molecules for the three adaptive QM/MM models, DAS, abrupt, and buffered-force (left), and the two restrictive models, FIRES and microsolvation (right). The reference is a full QM (PM6-DH+) simulation of a 14.2 Å cubic box containing the NCO molecule and 87 water molecules. The position of the QM and MM boundaries are indicated (left), and for the FIRES method, the position of the spherical wall is indicated. The average (and median) of the wall is located at 4.245 Å, and the shaded rectangle indicates 90% of the wall distances.

Global Solvent Structure

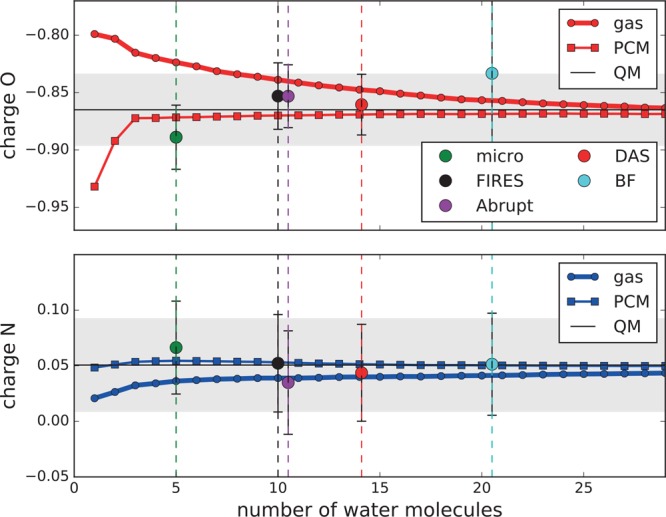
Beyond the first solvation shell, the O*–O radial distribution obtained with buffered-force severely deviates from the other models. This deviation is caused by the violation of total momentum in our system. This results in unidirectional forces on molecules on both sides of the boundary (as opposed to opposite forces for the other adaptive QM/MM models). These forces push both molecules out/away from the A-region, causing a small depletion near the A/T boundary and an aggregation of molecules just outside the buffer region. This can be better understood if we consider a QM molecule, denoted by 1, close to the A/T boundary and a second molecule, denoted by 2, in the T-region (Figure 5). The equilibrium distance between water molecules is smaller with the QM description than with the MM description.31 With buffered-force, the force exerted on molecule 1 by molecule 2 is described quantum mechanically (partition 1, Figure 5, solid arrow), but the exertion on molecule 2 by molecule 1 is described by the MM method (partition 2, solid arrow). This means that molecule 1 is attracted to molecule 2, but molecule 2 does not feel this attraction to molecule 1. As a result, the QM molecule moves closer to the MM molecule (in other words closer to the boundary), thereby pushing molecule 2 further away. Therefore, both molecules experience a force away from the QM center of the simulation (Figure 5, solid arrows). The net effect is a shift to a new equilibrium with low density at the A/T boundary, causing the small depletion of the QM region and an aggregation just outside the T-region. The diminished number of QM water molecules in the second solvation shell is something that buffered-force has in common with abrupt (abrupt does have water molecules in the second solvation shell, but they are all MM). This common feature may explain why the coordination of the first solvation shell water molecules to the C=O oxygen is too large with these models (Table 4).

Figure 5.

Figure 5

Open in a new tab

Schematic representation of the two different partitions for which buffered-force calculates the forces each time step. QM molecules are depicted as ball and stick and MM molecules as thick lines. Background colors are used to indicate the different regions: orange (A-region), yellow (T-region), and white (environment).

The solvent structure beyond the first solvation shell obtained with all the adaptive QM/MM models is less defined than the reference structure. We attribute this to the difference in interaction between the QM and MM solvent molecules, which leads to a loss of structure near the QM/MM boundary. It can be seen in Figure 4 (right) that both restrictive models yield a more defined solvent structure beyond the first solvation peak. The microsolvation model has no explicit solvent beyond a 4 Å radius and can therefore not properly describe it. The g(r) obtained with the FIRES model matches the reference very well, apart from a small aggregation of molecules near the position of the wall. This aggregation is a known consequence of FIRES, but in this instance, it is not dramatic because the position of the wall coincides roughly with this second solvation peak. The aggregation is an entropic effect of the penetration of MM water molecules into the QM region, which is a consequence of the soft (elastic) wall that is used.45 Overall, global water structure in a QM/MM simulation will always differ from a QM reference due to the inherent difference between a QM and an MM description. More details on this can be found in the Supporting Information in the discussion of the g(r) of oxygen around the nitrogen atom of the NCO molecule. Considering all the data presented above, the global water structure is best described by FIRES, with DAS following as a close second.

Summary

Out of the four models to describe explicit solvation, two models are less accurate than the others; the abrupt model describes the structure of the closed state of the NCO molecule less accurately than all other models, and buffered-force yields deviations in the O*–O g(r) caused by a violation of Newton’s third law. Since the buffered-force model describes the closed state NCO structure accurately, we cannot ascertain whether it can properly simulate the N|···C+–O– bond breaking process. To be on the safe side, however, we eliminate this model. This leaves two models, DAS and FIRES, that describe the solvated closed N|···C state of the NCO molecule accurately. The microsolvation model may slightly overestimate the strength of the N|···C bond, but the observed effects on the charges and bond lengths are small. This leaves a pressing question: Is the interaction with explicit water molecules across long distances necessary to obtain accurate reaction energies for the N|···C+–O– bond? In the next section we compute the reaction free energy profile with one of the two well-performing explicit solvation models assessed in this section and compare it to the profile obtained in the same manner with microsolvation. We selected DAS as the representative explicit solvation model.

3.2. The N|···C+–O– Bond Breaking Process

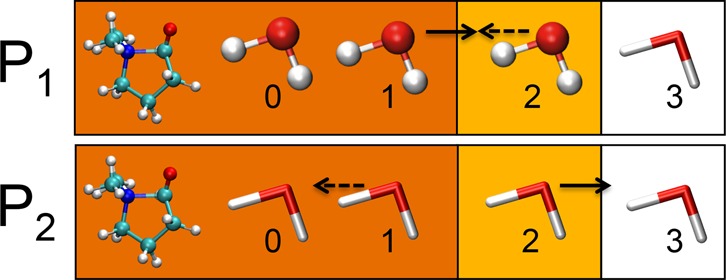
Metadynamics69−72 is used to simulate the rare event of opening and closing the N|···C bond. In Figure 6, the N|···C distance (in red) and a running average (over 100 time steps) of the number of hydrogen bonds toward the oxygen of the NCO molecule (in blue) are shown for one typical metadynamics simulation with both the DAS and microsolvation model. It can be seen that when the N|···C distance is in the bonded regime, there are two to three hydrogen bonds toward the oxygen of the NCO molecule, and there is a negative correlation (ρ = −0.76, see Supporting Information for the expression used) between the N|···C bond length and the number of hydrogen bonds. This means that when the N|···C distance increases, the number of hydrogen bonds decreases at the same time. This value is approximately 1 when the N|···C bond length is larger than 3 Å.

Figure 6.

Figure 6

Open in a new tab

N|···C distance and average number of hydrogen bonds toward the oxygen of the aldehyde group of the NCO molecule of a typical metadynamics run for the DAS and microsolvation models.

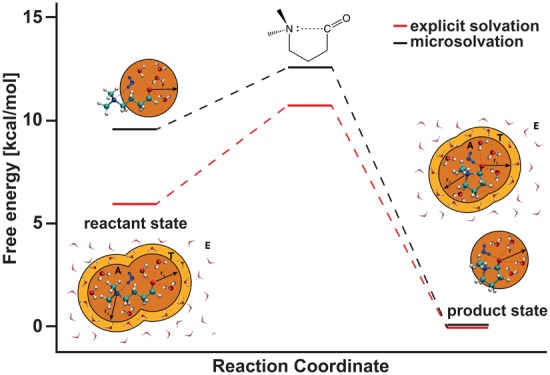
Free Energy Barrier

DAS yields a barrier of 10.7 ± 0.8 kcal/mol, whereas the microsolvation model yields a barrier of 12.6 ± 0.3 kcal/mol (Figure 7, Table 5). The difference in barrier height is in line with the observation in Section 3.1.2 that the microsolvation model appears to overestimate the N|···C interaction. If this electronic effect is indeed the cause of the free energy difference, then the difference must also be present in the potential energy contribution to the barrier. As a rough estimate of the potential energy barriers, we extracted the average potential energy value associated with the structures that correspond to the transition state and compared it to the average value extracted for the closed state structures. We found that the average potential energy barrier is 1.90 kcal/mol higher with the microsolvation model than with adaptive QM/MM (see Supporting Information for absolute values). This is approximately equal to the difference in free energy barriers (1.86 kcal/mol), supporting our assumption that the observed difference in free energy barriers comes from the bond potential energy.

Figure 7.

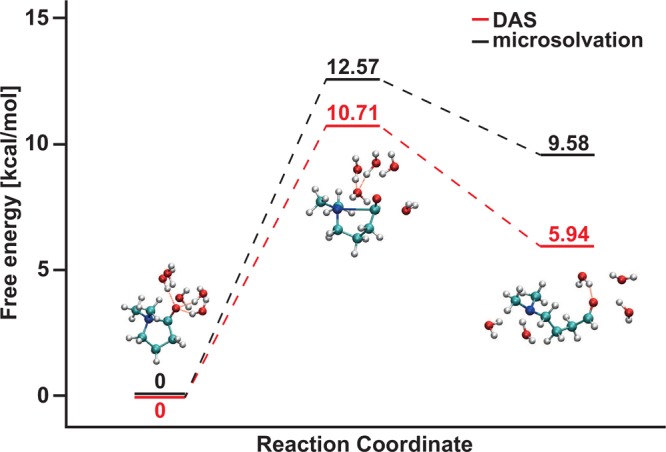
Figure 7

Open in a new tab

Schematic representation of the free energy profile of the N|···C+–O– bond breaking reaction. Typical snapshots of a DAS simulation are shown for the closed, transition, and open state of the NCO molecule.

Table 5. Barrier Height (ΔF‡) of Breaking of N|···C Bond and Free Energy Difference (ΔF) of N|···C+–O– Interaction with DAS and Microsolvation Modelsa.
  ΔF‡ [kcal/mol] smean of ΔF‡[kcal/mol] ΔF [kcal/mol] smean of ΔF [kcal/mol]
         
DAS 10.71 0.78 5.94 0.51
Microsolvation 12.57 0.27 9.58 0.32
Open in a new tab
a

Also the standard error of the mean is tabulated: 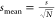Inline graphic

Free Energy Difference

The computed free energy difference ΔF between the open and the closed states (Table 5) obtained with the microsolvation model (9.6 ± 0.3 kcal/mol) agrees well with the previously obtained (static) binding energies of ref (42). In explicit solvent, the binding energy of 5.9 ± 0.5 kcal/mol is about 40% weaker than the previously obtained value,42 but it is still about 20% stronger than an average hydrogen bond in water. The error in the average value of ΔG obtained with the microsolvation model (Table 5) is smaller than that of the DAS model (0.32 vs 0.51 kcal/mol), but this is mainly caused by the improved statistics. Out of the 10 metadynamics simulations, only 7 trajectories did recross for DAS after 250,000 steps. We disregarded the three nonrecrossed trajectories, which may mean that the open state for DAS is even more stable than our results indicate.

In contrast to the barrier heights, the free energies difference is much smaller with the DAS model than with the microsolvation model. Part of this effect is again due to the energetic overstabilization of the closed state by the microsolvation model (∼2 kcal/mol). Examination of the trajectores also reveals an energetic destabilization of the open state in the microsolvation model. We observed an undercoordination of the nitrogen atom in the NCO molecule compared to the DAS result (Table 6). In the open state, the number of N-coordinated water computed with DAS equals 0.78, while with the microsolvation model only 0.59 water molecules are coordinated (Table 6). This problem is unique to the microsolvation model since the single wall around the oxygen atom of the NCO molecule prevents water from coordinating to the nitrogen atom in the open state. The single wall around the oxygen atom of the NCO molecule prevents water from coordinating to the nitrogen atom in the open state. On the other hand, the dual-sphere approach adopted in the DAS simulations allows QM solvation of both the oxygen and the nitrogen atoms throughout the reaction process. The average potential energy obtained with the microsolvation model for frames where one water molecule is hydrogen bonded to nitrogen is 5.5 kcal/mol lower than for frames without such a water. The average NCO geometries are slightly different for frames with and without a hydrogen-bonded water (average N–C distance 4.75 and 4.91 Å, respectively), but we feel confident that we can attribute the larger part of the energetic difference to the difference in hydrogen bonds. We can now quantify the relative destabilization of the microsolvated open state by this coordination effect. On average, the number of hydrogen-bonded water molecules to nitrogen is only 0.19 lower for the microsolvation model compared with DAS, indicating that the energetic destabilization is around 19% of the value of the hydrogen bond (5.5 kcal/mol). We then estimate the destabilization by the microsolvation model to be a little over 1 kcal/mol. In combination with the ∼2 kcal/mol overstabilization of the closed state, this adequately explains the observed total discrepancy from the DAS result of 3.64 kcal/mol.

Table 6. Average Number of Hydrogen-Bonded Water to Nitrogen Atom in Closed, Transition, and Open States of NCO Molecule for DAS and Microsolvation Modela.
  H-bonds to N
  DAS Microsolvation
Closed state (<2.25 Å) 0.00 0.00
Transition state (2.25 ≤ 3.00 Å) 0.05 0.07
Open state (>3.00 Å) 0.78 0.59
Open in a new tab
a

Closed state: N|···C < 2.25 Å. Open state: N|···C > 3.00 Å. Transition State: 2.25 Å < N|···C < 3.00 Å. Only frames from a completed opening or closing event are included.

Summary

In summary, the majority of the difference between the free energy profiles obtained with the DAS and the microsolvation model is caused by an overstabilization of the N–C bond by the polarizable medium of the microsolvation model. An additional difference stems from the nonadaptive nature of the microsolvation model, which cannot adjust to changing solvation preferences. An important advantage of adaptive QM/MM models is therefore that they can provide water molecules for coordination in any desired location. The explicit solvation provided by these models thus affects the quality of the solute description along the reaction path in an indirect manner by providing a reservoir of water molecules that can be incorporated in the first solvation shell.

We can extrapolate our findings to intermediate states in nucleophilic substitution reactions featuring very polarized transition states. Water molecules coordinating the lone pair of the nucleophile need to be removed, which is energetically unfavorable. The reaction can be made more favorable if the nucleophilic moiety is located in a solvent-free environment. Such a situation can conceivably be achieved in the active site of a protein or in a well-designed molecular catalyst.

4. Summary and Conclusion

We compare the performance of five different multiscale models to accurately describe the effect of explicit solvation on a sensitive probe molecule that mimics the transition state of a nucleophilic substitution reaction. The explicit solvation models DAS, abrupt, buffered-force, and FIRES employ two spherical QM regions, encompassing the two reactive moieties in the Me2N–(CH2)3–CH=O (NCO) molecule, while the microsolvation model confines its five QM water molecules near the C=O moiety at all times. Among the adaptive models, the abrupt model does not describe the structure of the closed NCO molecule as accurately as the other models, most likely due to the effectively small QM region. Buffered-force yields a discrepancy in the solvent structure caused by a violation of Newton’s third law. In addition, abrupt and buffered-force require strong thermostats, which affect the structure of the first solvation shell. DAS yields excellent agreement with our reference simulation for the structure of the closed N|···C state. FIRES (a restrictive QM/MM model) also provides a good description of the geometry of NCO in the closed state, and the solvent structure is in excellent agreement with the reference. The microsolvation model appears to overestimate the interaction in the N|···C bond. Metadynamics simulations with the DAS and microsolvation models reveal that the free energy barriers for the N|···C bond opening, as well as the free energy differences between the closed and the open state, are affected differently by the two models. The dual-sphere explicit solvation of DAS allows a superior description of solvent rearrangement along the entire reaction path. This yields a binding free energy of 6 kcal/mol, which is about 40% lower than the binding energy obtained with a microsolvation model. This value is still roughly 20% stronger than an average hydrogen bond.

Acknowledgments

The research was supported by The Netherlands Organization for Scientific Research (NWO) (Vidi 723.012.104). Simulations were carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. This work is supported by the CNRS, Université de Bourgogne, Conseil Régional de Bourgogne through the plan d’actions régional pour l’innovation (PARI) and the fonds européen de développement regional (FEDER) programs. Gaussian calculations were performed using HPC resources from DNUM CCUB (Centre de Calcul de l’Université de Bourgogne).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.7b01206.

  • Background information is provided on (A) the QM/MM solvation models and (B) the metadynamics approach and the collective variables used. Additional tests of the PM6-DH+ level of theory are presented (C). Several tests of the solvation models are provided: The mechanical embedding scheme is tested against electrostatic embedding (D), the dual-sphere scheme is evaluated (E), and the size of the microsolvation cluster is tested (F). Additional data is listed from simulations of the closed state of the NCO molecule with the different solvation models (G): Bond distances, N-coordination, and local heating. Additional metadynamics results are presented (H). XYZ files are provided for geometry optimized structures and selected MD snapshots (I). (PDF)

The authors declare no competing financial interest.

Supplementary Material

ct7b01206_si_001.pdf (3.4MB, pdf)

References

  1. Berthelot M.; Péan de Saint-Gilles L. De la Formation et de la decomposition des Ethers. Ann. Chim. Phys. 1862, 65, 385–422. [Google Scholar]
  2. Menschutkin Z. Beitraegen zur Kenntnis der Affinitaetskoeffizienten der Alkylhaloide und der organischen chemie. Z. Phys. Chem. 1890, 5U, 589–600. 10.1515/zpch-1890-0546. [DOI] [Google Scholar]
  3. Kropman M. F.; Bakker H. J. Dynamics of Water Molecules in Aqueous Solvation Shells. Science 2001, 291, 2118–2120. 10.1126/science.1058190. [DOI] [PubMed] [Google Scholar]
  4. Laage D.; Hynes J. T. Reorientional dynamics of water molecules in anionic hydration shells. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 11167–11172. 10.1073/pnas.0701699104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Park S.; Fayer M. D. Hydrogen bond dynamics in aqueous NaBr solutions. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 16731–16738. 10.1073/pnas.0707824104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Park J. M.; Laio A.; Iannuzzi M.; Parrinello M. Dissociation Mechanism of Acetic Acid in Water. J. Am. Chem. Soc. 2006, 128, 11318–11319. 10.1021/ja060454h. [DOI] [PubMed] [Google Scholar]
  7. Michel C.; Auneau F.; Delbecq F.; Sautet P. C-H versus O-H Bond Dissociation for Alcohols on a Rh(111) Surface: A Strong Assistance from Hydrogen Bonded Neighbors. ACS Catal. 2011, 1, 1430–1440. 10.1021/cs200370g. [DOI] [Google Scholar]
  8. Trinh T. T.; Rozanska X.; Delbecq F.; Sautet P. The initial step of silicate versusaluminosilicate formation in zeolite synthesis: a reaction mechanism in water with a tetrapropylammonium template. Phys. Chem. Chem. Phys. 2012, 14, 3369–3380. 10.1039/c2cp23370c. [DOI] [PubMed] [Google Scholar]
  9. Pavlova A.; Meijer E. J. Understanding the Role of Water in Aqueous Ruthenium-Catalyzed Transfer Hydrogenation of Ketones. ChemPhysChem 2012, 13, 3492–3496. 10.1002/cphc.201200454. [DOI] [PubMed] [Google Scholar]
  10. Glaves R.; Mathias G.; Marx D. Mechanistic Insights into the Hydrolysis of a Nucleoside Triphosphate Model in Neutral and Acidic Solution. J. Am. Chem. Soc. 2012, 134, 6995–7000. 10.1021/ja2101533. [DOI] [PubMed] [Google Scholar]
  11. Chibani S.; Michel C.; Delbecq F.; Pinel C.; Besson M. On the key role of hydroxyl groups in platinum-catalysed alcohol oxidation in aqueous medium. Catal. Sci. Technol. 2013, 3, 339–350. 10.1039/C2CY20363D. [DOI] [Google Scholar]
  12. De Wispelaere K.; Wondergem C. S.; Ensing B.; Hemelsoet K.; Meijer E. J.; Weckhuysen B. M.; Van Speybroeck V.; Ruiz-Martínez J. Insight into the Effect of Water on the Methanol-to-Olefins Conversion in H-SAPO-34 from Molecular Simulations and in Situ Microspectroscopy. ACS Catal. 2016, 6, 1991–2002. 10.1021/acscatal.5b02139. [DOI] [Google Scholar]
  13. Miertuš S.; Scrocco E.; Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of {AB} initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
  14. Warshel A.; Levitt M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
  15. Field M. J.; Bash P. A.; Karplus M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. 10.1002/jcc.540110605. [DOI] [Google Scholar]
  16. Kerdcharoen T.; Liedl K. R.; Rode B. M. A QM/MM simulation method applied to the solution of Li+ in liquid ammonia. Chem. Phys. 1996, 211, 313–323. 10.1016/0301-0104(96)00152-8. [DOI] [Google Scholar]
  17. Kerdcharoen T.; Morokuma K. ONIOM-XS: an extension of the ONIOM method for molecular simulation in condensed phase. Chem. Phys. Lett. 2002, 355, 257–262. 10.1016/S0009-2614(02)00210-5. [DOI] [Google Scholar]
  18. Heyden A.; Lin H.; Truhlar D. G. Adaptive Partitioning in Combined Quantum Mechanical and Molecular Mechanical Calculations of Potential Energy Functions for Multiscale Simulations. J. Phys. Chem. B 2007, 111, 2231–2241. 10.1021/jp0673617. [DOI] [PubMed] [Google Scholar]
  19. Bulo R. E.; Ensing B.; Sikkema J.; Visscher L. Toward a Practical Method for Adaptive QM/MM Simulations. J. Chem. Theory Comput. 2009, 5, 2212–2221. 10.1021/ct900148e. [DOI] [PubMed] [Google Scholar]
  20. Bernstein N.; Varnai C.; Solt I.; Winfield S. A.; Payne M. C.; Simon I.; Fuxreiter M.; Csanyi G. QM/MM simulation of liquid water with an adaptive quantum region. Phys. Chem. Chem. Phys. 2012, 14, 646–656. 10.1039/C1CP22600B. [DOI] [PubMed] [Google Scholar]
  21. Rowley C. N.; Roux B. The Solvation Structure of Na+ and K+ in Liquid Water Determined from High Level ab Initio Molecular Dynamics Simulations. J. Chem. Theory Comput. 2012, 8, 3526–3535. 10.1021/ct300091w. [DOI] [PubMed] [Google Scholar]
  22. Pezeshki S.; Lin H. Molecular dynamics simulations of ion solvation by flexible-boundary QM/MM: On-the-fly partial charge transfer between QM and MM subsystems. J. Comput. Chem. 2014, 35, 1778–1788. 10.1002/jcc.23685. [DOI] [PubMed] [Google Scholar]
  23. Watanabe H. C.; Kubař T.; Elstner M. Size-Consistent Multipartitioning QM/MM: A Stable and Efficient Adaptive QM/MM Method. J. Chem. Theory Comput. 2014, 10, 4242–4252. 10.1021/ct5005593. [DOI] [PubMed] [Google Scholar]
  24. Böckmann M.; Doltsinis N. L.; Marx D. Adaptive Switching of Interaction Potentials in the Time Domain: An Extended Lagrangian Approach Tailored to Transmute Force Field to QM/MM Simulations and Back. J. Chem. Theory Comput. 2015, 11, 2429–2439. 10.1021/acs.jctc.5b00142. [DOI] [PubMed] [Google Scholar]
  25. Boereboom J. M.; Potestio R.; Donadio D.; Bulo R. E. Toward Hamiltonian Adaptive QM/MM: Accurate Solvent Structures Using Many-Body Potentials. J. Chem. Theory Comput. 2016, 12, 3441–3448. 10.1021/acs.jctc.6b00205. [DOI] [PubMed] [Google Scholar]
  26. Praprotnik M.; Delle Site L.; Kremer K. Adaptive resolution molecular-dynamics simulation: Changing the degrees of freedom on the fly. J. Chem. Phys. 2005, 123, 224106. 10.1063/1.2132286. [DOI] [PubMed] [Google Scholar]
  27. Praprotnik M.; Site L. D.; Kremer K. Multiscale Simulation of Soft Matter: From Scale Bridging to Adaptive Resolution. Annu. Rev. Phys. Chem. 2008, 59, 545–571. 10.1146/annurev.physchem.59.032607.093707. [DOI] [PubMed] [Google Scholar]
  28. Heyden A.; Truhlar D. G. Conservative Algorithm for an Adaptive Change of Resolution in Mixed Atomistic/Coarse-Grained Multiscale Simulations. J. Chem. Theory Comput. 2008, 4, 217–221. 10.1021/ct700269m. [DOI] [PubMed] [Google Scholar]
  29. Park J. H.; Heyden A. Solving the equations of motion for mixed atomistic and coarse-grained systems. Mol. Simul. 2009, 35, 962–973. 10.1080/08927020902902759. [DOI] [Google Scholar]
  30. Potestio R.; Fritsch S.; Español P.; Delgado-Buscalioni R.; Kremer K.; Everaers R.; Donadio D. Hamiltonian Adaptive Resolution Simulation for Molecular Liquids. Phys. Rev. Lett. 2013, 110, 108301. 10.1103/PhysRevLett.110.108301. [DOI] [PubMed] [Google Scholar]
  31. Bulo R. E.; Michel C.; Fleurat-Lessard P.; Sautet P. Multiscale Modeling of Chemistry in Water: Are We There Yet?. J. Chem. Theory Comput. 2013, 9, 5567–5577. 10.1021/ct4005596. [DOI] [PubMed] [Google Scholar]
  32. Carey F.; Sundberg R.. Advanced Organic Chemistry; Springer, 2000. [Google Scholar]
  33. Bentley T. W.; Llewellyn G.; McAlister J. A. SN2 Mechanism for Alcoholysis, Aminolysis, and Hydrolysis of Acetyl Chloride. J. Org. Chem. 1996, 61, 7927–7932. 10.1021/jo9609844. [DOI] [PubMed] [Google Scholar]
  34. Fox J. M.; Dmitrenko O.; Liao L. A.; Bach R. D. Computational Studies of Nucleophilic Substitution at Carbonyl Carbon: the SN2 Mechanism versus the Tetrahedral Intermediate in Organic Synthesis. J. Org. Chem. 2004, 69, 7317–7328. 10.1021/jo049494z. [DOI] [PubMed] [Google Scholar]
  35. Chéron N.; El Kaïm L.; Grimaud L.; Fleurat-Lessard P. A DFT study of the Nef-Isocyanide reaction: mechanism, influence of parameters and scope. J. Phys. Chem. A 2011, 115, 10106–10112. 10.1021/jp205909d. [DOI] [PubMed] [Google Scholar]
  36. Chéron N.; Jacquemin D.; Fleurat-Lessard P. A qualitative failure of B3LYP for textbook organic reactions. Phys. Chem. Chem. Phys. 2012, 14, 7170–7175. 10.1039/c2cp40438a. [DOI] [PubMed] [Google Scholar]
  37. Bürgi H. B.; Dunitz J. D.; Lehn J. M.; Wipff G. Stereochemistry of reaction paths at carbonyl centres. Tetrahedron 1974, 30, 1563–1572. 10.1016/S0040-4020(01)90678-7. [DOI] [Google Scholar]
  38. Gautier A.; Pitrat D.; Hasserodt J. An unusual functional group interaction and its potential to reproduce steric and electrostatic features of the transition states of peptidolysis. Bioorg. Med. Chem. 2006, 14, 3835–3847. 10.1016/j.bmc.2006.01.031. [DOI] [PubMed] [Google Scholar]
  39. Garrec J.; Sautet P.; Fleurat-Lessard P. Understanding the HIV-1 Protease Reactivity with DFT: What do We Gain from Recent Functionals?. J. Phys. Chem. B 2011, 115, 8545–8558. 10.1021/jp200565w. [DOI] [PubMed] [Google Scholar]
  40. de M Carneiro J. W.; de Oliveira C. d. S.; Passos F. B.; Aranda D. A.; de Souza P. R. N.; Antunes O. A. Host-guest interactions and their role in enantioselective hydrogenation of α-keto esters: An analysis of model systems. J. Mol. Catal. A: Chem. 2001, 170, 235–243. 10.1016/S1381-1169(01)00075-9. [DOI] [Google Scholar]
  41. Studer M.; Blaser H.-U.; Exner C. Enantioselective Hydrogenation Using Heterogeneous Modified Catalysts: An Update. Adv. Synth. Catal. 2003, 345, 45–65. 10.1002/adsc.200390029. [DOI] [Google Scholar]
  42. Pilmé J.; Berthoumieux H.; Robert V.; Fleurat-Lessard P. Unusual Bond Formation in Aspartic Protease Inhibitors: A Theoretical Study. Chem. - Eur. J. 2007, 13, 5388–5393. 10.1002/chem.200601250. [DOI] [PubMed] [Google Scholar]
  43. Piquemal J.-P.; Pilmé J.; Parisel O.; Gerard H.; Fourre I.; Berges J.; Gourlaouen C.; De La Lande A.; Van Severen M.-C.; Silvi B. What can be learnt on biologically relevant systems from the topological analysis of the electron localization function?. Int. J. Quantum Chem. 2008, 108, 1951–1969. 10.1002/qua.21711. [DOI] [Google Scholar]
  44. Kozlowski D.; Pilmé J.; Fleurat-Lessard P. Using the unusual weak N ··· CO bond as a solvation probe. Mol. Simul. 2014, 40, 185–195. 10.1080/08927022.2013.842995. [DOI] [Google Scholar]
  45. Jiang T.; Boereboom J. M.; Michel C.; Fleurat-Lessard P.; Bulo R. E. In Quantum Modeling of Complex Molecular Systems; Rivail J.-L., Ruiz-Lopez M., Assfeld X., Eds.; Challenges and Advances in Computational Chemistry and Physics Series; Springer International Publishing: Switzerland, 2015; Vol. 21; Chapter 2, pp 51–91. [Google Scholar]
  46. Zheng M.; Waller M. P. Adaptive quantum mechanics/molecular mechanics methods. WIREs: Comput. Mol. Sci. 2016, 6, 369–385. 10.1002/wcms.1255. [DOI] [Google Scholar]
  47. Fleurat-Lessard P.; Michel C.; Bulo R. E. Energy extrapolation schemes for adaptive multi-scale molecular dynamics simulations. J. Chem. Phys. 2012, 137, 074111. 10.1063/1.4739743. [DOI] [PubMed] [Google Scholar]
  48. ADF2014, SCM. Vrije Universiteit, Amsterdam, The Netherlands. http://www.scm.com (accessed February 2018).
  49. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  50. Bahn S.; Jacobsen K. W. An object-oriented scripting interface to a legacy electronic structure code. Comput. Sci. Eng. 2002, 4, 56–66. 10.1109/5992.998641. [DOI] [Google Scholar]
  51. van Duin A. C. T.; Dasgupta S.; Lorant F.; Goddard W. A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. 10.1021/jp004368u. [DOI] [Google Scholar]
  52. Rahaman O.; van Duin A. C. T.; Goddard W. A.; Doren D. J. Development of a ReaxFF Reactive Force Field for Glycine and Application to Solvent Effect and Tautomerization. J. Phys. Chem. B 2011, 115, 249–261. 10.1021/jp108642r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Stewart J. J. P. Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. 10.1007/s00894-012-1667-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. MOPAC2012, Stewart Computational Chemistry, Colorado Springs, CO. http://openmopac.net/mopac2012.html (accessed February 2018). [Google Scholar]
  55. Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N · log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
  56. Maseras F.; Morokuma K. IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J. Comput. Chem. 1995, 16, 1170–1179. 10.1002/jcc.540160911. [DOI] [Google Scholar]
  57. Bakowies D.; Thiel W. Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches. J. Phys. Chem. 1996, 100, 10580–10594. 10.1021/jp9536514. [DOI] [Google Scholar]
  58. Scalmani G.; Frisch M. J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. 10.1063/1.3359469. [DOI] [PubMed] [Google Scholar]
  59. Klamt A.; Schüürmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2 1993, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  60. Laio A.; Gervasio F. L. Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. 10.1088/0034-4885/71/12/126601. [DOI] [Google Scholar]
  61. Barducci A.; Bonomi M.; Parrinello M. Metadynamics. WIREs: Comput. Mol. Sci. 2011, 1, 826–843. 10.1002/wcms.31. [DOI] [Google Scholar]
  62. Møller C.; Plesset M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
  63. Frisch M. J.; Head-Gordon M.; Pople J. A. A direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. 10.1016/0009-2614(90)80029-D. [DOI] [Google Scholar]
  64. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  65. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  66. Ditchfield R.; Hehre W. J.; Pople J. A. Self-Consistent Molecular Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. 10.1063/1.1674902. [DOI] [Google Scholar]
  67. Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  68. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta P. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
  69. Laio A.; Parrinello M. Escaping free-energy minima. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 12562–12566. 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Laio A.; Rodriguez-Fortea A.; Gervasio F.; Ceccarelli M.; Parrinello M. Assessing the accuracy of metadynamics. J. Phys. Chem. B 2005, 109, 6714–6721. 10.1021/jp045424k. [DOI] [PubMed] [Google Scholar]
  71. Laio A.; Parrinello M. In Computer Simulations in Condensed Matter Systems: From Materials to Chemical Biology Vol. 1; Ferrario M., Ciccotti G., Binder K., Eds.; Lecture Notes in Physics; Springer: Berlin, Heidelberg, 2006; Vol. 703; pp 315–347. [Google Scholar]
  72. Bulo R. E.; Van Schoot H.; Rohr D.; Michel C. Bias-exchange metadynamics applied to the study of chemical reactivity. Int. J. Quantum Chem. 2010, 110, 2299–2307. 10.1002/qua.22554. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct7b01206_si_001.pdf (3.4MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES