Direct Observation of Cr³⁺ 3d States in Ruby: Toward Experimental Mechanistic Evidence of Metal Chemistry

Abstract

The role of transition metals in chemical reactions is often derived from probing the metal 3d states. However, the relation between metal site geometry and 3d electronic states, arising from multielectronic effects, makes the spectral data interpretation and modeling of these optical excited states a challenge. Here we show, using the well-known case of red ruby, that unique insights into the density of transition metal 3d excited states can be gained with 2p3d resonant inelastic X-ray scattering (RIXS). We compare the experimental determination of the 3d excited states of Cr³⁺ impurities in Al₂O₃ with 190 meV resolution 2p3d RIXS to optical absorption spectroscopy and to simulations. Using the crystal field multiplet theory, we calculate jointly for the first time the Cr³⁺ multielectronic states, RIXS, and optical spectra based on a unique set of parameters. We demonstrate that (i) anisotropic 3d multielectronic interactions causes different scaling of Slater integrals, and (ii) a previously not observed doublet excited state exists around 3.35 eV. These results allow to discuss the influence of interferences in the RIXS intermediate state, of core–hole lifetime broadenings, and of selection rules on the RIXS intensities. Finally, our results demonstrate that using an intermediate excitation energy between L₃ and L₂ edges allows measurement of the density of 3d excited states as a fingerprint of the metal local structure. This opens up a new direction to pump-before-destroy investigations of transition metal complex structures and reaction mechanisms.

Introduction

Determination of the reaction mechanisms is the holey grail of metal chemistry. In particular, the 3d states of transition metal ions play a crucial role in the reactivity of the metal active site. The relation between the atomic structure and electronic structure involves multielectronic and nonlocal electronic effects, which are of great importance in the reactivity but so far escape any complete and exact modeling. Spectroscopy is the only method that allows to probe experimentally and directly the metal electronic states and to derive information about the chemical bonds involving the metal.

Ultraviolet–visible (UV/vis) or optical absorption spectroscopy (OAS) is often the most straightforward method to study compound electronic details such as HOMO–LUMO, charge transfer (CT; for example ligand-to-metal) or metal d–d excitations. Synchrotron-based X-ray spectroscopies are less accessible but can provide considerable more details on for example oxidation states, coordination numbers, and bond covalency. Among them, 2p3d resonant inelastic X-ray scattering (RIXS; also resonant X-ray emission spectroscopy, RXES) is able to probe the transitions in the optical range, but with several advantages over UV/vis:¹ (1) The technique is element-specific, allowing selective transition-probing in the presence of multiple, competing chromophores (even black samples). (2) It probes transitions with energies between 0 and 20 eV, a range considerably larger than the optical one. (3) It probes d-orbital rich states with fully allowed electric dipole transitions, preventing d–d excitation intensity loss by the parity selection rule. (4) Optically spin-forbidden transitions are measured (with more efficiency). (5) 2p3d RIXS is successfully calculated by various (multielectron) methods.²⁻¹¹

For a basic explanation of 2p3d RIXS, we refer to previous works.^1,12,13 In short, ion valence electrons are first photoexcited from a 2p⁶3dⁿ ground state to a 2p⁵3dⁿ⁺¹ intermediate state. When this is followed by radiative electron decay back to a 2p⁶3dⁿ state, it is possible to measure the multielectronic 3d states of a metal ion in a RIXS spectrum. Part of these 3d states are also measurable with optical spectroscopies through d–d excitations, and for the sake of simplicity, we will refer to these charge neutral, excited 3d states as the optical density-of-states (3d o-DOS). This terminology is chosen to discriminate from the empty density-of-states (DOS) of the ground state, which can be probed by adding an electron to the conduction band of the system as in inverse photoemission spectroscopy (IPES).

Despite the above advantages over optical spectroscopies several questions regarding the use of 2p3d RIXS remain unanswered: (1) to what extent is the spin-selection rule (ΔS = 0) obeyed in the RIXS process? (2) Is there an intrinsic difference in the energies of observed 3d excited states as measured by OAS and 2p3d RIXS? (3) On which factors do the 2p3d RIXS spectral intensities depend? (4) To what extent is 2p3d RIXS able to measure the full 3d optical density-of-states of a metal ion?

To quantitatively address these issues we have studied the Cr³⁺ d–d excitations in the gemstone ruby, namely α-Al₂O₃ doped with 2 wt % Cr³⁺. It is an ideal model system because: (a) The system was extensively studied by (polarized) optical and electron paramagnetic resonance spectroscopies, which enabled assignment of many Cr³⁺ excited electronic states, including the effects of C₃ site symmetry and valence spin–orbit coupling on their energies. It also revealed which states are (not) coupled to phonons.^14,15 (b) The low Cr³⁺ content prevents the large-scale formation of Cr³⁺–Cr³⁺ bonds, allowing the neglect of interatomic metal–metal transitions in the spectral analysis. (c) Ligand-to-metal charge transfer effects are relatively small. (d) Temperature effects are little due to the four microstates of the ground state being almost degenerate.^16,17 (e) The 3d electronic state energies are almost constant for different RIXS excitation energies and polarizations (vide infra). Points (b–c) enable, and points (d–e) simplify, the use of a crystal field model to calculate the multielectronic states of Cr³⁺ in ruby.

All this, together with our recently developed abilities to calculate both optical¹⁸ as well as 2p3d RIXS spectra in C_3v symmetry, allows us to present here for the first time a complete simultaneous experimental and theoretical comparison of OAS versus 2p3d RIXS probed 3d excited states. The comparison is further strengthened by experimental and simulated 2p X-ray absorption spectroscopy (XAS) data. The combined approach, using unified crystal field electronic structure parameters to simulate all data, reveals (1) that strong correlations are found between the dominant spin-multiplicity at an energy in the XAS spectrum and those that are enhanced in a RIXS spectrum. It is thereby demonstrated that RIXS has the ability to be spin-selective in the transitions that it probes. We further show that (2) no significant energy differences exist between d–d excitation energies as probed by OAS and 2p3d RIXS in the case of ruby. Consideration of the electronic structure and the selection rules is enough to explain minor energy differences between the main features as seen by both techniques. Detailed analysis further identifies, for the first time, how (3) the RIXS intensity depends on incident light polarization, light interferences in the RIXS intermediate state, natural lifetime broadening, and other broadening effects. And importantly (4), it is shown here for the first time, to what extent 2p3d RIXS is able to measure all multielectronic excited 3d states. We identify a RIXS excitation energy range, within the metal 2p XAS spectrum, where at least all 3d excited states below 6 eV are measured with an even probability resulting in an intensity profile that largely scales with the multiplicity of the multielectronic energy levels. In the case of OAS, a selective view of these 3d states is obtained as spectral intensity is related to many entangled effects. This implies that 2p3d RIXS is a perfect technique to inquire the role that 3d states play in transition metal chemistry.

While answering the above questions, we further revealed novel insights in the electronic structure of ruby, the most important being that noncommon ratios between the F_dd²/F_dd Coulomb Slater integrals of Cr³⁺ are needed to reproduce the experimentally observed electronic structure of ruby.

Experimental Section

Material Synthesis and Characterization

Aluminum nitrate nonahydrate, urea, and chromium nitrate nonahydrate were obtained from Sigma-Aldrich. Ruby powder was synthesized according to a literature procedure.¹⁹ The chromium content of the obtained α-Al₂O₃ (corundum) doped with chromium was analyzed by atomic absorption spectroscopy analysis. For this purpose, the powder was preprocessed using an acid method and analyzed on a PerkinElmer model A Analyst 200. Structural analysis was performed by obtaining an X-ray diffraction pattern on a Bruker D8 Advance diffractometer. A cobalt Kα_1,2 X-ray tube (k = 1.790 Å) operating at 30 kV was used with a current of 45 mA. Data were recorded in a step-scan mode between 2θ values of 25° and 85° with 0.2° steps. Sample uniformity and microstructure was further assessed by scanning electron microscopy images, obtained using a Phenom Pro microscope from PhenomWorld equipped with a backscattered detector.

Optical Absorption, XAS, and RIXS measurements

Diffuse reflectance OAS data were acquired on finely ground powder on a PerkinElmer Lambda 1050 spectrophotometer in the 0.5–5.7 eV (≈4000–46000 cm^–1) energy range. A chromium L_2,3 XAS transmission spectrum was obtained at the Soft X-ray Spectromicroscopy 10ID-1 beamline of the Canadian Light Source (CLS) synchrotron. During acquisition the light source operated at 2.9 GeV, ≈ 200 mA, in normal mode and with a flux density of ≈5 × 10¹⁰ photons (ph) s^–1 μm^–2.²⁰ For RIXS measurements, finely ground ruby powder was pelletized (1 mm thick) and attached to a copper holder. Cr L_2,3 edge XAS (2p XAS) and 2p3d RIXS were measured at the HORNET endstation,²¹ BL07LSU, SPring-8 synchrotron (8 GeV; 100 mA; top-up mode), Japan (see for beamline lay-out and optics refs (22, 23)). The XAS was acquired in inverse partial fluorescence yield mode using a silicon drift detector and was used to match CLS Cr XAS data to determine RIXS excitation energies. Experiments were performed at room temperature and 35 K at pressures <5 × 10^–9 mbar. The incident energy had a total energy resolution of 125 meV full width at half-maximum (fwhm). The beam energy was calibrated to ±0.5 eV absolute energy by measuring the N 1s photoemission line of N₂ (g). The energy span is further calibrated against the Cr L-edge inverse partial fluorescence yield XAS spectrum, giving a variation of no more than 10 meV within 10 eV (energy span used for the RIXS data). A scattering geometry was used in which the angle between the incoming and outgoing light vector was 90°. The sample pellet was positioned vertically with respect to the plane of the laboratory. The incoming light was polarized with its electric component either linear parallel (depolarized geometry or linear horizontal; LH) or linear perpendicular (polarized geometry or linear vertical; LV) to the scattering plane. The incident angle of the light with respect to the sample surface was 45.5°. The RIXS energy scale was calibrated by measuring the elastic scattering of a nonchromium containing reference with the incoming energy varying from 576 to 586 eV. The total energy resolution of the RIXS zero-loss peak was found to be 152 meV fwhm at the Cr L₃-edge (577 eV). RIXS spectra were measured at 12 excitation energies (573 until 584 eV; every 1 eV; labeled from a to l in ascending order) in the Cr L_2,3 XAS edge. During RIXS acquisition, the flux was 2 × 10¹² ph s^–1 and the beam spot size at the sample was 1.5 μm × 45 μm, resulting in a flux density of 3 × 10¹⁰ ph s^–1 μm^–2. Measurements were performed at a single fixed physical position for all excitation energies at one polarization geometry and/or temperature, i.e., for each temperature or polarization change a previously nonirradiated sample spot was measured. Each spectrum was acquired in 1800 s (no detector saturation observed). Using the freely available Matlab script XASskindose²⁴ and a sample density ρ = 4 g cm^–3, the skin dose for each spectrum was estimated to be 5.1–5.2 TGy depending on the excitation energy. RIXS spectra were acquired subsequently from low to high excitation energies. This implies that for each combination of polarization and temperature measurements, the accumulated skin dose increased to 62 TGy post acquisition. Throughout this work all RIXS spectra are normalized to their acquisition time, hence relative intensity differences per excitation energy and polarization can be considered to result from RIXS scattering probabilities. All RIXS spectra are displayed on an energy transfer scale, i.e., the excitation energy of each spectrum is subtracted from the energy scales of the acquired RIXS spectra, which are subsequently multiplied by minus one and displayed with descending energy from left to right. This common RIXS description allows the determination of the energy of the probed valence transitions. For reasons of consistency the OAS data are given in an identical fashion.

Computational Details

Semiempirical crystal field multiplet (CFM) calculations^25,26 were performed to simulate the OAS, XAS, and RIXS spectra using the quantum many-body script code Quanty that uses second quantization and Lanczos recursion method to calculate Green functions.^3,9,27 The Cr³⁺ electronic configurations of relevance in our description are 3d³ and 2p⁵3d⁴. They result in atomic multiplets, which are described by 3d–3d Coulomb and 2p–3d Coulomb and exchange interactions parametrized in Slater–Condon integrals F_dd^k, F_pd (Coulomb) and G_pd^k (exchange) for Hartree–Fock calculations. Relativistic effects resulting in 2p and 3d spin–orbit coupling are equally calculated and affect the atomic multiplet energies. The effect of the solid state is described by considering the Racah parameters B and C to account for the ion covalency (e.g., the nephelauxetic effect) and a crystal field. In the CFM model of the initial state, Racah B and C are defined by F_dd and F_dd⁴ through: B = (9 F_dd – 5 F_dd⁴)/441 and C = 5 F_dd/63.^28,29 The crystal field in the C_3v point group symmetry is parametrized using crystal field parameters Dq, Dσ, and Dτ, following Vercamer et al.¹⁸ A magnetic superexchange field M is not included in the calculations as no superexchange is detectable due to the lack of close Cr³⁺–Cr³⁺ distances. Additional electron configurations resulting from ligand charge transfer (e.g., 3dⁿ⁺¹L) can equally be neglected (see Discussion). To calculate electric dipole transitions in the optical spectra, it is necessary to consider intra-atomic p–d mixing of the ion, captured in V_pd mixing variables (vide infra). Values and a discussion of the obtained electronic structure parameters in the CFM simulations are given in Table 1 in the Results. For a more detailed, basic description of the parameters, we refer to previous work.^18,30 For all simulated spectra, an appropriate Boltzmann-population weighted ground state contribution is considered.

Table 1. Energetic Values of the Electronic Structure Parameters of Cr³⁺ in Ruby Used in the CFM Calculations^a.

parameter	ground state 3d3	core–hole excited state 2p53d4
Fdd2	6.466	6.958
Fdd4	5.404	5.816
Racah B	0.071	0.076
Racah C	0.429	0.462
C/B	6.067	6.067
Fpd2		5.221
Gpd1		3.591
Gpd3		2.722
ζ2p		5.667
ζ3d	0.018	0.024
10Dq	2.320	2.320
Dσ	–0.057	–0.057
Dτ	–0.012	–0.012
Vpd(a1)	0.18
Vpd(e)	0.12
Vpd(e′)	0.06

^aAll energies are in eV.

Optical Absorption Spectrum Calcultations

Calculating the intensities of OAS spectra is a long-standing topic of interest (p–d mixing has been considered since the works of Liehr and Ballhausen³¹). The intensity of the observed transitions arise from the parity-forbidden electric dipole transitions, which become allowed by some p-character brought to the 3d states by static or dynamic (vibronic) p–d mixing.^18,31−33 Optical absorption spectra were calculated following Vercamer et al.¹⁸ by considering on-site p–d mixing via configuration interaction and calculating the electric dipole transitions from [3d³ + 3d²4p¹] to [3d³ + 3d²4p¹] mixed electronic configurations. On site p–d mixing is described by a hybridization Hamiltonian which mixes p and d states of the same symmetry. It is crucial to mix in some of the p-character of the on-site 3d²4p¹ electron configuration (here ca. 0.01% of the total) to allow for the otherwise dipole-forbidden 3d³ to 3d³ transitions. The electron–electron interactions in the 3d²4p¹ electronic configuration are neglected because (i) they are very small and (ii) it aims at reproducing the effect of a p-character band (4p states being more delocalized than 3d states). Only a very small amount of p-character is required to calculate optical transitions, and therefore the contribution of the hybridization Hamiltonian to the total Hamiltonian of the system is negligible and barely modifies the energies of the multielectronic solutions. The applied method and its limitations are discussed in detail elsewhere.^18,33 In the case of C_3v point group, the 4p and 3d orbitals of a₁ and e symmetries can be mixed, which results in three hybridization parameters V_pd(a₁), V_pd(e), and V_pd(e′). The broadening of the simulated OAS spectra is set by convoluting electronic states with Gaussian functions (150 and 5 meV fwhm for states with a quartet or doublet spin multiplicity, respectively) to reproduce the experimentally observed bandwidth.

XAS/RIXS Spectrum Calculations

Chromium 2p XAS and 2p3d RIXS spectra were calculated for Cr³⁺ ions, for which the relevant electron configurations of the system ground and core–hole excited states are described as 2p⁶3d³ and 2p⁵3d⁴, respectively. For XAS, transitions from the ground state to the core–hole excited state are considered, followed by the reverse radiative transitions in RIXS. The Kramers–Heisenberg equation^12,26,34 is used to evaluate the RIXS spectra. Also, consecutive X-ray absorption and emission spectra are calculated without interference terms between the two processes as important in RIXS and naturally included in the Kramers–Heisenberg equation. The generated theoretical spectra yield insight in the effect of these interference terms on the RIXS intensities. Note that inclusion of the 3d²4p¹ configuration is not needed for XAS/RIXS because, while 2p⁶3d²4p¹ to 2p⁵3d³4p¹ (or vice versa) is electric dipole in nature, its probability is 10^–4 smaller than the 2p⁶3d³ to 2p⁵3d⁴ (or vice versa) transition (vide supra, 3d²4p¹ makes up 0.01% of the electron configuration). The X-ray absorption transitions from 2p⁶3d³ to 2p⁵3d³4p¹ and from 2p⁶3d²4p¹ to 2p⁵3d²4p² are electric quadrupole transitions and can be neglected. The same reasoning applies for the X-ray emission transitions from 2p⁵3d³4p¹ to 2p⁶3d³ and from 2p⁵3d²4p² to 2p⁶3d²4p¹.

Further, in the depolarized RIXS configuration, the electric component of the incident light polarization is collinear with the direction of the detected emitted beam, resulting is a necessary change of light polarization in the RIXS process. On the contrary in the polarized RIXS configuration, the incident light polarization is orthogonal to the detection direction. As a consequence, in first approximation, depolarized RIXS is calculated as incident circular polarized light and emitted linear parallel polarized light transitions, [σ(±1) to π(0)], plus incident linear parallel polarized light and emitted circular polarized light transitions, [π(0) to σ(±1)]. In polarized RIXS the sum of incident circular polarized light and emitted circular polarized light, [σ(±1) to σ(±1)], plus incident parallel polarized light and emitted parallel polarized light, [π(0) to π(0)], is calculated. The resulting selection rules for the (de)polarized configurations were derived for the C_3v and C₃ point groups following Matsubara et al.³⁵ without spin–orbit coupling and are given in the Supporting Information.

Finally, the calculated 2p XAS electronic states are convoluted with a Lorentzian with a fwhm of 0.2 eV (up to 577.5 eV), 0.4 eV (577.5–584 eV), and 1.2 eV (above 584 eV) and convoluted with a Gaussian of 0.125 eV fwhm (full E-range) to describe the natural broadening and instrumental resolution, respectively. For RIXS, the intermediate lifetime Γ_C (core–hole state) of each spectrum was set identical to the 2p XAS lifetimes (thus increasing over the edge). The final state lifetime Lorentzian broadening Γ_F (dd-excited final state) was constant at 50 meV. Gaussian broadenings, accounting for the experimental resolution, were also applied (125 and 150 meV for the incoming and emitted beam, respectively).

3d o-DOS Calculations

The obtained CFM model parameters that allow a description of the OAS, XAS, and RIXS data of ruby were used to generate the density of 3d multielectronic states of Cr³⁺ in ruby: optical DOS (o-DOS). To that end, each one of the 120 multielectronic state energies of the ground state 3d³ electronic configuration was calculated and convoluted with a normalized Gaussian function (where the middle of the Gaussian has the state energy and the fwhm of the Gaussian is set to match the RIXS instrumental resolution). All state Gaussians are summed to generate a curve of the 3d optical density-of-states as it would be seen in the current RIXS experiment. The intensities scale automatically with the degeneracies of states, as each individual state is convoluted and their sum is the 3d o-DOS curve.

State projection analyses

The number of electrons (e.g., N(t_2g), N(e_g) in O_h) and the spin multiplicity are evaluated as the expectation values of the respective operators Ô for each multielectronic wave function Ψ_i of the system: ⟨Ψ_i|Ô|Ψ_i⟩. The number of electrons is evaluated by the expectation value of the number operator n, which counts the number of electrons and is defined in second quantization by

where k spans all the 3d spin orbitals of a given symmetry X. The spin-multiplicity 2S + 1 of the multielectronic states is determined from the calculation of the expectation value (S(S + 1)) of the S² spin magnitude operator (norm of the spin angular momentum) for each state, where S is the total spin quantum number equal to the number of unpaired electrons.

Energy Level Diagrams

The energy-level diagrams were obtained by diagonalizing the standard crystal field multiplet Hamiltonian²⁶ of the Cr³⁺ multielectronic system, which accounts for the electron Coulomb interactions and a crystal field potential, for varying parameter values. These energy-level-diagrams do not account for spin–orbit coupling interactions and p–d mixing.

Results

A picture of the examined ruby powder is given in Figure 1a. Atomic absorption spectroscopy revealed the presence of 2.16 wt % of chromium in the pink sample. Scanning electron micrographs (see Supporting Information, Figure S1a) showed the material to be uniform on the micrometer scale. The sample powder X-ray diffractogram (Supporting Information, Figure S1b) revealed a single crystal phase with a perfect match to a database reference of ruby (PDF 01-073-0027³⁶).

Figure 1.

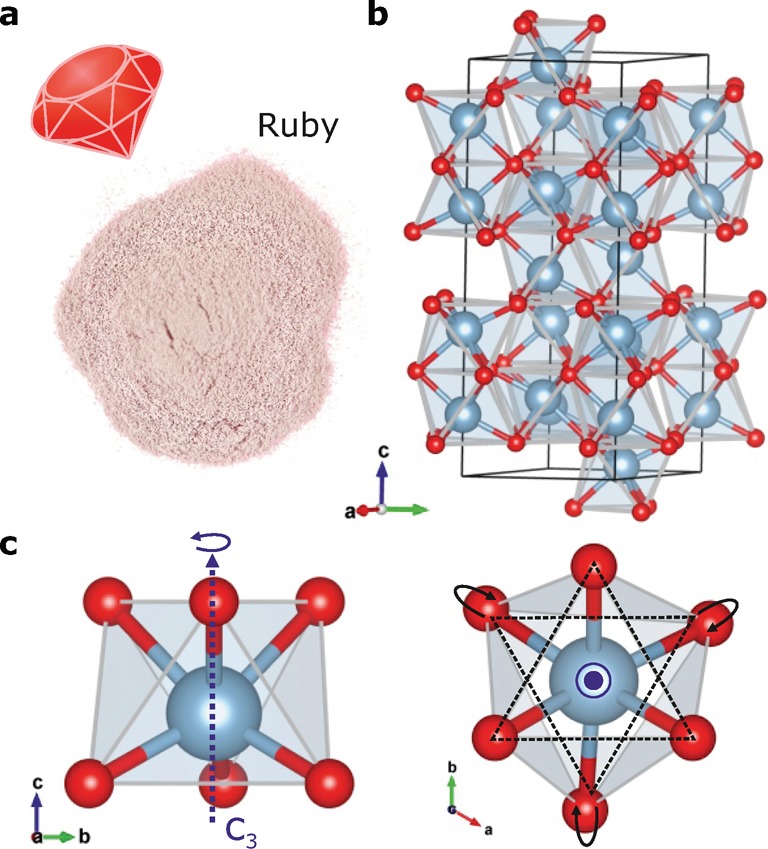
(a) Picture of the studied ruby powder: Al₂O₃ doped with 2.16 wt % Cr³⁺. (b) Crystal structure representation of α-Al₂O₃ (red/gray balls represent O^2–/Al³⁺ ions, respectively). (c) Representations of the Al³⁺ site in Al₂O₃ along the a (left) and c (right) axes of the crystal structure. A minority of the Al³⁺ are replaced by Cr³⁺ ions.

In ruby, the chromium is present as Cr³⁺ impurities in corundum (α-Al₂O₃; see Figure 1b for a crystal structure representation). The Cr³⁺ ions occupy a minor fraction of the 6-fold oxygen coordinated Al³⁺ sites as shown in Figure 1c. The exact point group symmetry of the Al³⁺ site is C₃, accounting for the trigonal distortion of the approximate octahedral (O_h) symmetry: Al³⁺ is displaced along the C₃ axis relative to the octahedron center and the upper equilateral triangle formed by three oxygen ions is rotated with respect to the lower triangle formed by the remaining three oxygen ions as shown in Figure 1c.³⁷ Experimental EXAFS^38,39 and DFT optimization⁴⁰ showed that the substitution of Al³⁺ by Cr³⁺ revealed no deep modification of the site symmetry for low chromium concentrations. While the Cr³⁺ site symmetry is thus also C₃, we use in the following spectroscopic descriptions the C_3v higher point group symmetry to define its crystal field. The actual deviation from the C_3v point group is due to the small rotation of the upper and lower equilateral oxygen ion triangles as mentioned above. The angle of rotation is 2° 8,5′ and is thus so small that the C_3v point group is a reasonable approximation,^41,42 previously successfully applied to explain optical (polarization) data of ruby.^16,43

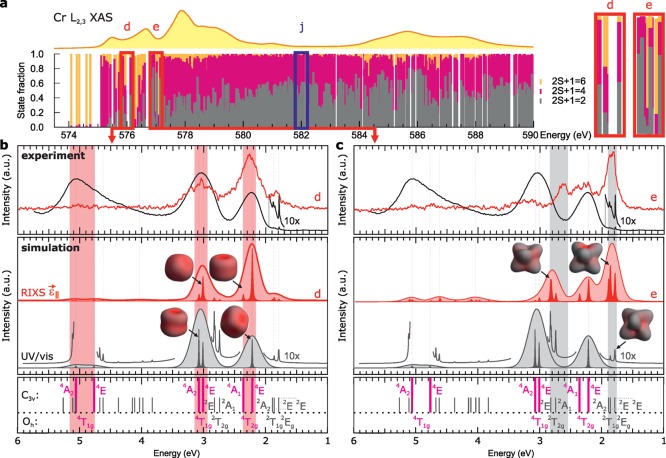
The C_3v symmetry description was then used to obtain a single parameter set for crystal field multiplet simulations that describes all the experimental Cr 2p XAS, Cr 2p3d RIXS, and OAS data of ruby. Figure 2 illustrates the rationale behind the derivation of the main octahedral crystal field parameter 10Dq and 3d–3d electron interaction parameters Racah B and C. The Cr 2p XAS spectrum (Figure 3a) agrees with a previously measured ruby spectrum.³⁹ The RIXS spectra (Figure 3b) show seven sharp features in the 0–6 eV range, which are more than the typical three optical absorption bands (Figure 3c).^{15,16,42−44} The final state of RIXS is identical to the final state of optical absorption, hence the same electronic states are present a priori. The additional observed states in RIXS, result from the technique’s ability to strongly probe both states with doublet and quartet spin multiplicity that for the ruby XAS and RIXS data this is the first description in a symmetry lower than the ideal octahedral case plus that these are the first soft RIXS data on ruby reported. The experimental data (including 0–12 eV energy-range extended RIXS spectra, plus those at a–c) without the theoretical spectra overlaid are given in Supporting Information, Figure S2.

Figure 2.

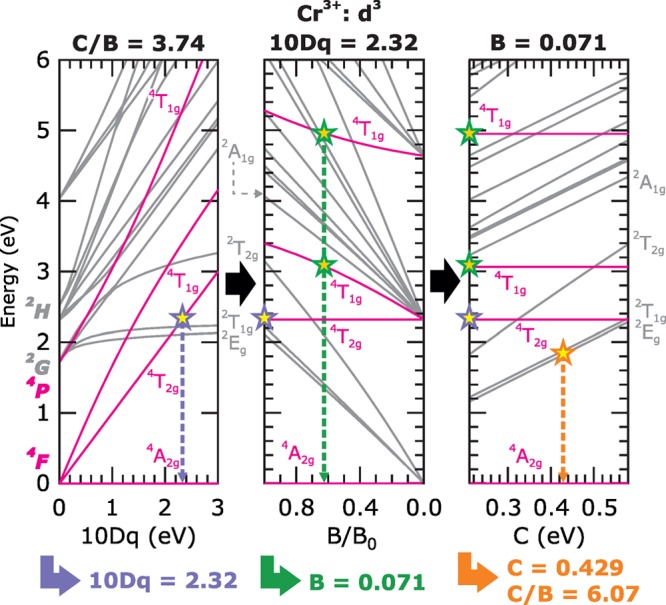
Energy-level diagrams showing quartet (magenta) and doublet (gray) 3d³ states for Cr³⁺ as a function of the crystal field strength 10Dq (left), Racah B (middle), and Racah C (right), used to determine their values in ruby. The spectroscopic terms are labeled in O_h symmetry.

Figure 3.

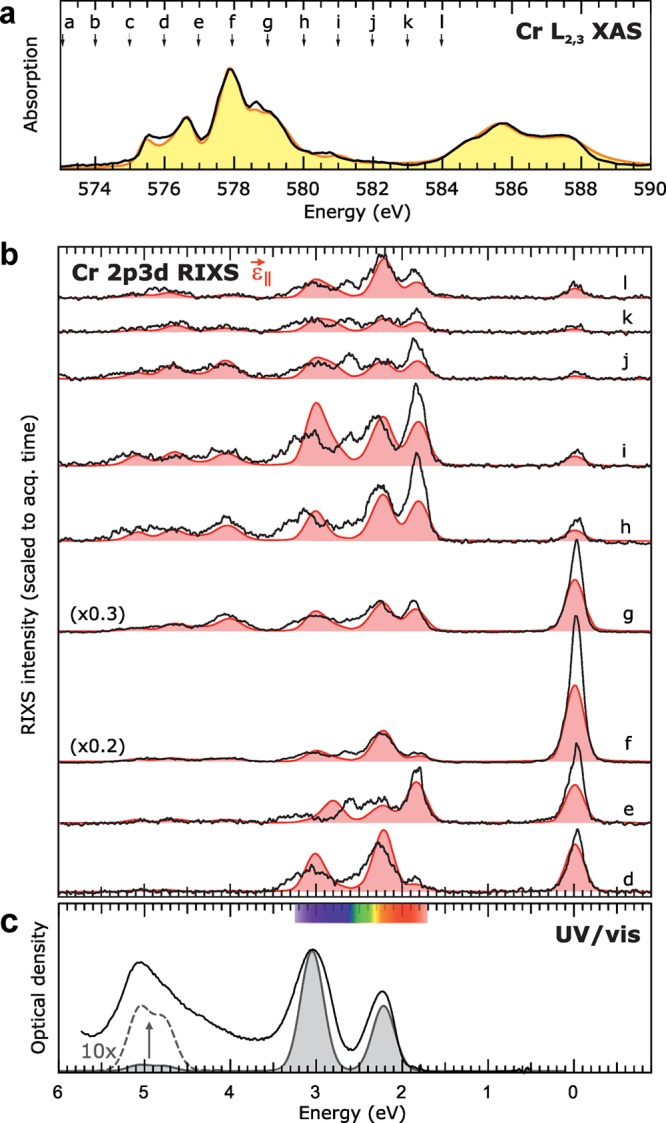
Experimental (black solid lines) and calculated (colored lines/fillings): (a) Cr L_2,3 XAS, (b) depolarized Cr 2p3d RIXS, and (c) UV/vis spectra for ruby with the LFM calculations.

To describe the derivation of the crystal field parameters, we temporarily use a simplified description of the Cr³⁺ in the O_h point group: the left panel of Figure 2 shows an energy level (Tanabe–Sugano like) diagram in which the splitting of the atomic Russel–Sanders terms as a function of 10Dq is given. The crystal field splits the 3d³ multielectronic atomic quartet ⁴F and ⁴P states into the manifolds ⁴A_2g, ⁴T_1g plus ⁴T_2g, and ⁴T_1g, respectively. These levels give rise to broad optical transitions in the visible range responsible for the famous red color of ruby. The energy difference between ⁴A_2g(⁴F) and ⁴T_1g(⁴F) is set by an effective 10Dq, and its value is readily obtained from the maximum of the first quartet excitation as seen in the UV/vis spectrum. The effective 10Dq is found to be 2.24 eV, as indicated by the violet star on Figure 2 (the actual 10Dq in the CFM calculations is corrected to be 2.32 eV as a result of the interfering Dτ value of the additional C_3v distortion). At this effective 10Dq, the energy positions of the remaining quartet states are now lowered to their experimental UV/vis values by lowering the Racah B parameter in the middle panel of Figure 2. Racah B is initially lowered by scaling F_dd² and F_dd with the same percentage, where a scaling of 80% (from Hartree–Fock values) corresponds to the ionic case and lower values to more covalently interacting ions.²⁵ Scaling both F_dd^k interactions to 50% yields a reasonable match for the second and third quartet states (⁴T_1g(⁴F) at 3 eV and ⁴T_1g(⁴P) at 5 eV) at a Racah B value of 0.071 eV as shown by the green stars on Figure 2.

However, the energy-level diagrams in Figure 2 also count numerous states with a doublet spin multiplicity, and in particular the first ones arising from the ²G atomic term, result in sharp lines in the red (R) and blue (B) energy ranges of the visible spectrum. It is the emission from the R-lines that is employed in ruby lasers^45,46 as well as in high-pressure measurements.⁴⁷ Unlike the quartet states, these doublets do not only depend on Racah B but also on Racah C. It is seen from the middle panel of Figure 2 that the energies of the R- and B-lines were moved to too low values with an identical scaling of F_dd² and F_dd. By increasing F_dd⁴ and F_dd back to 80% and 60%, respectively, and thereby increasing Racah C to 0.429 eV while keeping Racah B constant (and thus increasing the C/B ratio to 6.07), the quartets remain at the correct experimental energies, while the R-lines are matched to their experimental energies of 1.79, 1.86, and 1.88 eV. Also, the majority of the other doublet states are now well matching their experimental features (vide infra RIXS spectra), with an exception for the B-lines that are 0.1 eV above their measured values of 2.60 and 2.64 eV. This is illustrated in the right panel of Figure 2, where the correct match is shown by the orange star. The here described procedure using energy-level diagrams is represented in a less abstract manner in Supporting Information, Figure S3, in which the experimental UV/vis spectrum is compared to calculations employing three different cases of F_dd² and F_dd scaling. Note that for the core–hole excited 2p⁵3d⁴ state, relevant in the XAS and RIXS calculations, additional G_pd¹ and G_pd electron exchange Slater parameters are used, which also require a similar unequal scaling as F_dd² and F_dd. In Supporting Information, Figure S4, it is shown that a G_pd¹/G_pd scaling of 75%/100% of original (Hartree–Fock) calculated values, respectively, improves the theoretical match to the experiment even further.

Having established the main crystal field effect and a description of on-site electron–electron interactions, we return to a description of the Cr³⁺ in the C_3v point group. This is crucial to explain the polarization behavior of OAS spectra and the relative order of state energies. This is elaborated upon in the Supporting Information. In Supporting Information, Figures S5 and S6, we focus on the determination of the actual signs and values of the Dσ and Dτ crystal field parameters^16,48 used in the spectral calculations. They are found to be −0.057 eV for Dσ and −0.012 eV for Dτ. From O_h to C_3v description, the ²T_2g and ²E_g doublets of the R-lines are further split in ²A₂, ²E, and ²E lines. In the UV/vis spectrum, indeed, three lines are observed and their energies, their relative intensities, and their optical dichroic behavior¹⁵ are well matched using the specified Dσ/Dτ values. The trigonal distortion induces further splitting of the ⁴T_1g and ⁴T_2g states into ⁴A₂ plus ⁴E and ⁴A₁ plus ⁴E states, respectively. The splitting of the ⁴T_1g(⁴F) state is evidenced in the dichroic behavior of its optical absorption band,^15,16,43 revealing that the ⁴A₂ state energy is higher than the ⁴E state energy by approximately 60–100 meV, which is reproduced here. Additionally, note that the intensities of the optical absorption bands depend on hybridization parameters V_pd that describe the on-site mixing of 3d and 4p orbitals. While only 0.01% of 4p character is mixed in the 3d electron configuration, it is this mixing that allows for the dipole-forbidden 3d–3d transitions to gain intensity in the OAS calculations. The V_pd(a₁), V_pd(e), and V_pd(e′) mixing parameters are set to 0.18, 0.12, and 0.06 eV, respectively, to reproduce the optical (polarized) spectra. This suggests that the strongest mixing happens with the A₁ vibration mode that relates to the vibrations along the c axis of the hexagonal unit cell of the Al₂O₃ host lattice. Their individual effect on the optical spectra is shown in Supporting Information, Figure S6.

Figure 3a–c show that the simulated XAS, depolarized RIXS, and OAS data using this CFM model match the experimental data well. Low temperature (35 K) RIXS and polarized RIXS spectra are also excellently reproduced by the model as shown in Supporting Information, Figure S7. That is, however, not the whole story, as it is clear from Figure 3b that the RIXS spectra acquired at different excitation energies are highly different in the number of probed features and the relative intensities of these features. All the determined CFM parameters are summarized in Table 1.

In Figure 4, both the energies and intensities of the observed 3d–3d transitions as seen in RIXS at different excitation energies and in OAS are compared. Therefore, RIXS slices at energies d and e (Figure 4a) are compared to UV/vis spectra in Figure 4b,c. We first focus on the differences between the RIXS slices and start by an analysis of the spin multiplicities of the core–hole excited states present in the RIXS intermediate step, i.e., the states forming the Cr 2p XAS spectrum of ruby. This is shown in Figure 4a. The bars under the XAS spectrum indicate the fractions of atomic states with a spin multiplicity (2S + 1) of 6, 4, or 2 that contribute to each 2p⁵3d⁴ multielectronic state of the spectrum. Boxes at energies d and e are indicating the state decompositions at those excitation energies and they are enlarged to the right of the figure. It is observed that, at energy e, significantly more spin-doublet character is present in the bars compared to energy d. This correlates to the observation in the top panels of Figures 4b,c that the (depolarized) RIXS spectrum at energy e is revealing mainly d–d states with spin-doublet character, while the RIXS spectrum at energy d shows doublet states weakly. The same behavior holds for the polarized case (see Supporting Information, Figure S8). The 3d state labeling is given at the bottom of Figure 4b,c, in which doublet and quartet states correlate in color to those in Figure 4a. The middle panels of Figure 4b,c show the RIXS calculations at the corresponding energies. A deliberately under-broadened, fine spectral shape displays the energy positions of different states and indicates which are responsible for the main intensities. Overall, Figures 4b,c clearly show that RIXS has the ability to selectively probe states with different spin-multiplicities.

Figure 4.

(a) Analysis of the spin multiplicity of all electronic states forming the displayed Cr L_2,3 XAS spectrum. The labels d, e, and j refer to the excitation energies of the RIXS spectra given in Figure 2. Red/blue boxes (widths 0.5 eV) and spectra refer to depolarized/polarized spectra, respectively. The states in the vicinity of energies d and e are given enlarged to the right. (b) Top: experimental UV/vis (black solid line; R-line doublets multiplied by 10) and depolarized RIXS (red solid line) spectrum at d. Middle: calculated analogues of the top spectra (all doublets multiplied by 10 in the UV/vis case). Graphical representations of selected doublet state electron densities are shown. Bottom: spectroscopic term labels given in O_h and C_3v symmetries. (c) Panel identical to (b), but with the RIXS spectra at e. Selected quartet state electron densities are illustrated. (b,c) Pink/gray bands indicate quartet/doublet states, respectively.

In addition, in the top panels of Figure 4b,c, the experimental UV/vis spectrum is compared to the experimental RIXS spectra at d and e. In the middle panels, the respective calculations are compared. The RIXS at d and the UV/vis spectrum are highly similar in the respect that they possess two main features below 4 eV. The relative intensities of the two quartet bands, the ⁴T_2g and ⁴T_1g (in O_h), are reversed in the spectra. This is explained from the selection rules (derivation in the Supporting Information). They show that in C_3v, in depolarized RIXS spectra, the ⁴A₁ at 2.37 eV and ⁴A₂ at 3.09 eV states (C_3v branches of the discussed quartet bands) are not probed. While in calculated isotropic UV/vis spectra the ⁴A₂ state is probed and the ⁴A₁ state is not. This leads to additional intensity for the second quartet band in UV/vis compared to depolarized RIXS. The calculations also explain that the lowest energy quartet, the ⁴T_2g (O_h) band, has its maximum at slightly higher values (<50 meV) in RIXS at d, compared to the UV/vis spectrum. It is the small amount of intensity (through interference and spin–orbit coupling) that the ⁴A₁ (C_3v) state at 2.37 eV has gained in the RIXS spectrum that causes this (see Figure 4b). Note further that in the RIXS spectrum, the doublet R-lines have gained relatively more intensity in RIXS than in OAS, which results from the small amount of doublet character in the XAS intermediate state (in optics the intensity of the doublet lines arises only from the spin–orbit coupling between doublet and quartet states¹⁶). It is important to see in Figure 4b that the energies of the R-lines as seen by both spectroscopies are identical. The comparison between UV/vis and RIXS at energy e yields similar insights. Note that the ²A₂ and ²E (in C_3v; from the parent term ²T_1g in O_h) and ²E (from ²E_g) states, the R-lines, are probed with similar intensities in RIXS, as opposed to the stronger intensity of the lowest energy ²E line compared to the other R-lines in the optical absorption spectrum. Finally, electron density projections of the discussed states in Figure 4b,c show the R- and B-line doublets to be more anisotropic in shape compared to the ⁴T_2g and ⁴T_1g (O_h) quartets.

In Figure 5, we return briefly to the comparison of RIXS spectra at different excitation energies. Next to the spectra at d and e, the depolarized RIXS spectrum at f is shown. The spectra are scaled as to give the ⁴T_1g (O_h) manifold at 3.1 eV a similar intensity. It is obvious that RIXS at d and f are highly similar and probing preferentially quartet 3d states as explained above, while RIXS at e is very different and probes mainly doublet 3d states. In this respect, the spectral weight observed in the RIXS spectrum at e at 3.35 eV, above the ⁴T_1g experimental energy of 3.1 eV, is interesting. To the best of our knowledge, there has been no electronic state observed at this energy for ruby by any previous measurement (with any technique). Our data are suggesting that a 3d state with a doublet spin multiplicity could be present here. The excited-state absorption measurements by Fairbank et al.,¹⁵ together with our energy level diagram calculations, would suggest that this is potentially the ²A_1g(²G) state (see the fourth gray line from the bottom in the right panel of Figure 2). The transition occurs, however, at the limit of the energy range of Fairbank’s experiment (around 3.6 eV) and our calculations predict this state at 3.8 eV. This discrepancy could arise from similar limitations as for the modeling of the B-line energies. This points out the limits of our simulation based on only two values, F_dd² and F_dd, to interpret the 3d electron–electron interactions. The importance of this observation is that it demonstrates that RIXS can observe weak, previously unknown, spectroscopic features hidden under a strongly probed state, for example, a state with identical spin multiplicity as the ground state (here a quartet state).

Figure 5.

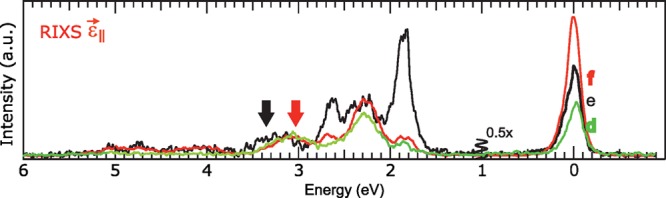
Comparison of experimental, depolarized RIXS spectra at d (green) and f (red) versus e (black). The black arrow around 3.35 eV indicates additional intensity above the ⁴T_1g ground state at 3.1 eV (red arrow).

We return to energy shifts of d–d excitations as probed in RIXS and OAS. In Figure 4b, it was explained that observed shifts in peak maxima could result from probing different electronic states, present under one peak, with different probabilities, following the spectroscopic selection rules. We observed such a shift for the ⁴T_2g (O_h) manifold as seen in RIXS at slice d versus OAS. In addition to electronic effects, we consider the role of phonons in causing observed peak shifts. No differences in the energy positions of the R-lines were measured between the two techniques. The R-lines are known to be pure electronic excitations, i.e., they are not coupled to phonons.^14,15 In principle, however, it remains a question whether energy differences as seen in RIXS and OAS could result from probing electron–phonon states with different amounts of phonon energy contributing to the total excitation energy.¹ Given that (a) the ⁴T_2g and ⁴T_1g (O_h) features are seen at approximately 2.25 and 3.1 eV, respectively, in both techniques, that (b) the small energy differences are explainable from pure electronic arguments, and (c) knowing that these states are coupled to phonons,¹⁴ it is likely that RIXS and OAS probe the same electron–phonon states. This may result from the femtosecond lifetime of the intermediate RIXS state,^49,50 preventing relaxation to the lowest phononic core–hole excited state before photoemission. This results in two vertical transitions at the same nuclear coordinate in the left diagram of Figure 6. As a consequence the same electron–phonon coupled 3d state is reached in 2p3d RIXS as in OAS. The OAS diagram is given to the right of Figure 6 for an example in which the d–d excitation is combined with the excitation of the second phonon level.

Figure 6.

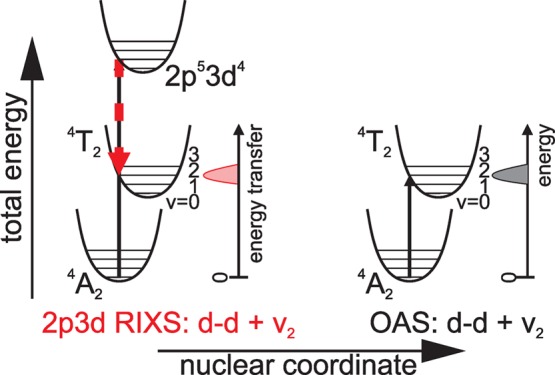
Schematic diagram illustrating that phonons (or vibrons) coupled to electronic transitions are expected to be probed in 2p3d RIXS and UV/vis in identical ways.

The accuracy of the current, single CFM solution in reproducing both the experimental XAS, RIXS, and OAS spectra, plus the small error in the determined model parameters, ensure with high degree of certainty the correctness of our 3d electronic structure description of ruby. On the basis of this strongly affirmed theoretical model, we can now extract valuable information from the simulations. One of the main open questions in stirring the application of RIXS to metal chemistry is to what extent the observed RIXS features are actually probing all 3d states of a metal ion. By extracting from the calculation the energies of all the Cr³⁺ 3d states, one can answer this question. In the top panel of Figure 7, the orange curve (plus yellow area under the curve) shows the multielectronic 3d optical DOS (o-DOS) of the Cr³⁺ ion in ruby.

Figure 7.

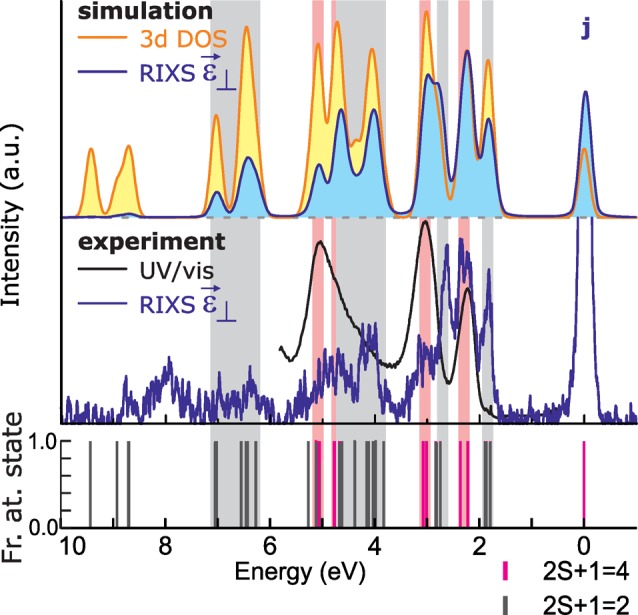
Top: the calculated, 3d optical density-of-states (o-DOS; orange line) of ruby together with the calculated, polarized RIXS spectrum at energy j (blue line). Middle: the experimental UV/vis (black line) and polarized RIXS spectrum at j (blue line). Bottom: spin-multiplicity analysis of ruby 3d–3d states. Pink/gray bands indicate quartets/doublets visible in the RIXS experiment, respectively. The experimental versus theoretical comparison reveals that RIXS at energy j probes a large part of the 3d o-DOS and does so with an unprecedented level of detail.

Having this valuable simulation in hand, based on sound experimental observations, it is possible to investigate at which incident energy (or combinations of them) the metal 3d o-DOS is best measured by 2p3d RIXS. To answer this question, it is good to realize that, due to selection rules, the polarized RIXS spectra reach all the multielectronic 3d states, while the depolarized spectra in C_3v only weakly measure the A₁ and A₂ states of Cr³⁺ (see the appendix in the Supporting Information). Therefore, we will compare polarized RIXS to the 3d o-DOS curve. Calculations allow the largest flexibility in making the comparison. Through them we find that RIXS spectra at high energies above the XAS L₃ edge, but before the XAS L₂ edge, measure the most significant part of the 3d o-DOS, with an intensity profile similar to the 3d o-DOS. In the top panel of Figure 7, this is highlighted by the comparison of the RIXS spectrum at j to the 3d o-DOS curve. Large overlap between the two curves is found, especially below 6 eV. Importantly, the polarized RIXS experimental spectrum at this energy, shown in the middle panel of Figure 7, resembles the calculated RIXS spectrum to a high degree. This proves that RIXS is able to actually measure a large part of the 3d o-DOS in a single spectrum. Note how different the obtained image of the electronic structure is compared to the experimental OAS spectrum of ruby, also shown in the middle panel of Figure 7. Clearly, RIXS has a very strong advantage over UV/vis to be able to map the full metal ion 3d o-DOS. The sticks in the bottom panel indicate the spin-multiplicities of the probed states and confirm that RIXS at j probes both doublet and quartet states, as is also expected when considering the state spin-multiplicities at j in the XAS spectrum (see the blue box in Figure 4a).

Comparisons for (both polarized and depolarized) RIXS spectra at other energies, plus detailed explanations of why the inter L-edge energy range is suitable to probe the metal 3d o-DOS, are given in Supporting Information, Figures S8–S10. For the interested reader, we point out that Supporting Information, Figure S10, also demonstrates that the well-known, typical elastic line intensity behavior as a function of linear polarization (depolarized, small/equal intensity compared to inelastic features; polarized, large intensity compared to inelastic features) is in fact not a “selection rule”-only effect as previously suggested,³⁵ but a combined “selection rule” plus “RIXS interference” effect.

Discussion

We will first discuss the reliability and consequences of the obtained crystal field multiplet model parameters and what new we have learned about ruby. This is followed by what new we have learned about RIXS and what kind of future studies it will enable.

Updated Insights into Electronic Structure of Ruby

We explained that the effective crystal field strength 10Dq and 3d electron–electron interaction parameters F_dd² and F_dd, were determined from the experimental spectra with high accuracy and that the energies of the spin-quartet states and spin-doublet R-lines are consistent with common knowledge on ruby. Here we discuss how the obtained values relate to previous determined ones for ruby and how they relate to the color and electronic structure of ruby. The obtained 10Dq value of 2.24 eV for ruby is consistent with previously determined values of 2.20–2.24 eV⁴⁴ and references therein, 2.25 eV¹⁵ and 2.24 eV.³⁹ This is no surprise as it is set equal to the optically observed ⁴A_2g(⁴F) → ⁴T_2g(⁴F) (O_h) transition. The value is however relatively high for Cr³⁺ ions in minerals. This becomes clear from a comparison with isostructural α-Cr₂O₃ (eskolaite; 10Dq is 2.07 eV^39,44), Cr³⁺-doped Ga₂O₃ (2.06 eV⁵¹) and emerald (Cr³⁺-doped Be₃Al₂(SiO₃)₆; 10Dq is 2.0 eV^15,52), of which all three also contain Cr³⁺ in 6-fold coordinated sites. Many other Cr³⁺ containing gemstones have a 10Dq of 2 eV, but ruby is however not unique in exhibiting a higher 10Dq value, as for example, Cr³⁺ doped MgAl₂O₄ and YAl₂O₄ spinels^53,54 and topaz and pyrope⁴² equally have 10Dq values of 2.23–2.32 eV. It is known that the Cr³⁺ 10Dq value decreases with increasing Cr³⁺ doping in the α-Al₂O₃ lattice of ruby and that rubies appear red (green) for x < (>) 0.25 for α-(1 – x)Al₂O₃·xCr₂O₃.⁴⁴ Similar trends are observed for increasing Cr³⁺ concentrations in the (1 – x)MgAl₂O₄·xMgCr₂O₄ systems.⁵⁵ The gradual change in color from red to green in the ruby series is a result of a shift of the ⁴T_2g(⁴F) (O_h) manifold to 0.2 eV lower values upon increasing Cr³⁺ content, hence a shift of 10Dq. The consequence is that low (high) Cr³⁺ concentrations in ruby lead to the absorption in the green (red) part of the visible spectrum, yielding their apparent inverse colors (all absorb blue).

Many studies addressed the origin of the relatively high 10Dq in ruby compared to for example emerald as it explains the color difference between the two famous gemstones. Initially it was assumed that, according to the simple point charge model, the average Cr³⁺–O^2– distance in emerald was higher than in ruby, giving rise to the observed 10Dq difference. Short reviews of this interpretation are given in, for example, the introductions of the works by Moreno et al.^54,56 It is essential that Gaudry et al. showed by EXAFS measurements^39,52 that the average Cr³⁺–O^2– distance in ruby coincides with that for eskolaite and emerald within the experimental uncertainty (in all three compounds, the bond lengths are 1.965–1.980 Å). Such differences could at maximum explain variations in 10Dq of 0.075 eV, not the observed 0.20–0.25 eV. It was also shown by DFT calculations that Cr³⁺ site relaxation, when replacing Al³⁺ in corundum, is not strongly influencing the optical excitations.^38,40

Alternatively, it has been argued that the electrons from the CrO₆^9– complex are not fully localized but extend partially to the Al sites in ruby, thereby potentially influencing 10Dq.^44,57,58 Electron nuclear double resonance (ENDOR) measurements⁵⁹ as well as DFT calculations⁶⁰ contradict the idea that electrons from the CrO₆ complex are delocalized outside the complex by showing that the actual average Al valency is very close to the formal Al³⁺ valency.

Electron transfer from the O to the Cr would be more likely for α-Cr₂O₃ than for α-Al₂O₃:Cr³⁺. This is evidenced in the decreasing Racah B values for Cr³⁺ when going gradually from dilute ruby, α-Al₂O₃:Cr³⁺, to eskolaite, α-Cr₂O₃.^39,44 In fact, Cr³⁺ in low concentrations in ruby is typically well described without ligand-to-metal CT effects.^39,42,43 The above concurs with the weak signature of antibonding charge transfer states observed here for ruby in RIXS slices d–g in Supporting Information, Figure S2. The broad and nonintense features are attributed to O to Cr CT, following previous interpretations.¹³ The relative energy position of this feature shifts according to the incident energy from 8.4, to 9.5, to 10.4, to 11.2 eV for slices d, e, f, and g, respectively.⁶¹ Because the CT feature has a low intensity and is observed at relatively high energies, it will not affect the d–d excitation features in the first 6 eV as discussed in this article.^30,62 Also, the L₃ XAS reveals no substantial CT shoulder on the high-energy-side of the L₃ edge, typical for systems in which CT plays a large role.⁶² The omission of antibonding Cr–O CT effects in the simulations is thus justified and further substantiated by an excellent match of the calculations with both experimental XAS and RIXS data.

Nevertheless, Cr–O bond covalency, without the transfer of a full electron from the ligand to the metal as in formal charge transfer descriptions, is important to consider when interpreting the Cr³⁺ electronic structure exhibited in the spectra and colors of various minerals. It has been argued that, although Cr–O bond covalency is changing between ruby and eskolaite or emerald, it has a minor effect on the strength of the crystal field 10Dq.⁵⁶ Others have argued that the difference in 10Dq between ruby and eskolaite is 35% due to covalency effects.³⁹ Cr K edge XANES experiments and DFT calculations reveal that the gradual change of the nature of the second neighbor in the coordination shell of the Cr³⁺ ion in a series of ZnAl_2–xCr_xO compounds affects its electronic structure via the O ligands. The DFT study by Verger et al.⁶³ confirms the suggestion from previous observations^57,64 that the 10Dq value includes effects of the nature of the (second nearest neighbor) cationic environment. Moreno and co-workers have systematically worked along these lines, as they have shown by many DFT calculations^{53,54,56,65−68} that the inclusion of a nonlocal electric field E(r) of the host lattice, acting on the localized electrons of the chromium ions, is causing nonzero additions to the local 10Dq, depending on how the additional electric field works along different spatial directions of the ion. Inclusion of such E(r) helps for example to explain why the spinel MgAl₂O₄:Cr³⁺ and ruby appear red and emerald green.^54,66

The works by Moreno et al. focus largely on the precise calculation of the 10Dq value of different systems using quantum chemistry methods. In a recent study also the energies of the R-lines and the second spin-quartet band (from the ⁴A_2g to the ⁴T_1g(⁴F)) are considered.⁶⁹ It is argued that a typical Tanabe Sugano approach, using only Racah B and C parameters, fails to explain spectra for systems such as ruby because not all 10 independent two-electron integrals, used to describe the dⁿ electron interactions on for example Cr³⁺ in ruby, are considered.

Here we argue however that a typical Tanabe Sugano approach, using only Racah B and C, works well to explain the OAS, XAS, and RIXS spectra of ruby, given that one does not hold on to the restriction that Racah C/B should be 4. In an educational contribution, Schmidtke explains the origin of this restriction to lie in the classical works of Sugano, Liehr, and Jorgensen.⁷⁰ Schmidtke continues by mathematically proving that it is a consequence of the model, that F_dd⁰ > F_dd > F_dd⁴ and hence B < C. In the case of describing a (partially) covalent ion, this also implies ΔF_dd > ΔF_dd² > ΔF_dd and, as a consequence, it follows that C/B can easily be larger than 4 when F_dd² and F_dd are reduced from their ionic values (remember B = (9F_dd² – 5F_dd)/441 and C = 5F_dd⁴/63). In fact, Schmidtke calls for a re-evaluation of crystal field interpretations of ions in complexes in which Racah B and C are not varied independently (those in which C/B are fixed a priori to a value close to 4). The notion that F_dd and F_dd⁴ need not always to be reduced with similar ratios is already present in the work by Ranson and Warren⁷¹ and references therein.

Analyzing the combined experimental OAS, XAS, and RIXS spectra in a systematic manner using a crystal field (Tanabe Sugano) approach led to the here obtained F_dd² and F_dd values, which differ from previous results for ruby. We established that F_dd² and F_dd were reduced in different manners (60% and 80% from Hartree–Fock values, respectively), yielding a relatively high Racah C/B ratio of 6.07 (where 3.75 is standard in multiplet codes²⁶). The experimental chromium 2p XAS spectrum of ruby was excellently matched by simulation, mainly as a result of the applied F_dd²/F_dd scaling. This was shown in detail in Supporting Information, Figure S4. We note that our XAS simulation matches the experimental data to a considerable higher degree of accuracy than previous presented results.^39,72 In fact, Gaudry et al. used an identical scaling of F_dd² and F_dd, being 56% of the Hartree–Fock values (70% of the ionic Cr³⁺ case; the nephelauxetic ratio being 0.7). Such identical scaling was also applied in one of the spectra of Supporting Information, Figure S4, and yields a similar curve as the one presented by Gaudry et al. These parameters are able to simulate the chromium 2p XAS spectrum of, for example, α-Cr₂O₃,³⁹ but not that of ruby, confirming that the odd F_dd²/F_dd scaling relates to low-concentrated Cr³⁺ in ruby. Also, only with this F_dd²/F_dd scaling, the energy positions of almost all OAS and RIXS observed doublet and quartet 3d states were tuned to match their calculated counterparts, as demonstrated in Figure 3b and Supporting Information, Figure S3. Concerning this topic, we note that, in optical absorption literature, it is not uncommon to present different Racah B values for different spectral features,^44,73 and more recent work on nonresonant inelastic spectroscopy also led to similar necessities.^3,74 For ruby (containing 5 wt % of Cr³⁺) B₃₅ and B₅₅ parameters (definitions related to the degree of e_g/t_2g character in a band) of 0.083 eV (670 cm^–1) and 0.092 eV (740 cm^–1) were reported, respectively, for different spectroscopic peaks.⁴⁴ The authors assumed a constant C/B ratio of 4 in energy-level calculations. The B₃₅ parameter for ruby with 2.5 wt % Cr³⁺ was also reported to be 0.079 eV (640 cm^–1).⁷⁵ Alternatively, a single B value was reported to be 0.080 eV (645 cm^–1) for ruby containing 3.5 wt % of Cr³⁺ and a C/B ratio of 3.75, but these parameters fail to predict the R-line (and other spin-doublet state) energies correctly. The single B value of 0.071 eV (570 cm^–1) and C/B ratio of 6.07 applied here are instead able to reproduce the energy positions of almost all features, with the exception of the B-line doublet states (and possibly the ²A_1g(²G) (O_h) state as suggested in Figure 4), without the need of invoking different parameters for different features. As discussed in the previous paragraph, the here obtained result that ΔF_dd² > ΔF_dd is a natural consequence of describing covalency within the crystal field model. Finally, we note that OAS spectra of other Cr³⁺ containing systems have been successfully described using C/B = 5.25 for Cs₂NaYCl₆:Cr³⁺⁷⁶ and C/B = 6.15 for tr-[Cr(NH₃)₄(CN)₂](ClO₄).⁷⁷

In summary, the nature of the second nearest neighbors or host lattice around the color-causing Cr³⁺ ions in ruby may lead to a relatively high 10Dq value (transition energy of the ⁴A_2g to ⁴T_2g (O_h)) compared to the case of CrO₆^9– clusters in vacuo or other minerals, as was shown by many (first-principle) calculations by Moreno et al. The origin is an additional electric potential acting locally upon the Cr³⁺ 3d electrons caused by the surroundings. Here we add to the discussion that within a Tanabe Sugano approach additional electric screening will naturally lead to ΔF_dd > ΔF_dd⁴ and that the obtained, new Racah C/B of 6.07 for ruby, also captures the influence of the solid matrix embedding the absorbing Cr and yields a local electronic description that explains the energies of almost all other d–d excitations. While the crystal field model cannot explain the origin of the relatively high 10Dq value, it does lead, in a transparent and secure manner, to the full and correct calculation of the OAS, XAS, and RIXS spectra using a single parameter set that includes a parametrized 10Dq.

Finally, despite the use of fitting parameters, we stress that the semiempirical crystal field model captures the essence of the OAS, 2p XAS, and 2p3d RIXS spectra in a relatively simple, but physically correct view, with a limited number of justifiable parameters. It is not the aim of such models to replace first-principle interpretations. First-principle calculations ultimately correlate the atomic structure with the electronic structure and subsequently with the excited state properties such as X-ray spectra. At this stage, however, ab initio methods are not capable yet of calculating the 2p3d RIXS spectra of open 3d shell ions as accurate as semiempirical codes, especially given the high resolution in such experiments. This holds for both solid-state based methods of Haverkort et al.,^,9 and Hariki et al.^4,11 and quantum-chemistry based methods from the groups of Neese,^6,7 Lundberg,⁵ Odelius,¹⁰ and Kühn.⁸ Ogasawara et al. have further described the challenges met when calculating the OAS^78,79 and 2p XAS⁷² spectra of ruby using first-principle methods.

What New Did We Learn about RIXS, RIXS versus OAS, and What Could It Lead to

We have identified and investigated different factors that influence the RIXS spectral intensities in great detail. It is known that the overall intensity of RIXS spectra (area under curve), as a function of the incident energy, follows roughly the intensity of the XAS spectrum. In Figure 3, we add to this that the relative intensities of inelastic features within a single-energy RIXS spectrum, have a clear correlation to the mix of atomic states with different spin multiplicities that contribute to the XAS states at which the RIXS was acquired. Recall that at excitation energy d, only a small spectral weight was seen for the doublet R-lines in the RIXS spectrum and that only 20–30% of doublet character was present at that excitation energy in the XAS spectrum. At excitation energy e, the RIXS spectrum was dominated by the doublet R- and B-lines, while the XAS cross-section at that energy consisted of 70% of doublet character. It seems thus that the spin-selection rule is still largely followed in the RIXS process, i.e., transitions with ΔS = 0 are more likely than those with ΔS ≠ 0. The 2p core–hole and its spin–orbit coupling are not completely canceling the spin-selection rule but create strong mixes of states with different spin multiplicity, thereby allowing the observation of 3d states with different spin character. As opposed to the strong parity and spin-forbidden electric dipole transitions of the optical absorption spectrum, the additional RIXS features arise from the fully allowed electric-dipole transitions involved and the strong state mixing occurring in the intermediate state as described above.

A second group of factors governing the relative intensities of RIXS features are broadening effects. RIXS is limited in this experiment by instrumental broadening (the natural broadening is identical to the one in OAS and much smaller¹). It is clear that an overall increased instrumental broadening (applied as a Gaussian broadening) will flatten the RIXS spectra (the differences in peak maxima will become smaller as all features are spread out). It is also good to realize that the width of the incoming X-ray beam has only little effect on the relative intensity profile of a RIXS spectrum. The effect of exciting several excitation energies simultaneously around the main excitation energy, weighted by a Gaussian width, is shown in Supporting Information, Figure S12. It is observed that, only when the incoming beam is fairly polychromatic, following an energy distribution with a fwhm above 0.5 eV, the relative intensity profile of the RIXS spectrum becomes severely affected. Here the incoming beam has an fwhm of 0.125 eV, and Supporting Information, Figure S12 shows that, in such case, it is perfectly possible to calculate the RIXS spectra at a single excitation energy instead (as was thus done here).

The broadening effect of most interest is the Lorentzian broadening applied to simulate the natural line width of the spectra. In the Kramers–Heisenberg equation, used to calculate RIXS spectra, the lifetime of the core–hole excited RIXS state is directly related to the degree of interference that occurs in the RIXS process. Therefore, identical alternation of the Lorentzian broadening of each state does not simply result in identical modifications of the intensities of each transition. It also redistributes intensities over the 3d states in the RIXS spectra. The effect of calculating the RIXS spectra with the obtained crystal field multiplet parameters, but with alternating values of the Lorentzian broadening of the core-hole excited state, is given in Supporting Information, Figure S13. It can, for example, be seen that only for low values of the Lorentzian broadening (≤0.2 eV fwhm) the R-lines in the RIXS spectrum at energy e gain sufficient intensity with respect to the other states. Similarly, at other excitation energies, relative intensity redistributions between features can be observed. This was also clearly seen in Supporting Information, Figure S10, where it was explained that it is “selection rules plus RIXS interference” (and not “selection rules only”) that explain the typical polarization-dependent behavior of the elastic line. The results presented in Supporting Information, Figure S13 teach us that no single value of the (core–hole excited state) Lorentzian broadening could explain the experimental RIXS intensities over the whole edge. From careful comparisons with the experiment, it was established that the Lorentzian broadening increases over the XAS edge, implying shorter lifetimes for higher energy core–hole excited states. At the beginning of the XAS L₃ edge, Figure 4a showed the presence of a relatively large degree of states with sextet spin multiplicity, which indeed are expected to live longer as no such states are available in the 3d ground state. Moreover, it is well established that simulation of the XAS L₂ edge needs relatively large Lorentzian broadenings. It is not surprising that the width for the L₂ edge is larger in a solid than the atomic values given by Krause and Oliver,⁸⁰ in particular due to the Coster–Kronig decay, which appears to be very large for ruby. This corresponds to the values used here at excitation energy l at the foot of this edge.

In addition to the differences in the intensity of the OAS versus RIXS spectra, as treated in Figure 4, the broadenings in the OAS spectra have a different origin. The OAS transitions to states with a doublet spin multiplicity are calculated as sharp lines (5 meV fwhm), whereas those to quartet states are broadened substantially more (150 meV fwhm). This is done to reproduce the experiment and is normally considered to be a result of a distribution of crystal field 10Dq values being present in the sample. A small distribution (due to minor variations in the Cr³⁺ site geometries) would yield broad (sharp) features for most quartets (doublets), in agreement with the slopes of the lines in the energy-level diagram of Figure 2.

The comparison of the energy positions of the RIXS and OAS spectral features showed only very small differences between them. We found no evidence for this compound that OAS and RIXS probe electron–phonon states differently within our experimental resolution. We ascribe this to the decay of the 2p core–hole excited state being faster than the decay of a high to a low phononic state of the same electronic configuration (see Figure 6). The absence of temperature dependence in the RIXS spectra further showed that (within our experimental resolution) phonon effects are not observable. This observation is important to understand previous results. For example, we have reported blue-shifts between d–d transitions probed by OAS compared to RIXS for a set of cobalt carboxylate compounds.¹ The energy shift was qualitatively discussed to be possibly originating from (a) dispersion effects in RIXS as a function of excitation energy and due to metal–metal interactions, (b) light polarization effects in RIXS, (c) temperature population effects, and (d) phonon–electron excitations being potentially probed different in OAS and RIXS. The last argument possibility can be excluded based on the current measurements.

Toward Experimental Evidence of Mechanisms in Metal Chemistry

Although the above observations are of interest to the specialist, the most interesting question this study has answered is to what extent can 2p3d RIXS observe the whole, charge neutral 3d optical density-of-states, 3d o-DOS, of a transition metal ion and how?

The importance of being able to measure the excited 3d o-DOS of a metal, is that it opens up a rich, new world of metal chemistry characterization. In the first place, it allows for spectral fingerprinting due to the large number of 3d states in most transition metal ions. This is shown in Figure 8. It illustrates how measuring the 3d o-DOS during a hypothetical, chemical reaction can yield experimental evidence for the reaction mechanism occurring around a metal ion. The energies and intensities of the 3d o-DOS are shown for a conversion of an octahedral to tetrahedral ligand-surrounded Cr³⁺ ion through a square planar transition phase. The overall intensity profiles (neglecting for now the color coded fillings) change dramatically as a result of the changing ligand geometry and this behavior will (a) be applicable to most transition metal ions and (b) be largely measurable as shown in Figure 7.

Figure 8.

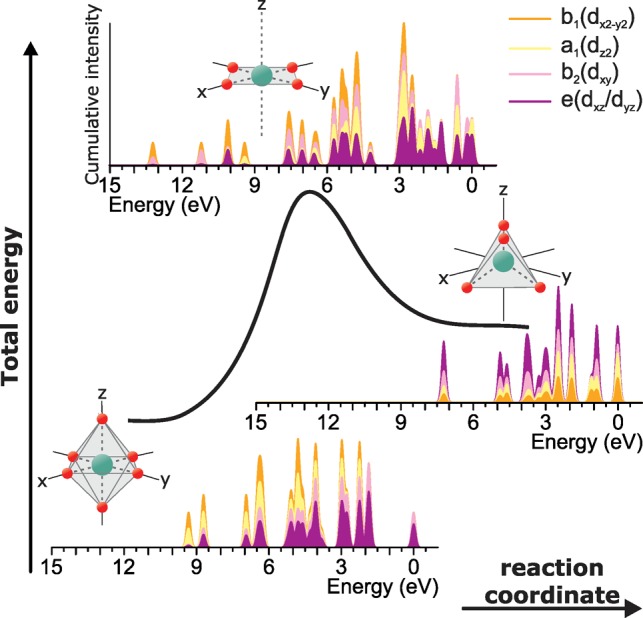
Total energy curve of a hypothetical, chemical conversion of an octahedral to tetrahedral ligand-surrounded Cr³⁺ ion through a square planar transition phase. For the initial, transition, and final states, the calculated 3d o-DOS is shown and broken down in the 3d orbital contributions to each 3d state. At each energy, the sum of the four colors (purple, pink, yellow, and orange) form 100% of the intensity.

Moreover, the calculations can equally be used to decompose the quantum many-body 3d electron states into contributions from the individual 3d orbitals to each state.^81,82 In Figure 4b, the excited 3d o-DOS curves show purple, pink, yellow, and orange areas under the curves. These relate to the individual contributions of d_xz/dyz, d_xy, d_z² and d_x²–y² orbitals to the 3d o-DOS, respectively. The representation is cumulative, meaning that the visible areas at each energy relate to the percentage contributions of each orbital. Such information could be related to specific compound reactivity with a transition metal ion. Supporting Information, Figure S11, shows how the RIXS signatures would evolve in nine spectra during the first part of this hypothetical reaction, from the initial toward the transition state.

However, it is not straightforward to use this information in the prediction of a chemical reaction because the mix of orbitals contributing to a state is not a fixed property, but changes continuously upon geometry changes of the ion or its ligands. Perhaps two things are most valuable to consider: (1) to simply use the rich RIXS spectra as fingerprints for a metal reaction mechanism without looking at particular 3d orbital compositions of each state, and (2) to consider only the 3d orbital contribution changes to the 3d state at 0 eV, that is the ground state of the system, as a function of for example changing ligand geometry. The change in the 3d orbital population of the ground state reflects the bonding combination of the 3d orbitals of the metal ion with ligand orbitals. The first point will become more relevant and feasible with the advent of the X-ray free electron lasers (XFELs). They allow the measurement of soft RIXS spectra with femto- to picosecond time resolution, time-scales fast enough to capture chemical reactivity. This was already demonstrated to yield new insight in the ligand exchange reaction of iron pentacarbonyl dissolved in ethanol⁸³ through an analysis of charge transfer interactions. If such experiment and analysis would be combined with the here presented, detailed measurement of a large part of the local, excited 3d o-DOS of a metal, complementary and spectacular experimental evidence of dynamic metal reaction mechanisms will become available.

In general, soft RIXS is becoming more accessible and by now 12 user beamlines fall in the right energy and resolution window (3d metal L-edge at E/ΔE ≥ 5000) to perform this type of research (for example, SLS-ADRESS, Spring8-BL07LSU, SOLEIL-Sextants, NSRRC-I511, and CLS-10ID-2). The new beamline ID32 in the European Synchrotron Radiation Facility (ESRF; Grenoble, France) reaches a record energy resolution of E/ΔE = 30000, implying 20 meV at the Cr L-edge. This means a 7.5 times improvement compared to the resolution in the current experiment. Such resolution is expected to sharpen the RIXS doublet features such as R- and B-lines for ruby. It will allow a better disentanglement of the suggested doublet contribution at 3.35 eV to the ⁴T_1g (O_h) feature at 3 eV as shown in Figure 4d. Moreover, novel electronic features of ruby could possibly be discovered. In general, a drastically improved resolution is expected to result in the observation of previously unidentified excited state signatures. Higher resolution comes at a cost of a higher applied X-ray dose (in the current set-ups) and hence a significantly larger chance to observe radiation induced chemistry or physics, see for example photoreduction processes at the metal XAS L-edges.²⁴ Luckily, with the advent of XFELs, such damage effects may be limited due to the beneficial dose rate effect. We refer to Kunnus et al. for a comparison of radiation parameters between a third generation synchrotron and an XFEL.⁸⁴

Conclusion

We have measured OAS, Cr 2p XAS, and Cr 2p3d RIXS spectra of the gemstone ruby. By considering these data, plus available literature data on ruby, we were able to describe the spectra with a single, unified crystal field multiplet interpretation. The errors in the obtained parameters (given in Table 1) used to describe the Cr 3d electronic states are small as shown in sensitivity analyses. It is found that nonidentical scaling of the Slater–Condon parameters F_dd² and F_dd is needed to describe the spectra. This is an uncommon result for a crystal field description, likely caused by the (relatively low) C₃ point group of the Cr³⁺ ion in ruby. The obtained values lead to a Racah C/B value of 6.07, which predicts the majority of 3d state energies correct. Careful analysis of RIXS spectra further hinted at the existence of a previously nonobserved state with doublet spin-multiplicity character around 3.35 eV, above the 3 eV ⁴T_1g(⁴F) (O_h) manifold. Furthermore, no significant energy differences were found between the 3d (plus phonon) states as seen by OAS and RIXS. Small changes could be explained by considering the selection rules of the different spectroscopies and the presence of different electronic states under a single broad RIXS or OAS peak. When it comes to RIXS, it was seen that relative intensity differences between RIXS spectra, acquired at different excitation energies, were understandable from considering the spin-state character of energy levels forming the XAS spectrum. Detailed insights on the role of RIXS interference, and broadenings on the RIXS intensities were equally obtained. An interesting insight is that the polarization-dependent intensity behavior of the elastic line (versus inelastic feature intensity) is not a selection rule only but a selection rule plus RIXS interference effect. The most important observation is however that, although 2p3d RIXS was not able to measure the full 3d o-DOS, it is able to measure a large part of the 3d o-DOS with a high resolution and with an intensity profile close to the original 3d o-DOS when measuring at selected X-ray excitation energies. For ruby at least, it was demonstrated here that measuring high above the XAS L₃ edge, but below the XAS L₂ edge, is a good energy range for the purpose. The further decomposition of the 3d o-DOS in contributions of individual 3d orbitals, plus the coming of age of many synchrotron and XFEL RIXS setups, will enable 2p3d metal RIXS spectroscopy fingerprinting as experimental evidence of reaction mechanisms that occur at a metal site during a chemical reaction.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpca.8b00984.

• Experimental details of sample characterization; raw experimental RIXS data; determination of the crystal field multiplet calculation parameters; RIXS polarization and temperature effects; additional calculations showing where to best measure o-DOS with RIXS and effect of interferences on RIXS intensity; derivation of the polarization dependent selection rules of optics and RIXS (PDF)

• Input file for CFM calculations (ZIP)

The authors declare no competing financial interest.