Abstract
We report a detailed study of the effects of anions on the rates of the amination of aryl halides catalyzed by palladium complexes of the hindered alkylmonophosphine PtBu3. These reactions occur by turnover-limiting oxidative addition. The extent of the dependence of the rates on the concentration and identity of bases was found to depend on the electronic properties of the haloarenes. The rates of reactions of electron-rich and electron-neutral chloroarenes were independent of the concentration of the bulky alkoxide base OCEt3−, but they were dependent on the concentrations of the less hindered OtBu− and the softer 2,4,6-tri-tert-butylphenoxide bases. The reactions were fastest when 2,4,6-tri-tert-butylphenoxide was used as base and slowest when NaOCEt3 was used as base. A concurrent reaction pathway involving simultaneous oxidative addition of chloroarenes to [Pd(PtBu3)] and [(PtBu3)Pd(OR)]− may explain the dependence of the rates of reactions of electron-rich and electron-neutral chloroarenes on the identity and concentration of bases. The rates of reactions of electron-poor chloroarenes and the reactions of bromoarenes were independent of the concentration of OCEt3−, OtBu−, or 2,4,6-tri-tert-butylphenoxide bases but were dependent on the identity of bases, even though an adduct of the base did not accumulate in any observable amounts. Further, long induction periods were observed for the reactions of electron-poor chloroarenes. These long induction periods suggest that the complex kinetic behavior could result from the generation of several catalytically active species.
Introduction
Metal-catalyzed coupling reactions of chloroarenes are highly desirable, because these haloarenes are the least expensive and most widely available. However, chloroarenes are the least reactive of the haloarenes. Thus, most of the early developments in palladium-catalyzed coupling to form carbon-carbon and carbon-heteroatom bonds occurred with bromoarenes and iodoarenes as electrophiles. Due to the growing importance of coupling chemistry, there has been extensive effort to extend the scope of Heck, Suzuki, Stille, Kumada, amination, and etherification reactions to include chloroarenes. Several sterically hindered alkylmonophosphines, chelating alkylphosphines, and sterically hindered carbene ligands have been identified that make coupling reactions of unactivated chloroarenes feasible.1–24 Chloroarene aminations were some of the first coupling reactions of chloroarenes at low temperature.3,6,25
Much effort has been devoted to ligand and reaction design, but surprisingly little mechanistic information has been generated on chloroarene coupling.26–29 Oxidative addition of chloroarenes to a mono- or bisphosphine Pd(0) complex is generally considered to be the turnover-limiting step of a catalytic cycle that involves oxidative addition, transmetalation, and reductive elimination. However, several results are inconsistent with this proposal. For example, Heck, Suzuki, Stille, amination, and etherification reactions require different temperatures and reaction times for the same chloroarene and catalyst.3,6,7,9,12,17,25,30 Further, dramatically different temperatures and catalyst loadings are needed for the amination of chloroarenes in the presence of strong and weak bases.7,25 Finally, added halides and acetate anions have been observed to affect the rates of coupling reactions.31–35
Several reports show that added halide and acetate anions influence the mechanism of oxidative addition.33,34,36–38 In some cases, the effect of anions on the rate of oxidative addition has been attributed to the coordination of halide to palladium prior to oxidative addition.33,34,39–43 For example, data in reports by Amatore, Jutand, and co-workers indicate that oxidative additions of aryl iodides and triflates to Pd(PPh3)4 were faster in the presence of Cl−. The authors concluded that the oxidative addition proceeded via Pd(PPh3)2 in the absence of any added Cl− 42,44 but through Pd(PPh3)2Cl− in the presence of Cl−. The reaction occurred to this anionic complex because it was present in much higher concentrations than the neutral 14-electron complex Pd(PPh3)2.33,34
Computational studies on the cross-coupling of phenylboronic acid with acetic anhydride catalyzed by Pd(PMe3)2, which is mechanistically related to the coupling of chloroarenes,45,46 and oxidative addition of iodobenzene to anionic two-coordinate and three-coordinate Pd(0) complexes have also been conducted.47 Some of these computational results imply that oxidative addition occurs to the anionic bisphosphine intermediate [(PMe3)2Pd(OAc)]− or the anionic monophosphine species [(PMe3)Pd(OAc)]−, rather than to the neutral species Pd(PMe3)2 and Pd(PMe3),36,37 while other computational results on the reactions of PPh3-ligated palladium(0) lead to the conclusion that the barrier to C–X bond cleavage by the neutral monoco-ordinate LPd (L = PPh3) species is lower than that by the anionic dicoordinate LPdX−.47
Fewer experimental studies have been conducted to explain the effect of bases and additives on the rate of catalytic cross-coupling reactions. Studies by Espinet and co-workers revealed that added chloride ions accelerated the rate of Stille reactions when AsPh3 was used as ligand and the oxidative addition of aryl triflate was turnover-limiting. In contrast, added chloride ions retarded the overall rate of the reaction catalyzed by PPh3 complexes of palladium when transmetalation was turnover-limiting.48 Alcazar-Roman and Hartwig studied the effect of alkoxide and aryloxide bases and halide anions on the rate of reaction of chlorobenzene with N-methylbenzylamine catalyzed by Pd(PtBu3)228. The data from these studies implied that the reaction proceeded by two concurrent mechanisms: one by oxidative addition of chloroarene to the 12-electron Pd(0) complex ligated by a single monophosphine and one by oxidative addition of chloroarene to an anionic, 14-electron Pd-(0) complex containing an alkoxide, aryloxide, or bromide anion.
Herein, we report mechanistic studies on reactions of N-methylbenzylamine with various chloroarenes possessing distinct electron-donating properties catalyzed by Pd(PtBu3)2. These studies were conducted to determine if chloroarenes possessing distinct electronic properties follow the two mechanisms proposed for reactions of chlorobenzene and whether the balance between the two mechanisms is affected by the electronic properties of the aryl group. Our data are consistent with the reactions of electron-neutral and electron-rich chloroarenes occurring through concurrent oxidative addition to neutral and anionic Pd(0) species. Reactions of electron-poor chloroarenes and of bromoarenes appear to be more complex.
Results
The rates of reactions of N-methylbenzylamine (1) with 4-chloroanisole (2a), chlorobenzene (2b), 4-chlorobenzotrifluo-ride (2c), and bromobenzene (2d) catalyzed by Pd(PtBu3)2 (Scheme 1) were examined. The reactions were conducted with 5–10 mol % of Pd(PtBu3)2 as the catalyst, amine as the limiting reagent, and an excess of aryl halide and base. The final concentrations of the reaction components were 21.2 mM N-methylbenzylamine, 50.0–250 mM haloarene, 100–300 mM base, 5.0–15.0 mM added [(C8H17)4N]Br or [(C8H17)4N]Cl, 1.02–2.02 mM Pd(PtBu3)2 (5–10 mol %), 0.21–1.26 mM P(tBu3) (1–6 mol %), and 2.92 mM 1,3,5-trimethoxybenzene as internal standard. Quantitative yields of the tertiary amine products were observed in all cases, as determined by 1H NMR spectroscopy with an internal standard. No measurable consumption of the Pd(PtBu3)2 was observed during the reaction, as determined by 31P{1H} NMR spectroscopy with an external standard, and no additional species were observed by 31P{1H} NMR spectroscopy (vide infra). Observed rate constants (kobs) for the reaction of N-methylbenzylamine with haloarenes (2a–d) and various alkoxide and aryloxide bases and added anions were determined from plots of the decay of N-methylbenzylamine vs time generated from 1H NMR spectra obtained over a reaction time that led to greater than 95% conversion. The values of the observed rate constants typically varied by less than 10% for duplicate runs.
Scheme 1.
1
a. Reaction of N-Methylbenzylamine with Electron-Rich 4-Chloroanisole
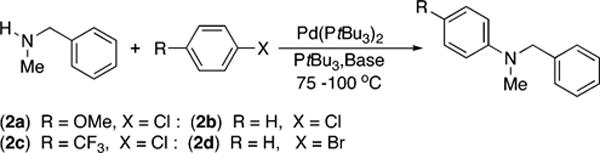
Linear plots of the decay of amine vs time were obtained during the reactions of 4-chloroanisole (2a; 119 mM) with N-methylbenzylamine (21.2 mM) and NaOCEt3 (0.10–0.30 M), NaOtBu (0.10–0.30 M), or 2,4,6-tri-tert-butylphenoxide (0.50–0.15 M) as base catalyzed by 10 mol % Pd(PtBu3)2 with 1 mol % added PtBu3 (Figure 1A–C). Linear plots of the decay of amine vs time were also obtained for the reactions of the same amine, chloroarene, and NaOCEt3 as base, but with added [(C8H17)4N]Br (5.0–15 mM) (Figure 1D). Thus, rates of amination of 2a occurred with a zero-order dependence of the rate on the concentration of N-methylbenzylamine.
Figure 1.
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with 4-chloroanisole (2a; 119 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) and PtBu3 (0.21 mM, 1%) at 100 2°C and (A) NaOCEt3 (0.10–0.30 M) as base, (B) NaOtBu (0.10–0.30 M) as base, (C) 2,4,6-tri-tert-butylphenoxide (0.50–0.15 M) as base, and (D) 0.20 M NaOCEt3 as base with added [(C8H17)4N]-Br (5.0–15 mM).
b. Reaction of N-Methylbenzylamine with the Electron-Neutral Chlorobenzene
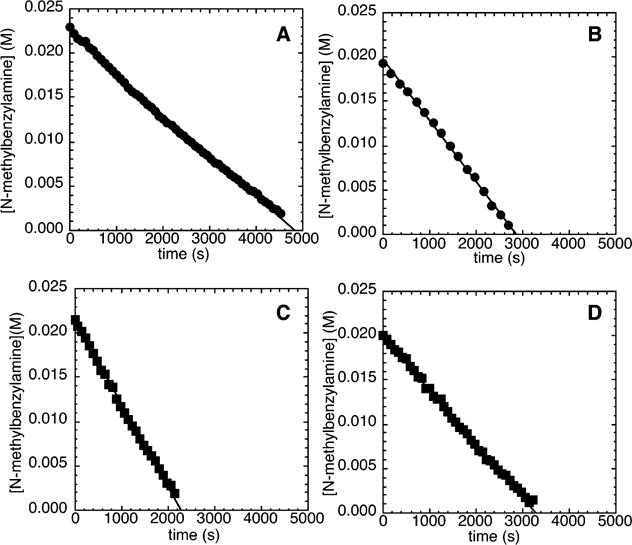
Reactions of the electron-neutral chlorobenzene 2b (140 mM) with N-methylbenzylamine (21.2 mM) and NaOCEt3 (0.10–0.30 M) as base catalyzed by 10% Pd(PtBu3)2 in the presence of 0–1% added PtBu3 occurred with a detectable induction period (Figure 2A). This observation contrasts the absence of any induction period during the reactions of the electron-rich chloroarene 2a with N-methylbenzylamine under similar conditions. The reaction of 2b with N-methylbenzylamine and NaOCEt3 (0.10–0.30 M) conducted with added [(C8H17)4N]Br (5.0–15 mM) occurred without any measurable induction period (Figure 2B), just as the reaction of the electron-rich 2a occurred without a detectable induction period under similar conditions. Reactions of N-methylbenzylamine with 2b and NaOtBu (0.10–0.30 M), instead of NaOCEt3, as base, in the presence of 1–5 mol % of added PtBu3 and 10 mol % Pd(PtBu3)2 as catalyst also occurred without any measurable induction period (Figure 3).
Figure 2.
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with chlorobenzene (2b; 140 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) and PtBu3 (0.21 mM, 1%) at 90 °C with (A) NaOCEt3 (0.10–0.30 M) as base and (B) 0.200 M NaOCEt3 as base with added [(C8H17)4N]Br (5.0–15 mM).
Figure 3.
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with chlorobenzene (2b; 140 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) and PtBu3 (0.21 mM, 1%) at 90 °C with NaOtBu (0.10–0.30 M) as base.
c. Reactions of N-Methylbenzylamine with the Electron-Deficient 4-Chlorobenzotrifluoride
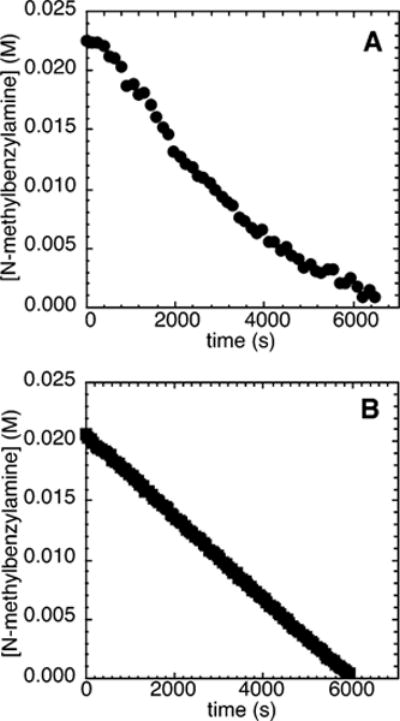
Figure 4A shows a typical plot of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with an excess of an electron-deficient chloroarene, 4-chlorobenzotrifluoride (2c; 109 mM), and NaOCEt3 (0.10–0.30 M) as base catalyzed by 10% Pd(PtBu3)2 in the presence of 0–3 mol % PtBu3. The reaction proceeded with a detectable induction period before the amine started to decay linearly with time. This observance of induction period matches the observation of an induction period during the reactions of electron-neutral chloroarene 2b and contrasts the absence of an induction period during the reactions of the electron-rich chloroarene 2a.
Figure 4.
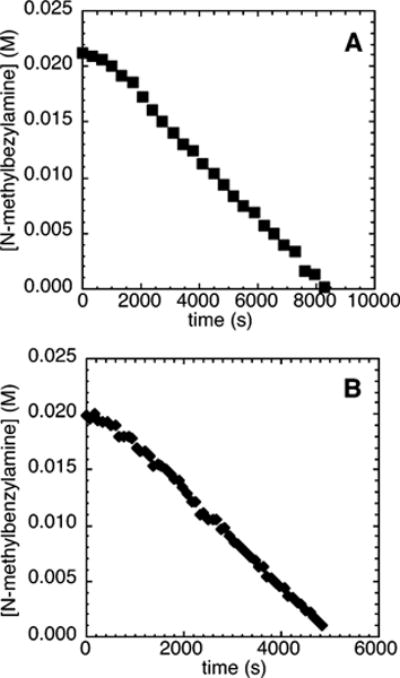
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with 4-chlorobenzotrifluoride (2c; 109 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%), with added PtBu3 (0.21 mM, 1%) at 75 °C and (A) NaOCEt3 (0.10–0.30 M) as base and (B) 0.20 M NaOCEt3 as base with added [(C8H17)4N]-Br.
The reaction of the electron-poor chloroarene 2c with N-methylbenzylamine and NaOCEt3 (0.10–0.30 M) conducted with added [(C8H17)4N]Br also occurred with a kinetically significant induction period (Figure 4B). The observation of an induction period in this case contrasts the absence of an induction period during the reactions of both electron-neutral and electron-rich chloroarenes in the presence of added [(C8H17)4N]Br.
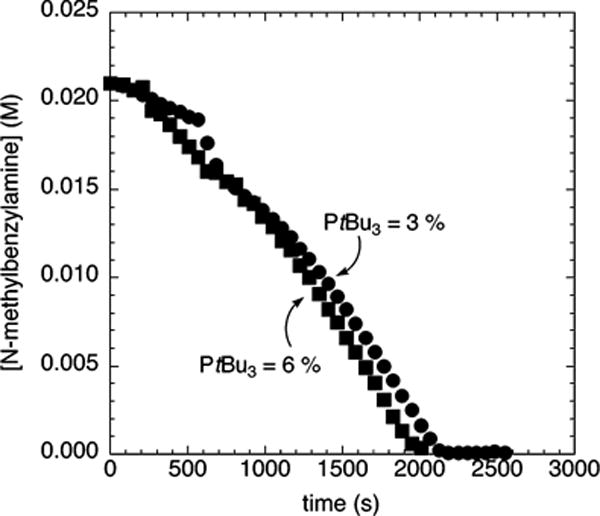
The length of induction period observed during the reaction of the electron-poor chloroarene 2c with N-methylbenzylamine and NaOCEt3 was found to depend on the concentration of added PtBu3. Figure 5 shows the reactions of N-methylbenzylamine (21.2 mM) with 4-chlorobenzotrifluoride (2c; 109 mM) and NaOCEt3 (0.10–0.30 M) as base catalyzed by 10% Pd-(PtBu3)2 in the presence of a larger amount of added PtBu3 (5 mol %). In the presence of this larger amount of added ligand, the reaction occurred without an induction period. The same reaction in the presence of 0–3 mol % PtBu3 occurred with a detectable induction period (Figure 4A).
Figure 5.
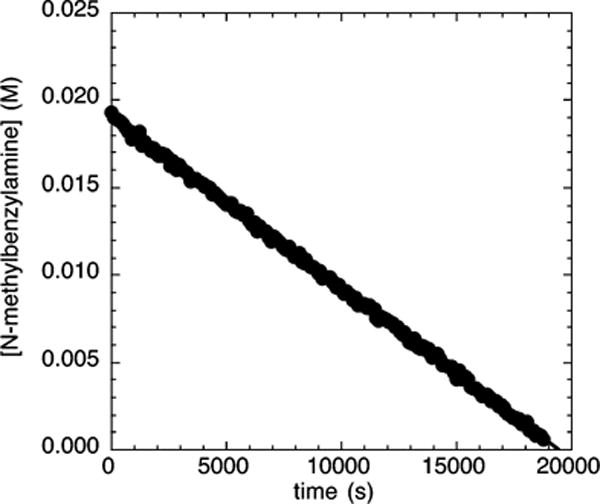
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with 4-chlorobenzotrifluoride (2c; 109 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) with added PtBu3 (1.1 mM, 5%) at 75 °C and NaOCEt3 (0.10–0.30 M) as base.
Reactions of N-methylbenzylamine with 4-chlorobenzotrifluoride (2c) and NaOtBu (0.10–0.30 M) or 2,4,6-tri-tert-butylphenoxide (0.05–0.15 M) as base, instead of NaOCEt3, catalyzed by 10 mol % Pd(PtBu3)2 in the presence of 1.0–5.9 mol % of added PtBu3 occurred without any kinetically significant induction period. The concentration of amine decayed linearly with time, indicating a zero-order dependence of the rate of reaction on the concentration of amine (Figure 6).
Figure 6.
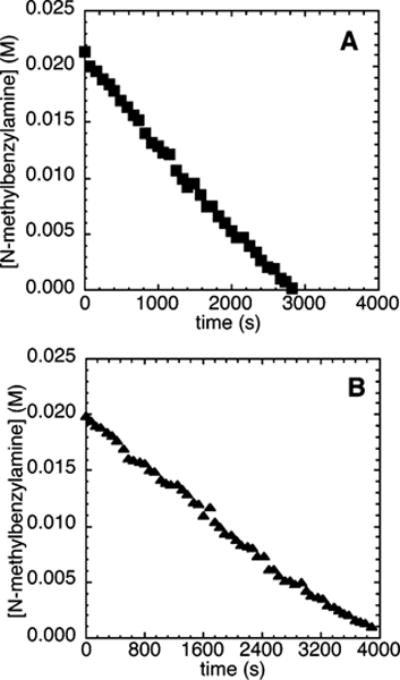
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with 4-chlorobenzotrifluoride (2c; 109 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%), with added PtBu3 (0.21 mM, 1%) at 75 °C and (A) 2,4,6-tri-tert-butylphenoxide (0.05–0.15 M) as base and (B) NaOtBu (0.10–0.30 M) as base.
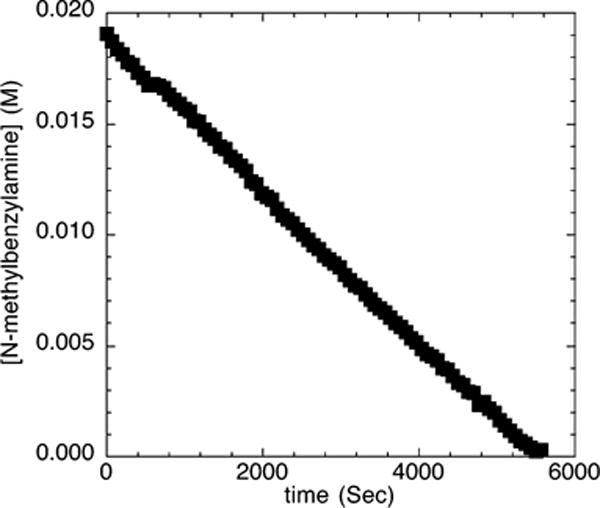
d. Reaction of N-Methylbenzylamine with Bromobenzene
One might expect that the profile of the decay of amine during the reactions of N-methylbenzylamine with bromobenzene (2d) would be similar to that of reactions with the electron-poor chloroarene 2c. Indeed, the reactions of an excess of bromobenzene (2d; 110 mM) with N-methylbenzylamine (21.2 mM) and NaOCEt3 (0.10–0.30 M) catalyzed by 10 mol % Pd(PtBu3)2 and 1 mol % added ligand proceeded with measurable induction periods (Figure 7A). The induction period was longer than the induction period observed during the reactions of the electron-poor 4-chlorobenzotrifluoride (2c). In contrast to the reactions of N-methylbenzylamine with 4-chlorobenzotrifluoride in the presence of NaOtBu as base, the reaction of N-methylbenzylamine with bromobenzene in the presence of NaOtBu as base (Figure 7B) occurred with a detectable induction period.
Figure 7.
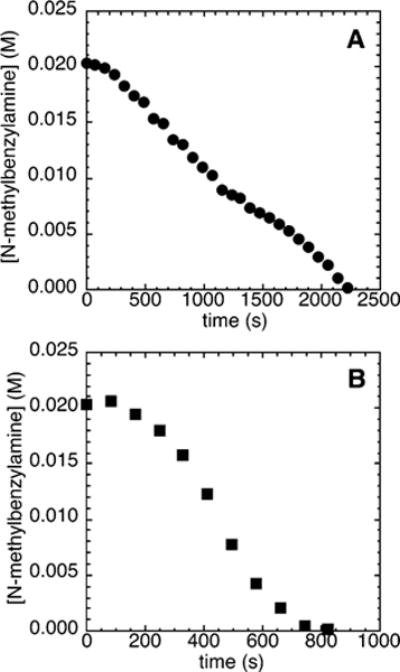
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with bromobenzene (2d; 110 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) and PtBu3 (0.21 mM, 1%) at 70 °C with (A) NaOCEt3 (0.10–0.30 M) as base and (B) NaOtBu (0.10–0.30 M) as base.
The reaction of 110 mM bromobenzene and 21.2 mM N-methylbenzylamine with 200 mM NaOCEt3 as base and 5.0–15 mM added bromide occurred without a detectable induction period and was clearly zero-order in amine (Figure 8A). The reactions of bromobenzene with 2,4,6-tri-tert-butylphenoxide as base also occurred without any detectable induction period (Figure 8B).
Figure 8.
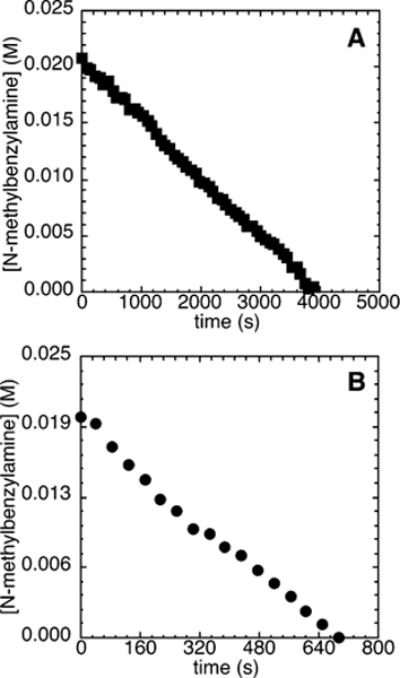
Typical profile of the decay of amine during the reaction of N-methylbenzylamine (21.2 mM) with bromobenzene (2d; 110 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) and PtBu3 (0.21 mM, 1%) at 70 °C with (A) 0.20 M NaOCEt3 as base and added [(C8H17)4N]Br (5.0–15 mM) and (B) 2,4,6-tri-tert-butylphenoxide (0.50–0.15 M) as base.
2. Dependence of the Reactions of N-Methylbenzylamine with Aryl Halides on [PtBu3]
The dependence of the rates of the amination reactions of electron-rich and electron-poor chloroarenes on the concentration of ligand were determined by following the rates of reactions of N-methylbenzylamine (21.2 mM) with 100 mM chloroarene and NaOCEt3 or NaOtBu (0.20 M) base by 1H NMR spectroscopy. The data were obtained with 0.5–5.9 mol % added PtBu3 and NaOtBu as base, because the reactions with added phosphine and this base occurred with a linear decay of amine. The plots of 1/kobs vs [PtBu3] for reactions of both electron-rich and electron-poor chloroarenes were linear (Figure 9). These data indicate that the rates of reaction were inversely dependent on the ligand concentration. The reactions of the electron-neutral chlorobenzene 2b with N-methylbenzylamine catalyzed by 10 mol % Pd(PtBu3)2 were also inversely dependent on the concentration of PtBu3.28 In contrast, the rates of reaction of bromobenzene (100 mM) with N-methylbenzylamine (21.2 mM) and NaOCEt3 or NaOtBu (0.10 M) as base catalyzed by 5% Pd(PtBu3)2 (1.01 mM) were independent of the concentration of added PtBu3 (0.628–1.25 mM) (Figure 10).
Figure 9.
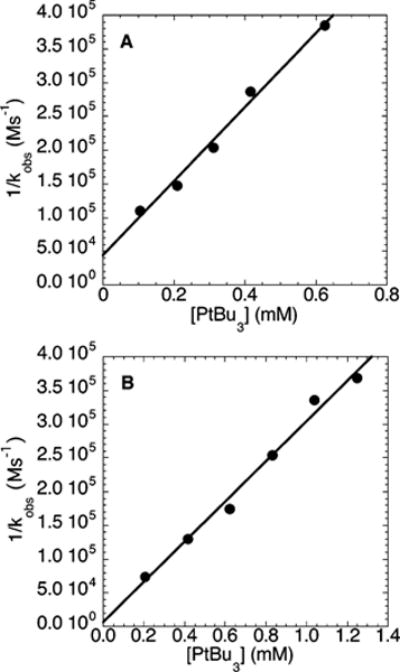
Plot of 1/kobs vs [PtBu3] obtained during the reactions of N-methylbenzylamine (21.2 mM) and NaOtBu (0.20 M) with (A) 4-chloroanisole (2a; 100 mM) at 100 °C and (B) 4-chloroben-zotrifluoride (2c; 100 mM) at 75 °C catalyzed by 10 mol % Pd-(PtBu3)2.
Figure 10.
Comparison of decay of [N-methylbenzylamine] with time during the reactions of bromobenzene (2d; 0.10 M) with N-methylbenzylamine (21.2 mM) and NaOtBu (0.10 M) catalyzed by 5 mol % Pd(PtBu3)2 (1.1 mM) in the presence of 3 mol % (0.64 mM) and 6 mol % (0.13 mM) PtBu3 at 70 °C.
3. Dependence of the Rates of Reactions of N-Methylbenzylamine with Haloarenes on [ArCl]
The dependence of the rates of the amination of electron-rich and electron-poor chloroarenes on the concentration of chloroarene was determined by measuring the rates of reactions of N-methylbenzylamine (21.2 mM) with 50–250 mM chloroarene and NaOCEt3 or NaOtBu (0.20 M) as base by 1H NMR spectroscopy. The data were obtained with 1 or 5 mol % added PtBu3 and NaOtBu as base, because these reactions occurred without an induction period. The plots of kobs vs [ArCl] were linear (Figure 11). These data indicate that the reactions are first-order in chloroarene. The reactions of the electron-neutral chlorobenzene with N-methylbenzylamine catalyzed by 10 mol % Pd(PtBu3)2 were also found to depend linearly on the concentration of PhCl.28 Likewise, the rates of reaction of bromobenzene (100–300 mM) with N-methylbenzylamine (21.2 mM) and NaOCEt3 or NaOtBu (0.20 M) as base catalyzed by 5% Pd(PtBu3)2 in the presence of 3% PtBu3 were found to depend on the concentration of bromoarene (Figure 12). Although the induction periods prevent quantifying the reaction order in a meaningful way (see Figure 12), there was clearly a positive dependence of the rate on the concentration of bromoarene.
Figure 11.
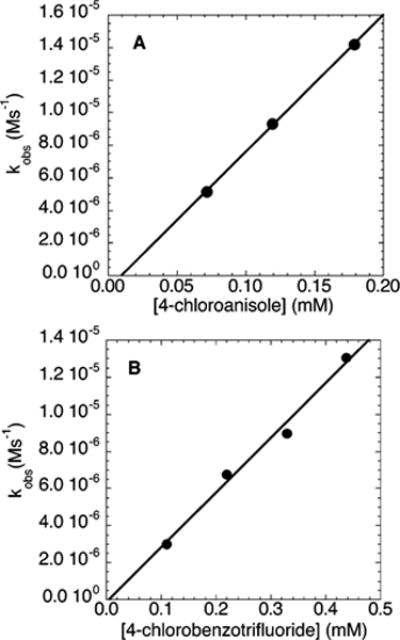
Plot of kobs vs [chloroarene] obtained during the reactions of N-methylbenzylamine (21.2 mM) and NaOtBu (0.20 M) with (A) 4-chloroanisole (2a) at 100 °C and (B) 4-chlorobenzotrifluoride (2c) at 75 °C catalyzed by 10 mol % Pd(PtBu3)2 (2.1 mM) in the presence of 1 mol % PtBu3 (0.21 mM).
Figure 12.
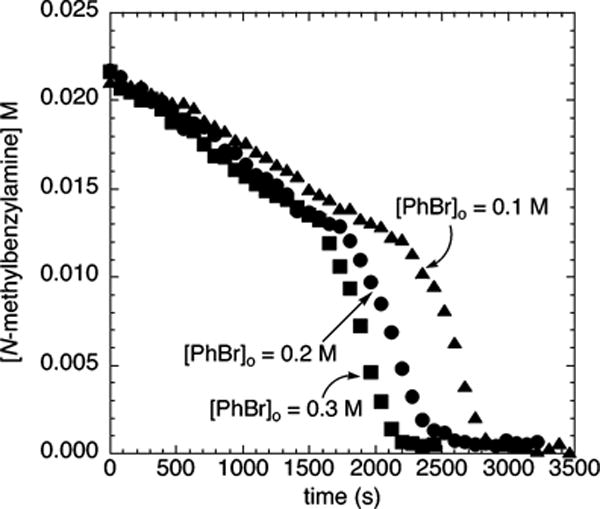
Comparison of decay of [N-methylbenzylamine] with time during the reactions of bromobenzene (2d; 0.10–0.30 M) with N-methylbenzylamine (21.2 mM), and NaOCEt3 (0.20 M) catalyzed by 5 mol % Pd(PtBu3)2 (1.1 mM) in the presence of 3 mol % PtBu3 (0.64 mM) at 70 °C.
4. Effect of the Identity and Concentration of Alkoxide and Aryloxide Bases and Additives
The dependence of the rates of amination of haloarenes on the identity and concentration of alkoxide and aryloxide bases and on the concentration of added halide ions was determined. This dependence of the rates of reactions of each aryl halide (2a–d) on the identity and concentration of bases and additives is presented in sections 4a–d. These data proved difficult to interpret.
a. Reactions of N-Methylbenzylamine with the Electron-Rich 4-Chloroanisole
The plots of the dependence of kobs on the concentration of the anions for the reaction of the electron-rich 4-chloroanisole 2a are shown in Figure 13. The halide and BF4 anions in these and all other experiments were added as soluble ammonium salts (see the Supporting Information for details). The sodium alkoxides and phenoxides were soluble at the reaction temperature at the concentrations used. These data show that kobs for this reaction is independent of the concentration of NaOCEt3 and linearly dependent on the concentration of Br−, 2,4,6-tri-tert-butylphenoxide, and tBuO−. These plots all contained a nonzero y intercept, and the values of these y intercepts were within a factor of 2 of each other. The slope of the plot of kobs vs [Br−] was larger than the slope of the plot of kobs vs [2,4,6-tri-tert-butylphenoxide] or [tBuO−]. Added weakly coordinating anions such as BF4− did not affect the rate of the reaction. The values of kobs in the presence of 0.005, 0.010, and 0.0015 M BF4− were 5.7 × 10−6, 5.5 × 10−6 and 5.4 × 10−6M s−1, respectively.
Figure 13.
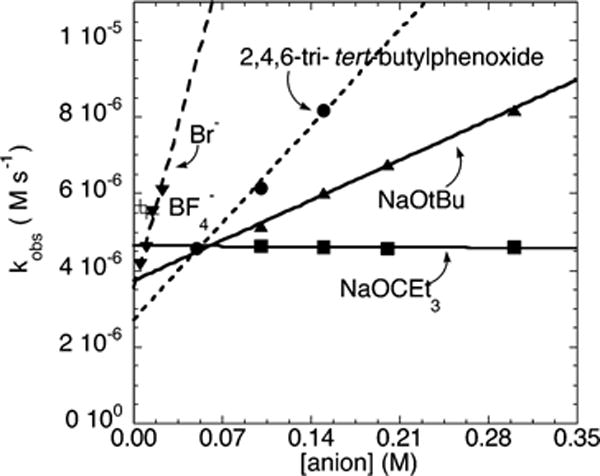
Dependence of kobs on [anion] for the reaction of 4-chloroanisole (2a, 119 mM) with N-methylbenzylamine (21.2 mM) catalyzed by 10 mol % Pd(PtBu3)2 (2.1 mM) in the presence of 1 mol % added (PtBu3)2 at 100 °C.
b. Reactions of N-Methylbenzylamine with the Electron-Neutral Chlorobenzene
The plots of the dependence of kobs on the concentration of the anions for the reaction of the electron-neutral chlorobenzene 2b are shown in Figure 14.28 The rate of the amination of chlorobenzene was found to be zero-order in [OCEt3−]. The plots of kobs vs the concentration of tBuO−, 2,4,6-tri-tert-butylphenoxide anion, and Br− were all linear, with a positive slope and a nonzero y intercept. The slope of the plot of kobs vs [Br−] was the largest, followed by the slope of the plot of kobs vs [2,4,6-tri-tert-butylphenoxide] and [tBuO−]. The y intercepts of these lines obtained from reactions of the different anions were indistinguishable. These data are analogous to those from the reactions of the electron-rich 4-chloroanisole.
Figure 14.
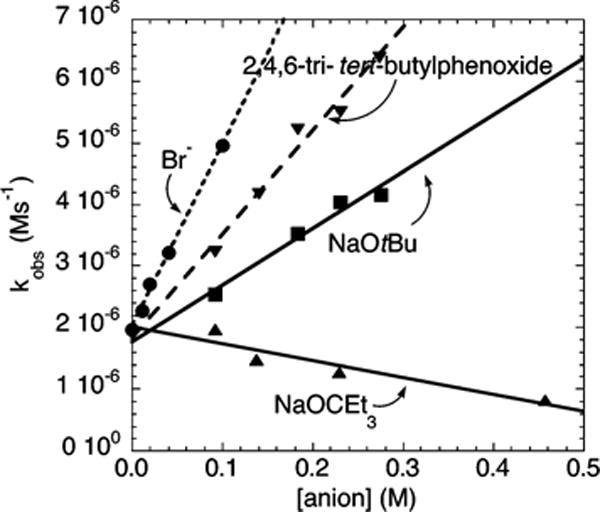
Dependence of kobs on [anion] for the reaction of chlorobenzene (2b; 97.5 mM) with N-methylbenzylamine (19.5 mM) catalyzed by 10 mol % Pd(PtBu3)2 (1.9 mM) in the presence of 1 mol % added P(tBu3)2 (0.19 mM) at 90 °C.
c. Reactions of N-Methylbenzylamine with the Electron-Deficient 4-Chlorobenzotrifluoride
The correlation between the rate constants for the reactions of 4-chlorobenzotrifluoride (2c) with N-methylbenzylamine on the identity and concentration of alkoxide and aryloxide bases and on the concentration of additives was determined from plots of kobs vs [anion]. As illustrated in Figure 15, the rate of the amination of 4-chlo-robenzotrifluoride (2c) was essentially zero-order in [OCEt3−] and [Cl−]. The plots of kobs vs the concentration of tBuO−, 2,4,6-tri-tert-butylphenoxide anion, and Br− were all linear, with a small positive slope. The plots of the reactions conducted with the different alkoxide bases with no added bromide also have a y intercept that is close to the values of each of the individual data points, and the lines do not converge at a common y intercept. The y intercept of the plot of kobs vs [2,4,6-tri-tert-butylphenoxide anion] was the largest, followed by the y intercept of the plot of kobs vs [NaOtBu], the y intercept of the plot of kobs vs [Br−], and the y intercept of the plot of kobs vs [NaOCEt3]. The different y intercepts of these plots contrast the similar values of the y intercept of plots obtained from reactions of electron-rich and electron-neutral chloroarenes with different anions.
Figure 15.
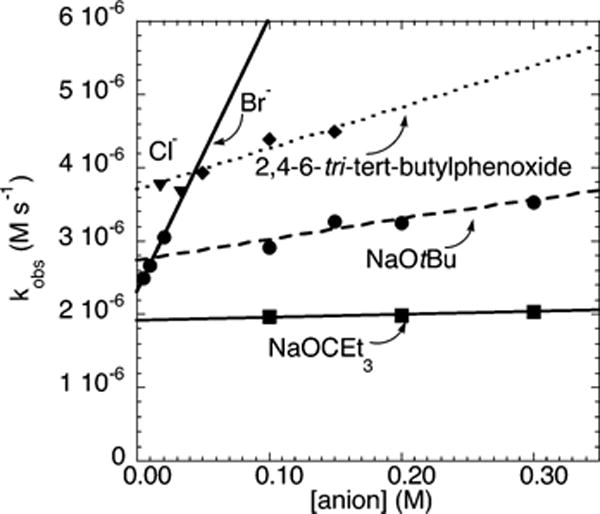
Dependence of kobs on [anion] for the reaction of 4-chlorobenzotrifluoride (2c; 109 mM) with N-methylbenzylamine (21.2 mM) catalyzed by Pd(PtBu3)2 (2.1 mM, 10%) in the presence of of added P(tBu3)2 (1.1 mM, 5%) at 85 °C.
d. Reactions of N-Methylbenzylamine with Bromobenzene
The amination of bromobenzene, which generally occurred more quickly than the amination of any of the chloroarenes, was fastest when 2,4,6-tri-tert-butylphenoxide or NaOtBu was used as base. The reactions were the slowest when NaOCEt3 was used as the base (Figures 7 and 8). Because the induction periods in these reactions were long, it was not possible to fit the decomposition of amine to a linear equation. However, the rate of the amination with NaOtBu or 2,4,6-tri-tert-butylphenoxide as base occurred in approximately one-fourth of the time of the amination with NaOCEt3 as base.
5. Monitoring the Reactions of N-Methylbenzylamine with Haloarenes by 31P NMR Spectroscopy
The reactions of aryl chlorides and bromobenzene with N-methylbenzylamine and various alkoxide and aryloxide bases in the concentration ranges described above were monitored by 31P NMR spectroscopy. Pd-(PtBu3)2 was the only palladium complex observed during the catalytic reactions. No measurable increase in the concentration of free P(tBu)3 or accumulation of [Pd(PtBu3)(Ar)(X)] or [Pd-(PtBu3)Br]2 was observed. Further, integration of the 1H NMR signals due to Pd(PtBu3)2 showed that the concentration of this species during the reaction was within 10% of the concentration of this species at the start of the reaction.
Discussion
1. Mechanism of Pd(PtBu3)2-Catalyzed Amination of Haloarenes
Six conventional classes of mechanisms that can be envisaged for the amination of aryl chlorides catalyzed by Pd(PtBu3)2 (3), with this Pd(0) species as the only observable species in solution, are shown in Schemes 2–7.
Scheme 2.
Scheme 7.
Scheme 2 consists of a turnover-limiting oxidative addition of chloroarenes to the Pd(0) species 3 to form the aryl halide complex (PtBu3)2Pd(Ar)(Cl) (4), followed by the reaction of 4 with amine and base to generate the aryl amide complex (PtBu3)2Pd(Ar)(NR1R2) (5). Reductive elimination from 5 would then form the arylamine product and regenerate 3. The full rate equation for this pathway derived by assuming steady-state conditions is shown in eq 1. A simplified version of this rate equation is shown in eq 2. The set of assumptions used to simplify eq 1 to eq 2 is discussed in the Supporting Information (Scheme S1).
| (1) |
| (2) |
The mechanism depicted in Scheme 3 begins with reversible ligand dissociation from the Pd(0) species 3 to generate the 12-electron Pd complex [Pd(tBu3)] (6), followed by turnover-limiting oxidative addition to the monophosphine complex 6 to form the arylpalladium halide complex (PtBu3)Pd(Ar)(Cl) (7). Reaction of 7 with amine and base would then generate the arylpalladium amide complex (PtBu3)Pd(Ar)(NR1R2) (8), and reductive elimination from 8 would release the arylamine product and regenerate 6. The full rate equation for this pathway derived by assuming steady-state conditions is shown in eq 3, and the simplified rate equation is shown in eq 4. The set of assumptions used to simplify eq 3 to eq 4 is discussed in the Supporting Information (Scheme S2).
| (3) |
| (4) |
Scheme 3.
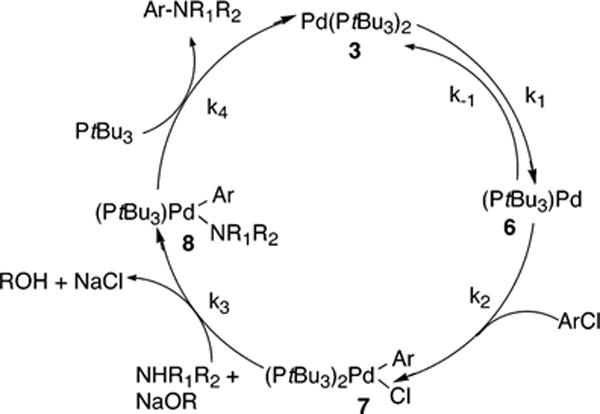
The mechanism in Scheme 4 occurs by oxidative addition of the chloroarene after reversible dissociation of ligand from 3. This reaction pathway in Scheme 4 differs from the reaction pathway in Scheme 3 by the position of the bisphosphine complex 3. In Scheme 3, the starting palladium complex Pd-(PtBu3)2 3 lies off the catalytic cycle, and in Scheme 4 it lies on the catalytic cycle. In other words, the product amine formed by reductive elimination from 8 dissociates from the [(PtBu3)-Pd(product)] complex to regenerate 6 in Scheme 3, whereas the product amine is associatively displaced by PtBu3 to regenerate 3 in Scheme 4. The full rate equation for the pathway in Scheme 4 derived by assuming steady-state conditions is shown in eq 5, and the simplified rate equation is shown in eq 6. The set of assumptions used to simplify eq 5 to eq 6 is discussed in the Supporting Information (Scheme S3).
| (5) |
| (6) |
Scheme 4.
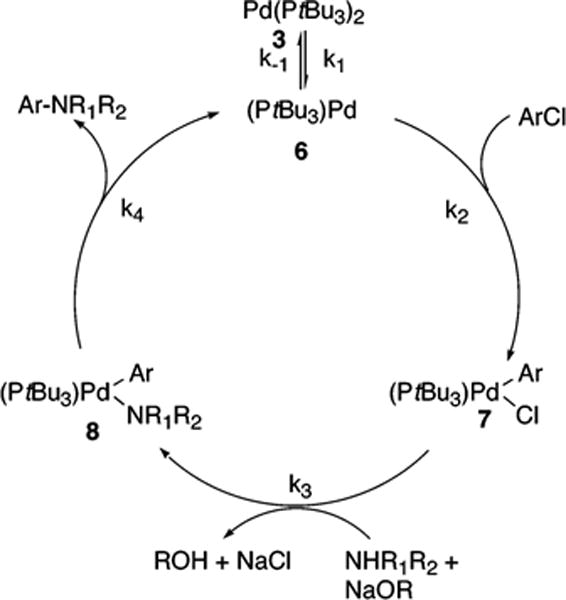
The mechanism in Scheme 5 begins with reversible ligand dissociation from the Pd(0) complex 3 to generate 6, followed by reversible oxidative addition of ArCl to 6 to produce 7. By this pathway, complex 7 undergoes irreversible reaction with base to generate the palladium-alkoxide complex 7′. Reaction of 7′ with amine would then form the palladium-amide complex 8, and reductive elimination of product amine from 8 would regenerate 6. The full rate equation for the pathway in Scheme 5 under steady-state conditions is shown in eq 7, and the simplified rate equation is shown in eq 8. The set of assumptions used to simplify eq 7 to eq 8 is discussed in the Supporting Information (Scheme S4).
| (7) |
| (8) |
Scheme 5.
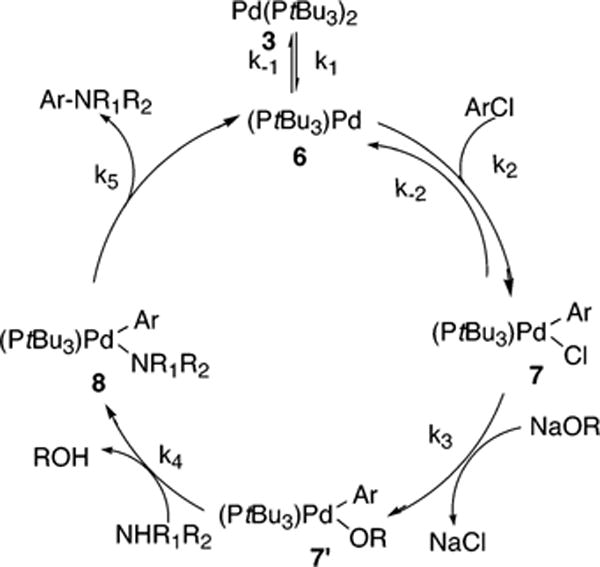
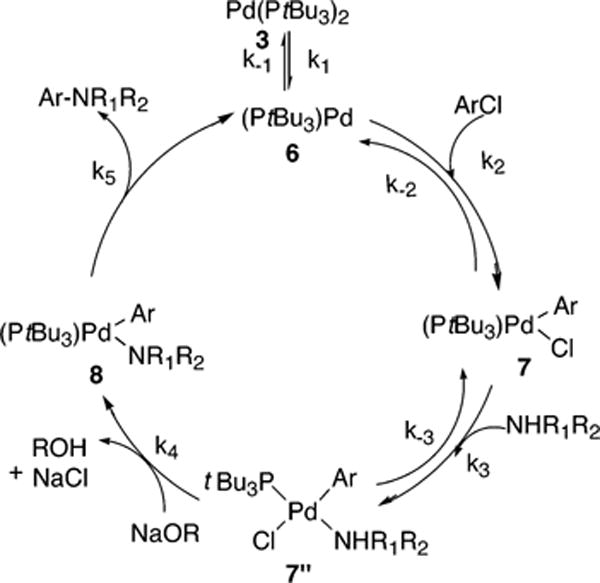
The mechanism in Scheme 6 begins with reversible ligand dissociation from the Pd(0) complex 3 to generate 6, followed by reversible oxidative addition of ArCl to 6 to generate 7. By this pathway, reversible reaction of 7 with amine forms the four-coordinate complex 7″. Reaction of 7″ with base forms the palladium-amide complex 8, and reductive alimination of product amine from 8 regenerates 6. The full rate equation for the pathway in Scheme 6 derived by assuming steady-state conditions is shown in eq 9, and the simplified rate equation is shown in eq 10. The set of assumptions used to simplify eq 9 to eq 10 is discussed in the Supporting Information (Scheme S5).
| (9) |
| (10) |
Scheme 6.
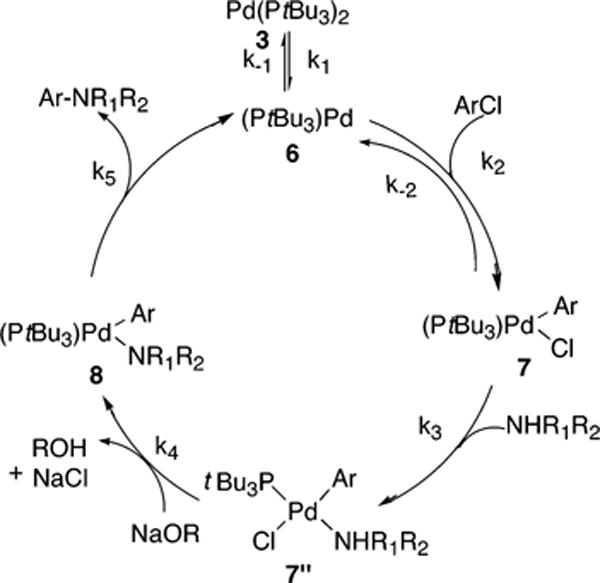
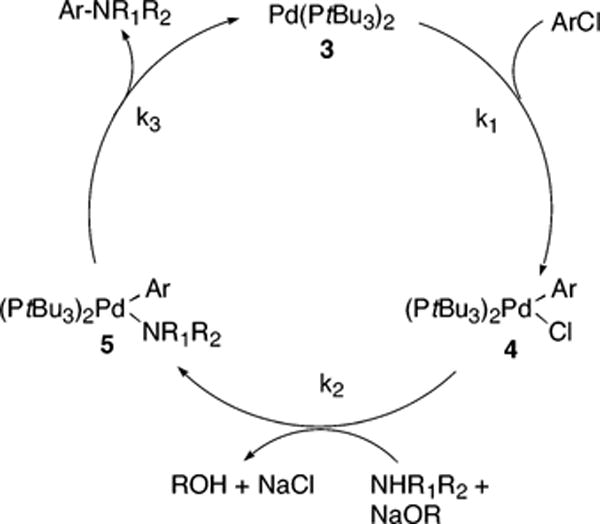
A final reaction pathway is shown in Scheme 7. This pathway is similar to the one shown in Scheme 6, except that the binding of amine to 7 to form 7″ is reversible in Scheme 7 and is irreversible in Scheme 6. The full rate equation for the pathway in Scheme 7 under steady-state conditions is shown in eq 11, and the simplified rate equation is shown in eq 12. The set of assumptions for simplifying eq 11 to eq 12 is discussed in the Supporting Information (Scheme S6).
| (11) |
| (12) |
Each of the pathways in Schemes 2–7 can be distinguished by the dependence of kobs on the concentrations of ligand, chloroarene, base, and amine. The correlation between these data and the predicted behavior for each of these reaction pathways is discussed in the following sections.
2. Correlation between the Data for the Reactions of Chloroarenes with N-Methylbenzylamine and the Predicted Behavior for Reactions by the Pathways in Schemes 2–7
The simplified rate equation (eq 2) for the pathway shown in Scheme 2 predicts a first-order dependence of the rate of the reaction on the concentration of haloarenes and no dependence of the rate on the concentration of added ligand, amine, and base. The prediction that the rate of reaction should be independent of the concentration of ligand is inconsistent with linear plots of 1/kobs vs [PtBu3] (Figure 9 and data in ref 28) obtained for the reactions of chloroarenes 2a–c with N-methylbenzylamine in the presence of NaOCEt3 or NaOtBu as base.
The simplified rate equation (eq 4) for the pathway in Scheme 3 predicts a first-order dependence of the rate on the concentration of haloarene, inverse first-order dependence on the concentration of added ligand, and no dependence of the rate on the concentrations of amine and base. These predictions are consistent with our data for the reactions of chloroarenes 2a–c with N-methylbenzylamine and NaOCEt3 as base. However, these data are inconsistent with the predicted behavior for reactions of 2a–c with N-methylbenzylamine and NaOtBu or 2,4,6-tri-tert-butylphenoxide as base by the same mechanism. Data in Figures 13–15 show that the rate of the reaction is dependent on the concentration of NaOtBu and 2,4,6-tri-tert-butylphenoxide. Thus, our data on the reactions of chloroarenes with bases other than NaOCEt3 are inconsistent with reaction solely by the pathway shown in Scheme 3.
The simplified rate equation (eq 6) for the pathway in Scheme 4 predicts a dependence of the rate of the reaction on the concentration of haloarenes that would be positive, but can be less than 1, a dependence on the concentration of added ligand that would be inverse, but can be less than fully inverse-first order, and no dependence of the rate on the concentrations of amine and base. Figures 9 and 11 and data in ref 27 show that there is a simple first-order dependence of the rate on [haloarene] and simple inverse-order dependence on [PtBu3]. These data may be consistent with the rate behavior predicted for the pathway in Scheme 4, but the dependence of the rate of the reaction on the identity and concentration of bases is clearly inconsistent with the rate behavior predicted for the pathway in Scheme 4.
The simplified rate equation (eq 8) for the pathway in Scheme 5 predicts a first-order dependence of the rate of the reaction on the concentration of haloarene, positive-order dependence on the concentration of base, inverse first-order dependence on the concentration of added ligand, and no dependence of the rate on the concentration of amine. These predictions are consistent with the measured dependence of the rates of reactions on [ArCl] and [amine] and have some of the characteristics of the measured dependence of the reaction on [base]. However, the rate equation for this mechanism predicts that the dependence of the rate of the reaction on the concentration of base saturates at high concentrations of base and saturates at the same rate constant for reactions with different bases. Further, it predicts that a plot of kobs vs [base] will intersect the y axis at zero. These predictions about the dependence of kobs on [base] are inconsistent with our data. The curves of kobs vs [anions] in Figure 13–15 clearly do not saturate at the same value of kobs, if they saturate at all. Further, the plot of kobs vs [base] for reactions with each of the bases has a clear nonzero y intercept.
The simplified rate equation (eq 10) for the pathway in Scheme 6 predicts a first-order dependence of the rate of the reaction on the concentration of haloarene, positive dependence on the concentration of amine, inverse first-order dependence on the concentration of added ligand, and no dependence of the rate on the concentration of base. The reactions of 2a–c with N-methylbenzylamine are zero-order in [amine] and positive-order in [NaOtBu] and [2,4,6-tri-tert-butylphenoxide]. These data are inconsistent with the mechanism in Scheme 6.
The simplified rate equation (eq 12) for the pathway in Scheme 7 predicts a first-order dependence of the rate of the reaction on the concentration of haloarene, positive-order dependence on the concentration of amine and base, and inverse first-order dependence on the concentration of added ligand. Thus, our data are also inconsistent with the mechanism in Scheme 7.
In summary, our kinetic data on the reactions of chloroarenes 2a–c with N-methylbenzylamine in the presence of the various bases are inconsistent with each of the conventional pathways discussed in section 2 of the Discussion. The complex dependence of the rates of the reactions on the identity and concentration of bases makes none of the pathways in Schemes 2–7 alone suitable for describing the mechanism of the catalytic reactions.
3. Mechanisms for the Reactions of Chloroarenes with N-Methylbenzylamine and Base via Anionic Pd(0)
Because our kinetic data are inconsistent with all of the conventional pathways discussed in section 2 of the Discussion, we present in Scheme 8 an alternative pathway. In this mechanism, the base reversibly replaces PtBu3 in 3 to form the anionic Pd(0) monophosphine complex 6′, which adds aryl chloride. Several experimental and theoretical studies have suggested that oxidative addition of aryl halides occur to anionic palladium complexes, such as 6′ in Scheme 8.33,36,37,47 The full rate equation for the pathway in Scheme 8 under steady-state conditions is shown in eq 13, and the simplified rate equation is shown in eq 14. The set of assumptions for simplifying eq 13 to eq 14 is discussed in the Supporting Information (Scheme S7).
| (13) |
| (14) |
Scheme 8.
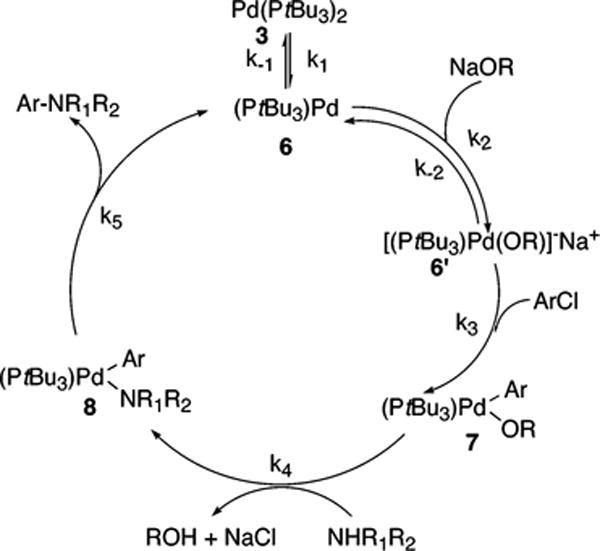
Equation 14 predicts that a plot of kobs vs [NaOR] would be linear with a positive slope and a zero y intercept. However, our data in Figures 13–15 clearly contain a large nonzero y intercept.
4. Concurrent Mechanisms for the Reactions of Chloroarenes with N-Methylbenzylamine and Base
Because no single pathway can account for our observed kinetic data, we considered the possibility that two mechanisms occur concurrently. A scheme that is consistent with most of our data involves reactions by a combination of the two pathways in Schemes 3 and 8. kobs for the concurrent pathways is shown in eq 15. This
| (15) |
equation shows that the kobs value corresponding to reaction by the mechanism in Scheme 3, which is independent of [base], would correspond to the y intercept of the plots in Figures 13–15. The slopes of the plots of kobs vs [anion] would correspond to the dependence of the rate constants on the concentrations of bases.
The relative magnitudes of the effect of anions on the reactions of each of the aryl chlorides 2a–c follow the order 2,4,6-tri-tert-butylphenoxide > OtBu− > OCEt3−. Hartwig and Alcazar-Roman had proposed that the relative magnitude of the effects of anions on the rates of amination might be explained by the relative binding constants (k2 in Scheme 8) for the reactions of anions with Pd(0). The bulky anion OCEt3− might be expected to have the smallest binding constant, and the softest anion, 2,4,6-tri-tert-butylphenoxide, might be expected to have the largest binding constant.
One might consider that the added halides and differences in base would reflect a dependence of the rate of the reaction on the ionic strength or polarity of the medium. However, the lack of a dependence on the concentration of added [(C8H17)4N]Cl showed that the rate does not depend significantly on these properties of the medium. The absence of an effect of the polarity or ionic strength of the medium was further demonstrated by the lack of dependence of kobs on added noncoordinating anions, such as BF4−.
The value of kobs corresponding to the neutral pathway (Scheme 3) is given by the y intercept in the plots of kobs vs [anion]. Thus, concurrent reactions by the two mechanisms in Schemes 3 and 8 would predict similar y intercepts for the plots of kobs vs [NaOCEt3], kobs vs [NaOtBu], and kobs vs [2,4,6-tri-tert-butylphenoxide]. This predicted rate behavior was observed for the reactions of electron-rich and electron-neutral aryl chlorides 2b,c.
However, this predicted rate behavior was not observed for the reactions of the electron-poor chloroarene 2c (Figure 14). The large dependence of the rates of reactions of 2c on the identity of the base and the distinct y intercepts in plots of kobs vs [base] for the reactions of electron-poor chloroarene 2c are inconsistent with reaction by the pathways in Schemes 3 and 8 involving one neutral and one ionic pathway. Similarly, the dependence of the observed rate constant of reactions of bromoarene 2d on the identity of the base without a dependence on the concentration of the base is inconsistent with reaction by the two concurrent pathways. However, these arguments assume that the concentrations of active catalyst are the same in the reactions with the different bases. We suggest, albeit tentatively, that the correlation between reactions of haloarenes that occur with an induction period and the unusual dependence of the rate on the identity of the base without a dependence on the concentration of the base implies that the concentrations of active catalyst may be different in the presence of the different bases.49
Conclusions
We have described our efforts to elucidate the potential effects of anions on the rates of Pd-catalyzed amination reactions catalyzed by complexes of hindered alkyl monophosphines. These experiments complement the large number of recent theoretical and experimental studies examining the effects of anions on the rates of oxidative addition to Pd complexes. The reactions in the current study proceed via rate-limiting oxidative addition to a Pd(0) complex containing a single phosphine, as revealed by the first-order behavior of the reaction in haloarene and zero-order behavior in amine. The relative rates for reaction of different haloarenes followed the typical order 4-MeOC6H4-Cl < PhCl < 4-F3CC6H4Cl < PhBr. The extent of the dependence of the rates of reactions on the concentration and identity of bases was found to depend on the electron-donating capacities of haloarenes.
The rates of reactions of electron-rich and electron-neutral chloroarenes were independent of the concentration of the bulky alkoxide base OCEt3− but were dependent on the concentrations of the less hindered OtBu− and the softer 2,4,6-tri-tert-butylphenoxide bases. The rates of reactions were independent of the ionic strength or polarity of the reaction medium. Concurrent reactions involving simultaneous oxidative addition of chloroarenes to [Pd(PtBu3)] and [(PtBu3)Pd(OR)]− are consistent with the dependence of the rates of reactions of electron-rich and electron-neutral chloroarenes on the identity and concentration of bases. The relative magnitudes of the two pathways depended on the haloarene and anion; reaction by the anion-dependent pathway was never the exclusive path but was the major pathway under some conditions.
The effects of base on the catalytic amination of electron-poor chloroarenes and bromoarenes were similar and contrasted in some ways with the effect of base on the reactions of electron-rich and electron-neutral choroarenes. For example, the amination of the more reactive haloarenes depended on the identity but not the concentrations of the base, while the amination of the less reactive electron-neutral and electron-rich haloarenes depended on both the identity and concentration of the base. At the same time, the orders of the rates of reactions in the presence of the different bases were the same for the activated chloroarene 2c and the bromoarene 2d, as was the case for the electron-rich and electron-neutral haloarenes 2a,b: the reactions of all the haloarenes 2a–d were fastest when 2,4,6-tri-tert-butylphenoxide was used as base and slowest when NaOCEt3 was used as base.
We do not have a firm explanation for the unusual combination of a dependence of the rate of the reaction of the more reactive haloarenes 2c,d on the identity, but not the concentration, of base. An effect of rate on the identity, but not the concentration, of a reagent can arise if the precatalyst is converted into a complex of the reagent. However, we did not observe any accumulation of an adduct between the Pd(PtBu3)2 catalyst and the base. The observation of long induction periods during the reactions of the more reactive haloarenes 2c,d could imply that several catalytically active species are generated during the reactions. In this case, the presence of a set of active catalysts could lead to the observed complex kinetic behavior. Clearly, additional experiments and theoretical studies are needed to understand the role of anions in these reactions.
Experimental Section
General Considerations
Unless otherwise noted, all manipulations were conducted using standard Schlenk techniques or in an inert-atmosphere glove box. 1H NMR spectra were obtained at 500 or 400 MHz and recorded relative to residual protio solvent. 31P-{1H} NMR spectra were obtained at 300 or 500 MHz and recorded relative to 85% H3PO4 as external standard. The temperature in the probe cavity was measured with a copper thermocouple inserted into toluene in an NMR sample tube in the probe.
Unless specified otherwise, all reagents were purchased from commercial suppliers and used without further purification. N-Methylbenzylamine was dried over CaH2 and purified by distillation. Pd(PtBu3)250 was prepared using literature procedures. NaOCEt328 and 2,4,6-tri-tert-butylphenoxides28 were synthesized according to literature procedures. Deuterated solvents were dried over sodium-benzophenone ketyl and were collected by vacuum transfer.
General Procedure for Measurement of the Rates of Reactions of Haloarenes (2a–d) with N-Methylbenzylamine
Stock solutions of 23.0 mM Pd(PtBu)2, 11.8 mM P(tBu3), 0.23 M N-methylbenzylamine, 1.25 M 4-chlorobenzotrifluoride, 1.36 M 4-chloroanisole, 1.64 M chlorobenzene, 1.24 M bromobenzene, 0.03 M tetraoctylammonium bromide, and 0.17 M 1,3,5-trimethoxybenzene were prepared in either C6D6 or toluene-d8. A typical reaction mixture was prepared by combining 50 μL of the stock solution of Pd(PtBu3)2, 10–50 µL of the stock solution of PtBu3, 50 µL of the stock solution of haloarene, 50 µL of the stock solution of N-methylbenzylamine, and 10 µL of the stock solution of 1,3,5-trimethoxybenzene (internal standard) in a screw-capped NMR tube. The appropriate amounts of NaOtBu, NaOCEt3, and 2,4,6-tri-tert-butylphenoxide were weighed directly into the NMR tube to give 0.1–0.3 M concentrations of base. When needed, 100–300 µL of the stock solution of tetraoctylammonium bromide was added to the NMR tube. Appropriate amounts of the deuterated solvent were added to generate a solution with a total volume of 0.6 mL. The NMR tube was placed into a preheated NMR probe, and automated data acquisition was started. Zero-order rate constants were obtained by fitting plots of the concentration of N-methylbenzylamine, determined from the peak intensity vs the internal standard, versus time to the expression Y = mt + c, in which m is the zero-order rate constant kobs.
Supplementary Material
Acknowledgments
We thank the NIH (NIGMS GM-55382) for support of this work. We also thank Johnson-Matthey for a gift of palladium complexes.
Footnotes
Supporting Information Available: Derivations of the simplified rate equations for the catalytic cycles of Schemes 1–7. This material is available free of charge via the Internet at http://pubs.acs.org. OM0607548
References
- 1.Nishiyama M, Yamamoto T, Koie Y. Tetrahedron Lett. 1998;39:617. [Google Scholar]
- 2.Yamamoto T, Nishiyama M, Koie Y. Tetrahedron Lett. 1998;39:2367. [Google Scholar]
- 3.Hamann BC, Hartwig JF. J Am Chem Soc. 1998;120:7369. [Google Scholar]
- 4.Mann G, Incarvito C, Rheingold AL, Hartwig JF. J Am Chem Soc. 1999;121:3224. [Google Scholar]
- 5.Shaughnessy KH, Kim P, Hartwig JF. J Am Chem Soc. 1999;121:2123. [Google Scholar]
- 6.Old DW, Wolfe JP, Buchwald SL. J Am Chem Soc. 1999;120:9722. [Google Scholar]
- 7.Wolfe JP, Tomori H, Sadighi JP, Yin J, Buchwald SL. J Org Chem. 2000;65:1158. doi: 10.1021/jo991699y. [DOI] [PubMed] [Google Scholar]
- 8.Littke AF, Fu GC. Angew Chem Int Ed. 1998;37:3387. doi: 10.1002/(SICI)1521-3773(19981231)37:24<3387::AID-ANIE3387>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 9.Littke AF, Fu GC. Angew Chem Int Ed. 1999;38:2411. doi: 10.1002/(sici)1521-3773(19990816)38:16<2411::aid-anie2411>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 10.Littke AF, Fu GC. Angew Chem Int Ed. 2002;41:4176. doi: 10.1002/1521-3773(20021115)41:22<4176::AID-ANIE4176>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
- 11.Littke AF, Fu GC. J Org Chem. 1999;64:10. doi: 10.1021/jo9820059. [DOI] [PubMed] [Google Scholar]
- 12.Littke AF, Dai C, Fu GC. J Am Chem Soc. 2000;122:4020. [Google Scholar]
- 13.Huang J, Grasa G, Nolan S. P Org Lett. 1999;1:1307. [Google Scholar]
- 14.Huang J, Nolan SP. J Am Chem Soc. 1999;121:9889. [Google Scholar]
- 15.Zhang C, Trudell ML. Tetrahedron Lett. 2000;41:595. [Google Scholar]
- 16.Stauffer SR, Lee S, Stambuli JP, Hauck SI, Hartwig JF. Org Lett. 2000;2:1423. doi: 10.1021/ol005751k. [DOI] [PubMed] [Google Scholar]
- 17.Shelby Q, Kataoka N, Mann G, Hartwig JF. J Am Chem Soc. 2000;122:10718. [Google Scholar]
- 18.Navarro O, Kelly RA, III, Nolan SP. J Am Chem Soc. 2003;125:16194. doi: 10.1021/ja038631r. [DOI] [PubMed] [Google Scholar]
- 19.Viciu MS, Kelly RA, III, Stevens ED, Naud F, Studer M, Nolan SP. Org Lett. 2003;5:1479. doi: 10.1021/ol034264c. [DOI] [PubMed] [Google Scholar]
- 20.Viciu MS, Kissling RM, Stevens ED, Nolan SP. Org Lett. 2002;4:2229. doi: 10.1021/ol0260831. [DOI] [PubMed] [Google Scholar]
- 21.Navarro O, Kaur H, Mahjoor P, Nolan SP. J Org Chem. 2004;69:3173. doi: 10.1021/jo035834p. [DOI] [PubMed] [Google Scholar]
- 22.Navarro O, Marion N, Scott NM, Gonzalez J, Amoroso D, Bell A, Nolan SP. Tetrahedron. 2005;61:9716. [Google Scholar]
- 23.Shen Q, Shekhar S, Stambuli JP, Hartwig JF. Angew Chem Int Ed. 2005;44:1371. doi: 10.1002/anie.200462629. [DOI] [PubMed] [Google Scholar]
- 24.Fernandez-Rodriguez MA, Shen Q, Hartwig JF. J Am Chem Soc. 2006;128:2180. doi: 10.1021/ja0580340. [DOI] [PubMed] [Google Scholar]
- 25.Hartwig JF, Kawastura M, Hauck SI, Shaughnessy KH, Alcazar-Roman LM. J Org Chem. 1999;64:5575. doi: 10.1021/jo990408i. [DOI] [PubMed] [Google Scholar]
- 26.Portnoy M, Milstein D. Organometallics. 1993;12:1665. [Google Scholar]
- 27.Barrios-Landeros F, Hartwig JF. J Am Chem Soc. 2005;127:6944. doi: 10.1021/ja042959i. [DOI] [PubMed] [Google Scholar]
- 28.Alcazar-Roman LM, Hartwig JF. J Am Chem Soc. 2001;123:12905. doi: 10.1021/ja016491k. [DOI] [PubMed] [Google Scholar]
- 29.Senn HM, Ziegler T. Organometallics. 2004;23:2980. [Google Scholar]
- 30.Littke AF, Fu GC. J Org Chem. 1999;64:10. doi: 10.1021/jo9820059. [DOI] [PubMed] [Google Scholar]
- 31.Jeffery T. J Chem Soc Chem Commun. 1984:1287. [Google Scholar]
- 32.Farina V, Krishnan B, Marshall DR, Roth GP. J Org Chem. 1993;58:5434. [Google Scholar]
- 33.Amatore C, Jutand A. Acc Chem Res. 2000;33:314. doi: 10.1021/ar980063a. [DOI] [PubMed] [Google Scholar]
- 34.Amatore C, Azzabi M, Jutand A. J Am Chem Soc. 1991;113:8375. [Google Scholar]
- 35.Suzuki A. Metal-Catalyzed Cross-Coupling Reactions. Wiley-VCH; Weinheim, Germany: 1998. p. 49. [Google Scholar]
- 36.Goossen LJ, Koley D, Hermann HL, Thiel W. Organometallics. 2006;25:54. [Google Scholar]
- 37.Goossen LJ, Koley D, Hermann HL, Thiel W. J Am Chem Soc. 2005;127:11102. doi: 10.1021/ja052435y. [DOI] [PubMed] [Google Scholar]
- 38.Goossen LJ, Koley D, Hermann HL, Thiel W. Organometallics. 2005;24:2398. [Google Scholar]
- 39.Amatore C, Jutand A, Meyer G. Inorg Chim Acta. 1998;273:76. [Google Scholar]
- 40.Amatore C, Broeker G, Jutand A, Khalil F. J Am Chem Soc. 1997;119:5176. [Google Scholar]
- 41.Amatore C, Jutand A, M’Barki MA. Organometallics. 1992;11:3009. [Google Scholar]
- 42.Amatore C, Pfluger F. Organometallics. 1990;9:2276. [Google Scholar]
- 43.Alami M, Amatore C, Bensalem S, Choukchou-Brahim A, Jutand A. Eur J Inorg Chem. 2001;2675 [Google Scholar]
- 44.Fauvarque J-F, Pfluger F. J Organomet Chem. 1981;208:419. [Google Scholar]
- 45.Nagayama K, Kawataka F, Sakamoto M, Shimizu I, Yamamoto A. Chem Lett. 1995;367 [Google Scholar]
- 46.Jutand A, Negri S, de Vries JG. Eur J Inorg Chem. 2002;1711 [Google Scholar]
- 47.Ahlquist M, Fristrup P, Tanner D, Norrby P-O. Organometallics. 2006;25:2066. [Google Scholar]
- 48.Casado AL, Espinet P. J Am Chem Soc. 1998;120:8978. [Google Scholar]
- 49.Hooper MW, Utsunomiya M, Hartwig JF. J Org Chem. 2003;68:2861. doi: 10.1021/jo0266339. [DOI] [PubMed] [Google Scholar]
- 50.Yoshida T, Ostuka S. Inorg Synth. 1990;28:113. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


