The force and stiffness of myosin motors in the isometric twitch of a cardiac trabecula and the effect of the extracellular calcium concentration

Abstract

Key points

• Fast sarcomere‐level mechanics in intact trabeculae, which allows the definition of the mechano‐kinetic properties of cardiac myosin in situ, is a fundamental tool not only for understanding the molecular mechanisms of heart performance and regulation, but also for investigating the mechanisms of the cardiomyopathy‐causing mutations in the myosin and testing small molecules for therapeutic interventions.

• The approach has been applied to measure the stiffness and force of the myosin motor and the fraction of motors attached during isometric twitches of electrically paced trabeculae under different extracellular Ca²⁺ concentrations.

• Although the average force of the cardiac myosin motor (∼6 pN) is similar to that of the fast myosin isoform of skeletal muscle, the stiffness (1.07 pN nm^–1) is 2‐ to 3‐fold smaller.

• The increase in the twitch force developed in the presence of larger extracellular Ca²⁺ concentrations is fully accounted for by a proportional increase in the number of attached motors.

Abstract

The mechano‐kinetic properties of the cardiac myosin were studied in situ, in trabeculae dissected from the right ventricle of the rat heart, by measuring the stiffness of the half‐sarcomere both at the twitch force peak (T _p) of an electrically paced intact trabecula at different extracellular Ca²⁺ concentrations ([Ca²⁺]_o), and in the same trabecula after skinning and induction of rigor. Taking into account the contribution of filament compliance to half‐sarcomere compliance and the lattice geometry, we found that the stiffness of the cardiac myosin motor is 1.07 ± 0.09 pN nm^–1, which is slightly larger than that of the slow myosin isoform of skeletal muscle (0.6‐0.8 pN nm^–1) and 2‐ to 3‐fold smaller than that of the fast skeletal muscle isoform. The increase in T _p from 61 ± 4 kPa to 93 ± 9 kPa, induced by raising [Ca²⁺]_o from 1 to 2.5 mm at sarcomere length ∼2.2 μm, is accompanied by an increase of the half‐sarcomere stiffness that is explained by an increase of the fraction of actin‐attached motors from 0.08 ± 0.01 to 0.12 ± 0.02, proportional to T _p. Consequently, each myosin motor bears an average force of 6.14 ± 0.52 pN independently of T _p and [Ca²⁺]_o. The application of fast sarcomere‐level mechanics to intact trabeculae to define the mechano‐kinetic properties of the cardiac myosin in situ represents a powerful tool for investigating cardiomyopathy‐causing mutations in the myosin motor and testing specific therapeutic interventions.

Key points

• Fast sarcomere‐level mechanics in intact trabeculae, which allows the definition of the mechano‐kinetic properties of cardiac myosin in situ, is a fundamental tool not only for understanding the molecular mechanisms of heart performance and regulation, but also for investigating the mechanisms of the cardiomyopathy‐causing mutations in the myosin and testing small molecules for therapeutic interventions.

• The approach has been applied to measure the stiffness and force of the myosin motor and the fraction of motors attached during isometric twitches of electrically paced trabeculae under different extracellular Ca²⁺ concentrations.

• Although the average force of the cardiac myosin motor (∼6 pN) is similar to that of the fast myosin isoform of skeletal muscle, the stiffness (1.07 pN nm^–1) is 2‐ to 3‐fold smaller.

• The increase in the twitch force developed in the presence of larger extracellular Ca²⁺ concentrations is fully accounted for by a proportional increase in the number of attached motors.

Introduction

The cardiac muscle is the pump that propels the blood into the circulatory system with a myogenic rhythm made by twitches (systoles) separated by relaxation periods (diastoles), during which the blood fills the ventricle. Similar to the skeletal muscle, the cardiac muscle is a striated muscle, in which the contractile material is organized in sarcomeres, the 2 μm long structural units comprising two anti‐parallel arrays of myosin motors, extending from the thick filament and overlapping with the nearby thin, actin‐containing, filaments originating from the opposite extremities of the sarcomere. Force and shortening during the twitch are generated by the cyclical, ATP‐driven interactions of the myosin motors with the thin filaments (Huxley, 1957; Lymn & Taylor, 1971). During each interaction, a working stroke in the myosin motor pulls the thin filament towards the centre of the sarcomere (Huxley, 1969; Huxley & Simmons, 1971; Rayment et al. 1993). The twitch is initiated by a signalling pathway, which starts with an action potential triggering the rise of intracellular calcium concentration ([Ca²⁺]_i) to promote a series of Ca²⁺‐dependent structural changes in the regulatory proteins on the thin filament and release the actin sites for binding of the myosin motors (Gordon et al. 2000). A second regulatory mechanism based on thick filament mechano‐sensing, which allows the recruitment of myosin motors from the resting state in relation to the load during the contraction, has been found recently in both skeletal muscle (Linari et al. 2015) and cardiac muscle (Reconditi et al. 2017).

By contrast to skeletal muscle, in cardiac muscle, the internal calcium concentration may not reach the level for full activation during heart contraction, so that the mechanical response depends on both [Ca²⁺]_i and the sensitivity of the thin filament to Ca²⁺ (Allen et al. 1985; ter Keurs, 2012). For a given [Ca²⁺]_i, the maximal force is larger at longer sarcomere lengths, a property known as length‐dependent activation (LDA). LDA is the cellular basis of the Frank–Starling law of the heart that relates the pressure exerted on the blood during the contraction of the ventricle (end‐systolic pressure) to its filling during the relaxation (end‐diastolic volume) (Sagawa et al. 1988; de Tombe et al. 2010). In addition, both the sensitivity of the filaments to Ca²⁺ and its dependence on LDA are modulated by neurohumoral control of the degree of phosphorylation of many sarcomeric proteins (Konhilas et al. 2003; Pfuhl & Gautel, 2012; Hanft et al. 2013; Hidalgo & Granzier, 2013; Sequeira et al. 2013; Methawasin et al. 2014; Kumar et al. 2015; Ait‐Mou et al. 2016; Kensler et al. 2017).

The performance of the heart in terms of force and power during the systole relies, at the level of the half‐sarcomere, on the integration of the mechano‐kinetic properties of the cardiac myosin (i.e. the force and the stiffness of the motor, the size and the speed of the working stroke, the rate of ATP hydrolysis) and the properties emerging from its array arrangement in the half‐sarcomere (i.e. the number of motors attached to actin and the degree of their co‐ordination). Defining these properties of the cardiac myosin in situ is fundamental not only for understanding the molecular mechanisms of heart performance and its regulation, but also for investigating the pathomechanisms of the cardiomyopathies based on mutations in the myosin and to provide therapeutic opportunities.

Recently, the sarcomere‐level mechanics made possible by the striation follower apparatus (Huxley et al. 1981; Lombardi & Piazzesi, 1990) has been successfully applied to intact trabeculae dissected from the right ventricle of the rat heart (Caremani et al. 2016), allowing the recording of changes in the half‐sarcomere length during the isotonic velocity transients following stepwise changes in force superimposed on the isometric twitch. The early phase of the transient represents the mechanical manifestation of the working stroke in the attached motors synchronized by the step (Piazzesi et al. 2002), whereas the later steady shortening occurs at a velocity characteristic of the steady‐state relationship between force and shortening velocity (T–V relationship) (Hill, 1938), governed by the strain‐dependent kinetics of motor attachment/detachment (Huxley, 1957). We found that increases in twitch isometric force and isotonic power induced by inotropic interventions, such as the increase in sarcomere length (SL) (1.9–2.2 μm) or in the extracellular Ca²⁺ concentration ([Ca²⁺]_o) (1–2.5 mm), are not accompanied by changes either in the working stroke parameters of the myosin motors or in the kinetics of motor attachment/detachment, suggesting that the inotropic mechanism acts uniquely through an increase of the number of motors, an emergent property of the array arrangement of motors in the half‐thick filament.

The need for a direct measurement of the number of motors attached at the peak of the cardiac twitch acquired even more importance following the demonstration by X‐ray diffraction from intact trabeculae that modulating the peak twitch force (T _p) with different loading conditions implies a modulation of the degree of activation of the thick filament via a positive feedback that rapidly adjusts the number of switched ON motors and, consequently, the number of attached motors with respect to the stress on the filament (Reconditi et al. 2017). In the study by Reconditi et al. (2017, the evidence that T _p varies in proportion to the number of attached motors was somewhat indirect, based on the finding that inotropic agents such as increase in SL or in Ca²⁺ do not affect the mechano‐kinetics of force generation by the motors (Caremani et al. 2016).

In the present study, with further refinement of the procedure to minimize compliance of the attachment of the trabeculae to the transducer levers, we have implemented the time resolution of the mechanical protocols up to a level that makes it possible to estimate the stiffness of the half‐sarcomere during the isometric twitch, minimizing the truncation of the elastic response by the quick recovery (Ford et al. 1977). We exploited the above method for the analysis of the mechanism that underlies a well‐established inotropic intervention, namely the potentiation of the twitch peak force with the increase in [Ca²⁺]_o (Gordon & Pollack, 1980; ter Keurs et al. 1980; Schouten et al. 1990; Caremani et al. 2016). Experiments are conducted at 27°C, representing a temperature lower than the physiological temperature of the rat heart (35–40°C), aiming to reduce the truncation of the elastic response by the quick tension recovery following the step (Ford et al. 1977) and to integrate the findings obtained in the present study within the framework of previous study, which has been systematically conducted at 25–27°C (ter Keurs et al. 1980; Caremani et al. 2016; Reconditi et al. 2017). The results have been analysed on the basis of a mechanical model of the half‐sarcomere (Fusi et al. 2014) to extract the stiffness of the array of attached motors. The stiffness of the single motor has been obtained by applying the same analysis to trabeculae in rigor, a condition in which all motors in the overlap region are attached to actin (Cooke & Franks, 1980; Thomas & Cooke, 1980; Lovell et al. 1981). Moreover, from the ratio of the stiffness measured at the peak of the twitch and in rigor, the fraction of the motors attached to actin during an isometric twitch and thus the force of the motor has been determined. The results provide the first definition of the mechanical parameters of cardiac myosin in situ and demonstrate that the Ca²⁺‐dependent potentiation of the twitch does not imply any increase in the force of the myosin motor and also that it is fully explained by a proportional increase of the number of attached motors.

Methods

Animals and ethical approval

All animals were treated in accordance with both the Italian regulation on animal experimentation (authorization no. 956/2015 PR) in compliance with Decreto Legislativo 26/2014 and the EU regulation (directive 2010/63). Male rats (Rattus norvegicus, strain Wistar Han, 230–280 g, aged 2–3 months) were anaesthetized with isoflurane (5%, v/v). As soon as the animal was deeply anaesthetised, as judged by the absence of the pedal reflex and the loss of the muscle tone in the hindlimb, the heart was rapidly excised, placed in a dissection dish and retrogradely perfused with a modified Krebs‐Henseleit (K‐H) solution (in mm: 115 NaCl, 4.7 KCl, 1.2 MgSO₄, 1.2 KH₂PO₄, 25 NaHCO₃, 0.5 CaCl₂ and 10 glucose), containing 20 mm 2,3‐butanedione monoxime (BDM) and equilibrated with carbogen (95% O₂, 5% CO₂, pH 7.4). All animals were kept with free access to food and water prior to use.

Sample preparation

A thin, unbranched trabecula was dissected from the right ventricle under a stereomicroscope. The trabecula was set at the length (L _t) at which it was just taut and the width (w) and the thickness (h) were measured using an eyepiece with a graduate scale. The cross‐sectional area (CSA) was calculated as w × h × π/4. The trabecula was then transferred into a temperature‐controlled trough (volume of 1.2 mL) perfused at 1.2 mL min^–1 with oxygenated K‐H solution (27°C) and attached, via titanium double hooks anchored to aluminium strips clamping the extremities, to the lever arms of a capacitance gauge force transducer (valve side) and a loudspeaker motor (wall side) for mechanical measurements. The temperature chosen for the experiments (27°C) is lower than the physiological temperature of the rat heart but matches that canonically used for high‐resolution mechanical experiments (de Tombe & ter Keurs, 1991, 1992; Caremani et al. 2016) to minimize the truncation of the elastic response elicited by a step perturbation in length by the quick force recovery (Huxley & Simmons, 1971; Ford et al. 1977). The characteristics of the force and length transducers and the procedure of attachment of the trabecula to the levers have been described previously (Lombardi & Piazzesi, 1990; Caremani et al. 2016). The sarcomere length (SL) was set at ∼2.2 μm at rest using a 40× dry objective and a 25× eyepiece and the corresponding trabecula length (L ₀) was measured again and the CSA corrected for the change in length (L ₀–L _t) assuming constant volume behaviour. The dimensions of the preparations were in the following ranges (mean ± SD, n = 9): w, 117–350 μm (194 ± 69 μm); h, 44–120 μm (76 ± 27 μm); cross‐sectional area, 4,900–27,500 μm² (11,800 ± 7,500 μm²); and L ₀, 1.6–3.0 mm (2.2 ± 0.5 mm).

For the rigor experiments (three trabeculae out of the nine used), following the measurements during the active contractions, the trabecula was skinned by 30 min of perfusion (room temperature) with 1% (v/v) Triton X‐100 in relaxing solution (Table 1) containing 20 mm BDM (Kentish et al. 1986). To minimize the end compliance, the extremities of the skinned trabecula were clamped with aluminium T‐clips for attachment to the transducer levers, fixed with glutaraldehyde and glued to the clips with shellac dissolved in ethanol (Linari et al. 1998; Linari et al. 2007). Both the width of the trabecula and the distance between myofilaments increased following skinning for the osmotic recall of water into the myocytes. The osmotic agent dextran T‐500 was used to restore the pre‐skinning dimensions. The correct concentration of dextran (5%) was tested with X‐ray diffraction measurements of the interfilament distance (at the same SL as that of the mechanical experiments) of trabeculae mounted at the beamline ID02 of the European Synchrotron (ESRF, Grenoble, France) before and after skinning.

Table 1.

Composition of solutions

	Na2ATP	MgCl2	EGTA	TES	Na2CP	GSH
Relaxing	5.44	7.7	25	100	19.11	10
Rigor	–	3.22	53	100	–	10

All concentrations are in mm. CP, phosphocreatine disodium salt hydrate; GSH, glutathione. pH (adjusted with KOH) was 7.1 at 20°C. Ionic strength, 190 mm. Dextran T‐500 (5% w/v) was added to the final solution. Protease inhibitors [10 μm trans‐epoxysuccinyl‐l‐leucylamido‐(4‐guanidino) butane (E‐64) and 20 μg mL^–1 leupeptin] were added to the solutions. All chemicals, except dextran (Pharmacia Biotech, Uppsala, Sweden), were obtained from Sigma (St Louis, MO, USA).

Rigor (solution composition is provided in Table 1) was induced at low temperature (∼1°C) by MgATP depletion. The temperature was returned to 27°C for mechanical measurements. Rigor induction did not change the dimension of the skinned trabecula (w, 1.03 ± 0.05 the value in relaxing solution with 5% dextran).

Myosin isoform identification

The myosin heavy chain (MHC) isoform composition was determined in three trabeculae, isolated from rats of the same strain and age as those used for mechanical experiments by means of 8% PAGE after denaturation in SDS‐PAGE, in accordance with the procedure described by (Reiser & Kline, 1998). The amount of protein loaded was 1–2 μg per lane; the gel was run at a constant voltage of 70 V for 24 h and then stained with Coomassie blue.

Experimental protocols

Mechanical measurements

Intact trabeculae were electrically stimulated by means of two platinum plate electrodes, 4 mm apart, with bipolar pulses of 0.5 ms in duration and an amplitude 1.5 times the threshold voltage. A striation follower (Huxley et al. 1981) was used to record SL changes in a 0.7–1.5 mm long segment selected along the central region of the preparation. During the twitch used for stiffness measurements, the sarcomere length was kept constant at ∼2.2 μm by using the feed‐forward method described previously (sarcomere length clamp) (Caremani et al. 2016). Stiffness measurements were performed on trabeculae electrically paced at 0.5 Hz by superimposing small stepwise length changes (ranging from −3 to +4 nm per half‐sarcomere, stretch positive, complete in 110–130 μs) on the isometric contraction at ∼95% of the twitch peak force attained in solution with different [Ca²⁺]_o (0.5, 1.0 and 2.5 mm).

To determine the stiffness at various steady forces in rigor, rigorized trabeculae were slowly lengthened, starting from the low level of force developed at the end of the rigorization procedure (0.05–0.1 T _p). The amplitude of the slow lengthening varied to attain different levels of steady force up to and above the levels of force developed by the intact trabeculae at different [Ca²⁺]_o. The half‐sarcomere stiffness in rigor was measured by imposing a train of different‐sized steps at 200 ms intervals on the steady rigor force. The force before the next step in the series was restored by imposing, 50 ms after each step, a step of the same size in the opposite direction (Linari et al. 1998; Linari et al. 2007).

Mechanical data collection and analysis

Force, motor lever position and sarcomere length signals were recorded at sampling intervals of 10 μs with a multifunction input/output board (PXIE‐6358; National Instruments, Austin, TX, USA). Dedicated computer software written in LabVIEW (National Instruments) and Origin 2015 (OriginLab Corp., Northampton, MA, USA) were used for the analysis.

X‐ray diffraction measurements

To measure the interfilament distance, X‐ray diffraction patterns were collected from intact trabeculae in diastole and from skinned trabeculae in relaxing solution. Trabeculae were vertically mounted at the beamline ID02 of the ESRF (van Vaerenbergh et al. 2016), which provides up to 2 × 10¹³ photons s^–1 with 0.1 nm wavelength in a beam of size, at the trabecula, ∼300 μm (horizontal, full width at half‐maximum) and ∼70 μm (vertical). The beam was attenuated for trabecula alignment. To minimize radiation damage, X‐ray exposure was limited to the data collection period using a fast electromagnetic shutter (model LS500; nmLaser Products, Inc., San Jose, CA, USA) and the trabecula was shifted along its axis by 100–200 μm between exposures. X‐ray diffraction patterns were recorded using the FReLoN charge‐coupled device‐based detector with 2,048 × 2,048 pixels (50 × 50 mm² active area). Pixels were binned by 8 in the equatorial direction (perpendicular to the trabecula axis) before the readout to increase the signal‐to‐noise ratio. Patterns were first collected with the X‐ray detector at 31 m from the preparation to record the sarcomere length (Reconditi et al. 2017). Then, the detector was moved to 3 m from the preparation to collect equatorial reflections from the lattice planes formed by the double hexagonal array of the myofilaments: the 1,0 reflection, associated with the planes passing through the centres of thick filaments, and the 1,1 reflection, associated with the planes passing through the centres of both thin and thick filaments. In the skinned trabecula, 2‐D patterns were collected at different concentrations of dextran T500 (range 0–8%, w/v) in the relaxing solution to determine the relationship between interfilament distance and dextran concentration and find the dextran concentration that restores the pre‐skinning distance.

X‐ray data analysis

X‐ray diffraction data were analysed using Fit2D (A. Hammersley, ESRF) and OriginPro 2015. 2‐D patterns were centred and aligned using either the third‐order sarcomere reflections (31 m camera) or the equatorial 1,0 reflections (3 m camera). The total intensity in one quadrant was obtained by horizontal and vertical mirroring. In the patterns at 3 m, the distribution of diffracted intensity along the equatorial axis of the pattern (perpendicular to the trabecula axis) was obtained by integrating the 2‐D pattern from 0.0036 nm⁻¹ on either side of the equator; in the patterns at 31 m, the intensity distribution on the meridian of the X‐ray pattern was determined by integrating from 0.25 μm⁻¹ on either side of the meridional axis (parallel to the trabecula axis). Background intensity distribution was removed using a convex hull algorithm. The spacing of the sarcomeric reflections and of the 1,0 equatorial reflection, used to estimate the interfilament distance, was determined by fitting a Gaussian peak to the reflection.

Results

MHC composition

The MHC composition is an important determinant of the mechanical parameters of the half‐sarcomere and may vary with the strain and age of the rat (see Discussion). The SDS‐PAGE gel from the trabeculae of our rat strain, 2–3 months old, shows two bands in the region of the molecular mass corresponding to that of the MHC (Fig. 1). The fraction of the β‐MHC isoform with respect to the α‐MHC isoform is 0.16 ± 0.01, corresponding to a ratio α‐to‐β cardiac myosin of 6:1. Thus, the α‐MHC isoform is dominant, in accordance with what is reported in the literature (Reiser & Kline, 1998; Carnes et al., 2004; Rundell et al., 2005).

Figure 1. Identification of MHC isoforms.

Left: SDS‐PAGE gel of the area of migration of myosin heavy chain from a single trabecula from rat heart. Upper line: α myosin isoform, lower line: β myosin isoform. Right: projection of the mass density along the vertical axis after horizontal integration.

The stiffness of the half‐sarcomere in the active contraction

The mechanical protocol for measuring half‐sarcomere stiffness at the peak of an isometric twitch is shown in Fig. 2 A and B ([Ca²⁺]_o 1 mm). During force development (Fig. 2 A, top trace), the half‐sarcomere length trace (Fig. 2 A, middle trace) is almost constant as the shortening against the end compliance is prevented by a feed‐forward exponential lengthening imposed at the motor end (Fig. 2 A, bottom trace). At ∼95% T _p, a small step release is imposed that elicits simultaneous half‐sarcomere shortening and drop in force, which is followed by a quick force recovery. The responses to three different step sizes at 1 mM [Ca²⁺]_o are shown on a faster time base in Fig. 2 B. The force response simultaneous with the step reflects the elastic properties of the half‐sarcomere and the plot of the force attained at the end of the step (T ₁) against the size of the imposed length step provides an almost linear relationship with a slope that estimates the stiffness of the half‐sarcomere (k ₀) (Fig. 2 C). The T ₁ relationship of the trabecula (Fig. 2 C, filled circles, length step size measured from the movement of the lever of the motor) is less steep than that of the selected sarcomere population (Fig. 2 C, open circles, length step size measured by the signal from the striation follower). The difference between the two relationships reflects the lower stiffness of the trabecula as a result of the contribution of the compliance of the attachments, which accounts for 40% of the overall compliance of the trabecula.

Figure 2. Stiffness measurements during isometric contraction.

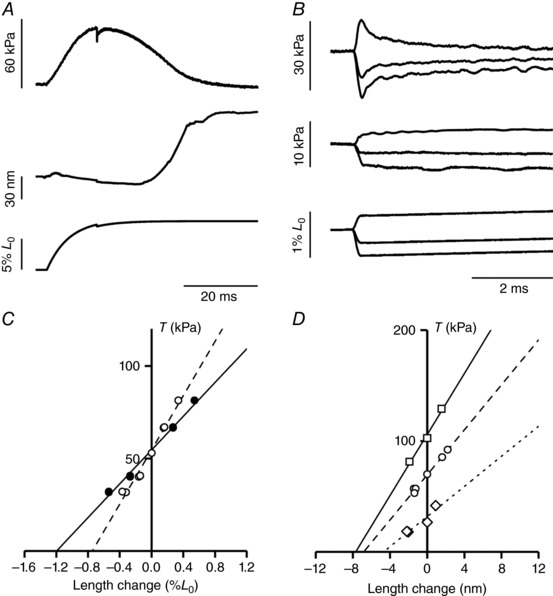
A, force development in a sarcomere length clamped twitch (1 mm [Ca²⁺]_o, SL 2.19 μm) with a stepwise reduction in length applied at 95% of T _p. Upper trace: force; middle trace: half‐sarcomere length change; lower trace: motor position. B, superimposed records of force responses (upper traces) and half‐sarcomere length changes (middle traces) elicited by length steps of different sizes imposed by the motor (lower traces). C, T ₁ relationships from data in (B): filled symbols, trabecula; open symbols, half‐sarcomere. The lines are linear regression fits to each set of points. The slopes of the two T ₁ relationships are 0.94 ± 0.02 %/L ₀ (continuous line) and 1.59 ± 0.02 %/L ₀ (dashed line). D, T ₁ relationships of the half‐sarcomere at three different [Ca²⁺]_o: 0.5 mm (diamonds), 1 mm (circles) and 2.5 mm (squares). The lines are linear regression fits to the experimental points. Length of the trabecula, 2.97 mm; segment length, 0.98 mm; average segment sarcomere length, 2.20 μm; cross‐sectional area, 7,600 μm²; temperature, 27°C.

T ₁ relationships were determined at different T _p obtained by changing [Ca²⁺]_o. The mean T _p values for the three different [Ca²⁺]_o used are reported in Table 2. The T ₁ relationships for one experiment and the respective linear fits to data are shown in Fig. 2 D (Fig. 2 D, diamonds and dotted line 0.5 mM Ca²⁺, T _p 26 kPa; Fig. 2 D, circles and dashed line 1 mM Ca²⁺, T _p 70 kPa; Fig. 2 D, squares and continuous line 2.5 mM Ca²⁺, T _p 102 kPa). It can be seen that not only the slope of the relationship, which is k ₀, but also the abscissa intercept, which estimates the half‐sarcomere (hs) strain just before the length step (s _hs), increases with the increase in T _p. This result indicates that the stiffness increases less than in proportion to the Ca²⁺‐modulated force, as expected on the basis of a simple two‐component mechanical model of the half‐sarcomere (Fig. 3 A, Model 1), in which the elasticity is given by an element with constant stiffness, the myofilaments, in series with an element, the array of myosin motors, which changes its stiffness in proportion to force (Ford et al. 1981; Brunello et al. 2006; Colombini et al. 2010; Fusi et al. 2014).

Table 2.

Estimates of the mechanical parameters of the half‐sarcomere and of the myosin motor at [Ca²⁺]_o ranging between 0.5 and 2.5 mM and at temperature 27°C

[Ca2+]o	(mm)	0.5	1	2.5
Measured parameters
Peak force (T p)	(kPa)	24.9 ± 3.6	61.1 ± 3.5	93.1 ± 9.2
Filament compliance (C f)a ,*	(nm MPa–1)		17.1 ± 0.3
hs‐compliance in activated trabeculae (C hs)	(nm MPa–1)	182 ± 22	112 ± 6	80 ± 6
hs‐compliance in rigor (C hsr)*	(nm MPa–1)		24.6 ± 0.6
Myosin motor strain (s 0)* *	(nm)		5.74 ± 0.02
Lattice geometry and force per myosin motor
Myosin to myosin spacingb ,*	(nm)	40.4
Myofibrillar volume densityc ,*	(%)	60
Number of myosin motors per CSAd ,*	(m−2)	1.25 × 1017
Fraction of attached myosin motors and derived parameters
Fraction of attached myosin motors			0.08 ± 0.01	0.12 ± 0.02
Force per attached myosin motor**	(pN)		6.14 ± 0.52
Stiffness of the attached myosin motor**	(pN nm–1)		1.07 ± 0.09

^aSee Appendix.

^bThe myosin‐to‐myosin spacing is obtained by multiplying the spacing of the 1,0 equatorial reflection (d _1,0) by 2/√3⋅ d ₁₀ = 40.4 nm in intact trabecula (Irving et al. 2000; Reconditi et al. 2017).

^cSchaper et al. (1985); Barth et al. (1992).

^dWith a myosin‐to‐myosin distance of 40.4 nm, the unit cell area containing one myosin filament is (sin60° × (40.4 nm)² = ) 1413  nm². The density of myosin filaments per CSA is (1/1413 nm² = ) 707 filaments μm^–2. With a myofibrillar volume density of 60%, the density of myosin filaments becomes (0.6 × 707 filaments/μm² = ) 424 filaments μm^–2. With 294 myosin motors per hs, the myosin motors per unit area is (294 × 424 filaments μm⁻² = ) 124797 μm^–2 or 1.25 × 10¹⁷ m^–2.

^*Same value at the three [Ca²⁺]_o.

^**Same value at 1 mM and 2.5 mM [Ca²⁺]_o.

Figure 3. Mechanical models of the hs (A) and dependence of the hs compliance C _hs (B) and hs strain s _hs (C) on force.

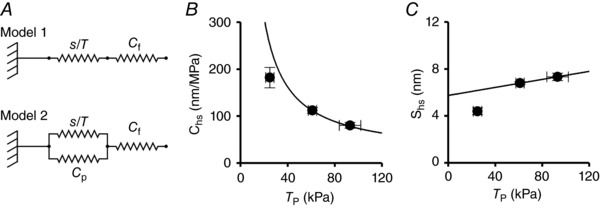
A, two component model (Model 1) and two component model with an elastic element in parallel with myosin motors (Model 2). Parameters defined in the text. B and C, dependence of C_hs (B) and s_hs (C) on T _p modulated by [Ca²⁺]_o. The line in (C) is calculated by fitting a first‐order regression to the two data points at T _p > 40 kPa with fixed slope given by C _f (17.1 nm MPa^–1; see Appendix). The ordinate intercept (5.74 ± 0.02 nm) is the only free parameter and estimates the average strain of the attached myosin motors (s ₀) at the peak of the twitch. The line in (B) is C _hs at any force calculated from the straight line in (C). Data are the mean ± SEM from nine trabeculae.

For the analysis of the components of the half‐sarcomere elasticity, it is convenient to use the half‐sarcomere compliance, C _hs, the reciprocal of k ₀, because C _hs (nm MPa^–1) is given by the sum of the contributions of its in series components:

$$C_{\mathrm{hs}}=C_{\mathrm{f}}+1/\phantom{1\left(\beta e_{\mathrm{r}}\right)}\left(\beta e_{\mathrm{r}}\right)$$ (1)

where C _f is the equivalent myofilament compliance and 1/(β⋅e _r) is the compliance of the array of myosin motors in the hs, with e _r being the stiffness of the array when all of the motors are attached, and β being the fraction of attached motors. C _hs can also be expressed as:

$$C_{\mathrm{hs}}=C_{\mathrm{f}}+s_0/\phantom{s_0{T}_{\mathrm{p}}}{T}_{\mathrm{p}}$$ (2)

where s ₀ is the average strain of the motors at T _p. Accordingly, C _hs decreases with the increase in T _p in a hyperbolic‐like manner (Fig. 3 B, circles).

The Ca²⁺‐dependent increase in force is explained by the increase in the number of attached motors, whereas the force and the strain per myosin motor remain constant. Consequently, under the assumptions of the simple two‐component model (Model 1), the half‐sarcomere strain (s _hs) increases with force in proportion to the increase in the strain of myofilaments with constant compliance C _f. s _hs at any T _p can be derived from C _hs as s _hs = C _hs⋅T _p (Fig. 3 C, circles) and is the sum of the strain in the force generating motors, s ₀, which is constant, and the strain in the myofilaments, which increases in proportion to T _p, according to the first order equation, derived from Eqn (2) multiplying both sides by T _p:

$$S_{\mathrm{hs}}=C_{\mathrm{f}}{T}_{\mathrm{p}}+s_0$$ (3)

where s ₀ is the ordinate intercept and C _f is the slope. As a result of both the paucity of the points describing the s _hs–T _p relationship and the deviation from the linearity at low values of force (<40 kPa) for the effect of an elastic element, in parallel with myosin motors, with constant compliance C _P (Fig. 3 A, Model 2), it appears evident that, in cardiac trabeculae, it is impossible to directly estimate C _f from the slope of the observed relationship. The problem can be resolved (see Appendix) by using an independent estimate of C _f, obtained from data in the literature. The value of C _f in the heart trabecula (calculated in accordance with the method detailed in the Appendix) is 17.1 ± 0.3 nm MPa^–1. With C _f constrained in this way, the fit of Eqn (3) to the two points at forces >40 kPa (continuous line in Fig. 3 C) gives an estimate of s ₀ (the only free parameter) of 5.74 ± 0.02 nm. The experimental points at T _p > 40 kPa lie on the fitted line, whereas the point at T _p < 40 kPa is lower, indicating that the half‐sarcomere strain–force relationship of the trabecula has remarkable similarities with that of fast skeletal muscle: (i) the slope of the linear part is explained by a myofilament compliance, which is just the same as that of skeletal muscle (see Appendix), and (ii) at forces <40 kPa, the relationship is shifted downward by the contribution, to C _hs, of a parallel elastic element, the stiffness of which is so small that it emerges only when T _p and the number of attached motors are reduced to one‐third of the respective values at saturating [Ca²⁺]_o. Knowing s ₀, the expected C _hs on the basis of Model 1 can be calculated according to Eqn (2) (continuous line in Fig. 3 B).

It is evident that at T _p = 24.9 kPa ([Ca²⁺]_o 0.5 mm), the observed C _hs is 30% lower than that expected from Model 1 because of the presence of the parallel elastic element (Fusi et al. 2014). The results obtained in cardiac trabeculae, under conditions where the isometric force is modulated by [Ca²⁺]_o, are in remarkable agreement with those obtained in fast skeletal muscle: the change in half‐sarcomere strain with isometric force is explained by filament compliance, whereas the strain of the motors s ₀ remains constant as their number increases in proportion to force.

The half‐sarcomere stiffness in rigor

Three trabeculae were used for half‐sarcomere stiffness measurements in rigor. Under this condition, all of the myosin motors are attached to actin (Cooke & Franks, 1980; Thomas & Cooke, 1980; Lovell et al. 1981); thus, the stiffness of the myosin motor can be calculated from the half‐sarcomere compliance analysis and simple geometrical considerations. In these experiments, at the end of the mechanical measurements during active contractions, the trabecula was skinned (see Methods) and rigor was developed by deprivation of ATP. The width of the trabecula, which is the dimension parameter that could be measured at this stage of the experiment, increased following skinning for the osmotic entrance of water by 15 ± 6% with respect to the value before skinning. This increase is accompanied by an increase in interfilament spacing and this effect has been shown to influence the half‐sarcomere stiffness (Goldman & Simmons, 1986; Brenner & Yu, 1991; Linari et al. 2007). The effect can be reversed using the osmotic agent dextran T‐500. The amount of dextran necessary to restore the pre‐skinning interfilament spacing was determined in dedicated measurements using X‐ray diffraction on trabeculae mounted at the beamline ID02 of the European Synchrotron ESRF (Fig. 4 A). First, the camera length was set to 31 m to collect the first orders of the sarcomeric reflections. In this way, sarcomere length could be set to 2.2 μm by adjusting the length of the trabecula. Then, the camera length was reduced to 3 m to collect the equatorial reflections from the filament lattice. The interfilament spacing (d _1,0), measured as the distance between the lattice planes formed by the myosin filaments, was 34.8 ± 0.2 nm in five intact trabeculae (sarcomere length 2.21 ± 0.01 μm) and, after skinning (two trabeculae), became 39.6 ± 1.8 nm (+13%, sarcomere length 2.23 ± 0.04 μm). The addition of dextran induced osmotic shrinkage so that d _1,0 decreased in proportion to the dextran concentration (Fig. 4 B). From the relationship of (d _1,0) against dextran concentration it appears that, in agreement with previous measurements (Irving et al. 2000), a concentration of 5% dextran is necessary to restore the pre‐skinning interfilament spacing. Noteworthy, with 5% dextran, which was used in all of the mechanical experiments in rigor, the width of the relaxed skinned trabeculae was 0.96 ± 0.06 that of the intact trabeculae. The induction of rigor after the osmotic recovery by dextran did not change the dimension of the skinned trabecula significantly (w, 1.03 ± 0.05 the value in relaxing solution with 5% dextran).

Figure 4. Effect of the increase of dextran concentration on the lattice spacing of skinned trabeculae.

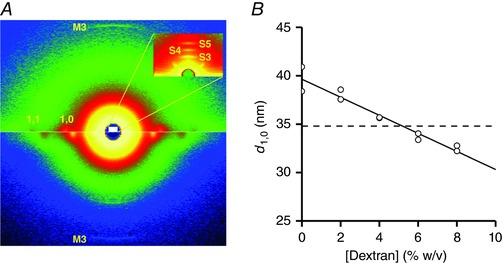
A, 2‐D diffraction patterns from a skinned trabecula in a solution without dextran (lower half) and with 8% dextran (upper half) collected with a sample to detector distance of 3 m and a 40 ms exposure time each. The equatorial 1,0 and 1,1 and meridional M3 reflections are indicated. The white area corresponds, in the reciprocal space, to the inset that shows a detail of a pattern collected with 31 m sample‐to‐detector distance (2 ms exposure time). The third‐ to fifth‐order sarcomeric reflections are indicated: their positions in the reciprocal space correspond to a sarcomere length of 2.2 μm. B, lattice spacing estimated as the distance between the lattice planes made by the myosin filaments (d _1,0). The line is the linear regression fit to the data (pooled from two trabeculae). The slope of the line is –0.93 ± 0.09 nm per 1% change in dextran concentration. Dashed line, d _1,0 value from intact rat trabeculae at sarcomere length 2.2 μm.

The half‐sarcomere stiffness in rigor was determined by superimposing a sequence of length steps on the steady force (T) attained following the end of slow ramp lengthening (step amplitude L, 2–6 nm per half‐sarcomere). Sample records of responses elicited at T = 70 kPa (attained with a slow lengthening of 4.8 nm per half‐sarcomere) are shown in Fig. 5 A. In rigor, the length step induces a response that is almost purely elastic and, to recover the original steady force, a similar step is imposed in the opposite direction 50 ms after each step. The responses of force and length changes to four different steps on a fast time base are superimposed in Fig. 5 B. The relationships between the force attained at the end of the step and the corresponding change in the half‐sarcomere length (T ₁ relationship) at three different steady forces T are shown by the different open symbols in Fig. 5 C). T is normalized for T _p (60 kPa), the peak force attained by the same trabecula in the active contraction in 1 mM Ca²⁺.

Figure 5. Half‐sarcomere stiffness measurements in rigor at different steady forces.

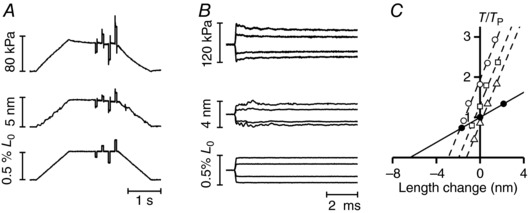
A, sample records of force responses (upper traces), half‐sarcomere length changes (middle traces) and change in motor position (lower traces) in a trabecula in rigor at a force of ∼70 kPa, obtained by slowly stretching the trabecula. Force per unit cross‐sectional area is expressed relative to the CSA in the relaxed trabecula in the presence of 5% dextran. B, superimposed records of force responses (upper panel), half‐sarcomere length changes (middle panel) and motor position (lower panel) as in (A) on a faster time base. C, T ₁ relationships either in the active trabecula at T _p (60 kPa, [Ca²⁺]_o = 1 mm, filled circles) or in rigor (open symbols) at different steady forces T (normalized for T _p: triangles, 0.83 T _p; diamonds, 1.30 T _p; circles, 1.88 T _p). The lines are linear regressions fitted to the experimental points. Active, continuous line; rigor, dashed lines. Length of the trabecula, 2.53 mm; segment length, 0.73 mm; average segment sarcomere length, 2.19 μm; cross‐sectional area, 10,650 μm²; temperature, 27.1°C.

The slopes of the three T ₁ relationships shown by the open symbols in Fig. 5 C, which measure the half‐sarcomere stiffness in rigor (k _r), are larger than that of the T ₁ relationship in the active contraction (filled circles). The estimates of the parameters from the linear regression fits to the three T ₁ relationships in rigor (dashed lines) indicate that k _r is not significantly different at the different T, with an average value of 40.2 ± 0.1 kPa nm^–1, whereas the abscissa intercept (the hs strain in rigor, s _hsr), is larger at larger T. The plot of s _hsr vs. T (Fig. 6 A), obtained by pooling the data from the three trabeculae, shows that s _hsr increases in direct proportion to T, as demonstrated by the linear regression fit (dashed line) that is a straight line passing through the origin. The slope of the line estimates the half‐sarcomere compliance in rigor (C _hsr) that is 24.6 ± 0.6 nm MPa^–1.

Figure 6. Half‐sarcormere compliance and fraction of attached myosin motors.

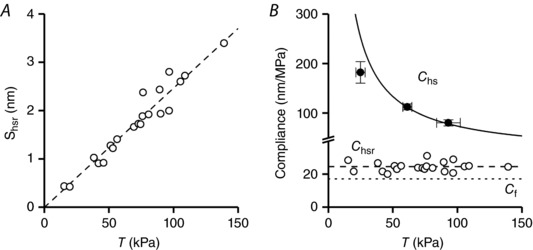
A, relationship of half‐sarcomere strain (s _hsr) vs. the steady force (T) in rigor. The dashed line is the linear regression fit forced to pass through zero. The slope of the line, the half‐sarcomere compliance in rigor, is 24.6 ± 0.6 nm MPa^–1. Data from three trabeculae. B, force dependence of the hs compliance in active (C _hs, filled circles) and in rigorized trabeculae (C _hsr, open circles). Filled circles and continuous line from Fig. 3 B. C _hsr is calculated from data in (A) as the ratio s _hsr/T; the dashed line is the C _hsr as determined by the fit in (A). The dotted line is the filament compliance (C _f).

In Fig. 6 B, individual C _hsr points have been calculated at each T by the ratio s _hsr/T and plotted vs. T (open circles, data pooled from the three trabeculae). C _hsr remains constant independent of T, as demonstrated also by the interpolation of the dashed line which represents the slope of the line in A. This analysis indicates that the half‐sarcomere in rigor responds as an elastic element with a constant compliance and that the stiffness of the array of motors and the stiffness of each motor in the array is constant over the full range of forces investigated. The dotted line in Fig. 6 B is C _f, 17.1 nm MPa^–1 (see Appendix). The C _hs–T relationship from the active contraction (filled circles and continuous line from Fig. 3 B) is also shown to illustrate the difference in the contribution of the motor array to half‐sarcomere compliance. In rigor, the compliance of the motor array is 1/e _r = (C _hsr – C _f = 24.6 ± 0.6 – 17.1 ± 0.3 =) 7.5 ± 0.7 nm MPa^–1 (the distance between the dashed and the dotted lines) and is smaller than the myofilament compliance. In the active contraction at T _p > 40 kPa, the compliance of the motor array, that is 1/β·e _r = C _hs – C _f (the distance between the continuous and the dotted line), is much larger than the myofilament compliance: even at [Ca²⁺]_o = 2.5 mm, when it attains the minimum observed value, 1/β·e _r (80.4 nm MPa^–1 – 17.1 nm MPa^–1 = 63.3 nm MPa^–1), accounts for (63.3 nm MPa^–1/80.4 nm MPa^–1·100 =) 79% of the half‐sarcomere compliance.

The linearity of the T ₁ relationships both in the active contraction and in rigor represents compelling evidence that the stiffness of the actin‐attached motor is constant independent of both motor strain and whether it is active or in rigor. Under these conditions at Ca²⁺‐modulated T _p > 40 kPa (the range within which the half‐sarcomere can be represented by the simple two‐component mechanical model (Model 1) of Fig. 3 A), the fraction of myosin motors responsible for the force generated at T _p, β, can be determined by the ratio between the compliance of the half‐sarcomere in rigor over that in the active contraction, once the filament compliance has been taken into account: β = (C _hsr – C _f)/(C _hs – C _f). β is (7.5/95.3 = ) 0.08 ± 0.01 in 1 mm Ca²⁺ (T _p = 61 ± 4 kPa) and (7.5/63.3 = ) 0.12 ± 0.02 in 2.5 mm Ca²⁺ (T _p = 93 ± 9 kPa). The result demonstrates that, within the experimental error, the Ca²⁺‐dependent increase in force at 2.5 mm Ca²⁺ relative to 1 mm Ca²⁺ (1.52 ± 0.17) is accounted for by the increase in the number of motors (1.51 ± 0.17) (P > 0.7; Student's t test).

The stiffness and the force of the myosin motor

The compliance of the array of motors in rigor is 1/e _r = 7.5 nm MPa^–1. Its reciprocal (e _r) is the stiffness of the motor array when all motors are attached (133 ± 12 kPa nm^–1) and can be used to calculate the stiffness of the myosin motor (ε) by simple lattice geometry considerations. At 2.2 μm sarcomere length, d _1,0 in the intact trabecula at rest is 35 nm (Fig. 4 B). The corresponding distance between myosin filaments is (2/√3⋅ d _1,0 = ) 40.4 nm. Considering a myofibrillar volume density of 0.60 (Schaper et al. 1985; Barth et al. 1992), the density of myosin filaments is 4.24⋅10¹⁴m⁻². Thus the stiffness of the motor array per half‐thick filament in rigor is 314 ± 28 pN nm^–1. Because all of the 294 motors are attached in rigor, the stiffness per motor, ε, is (314 pN nm^–1/294 = ) 1.07 ± 0.09 pN nm^–1. From ε, knowing that the average strain of the force‐generating motors in the active contraction (s ₀) is 5.74 nm (Fig. 3 C), the average force per myosin motor can be calculated as F ₀ = ε⋅s ₀, and is (1.07 pN nm^–1⋅5.74 nm = ) 6.14 ± 0.52 pN.

Discussion

Fast sarcomere level mechanics in rat trabeculae is used to define the elastic characteristics of the components of the cardiac half‐sarcomere during active contractions in which force is modulated by [Ca²⁺]_o. It is found that, over the range of forces >40 kPa, the stiffness of the array of the actin‐attached motors is proportional to the force attained during the twitch. The comparison with the stiffness of the motor array in rigor allows the stiffness and force of the motor to be defined, as well as the number of motors attached at the peak of the twitch and its dependence on [Ca²⁺]_o. Independently of [Ca²⁺]_o, during isometric contraction, the average force of the attached myosin motor is 6.1 pN and its average strain is 5.7 nm, underlying a motor compliance of 0.93 nm pN^–1 or a stiffness of 1.07 pN nm^–1. Thus, although the force of the motor is comparable to that in fast skeletal muscle (5–6 pN, (Linari et al. 2007; Brunello et al. 2014)), its stiffness is 2‐ to 3‐fold smaller than that of fast skeletal muscle (1.7–2.8 pN nm^–1). It is worth noting that all of the above comparisons do not take into account the different temperature of the experiments, that is 12°C in skinned fibres from rabbit psoas (Linari et al. 2007), 4°C for the intact fibres from frog muscle (Brunello et al. 2014) and 27°C for intact trabeculae from rat heart. However, although the average force and strain of the motors responsible for isometric force in skeletal muscle have been found to increase with temperature, the stiffness of the motor is a parameter that does not depend on temperature (Decostre et al. 2005; Linari et al. 2007). Thus, the difference in stiffness of the myosin motors between the trabecula and fast skeletal muscle should be genuine and somewhat expected considering that an even slightly larger difference has been found between the myosin isoforms of the slow and fast skeletal muscle of mammals (Percario et al. 2018; Brenner et al. 2012) and that, in mammals, the MHC isoforms of slow skeletal muscle and cardiac muscle are similar (Brenner et al. 2012).

The proportionality between the stiffness of the array and the [Ca²⁺]_o‐dependent increase in the force of the twitch is explained by a proportional increase in the number of attached motors: an increase in [Ca²⁺]_o from 1 to 2.5 mm, which increases the peak force from 61 to 93 kPa, induces an increase of the fraction of attached myosin motors from 0.08 to 0.12, which fully accounts for the increase in force. Noteworthy, the estimate of the fraction of attached motors from X‐ray diffraction experiments with the same [Ca²⁺]_o (2.5 mm) is slightly larger (0.18 ± 0.01) (Reconditi et al. 2017).

A reduction in [Ca²⁺]_o to 0.5 mm reduces the force to 25 kPa and, at these low force values, an additional elasticity in parallel with the array of myosin motors becomes evident (Fig. 3 B). The contribution of a parallel elasticity, which at low forces reduces the half‐sarcomere compliance below the value expected on the basis of the two component mechanical model (Model 1), is in agreement with that found in the skeletal muscle sarcomere (Colombini et al. 2010; Fusi et al. 2014; Fusi et al. 2017). In the cardiac sarcomere, the deviation cannot be resolved with the same detail, given the paucity of data, although the reduction of C _hs by 30% at a force of 25 kPa appears to be larger than the reduction produced by the parallel elastic element in the corresponding low force range of frog skeletal muscle fibres (Fusi et al. 2014).

This parallel elasticity has been attributed to either titin or a population of non‐force generating motors weakly bound to actin or both (Fusi et al. 2014). The larger effect of the parallel elasticity found in the present study for the trabeculae, if significant, could indicate some other source, such as the microtubules, which, in cardiomyocytes, have been identified as a supplementary element in parallel with sarcomere (Robison et al. 2016).

The mechanical parameters of the half‐sarcomere in the heart muscle, estimated at [Ca²⁺]_o in the range 0.5–2.5 mm, are summarized, together with the relevant lattice parameters, in Table 2.

Comparison with in vitro measurements

In vitro determination of the force of a single myosin motor at high load (corresponding to the isometric contraction) is difficult to achieve as a result of the relatively large compliance connecting the motor system to the transducers. In the three bead assay (TBA) configuration (Finer et al. 1994), the laser beam is split in two to trap the two beads to which the actin filament is attached and to bring the filament in proximity of a myosin molecule attached to a third bead stuck to the coverslip. Each interaction is detected by the reduction of the thermal noise in the bead position. The stiffness of the trap is intrinsically very low and limits the possibility of applying this technique to high load measurements. However, Finer et al. (1994) describe experiments on skeletal muscle myosin where a feedback circuit prevented the movement of the bead during force generating actomyosin interaction, increasing the stiffness of the trap to 6 pN nm^–1. Under these conditions, the average force per interaction of skeletal muscle myosin was 3.4 pN, with an upper limit of 11 pN. Using the same technique, the force per interaction of cardiac myosin shows a large range of values, from 1.5–2 pN (subfragment 1 of human β‐cardiac myosin) (Sommese et al. 2013; Spudich, 2014) to 5 pN (full length porcine β‐cardiac myosin) (Greenberg et al. 2014). Thus, the larger values are 50% lower than those reported for skeletal muscle myosin. Laser trapping allowed comparative measurements on the two isoforms of the cardiac myosin (the slow β‐cardiac myosin, extracted from large mammal and human hearts, and the fast α‐cardiac myosin, extracted from small mammal hearts). The high load force of β‐cardiac myosin was found to be similar (Alpert et al. 2002; Noguchi et al. 2003; Malmqvist et al. 2004) or higher than that of the α‐cardiac myosin (VanBuren et al. 1995; Aksel et al. 2015). The ratio α‐to‐β cardiac myosin isoforms in the 2–3‐month‐old rats used in our experiments is 6:1 (Fig. 1); thus, the value of the isometric force we found (6.1 pN) arises mostly from the α‐cardiac myosin (which is 86% of the total). Nonetheless, our estimate of the force per motor is in the upper range of the values obtained with in vitro studies. In this respect, it must be noted that, apart the different temperature (room temperature for most in vitro measurements vs. 27°C in the present study), in the native half‐thick filament, all of the myosin motors are correctly oriented with respect to the actin filament, whereas, in the TBA, the myosin molecules are attached to the third bead with a random orientation and this could reduce the efficiency of force generation (Ishijima et al. 1996).

In face of the limits of in vitro mechanical measurements in relation to either the large series compliance or the intrinsic impossibility of studying the motor co‐ordination emerging from the array arrangement of motors in situ, the application of our fast sarcomere level mechanics to intact trabeculae is unique in allowing the definition of the mechano‐kinetics properties of the cardiac myosin, as demonstrated in the present study for the force and stiffness of the myosin motor and in a previous study (Caremani et al. 2016) for the motor working stroke and its attachment‐detachment kinetics. Moreover, trabeculae mechanics can be combined with time resolved X‐ray diffraction to investigate the structural dynamics of the cardiac sarcomeric proteins in situ (Reconditi et al. 2017). This combined approach can be applied also to skinned muscle strips from human myocardium and rodent models with selective cardiomyopathy causing mutations, opening new possibilities for the investigation of the pathomechanisms of the cardiomyopathies and testing small molecules as potential therapeutic tools.

Relevance of results in relation to mechano‐kinetic properties of the cardiac myosin and its regulation

The main aim of the present study was to directly test the correctness of a paradigm accompanying the performance of cardiac muscle that so far has been only supported indirectly. The paradigm states that the force at the peak of the twitch (T _p) of a cardiac trabecula is modulated by inotropic interventions (sarcomere length, external [Ca²⁺]) via the modulation of the number of attached motors, so that the force per motor remains constant. The most recent indirect evidence comprised the demonstration that an increase in either [Ca²⁺]_o or sarcomere length that double T _p does not affect the speed and the size of the working stroke in the attached motors (Caremani et al. 2016), leading to the conclusion that the parameter modulated by the inotropic intervention is the number of attached motors. In recent X‐ray diffraction experiments on intact trabeculae (Reconditi et al. 2017), it was shown that modulating T _p with different loading conditions implies a modulation of the degree of activation of the thick filament via a positive feedback, based on thick filament mechano‐sensing, which adjusts the number of switched ON motors to the stress on the filament. According to Caremani et al. (2016), who propose that T _p varies in proportion to the number of attached motors, it could be concluded that the duty ratio (i.e. the ratio between attached and available motors) is constant independent of T _p. However, a direct test concerning the relationship between T _p and number of attached motors was absent. In the present study, the question of estimating the number of attached motors in a twitching trabecula was directly addressed under the same experimental conditions (temperature 27°C, pacing frequency 0.5 Hz) as those that were used in previous experiments and established as efficient protocols for mechanical studies of the cardiac myosin in situ (ter Keurs et al. 1980; de Tombe & ter Keurs, 1991, 1992; Kentish & Wrzosek, 1998; Caremani et al. 2016). It should be noted that a higher, more physiological, temperature (35–40°C) would have not increased T _p of the rat trabecula further (de Tombe & ter Keurs, 1990; Raman et al. 2006) and, at the same time, it would have reduced the resolution of the method for the measurement of half‐sarcomere stiffness (see Methods). Finally, it should be noted that, in general, temperature does not affect the half‐sarcomere stiffness of the myosin motor per se (Decostre et al. 2005; Linari et al. 2007; Park‐Holohan et al. 2012) and, even if this finding were not valid for cardiac muscle, there would be an even more stringent reasons for keeping the temperature at the same value (27°C) as that used in the two most recent studies (Caremani et al. 2016; Reconditi et al. 2017), where fundamental new properties of cardiac myosin in situ were revealed in relation to the mechano‐kinetics of the actin‐attached motor and the mechanism of its recruitment from the energetically convenient OFF state.

Additional information

Competing interests

The authors declare that they have no competing interests.

Author contributions

FP, IP, MR, TN, GJMS, GP, VL, ML and MC performed the experiments. All of the authors contributed to the conception and design of the experiments; the collection, analysis and interpretation of data; and drafting the article or revising it critically for important intellectual content. All authors approved the final version of the manuscript submitted for publication, and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. All persons designated as authors qualify for authorship and all those who qualify for authorship are listed.

Funding

This work was supported by MIUR‐PRIN Project 2010R8JK2X (Italy), Ente Cassa di Risparmio di Firenze Project 012.0611 (Italy), Telethon Project GGP12282 (Italy) and University of Florence (competitive project rictd1819) (Italy).

Biography

Francesca Pinzauti obtained her master's degree in Biology at the University of Florence, Italy, in 2014. She is currently a PhD student working in the Department of Biology (PhysioLab) of the University of Florence. Her research is aimed at investigating the molecular basis of the performance of the cardiac muscle and its regulation using biophysical techniques that combine sarcomere‐level mechanics and X‐ray diffraction in intact trabeculae isolated from the rat heart. Recently, she found that the energetic cost of the heartbeat is tuned to the afterload by a stress‐sensing mechanism in the thick filament.

Appendix

Filament compliance in heart muscle

The myofilament compliance (C _f) used in the present study for the half‐sarcomere compliance analysis of the rat trabecula is calculated from the C _f estimated in single fibres from fast skeletal muscle of the frog (12.8 ± 0.3 nm MPa^–1) (Piazzesi et al. 2007; Brunello et al. 2009; Linari et al. 2009; Fusi et al. 2010; Fusi et al. 2014), taking into account the SL, the myofibrillar fractional occupancy in the myocyte and the thin filament length.

The average SL at which C _f is measured in skeletal muscle is 2.15 μm, whereas the measurements in the trabeculae of the present study are conducted at SL = 2.19 μm. However, because the length of the Z line is 30–50 nm in fast skeletal muscle and ∼100 nm in slow skeletal and cardiac muscle (Luther 2009), in the sarcomere, the myofilaments span a similar length in both preparations [∼(2.15–0.04 = ) 2.11 μm in skeletal muscle and (2.19–0.10 = ) 2.09 μm in the trabeculae]. Consequently, the fact that the actin filament has a length of 0.94 μm in the skeletal muscle and 1.04 μm in the heart trabecula (Burgoyne et al. 2008) does not substantially affect the length of actin filament overlapped with the myosin motor array. Thus, assuming that the compliances per unit length of the actin and myosin filaments are the same in skeletal and heart muscle, the contribution of the myofilaments to the half‐sarcomere compliance is expected to be the same in the skeletal and trabecular myofibrils.

Once the different myofibrillar volume density in skeletal muscle fibre of frog (0.8) (Mobley & Eisenberg, 1975) and rat heart trabecula (0.6) (Schaper et al. 1985; Barth et al. 1992) is taken into account, a C _f per cross‐sectional area of 12.8 nm MPa^–1 in the skeletal muscle corresponds to a C _f of (12.8 nm MPa^–1·0.8/0.6 = ) 17.1 ± 0.3 nm MPa^–1 in the heart trabecula.