Abstract
Consensus pattern and matrix-based searches designed to predict cis-acting transcriptional regulatory sequences have historically been subject to large numbers of false positives. We sought to decrease false positives by incorporating expression profile data into a consensus pattern-based search method. We have systematically analyzed the expression phenotypes of over 6000 yeast genes, across 121 expression profile experiments, and correlated them with the distribution of 14 known regulatory elements over sequences upstream of the genes. Our method is based on a metric we term probabilistic element assessment (PEA), which is a ranking of potential sites based on sequence similarity in the upstream regions of genes with similar expression phenotypes. For eight of the 14 known elements that we examined, our method had a much higher selectivity than a naïve consensus pattern search. Based on our analysis, we have developed a web-based tool called PROSPECT, which allows consensus pattern-based searching of gene clusters obtained from microarray data.
INTRODUCTION
The availability of numerous completely sequenced eukaryotic genomes and the constantly expanding amount of DNA microarray data have made computationally based strategies aimed at deciphering genetic regulatory networks more feasible. To date, computational analysis of transcriptional mechanisms has largely been focused on identification of potential regulatory factor-binding sites in the DNA sequences upstream of genes (1–4). The methods used have been quite varied, ranging from sophisticated Gibbs sampling-based algorithms to more ‘brute force’ counting and analysis of fixed length oligonucleotide words (so-called kmer or ktuple word searching). Subsequent work is necessary to validate the cis-acting elements predicted by these methods. However, searches of this sort nonetheless serve a purpose, in that they provide experimental targets for ‘wet bench’ researchers.
Another method of element prediction which was frequently used before the advent of complete genome sequences and expression profile data is the consensus sequence or matrix method (5). Theoretically, by searching upstream regions for sequences which have previously been shown to act as cis-regulatory elements, the number of false positive predictions should be greatly reduced. In practice, the consensus sequence or matrix scan method is often just as inefficient as the newer methodologies. Lavorgna et al. (6) have described some methods to reduce the high rate of false positives, by selectively excluding known non-regulatory sequences. Unfortunately, this method fails to address the real cause of the false positives, which is that known cis-acting element sequences are often inadequately defined and often do not contain sufficient information to allow them to be used to predict sites in a large (e.g. genome sized) amount of sequence.
The advent of large-scale transcription or expression ‘profiles’ allows the refinement of ‘classical’ consensus pattern/matrix-based searches into a useful predictive tool. First, by applying clustering techniques to the data from the expression profile studies, we can obtain groups of genes that are likely to be co-regulated (i.e. likely to have functionally similar cis-acting elements in their upstream regions). Additionally, the availability of complete genome sequences means that it is trivially possible to search these upstream sequences for sequences common to some or all of them. It has been suggested that this combination of expression phenotype and sequence similarity could lead to a large increase in the efficiency of cis-acting element prediction. This combinatorial approach has been critical to some recent regulatory element prediction techniques (7,8), but none of the described techniques were systematically evaluated to determine if known elements were detected with a higher selectivity than in naïve searches.
In this paper we report on a technique that combines clustering of expression profile data with sequence similarity searches of upstream regions. We have systematically analyzed the correlation between expression phenotype and presence of known regulatory sequences, across 121 transcript profile experiments, with 14 different known elements. In the method that we describe, a binomial distribution model is used to give potential sites a probabilistic rank based on the observed degree of sequence similarity in clusters of genes with a similar expression phenotype. We refer to this metric as probabilistic element assessment (PEA). Analysis of the results of applying our method showed that sites with a favorable PEA (≤0.1) were at least two to five times more likely to represent experimentally confirmed regulatory sites, relative to a typical consensus pattern or matrix-based search.
MATERIALS AND METHODS
Consensus pattern and sequence nomenclature
All consensus patterns presented and referred to in this work are encoded using the standard IUPAC nucleotide symbols (e.g. W at a given position in a consensus indicates that either A or T may be present) (9). Additionally, all nucleotide sequences are shown with 5′→3′ polarity relative to the sense strand of the downstream open reading frame. We have incorporated data from both SCPD (10) and TRANSFAC (11) in this study (see below). SCPD assigns names to regulatory element sequences, while TRANSFAC is organized in terms of the regulatory factor that recognizes the element. Because of the different organizations of these two databases, merging their name spaces was not attempted; instead, we have chosen to use the SCPD naming scheme.
Regulatory element dataset
We prepared a dataset of Saccharomyces cerevisiae transcriptional regulatory elements by merging data from the SCPD and TRANSFAC databases. After starting with 50 consensus patterns from the SCPD, we merged in by manual inspection 298 yeast sites from the TRANSFAC database. After redundancies were eliminated, there were 149 different recognition sites. Because some sites consist of patterns that cannot be combined into a sensible consensus, these 149 consensus patterns correspond to 66 site/factor names. Since several sites only contained data for single-stranded sequences, we created opposite strand sequences where necessary, resulting in 271 patterns on both strands. After duplicated patterns had been removed, the dataset contained a total of 139 unique patterns.
Upstream sequence dataset
We chose to focus our search for regulatory elements on the sequences upstream of open reading frames in S.cerevisiae. Using a tool developed by Wolfsberg et al. (http://www.nci.nlm.nih.gov/CBBresearch/Landsman/Cell_cycle_data/upstream_seq.html), we extracted 1000 bp 5′ of the translation start site of each of 6194 yeast open reading frames. Seven of these sequences (YAL069W, YFL067W, YFL068W, YJR162C, YKL225W, YMR326C and YNR077C) do not consist of a full 1000 bases, because they occur close to a chromosome end. Since there is some question about the ability of distant elements to effectively influence transcription, we also prepared datasets consisting of sequences of 600 and 200 bases upstream of each open reading frame. The subsequent analysis was independently carried out on all three datasets, and when results differed, it will be mentioned.
Expression profile dataset
We constructed a database, GExDB-Yeast, from publicly available data that had been presented in eight different manuscripts (12–19; summarized in Table 1). Four of these manuscripts reported time course experiments involving multiple samples compared to a common reference or base sample. Once redundancies were eliminated, we obtained 121 experimental values for each yeast gene, 103 of which came from time course-based experiments.
Table 1. Summary of data sources and clustering in the PROSPECT system: gene expression profile datasets.
| Dataset |
Description |
Experiments |
| DeRisi et al. (12) | Diauxic shift, repressor TUP deletion, activator YAP1 overexpression | 9 |
| Eisen et al. (13), Lashkari et al. (14) | Cell cycle elutriation, cdc15 arrest, sporulation, sporulation ndt80 knockout, heat shock, DTT shock, cold shock | 14 |
| Chu et al. (15) | Sporulation, sporulation ndt80 knockout | 9 |
| Holstege et al. (16) | Transcription factor mutant, SAGA chromatin modification complex mutant | 11 |
| Spellman et al. (17), Cho et al. (18) | Cell cycle α-factor arrest, cell cycle elutriation, cdc15 arrest, cdc28 arrest | 77 |
| Jelinsky and Samson (19) | Alkylating agents, methyl methanesulfonate | 1 |
| Total | 121 |
The original citations for the various datasets used in the PROSPECT system, as well as a description of the type of experiment that gave rise to the data and the number of individual ‘experiments’ in each dataset (where an experiment reflects comparison of one ‘experimental’ expression state with a ‘control’ baseline state) are listed and described.
Internally, gene data points in GExDB are stored as the ratio between two values, the value for the gene in the experimental state and the value for that same gene in the reference state [with the exception of the data of Cho et al. (18), where a single value is available in the original work]. These experimental and reference state values are expressed in units of bits and have been calibrated against an experiment- or time point-specific background value. As per Spellman et al. (17), the sum of all values within a particular experiment is normalized to 0.
The results of subsequent clustering of these expression profile experiments were collected in a linked database, GExCluster, which contains the results of clustering the expression profile data via a Pearson correlation coefficient-based hierarchical clustering algorithm, as described by Eisen et al. (13) and implemented by us. We empirically derived the cluster cut-off by examining the effects of using increasing correlation coefficients (summarized in Table 2), finally choosing a value of 0.7. This value was chosen because it was the smallest value that resulted in co-clustering of the majority of the histone genes (which we chose because they represent a distinct expression coherency with high variances). The chosen correlation coefficient cut-off of 0.7 clusters nine of the 10 histone genes together (H1 and both copies of H2A, H2B, H3 and H4). The failure of the other histone locus to co-cluster is due to a lack of data in some of the expression profile experiments (data not shown). Using the empirically determined cut-off value, the GExCluster database contains 6386 genes in 3998 clusters, an average of 1.6 genes/cluster. The largest observed cluster contains 377 genes; the smallest clusters contain only one gene (see Table 3 for additional data about the size distribution of the clusters obtained).
Table 2. Summary of data sources and clustering in the PROSPECT system: increasing the correlation coefficient cut-off increases the number of gene clusters.
| Cut-off |
Gene clusters |
| ≥0.1 | 185 |
| ≥0.3 | 547 |
| ≥0.5 | 1531 |
| ≥0.7 | 3998 |
| ≥0.9 | 6272 |
| 1.0 | 6386 |
The numbers of gene clusters obtained with increasing correlation coefficient cut-off thresholds are shown. The 0.7 line (bold) is the cut-off used to cluster genes in the GExCluster database.
Table 3. Summary of data sources and clustering in the PROSPECT system: size distribution of gene clusters.
| Size |
Number |
Genes |
| 1 | 3509 | 3509 |
| 2–10 | 459 | 1377 |
| 11–100 | 27 | 616 |
| 101–400 | 3 | 884 |
| Total | 3998 | 6386 |
The distribution of cluster sizes (in terms of genes per cluster) and the number of genes included at a correlation coefficient cut-off of 0.7 are shown.
Matrix search
A typical type of element search is carried out by looking for matches to patterns specified as matrix files. While relatively few (only 24) of the patterns in SCPD are available in this form, we chose to also characterize the effects of a matrix search in combination with PROSPECT and to compare them to the results obtained with PROSPECT alone. These searches were carried out using the MatInd/MatInspector software package (5) (http://www.gsf.de/biodv/mtinspector.html). SCPD patterns were imported into MatInd and then MatInspector was used to search upstream regions without a primal core search and with a low cut-off (0.7) for all matrices, in an attempt to match all known genes. After this initial step, we reiterated, raising the search cut-off until we began to fail to detect matches to known regulatory sites.
RESULTS AND DISCUSSION
PROSPECT: correlation between expression patterns and element distributions on upstream sequences
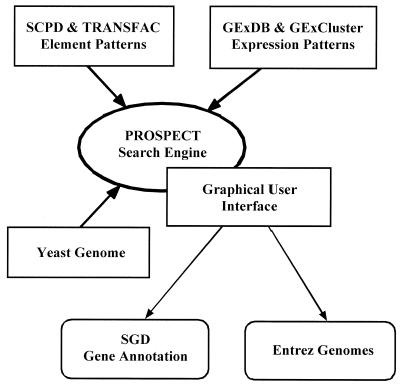
We hypothesized that detection of a particular known cis-acting element in all or many of the genes in a particular expression cluster would predict that the genes were co-regulated via that element. Furthermore, we hypothesized that the quality of this prediction would be directly proportional to the number of genes in the cluster. With these two hypotheses in mind, we developed a new tool, PROSPECT, which combines a typical consensus pattern search with the results stored in GExDB and GExCluster. This system is schematically outlined in Figure 1. Besides the basic components depicted in the diagram, PROSPECT is also linked to gene level annotation information in the Saccharomyces Genome Database (SGD) (20) and to genome level annotation information in the Entrez Genomes database (21).
Figure 1.
General architecture of the PROSPECT system. The PROSPECT search engine integrates sequence data from Wolfsberg et al. (http://www.ncbi.nlm.nih.gov/CBBresearch/Landsman/Cell_cycle_data/upstream_seq.html), cis-acting element sites and consensus sequences from SCPD (10) and TRANSFAC (11) and expression pattern data in GExDB and GExCluster (see text). A web-based graphical user interface provides access to that data, as well as links to SGD (20) and Entrez Genomes (21).
Evaluating the probability of element conservation in expression clusters
The basic concept in the search step of PROSPECT is an expression-limited element search method, where a pattern-based search is made against a subset of the genes represented by each expression cluster. When a pattern is observed more often than expected, this indicates that the pattern may be a regulatory element (or part of a regulatory element) which plays a role in determining co-expression of the genes in the cluster. The expectation value is calculated as a function of the size of the group of co-expressed genes, using a model based on a binomial distribution. When a given pattern occurs more than once in an upstream sequence, it is only counted once, i.e. pattern counting is done on an all-or-none basis. This constraint, which fails to adequately model the known biological situation (where multiple elements are generally more indicative of regulation than single elements) is a limitation of current statistical techniques, which cannot easily handle evaluation of multiple element data. It is important to note that the all-or-none counting method that was used will generally result in an under-estimation of element frequencies, with a concomitant under-estimation of statistical significance.
The PEA is calculated according to the following equation:
P(k ≥ x) = ∑ Ni = x[Ni]mi(1 – m)N – i 1
where P is the probability of finding x or more sequences that contain a given pattern by chance, assuming a binomial distribution with expected value m over an expression cluster with N members. The expected value (m) is estimated from the fraction of total sequences that have the pattern.
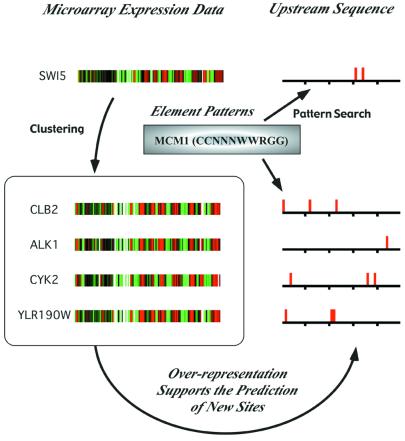
For example, in Figure 2 a search for the MCM1 element (CCNNNWWRGG) is shown. The SWI5 promoter is found to have a match to the MCM1 consensus pattern, confirming the experimental finding that SWI5 is regulated by MCM1 (22). When the search is extended to the set of genes that SWI5 clusters with, matches to the MCM1 consensus pattern are also found in the upstream regions of the other four genes in the cluster. One of these other genes, CLB2, is also known to be regulated by MCM1 (22); at this time, no data are available on whether the remaining three genes are also regulated by MCM1. Additionally, it is known that genes regulated by MCM1 have additional regulators. Consistent with these observations, we also find that all five upstream regions of the genes in the expression group contain a match to the consensus pattern of the SFF element, as reported by Spellman et al. (17). This suggests that the PROSPECT search technique may be useful in deciphering combinatorial regulatory networks.
Figure 2.
Example of a PROSPECT search. The MCM1 gene product is known to recognize an element upstream of the SWI5 gene. Previously generated clusters (based on data from GExDB and stored in GExCluster) contain a cluster of the SWI5, CLB2, ALK1, CYK2 and YLR190W genes. Each of these genes contains at least one MCM1 site in the sequence upstream of the start codon.
In order to evaluate the effect of varying PEA cut-off values on the results we obtained, we examined how decreasing the PEA (making the search more selective) affected both the number of elements and clusters identified and what selectivity increase over a random background level we obtained. As summarized in Table 4, we found that decreasing the PEA led, as expected, to a decrease in the number of genes and clusters that were identified as containing matches to the MCM1 consensus pattern. It is important to note that the decrease in the number of elements predicted by PROSPECT was less dramatic than the decrease in the number of elements expected to be found. This is significant, as the expected number of elements is equivalent to a classical pattern search, suggesting that the PROSPECT search technique greatly reduces the number of false positives found in a traditional pattern search. Unfortunately, since the location of all ‘real’ occurrences of any given element (i.e. examples that are recognized and bound by a protein to produce a regulatory event) is unknown, it is not possible to calculate the number of observed false positives. We can determine the number of false negatives, i.e. the number of known elements that are not detected by the PROSPECT search, and we have found this to be equal to or less than the number of false positives produced by a traditional pattern search in all cases. For example, Table 4 shows data for the MCM1 element, which has 25 known occurrences. At a PEA of ≤0.5 the PROSPECT search fails to identify four of the 25, while a traditional pattern search would have missed seven.
Table 4. PROSPECT searches have higher selectivity than simple pattern-based searches.
| PEA cut-off | Candidate genes (clusters) | Annotated sites correctly identified |
|
Selectivity ratio |
| |
|
PROSPECT (predicted) |
Pattern search (expected) |
|
| 1.0 | 2498 (1703) | 25 | 25.00 | 1.0 |
| ≤0.5 | 1722 (1460) | 21 | 17.23 | 1.2 |
| ≤0.4 | 1712 (1457) | 21 | 17.13 | 1.2 |
| ≤0.3 | 285 (86) | 5 | 2.85 | 1.8 |
| ≤0.2 | 255 (80) | 5 | 2.55 | 2.0 |
| ≤0.1 | 128 (23) | 5 | 1.28 | 3.9 |
| ≤0.01 | 5 (1) | 2 | 0.05 | 40a |
This table summarizes the results of searching for matches to the MCM1 consensus at a variety of PEA levels. The Candidate genes (clusters) column gives the number of genes and clusters searched (those for which PROSPECT detected a match to the MCM1 consensus) at the given PEA level. The Annotated sites correctly identified columns give the number of annotated sites (10; see also Materials and Methods) correctly predicted by PROSPECT and the expected number that would have been detected in the same set of genes by a typical pattern-based search. The final column gives the selectivity ratio, which measures the increase in selectivity given via the PROSPECT method (see Results for details).
aThis number is misleadingly high and should be interpreted with caution. The example discussed in the text is more realistic.
PROSPECT is more selective than a simple consensus pattern search
Because the initial MCM1 experiment suggested that a PROSPECT search could be significantly more selective than a naïve pattern search, we wanted to characterize the performance of the method over several patterns. In order to accomplish this, we elected to analyze a dataset containing numerous annotated (experimentally confirmed) regulatory sites and quantify how many were detected, as well as how many false positives were predicted. Since the SCPD contains a substantial number of annotated sites (580) distributed over a significant number of genes (205), we selected it as the dataset for this evaluation. We picked the 14 elements with the highest numbers of annotated binding sites in the 1000 bp upstream region that we were going to search in. These elements are ABF1 (19), GAL4 (6), GCN4 (9), GCR1 (6), HSE/HSTF (6), MATα2 (7), MCB (6), MCM1 (25), MIG1 (8), PDR3 (7), RAP1 (15), REB1 (12), repressor of CAR1 (13) and TATA (16); the numbers of genes which contain a particular element in their upstream region are indicated in parentheses.
In order to evaluate the two element prediction methods relative to each other, we devised a metric which we term the selectivity ratio. Selectivity for a particular method is measured as the fraction of correctly predicted elements (out of all elements predicted); the selectivity ratio is then the ratio of the selectivity of the PROSPECT method to the selectivity of the naïve consensus pattern search. Consequently, ratios >1 indicate that the PROSPECT method is more sensitive than the basic search, while ratios <1 indicate the opposite. For example, as described in the second last line of Table 4, we correctly predicted five elements out of 128 candidates with the PROSPECT method, while the standard consensus pattern search correctly predicted 25 elements in 2498 candidates, so the selectivity ratio is calculated as:
(5/128)/(25/2498) = ~3.9 2
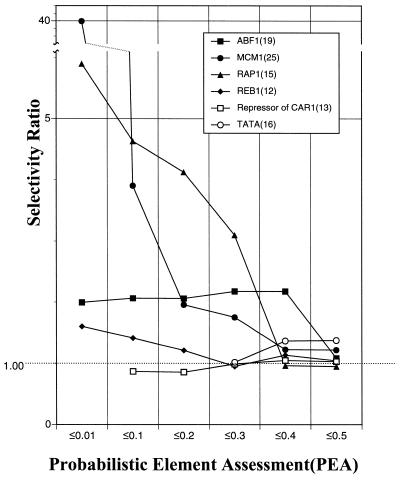
The data presented in Figure 3 demonstrate that the PROSPECT search method generally produces a large increase in search selectivity, especially at lower PEA values. Notably, searches for the MCM1 and RAP1 elements were more than five times more selective than a naïve consensus pattern search at a PEA of 0.01. In contrast, lowering the PEA cut-off did not improve the selectivity when searching for certain elements, such as repressor of CAR1. Furthermore, the selectivity ratios in searches for the ABF1 element plateau at a value of ∼2.0 at PEA levels ≤0.4.
Figure 3.
PROSPECT searches are more selective than traditional pattern-based searches. This graph shows selectivity ratios for a number of different known regulatory element patterns as a function of PEA cut-off level. Note that not all element patterns were tested at all PEA cut-offs (see for example Table 3).
Detailed numerical data for all 14 elements (at a PEA ≥0.1) is presented in Table 5A. Both consensus patterns from SCPD and individual patterns from TRANSFAC were used in the searches. Because the number of genes containing annotated sites was small (as low as six genes), we added additional regulatory data obtained from the Yeast Protein Database (YPD) (23) so as to improve the statistical calculations; this data is presented in Table 5B. Because the YPD data is in the form of trans-acting factors and the genes they regulate, we needed to map these factor names onto our element patterns. Note that in some cases the site names obtained from YPD do not identically match named patterns from SCPD. Three different selectivity ratios were calculated for three different upstream regions, of 200, 600 and 1000 bp.
Table 5. Summary of elements and data from the analysis.
| Element name | Sequence region (bp) | Candidate genes from search type | Selectivity ratios | |||
| |
|
Pattern |
PROSPECT |
Matrix + PROSPECT |
PROSPECT |
Matrix + PROSPECT |
| (A) Site data derived from SCPD | ||||||
| MCM1 | 200 | 440 (7) | 268 (6) | 65 (2) | 1.4 | 1.9 |
| 600 | 1631 (22) | 114 (5) | 379 (1) | 3.3 | NA | |
| 1000 | 2498 (25) | 128 (5) | 366 (1) | 3.9 | NA | |
| RAP1 | 200 | 338 (3) | 186 (0) | 85 (3) | ND | 4.0 |
| 600 | 1231 (13) | 176 (6) | 622 (8) | 3.2 | 1.2 | |
| 1000 | 2035 (15) | 205 (7) | 715 (7) | 4.6 | NA | |
| MCB | 200 | 507 (4) | 319 (4) | 116 (3) | 1.6 | 3.3 |
| 600 | 1218 (6) | 200 (3) | 246 (5) | 3.0 | 4.1 | |
| 1000 | 1677 (6) | 214 (3) | 326 (6) | 3.9 | 5.1 | |
| ABF1 | 200 | 837 (8) | 208 (6) | 210 (7) | 3.0 | 3.5 |
| 600 | 2144 (15) | 458 (7) | 425 (8) | 2.2 | 2.7 | |
| 1000 | 2974 (19) | 607 (8) | 333 (4) | 2.1 | 1.9 | |
| REB1 | 200 | 494 (2) | 363 (0) | 217 (2) | ND | 2.5 |
| 600 | 1097 (10) | 314 (4) | 360 (2) | 1.4 | 0.6 | |
| 1000 | 1440 (12) | 340 (4) | 418 (5) | 1.4 | 1.4 | |
| MIG1 | 200 | 143 (3) | 117 (3) | 83 (3) | 1.2 | 1.7 |
| 600 | 414 (7) | 247 (6) | 225 (6) | 1.4 | 1.6 | |
| 1000 | 652 (8) | 34 (0) | 315 (6) | ND | 1.6 | |
| GAL4 | 200 | 51 (2) | 35 (2) | 5 (2) | 1.5 | 10.2 |
| 600 | 214 (6) | 149 (6) | 21 (6) | 1.4 | 10.2 | |
| 1000 | 349 (6) | 230 (5) | 27 (6) | 1.3 | 12.9 | |
| PDR3 | 200 | 24 (1) | 17 (1) | 40 (1) | 2.0 | 0.8 |
| 600 | 118 (7) | 97 (7) | 144 (7) | 1.2 | 0.8 | |
| 1000 | 182 (7) | 142 97) | 206 (7) | 1.3 | 0.9 | |
| Repressor of CAR3 | 200 | 90 (3) | 75 (3) | 51 (1) | 1.2 | 0.6 |
| 600 | 292 (11) | 212 (5) | 119 (3) | 0.6 | 0.7 | |
| 1000 | 471 (13) | 292 (7) | 33 (0) | 0.9 | ND | |
| MATα2 | 200 | 554 (1) | 313 (1) | 143 (0) | 1.8 | 0.0 |
| 600 | 1476 (7) | 99 (0) | 199 (0) | ND | ND | |
| 1000 | 2178 (7) | 103 (0) | 364 (0) | ND | ND | |
| TATA | 200 | 2497 (15) | 128 (0) | 141 (0) | ND | ND |
| 600 | 4275 (16) | 66 (0) | 49 (0) | ND | ND | |
| 1000 | 4944 (16) | 327 (0) | 30 (0) | ND | NA | |
| HSE, HSTF | 200 | 1641 (3) | 95 (0) | NM | ND | NM |
| 600 | 4042 (6) | 39 (0) | ND | |||
| 1000 | 5225 (6) | 27 (0) | NA | |||
| GCR1 | 200 | 2778 (4) | 75 (0) | 119 (0) | ND | ND |
| 600 | 5409 (6) | 209 (0) | 167 (0) | NA | ND | |
| 1000 | 6016 (6) | 906 (0) | 227 (0) | NA | NA | |
| GCN4 | 200 | 5177 (8) | 672 (0) | 38 (0) | NA | ND |
| 600 | 6162 (9) | 717 (0) | 216 (1) | NA | 3.2 | |
| 1000 | 6193 (9) | 881 (0) | 193 (0) | NA | NA | |
| (B) Site data derived from SCPD and YPD | ||||||
| MCM1 | 200 | 440 (8) | 268 (7) | 65 (2) | 1.4 | 1.7 |
| 600 | 1631 (24) | 114 (6) | 379 (1) | 3.6 | NA | |
| 1000 | 2498 (28) | 128 (6) | 366 (1) | 4.2 | NA | |
| RAP1 | 200 | 338 (3) | 186 (0) | 85 (3) | ND | 4.0 |
| 600 | 1231 (14) | 176 (7) | 622 (10) | 3.5 | 1.4 | |
| 1000 | 2035 (18) | 205 (9) | 715 (9) | 5.0 | NA | |
| MCB | 200 | 507 (23) | 319 (20) | 116 (17) | 1.4 | 3.2 |
| 600 | 1218 (33) | 200 (16) | 246 (23) | 3.0 | 3.5 | |
| 1000 | 1677 (33) | 214 (16) | 326 (24) | 3.8 | 3.7 | |
| ABF1 | 200 | 837 (11) | 208 (7) | 210 (7) | 2.6 | 2.5 |
| 600 | 2144 (19) | 458 (8) | 425 (9) | 2.0 | 2.4 | |
| 1000 | 2974 (23) | 607 (9) | 333 (5) | 1.9 | 1.9 | |
| REB1 | 200 | 494 (20 | 363 (0) | 217 (2) | ND | 2.5 |
| 600 | 1097 (10) | 314 (4) | 360 (2) | 1.4 | 0.6 | |
| 1000 | 1440 (13) | 340 (4) | 418 (8) | 1.3 | 2.1 | |
| MIG1 | 200 | 143 (6) | 117 (6) | 83 (6) | 1.2 | 1.7 |
| 600 | 414 (15) | 247 (12) | 225 (14) | 1.3 | 1.7 | |
| 1000 | 652 (18) | 34 (1) | 315 (14) | ND | 1.6 | |
| GAL4 | 200 | 51 (3) | 35 (2) | 5 (2) | 1.0 | 6.8 |
| 600 | 214 (7) | 149 (6) | 21 (6) | 1.2 | 8.7 | |
| 1000 | 349 (7) | 230 (5) | 27 (6) | 1.1 | 11.1 | |
| PDR3 | 200 | 24 (1) | 17 (1) | 40 (1) | 2.0 | 0.8 |
| 600 | 118 (7) | 97 (7) | 144 (7) | 1.2 | 0.8 | |
| 1000 | 182 (7) | 142 (7) | 206 (7) | 1.2 | 0.9 | |
| Repressor of CAR3 | 200 | 90 (9) | 75 (9) | 51 (1) | 1.2 | 0.2 |
| 600 | 292 (21) | 212 (15) | 119 (3) | 1.0 | 0.4 | |
| 1000 | 471 (24) | 292 (17) | 33 (0) | 1.1 | ND | |
| MATα2 | 200 | 554 (1) | 313 (1) | 143 (0) | 1.8 | ND |
| 600 | 1476 (7) | 99 (0) | 199 (0) | ND | ND | |
| 1000 | 2178 (7) | 103 (0) | 364 (0) | ND | ND | |
| TATA | 200 | 2497 (15) | 128 (0) | 141 (0) | ND | ND |
| 600 | 4275 (16) | 66 (0) | 49 (0) | ND | ND | |
| 1000 | 4944 (16) | 327 (0) | 30 (0) | ND | NA | |
| HSE, HSTF | 200 | 1641 (8) | 95 (1) | NM | 2.2 | NM |
| 600 | 4042 (12) | 39 (0) | ND | |||
| 1000 | 5225 (14) | 27 (0) | NA | |||
| GCR1 | 200 | 2778 (9) | 75 (0) | 119 (0) | ND | ND |
| 600 | 5409 (15) | 209 (0) | 167 (0) | NA | ND | |
| 1000 | 6016 (15) | 906 (3) | 227 (0) | 1.3 | NA | |
| GCN4 | 200 | 5177 (44) | 672 (5) | 38 (2) | NA | 6.2 |
| 600 | 6162 (50) | 717 (6) | 216 (3) | NA | 1.7 | |
| 1000 | 6193 (50) | 881 (8) | 193 (3) | NA | NA |
Numbers under the Candidate genes from search type columns show the number of candidates predicted with each method in each set of upstream sequences. Numbers in parentheses are the annotated elements (10; see also Materials and Methods) that were correctly predicted. The PEA value was ≤0.1 for all searches.
ND, no data obtained at this threshold; NA, not applicable for the analysis due to the large number of candidates detected in the pattern search; NM, no matrix available for this element.
Consistent with the initial MCM1 experiment, we found that the PROSPECT search method was significantly more selective than the naïve pattern search. The top four elements were consistently observed to have high selectivity ratios (typically >2). Five other elements (REB1, GAL4, MIG1, PDR3 and repressor of CAR1) had somewhat lower selectivity, but their ratios were almost always ≥1. Unfortunately, it was necessary to exclude three elements (HSE/HSTF, GCR1 and GCN4) in some cases, because their consensus patterns matched a significant fraction of the available gene sequences (>5000 out of ∼6000 sequences), which skewed the statistical calculations. As might be expected, these three elements have the least stringent consensus patterns of the 14 elements we tested, suggesting that a PROSPECT search may not be appropriate when dealing with inadequately defined sites.
Additionally, we observed that addition of the matrix pattern information produced a slight, but noticeable, increase in selectivity. This can be seen in the data for MCB, MIG1, GAL4, GCR1 and GCN4 (Table 5); it is most evident for GAL4. The patterns for these elements have less information, relative to the other elements that have higher selectivity ratios, suggesting that inclusion of a matrix search before PROSPECT analysis improves selectivity because it provides additional information in the pattern search step.
Finally, we observed a distinct effect of the length of the sequence analyzed. Generally speaking, the datasets with longer sequences had higher selectivity than datasets with shorter sequences. Intuitively, it seems likely that this is due to the increased probability of a false positive match as the sequence length increases; since these matches are less likely to be detected by the PROSPECT search, the overall selectivity increases. There was one notable exception to this pattern, the selectivity ratio for the ABF1 element decreased with increasing sequence length. This likely reflects a need for ABF1 elements to be positioned very close to the start of transcription, which is consistent with the high positional bias of the element as reported in the literature (2).
Web-based PROSPECT search tool
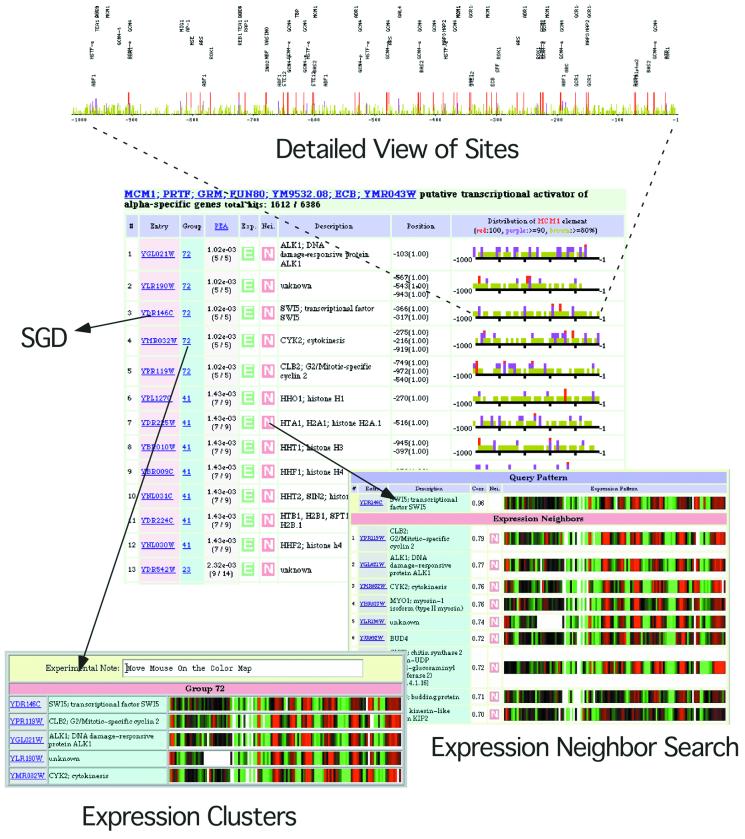
In order to maximize its utility, we have made a version of PROSPECT available on the World Wide Web at http://www.ncbi.nlm.nih.gov/CBBresearch/Postdocs/Wataru/PROSPECT/. Figure 4 shows the output from a search for MCM1 sites in the set of 1000 bp upstream regions. Genes can be searched for elements based on the name of the element or via a keyword-based mechanism. Alternatively, patterns can be specified via a regular expression-based mechanism. Results are returned sorted in order of ascending PEA values of the found matches to the element pattern. Gene names are hyperlinked to further information in the Saccharomyces Genome Database (SGD) (20).
Figure 4.
PROSPECT is available as a web-based element search tool. This diagram depicts the results of a PROSPECT search for MCM1-binding sites. In the main list view, genes containing a match to the MCM1 consensus are returned, sorted by PEA value. The Group links link individual genes to their expression cluster; E links provide a view of the comparison of the expression pattern for a particular gene to that of the factor that recognizes the element that was searched for; N links point to an alternative expression comparison method which uses a distance-based metric to group related expression patterns. A detailed view of element distribution on the upstream sequences is shown.
Additionally, from the results page it is possible to search for additional genes with expression patterns similar to the current gene. This ‘expression neighbor search’ is based on pre-calculated correlation coefficient scores from the initial clustering of the microarray dataset. A graphical interface that displays the positions of pattern matches on the upstream sequence is also provided and hyperlinked to the Entrez Genomes database (21), making it possible to obtain information about gene distributions and orientations.
We have developed a regulatory element prediction method that integrates traditional consensus-based searches with data from expression profile experiments. We have characterized this method by using it to ‘predict’ the locations of known regulatory elements, and have found that the PROSPECT method can significantly reduce the number of false positives typically generated by a pattern-based search. Furthermore, we have developed a web-based search tool so that other researchers may apply the PROSPECT search method to genes or elements that they are interested in. Researchers are able to specify arbitrary patterns to be searched, and these searches are relatively fast; over 6000 upstream sequences can be searched in <30 s. Since combinatorial regulation seems quite likely to be the underlying paradigm by which gene expression is organized, we consider the development of the ability to do complex searches of this nature to be a critical task in the overall process of determining how to extract maximum information from expression profiles.
Acknowledgments
ACKNOWLEDGEMENTS
We gratefully thank John Spouge and Tyra Wolfsberg for helpful discussions and useful comments on the manuscript. We also thank Alex Lash and Robert Ploger IV for careful reading of the manuscript.
References
- 1.Lawrence C.E., Altschul,S.F., Boguski,M.S., Liu,J.S., Neuwald,A.F. and Wootton,J.C. (1993) Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science, 262, 208–214. [DOI] [PubMed] [Google Scholar]
- 2.Hughes J.D., Estep,P.W., Tavazoie,S. and Church,G.M. (2000) Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae. J. Mol. Biol., 296, 1205–1214. [DOI] [PubMed] [Google Scholar]
- 3.van Helden J., André,B. and Collado-Vides,J. (1998) Extracting regulatory sites from the upstream region of yeast genes by computational analysis of oligonucleotide frequencies. J. Mol. Biol., 281, 827–842. [DOI] [PubMed] [Google Scholar]
- 4.Brazma A., Jonassen,I., Vilo,J. and Ukkonen,E. (1998) Predicting gene regulatory elements in silico on a genomic scale. Genome Res., 8, 1202–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Quandt K., Frech,K., Karas,H., Wingender,E. and Werner,T. (1995) MatInd and MatInspector: new fast and versatile tools for detection of consensus matches in nucleotide sequence data. Nucleic Acids Res., 23, 4878–4884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lavorgna G., Guffanti,A., Borsani,G., Bllabio,A. and Boncinelli,E. (1999) TargetFinder: searching annotated sequence databases for target genes of transcription factors. Bioinformatics, 15, 172–173. [DOI] [PubMed] [Google Scholar]
- 7.Zhang M.Q. (1999) Promoter analysis of co-regulated genes in the yeast genome. Comput. Chem., 23, 233–250. [DOI] [PubMed] [Google Scholar]
- 8.Wolfsberg T.G., Gabrielian,A.E., Campbell,M.J., Cho,R.J., Spouge,J.L. and Landsman,D. (1999) Candidate regulatory sequence elements for cell cycle-dependent transcription in Saccharomyces cerevisiae. Genome Res., 9, 775–792. [PMC free article] [PubMed] [Google Scholar]
- 9.Cornish-Bowden A. (1985) Nomenclature for incompletely specified bases in nucleic acid sequences: recommendations 1984. Nucleic Acids Res., 13, 3021–3030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhu J. and Zhang,M.Q. (1999) SCPD: a promoter database of the yeast Saccharomyces cerevisiae. Bioinformatics, 15, 607–611. [DOI] [PubMed] [Google Scholar]
- 11.Wingender E., Chen,X., Hehl,R., Karas,H., Liebich, I, Matys,V., Meinhardt,T., Pruss,M., Reuter,I. and Schacherer,F. (2000) TRANSFAC: an integrated system for gene expression regulation. Nucleic Acids Res., 28, 316–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.DeRisi J.L., Iyer,V.R. and Brown,P.O. (1997) Exploring the metabolic and genetic control of gene expression on a genomic scale. Science, 278, 680–686. [DOI] [PubMed] [Google Scholar]
- 13.Eisen M.B., Spellman,P.T., Brown,P.O. and Botstein,D. (1998) Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA, 95, 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lashkari D.A., DeRisi,J.L., McCusker,J.H., Namath,A.F., Gentile,C., Hwang S.Y., Brown,P.O. and Davis R.W. (1997) Yeast microarrays for genome wide parallel genetic and gene expression analysis. Proc. Natl Acad. Sci. USA, 94, 13057–13062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chu S., DeRisi,J., Eisen,M., Mulholland,J., Botstein,D., Brown,P.O. and Herskowitz,I. (1998) The transcriptional program of sporulation in budding yeast. Science, 282, 699–705. [DOI] [PubMed] [Google Scholar]
- 16.Holstege F.C., Jennings,E.G., Wyrick,J.J., Lee,T.I., Hengartner,C.J., Green,M.R., Golub,T.R., Lander,E.S. and Young,R.A. (1998) Dissecting the regulatory circuitry of a eukaryotic genome. Cell, 95, 717–728. [DOI] [PubMed] [Google Scholar]
- 17.Spellman P.T., Sherlock,G., Zhang,M.Q., Iyer,V.R., Anders,K., Eisen,M.B., Brown,P.O., Botstein,D. and Futcher,B. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell, 9, 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cho R.J., Campbell,M.J., Winzeler,E.A., Steinmetz,L., Conway,A., Wodicka,L., Wolfsberg,T.G., Gabrielian,A.E., Landsman,D., Lockhart,D.J. and Davis,R.W. (1998) A genome-wide transcriptional analysis of the mitotic cell cycle. Mol. Cell, 2, 65–73. [DOI] [PubMed] [Google Scholar]
- 19.Jelinsky S.A. and Samson,L.D. (1999) Global response of Saccharomyces cerevisiae to an alkylating agent. Proc. Natl Acad. Sci. USA, 96, 1486–1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ball C.A., Dolinski,K., Dwight,S.S., Harris,M.A., Issel-Tarver,L., Kasarskis,A., Scafe,C.R., Sherlock,G., Binkley,G., Jin,H., Kaloper,M., Orr,S.D., Schroeder,M., Weng S., Zhu,Y., Botstein,D. and Cherry,J.M. (2000) Integrating functional genomic information into the Saccharomyces genome database. Nucleic Acids Res., 28, 77–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wheeler D.L., Church,D.M., Lash,A.E., Leipe,D.D., Madden,T.L., Pontius,J.U., Schuler,G.D., Schriml,L.M., Tatusova,T.A., Wagner,L. and Rapp,B.A. (2001) Database resources of the National Center for Biotechnology Information. Nucleic Acids Res., 29, 11–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Althoefer H., Schleiffer,A., Wassmann,K., Nordheim,A. and Ammerer,G. (1995) Mcm1 is required to coordinate G2-specific transcription in Saccharomyces cerevisiae. Mol. Cell. Biol., 15, 5917–5928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Costanzo M.C., Hogan,J.D., Cusick,M.E., Davis,B.P., Fancher,A.M., Hodges,P.E., Kondu,P., Lengieza,C., Lew-Smith,J.E., Lingner,C., Roberg-Perez,K.J., Tillberg,M., Brooks,J.E. and Garrels,J.I. (2000) The yeast proteome database (YPD) and Caenorhabditis elegans proteome database (WormPD): comprehensive resources for the organization and comparison of model organism protein information. Nucleic Acids Res., 28, 73–76. [DOI] [PMC free article] [PubMed] [Google Scholar]