Digital holography and its multidimensional imaging applications: a review

We introduce digital holographic techniques and recent progress in multidimensional sensing. Digital holography can be used to perform multidimensional imaging of three-dimensional structure, dynamics, quantitative phase, multiple wavelengths, and polarization state of light and sensing of a holographic image of nonlinear light and a three-dimensional image of incoherent light.

Abstract

In this review, we introduce digital holographic techniques and recent progress in multidimensional sensing by using digital holography. Digital holography is an interferometric imaging technique that does not require an imaging lens and can be used to perform simultaneous imaging of multidimensional information, such as three-dimensional structure, dynamics, quantitative phase, multiple wavelengths and polarization state of light. The technique can also obtain a holographic image of nonlinear light and a three-dimensional image of incoherent light with a single-shot exposure. The holographic recording ability of this technique has enabled a variety of applications.

Introduction

Holography [1–4] is a technique used to record a wavefront diffracted from an object. Both amplitude and phase information of an object wave are recorded by utilizing the interference of light. A medium containing the information is called a ‘hologram’. A three-dimensional (3D) image can be reconstructed from a hologram by utilizing the theory of diffraction of light. Holography has been utilized as both a natural 3D display and a lensless 3D image recording technique. One of the most remarkable features of holography is that 3D motion-picture recording of any ultrafast physical phenomenon can be achieved with light-in-flight recording, even for light pulse propagation in 3D space [5].

In recent years, there have been rapid improvements in electronic devices such as image sensors, spatial light modulators (SLM) and computers. An SLM with high pixel density enables natural, colorful and high-quality lensless 3D motion-picture image formation on a holographic display [6–9]. A lensless image sensor with high pixel density and a large number of pixels can capture an image of fine interference fringes digitally, and a computer with high computational performance can then reconstruct a holographic image numerically with high throughput from a digitally recorded hologram. Digital holography (DH) [10–16] is a technique in which a digital hologram that contains an object wavefront is recorded, and both 3D and quantitative phase images of an object are reconstructed using a computer. This technique has potential application to the fields of microscopy [14, 17, 18], quantitative phase imaging (QPI) [14, 17, 19], particles and flow measurement in 3D space [20], 3D imaging of biological specimens [21], multiple 3D image encryption [22], 3D object recognition [23], 3D tomographic imaging of amplitude and phase distributions [24], 3D surface shape measurements with nanometer accuracy in the depth direction [25], ultrafast 3D optical imaging with an ultrashort pulsed laser [26], and holographic 3D imaging with a single photo detector [27, 28].

There has been an increase in demand for sensing multidimensional information, such as 3D space, time, wavelength, state of polarization, refractive index and various light waves, including second harmonic generation (SHG), coherent anti-Stokes Raman scattering (CARS), stimulated Raman scattering (SRS), evanescent waves and natural light. Holography has the ability to record a multidimensional image and various light waves with a single-shot exposure of a lensless monochrome image sensor [29]. Until now, multidimensional imaging techniques based on DH have emerged in coordination with electronic devices and signal theory. As an example, the development and improvement of high-speed cameras and the application of digital signal processing help the technique to capture the 3D dynamics of multiple living micro-biological specimens simultaneously at a frame rate of more than 10 000 fps [30]. In this article, we review digital holographic techniques and recent multidimensional digital holographic imaging and various light-waves sensing applications.

Digital holography

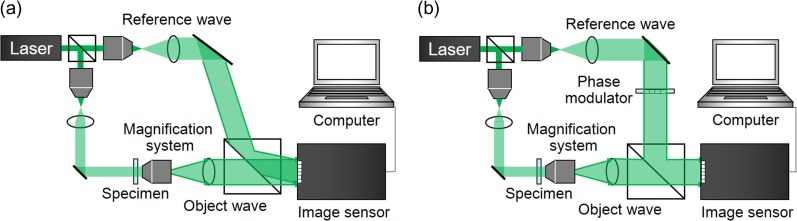
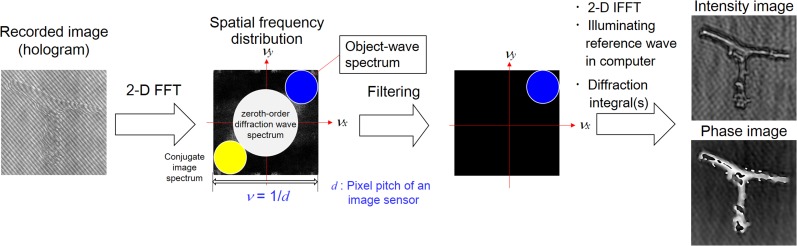
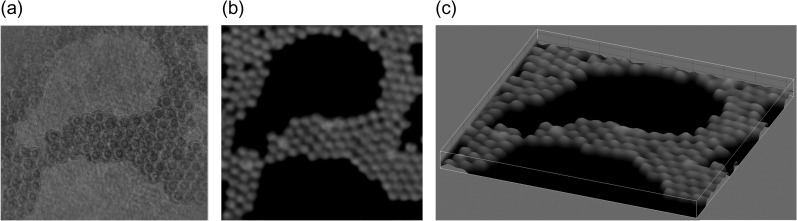
DH [10–16] is an interferometric imaging technique. DH requires two waves to generate a hologram and to obtain amplitude as well as quantitative phase images simultaneously. The two waves are called an ‘object wave’ and a ‘reference wave’, respectively. Two types of representative configurations are generally adopted in DH: off-axis DH [11] and phase-shifting DH [31, 32]. Figure 1 schematically shows these techniques. Two laser light waves are generated by dividing a laser beam with a beam splitter, and one laser light beam illuminates an object. The light diffracted from the object is the object wave, which illuminates an image sensor. The other light beam, serving as a reference wave, directly arrives at the image sensor. These waves interfere with each other, and an interference fringe image is formed on the image sensor plane. In Fig. 1a, the optical axis directions of the two waves differ from each other. The incident angle difference between the two waves results in a fine fringe pattern, and the image sensor records a single off-axis hologram. In Fig. 1b, two illumination waves come from the same direction and an image sensor records multiple in-line holograms by changing the phase of a reference wave with a phase modulator. Figure 2 schematically illustrates the image-reconstruction procedure of DH using the Fourier-transform method [11], which is frequently used for off-axis DH. A 2D Fourier transform (FT) localizes the object-wave information, and the large angle difference separates the object wave from unwanted image components of the hologram in the spatial frequency domain ν_x−ν_y. Due to the filtering in the spatial frequency domain, only the object-wave information is obtained. After the calculation of a 2D inverse FT (IFT), removal of the spatial carrier generated by tilting the reference wave, and calculation of diffraction integrals, focused intensity and quantitative phase images are obtained from a single hologram. A 2D fast Fourier transform (FFT) is used to accelerate the calculation, and methods to calculate diffraction integrals are described in [12–16]. Although spatial characteristics, such as field of view and resolution, are partially sacrificed to obtain intensity and phase images of an object from a hologram, single-shot holographic imaging can be achieved. Figure 3 shows an example of experimental results obtained from a single off-axis hologram. From a single hologram of polystyrene beads, whose diameters were 5 μm, transparent and phase images were retrieved as shown in Fig. 3a and b, and the 3D rendering shown in Fig. 3c was obtained from the phase image.

Fig. 1.

Schematic diagrams of (a) off-axis and (b) in-line digital holography systems with phase-shifting interferometry. Object and reference waves are generated from the same laser light source.

Fig. 2.

Image-reconstruction procedure in off-axis digital holography with the Fourier transform method.

Fig. 3.

(a) Intensity and (b) phase images of polystyrene beads whose diameters are 5 μm, which are obtained with a hologram at a wavelength of 532 nm. (c) 3D rendering image obtained from (b).

Figure 1b shows multiple holograms with different phases sequentially recorded with a phase modulator, such as a piezo-driven mirror, an SLM, an acousto-optic modulator, or an electro-optic modulator. Based on phase-shifting interferometry [31, 32], only the object-wave information is extracted with multiple phase-shifted holograms. After extraction, a holographic image of an object is obtained by calculating diffraction integral(s). Although recording of multiple holograms is required, the full space-bandwidth product of an image sensor can be utilized to record an object wave, and both a wide field of view and high resolution are obtained. To achieve high temporal resolution with phase-shifting interferometry, parallel phase-shifting DH, which uses space-division multiplexing of multiple phase-shifted holograms, was proposed by Awatsuji and Wyant around the same time [33–36]. By using a single-shot phase-shifting technique, a larger recordable space-bandwidth product is obtained in comparison to an off-axis configuration with the FT method [37].

The measurement speed is determined by the frame rate of the image sensor, the data transfer speed, and the calculation time for the image-reconstruction procedure. A modern high-speed camera has a frame rate of 1 Mfps, and such a camera has been used to perform digital holographic recording with a frame rate of 10⁶ fps [38]. In contrast, the high calculation cost is a problem that should be solved. It takes much more time to compute the diffraction integral(s) with a commercially available computer because of the demanding calculation requirements for the 2D FFTs. Use of a graphics processing unit (GPU) and a field-programmable gate array (FPGA) are possible solutions to achieve holographic image reconstruction with extremely high throughput [39, 40].

Multidimensional imaging and various light-wave recording by DH

Quantitative phase imaging

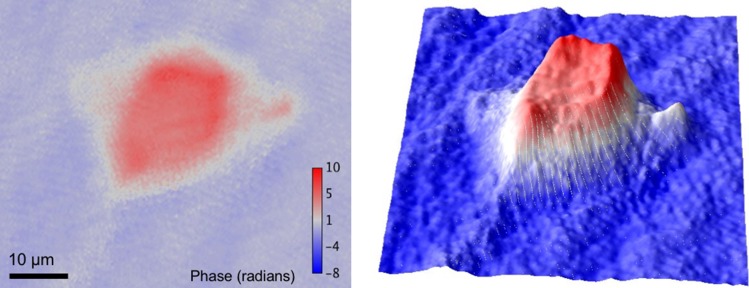
DH obtains both amplitude and phase distributions of an object wave simultaneously and quantitatively. The application of DH to microscopy is called digital holographic microscopy (DHM). DHM is also called 3D microscopy [14, 18] and quantitative phase microscopy [14, 17, 19]. QPI is an emerging field in 3D shape measurement, where it enables a high axial resolution on the scale of the light wavelength, and in biological imaging, where it is possible to visualize or quantify optical-path-length differences [14, 17, 19]. The path difference is a product of the physical thickness of an object in the axial direction and the difference in refractive index between the object and the surrounding medium. Figure 4 is an example of QPI for a HeLa cell, which is obtained with an off-axis digital holographic microscope that is described in Ref. [41]. As shown in Fig. 4, a transparent cell was recorded and imaged without labeling. Cuche et al., Takaki et al. [17, 42], and several other research groups presented not only 3D intensity imaging but also QPI with DHM around the year 2000. Mann et al. [19] demonstrated label-free imaging of cells with high axial resolution. After that, they showed QPI with higher resolution and quantitative phase movies of cells [43]. Label-free imaging of cells has also been performed successfully by many researchers to observe dynamics and to achieve time-lapse imaging without staining [44–46]. Kemper and Gert [47] demonstrated QPI with DHM for living cells and Watanabe et al. [48] reported cancer cell identification without staining using QPI . Another aspect of DHM is that its measurement performance is strongly affected by vibrations, and the construction of apparatus insensitive to disturbances is an important research theme. A common-path interferometer is stable and is suitable for QPI with a high tolerance against vibrational disturbances. Popescu et al. [49] constructed a common-path setup with a grating and 4f optical system and demonstrated its stability. Then, Lue et al. [50] presented another simple common-path DHM with Fresnel mirrors. QPI can be used in the fields of not only DH but also electron microscopy [51] and interference-less technique [52].

Fig. 4.

Phase image of a HeLa cell. Left: 2D phase image. Right: 3D surface plot of the phase image.

As a promising application of DHM, quantitative phase tomography has been actively researched [24]. A combination of DH and coherence tomography or diffraction tomography makes it possible to conduct complex-amplitude tomographic 3D imaging of an object such as a transparent material [24,53–58]. DHM has employed multidirectional illumination [24, 55, 58], low-coherence light [53], rotation of a specimen [54, 56], or multiple wavelengths [57] and multiple recording of sub-holograms to conduct phase tomographic 3D imaging of a specimen. Multidirectional illumination and recording of sub-holograms has also been applied to achieve super-resolution complex amplitude imaging [59–61].

A quantitative phase image contains information about the optical thickness distribution of a specimen, where optical thickness means the product of physical thickness and refractive index. Therefore, it is difficult to separate physical thickness and refractive index by ordinary DH. However, simultaneous measurements of physical thickness and refractive index distributions have been performed by recording multiple phase images at multiple illumination angles [24], multiple viewing angles [54] or multiple wavelengths [62] or by using low-coherence light and mechanical scanning [63]. By utilizing a tomographic imaging technique, a 3D refractive index distribution has been visualized. Kim et al. [64] demonstrated tomographic imaging of the 3D refractive index distribution of cells with multiple illumination angles, and subsequently, Yoon et al. [65] applied this technique to the characterization of white blood cells. Chowdhury et al. [66] alternatively proposed quantitative phase tomography utilizing structured illumination to visualize depth-resolved 3D refractive index distributions.

Multiwavelength 3D imaging with holographic multiplexing

One of the particular features in holography is its ability to simultaneously record multidimensional object waves that contain intensity in 3D space, phase, wavelength and polarization information [29]. Multiwavelength object-wave information contains the wavelength dependencies of absorption, reflectance and refractive index. Thanks to the recording of complex amplitude information at multiple wavelengths, multiwavelength DH can be applied to not only color 3D imaging [67] but also dispersion imaging [68], 3D shape measurement with a wide depth range by using multiwavelength phase unwrapping [25], depth-resolved 3D imaging [53], simultaneous measurements of 3D morphology and refractive index distribution [62], and even tomographic 3D imaging of dispersion [69].

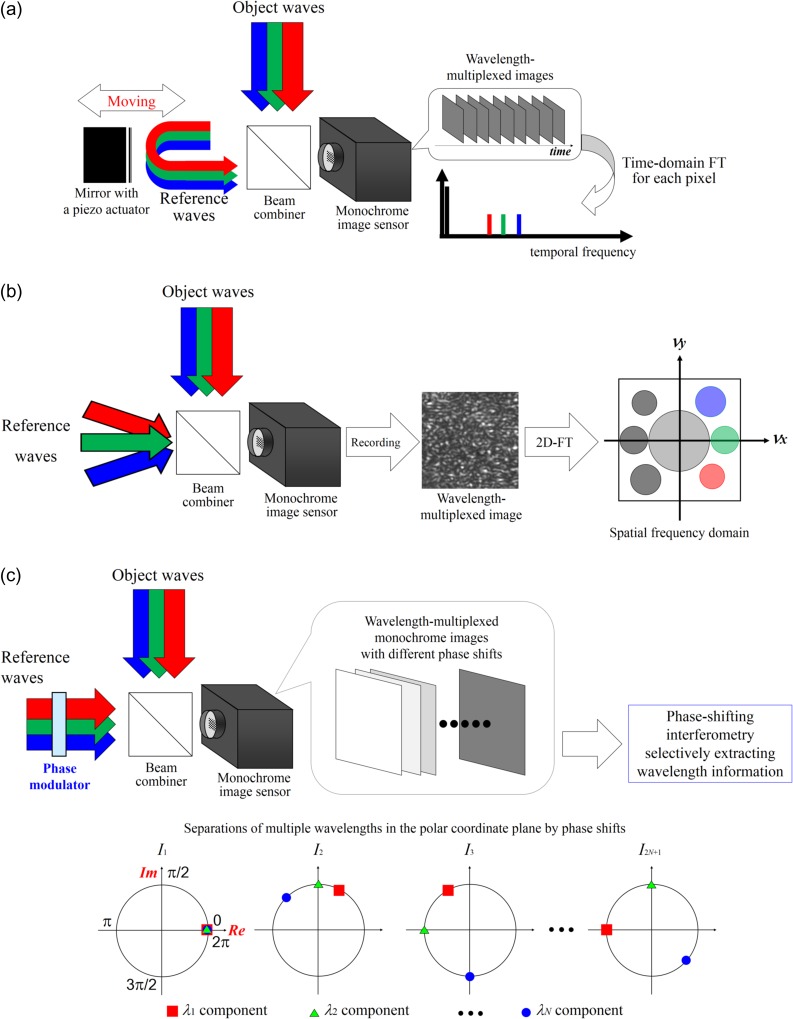
Wavelength information is obtained generally by using temporal [70] and spatial [71] divisions and space-division multiplexing [67, 72]. However, holographic techniques make it possible to record multiwavelength/color information using a monochrome image sensor and to reconstruct it from wavelength-multiplexed image(s). Therefore, a wavelength filter is not required and multiwavelength information can be rapidly recorded without any color absorption. As a result, DH can realize multiwavelength 3D imaging with high light use efficiency. In holography, multiple wavelength information is obtained also by utilizing temporal frequency-division multiplexing (TFDM) [73–75], spatial frequency-division multiplexing (SFDM) [29,76–78] and phase-division multiplexing (PDM) [79–82]. Figure 5 illustrates the schematics of TFDM, SFDM and PDM. DH with TFDM records a series of wavelength-multiplexed holograms with a monochrome image sensor by changing the optical path of a reference arm. The periods of intensity changes at certain wavelengths are different from each other. A 1D FT is calculated for each pixel in the recorded images and wavelength information is separated in the temporal frequency domain. DH with TFDM has been used to perform not only 3D shape measurement with multiwavelength phase unwrapping [73, 74] but also multicolor 3D imaging of incoherent light [75]. DH with SFDM generates different spatial carrier frequencies for respective wavelengths by using single or multiple reference beams. The spatial carrier frequency ν is sinθ/λ. Therefore, wavelength information can be separated in the spatial frequency domain by changing θ [29, 77, 78] for respective wavelengths or utilizing the difference of λ [76]. SFDM has the ability to record multiwavelength holographic images with a single-shot exposure at the expense of recordable spatial information, and therefore is suitable for observing dynamics in 3D scenes. 3D motion-picture imaging of micrometer-order movements of a mirror has been demonstrated [77] and high-speed color 3D motion-picture recording at 20 000 fps with a monochrome image sensor by using SFDM was reported [78]. SFDM was also applied to DHM to measure the dispersion distributions of cells with a single-shot exposure because multiwavelength DH can obtain quantitative phase images at multiple wavelengths [52]. Another suitable method to record multiwavelength object waves with high light efficiency is PDM [79–82]. Figure 5c represents the principle of PDM. A monochrome image sensor records 2N + 1 wavelength-multiplexed holograms sequentially while changing the phases of holograms at respective wavelengths with a phase modulator, such as a mirror with a piezo actuator or an SLM, where N denotes the number of wavelengths measured. Wavelength information is superimposed on space and spatial frequency domains, and is separated in the polar coordinate plane by introducing phase shifts, as in Fig. 5c. From the recorded wavelength-multiplexed phase-shifted holograms, object waves at the respective wavelengths are separately obtained with the phase-shifting interferometry selectively extracting wavelength information [79–82] and without any FTs. PDM of multiple wavelengths was presented in 2013 initially [79], and then color 3D imaging by using PDM was experimentally demonstrated [80]. Multiwavelength imaging with holographic multiplexing (MIHOM) using 2N wavelength-multiplexed phase-shifted holograms was proposed as a multiwavelength 3D imaging technique [81], which can be said as a computational coherent superposition scheme with 2N wavelength-multiplexed intensities. The originally proposed scheme involved the 2π ambiguity of the phase, but PDM with arbitrary and regular phase shifts was also proposed [82]. As an example of holographically multiplexed recording, we show three-wavelength digital holographic imaging with DHM based on PDM. A constructed multicolor in-line digital holographic microscope was based on PDM [82]. A preparation of stained mouse kidney cells was set as a specimen. Figure 6 shows the experimental results. The DHM obtained wavelength-multiplexed phase-shifted holograms and therefore conducted holographically multiplexed recording without a wavelength filter. As seen in Fig. 6a–c, the image reconstructed by the PDM resembles the photograph, and the PDM obviously separates wavelength information from the recorded monochrome images. DHM based on PDM also successfully visualized an in-focus image of stained cell nuclei with 1 μm-order diameters shown in Fig. 6d by calculating diffraction integrals.

Fig. 5.

Schematic diagrams of multiwavelength digital holography with (a) temporal frequency-division multiplexing (TFDM), (b) spatial frequency-division multiplexing (SFDM) and (c) phase-division multiplexing (PDM) of multiple wavelengths, respectively.

Fig. 6.

Experimental results. (a) Photograph of a specimen illuminated by three lasers. (b) In-line wavelength-multiplexed phase-shifted hologram. (c) Image reconstructed by the PDM on the image sensor plane. (d) Image obtained by the PDM and the calculation of diffraction integrals. Magnified image was focused at a depth of 8 mm from the image sensor plane. Scale bar in (a) is 20 μm.

3D imaging of incoherent light with DH

Ordinary DH uses a coherent light source such as a laser to record a hologram. This is because spatially and temporally coherent light is needed to generate an interference fringe image. However, in order to achieve 3D imaging for incoherent light such as fluorescence, spontaneous Raman scattering, or sun light, there is a lot of literature introducing incoherent holography and DH to realize 3D incoherent imaging with holography [83]. Basic configurations are often discussed with incoherent DH. Incoherent holography and DH frequently adopts common-path [83–90], Michelson [91–98], triangular [99], Mach-Zehnder [75] and optical scanning [100–102] interferometers to record incoherent hologram(s). Fluorescence 3D imaging with incoherent DH was initially performed in 1997 [100] after which image-quality improvements were shown by several groups [85, 98, 101]. As a common-path incoherent interferometer, Fresnel incoherent correlation holography (FINCH) [83–90] is an actively researched implementation. Rosen and Brooker [85] demonstrated 3D fluorescence imaging of particles with a 1 μm-order diameter by a FINCH system, and subsequently, Abe and Hayasaki [98] performed 3D mapping of multiple fluorescence nanoparticles having diameters of 500 nm with a Michelson interferometer. Kim [94] proposed a multicolor natural light holographic camera and captured an image of a 3D scene. It is noted that, in a self-reference interferometer using two object waves to obtain an incoherent hologram, the Lagrange invariant is violated [103]. This means that the product of magnification M and the maximum angle of a reconstructed object wave θ_max is larger than that of an ordinary coherent imaging system. The magnification of FINCH is higher than that of an ordinary incoherent imaging system while the angle θ_max in the system is the same as that in a coherent imaging system. As a result, super-resolution imaging can be performed. The difference between FINCH and the initially presented common-path incoherent holography [83] is the uses of an SLM and digital signal processing. The SLM generates two waves with different radii of curvature from an incoherent object wave to obtain an incoherent hologram. Incoherent DH including FINCH frequently adopts in-line phase-shifting interferometry because of the short coherence length of incoherent light and high-quality 3D imaging with a large space-bandwidth product. However, phase-shifting interferometry generally requires multiple exposures and loses temporal resolution.

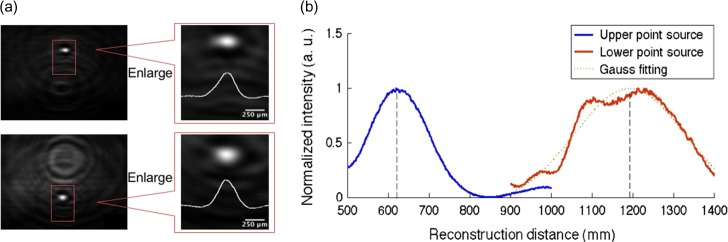
To realize single-shot incoherent 3D imaging with DH, incoherent DH setups with off-axis configurations [88, 95, 104] and single-shot phase-shifting interferometry [105, 106] have been proposed. In off-axis incoherent DH, Kelner and Rosen proposed a single-path FINCH system [88]. Hong and Kim [95] demonstrated single-shot incoherent 3D imaging with a Michelson interferometer. Quan et al. [104] introduced a method to realize common-path, stable, single-shot and incoherent DHM using a dual-focus lens and gratings. In single-shot in-line incoherent DH, incoherent DH and single-shot phase-shifting interferometry were successfully combined. Single-shot, common-path, in-line phase-shifting incoherent DH was presented to realize single-shot lensless 3D imaging of natural light with high temporal resolution [105, 106]. Figure 7 shows the results obtained by Quan’s system, which is described in Ref. [104]. A single incoherent hologram of two pinholes with 10 μm diameters, which were placed at different depths, was recorded and the respective focused images were reconstructed successfully.

Fig. 7.

Reconstructed images of two pinholes serving as point sources. These pinholes are placed at different depths. (a) The reconstructed images of point sources in the upper and lower sides. (b) Peak intensity obtained by calculating multiple diffraction integrals at multiple reconstruction distances and applying Gauss fitting. The depth information of each pinhole is derived from each peak intensity obtained after Gauss fitting. The depth positions of the magnified images of the pinholes were derived as 620 and 1190 mm, respectively.

As a method different from FINCH, a remarkable single-path incoherent DH method called coded aperture correlation holography (COACH) was recently proposed [107]. In COACH, coded phase-modulation (CPM) distributions are displayed on an SLM and point spread functions (PSFs) of CPMs at respective depths are measured in advance. After that, incoherent light in 3D space is recorded, and correlations between PSFs and recorded images are calculated. As a result, a 3D image of incoherent light is reconstructed without calculating diffraction integrals, while the Lagrange invariant is not violated. With COACH, incoherent 3D imaging [107], incoherent color 3D imaging [108], 3D imaging of a scattering object without interference [109] and single-shot COACH [110] have been demonstrated.

Other multidimensional imaging and special techniques in DH

DH has the ability to perform multiplexed recording of not only multiple wavelengths but also the polarization of a light wave and multiple object waves. The polarization of light is also an important physical parameter obtained by light wave recording. The polarization distribution of a 3D object can be recorded by sensing two object waves polarized in orthogonal directions and is obtained with SFDM [29, 111, 112], temporal division [113] and space-division multiplexing [114]. By using polarization-imaging DH, birefringent materials such as polarization optical elements [112] and biological polymers [114] were observed without staining. By recording multiple object waves, multiple physical information is simultaneously acquired. Object waves that reflected and transmitted a specimen were simultaneously captured with a single CCD image sensor. These waves were successfully and separately reconstructed and holographic reflection and transmission images were simultaneously visualized [115]. Multiplexed recording of multiple object waves were also applied to multiple 3D image encryption/decryption [116].

DH can be applied to not only multidimensional sensing but also holographic recording of various light waves such as nonlinear holographic 3D imaging. Nonlinear coherent light such as SHG, CARS and SRS waves can be recorded as a hologram by modulating not only an object wave but also a reference wave. Holographic imaging of nonlinear coherent light such as SHG [117, 118], CARS [119], SRS [120] and evanescent waves [121] has been performed. Holographic SHG imaging was used to visualize the 3D distribution of collagen in mouse tail dermis and epidermis [118]. CARS holography acquired a 3D image of polymeric beads with a single-shot exposure and no staining [119]. Time-resolved imaging of methane gas and its pressure were demonstrated with SRS holography [120]. Holographic imaging of evanescent waves was used to perform complex amplitude imaging of transparent objects such as water droplets and fused quartz plano-convex lens [121].

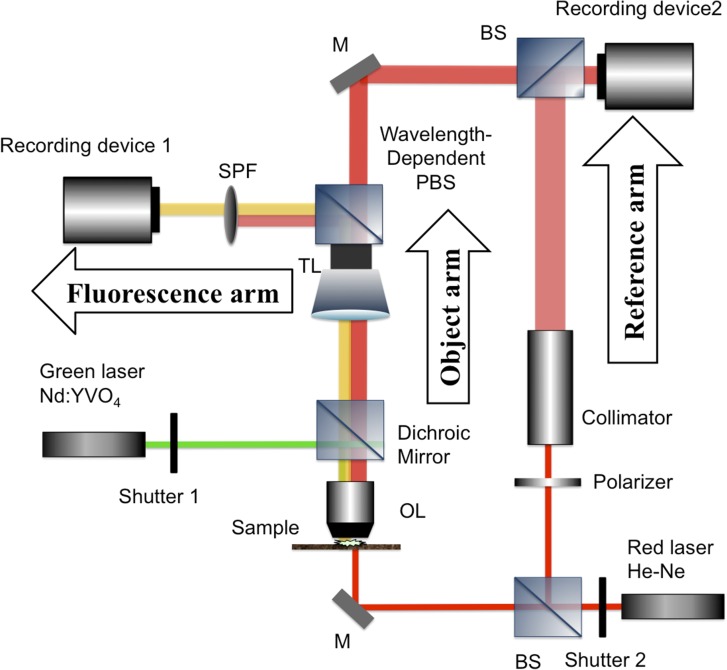
DH also has the ability to simultaneously record an interference fringe image and incoherent light, such as fluorescence and phosphorescence light [122, 123]. Fluorescence imaging in biology has proven valuable in detecting certain cells or cell components. In order to understand cell activities thoroughly, simultaneous detection of fluorescence and phase information from the same measuring object is desired. Several research groups have proposed single-shot implementations to record fluorescence light and quantitative phase images simultaneously [41, 122, 123]. Quan et al. [41] constructed a multimodal microscope that combines a conventional epifluorescence microscope and an off-axis digital holographic microscope. Figure 8 is a schematic diagram of multimodal DHM (MDHM), which is an implementation with two recording devices for recording a hologram and fluorescence light respectively. MDHM provides QPI and 2D fluorescence imaging. Recording device 1 in Fig. 8 only captures fluorescence light and recording device 2 only obtains an off-axis hologram. The recording devices are controlled by a computer for synchronization. Figure 9 is an example of a mouse brain slice recorded at the same time. From the 2D fluorescence image, neurons that expressed GFP were clearly imaged in Fig. 9a, while the boundary of white matter and grey matter was vague in the same image. From phase images in Fig. 9b and c, the boundaries were clearly imaged, as the white matter appeared darker due to the phase delay caused by the higher refractive index of lipid, compared to the surroundings of cells which are mainly composed of water.

Fig. 8.

A schematic diagram of multimodal digital holographic microscopy, which is an implementation for recording a hologram and fluorescence light simultaneously. The left part of the system is a conventional epifluorescence microscope, and the right part is off-axis DHM for QPI.

Fig. 9.

Part of a mouse brain slice measured in fluorescence and phase. (a) 2D fluorescence imaging of neurons. (b) 3D surface plot of phase. (c) Phase image in 2D, the boundaries between white and grey matters are indicated in dashed lines with arrows.

Image recovery for a defocused incoherent object image enables simultaneous 3D imaging of coherent and incoherent light without interference. The first method is to utilize PSF at each depth for the calculation of deconvolution [124, 125]. Second is COACH [107–110]. Structured illumination with multiple recording [126] and scanning in the depth direction [127] are also effective methods to visualize 3D images of coherent and incoherent light simultaneously. In particular, in Ref. [126], simultaneous depth-resolved 3D imaging of quantitative phase and fluorescence was performed by using structured illumination. Alternatively, a method of utilizing depth information obtained by DH was recently proposed by Quan et al. [128]. The method adopts MDHM and performs appropriate phase-compensation of the fluorescence image and numerical calculations of diffraction integrals with the obtained depth information in free space. Figure 10 shows an example of the recovery of defocused fluorescence images to demonstrate the simultaneous 3D imaging of coherent and incoherent light. Microbeads were immersed in water and freely moved. Figure 10a and b shows simultaneous recording of a 2D fluorescence image and a hologram by MDHM, respectively. As shown in Fig. 10c, the defocused fluorescence bead was successfully recovered. Phase images were also reconstructed as shown in Fig. 10d. From the results, both 3D fluorescence and phase imaging were realized.

Fig. 10.

Experimental results of obtaining a 3D fluorescence image from defocused one. (a) Recorded fluorescence image, (b) hologram, (c) fluorescence images recovered from (a) by the method of Ref. [128] and (d) reconstructed phase images.

Summary

In this review, we introduced digital holographic techniques, multidimensional imaging and its applications in holography, and recent progress in DH. DH has contributed to imaging science by performing quantitative phase, 3D intensity, motion picture and time-lapse imaging. DH can be applied to multidimensional imaging, complex amplitude 3D tomography, nonlinear holographic sensing and incoherent 3D imaging. Natural light, including fluorescence and spontaneous Raman scattering light can be recorded as a hologram, and lensless multicolor 3D motion-picture recording of incoherent light can be enabled by exploiting holographic techniques and improvements of electronic devices. DH with multidimensional imaging systems will extend the imaging ability to label-free living cells, transparent materials and dynamically changing phenomena.

Funding

Japan Science and Technology Agency (JST), PRESTO (Grant number JPMJPR16P8), Japan; Konica Minolta Science and Technology Foundation; Research Foundation for Opt-Science and Technology; The Nakajima Foundation; JSPS KAKENHI under (Grants 15H03580 and 16J05689), Japan.