Abstract
To date, reasons for the increase in liana abundance and biomass in the Neotropics are still unclear. One proposed hypothesis suggests that lianas, in comparison with trees, are more adaptable to drought conditions. Moreover, previous studies have assumed that lianas have a deeper root system, which provides access to deeper soil layers, thereby making them less susceptible to drought stress. The dual stable water isotope approach (δ18O and δ2H) enables below-ground vegetation competition for water to be studied. Based on the occurrence of a natural gradient in soil water isotopic signatures, with enriched signatures in shallow soil relative to deep soil, the origin of vegetation water sources can be derived. Our study was performed on canopy trees and lianas reaching canopy level in tropical forests of French Guiana. Our results show liana xylem water isotopic signatures to be enriched in heavy isotopes in comparison with those from trees, indicating differences in water source depths and a more superficial root activity for lianas during the dry season. This enables them to efficiently capture dry season precipitation. Our study does not support the liana deep root water extraction hypothesis. Additionally, we provide new insights into water competition between tropical canopy lianas and trees. Results suggest that this competition is mitigated during the dry season due to water resource partitioning.
Keywords: lianas, soil water competition, stable water isotopes, tropical forest, water resource partitioning
Introduction
The abundance of lianas (woody wines) has increased in the last three decades in Neotropical forest ecosystems (Phillips et al. 2002, Schnitzer and Bongers 2011). High liana abundance causes elevated tree mortality and reduced tree growth due to an increase in competition for light, nutrients and water (Ingwell et al. 2010, van der Heijden et al. 2015). Lianas therefore may play a key role in current tropical forest dynamics and functioning (Schnitzer et al. 2005). Increases in liana abundance have been shown to significantly reduce the carbon sequestration of tropical forests (van der Heijden et al. 2015), a biome that contributes 70% of the global gross forest carbon sink (Pan et al. 2011). However, further understanding of liana–tree competition for soil water is still needed to quantify and/or model the impact of lianas on tropical forests (Verbeeck and Kearsley 2016).
It has been proposed that lianas strongly compete with trees for the same below-ground water and nutrient resources (Schnitzer et al. 2005, Schnitzer and Bongers 2011). However, this hypothesis is mainly based on pot experiments or in situ liana removal studies where the removal of lianas resulted in an instantaneous increase of sap flow in the monitored trees (Schnitzer 2005, Toledo-Aceves and Swaine 2008, Alvarez-Cansino et al. 2015). Due to potential distinct competitive strategies between saplings and adult trees, and/or due to potential strong sap water influx in the soil released by the liana roots when cut, these studies might not represent actual in situ competition of adult lianas and trees (van der Sande et al. 2013). Moreover, it can be argued that the increase in sap flow from these previous studies were due to the elimination of light interception by liana leaves rather than a result of the alteration of below-ground water competition. It has also been hypothesized that lianas have an advantage over trees during dry season growth (Schnitzer 2005, Cai et al. 2009), the main tenant of this hypothesis being that lianas have a deeper rooting system compared with trees (Jackson et al. 1995, Schnitzer 2005). However, evidence to verify this deep root hypothesis is lacking due to the difficulty in undertaking large-scale excavation of lianas and tree root systems.
Stable isotope enrichment studies can provide indirect evidence for the depth of soil water extraction by vegetation, and the pioneering methodology devised by Ehleringer and Dawson (1992) on trees in a dry climate has now also been used in tropical regions (Romero-Saltos et al. 2005, Stahl et al. 2013). For lianas, Andrade et al. (2005) undertook a preliminary study that aimed to investigate the depth of soil-water uptake via the use of deuterium (δD, in this article referred to as δ2H). In addition to δ2H, oxygen stable isotopes (δ18O) can also help to unravel plant water sources (Zimmermann et al. 1967, Dawson and Ehleringer 1991, Dawson 1996, Hervé‐Fernández et al. 2016). The use of the combination of both δ18O and δ2H stable water isotopes has also been advocated by Stahl et al. (2013) and Evaristo et al. (2016) for resolving various ecohydrological questions related to the origin of extracted soil water. The depth of the source of the soil water can be estimated by taking into consideration that the isotopic composition of the extracted soil water for both δ18O and δ2H isotopes customarily varies with soil depth due to several environmentally driven processes, such as evaporative fractionation (Allison and Barnes 1983), infiltration rate (Dincer et al. 1974), isotopic seasonality in precipitation (temperature and volume effects) (Dansgaard 1964, Gat 2010) and prolonged drought events (Andrade et al. 2005). All of these processes contribute together to generate a specific dual isotopic profile of water in soils (Sprenger et al. 2016).
To date, the majority of studies characterizing partitioning of soil water resources undertaken in the tropics have adhered to the dual stable water isotope approach, rather than the single approach (the latter e.g., Jackson et al. 1995, Meinzer et al. 1999, Bonal et al. 2000). Single isotope studies form a small body of evidence for the conventional theory that lianas are able to tap deep sources of soil water at the beginning of the dry season. Andrade et al. (2005), who showed evidence for shallow soil water extraction by lianas, contradicted previous findings. In addition to this lack of consensus, the quality and interpretation of single isotope studies were recently questioned by Brooks et al. (2010), Stahl et al. (2013) and Evaristo et al. (2016), who instead advocated the use of dual isotope studies. The relative lack of observations about liana water uptake, and the arguments from these studies, inspired us to perform a new dual isotope study of water extraction by canopy-reaching lianas (henceforth indicated as ‘canopy lianas’).
The aim of our study is to verify whether tropical canopy lianas use deep water sources in the dry season. If so, this will provide evidence for the deep-rooted liana hypothesis. We applied the dual stable water isotope approach of Stahl et al. (2013) and Evaristo et al. (2016) in a tropical rainforest of French Guiana (Paracou site, 5°18′ N, 52°53′ W) and the differences in isotopic signature between canopy trees and canopy lianas during the dry season in two different edaphic habitats were examined. Our hypothesis is that in contrast to trees, most lianas are able to explore deep soil layers, which would be reflected in a more depleted isotopic signature in liana xylem water relative to that of trees. In Paracou, 105 canopy trees and 59 canopy lianas in two plots, located on different soil types, were analyzed. The study was performed in a clayey plot (terra firme forest sensu Baraloto et al. 2011) and a sandy plot (white sand forest sensu Baraloto et al. 2011), for which the speed of drought proliferation throughout the soil layers was expected to differ. The soil texture of sandy soils results in a higher percolation speed and a lower water holding capacity, which will accelerate soil layer drying. Additionally, these two distinct edaphic habitats were selected since edaphic habitat specialization might result in distinct ecophysiological and water competition strategies for tropical vegetation (Baltzer et al. 2005). Isotopic signatures of xylem water, precipitation, stream water and bulk soil water at multiple depths were compared. To our knowledge, this is the first study quantitatively investigating below-ground competition between canopy trees and canopy lianas in tropical forests.
Materials and methods
Site description
The field sampling campaign was conducted between 7 and 13 October 2015 (7th and 9th on sandy plots and 11th and 13th on clayey plots), within the lowland ‘terra firme’ rainforest of the Paracou Experimental Station (5°18′ N, 52°53′ W, French Guiana), located 12 km inland from the coast (Gourlet-Fleury et al. 2004). These forests are subject to mean annual rainfall and temperatures around 3000 mm and 26 ± 1.5 °C, respectively (Gourlet-Fleury et al. 2004). Due to the movement of the Intertropical Convergence Zone creating significant seasonal and inter-annual variations, French Guiana is characterized by two main climatic periods: a dry period (mid-August to mid-November) with monthly precipitation <100 mm, and a long wet period, which is regularly interrupted by a short drier period (March–April). Two additional datasets of rainfall isotopic signatures, retrieved from the Global Network of Isotopes in Precipitation (GNIP; IAEA/WMO; 2016; accessible at: http://www.iaea.org/water) were used in the analysis of our results. The first dataset describes long-term seasonal and monthly accumulated rainfall volumes (referred to as the ‘Cayenne data’) measured in Cayenne (~90 km away from our sampling site). The second dataset contains the seasonal pattern of the corresponding isotopic signature (δ18O and δ2H) as observed in Suzini (district located in Cayenne) for the monthly accumulated rainfall volumes in the year 1995 (referred to as ‘Cayenne 1995 data’; GNIP 2016). Due to their proximity to Paracou, the comparable meteorological conditions, height above sea level (a.s.l.) and similarity in position relative to the coast in comparison to the Paracou field station, both datasets were assumed appropriate for use in our study.
Plot selection
Two distinct edaphic habitats within the Paracou site were selected. The first habitat was located on top of a hill (40 m a.s.l.), hereafter referred to as the clayey plot. This is a terra firme forest (Baraloto et al. 2011) that is a nutrient poor acrisol (FAO-ISRIC 1998) and mainly characterized by a high clay content (43.2%) and a high sand content (47.8%). The second habitat was very nutrient poor, hereafter referred to as the sandy plot (located 10 m a.s.l.). This is a white sand forest (Baraloto et al. 2011) on a white sandy ultisol (FAO-ISRIC 1998), with clay and sand contents of 25.8% and 64.6%, respectively. Both plots lie in the close vicinity of the Guyaflux flux tower footprint (Bonal et al. 2008), potentially representative for the tropical rainforest in the coastal plains of French Guiana. Since both edaphic habitats are very close to each other (<1 km), meteorological conditions were considered similar. However, soil water-holding capacity, and thus the impact of the dry season on soil moisture, was expected to differ. Moreover, considering greater pore size and lower water holding capacity in the sandy soil, it was expected that drought would proliferate more strongly throughout the soil layers of the sandy habitat. Plot selection within each edaphic habitat was driven by the presence of climbable canopy trees containing multiple lianas in the canopy layer, or from which lianas could be sampled.
Sampling setup
Within each edaphic habitat (~1 ha) soil cores were sampled at eight depths (0.1, 0.2, 0.3, 0.45, 0.6, 0.9, 1.2 and 1.8 m) in close proximitry (<2 m) to the selected trees using a soil auger. A total of six soil cores per edaphic habitat were collected. It is important to note that groundwater was reached in the sandy soils below 1 m, which influences the isotopic profile of soil water. Since small catchment areas are considered in our dry season study, we assume that the isotopic composition of the stream is a proxy for ground water isotopic signature (Kendall and Coplen 2001). Although one precipitation event occurred (16.8 mm on 8 October; see Figure S1 available as Supplementary Data at Tree Physiology Online) between two sample collection days, no significant difference in the measured isotopic signatures of canopy lianas, trees and soil were observed before and after the rainfall event.
Within a perimeter of 20 m from the soil cores, xylem samples from trees and lianas were collected. Only mature canopy trees in full leaf-on conditions, with a minimum diameter of 10 cm, and lignified canopy-reaching lianas in full leaf-on conditions (diameter >2 cm at 1.3 m from the last rooting point), both independent of species, were considered for sampling. Tree xylem samples were collected using an increment borer (5 mm diameter) at breast height (±1.3 m), resulting in wooden cylinders from which the bark was removed. Coring was performed oblique to the trunk to maximize xylem sampling. Since coring of lianas was not feasible, in situ lignified liana branches were collected using a pruner (average height of sampling was 12.2 ± 7.0 m). Subsequently, a straight internodal branch part of ~5 cm was subsampled by removing both distal branch ends and the bark tissue using a knife. The remaining branch part represents only sapwood tissue of the liana. Isotopic signatures are assumed not to vary between stems and branches within one individual tree or liana due to the absence of fractionation throughout lignified plant tissues (Zimmermann et al. 1967, Brooks et al. 2010, Hervé‐Fernández et al. 2016, De Wispelaere et al. 2016).
Additionally, water from two nearby streams (300 m from the sampled plots) was sampled and precipitation water was collected via an evaporation-free sampler in an open field (bulk precipitation) and below the canopy (throughfall precipitation).
Sample processing and isotope analysis
Upon collection, samples were placed in pre-weighed glass vials and sealed with caps to avoid loss of water prior to cryogenic vacuum distillation (CVD). All fresh samples were weighed, transported in a cooler and frozen (−5 to −10°C) before CVD.
Water was extracted from all samples by CVD (4 h at 105 °C). For clayey soil samples, the isotope results strongly depend on the extraction conditions under low soil moisture conditions (<30%) (Orlowski et al. 2013, Oerter et al. 2014). Under these conditions, a combination of longer extraction times (>180 min), higher extraction temperatures (>90 °C) and lower pressure (<0.3 Pa) are needed to achieve reliable results (Orlowski et al. 2013). Water recovery rates were calculated by weighing the extracted samples, oven drying (48 h at 105 °C) and re-weighing. Whenever weight loss as a result of the extraction process was less than 98%, the sample was considered erroneous and thus removed from further analysis (Araguás‐Araguás et al. 1998). Sample isotopic signatures were measured by Wavelength Scan-Cavity Ringdown Spectrometer (WS-CRDS, L2120-i, Picarro, California, USA) coupled with a vaporizing module (A0211 high-precision vaporizer) through a micro combustion module to remove possible organic contamination (Martin-Gomez et al. 2015, Evaristo et al. 2016). Internal laboratory references were used for calibration of the measured samples. Each sample was measured eight times, of which only the last four measurements were considered for the estimation of the final isotopic signature and standard deviation of the analyzed sample. The ±1σ measurement uncertainty of the WS-CRDS was ±0.2‰ and ±1.0‰ for δ18O and δ2H, respectively.
Isotopic composition, expressed in terms of [18O]/[16O] and [2H]/[1H] ratios, is represented by δ-values (Eq. (1)), which indicate the deviation from a designated standard (i.e., V-SMOW, Vienna Standard Mean Ocean Water) in parts per thousand (‰), as
| (1) |
where R is the heavy to light isotope ratio measured in the sample or standard, respectively.
Data analysis and statistics
Calculations of the local meteoric water lines
The empiric relationship between δ18O and δ2H in rainwater typically results in a stable water isotope scatter around a geographically biased (due to meteorological conditions) regression line, i.e., the local meteoric water line (LMWL), which forms the baseline for the study area. Variation of individual isotopic signatures along the LMWL can, among others, originate from seasonality (i.e., differing temperature and rainfall amounts) in the isotopic signature of precipitation (Dansgaard 1964), while deviation from the LMWL can be attributed to inner forest circulation processes and evaporation conditions. The latter results in kinetic isotopic fractionation, which shows higher susceptibility of isotopically lighter molecules in comparison with isotopically heavier ones (for this study: water molecules containing 18O and/or 2H). This phenomenon is known as the Graham’s law of effusion. As a consequence, evaporated water will experience a signature shift diverging away from the LMWL during progressing kinetic isotopic fractionation. To obtain the function of the LMWL of Paracou, a reduced major axis regression (as in Crawford et al. 2014) was performed using the collected bulk precipitation data during the measurement period (September–October) at the Paracou flux tower station (Paracou LMWL: δ2H = 6.21 δ18O + 10.18). A similar approach was used to construct the LMWL of Cayenne based on long-term precipitation data in Cayenne (capital of French Guiana; GNIP 2016; Cayenne LMWL: δ2H = 6.15 δ18O + 4.95).
Evaporation line
Aiming to follow and describe the covariation between δ18O and δ2H of residual soil water caused by evaporation, the soil evaporation line of our study system needed to be obtained (Levia et al. 2011). However, when the atmosphere is mostly saturated (i.e., relative humidity (RH) ≈ 100%), a clear evaporation line is very close to that of the LMWL. Hence, using meteorological data and precipitation isotope signatures (Cayenne data; GNIP 2016), the slope of the local soil evaporation line (resulting SEL = 2.769), i.e., mainly driven by equilibrium fractionation, was derived using the Craig and Gordon model following Gibson et al. (2008):
| (2) |
where δA and δP are the isotopic signatures for δ18O and δ2H (‰, but for the formula provided in decimal notation) (in the denominator and numerator, respectively) of atmospheric moisture and precipitation, respectively; h represents the relative humidity (%, for the formula provided in decimal notation) corrected by the evaporating surface temperature; α+ is the liquid–vapor isotopic fractionation under equilibrium conditions as will be discussed below and ∆ε is the equivalent kinetic isotopic separation based on wind tunnel experiments (Merlivat 1978).
| (3) |
where is 25.0‰ and 28.6‰ for δ18O for and δ2H, respectively; n = 1, which is generally assumed when considering soil water (Gibson et al. 2008); and θ, being the advection term making account for the potential influence of humidity buildup, is usually considered θ ≈ 1 (Gat 1996).
Considering the precipitation-equilibrium assumption, the values for δA could be determined to conform to Gibson et al. (2008), where
| (4) |
With α+, the liquid–vapor isotopic fractionation (α+ > 1) under equilibrium conditions based on the empirical relations described by Horita and Wesolowski (1994):
| (5) |
and
| (6) |
With ε+ being the isotopic enrichment under equilibrium conditions between liquid and vapor, the latter variable is therefore calculated as:
| (7) |
Seasonality of precipitation source: LMWL intersection
As precipitation is considered to occur in equilibrium (RH ≈ 100%), it is therefore sensitive to changes in temperature. In this sense, it is shown that the precipitation signature can be related to the season in which precipitation occurs (Evaristo et al. 2015, Hervé‐Fernández et al. 2016). Since LMWL represents meteoric water inputs to the catchment, δ18OLMWLi and δ2HLMWLi (to be read as the stable isotope LMWL intersection) were calculated in order to trace the isotopic signature of the precipitation source for the water compartments measured in this study (i.e., bulk soil and xylem water). Each measured xylem and soil isotopic signature was projected upon the LMWL along the SEL line trajectory. This acquired variable therefore represents the precipitation source for each of the measured water compartments (Evaristo et al. 2015), preceding evaporative fractionation, i.e., the source of water origin. Calculations were made following Hervé‐Fernández et al. (2016) (Eq. (8) and (9)).
| (8) |
| (9) |
Water mobility range
A hypothetical approach to help understand below-ground water competition is to calculate the water mobility ranges of the vegetation root system. This is defined by the distance between the initial water source (the LMWL intersection), i.e., before being subjected to evaporative fractionation, and the measured isotopic water signature (in ‰), i.e., being subjected to evaporation (Eq. (10)). Hence, the distance between a specific measured isotopic signature and its LMWL intersection, measured along the line trajectory defined by the slope of the soil evaporation line (SEL), is a proxy for the severity of evaporative fractionation. A longer distance hypothetically corresponds to a larger loss of water by evaporation processes. However, drying of the soil by evapotranspiration loss corresponds to a higher likelihood that the remaining water is retracted to smaller pores and is hypothesized to be strongly bound to soil texture (Brooks et al. 2010, McDonnell 2014, Hervé‐Fernández et al. 2016, Zhang et al. 2016). When the higher physical effort required to extract these remaining water resources is taken into account, the variance range of the calculated distances per growth form (see Eq. (10)) can be considered as a proxy of a vegetation-specific water available range and the physical limits of extraction of more bound water. The range of vegetation variability, i.e., the assembly of all calculated ranges per vegetation type, is then considered as the water mobility range.
| (10) |
Statistics
All statistical analyses were performed using R and RStudio (version 3.3.3, Boston, MA, USA). Since data were non-normally distributed (Shapiro–Wilkinson normality test, P < 0.05), Kruskal–Wallis non-parametric statistical testing with Dunn’s post hoc analysis (henceforth indicated as Kruskal–Wallis test) was undertaken to study potential differences in median values among the sample groups. Data are provided in interquartile ranges (IQR). Due to its robustness against deviations from normality, the Fligner–Killeen test was selected to study the homogeneity of variances between sampled groups, i.e., in scope of studying the water mobility range (Conover et al. 1981). Unless otherwise stated, statistical significance was set to 0.05.
Results
Different signatures for lianas versus trees
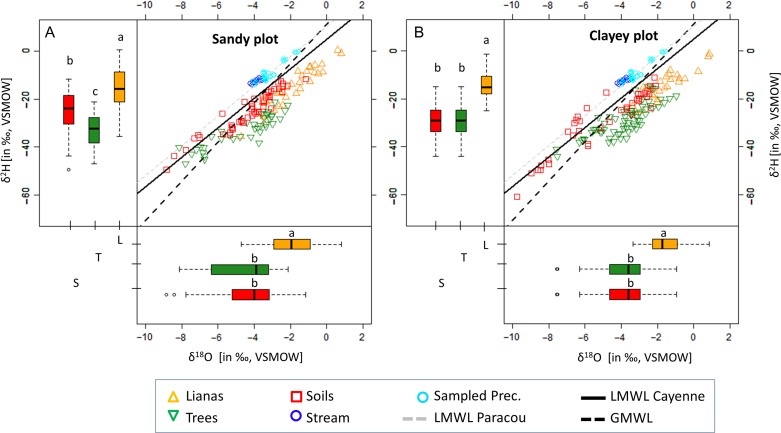
For both the sandy and clayey plot, the dual isotopic signature of all analyzed samples, i.e., xylem water, bulk soil water, stream and precipitation (for IQR and corresponding sample sizes see Table 1) were plotted along the Paracou and Cayenne LMWL (Figure 1). Since the LMWL of Cayenne is parallel to the LMWL of Paracou, but covers a longer measurement period and hence includes seasonality in the isotopic signature, the LMWL of Cayenne was used as the reference in this study as it is a more complete and reliable representation of the LMWL at Paracou (Kendall and Coplen 2001). Xylem water and bulk soil isotopic signatures are distributed extensively along the LMWL of Cayenne, suggesting that evaporation from the soil occured under or near equilibrium conditions, i.e., saturated environmental conditions (RH ≈ 100%) in both plots. Hence, the typical expected trend of the soil evaporation line, defined by the distribution of soil samples, deviated away from the LMWL due to an absence of mass-dependent effects (see Gat 2010 and Clark 2015). In the sandy and clayey plots, water xylem signatures of lianas were significantly enriched (P < 0.01, Kruskal–Wallis test) in comparison with those of trees (Table 1), which tap significantly depleted water sources (P < 0.01, Kruskal–Wallis test).
Table 1.
Interquartile ranges (IQR 25–75%) for measured δ18O and δ2H (in ‰,VSMOW) values, and for the derived LMWL intersections (δ18OLMWLi and δ2HLMWLi), given for all sample types in both plots (sandy and clayey plots). Precip contains both measured bulk precipitation as through-fall. Different letters per column represent statistical differences (non-parametric Kruskal–Wallis test with Dunn post hoc analysis, P < 0.05) between sample types with χ2 being the chi-squared value.
| Sandy plot | Clayey plot | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | δ18O | δ2H | δ18OLMWLi | δ2HLMWLi | n | δ18O | δ2H | δ18OLMWLi | δ2HLMWLi | |
| ‰ | ‰ | ‰ | ‰ | ‰ | ‰ | ‰ | ‰ | |||
| Lianas | 33 | [−2.91, −0.91]a | [−21.19, −8.68]a | [−5.34, −3.40]ab | [−27.90, −15.93]ab | 26 | [−2.27, −1.01]a | [−17.79, −10.87]a | [−4.94, −3.72]ab | [−25.39, −17.93]ab |
| Trees | 38 | [−6.21, −3.25]b | [−37.95, −27.84]b | [−8.06, −6.85]c | [−44.60, −37.15]c | 67 | [−4.65, −2.96]bc | [−33.81, −24.87]b | [−7.70, −6.27]c | [−42.41, −33.58]c |
| Soils | 48 | [−5.19, −3.18]b | [−30.21, −18.59]c | [−6.41, −4.26]bc | [−34.44, −21.25]bc | 38 | [−6.56, −3.02]b | [−35.02, −19.48]b | [−6.78, −4.88]b | [−36.71, −25.05]b |
| Stream | 18 | [−3.44, −2.39]b | [−11.78, −3.74]ad | [−3.07, −1.89]ad | [−13.91, −6.70]ad | 18 | [−3.44, −2.39]b | [−11.78, −3.74]a | [−3.07, −1.89]ad | [−13.91, −6.70]ad |
| Precip | 29 | [−3.98, −3.73]a | [−13.16, −12.07]d | [−3.46, −3.25]d | [−16.33, −15.01]d | 29 | [−3.98, −3.73]c | [−13.16, −12.07]a | [−3.46, −3.25]d | [−16.33, −15.01]d |
| χ2 | 60.29 | 109.34 | 117.87 | 117.87 | 56.2 | 118.79 | 122.39 | 122.39 | ||
Figure 1.
Dual stable water isotope signatures (δ18O and δ2H; in ‰, VSMOW) for both the sandy plot (A) and the clayey plot (B). The stable water isotopic signature is shown for canopy lianas (xylem water; orange triangles), trees (xylem water; inverted green triangles), bulk soil water (red squares), precipitation (through-fall + bulk; cyan circles) and stream (blue circles) samples. The local meteoric water line (LMWL) of both Paracou (gray dotted line, δ2H = 6.209 δ18O + 10.176) and Cayenne (black solid line, δ2H = 6.148 δ18O + 4.951) are depicted, as well as the global meteoric water line (GMWL; black dotted line, δ2H = 8.2 δ18O + 11.3; Rozanski et al. 1993). Vertical and horizontal boxplots display the δ2H and δ18O signatures (in ‰, VSMOW), respectively, for canopy liana xylem water (L, orange), tree xylem water (T, green) and bulk soil water (S, red). Boxplots show Q25 − 1.5 IQR, Q25, Q50, Q75 and Q75 + 1.5 IQR values. Outliers are shown by open circles. Statistical differences are indicated by different letters (non-parametric Kruskal–Wallis test with Dunn post hoc analyses, P < 0.05).
Seasonality of the isotopic signature of precipitation
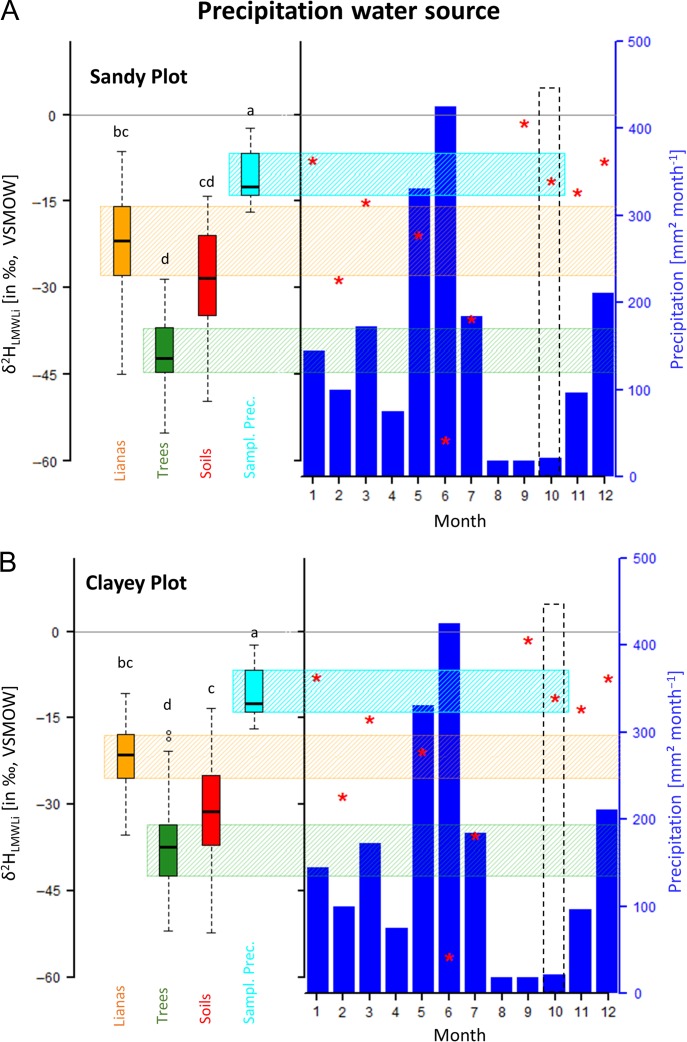
In both plots, the LMWL intersections of xylem water (δ18OLMWLi and δ2HLMWLi; Figure 2) of lianas and trees differed significantly (P < 0.05, Kruskal–Wallis test; see Table 1). Compared with trees, canopy lianas display enriched LMWL intersection signatures more or less in line with signatures measured in precipitation samples corresponding to the dry season (Table 1). On the other hand, LMWL intersections of the xylem isotopic signatures for trees are significantly depleted (P < 0.05, Kruskal–Wallis test). δ18OLMWLi and δ2HLMWLi of both canopy lianas and trees, representing the precipitation source water taken up by these vegetation types, can be linked with the seasonal trend of the isotopic signature in local precipitation. This phenomenon, described by Dansgaard (1964) and Gat (1996) as the ‘amount effect’ and ‘temperature effect’, respectively, dictates that depleted signatures correspond to high rainfall amounts or colder temperatures during precipitation, i.e., wet season precipitation, while enriched signatures are found in low precipitation volumes and/or higher temperatures during precipitation, usually found during the dry season (i.e., evaporated) (Gaines et al. 2016). In terms of soil water retention, it can be hypothesized that deeper soil water represents depleted wet season rainfall, while recent dry season rainfall events and evaporative fractionation influence enrichment of the surface soil water. Moreover, the difference is that δ18OLMWLi and δ2HLMWLi can not only be related to seasonality, they can also indirectly provide insight to water extraction depth.
Figure 2.
Boxplot panels showing the LMWL intersection signatures (δ2HLMWLi, ‰, in VSMOW) for both plots (sandy plot and clayey plot) derived from the measured canopy liana xylem water (orange), tree xylem water (green), bulk soil water (red), and bulk and through-fall precipitation (Sampl. Prec., cyan) sampled in Paracou. Boxplots show Q25 – 1.5 IQR, Q25, Q50, Q75 and Q75 + 1.5 IQR values. Outliers are shown by open circles. Different letters represent statistical differences (non-parametric Kruskal–Wallis test with Dunn post hoc analyze, P < 0.05). The bar plot panels show monthly precipitation amounts (blue bars, mm2 month–1) with the corresponding δ2HLMWLi bulk precipitation signatures (red asterisk, in ‰, VSMOW) observed in the Cayenne 1995 dataset. Cyan, orange and green shaded vertical strips represent the interquartile range (IQR, see Table 1) of the derived δ2HLMWLi (in ‰, VSMOW) signatures of the sampled precipitation (cyan), canopy lianas (orange) and trees (green). Black dotted square indicates the corresponding month of sample collection, i.e., in October 2015.
The measured monthly mean δ2H values from historical precipitation samples (Cayenne 1995 dataset) during the sampling period (September–October) were recorded within the interquartile range (IQR, Figure 2 cyan shaded box) of the precipitation δ2HLMWLi values sampled in Paracou. This finding justifies using the Cayenne 1995 dataset in this analysis. Additionally, it was observed that the δ2HLMWLi liana xylem signatures in both plots (Figure 2) correspond aproximately to the δ2H values from historical precipitation samples (Cayenne 1995 dataset) measured in the dry season (September–October) in Cayenne. Identical correspondences were also found for the δ18OLMWLi signatures (data not shown). However, xylem water isotopic signatures derived from the sampled trees were significantly (P < 0.05, Kruskal–Wallis test) depleted in comparison with the Cayenne 1995 dataset precipitation signature from September–October. Intriguingly, the signatures of the trees correspond to the wet season precipitation isotopic signatures in the Cayenne 1995 dataset (May–July, Figure 2), whilst signatures for lianas correspond to the dry season rainfall signature.
Isotope signatures along a soil depth profile
Both δ18O and δ2H in the bulk soil water show a clear isotopic depletion with depth (Figure 3). In the sandy plots (Figure 3A and B), due to the influence of groundwater, this isotopic depletion with depth disappears below 1 m. Groundwater enriched the isotopic signature by ~1‰ for δ18O and 8‰ for δ2H. In theory, the xylem signatures of plants should fall within the measured bulk soil water range of the studied system. However, measured xylem water isotopic signatures of many of the observed lianas (in both plots and for both stable water isotopes) extended beyond the measured bulk soil water range, displaying enriched isotope signatures. According to previous studies (Zimmermann et al. 1967, Allison 1998, Gazis and Feng 2004, Gat 2010), despite the investigations primarily describing dry ecosystems, an exponential isotopic signature trend might be expected in the upper soil layers due to strong evaporative fractionation (Allison 1988). Since no samples were taken above 0.1 m depth, such a trend is not identified by our sampled depths. Nonetheless, the observed enriched liana signatures likely represent bulk soil water signatures within the upper 0.1 m soil layer.
Figure 3.
Boxplot chart with (A and C) δ2H (in ‰, VSMOW) and (B and D) δ18O (in ‰, VSMOW) for the sampled xylem water of canopy lianas (orange), trees (green) and the bulk soil water samples at various depths (gray), derived from both the sandy (A and B) and clayey (C and D) plots. Orange and green shaded rectangles illustrate the interquartile range (IQR) of xylem water values for canopy lianas and trees, respectively. Boxplots show Q25 – 1.5 IQR, Q25, Q50, Q75 and Q75 + 1.5 IQR values. Outliers are shown by open circles. Statistical differences are indicated by different letters (non-parametric Kruskal–Wallis test with Dunn post hoc analyses, P < 0.05).
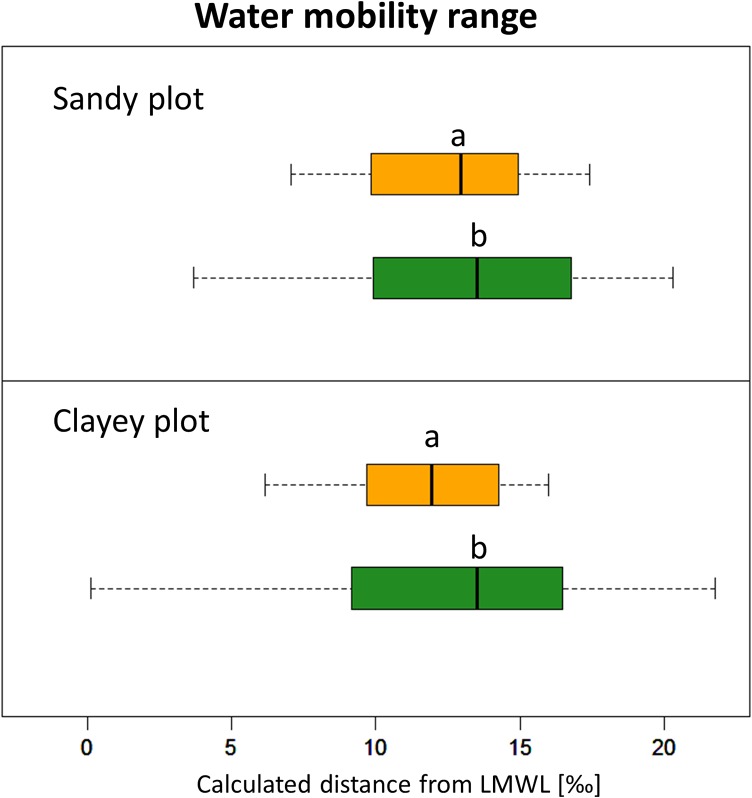
Conceptual water mobility range characterization
The resulting calculated distance from the LMWL, i.e., the water mobility range, for both the xylem water isotopic signatures of lianas and trees are displayed for both plots in Figure 4. A small but statistically significant difference between lianas and trees (P < 0.05, Kruskal–Wallis test) in median calculated distance (the water mobility range) is found for both plots. Notably, a significantly higher water mobility range variance for trees in comparison with canopy lianas is identified (P < 0.05, Fligner–Killeen).
Figure 4.
Water mobility range, i.e., the distance to the LMWL (in ‰), for canopy lianas (orange) and trees (green) within the clayey and sandy plots. The median value represents the isotopic signature of the fractionated water taken up by both vegetation types, with higher values representing more fractionated and less mobile water. Significant differences in the median values are shown by different letters per plot (non-parametric Kruskal–Wallis with Dunn post hoc, P < 0.05). The specific ranges, the within vegetation variance, is a proxy of the ability of the vegetation type to retrieve water found in smaller soil pores, i.e., being less mobile. Variance ranges are significantly larger for trees in both plots (non-normal Fligner–Killeen test; clayey plot: median of χ2 = 4.7467, df = 1, P < 0.05; sandy plot: median of χ2 = 8.3386, df = 1, P < 0.01).
Discussion
Different signatures for lianas versus trees
Xylem water isotopic measurements displayed significant differences between canopy lianas and trees, both in the measured isotopic signatures and in the isotopic signatures of the LMWL intersections (δ18OLMWLi and δ2HLMWLi). Canopy lianas and trees thus accessed distinct precipitation water sources at the time of sampling, with depth of water uptake and seasonal replenishment of these precipitation water sources differing. Despite carefully undertaking stem coring to only sample sapwood, it is possible that some traces of hardwood were contained in the samples, thus accounting for one of the uncertainties in the observed isotopic signals. Parenchyma cells within the hardwood tissue indeed store water that might, in contrast to water in sapwood, not fully represent the immediate water fluxes throughout the plant. Additionally note that, to the best of our knowledge, the potential occurrence of root system dimorphism and whether or not this is a more general trait for lianas than for trees has never been studied. Further research on this topic is greatly needed and should be considered in view of the presented findings.
Seasonality in water use of trees and lianas
The δ2HLMWLi of liana xylem water, having a close correspondence with the historical precipitation isotopic signatures of the Cayenne 1995 dataset (Figure 2), indicates that sampled canopy lianas are seemingly able to access dry season precipitation. The occurrence of the historical precipitation signature being close to, but not encompassed by, the IQR of the δ2HLMWLi of the lianas indicates a marginal contribution of depleted soil water found in deeper soil layers. In consideration of the time-dependent infiltration capacity of dry season rainfall, resulting in infiltration only into shallow soil layers and litter decomposition layers (see Figure S1 available as Supplementary Data at Tree Physiology Online) before complete evaporation loss, these findings suggest that lianas take up water mainly from superficial soil layers.
In strong contrast to our observations for canopy lianas, xylem samples from trees show depleted δ2HLMWLi ranges when compared with the Cayenne 1995 dataset precipitation signature in the sampling period of September–October (Figure 2). For trees, the δ2HLMWLi resembles the depleted precipitation isotopic signature collected during the wet season, suggesting that sampled trees mainly depend on wet season replenishment of their tapped soil water compartments. These depleted water resources typically originate from wet season rainfall that has infiltrated to deeper soil layers (Brooks et al. 2010, Gaines et al. 2016, Hervé‐Fernández et al. 2016, De Wispelaere et al. 2016).
Isotope signatures along a soil depth profile
The presented isotopic soil gradient (Figure 2) in relation to depleted δ18O and δ2H of xylem water from canopy lianas support the idea of an active shallow root system strategy in both edaphic habitats. Moreover, the liana isotopic signatures are significantly enriched in comparison with the measured bulk soil water range, suggesting that liana root activity may be assigned to the upper 10 cm soil layer. However, this statement needs to be verified by future investigations, which should consider sampling the upper soil layer in more detail. Our data do not allow definitive rejection of the alternative hypothesis that very deep soil water beyond a depth of 1.8 m (the deepest depth we reached) is significantly enriched and accessed by lianas as a water source. Root excavation or the examination of deeper soil samples in future investigations should resolve this uncertainty.
It is possible to hypothesize that since nutrients are mainly located in the upper soil layers (Jobbagy and Jackson 2001, Quesada et al. 2011), a strategy of localizing root activity and colonization in these relatively nutrient-rich layers is of essential importance in nutrient poor ecosystems, such as the very weathered soils of tropical biomes (Grau et al. 2017). Hence, this strategy might provide lianas an advantage over trees in the context of nutrient competition. The ability of lianas to adopt this strategy is consistent with their preference of not investing much energy into structural support roots and facilitating the growth of finer roots in contrast to trees (Putz 1991, Collins et al. 2016). In addition, the physiological capability of lianas to alter their internal water potential gradient enables them to secure their water uptake capacity in the upper soil layers under more demanding conditions (De Guzman et al. 2016, Maréchaux et al. 2017). However, greater seasonal osmotic adjustments and/or overall hydraulic trait plasticity does not necessarily imply increased tolerance to long-term droughts (Binks et al. 2016). In the context of short drought events and seasonal variations in soil moisture, these traits help to broaden the ecohydrological comfort zone of lianas, resulting in a competitive advantage for nutrient acquisition over trees in the upper soil layers.
In contrast, the isotopic soil gradient analysis (Figure 3) allocates the depleted isotopic signatures found in trees to the deeper soil layers in both edaphic habitats. Moreover, trees seemingly rely on deeper bulk soil water resources during dry season conditions, thus they are relying on deep roots, a phenomenon that can be considered as a drought avoidance strategy. The absence of active shallow root systems and importance of deep root activity of the sampled trees corborates with the study of Stahl et al. (2013) where more than 98% of the measured trees showed water uptake below 0.4 m.
During seasonally dry periods therefore, canopy lianas and trees show water resource partitioning by extracting water from distinct soil layers. This indicates that during the studied period, canopy lianas and trees had only limited competition for the same water sources (Walter 1939, Ehleringer et al. 1991, Ward et al. 2013), a finding that contradicts previous liana studies undertaken in the tropics (Jackson et al. 1995, Schnitzer 2005).
Mobility of water sources
Our conceptual approach defines distinct overall extractable ranges for both the sampled liana and tree communities in two contrasting habitats, with trees showing longer calculated distances from the LMWL before water uptake by the root system. Additionally, the variance of water mobility ranges of both life-forms appears to differ, with trees showing broader extractable ranges. This is a novel finding, and to our knowledge our study is the first to assess this in the tropics. These results may imply that trees are able to successfully access water retained in the smaller soil pores compared with lianas. Thus, trees can access water sources that are more strongly bound to the soil particles and correspond to higher static to labile water ratios. The results of this approach corroborate the findings of Collins et al. (2016), where roots from trees showed higher mycorrhizal colonization than those of lianas. Since mycorrhizal hyphae networks are able to explore water in smaller soil pores than root hairs, higher mycorrhizal colonization extends the physical range of extractable bulk soil water. This advantage could explain the large repartition for trees rather than for lianas across environmental gradients.
Potential underlying mechanisms
Our data, in combination with previous investigations, will assist in disentangling the potential driving force of water resource participation between lianas and trees during the dry season. Our hypothesis is that gradients in soil water potential (Ψsoil) may be considered as the driving factor in below-ground water competition between lianas and trees, which may explain differences in depth of water extraction during the dry and wet season. During the onset of the dry season, a relocation of root activity in trees might be expected as Ψsoil becomes more negative as the upper soil layer dries out (Stahl et al. 2013). This will result in the activity of tree roots literally being pushed to deeper soil layers where Ψsoil values are still less negative due to the presence of non-exhausted water reserves, which were replenished during the wet season. The ability of lianas to remain active in upper soil layers and to efficiently exploit the small rainfall input (see Figure S1 available as Supplementary Data at Tree Physiology Online) can potentially be attributed to the following reasons: (i) lianas are able to actively lower their osmotic potential to ensure the maintenance of a functional water potential gradient within the liana (De Guzman et al. 2016, Maréchaux et al. 2017); and (ii) lianas may be able to form hydraulic bridges by-passing embolized large vessels and ensuring an intact water column by their ability to anatomically adapt bimodal distribution of vessel diameter (i.e., vessel dimorphism) (Bastos et al. 2016). The strategy of maintaining an active upper root system might be very beneficial for lianas as this allows them to have a competitive advantage not only for water, but also a strong advantage for accessing nutrients in the upper soil layers, which may account for the dry season growth advantage of lianas as previously noted (Schnitzer 2005, Cai et al. 2009). In contrast, the wet season imposes high water availability and relatively similar bulk Ψsoil throughout all soil layers in a tropical forest. Under these specific conditions, the active part of tree root systems is designated to the upper soil layers (Sun et al. 2011), where nutrient availability is considered highest in tropical forests (Jobbagy and Jackson 2001, Quesada et al. 2011). This might imply that during the wet season, lianas and trees access the same soil water resources as the roots of both growth forms will exploit the nutrient-rich shallow soil layers. However, this hypothesis would need to be tested in year-round observational studies.
Conclusion
This study provides evidence that in tropical rainforests subjected to seasonal variations in soil water content, lianas and trees display clear water resource partitioning during the dry season. Additionally, rather than relying on deep roots for deep water access, as is generally accepted for lianas, our results show the opposite: lianas maintain an active root system in shallow soil layers during the dry season. This strategy was identified for both edaphic habitats, indictating avoidance of direct below-ground water competition with trees, and ensuring active exploitation of the nutrient-rich upper soil layers. Hence, lianas may be able to quickly and efficiently take up the small amount of dry season precipitation, but they may require stronger drought tolerance strategies. In contrast, our results show that trees relocate their root system activity to deeper and less dry soil layers. Such an water resource participation strategy provides favorable conditions for lianas that may promote their dry season growth advantage, as described by Schnitzer (2005) and Cai et al. (2009). Further research is needed (i) to assess whether lianas can maintain this competitive advantage during prolonged and/or repetitive drought events; (ii) to determine whether lianas and trees compete for the same water resources during the wet season; and (iii) to examine root profiles of both trees and lianas.
Supplementary Material
Acknowledgments
For all their highly appreciated efforts in the process of data collection, the authors like to thank E. Kearsley, N. Pausenberger, J. Roels, B. Leudet and J.Y. Goret. We would like to thank K. van Nieuland, S. Vandevoorde, M. Bauters, L. De Wispelaere, S. Bodé and H.R. Upadhayay for laboratory and analytical assistance. The authors also like to express their gratitude to various researchers who have provided feedback on analytical and interpretative aspects of the study. In this respect we thank J. Wright, S. Schnitzer, G. van der Heijden, J. McDonnell, F. Bongers, M. Combe and S. Moorthy Krishna Moorthy Parvathi. Additionally, we are thankful to J.F. Corr for English editing. Also, P.H.-F. would like to thank M. Aigner from the International Atomic Energy Agency (IAEA) for training in the cryogenic distillation method. Data can be made available to all interested researchers upon request.
Supplementary Data
Supplementary Data for this article are available at Tree Physiology Online.
Conflict of interest
The authors declare no conflicts of interest.
Funding
This research was funded by the European Research Council Starting Grant 637643 (TREECLIMBERS) and benefitted from an “Investissement d’Avenir” grant of the Agence Nationale de la Recherche (Centre d’étude de la biodiversité amazonienne - CEBA: ANR-10-LABX-25-01). The study was conducted at the Guyaflux site, which belongs to the SOERE F-ORE-T and which is supported annually by Ecofor, Allenvi and the French National Research Infrastructure ANAEE-F. Pedro Hervé-Fernández is funded by Programa de Formación de Personal Avanzado CONICYT, BECAS CHILE, by the Commissie Wetenschappelijk Onderzoek (CWO) and by the Bijzonder Onderzoeksfonds (BOF) of Ghent University.
Authors' contributions
H.V. supervised the research. H.D.D., P.H.-F., H.V., D.B. and C.S. designed the study. H.D.D. collected the samples and data during the field campaign. P.P., C.S. and B.H. performed species determination. B.B. provided technical support in the field. H.D.D. and P.H.-F. performed processing and analysis of the samples. Results were interpreted by H.D.D., P.H.-F., H.V., D.B. and P.B. All authors contributed to the text of the manuscript.
References
- Allison GB. (1988) A review of some of the physical, chemical and isotopic techniques available for estimating groundwater recharge In: Simmers I (ed). Estimation of natural groundwater recharge. Springer Netherlands, Dordrecht, pp 49–72. [Google Scholar]
- Allison GB. (1998) Stable isotopes in soil and water studies. In: Causse, C, Gasse F (ed) Colloques et Seminaires. Hydrology and isotope geochemistry. pp 23–38. France: Orstom editions
- Allison GB, Barnes CJ (1983) Estimation of evaporation from non-vegetated surfaces using natural deuterium. Nature 301:143–145. [Google Scholar]
- Alvarez-Cansino L, Schnitzer SA, Reid JP, Powers JS (2015) Liana competition with tropical trees varies seasonally but not with tree species identity. Ecology 96:39–45. [DOI] [PubMed] [Google Scholar]
- Andrade JL, Meinzer FC, Goldstein G, Schnitzer SA (2005) Water uptake and transport in lianas and co-occurring trees of a seasonally dry tropical forest. Trees 19:282–289. [Google Scholar]
- Araguás‐Araguás L, Froehlich K, Rozanski K (1998) Stable isotope composition of precipitation over southeast Asia. J Geophys Res 103:28721–28742. [Google Scholar]
- Baltzer JL, Thomas SC, Nilus R, Burslem DFRP (2005) Edaphic specialization in tropical trees: physiological correlates and responses to reciprocal transplantation. Ecology 86:3063–3077. [Google Scholar]
- Baraloto C, Rabaud S, Molto Q et al. (2011) Disentangling stand and environmental correlates of aboveground biomass in Amazonian forests. Glob Chang Biol 17:2677–2688. [Google Scholar]
- Bastos CL, Tamaio N, Angyalossy V (2016) Unravelling roots of lianas: a case study in Sapindaceae. Ann Bot (Lond) 118:733–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binks O, Meir P, Rowland L et al. (2016) Plasticity in leaf‐level water relations of tropical rainforest trees in response to experimental drought. New Phytol 211:477–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonal D, Atger C, Barigah TS, Ferhi A, Guehl J-M, Ferry B (2000) Water acquisition patterns of two wet tropical canopy tree species of French Guiana as inferred from H218O extraction profiles. Ann For Sci 57:717–724. [Google Scholar]
- Bonal D, Bosc A, Ponton S et al. (2008) Impact of severe dry season on net ecosystem exchange in the Neotropical rainforest of French Guiana. Glob Chang Biol 14:1917–1933. [Google Scholar]
- Brooks J, Barnard H, Coulombe R, McDonnell J (2010) Ecohydrologic separation of water between trees and streams in a Mediterranean climate. Nat Geosci 3:100–104. [Google Scholar]
- Cai Z-Q, Schnitzer SA, Bongers F (2009) Seasonal differences in leaf-level physiology give lianas a competitive advantage over trees in a tropical seasonal forest. Oecologia 161:25–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark I. (2015) Groundwater geochemistry and isotopes. CRC Press, Florida. [Google Scholar]
- Collins CG, Wright SJ, Wurzburger N (2016) Root and leaf traits reflect distinct resource acquisition strategies in tropical lianas and trees. Oecologia 180:1037–1047. [DOI] [PubMed] [Google Scholar]
- Conover WJ, Johnson ME, Johnson MM (1981) A comparative-study of tests for homogeneity of variances, with applications to the outer continental-shelf bidding data. Technometrics 23:351–361. [Google Scholar]
- Crawford J, Hughes CE, Lykoudis S (2014) Alternative least squares methods for determining the meteoric water line, demonstrated using GNIP data. J Hydrol 519:2331–2340. [Google Scholar]
- Dansgaard W. (1964) Stable isotopes in precipitation. Tellus 16:436–468. [Google Scholar]
- Dawson TE. (1996) Determining water use by trees and forests from isotopic, energy balance and transpiration analyses: The roles of tree size and hydraulic lift. Tree Physiol 16:263–272. [DOI] [PubMed] [Google Scholar]
- Dawson TE, Ehleringer JR (1991) Streamside trees that do not use stream water. Nature 350:335–337. [Google Scholar]
- De Guzman ME, Santiago LS, Schnitzer SA, Álvarez-Cansino L (2016) Trade-offs between water transport capacity and drought resistance in neotropical canopy liana and tree species. Tree Physiol 37:1404–1414. [DOI] [PubMed] [Google Scholar]
- De Wispelaere L, Bodé S, Hervé-Fernández P, Hemp A, Verschuren D, Boeckx P (2016) Plant water resource partitioning and xylem-leaf deuterium enrichment in a seasonally dry tropical climate. Biogeosci Discuss 2016:1–26. [Google Scholar]
- Dincer T, Al-Mugrin A, Zimmermann U (1974) Study of the infiltration and recharge through the sand dunes in arid zones with special reference to the stable isotopes and thermonuclear tritium. J Hydrol 23:79–109. [Google Scholar]
- Ehleringer JR, Dawson TE (1992) Water uptake by plants: perspectives from stable isotope composition. Plant Cell Environ 15:1073–1082. [Google Scholar]
- Ehleringer JR, Phillips SL, Schuster WSF, Sandquist DR (1991) Differential utilization of summer rains by desert plants. Oecologia 88:430–434. [DOI] [PubMed] [Google Scholar]
- Evaristo J, Jasechko S, McDonnell JJ (2015) Global separation of plant transpiration from groundwater and streamflow. Nature 525:91–94. [DOI] [PubMed] [Google Scholar]
- Evaristo J, McDonnell JJ, Scholl MA, Bruijnzeel LA, Chun KP (2016) Insights into plant water uptake from xylem-water isotope measurements in two tropical catchments with contrasting moisture conditions. Hydrol Process 30:3210–3227. [Google Scholar]
- FAO-ISRIC I (1998) World reference base for soil resources (WRB). World Soil Resources, FAO Rome. [Google Scholar]
- Gaines KP, Stanley JW, Meinzer FC, McCulloh KA, Woodruff DR, Chen W, Adams TS, Lin H, Eissenstat DM (2016) Reliance on shallow soil water in a mixed-hardwood forest in central Pennsylvania. Tree Physiol 36:444–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gat JR. (1996) Oxygen and hydrogen isotopes in the hydrologic cycle. Annu Rev Earth Planet Sci 24:225–262. [Google Scholar]
- Gat JR. (2010) Isotope hydrology: a study of the water cycle, vol. 6. World scientific, pp 51–66. Imperial College Press, London. [Google Scholar]
- Gazis C, Feng X (2004) A stable isotope study of soil water: evidence for mixing and preferential flow paths. Geoderma 119:97–111. [Google Scholar]
- Gibson JJ, Birks SJ, Edwards TWD (2008) Global prediction of δA and δ2H-δ18O evaporation slopes for lakes and soil water accounting for seasonality. Glob Biogeochem Cycles 22:GB2031. [Google Scholar]
- GNIP (2016) Global Network of Isotopes in Precipitation; IAEA/WMO. http://www.iaea.org/water (17 May 2016, date last accessed).
- Gourlet-Fleury S, Guehl JM, Laroussinie O (eds) (2004) Ecology and management of a neotropical rainforest: lessons drawn from Paracou, a long-term experimental research site in French Guiana. Elsevier, Paris, p 326. [Google Scholar]
- Grau O, Peñuelas J, Ferry B et al. (2017) Nutrient-cycling mechanisms other than the direct absorption from soil may control forest structure and dynamics in poor Amazonian soils. Sci Rep 7:45017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hervé‐Fernández P, Oyarzún C, Brumbt C, Huygens D, Bodé S, Verhoest NEC, Boeckx P (2016) Assessing the ‘two water worlds’ hypothesis and water sources for native and exotic evergreen species in south‐central Chile. Hydrol Process 30:4227–4241. [Google Scholar]
- Horita J, Wesolowski DJ (1994) Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature. Geochim Cosmochim Acta 58:3425–3437. [Google Scholar]
- Ingwell LL, Joseph Wright S, Becklund KK, Hubbell SP, Schnitzer SA (2010) The impact of lianas on 10 years of tree growth and mortality on Barro Colorado Island, Panama. J Ecol 98:879–887. [Google Scholar]
- Jackson PC, Cavelier J, Goldstein G, Meunzer FC, Holbrook NM (1995) Partitioning of water-resources among plants of a lowland tropical forest. Oecologia 101:197–203. [DOI] [PubMed] [Google Scholar]
- Jobbagy EG, Jackson RB (2001) The distribution of soil nutrients with depth: global patterns and the imprint of plants. Biogeochemistry 53:51–77. [Google Scholar]
- Kendall C, Coplen TB (2001) Distribution of oxygen‐18 and deuterium in river waters across the United States. Hydrol Process 15:1363–1393. [Google Scholar]
- Levia DF, Carlyle-Moses D, Tanaka T (2011) Forest hydrology and biogeochemistry: synthesis of past research and future directions. Springer, The Netherlands. [Google Scholar]
- Maréchaux I, Bartlett MK, Iribar A, Sack L, Chave J (2017) Stronger seasonal adjustment in leaf turgor loss point in lianas than trees in an Amazonian forest. Biol Lett 13:20160819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin-Gomez P, Barbeta A, Voltas J, Penuelas J, Dennis K, Palacio S, Dawson TE, Pedro Ferrio J (2015) Isotope-ratio infrared spectroscopy: a reliable tool for the investigation of plant-water sources? New Phytol 207:914–927. [DOI] [PubMed] [Google Scholar]
- McDonnell JJ. (2014) The two water worlds hypothesis: ecohydrological separation of water between streams and trees? Wiley Interdiscip Rev 1:323–329. [Google Scholar]
- Meinzer FC, Andrade JL, Goldstein G, Holbrook NM, Cavelier J, Wright SJ (1999) Partitioning of soil water among canopy trees in a seasonally dry tropical forest. Oecologia 121:293–301. [DOI] [PubMed] [Google Scholar]
- Merlivat L. (1978) Molecular diffusivities of H2 16O,HD16O, and H2 18O in gases. J Chem Phys 69:2864–2871. [Google Scholar]
- Oerter E, Finstad K, Schaefer J, Goldsmith GR, Dawson T, Amundson R (2014) Oxygen isotope fractionation effects in soil water via interaction with cations (Mg, Ca, K, Na) adsorbed to phyllosilicate clay minerals. J Hydrol 515:1–9. [Google Scholar]
- Orlowski N, Frede HG, Brüggemann N, Breuer L (2013) Validation and application of a cryogenic vacuum extraction system for soil and plant water extraction for isotope analysis. J Sens Sens Syst 2:179–193. [Google Scholar]
- Pan Y, Birdsey RA, Fang J et al. (2011) A large and persistent carbon sink in the world’s forests. Science 333:988–993. [DOI] [PubMed] [Google Scholar]
- Phillips OL, Martinez RV, Arroyo L et al. (2002) Increasing dominance of large lianas in Amazonian forests. Nature 418:770–774. [DOI] [PubMed] [Google Scholar]
- Putz FE. (1991) The biology of vines. Cambridge University Press, New York. [Google Scholar]
- Quesada CA, Lloyd J, Anderson LO, Fyllas NM, Schwarz M, Czimczik CI (2011) Soils of Amazonia with particular reference to the RAINFOR sites. Biogeosciences 8:1415–1440. [Google Scholar]
- Romero-Saltos H, Sternberg L, Moreira MZ, Nepstad DC (2005) Rainfall exclusion in an eastern amazonian forest alters soil water movement and depth of water uptake. Am J Bot 92:443–455. [DOI] [PubMed] [Google Scholar]
- Rozanski K, Araguás‐Araguás L, Gonfiantini R (1993) Isotopic patterns in modern global precipitation. Clim Change Cont Isotopic Rec 78:1–36. [Google Scholar]
- Schnitzer SA. (2005) A mechanistic explanation for global patterns of liana abundance and distribution. Am Nat 166:262–276. [DOI] [PubMed] [Google Scholar]
- Schnitzer SA, Bongers F (2011) Increasing liana abundance and biomass in tropical forests: emerging patterns and putative mechanisms. Ecol Lett 14:397–406. [DOI] [PubMed] [Google Scholar]
- Schnitzer SA, Kuzee ME, Bongers F (2005) Disentangling above- and below-ground competition between lianas and trees in a tropical forest. J Ecol 93:1115–1125. [Google Scholar]
- Sprenger M, Leistert H, Gimbel K, Weiler M (2016) Illuminating hydrological processes at the soil‐vegetation‐atmosphere interface with water stable isotopes. Rev Geophys 54:674–704. [Google Scholar]
- Stahl C, Herault B, Rossi V, Burban B, Brechet C, Bonal D (2013) Depth of soil water uptake by tropical rainforest trees during dry periods: does tree dimension matter? Oecologia 173:1191–1201. [DOI] [PubMed] [Google Scholar]
- Sun S-J, Meng P, Zhang J-S, Wan X (2011) Variation in soil water uptake and its effect on plant water status in Juglans regia L. during dry and wet seasons. Tree Physiol 31:1378–1389. [DOI] [PubMed] [Google Scholar]
- Toledo-Aceves T, Swaine MD (2008) Above- and below-ground competition between the liana Acacia kamerunensis and tree seedlings in contrasting light environments. Plant Ecol 196:233–244. [Google Scholar]
- van der Heijden GMF, Powers JS, Schnitzer SA (2015) Lianas reduce carbon accumulation and storage in tropical forests. Proc Natl Acad Sci USA 112:13267–13271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Sande MT, Poorter L, Schnitzer SA, Markesteijn L (2013) Are lianas more drought-tolerant than trees? A test for the role of hydraulic architecture and other stem and leaf traits. Oecologia 172:961–972. [DOI] [PubMed] [Google Scholar]
- Verbeeck H, Kearsley E (2016) The importance of including lianas in global vegetation models. Proc Natl Acad Sci USA 113:E4–E5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter H. (1939) Grasland: Savanne und Busch der arideren Teile Afrikas in ihrer ökologischen Bedingtheit. Jahrbücher für Wissenschaftliche Botanik, Berlin, pp 750–860.
- Ward D, Wiegand K, Getzin S (2013) Walter’s two-layer hypothesis revisited: back to the roots! Oecologia 172:617–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang ZQ, Si BC, Li Z, Evaristo J, McDonnell JJ (2016) Tritium analysis shows apple trees may be transpiring water several decades old. Hydrol Process 31:1196–1201. [Google Scholar]
- Zimmermann U, Ehhalt D, Münnich K (1967) Soil-water movement and evapotranspration: changes in the isotopic composition of the water. Conference on Isotopes in Hydrology, Vienna, , 14–18 November 1966, IAEA, pp 567–585.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.