The architecture of mutualistic networks as an evolutionary spandrel

Abstract

Mutualistic networks have been shown to involve complex patterns of interactions among animal and plant species, including a widespread presence of nestedness. The nested structure of these webs seems to be positively correlated with higher diversity and resilience. Moreover, these webs exhibit marked measurable structural patterns, including broad distributions of connectivity, strongly asymmetrical interactions and hierarchical organization. Hierarchical organization is an especially interesting property, since it is positively correlated with biodiversity and network resilience, thus suggesting potential selection processes favouring the observed web organization. However, here we show that all these structural quantitative patterns—and nestedness in particular—can be properly explained by means of a very simple dynamical model of speciation and divergence with no selection-driven coevolution of traits. The agreement between observed and modelled networks suggests that the patterns displayed by real mutualistic webs might actually represent evolutionary spandrels.

Ecological networks are known to exhibit a number of structural features associated with their interaction patterns^1–3. In particular, these include: (1) small-world structure⁴, where two given species are separated by a small number of links from any other species in the web^5–7; (2) heterogeneous distributions of connections^1,8, where the number of links between a given species and other species in the web can vary widely; (3) modular organization^7,9 implying that subsets of species exhibit more connections among them than with the rest of the network and (4) nestedness¹⁰, where specialists interact with a subset of the whole set of species that generalists interact with.

The presence of some of these traits has important implications. As an example, the architecture of ecological webs displays the 'robust-but-fragile' feature of many complex networks: random removal (extinction) has little effect, whereas the loss of certain species can lead to a cascade of extinctions^1,11. In this context, mutualistic networks have received special attention over the past decade^7–12. They are defined as a bipartite graph (Fig. 1a) involving interactions across two adjacent trophic levels, such as plants and the species that feed on and pollinate them (Fig. 1b). These graphs are often significantly nested¹³. Following an adaptationist view of naturally evolved systems, it has been argued that the presence of these properties—and nestedness in particular—is a consequence of some underlying selection that reduces competition relative to the benefits of facilitation and hence increases biodiversity and food web persistence or feasibility^3,14,15. The main arguments provided to support this view are grounded in the use of generalized Lotka–Volterra equations with different functional responses. Recent papers have challenged this view questioning the conclusion that nestedness has resulted from selection pressures favouring higher biodiversity^16,17. Instead, it has been suggested that nestedness is likely to be a consequence (rather than a causative property) of biodiversity, in particular of the heterogeneous distributions of connections¹⁸.

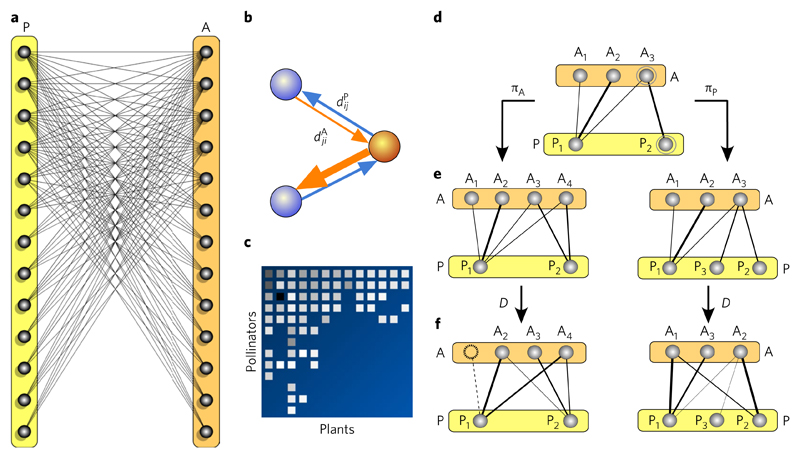
Fig. 1. Mutualistic webs and how to model their evolution.

a, Mutualistic networks are bipartite graphs involving two types of interacting species, such as plants (P) and animals (A). Each link in the graph indicates the existence of an ecological link, such as a frugivore–plant interaction. b, For each pairwise interaction between species i and j, we can obtain two values of mutual dependency: $d_{ji}^{\text{A}}$ for the dependence of the animal species j on plant species i (orange arrow), and $d_{ij}^{\text{P}}$ for the dependence of plant species i on animal species j (blue arrow). The arrows point to the intrinsic direction of the corresponding dependence. If the strength of this interaction is known, the resulting web is weighted. In this case, directional connections need to be considered. The strength might be estimated, for example, by the number of encounters among the members of the pair over a given time window. c, The structure of the interaction matrix resulting from this bipartite graph can be arranged in such a way that node labels are assigned in descending order of degree. d, A simple evolutionary model can be defined by means of a set of duplication-divergence rules. Here, the graph starts with S_A = 3 (upper) and S_P = 2 (lower) species, respectively. Speciation can affect either the A or the P sets with probabilities π_A and π_P, respectively. e, Each time a new species is added, the daughter species inherits all its interactions. f, Afterwards, the network experiences a divergence (D) affecting the weights and links.

In this context, previous work concerning the evolution of complex biological and artificial networks suggests that many architectural patterns displayed by these graphs are an inevitable byproduct of the way they are constructed¹⁸. This is, in fact, the consequence of processes involving network growth through duplication and rewiring^19–23. Specifically, evolution often proceeds by tinkering from available components^24,25, and a network resulting from a process of copy and further modification is likely to display complex features (as is the case of the proteome, metabolic networks and even technological graphs). Simple models involving no functionality or population dynamics can develop small-world or scale-free webs, which can be modular²⁶ despite the apparently well-established idea that modularity is an evolved, functionally relevant trait. If this were the case for mutualistic webs, their invariant features²⁷ would be a consequence of universal properties of the graphs and their growth rules, more akin to the idea of universality²⁸. When this occurs, very simple toy models are capable of accounting for the global features exhibited by the system.

The key lesson of the studies mentioned above is that when dealing with complex biological networks, some ubiquitous patterns might be a byproduct of given generative rules. The emergent patterns can thus be evolutionary spandrels; that is, phenotypic characteristics that evolved as a side effect of a true adaptation^29,30. Despite some criticisms related to the appropriateness of the architectural analogy³¹, the key concept of a non-adaptive structural pattern stands. An example of a spandrel is provided by the distribution of network motifs in cellular networks³², where it has been shown that most network properties can be explained by means of non-functional models. We define evolutionary spandrels as structures that: (1) are the byproduct of building rules; (2) have intrinsic, well-defined, non-random features; and (3) reveal some of the underlying rules of construction³².

Here, we aim to show that nestedness and other system-level network features in mutualistic webs are a byproduct of the generative rules associated with speciation-divergence mechanisms with no consideration of the underlying population dynamics. This approach ignores the ecological time scale (and thus all factors associated with standard stability criteria) by considering instead a scenario in which speciation and diversification events take place over very long (evolutionary) time scales. This approach has been used to model macroevolutionary dynamics, including climbing fitness landscapes as well as processes of network growth and extinction^33–37. In particular, these methods have revealed deep insights into the large-scale evolution of ecological networks (refs ^30,36,38,39 and the references therein).

Speciation-diversification model

Our model assumes a bipartite graph involving two subsets of vertices that correspond with animals and plants, respectively. These species are linked (Fig. 1) provided that a mutualistic relationship exists. This approach makes some strong assumptions. One is that species are either present or absent, with no role to be played by population size or other species-specific traits. Second, interactions are introduced as weighted links. The values of these links will evolve in time following very simple rules (see Methods). Alternatively, we could limit ourselves to a topological, undirected graph (see Supplementary Information).

The large-scale dynamics is obtained by a combination of two processes that occur over evolutionary time scales: new species are generated from old ones through speciation and coevolution, and external (either environmental or stochastic) factors modify the presence and strength of the interactions. Below, we summarize the observed patterns of network architecture generated by our model to be compared with a public database containing n = 25 weighted mutualistic webs (see Supplementary Information).

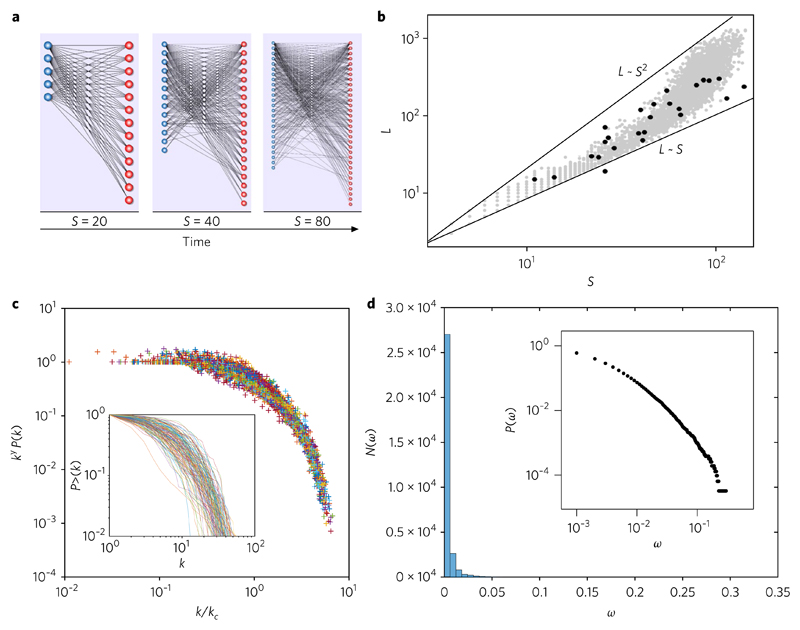
Network connectivity distributions. As a result of the previous evolutionary rules, complex bipartite graphs are generated in silico. In Fig. 2a, we show an example of the time evolution of a simulated bipartite network, starting from an initial condition (t = 1) with two species at each level, connected to each other with a small weight, ω_kl = 10⁻³. A first statistical measure to consider is the relation between the total number of links, L, displayed by the in silico webs against the total number of species, S, at the end of the simulation (Fig. 2b). Real webs are scattered within the two limits given by the linear L ~ S and square scaling L ~ S² bounds, as for our modelled networks (grey circles). As shown in the Supplementary Information, the topological version of this speciation-divergence scheme allows for an analytical prediction of the scaling bounds L ~ S^σ, with the constraint 1 < σ < 2.

Fig. 2. Connectivity patterns in evolved in silico mutualistic webs.

a, A typical sequence of growing in silico networks with size S = 20, 40, 80 showing a nested pattern that becomes more manifest with time. Here the parameters are β = 10⁻⁵, P = 0.1 and θ = 10⁻⁶ (pace of evolutionary change, probability of weight change and link removal threshold, respectively). b, Pattern of links–species relationships. The grey dots indicate the (S, L) pairs for each of the m = 4, 000 simulated networks, evolved over T = 500 steps, generated using randomly chosen pairs (p, β). Here, P ∈ (0, 1) and β ∈ (10⁻⁴, 10⁻¹). The black dots correspond to our benchmark data and the straight lines provide the limits associated with a purely linear L ~ S and the square L ~ S² limits, consistent with the mathematical model provided in the Supplementary Information. c, Series of simulated sequences, each of which is collapsed under the truncated power law scaling, P(k) ~ k^−γexp(−k/k_c). The inset shows the cumulative (undirected) degree distribution P_>(k) of these graphs (for all simulated networks with S > 100) in a log–log plot (to be compared with real webs; see Supplementary Fig. 2). d, Corresponding distribution of link weights aggregated over all our systems, shown in both linear and double logarithmic (inset) plots. The fat tail is difficult to see from the N(ω) frequency histogram, but is clearly observed in the cumulative form in the log scale. Here too, a truncated power law is found.

The previous scaling only represents a first level of analysis that ignores the underlying network. Peering deeper into its internal structure, let us study the distribution of connections. Allow the frequency of (any) species with a given number of links k to be denoted by P(k). Available data show that mutualistic webs display degree distributions that can be properly described by a truncated power law²⁷: P(k) ~ k^−γexp(−k/k_c), where γ is the exponent that indicates how rapidly the distribution falls at small k and k_c—a cut-off that effectively limits the spread of the distribution³⁶. The larger k_c is, the flatter the distribution and the higher the presence of highly connected species. In Fig. 2c, we represent the data collapse for every generated graph under the ansatz of a truncated power law distribution, following ref. 27. Also, we show (inset) the cumulative degree distribution P_>(k) for each system. Different colours indicate different networks. This method allows for a size-independent check on the structural features of the emerging bipartite networks, illustrating the robustness of our scaling ansatz.

These results are indicative of heterogeneity as a consequence of speciation-divergence phenomena, as suggested by previous studies¹⁹, but in this case applied to a bipartite system. Additionally, it is well known that the distribution of weights also decays in a broadscale shape, with a characteristic scaling exponent close to one. Our results are fully consistent with this prediction, as shown in Fig. 2d, where we plot the histogram of weights for all our sets. The logarithmic plot (inset) shows the cumulative probability distribution of weights.

Correlations and asymmetries

The previous results indicate that our model is capable of reproducing the distributions of connections, but there are several non-trivial ways in which the weighted network can be organized and, in particular, how different features are correlated. The use of a weighted network provides relevant information about its local and global organization^40–42 and was early identified as an essential feature of mutualistic interactions⁴³. In general, a scaling law relates strength and degree,

$$s\left(k\right)\sim k^{\eta },$$ (1)

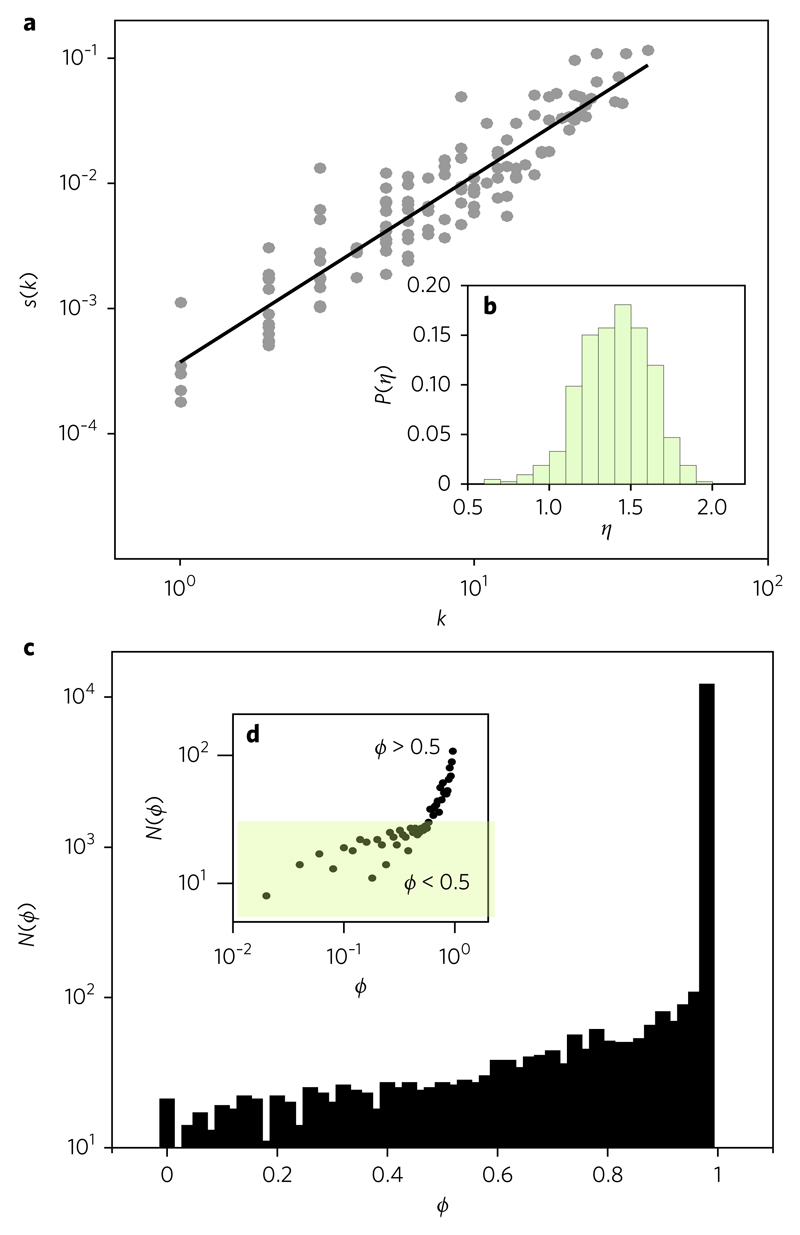
where the exponent η establishes the nature of the correlation. For a randomly distributed set of weights, it can be shown that a linear relation (η = 1) exists. If the importance of a given node in the network is lower than predicted by its degree, we would observe η < 1. In mutualistic webs, a superlinear behaviour is found (that is, η > 1), indicating that species with many connections tend to display stronger interactions than average⁸. Specifically, an exponent η_mut ≈ 1.45 has been reported for mutualistic nets⁴². In Fig. 3b, we display the distribution of exponent values η for a the subsample of generated networks with S > 100. Its corresponding mean value is η_model = 〈η〉 = 1.50, a result compatible with the measured exponent. Figure 3a shows an example of a single system adjust between strength and degree.

Fig. 3. Higher-order correlations and network asymmetries.

a, Scaling behaviour displayed by the strength–degree distribution for a single system. The adjusted exponent for this particular system gives η = 1.49. b, Distribution of exponents, P(η), for a subsample of 426 connected graphs with sizes S > 100. The average value for this distribution gives 〈η〉 = 1.50, which is consistent with the available data⁴². c, Frequency distribution of asymmetry values ϕ(i,j) between the two possible directed weights connecting a pair (i,j) of species. If we indicate these two values as ω_ij and ω_ji, the asymmetry of this pair is defined as $\varphi (i,j)=|{\omega }_{ij}-{\omega }_{ji}|/\max \left\{{\omega }_{ij},{\omega }_{ji}\right\}.$ The frequency of pairs gives an asymmetric distribution that is strongly skewed towards higher ϕ values. d, This asymmetry is also displayed in a log–log scale, markedly growing for ϕ > 0.5 values, as found in real webs⁸.

Along the lines of correlation between strength and degree, it has also been reported that weights are strongly asymmetrical⁸. The distribution N(ϕ) of asymmetry is strongly biased towards higher values of ϕ. The results of our model are shown in Fig. 3c,d. Additionally, Fig. 3c shows how the frequency rapidly grows for ϕ > 0.5, thus revealing a skewed increase for higher levels of asymmetry, as reported from real webs. These two measures match the observed low frequency of string dependences along with their marked asymmetry and heterogeneity. Although the ecological consequences can be interpreted under a coevolution–selection picture⁸, our model challenges the generality of this approach.

Nestedness

A final, ubiquitous pattern to be considered here is nestedness, which can be described as the tendency of low-degree species to interact with a subset of highly connected species. Once again, the standard interpretation of nestedness is tied to the likelihood of the underlying interactions. The traditional analysis of nested graphs uses topological matrices, which only account for the presence or absence of links. These matrices are typically nested, but, as pointed out by Staniczenko et al. ¹⁶, a better characterization of these webs using link weights reveals that only a small fraction of them exhibit nestedness¹⁶, thus suggesting that a truly meaningful measure requires considering a weighted interaction matrix.

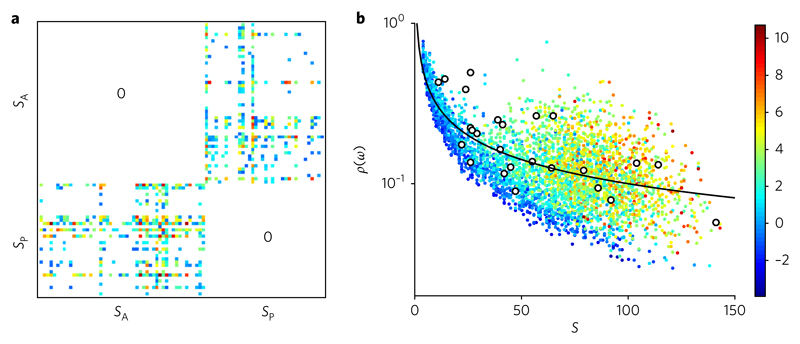
Edges in a nested network are organized in such a way that specialists interact with a subset of the species whom generalists interact with. This nested pattern can be detected in the specific arrangement of present and absent interactions in bipartite networks. This definition was extended to quantitative networks using spectral graph theory¹⁶. In Fig. 4b, the spectral radius is displayed against the number of species for our large set of m = 4, 000 generated mutualistic webs. The cloud of points (coloured dots) scatters around the predicted scaling exhibited by a random graph (see Supplementary Information), where the spectral radius follows ρ_rand(ω) ~ S^−1/2. The plot also shows the position of the real webs (open circles), which are shown to fit well within the bounds exhibited by our in silico data set.

Fig. 4. Nested evolved networks.

The networks generated by the rules described in the main text display nested structures. Nestedness in these weighted graphs is estimated by means of the spectral radius of the squared weighted matrices, ω, generated by the model¹⁶. a, An example of the matrices obtained from our digital mutualistic webs. b, The spectral radius ρ(ω) value has been calculated using the full sample of m = 4, 000 networks and plotted against their corresponding number of species S. The open circles correspond to a total of 25 real network data points (see Supplementary Information for sources). The line corresponds to the prediction for the random model, which follows from Wigner’s semi-cirle law (see Supplementary Information). The colour scale gives the corresponding Z-score (see Supplementary Information for details of the calculation).

For the in silico webs, the Z-score associated with the nestedness estimation has also been displayed by means of a colour scale to provide an assessment of its statistical significance. In general, statistical significance increases with degree, as expected from the impact of heterogeneity, which grows with network size. Webs with low S values are instead closer to the low-Z (blue) area. These graphs typically fail to display high connectivity and often exhibit tree-like features. The mutualistic network benchmark falls within the bounds defined by the in silico data set. In both cases, the graphs display higher ρ values as the number of species increases.

Discussion

This paper introduces a model of the large-scale evolution of mutualistic webs. This model involves only the minimal components related to the formation of new species through speciation and divergence (under constraints) of weights over evolutionary time. Despite its simplicity, the model is capable of consistently reproducing several well-known structural patterns of organization, suggesting that the generative rules responsible for network growth largely determine the presence of universal traits in empirical systems.

The model presented here does not stand alone in trying to explain the emergence of complex mutualistic networks. In ref. 44, the authors show that nestedness and heterogeneous degree distributions emerge from an optimization principle that maximizes species abundances. Their model, however, works over ecological time scales, whereas the question we pose here is to what extent simple evolutionary models can account for observed structural patterns. In this respect, Nuismer et al.⁴⁵ developed a quantitative genetic model that allows inference of network structure over evolutionary time. Their model was far more complex that the one presented here, yet emerging networks were only more nested than their random counterparts under very restrictive conditions: species interactions should be mediated by phenotype differences and coevolutionary selection should be weak. In the remaining cases, resulting networks were either not nested or anti-nested.

Our speciation-divergence rules belong to the broad class of duplication-rewiring models known to indirectly incorporate a preferential attachment rule, since duplication events are likely to increase the number of connections of those nodes that already have higher degrees. This rule is known to generate heterogeneous graphs⁴⁶. Once heterogeneous distributions arise, other features emerge 'for free'. Nestedness in particular seems to be a consequence of broad connectivities^47,48.

Additionally, our model incorporates evolutionary rules of speciation and drift that naturally provide a mechanism to explain the properties found in mutualistic webs. As it does not include the population size associated with each species nor the nonlinear dynamics of ecological interactions, our results suggest that the ecological scale plays a minor role in shaping the architecture of mutualistic webs. Instead, the universal constraints associated with the evolutionary unfolding of these webs would lead to the observed invariant properties. However, the advantages provided by these networks, such as robustness and evolvability, can be of great relevance at other scales. Tinkering can work as a bootstrapping process leading to population-level advantages that might, in turn, be the target of selection. Future work should further explore these mechanisms and their applicability to other types of webs; for example, networks involving both mutualistic and antagonistic interactions^7,9. An interesting candidate in this respect is the microbiome, which also exhibits complex ecological networks⁴⁹ and marked similarities with standard ecosystems, suggesting again the presence of universal rules⁵⁰. Given their potential for tracing evolutionary histories and their shorter evolutionary time scales, these systems will prove to be a useful test to some of the ideas described here.

Methods

Evolutionary rules

A bipartite graph G = (A, P, {ω_ij}) involving the two subsets of nodes A(t) and P(t) represents the animals and plants at a given evolutionary time step t. We define the quantitative effect of animals on plants through a matrix ω_ij = ω(A_i → P_j), which indicates the strength of the interaction between both partners and vice versa. The evolutionary dynamics of the graph is defined by speciation and divergence.

Speciation

We choose a given species A_i or P_j and create a speciation event. The new species inherits exactly the same list of links from its parent species. If A_k indicates the newly created species, we have ω_kj = ω_ij for all j = 1, ..., |P|.

Divergence

We redistribute the weights between parent and daughter species. A random number 0 < μ < 1 is generated and each pair of links {ω_kj, ω_ij} is updated to a new pair {μω_kj, (1−μ)ω_ij}. Additionally, for each link, we introduce, with a given probability p, a weight change; that is, we have a new value ω_ij → ω_ij + ξ being −β < ξ < β a small random number. Here, the parameter β weights how fast evolutionary changes occur at the level of single ecological links. If ω_ij falls below a threshold θ, it is removed. Finally, a maximum input weight is allowed for all plants. Specifically, if the sum ϕ(P_j)= ∑_i ω_ij over all animals acting on the plant P_j is larger than one, the change is not accepted. A symmetrical rule is used to constrain the links in the P → A direction. As a consequence of the threshold rule, species become extinct when no mutual support is present (that is, when ∑_j ω_ji = 0).

Numerical simulations

Our aim was to sample the parameter space defined by the space (P, β) with no other adjustment of our parameters. A set of m = 4, 000 simulated random bipartite grown graphs was generated from randomly chosen pairs (P, β) with P ∈ (0, 1) and β ∈ (10⁻⁴, 10⁻¹, respectively, using a uniform distribution. Lower values of β can be used, but their single effect is to slow down the rate of network evolution, not the final outcome. The same applies for the θ parameter, which leads to very similar results for a wide range, only leading to significant changes for very high (and probably unrealistic) values. Given the wide variations in the parameters, a broad range of network sizes was generated, from very small to a maximum size of S ~ 200 species.

Weighted network properties

We compared different properties measured in empirical and synthetic networks. The aggregated strength of the nodes is defined as the sum of all the dependencies in both link directions; that is, $s_i={\displaystyle {\sum }_{j=1}^{N_i}\left({\omega }_{ij}+{\omega }_{ji}\right)}$, where N_i indicates the number of interactions with other species. Asymmetry is calculated following ref. 8. If ω_ij and ω_ji are the links connecting the two elements A_i and P_j in the two possible directions, we define the asymmetry ϕ(i, j) of the pair as:

$$\varphi \left(i,j\right)=\frac{\left|{\omega }_{ij}-{\omega }_{ji}\right|}{\max \left\{{\omega }_{ij},{\omega }_{ji}\right\}},$$

which takes values within the range 0 ≤ ϕ(i, j) ≤ 1.

Nestedness based on the spectral radius

Nestedness is computed over the square S × S matrix ω (see Fig. 4a), where S = S_A + S_P is defined as:

$$\omega =\left[\begin{array}{cc}0& {\omega }_{S_{\text{A}}\times S_{\text{P}}}\\ {\omega }_{S_{\text{P}}\times S_{\text{A}}}& 0\end{array}\right],$$ (2)

where mutualistic interactions ω = [ω_ij] describe a block off-diagonal form. The eigenvalues of this matrix, {λ_k}(k = 1, ..., S), can be systematically calculated. In particular, it has been shown¹⁶ that the perfectly nested graph is associated with the so-called spectral radius ρ(ω), which is defined as:

$$\rho \left(\omega \right)=\max \{\left|{\lambda }_1\right|,\dots ,\left|{\lambda }_S\right|\},$$ (3)

that is, the largest eigenvalue.

Supplementary Material

Supplementary information is available for this paper at https://doi.org/10.1038/s41559-017-0383-4.