Abstract
In addition to the processes structuring free-living communities, host-associated microbiota are directly or indirectly shaped by the host. Therefore, microbiota data have a hierarchical structure where samples are nested under one or several variables representing host-specific factors, often spanning multiple levels of biological organization. Current statistical methods do not accommodate this hierarchical data structure and therefore cannot explicitly account for the effect of the host in structuring the microbiota. We introduce a novel extension of joint species distribution models (JSDMs) which can straightforwardly accommodate and discern between effects such as host phylogeny and traits, recorded covariates such as diet and collection site, among other ecological processes. Our proposed methodology includes powerful yet familiar outputs seen in community ecology overall, including (a) model-based ordination to visualize and quantify the main patterns in the data; (b) variance partitioning to assess how influential the included host-specific factors are in structuring the microbiota; and (c) co-occurrence networks to visualize microbe-to-microbe associations.
Keywords: Bayesian inference, generalized linear mixed models, host-associated, joint species distribution models, microbiome, microbiota
1. Introduction
Ecological communities are the product of stochastic and deterministic processes, while environmental factors may set the upper bound on carrying capacity, competitive and facilitative interactions within and among taxa determine the identity of the species present in local communities. Ecologists are often interested in inferring ecological processes from patterns and determining their relative importance for the community under study (Vellend, 2010). During the last few years, there has been a growing interest in developing new statistical tools aimed towards ecologists and the analysis of multivariate community data (see, e.g., Legendre & Legendre, 1983). Many of the distance-based approaches, however, have a number of drawbacks, including uncertainty of selecting the most appropriate null models, low statistical power and the lack of possibilities for making predictions (Warton, Wright, & Wang, 2012). One alternative, model-based framework which has become increasingly popular in community ecology, is joint species distribution models (JSDMs, (Pollock et al., 2014). Such models are an extension of generalized linear mixed models (GLMMs, Bolker et al., 2009), where multiple species are analysed simultaneously often together with environmental variables, thereby revealing community-level responses to environmental change. By incorporating both fixed and random effects, sometimes at multiple levels of biological organization, JSDMs have the capacity to assess the relative importance of processes such as environmental and biotic filtering versus stochastic variability. Furthermore, with the increase in trait-based and phylogenetic data in community ecology together with the growing appreciation that species interactions are constrained by the “phylogenetic baggage” they inherit from their ancestors (Thompson, 1994), JSDMs can further accommodate information on both species traits and phylogenetic relatedness among species (Aivelo & Norberg, 2018; Ives & Helmus, 2010; Kaldhusdal, Brandl, Müller, Möst, & Hothorn, 2015; Ovaskainen et al., 2017). At last, accounting for phylogenetic relatedness among species can greatly improve estimation accuracy and power when there is a phylogenetic signal in species traits and/or residual variation (Li & Ives, 2017).
To model covariances between a large number of species using a standard multivariate random effect, as a standard JSDM (Pollock et al., 2014; Xia, Chen, Fung, & Li, 2013) does, is computationally challenging; the number of parameters that needs to be estimated when assuming a completely unstructured covariance matrix increases rapidly (quadratically) with the number of species. An increasingly popular tool for overcoming this problem, which is capable of modelling such high-dimensional data, is latent factor models (Warton et al., 2015). In community ecology, latent factor models and JSDMs have been combined to allow for a more parsimonious yet flexible way of modelling species covariances in large communities (Letten, Keith, Tozer, & Hui, 2015; Ovaskainen et al., 2017). Such an approach offers a number of benefits. First, latent factors provide a method of explicitly accounting for residual correlation. This is important because missing covariates, ecological interactions and/or spatiotemporal correlation will induce residual correlation among species, which, if not accounted for, may lead to erroneous inference. Second, latent factors facilitate model-based ordination in order to visualize and quantify the main patterns in rows and/or columns of the data (Hui, 2016, 2017). While traditional distance-based ordination techniques may confound location (i.e., the mean abundance) and dispersion (i.e., the variability) effects (Warton et al., 2012), model-based ordination directly models the mean–variance relationship and can therefore accurately distinguish between the two effects (Sohn & Li, 2017; Hui, Taskinen, Pledger, Foster, & Warton, 2015). At last, the estimated factor loadings can be conveniently interpreted as indicating whether two species co-occur more or less often than by chance as well as the direction and strength of their co-occurrence, thus allowing a latent factor approach to robustly estimate large species-to-species co-occurrence networks (Ovaskainen, Abrego, Halme, & Dunson, 2016). Note that an important decision when fitting latent factor models is the choice of the number of latent factors. While less than five is usually sufficient for a good approximation to correlations, there is a trade-off between model complexity and the model’s capacity to capture the true correlation structure (Warton et al., 2015). An alternative approach is to use variable selection, which automatically shrinks less-informative latent factors to zero (Bhattacharya & Dunson, 2011).
In parallel to community ecology, there is a growing field of microbial ecology studying both free-living and host-associated microbiota. While microbial ecologists can adopt many of the same statistical tools developed for traditional multivariate abundance data (see, e.g., Balint et al., 2016), researchers studying host-associated microbiota need to consider an additional layer of processes structuring the focal community, namely that host-associated microbiota are additionally shaped directly or indirectly by their hosts. For example, interactions between hosts and microbes often involve long-lasting and sometimes extremely intimate relationships, where the host may have evolved the capacity to directly control the identity and/or abundance of its microbial symbionts (Berendsen, Pieterse, & Bakker, 2012; McFall-Ngai et al., 2013). Similar to an environmental niche, the host must be viewed as a multidimensional composite of all host-specific factors driving the occurrence and/or abundance of microbes within a host– everything from broad evolutionary relationships between host species (Groussin et al., 2017) to the direct production of specific biomolecules within a single host individual (Liu et al., 2016). As a result, host-associated microbiota have a hierarchical data structure where samples are nested under one or several variables representing recorded and/or measured host-specific factors sometimes spanning multiple levels of biological organization.
In this article, we propose a novel extension of JSDMs to analyse host-associated microbiota, based around explicitly modelling its characteristic hierarchical data structure. In doing so, our proposed model can straightforwardly accommodate and discriminate among any measured host-specific factors. Over the past few years, there has been an increase in model-based approaches aimed specifically towards the analysis of host-associated microbiota (see, e.g., Grantham, Reich, Borer, & Gross, 2017; Xia et al., 2013; Xu, Paterson, & Xu, 2017; Zhang et al., 2017). To our knowledge however, our proposed model is the first to explicitly and transparently account for the aforementioned hierarchical structure that is inherent in data on host-associated microbiota (Figure 1). Other key features of the proposed model, which are inherited from JSDMs and latent factor models, include the following: (a) parsimonious modelling of the high-dimensional correlation structures typical of host-associated microbiota; (b) model-based ordination to visualize and quantify the main patterns in the data; (c) variance partitioning to assess the explanatory power of the modelled host-specific factors and their influence in shaping the microbiota; and finally (d) co-occurrence networks to visualize microbe-to-microbe associations. Furthermore, by building our model in a probabilistic, that is, Bayesian framework, we can straightforwardly sample from the posterior probability distribution of the correlation matrix computed by the factor loadings; this means that we can choose to look at, or further analyse the correlations that have at least, for example, 95% (or even 97% or 99%) probability.
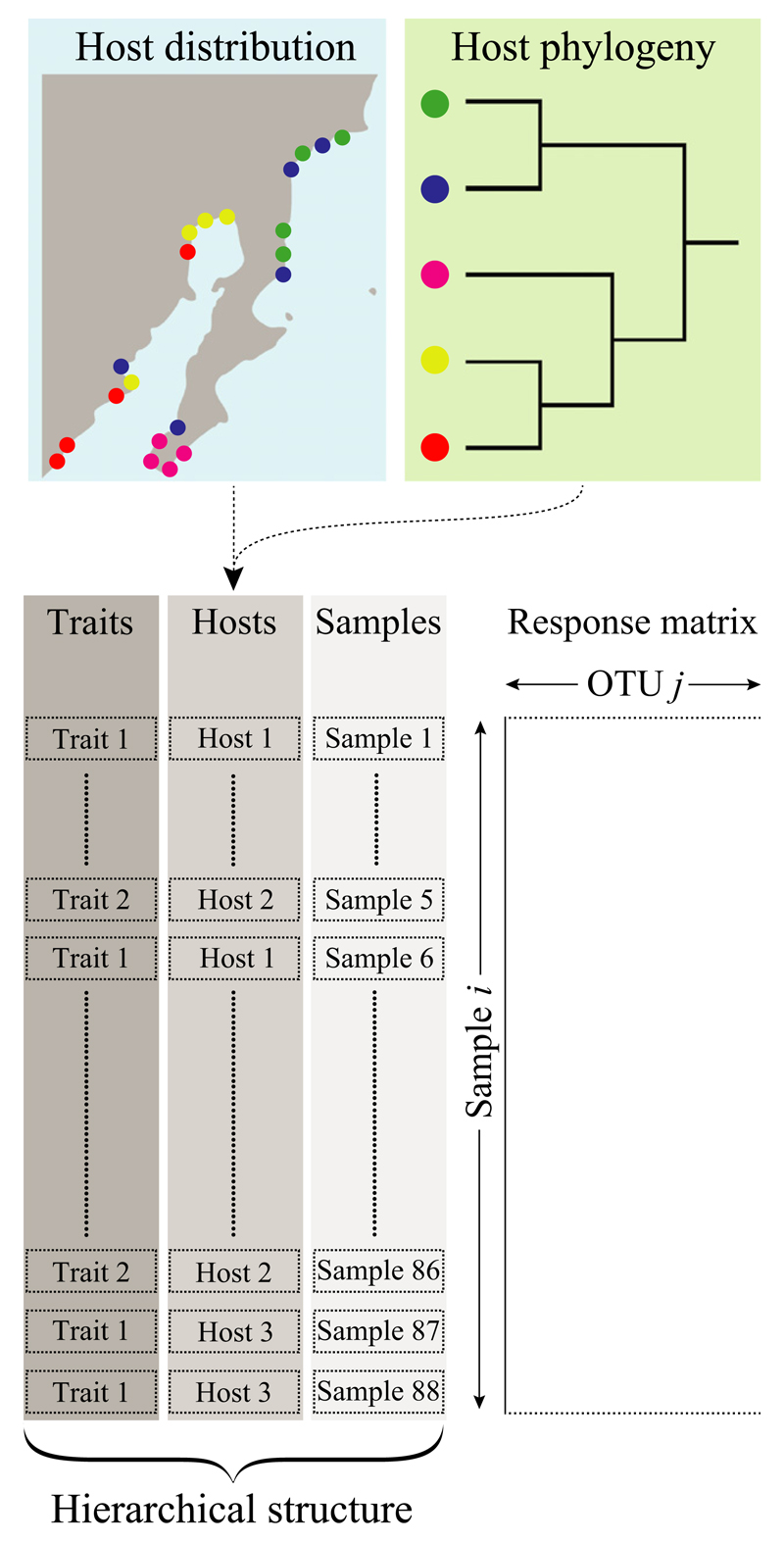
Figure 1.
Host-associated microbiota data have a hierarchical data structure. In this example, samples are nested within host species which in turn are nested under species traits. Additional data often available are, e.g., (part of) the geographic distribution of the focal host species, as well as the phylogenetic relatedness between those. This means that host species can be further nested within observation/collection sites, and linked to branches in a phylogeny. The proposed model extension can straightforwardly accommodate for this hierarchical data structure and discriminate their importance in structuring the microbiota [Colour figure can be viewed at wileyonlinelibrary.com]
We apply our proposed model to two published data sets. While we include the effect of host phylogenetic relatedness in both case studies, we illustrate the flexibility of our approach by adapting the proposed model to overdispersed counts and presence—absence responses, and study-specific metadata relevant to each case study. By utilizing recent progress in latent factor modelling, our proposed model can also assist in cases where metadata are scarce by finding latent “hidden” variables driving the microbiota.
2. Methods
We applied the proposed methodology to two published data sets on host-associated microbiota. Both data sets possess two main features which characterize many host-associated microbiota data, namely high dimensionality, that is, the number of OTUs is a non-negligible proportion of the number of samples, and sparsity, that is, most OTUs are rarely observed. The first data set comprise 90 samples from 20 sponge species collected in four closely located sites in the Bocas del Toro archipelago (Supporting Information Figure S1, for original study see Easson & Thacker, 2014). The metadata contain apart from collection site, a classification of hosts into either high microbial abundance (HMA) or low microbial abundance (LMA) sponges (hereafter termed ecotype). This classification is based on the abundance of microbes harboured by the host and determined by transmission electron microscopy (Gloeckner et al., 2014). The authors constructed a host phylogeny from 18S rRNA gene sequences (downloaded from GenBank) by implementing a relaxed-clock model in MrBayes. The data have a hierarchical structure with n = 90 samples nested within S = 20 host species and L = 4 collection sites. Host species are then further nested under one of R = 2 ecotypes. The response matrix had already been filtered to only include OTUs (defined at 97% similarity) with at least 500 reads, but we further removed OTUs with <20 presences across samples, resulting in m = 187 modelled OTUs.
The second data set consists of 59 Neotropical bird species with a total of 116 samples from the large intestine. Host species were collected from 12 lowland forests sites across Costa Rica and Peru (Supporting Information Figure S2, for original study see Hird, Sánchez, Carstens, & Brumfield, 2015). The metadata include bird taxonomy and several covariates–including dietary specialization, stomach contents and host habitat. The authors sequenced and used the mitochondrial locus ND2 to reconstruct the host phylogeny by implementing a partitioned GTR + Γ model in BEAST. Similar to the sponge data set, this data set has a hierarchical structure with n = 116 samples nested within S = 59 host species and L = 12 collection sites. We filtered the response matrix to include OTUs (defined at 97% similarity) with at least 50 reads and 40 presences across samples, resulting in m = 151 modelled OTUs. Of the full list of covariates available, we included diet, stomach content, sex, elevation and collection site as explanatory predictor variables in our model. While diet and geography have been shown to influence the human gut microbiota (see, e.g., Muegge et al., 2011; Yatsunenko et al., 2012), the effect of sex and elevation is less known.
2.1. Joint species distribution models
We considered two response types commonly encountered in host-associated microbiota data: counts and presence–absence. In a formal manner, let the response matrix being modelled consist of either counts or presence—absence records of m OTUs from n samples, and let yij denote the response of the j-th OTU in the i-th sample. Also, let denote a univariate normal distribution with mean μ and variance σ2, and analogously, let denote a multivariate normal distribution with mean vector and covariance matrix Σ. We now split our model formulation up into the two case studies/response types.
2.1.1. Case study 1 (Counts)
Due to the presence of overdispersion that was quadratic in nature, as confirmed by a mean–variance plot of the OTU counts (not shown), we assumed a negative binomial distribution for the responses. In a specific manner, we considered a negative binomial distribution with a quadratic mean—variance relationship for the element yij, such that where ϕj is the OTU-specific overdispersion parameter. The mean abundance was related to the covariates using a log-link function. Denoting the mean abundance of OTU j in sample i by ψij, then for Model 1 we have
| (1) |
| (2) |
To clarify the above formulation, s, r and l index effects that are attributed to the S = 20 host species, R = 2 ecotypes and L = 4 sites, respectively. For instance, “s[i]” and “r[s]” denote “sample i nested within host species s” and “host species s nested within ecotype r”, respectively (Figure 1). In Equation (1), the quantities αi and γj represent sample and OTU-specific effects, respectively. The former adjusts for differences in sequencing depth among samples, while the latter controls for differences in OTU total abundance. The inclusion of αi serves two main purposes. First and foremost, including αi allows us to account for the hierarchical data structure and its effect on sample total abundance specifically. In particular, to account for sample i being nested within host species s (which are further nested within ecotype r) and site l, the sample effects αi are drawn from a normal distribution with a mean that is a linear function of three host-specific effects: host ecotype μ(ecotype); host collection site μ(site); and host phylogeny μ(phylo). Furthermore, the host ecotype μ(ecotype) and host collection site μ(site) effects are themselves drawn from a normal distribution with an ecotype and site-specific mean, respectively. Second, the inclusion of αi means that the resulting ordinations constructed by the latent factors on the sample Ziq and host species level are in terms of species composition only, as opposed to a composite of abundance and composition if the site effects were not included in the formulation. We included five latent factors at both the sample and host species level, and both Ziq and were assigned standard normal priors with the assumption of zero mean and unit variance to fix the location and scale (see Chapter 5, Skrondal & Rabe-Hesketh, 2004). Furthermore, to address rotational variance, the upper triangular components of both loading matrices (i.e., sample λ and host species λH level) are fixed to zero with the diagonals constrained to be positive (Geweke & Zhou, 1996). As recommended by Polson and Scott (2012), and analogous to the prior distributions we use for the mean μr and μl, we used a weakly informative prior in the form of a half-Cauchy distribution with a centre and scale equal to 0 and 2.5 for the overdispersion parameter ϕ. Moreover, following Gelman, Jakulin, Pittau, and Su (2008), we used the same distribution with location and scale equal to 0 and 1 as prior information on the variance parameters: σ2(sample); σ2(ecotype); and σ2(site). Based on our empirical investigation, we found that the use of such priors stabilized the MCMC sampling substantially without introducing too much prior information, compared to using more uninformative prior distributions. At last, the quantity C(phylo) corresponds to a phylogenetic correlation matrix constructed from the host phylogeny by assuming Brownian motion evolution such that the covariances between host species are proportional to their shared branch length from the most recent common ancestor (Felsenstein, 1985). The phylogenetic parameter θphylo quantifies variance that can be attributed to the phylogenetic effect and is drawn from an exponential distribution with a rate parameter of 0.1. Similar to the Cauchy priors, this prior distribution provides a weak level of regularization—a rate parameter of 0.1 gives a prior mean of 10, thus preventing the estimated variance of getting implausibly large.
2.1.2. Case study 2 (Presence–absence)
We modelled the presence (yij = 1) or absence (yij = 0) of OTU j in sample i using probit regression, implemented via the indicator function yij = 1zij > 0 where the latent score zij is normally distributed with the mean equal to a linear function of the covariates and latent factors, and variance set equal to one. Model 2 was set up as follows:
| (3) |
| (4) |
| (5) |
While the above description is largely the same as that of Model 1, we also included here a linear predictor Lij to model the effects of five available covariates (represented by the model matrix Xik; k = 1, …, 5) on species composition (Equation 4). The linear predictor Lij thus acts to explain covariation between OTUs due to the measured explanatory predictor variables, while the latent factors account for the remaining, residual covariation. Similar to Model 1, including αi means that the covariation between OTUs is in terms of species composition only. By drawing the sample effects αi from a normal distribution with a mean that is a linear function of both nonphylogenetic μ(non-phylo) and phylogenetic μ(phylo) host effects (Equation 5), we account for the hierarchical structure present in the data. Furthermore, from the loading matrix λ, we computed a covariance matrix as Ω = λλ⊤, which we subsequently converted to a correlation matrix for studying the OTU-to-OTU co-occurrence network.
For both case studies, we used Markov Chain Monte Carlo (MCMC) to estimate the models via JAGS (Plummer, 2003) and the runjags package (Denwood, 2016) in R (R Core Team 2016). For each model, we ran one chain with dispersed initial values for 300,000 iterations saving every 10th sample and discarding the first 25% of samples as burn-in. We evaluated convergence of model parameters by visually inspecting trace and density plots using the R packages coda (Plummer, Best, Cowles, & Vines, 2016) and mcmcplots (McKay, 2015), as well as using the Geweke diagnostic (Geweke, 1991).
2.2. Variance partitioning
To discriminate among the relative contributions of the various factors driving covariation in the JSDMs, we partition the explained variance by the row effects (αi), the linear predictor (Lij), and the factor loadings (λqj and ) into components reflecting sample and host-level effects. Such a variance decomposition is analogous to the sum-of-squares and variance decompositions seen in analysis of variance (ANOVA) and linear mixed models (Nakagawa & Schielzeth, 2013). Depending on the response type, the row effects capture variance in relative abundance (Model 1) or species richness (Model 2), while the linear predictor and the factor loadings capture variance in species composition. As mentioned above, when the linear predictor is included in (Model 2), the loadings capture residual variation not accounted for by the modelled covariates. Variance partitioning therefore allows us to assess the explanatory power of the hierarchical data structure, and measured covariates including “hidden” factors, and how influential each of them are in structuring the host-associated microbiota (Ovaskainen et al., 2017).
We now discuss in more detail how we partition the explained variance into components attributed to the row effects (αi) for Model 1 and the factor loadings (λqj) together with the linear predictor (Lij) for Model 2. Let Vtotal denote the total variance of the αi, while Vsample, Vecotype, Vsite and Vphylo denote the variances for the sample, host ecotype, host collection site and host phylogeny, respectively. Then for Case Study 1 we have,
and for Case Study 2 we have,
In the second partitioning, the quantity Vlinpred represents the variance explained by the linear predictor Lij, the Vresidual represents the residual variance not accounted for by the modelled predictor variables, that is, as explained by the diagonal elements of the residual covariance matrix Ω, and finally, the Vsample, Vnon-phylo and Vphylo to variance attributed to the hierarchy present on the row effects αi.
3. Results
Below, we present the main results of each case study. We used the 95% highest density interval (HDI) as a measure of statistical significance; that is, if a parameter or a pairwise parameter comparison excludes zero, then we conclude that the posterior probability of the difference being significantly different from zero exceeds 95%.
3.1. Case study 1
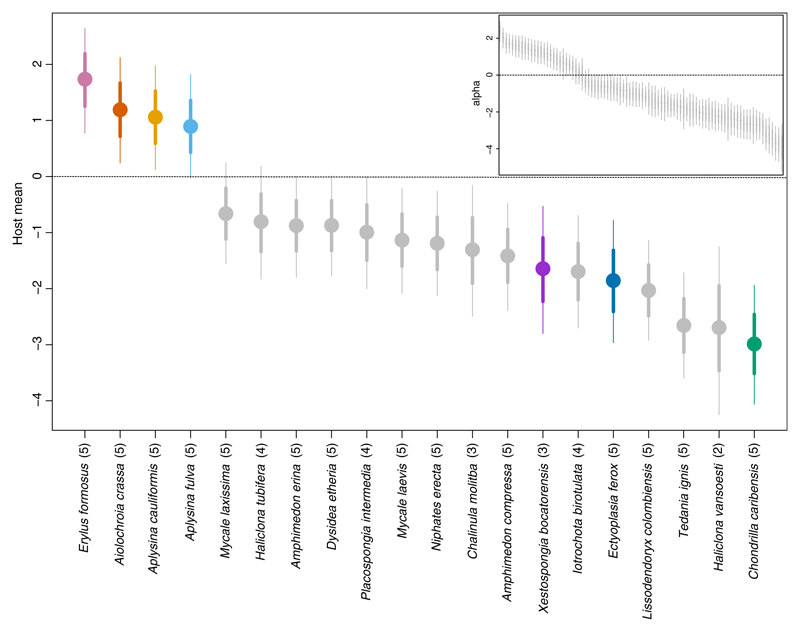
We applied Model 1 to data on sponge host-associated microbiota (Easson & Thacker, 2014). The fitted model revealed that more than 86% of the variation in relative abundance among samples could be attributed to processes operating on the host species level (Table 1; Figure 2). More specifically, 57% of this variation was explained by host phylogenetic relatedness, even though the 95% HDI for the phylogenetic effects did not exclude zero for any of the host species. While this suggests the presence of a phylogenetic signal in one or more host traits affecting microbial abundance and/or occurrence, it also indicates that no particular host species or host species clade have a stronger signal than the rest. Easson & Thacker, 2014 used the Bloomberg’s K statistic and found a significant signal of the host phylogeny on the inverse Simpson’s index. This index measures the diversity of a community, but is strongly influenced by the relative abundance of its most common species (Haegeman, Sen, Godon, & Hamelin, 2014). The authors specifically noted that host species Aiolochroia crassa, Aplysina cauliformis and Aplysina fulva from the order Verongida, along with host Erylus formosus from the order Astrophorida, had higher values of this index compared to the rest of the host species. In a similar manner, we found that the same four hosts harboured more abundant (Figure 2) and distinctively different microbiotas than the other host species (Figure 3). Pairwise comparisons of these four hosts showed that A. crassa harboured markedly different microbial composition compared to its two closest relatives A. cauliformis and A. fulva (Supporting Information Tables S1 and S2). These three hosts were nonetheless collected at the same site. The two species from the genus Aplysina, on the other hand, harboured very similar microbiota composition to that of host E. formosus even if they were collected some 17,000 km apart.
Table 1.
Variation explained by the hierarchy present on αi
| Phylogeny | 57.09% |
| Ecotype | 14.58% |
| Site | 14.51% |
| Sample | 13.82% |
Figure 2.
The main plot shows a caterpillar plot for the host means μ(host)s, with the colours representing the seven HMA hosts. The subplot shows a caterpillar plot for the row effects αi. The quantiles correspond to the 95% (thin lines) and 68% (thick lines) credible intervals, respectively. The number within the parentheses shows how many individuals per host species were availible to draw inference on [Colour figure can be viewed at wileyonlinelibrary.com]
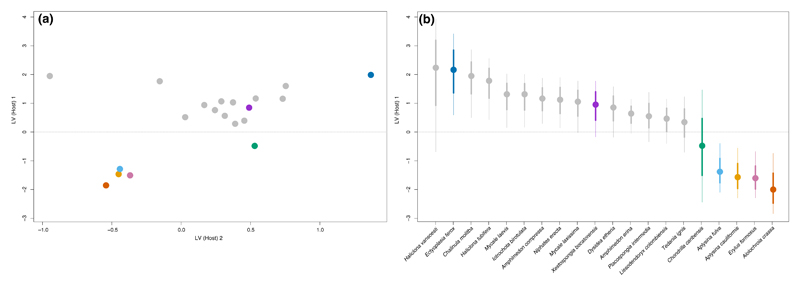
Figure 3.
Plot (a) shows the ordination constructed from the latent factors on the host species level ZH, and plot (b) shows the corresponding caterpillar for first latent factor The quantiles correspond to the 95% (thin lines) and 68% (thick lines) credible intervals, respectively [Colour figure can be viewed at wileyonlinelibrary.com]
Host ecotype and collection site roughly explained two-thirds of the remaining variation in relative abundance (Table 1). Furthermore, the host species level explained 39% of the variation beyond differences in relative abundance, with the remaining variation explained by the latent factors on the sample level. While samples did not cluster based on ecotype or sites, samples belonging to HMA hosts generally formed tighter clusters compared to samples from LMA hosts (Supporting Information Figure S3). Note however that because the sampling scheme in the original study confounded host ecotype and collection site, it is impossible to fully disentangle the two.
3.2. Case study 2
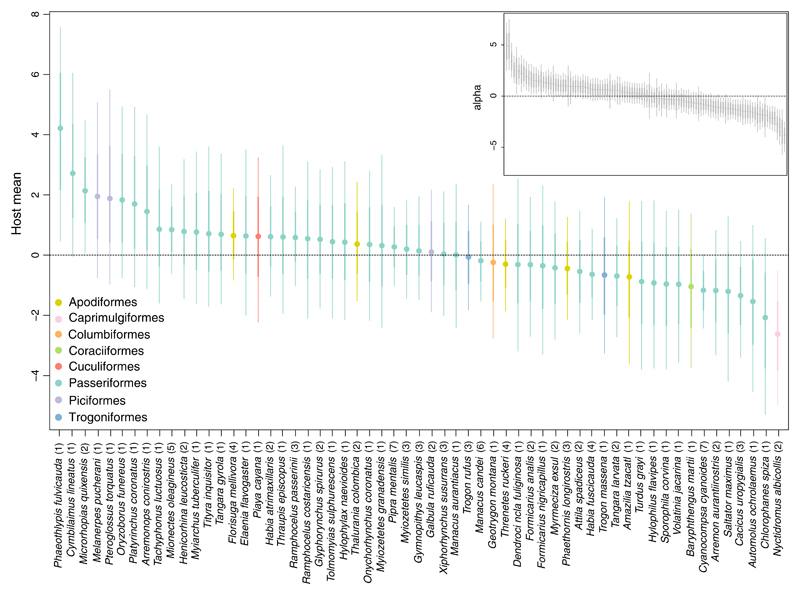
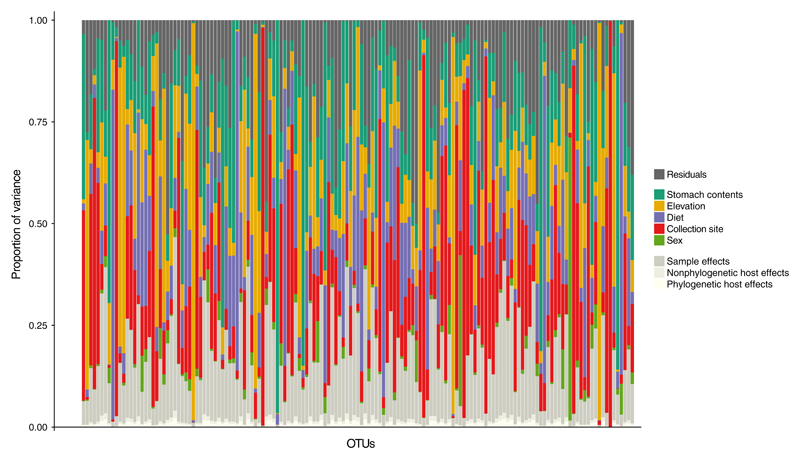
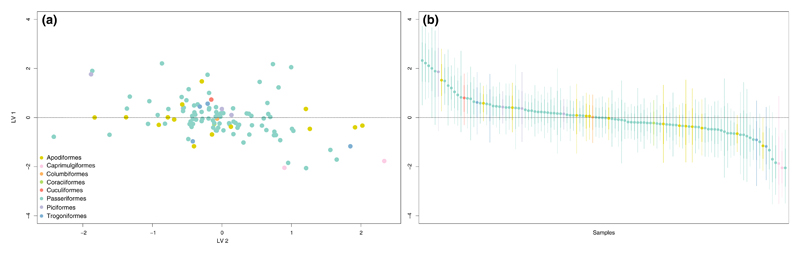
Fitting Model 2 to the data on Neotropical bird gut-associated microbiota (Hird et al., 2015) revealed that only 9% of the variation in species richness among samples could be explained by processes acting on the host species level, including processes related to the host phylogeny. The remaining 91% of this variation was captured by processes operating on the sample level (Table 2; Figure 4). Of the total variance in species occurrence, variation in species richness only accounted for, on average, about 17%. The modelled predictor variables explained 69% of the total variance and varied from a minimum of <0.01% to a maximum of 99.7% across all OTUs (Figure 5). The predictor variable that had the largest average effect on microbiota composition was collection site (21.33%; Table 2). However, none of the estimated regression coefficients for the predictor variables excluded zero (Supporting Information Figure S4). Furthermore, the ordination plots constructed from the first two latent factors did not reveal any obvious clustering by, for example, host taxonomy (at the order level), collection site or diet (broad dietary specialization) (Figure 6, Supporting Information Figures S5 and S6).
Table 2.
Variation attributed to the linear predictor Lij, the residual variation captured by the diagonal elements of the residual covariance matrix Ω, and by the hierarchy present on the row effects αi
| Collection site | 21.33% |
| Stomach contents | 16.13% |
| Elevation | 15.97% |
| Diet | 13.59% |
| Sex | 2.12% |
| Residuals | 13.89% |
| Sample | 15.5% |
| Nonphylogeny | 0.65% |
| Phylogeny | 0.82% |
Figure 4.
The main plot shows a caterpillar for the host means μ(host)s coloured by host taxonomy at the order level, while the subplot shows a caterpillar plot for the row effects αi. The quantiles correspond to the 95% (thin lines) and 68% (thick lines) credible intervals, respectively. The number within the parentheses shows how many individuals per host species were availible to draw inference on [Colour figure can be viewed at wileyonlinelibrary.com]
Figure 5.
The y-axis shows the relative proportion of variance in species occurrences explained by the hierarchy present on αi, the covariates included on the linear predictor Lij, and the residual variance not accounted for by the modelled effects, that is, the diagonal elements of the residual covariance matrix Ω, for each OTU (x-axis) [Colour figure can be viewed at wileyonlinelibrary.com]
Figure 6.
Plot (a) shows the ordination constructed from the latent factors Z coloured by host taxonomy (at the order level) and plot (b) shows the corresponding caterpillar plot for the first latent factor Zi1. The quantiles correspond to the 95% (thin lines) and 68% (thick lines) credible intervals, respectively [Colour figure can be viewed at wileyonlinelibrary.com]
We ran an edge betweenness community detection algorithm (Csardi & Nepusz, 2006) on the correlation matrix computed from the loading matrix λ where links represent positive and negative co-occurrences with at least 95% posterior probability. We coloured nodes by their bacterial taxonomic affiliation at the phylum level. This revealed a large tightly knit cluster with well-connected nodes in the centre and less-connected nodes in the periphery of the cluster. The network displayed similar proportions of positive and negative co-occurrences and with no apparent clustering of OTUs belonging to certain phyla (Supporting Information Figure S7). Caution should, however, be taken when interpreting statistical interactions: These are residual co-occurrences that can only be considered as hypotheses for ecological interactions, and without additional biological information, it is impossible to definitively confirm or assess their nature (Ovaskainen et al., 2016; Tikhonov, Abrego, Dunson, & Ovaskainen, 2017; Zurell, Pollock, & Thuiller, 2018).
4. Discussion
In this paper, we have developed a joint species distribution model (JSDM) aimed towards analysing host-associated microbiota data. The present work builds upon and extends existing JSDMs by specifically targeting the hierarchical structure implicit in host-associated microbiota studies, while also including several other features that are attractive for analysing such data. First, we have shown how overdispersed counts and presence-absence data, two common features of host–microbiota data can be modelled under a single framework by implementing a negative binomial and a probit distribution with the appropriate link function. Furthermore, we have utilized recent progress in latent factor modelling in order to represent the high-dimensional nature of host-microbiota data as a rank-reduced covariance matrix, thus making the estimation of large microbe-to-microbe covariance matrices computationally tractable. By doing so, we have also demonstrated how latent factors, both alone or together with measured covariates, can be used for variance partitioning and further visualized as ordinations and co-occurrence networks. At last, depending on the modelled response function, we have illustrated that the variance partitioning of the hierarchy present on the rows can be represented in terms of either relative abundance or species richness.
We adapted our proposed model to make use of two published data sets on host-associated microbiota. Although our goal was not to compare the results from these two case studies, such a systematic comparison can be made using a model-based approach like ours. In a broad manner, the data analysed here suggest that markedly different processes are shaping the microbiota harboured by these different host organisms. On an individual basis, the main results from each of our two models were generally in agreement with the results reported in their respective original study; for example, Model 1 identified the same four host species reported by Easson and Thacker (2014) to have more abundant and distinctively different microbiotas compared to the other analysed hosts. Similar to Hird et al. (2015), the ordinations produced by Model 2 did not cluster by host diet, host taxonomy nor collection site. By partitioning variance among fixed and random effects, Model 2 further showed that there was substantial variation across OTUs in terms of which predictor variables explained the most variance.
While distance-based methods such as PERMANOVA still remains one of the most widely used nonparametric methods to analyse host-associated microbiota data, model-based approaches are increasingly recognized to outperform such analyses (see, e.g., Grantham et al., 2017; Sohn & Li, 2017; Hui et al., 2015; Warton et al., 2012), and we see our proposed model as making a strong case for further empirical comparisons between distance-based and model-based approaches to analysing microbiota data.
There are a number of extensions one could make to the proposed model. Perhaps the most important of these stems from the growing recognition that high-throughput DNA sequencing produces compositional data, that is, non-negative counts with an arbitrary sum imposed by the sequencing platform, which can produce spurious correlations if not properly accounted for (see, e.g., Gloor, Macklaim, Pawlowsky-Glahn, & Egozcue, 2017; Li, 2015; Tsilimigras & Fodor, 2016). Because of the log-link function used in Model 1, it is possible to parameterize this model and regard it in terms of compositional effects (see Warton & Guttorp, 2011 and also noting the fact that the negative binomial distribution can itself be parameterized as a hierarchical Poisson model with Gamma-distributed random effects), although for ease of estimation and interpretation we chose to adopt the standard negative binomial parameterization. This topic remains an area of active research, and there are currently several model-based methods (see, e.g., Fang, Huang, Zhao, & Deng, 2015; Friedman & Alm, 2012; Kurtz et al., 2015; Schwager, Mallick, Ventz, & Huttenhower, 2017) to infer co-occurrence networks, each with its own set of assumptions–it is not yet conclusive that any one of these methods outperforms the rest.
Other model extensions and modifications can also be made to answer specific ecological questions of interest. For example, whether closely related host species harbour closely related microbes (i.e., host-microbiota phylogenetic congruence) or whether similarity among host-associated microbiota decreases as a function of increasing geographical distance or social connectance between hosts. Such questions may be answered for instance, by incorporating an additional phylogenetic effect acting on the columns of the response matrix, and by implementing a Gaussian process model that quantifies the degree of spatial and/or social autocorrelation between hosts, respectively. These two “flavours” of JSDMs and mixed models more generally have previously been considered in community ecology, both separately (Ives & Helmus, 2011; Ovaskainen, Roy, Fox, & Anderson, 2015; Thorson et al., 2015) and combined (Kaldhusdal et al., 2015), although both computation and successful estimation and inference of all the model parameters remain a major issue especially with the high-dimensional nature of host-associated microbiota data. In summary, while substantial methodological advances have been made over the past few years in developing an extensive model framework for community ecological data, to date there exists no similar unifying framework for modelling host-associated microbiota which is directly tailored to the hierarchical and correlation structures present as well as questions of interest specific to such data. Our proposed model, which explicitly accounts for the host’s effect in structuring its microbiota, takes us closer to that goal.
Acknowledgements
We thank Dr. Robert W. Thacker and Dr. Sarah Hird for sharing their data sets on the microbiota associated with marine sponges and Neotropical bird species, respectively. We further thank three anonymous reviewers for providing constructive feedback and comments. J.R.B was supported by an FPI Fellowship from the Spanish Government (BES-2011-049043). J.M.M. was supported by the French LabEx TULIP (ANR-10-LABX-41; ANR-11-IDEX-002-02), by the Region Midi-Pyrenees project (CNRS 121090) and by the FRAGCLIM Consolidator Grant, funded by the European Research Council under the European Union’s Horizon 2020 research and Innovation Programme (grant agreement number 726176).
Funding information
Spanish Government, Grant/Award Number: BES-2011-049043; LabEx TULIP, Grant/Award Number: ANR-10-LABX-41, ANR-11-IDEX-002-02; Region Midi-Pyrenees, Grant/Award Number: CNRS 121090; European Research Council
Footnotes
Code and Data Availability
All code and data are available on Open Science Framework (https://doi.org/10.17605/osf.io/t9nxh) with a tutorial on how to fit the model and analyse the output. While we used JAGS to fit the model in this study, we have translated the model into Greta (Golding, 2018), which is an R style probabilistic language that scales better to large data sets.
References
- Aivelo T, Norberg A. Parasite–microbiota interactions potentially affect intestinal communities in wild mammals. Journal of Animal Ecology. 2018;87(2):438–447. doi: 10.1111/1365-2656.12708. [DOI] [PubMed] [Google Scholar]
- Balint M, Bahram M, Eren AM, Faust K, Fuhrman JA, Lindahl B, et al. Tedersoo L. Millions of reads, thousands of taxa: Microbial community structure and associations analyzed via marker genes. FEMS Microbiology Reviews. 2016;40(5):686. doi: 10.1093/femsre/fuw017. [DOI] [PubMed] [Google Scholar]
- Berendsen RL, Pieterse CM, Bakker PA. The rhizosphere microbiome and plant health. Trends in Plant Science. 2012;17(8):478–486. doi: 10.1016/j.tplants.2012.04.001f. [DOI] [PubMed] [Google Scholar]
- Bhattacharya A, Dunson DB. Sparse Bayesian infinite factor models. Biometrika. 2011;98:291–306. doi: 10.1093/biomet/asr013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolker BM, Brooks ME, Clark CJ, Geange SW, Poulsen JR, Stevens MHH, White JSS. Generalized linear mixed models: A practical guide for ecology and evolution. Trends in Ecology & Evolution. 2009;24(3):127–135. doi: 10.1016/j.tree.2008.10.008. [DOI] [PubMed] [Google Scholar]
- Csardi G, Nepusz T. The igraph software package for complex network research. InterJournal Complex Systems. 2006;1695:1–9. [Google Scholar]
- Denwood M. runjags: An R package providing interface utilities, model templates, parallel computing methods and additional distributions for MCMC models in JAGS. Journal of Statistical Software. 2016;71(9):1–25. doi: 10.18637/jss.v071.i09. [DOI] [Google Scholar]
- Easson CG, Thacker RW. Phylogenetic signal in the community structure of host-specific microbiomes of tropical marine sponges. Frontiers in Microbiology. 2014;5:532. doi: 10.3389/fmicb.2014.00532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang H, Huang C, Zhao H, Deng M. CCLasso: correlation inference for compositional data through Lasso. Bioinformatics. 2015;31(19):3172–3180. doi: 10.1093/bioinformatics/btv349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Phylogenies and the comparative method. The American Naturalist. 1985;125(1):1–15. doi: 10.1086/284325. [DOI] [PubMed] [Google Scholar]
- Friedman J, Alm EJ. Inferring correlation networks from genomic survey data. PLOS Computational Biology. 2012;8(9):1–11. doi: 10.1371/journal.pcbi.1002687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A, Jakulin A, Pittau MG, Su YS. A weakly informative default prior distribution for logistic and other regression models. The Annals of Applied Statistics. 2008;2(4):1360–1383. doi: 10.1214/08-AOAS191. [DOI] [Google Scholar]
- Geweke JF. Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. Oxford, UK: Clarendon Press; 1991. [Google Scholar]
- Geweke J, Zhou G. Measuring the price of the Arbitrage Pricing Theory. The Review of Financial Studies. 1996;9(2):557–587. doi: 10.1093/rfs/9.2.557. [DOI] [Google Scholar]
- Gloeckner V, Wehrl M, Moitinho-Silva L, Gernert C, Schupp P, Pawlik R, et al. Hentschel U. The HMA-LMA dichotomy revisited: An electronmicroscopical survey of 56 sponge species. The Biological Bulletin. 2014;227(1):78–88. doi: 10.1086/BBLv227n1p78. [DOI] [PubMed] [Google Scholar]
- Gloor GB, Macklaim JM, Pawlowsky-Glahn V, Egozcue JJ. Microbiome datasets are compositional: And this is not optional. Frontiers in Microbiology. 2017;8:2224. doi: 10.3389/fmicb.2017.02224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding N. greta: Simple and Scalable Statistical Modelling in R. 2018 Retrieved from https://cran.r-project.org/web/packages/greta/
- Grantham NS, Reich BJ, Borer ET, Gross K. MIMIX: A bayesian mixed-effects model for microbiome data from designed experiments. 2017 eprint:arXiv: 1703.07747. [Google Scholar]
- Groussin M, Mazel F, Sanders JG, Smillie CS, Lavergne S, Thuiller W, Alm EJ. Unraveling the processes shaping mammalian gut microbiomes over evolutionary time. Nature Communications. 2017;8 doi: 10.1038/ncomms14319. 14319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haegeman B, Sen B, Godon JJ, Hamelin J. Only simpson diversity can be estimated accurately from microbial community fingerprints. Microbial Ecology. 2014;68(2):169–172. doi: 10.1007/s00248-014-0394-5. [DOI] [PubMed] [Google Scholar]
- Hird SM, Sánchez C, Carstens BC, Brumfield RT. Comparative gut microbiota of 59 neotropical bird species. Frontiers in Microbiology. 2015;6:1403. doi: 10.3389/fmicb.2015.01403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hui FKC. boral–Bayesian ordination and regression analysis of multivariate abundance data in R. Methods in Ecology and Evolution. 2016;7(6):744–750. doi: 10.1111/2041-210X.12514. [DOI] [Google Scholar]
- Hui FKC. Model-based simultaneous clustering and ordination of multivariate abundance data in ecology. Computational Statistics & Data Analysis. 2017;105:1–10. doi: 10.1016/j.csda.2016.07.008. [DOI] [Google Scholar]
- Hui FK, Taskinen S, Pledger S, Foster SD, Warton DI. Model-based approaches to unconstrained ordination. Methods in Ecology and Evolution. 2015;6(4):399–411. doi: 10.1111/2041-210X.12236. [DOI] [Google Scholar]
- Ives AR, Helmus MR. Phylogenetic metrics of community similarity. The American Naturalist. 2010;176(5):E128–E142. doi: 10.1086/656486. [DOI] [PubMed] [Google Scholar]
- Ives AR, Helmus MR. Generalized linear mixed models for phylogenetic analyses of community structure. Ecological Monographs. 2011;81(3):511–525. doi: 10.1890/10-1264.1. [DOI] [Google Scholar]
- Kaldhusdal A, Brandl R, Müller J, Möst L, Hothorn T. Spatio-phylogenetic multispecies distribution models. Methods in Ecology and Evolution. 2015;6:187–197. doi: 10.1111/2041-210X.12318. [DOI] [Google Scholar]
- Kurtz ZD, Müller CL, Miraldi ER, Littman DR, Blaser MJ, Bonneau RA. Sparse and compositionally robust inference of microbial ecological networks. PLOS Computational Biology. 2015;11(5):1–25. doi: 10.1371/journal.pcbi.1004226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legendre L, Legendre P. Numerical ecology. Developments in environmental modelling. Amsterdam, Netherlands: Elsevier; 1983. ISBN 9780444538680. [Google Scholar]
- Letten AD, Keith DA, Tozer MG, Hui FK. Fine-scale hydrological niche differentiation through the lens of multi-species cooccurrence models. Journal of Ecology. 2015;103(5):1264–1275. doi: 10.1111/1365-2745.12428. [DOI] [Google Scholar]
- Li H. Microbiome, metagenomics, and high-dimensional compositional data analysis. Annual Review of Statistics and Its Application. 2015;2(1):73–94. doi: 10.1146/annurev-statistics-010814-020351. [DOI] [Google Scholar]
- Li D, Ives AR. The statistical need to include phylogeny in traitbased analyses of community composition. Methods in Ecology and Evolution. 2017;8(10):1192–1199. doi: 10.1111/2041-210X.12767. [DOI] [Google Scholar]
- Liu S, da Cunha AP, Rezende RM, Cialic R, Wei Z, Bry L, et al. Weiner HL. The host shapes the gut microbiota via fecal microRNA. Cell Host & Microbe. 2016;19(1):32–43. doi: 10.1016/j.chom.2015.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFall-Ngai M, Hadfield MG, Bosch TC, Carey HV, Domazet-Lošo T, Douglas AE, et al. Hentschel U. Animals in a bacterial world, a new imperative for the life sciences. Proceedings of the National Academy of Sciences. 2013;110(9):3229–3236. doi: 10.1073/pnas.1218525110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKay CS. Create Plots from MCMC Output. 2015 Retrieved from https://cran.r-project.org/web/packages/mcmcplots/
- Muegge BD, Kuczynski J, Knights D, Clemente JC, González A, Fontana L, et al. Gordon JI. Diet drives convergence in gut microbiome functions across mammalian phylogeny and within humans. Science. 2011;332(6032):970–974. doi: 10.1126/science.1198719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagawa S, Schielzeth H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution. 2013;4(2):133–142. doi: 10.1111/j.2041-210x.2012.00261.x. [DOI] [Google Scholar]
- Ovaskainen O, Abrego N, Halme P, Dunson D. Using latent variable models to identify large networks of species-to-species associations at different spatial scales. Methods in Ecology and Evolution. 2016;7(5):549–555. doi: 10.1111/2041-210X.12501. [DOI] [Google Scholar]
- Ovaskainen O, Roy DB, Fox R, Anderson BJ. Uncovering hidden spatial structure in species communities with spatially explicit joint species distribution models. Methods in Ecology and Evolution. 2015;7(4):428–436. doi: 10.1111/2041-210X.12502. [DOI] [Google Scholar]
- Ovaskainen O, Tikhonov G, Norberg A, Guillaume Blanchet F, Duan L, Dunson D, et al. Abrego N. How to make more out of community data? A conceptual framework and its implementation as models and software. Ecology Letters. 2017;20(5):561–576. doi: 10.1111/ele.12757. [DOI] [PubMed] [Google Scholar]
- Plummer M. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. 2003 Retrieved from https://www.r-project.org/conferences/DSC-2003/
- Plummer M, Best N, Cowles K, Vines K. CODA: convergence diagnosis and output analysis for MCMC. 2016 Retrieved from https://cran.r-project.org/web/packages/coda/
- Pollock LJ, Tingley R, Morris WK, Golding N, O’Hara RB, Parris KM, et al. McCarthy MA. Understanding co-occurrence by modelling species simultaneously with a Joint Species Distribution Model (JSDM) Methods in Ecology and Evolution. 2014;5(5):397–406. doi: 10.1111/2041-210X.12180. [DOI] [Google Scholar]
- Polson NG, Scott JG. On the half-Cauchy prior for a global scale parameter. Bayesian Analysis. 2012;7(4):887–902. doi: 10.1214/12-BA730. [DOI] [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2016. [Google Scholar]
- Schwager E, Mallick H, Ventz S, Huttenhower C. A Bayesian method for detecting pairwise associations in compositional data. PLOS Computational Biology. 2017;13(11):1–21. doi: 10.1371/journal.pcbi.1005852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skrondal A, Rabe-Hesketh S. Chapman Hall & Hall/CRC Interdisciplinary Statistics. CRC Press; 2004. Generalized latent variable modeling: Multilevel, longitudinal, and structural equation models. ISBN: 9780203489437. Retrieved from https://books.google.com/books?id=YUpDqCzb-WMC. [Google Scholar]
- Sohn MB, Li H. A GLM-based latent variable ordination method for microbiome samples. Biometrics. 2017 doi: 10.1111/biom.12775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson JN. The coevolutionary process. Chicago, IL: University of Chicago Press; 1994. [DOI] [Google Scholar]
- Thorson JT, Scheuerell MD, Shelton AO, See KE, Skaug HJ, Kristensen K. Spatial factor analysis: A new tool for estimating joint species distributions and correlations in species range. Methods in Ecology and Evolution. 2015;6(6):627–637. doi: 10.1111/2041-210X.12359. [DOI] [Google Scholar]
- Tikhonov G, Abrego N, Dunson D, Ovaskainen O. Using joint species distribution models for evaluating how speciestospecies associations depend on the environmental context. Methods in Ecology and Evolution. 2017;8(4):443–452. doi: 10.1111/2041-210X.12723. [DOI] [Google Scholar]
- Tsilimigras MC, Fodor AA. Compositional data analysis of the microbiome: Fundamentals, tools, and challenges”. Annals of Epidemiology. 2016;26(5):330–335. doi: 10.1016/j.annepidem.2016.03.002. [DOI] [PubMed] [Google Scholar]
- Vellend M. Conceptual synthesis in community ecology. The Quarterly Review of Biology. 2010;85(2):183–206. doi: 10.1086/652373. [DOI] [PubMed] [Google Scholar]
- Warton DI, Blanchet FG, O’Hara RB, Ovaskainen O, Taskinen S, Walker SC, Hui FK. So many variables: Joint modeling in community ecology. Trends in Ecology and Evolution. 2015;30:1–14. doi: 10.1016/j.tree.2015.09.007. [DOI] [PubMed] [Google Scholar]
- Warton DI, Guttorp P. Compositional analysis of overdispersed counts using generalized estimating equations. Environmental and Ecological Statistics. 2011;18(3):427–446. doi: 10.1007/s10651-010-0145-9. [DOI] [Google Scholar]
- Warton DI, Wright ST, Wang Y. Distance-based multivariate analyses confound location and dispersion effects. Methods in Ecology and Evolution. 2012;3(1):89–101. doi: 10.1111/j.2041-210X.2011.00127.x. [DOI] [Google Scholar]
- Xia F, Chen J, Fung WK, Li H. A logistic normal multinomial regression model for microbiome compositional data analysis. Biometrics. 2013;69(4):1053–1063. doi: 10.1111/biom.12079. [DOI] [PubMed] [Google Scholar]
- Xu L, Paterson AD, Xu W. Bayesian latent variable models for hierarchical clustered count outcomes with repeated measures in microbiome studies. Genetic Epidemiology. 2017;41(3):221–232. doi: 10.1002/gepi.22031. [DOI] [PubMed] [Google Scholar]
- Yatsunenko T, Rey FE, Manary MJ, Trehan I, Dominguez-Bello MG, Contreras M, et al. Heath AC. Human gut microbiome viewed across age and geography. Nature. 2012;486(7402):222–227. doi: 10.1038/nature11053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Mallick H, Tang Z, Zhang L, Cui X, Benson AK, Yi N. Negative binomial mixed models for analyzing microbiome count data. BMC Bioinformatics. 2017;18(1):4. doi: 10.1186/s12859-016-1441-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zurell D, Pollock LJ, Thuiller W. Do joint species distribution models reliably detect interspecific interactions from co occurrence data in homogenous environments? Ecography. 2018 doi: 10.1111/ecog.03315. [DOI] [Google Scholar]