Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 May 29;9(12):3271–3277. doi: 10.1021/acs.jpclett.8b01470

Dissociative Chemisorption of O2 on Al(111): Dynamics on a Correlated Wave-Function-Based Potential Energy Surface

Rongrong Yin †, Yaolong Zhang †, Florian Libisch ‡, Emily A Carter §, Hua Guo ∥, Bin Jiang †,*
PMCID: PMC6025882  PMID: 29843512

Abstract

graphic file with name jz-2018-01470g_0006.jpg

Dissociative chemisorption of O2 on the Al(111) surface represents an extensively studied prototype for understanding the interaction between O2 and metal surfaces. It is well known that the experimentally observed activation barrier for O2 dissociation is not captured by conventional density functional theory. The interpretation of this barrier as a result of spin transitions along the reaction path has been challenged by recent embedded correlated wave function (ECW) calculations that naturally yield an adiabatic barrier. However, the ECW calculations have been limited to a static analysis of the reaction pathways and have not yet been tested by dynamics simulations. We present a global six-dimensional potential energy surface (PES) for this system parametrized with ECW data points. This new PES provides a reasonable description of the site-specific and orientation-dependent activation barriers. Quasi-classical trajectory calculations on this PES semiquantitatively reproduce both the observed translational energy dependence of the sticking probability and steric effects with aligned O2 molecules.

As the initial and often rate-determining step in heterogeneous catalysis, dissociative chemisorption of molecules on metal surfaces continues to attract much attention. Experimentally, energy- and quantum-state-resolved initial sticking probabilities have been measured for various molecules using the molecular beam approach under ultrahigh vacuum.1−3 These measurements are complemented by theoretical investigations of dissociation and scattering dynamics in high-dimensional spaces,4−8 which have been almost exclusively based on a density functional theory (DFT) characterization of the electronic structure. Over several decades, these studies have shed light on how molecular dissociation depends on translational and internal excitations as well as on the orientation of the incident molecule, greatly improving our understanding of this key elementary process at the gas–solid interface. In a few cases, such as H2 dissociation on Cu surfaces, quantitative understanding has been achieved.9

Despite much progress, however, there are several enigmatic systems where a clear understanding is still lacking.10 One such example is the dissociation of O2 on metals, which is of great fundamental and practical importance.11 It is well established that O2 has very small sticking probabilities on Al(111) at ambient temperatures, despite a large reaction exothermicity.12 Measurements by Kasemo and coworkers indicate that O2 directly dissociates on Al(111) and that the initial sticking probability strongly depends on the kinetic energy of the molecule perpendicular to the surface, rising from near zero to 90% within ∼0.6 eV.13 This energy dependence was later confirmed by Komrowski et al.14 In addition, vibrational excitations of the impinging molecule are found to enhance dissociation, although the evidence is less certain.13 These observations were rationalized by the existence of a dissociation barrier, which can be overcome with energy in either translational or vibrational degrees of freedom. Yet theoretical studies based on Kohn–Sham DFT within the generalized gradient approximation (GGA) found no adiabatic barrier for the dissociative process,15−17 in sharp contrast with the experimental findings. To resolve this apparent contradiction, Behler et al. proposed a spin-constrained model in which the spin of the entire system is restricted to a triplet state potential energy surface (PES). A small dissociation barrier on this triplet PES results from nonadiabatic crossing between the singlet and triplet states of the impinging O2 molecule, yielding a theoretical sticking probability curve that is quite similar to the experimental observation.18,19 Later, Carbogno et al. further included the nonadiabatic transitions between the two states using a surface-hopping (SH) approach and obtained a qualitatively similar result as that on the single triplet PES.20,21

Despite its appeal, the proposed spin-flip model has been challenged because of the approximations to exchange-correlation necessary within DFT.22−27 In particular, some of the current authors27 have demonstrated based on embedded correlated wave function (ECW) theory28 that the barrier for O2 dissociation on Al(111) emerges naturally on the adiabatic PES, thanks to an abrupt charge transfer,29 rather than a spin flip. Similar barriers were found for O2 dissociation on Al clusters using either a wave-function-based method23,25 or range-separated DFT24 and on Al slabs using hybrid functionals.26 It was argued that the intrinsic deficiencies within the GGA DFT framework, such as self-interaction errors and lack of derivative discontinuities, overly delocalize electrons and lead to the absence of a barrier.23,24,27 As a result, a higher-level description of the charge-transfer processes using, for example, ECW theory, seems necessary to provide a physically correct description. However, neither a full-dimensional global PES nor dynamics based on ECW theory have been reported, leaving a direct comparison with experimental observables still missing.

In addition to the aforementioned energy-resolved experiments, measurements have been reported on the steric effect in O2 dissociation on Al(111). Using an O2 (X3Σg–) beam aligned by a magnetic hexapole, Kurahashi and Yamauchi found that O2 dissociation is dominated by an initial orientation of the molecule parallel to the surface.30 This experimental observation is consistent with the anisotropy of the ECW data,31 providing further support of its validity. In this Letter, we report an analytical six-dimensional (6D) global PES based on over 700 ECW data points as well as the dissociation dynamics on this new PES. Good agreement with the experimentally observed energy and angular dependence of the sticking probability is obtained, firmly validating the accuracy of the PES.

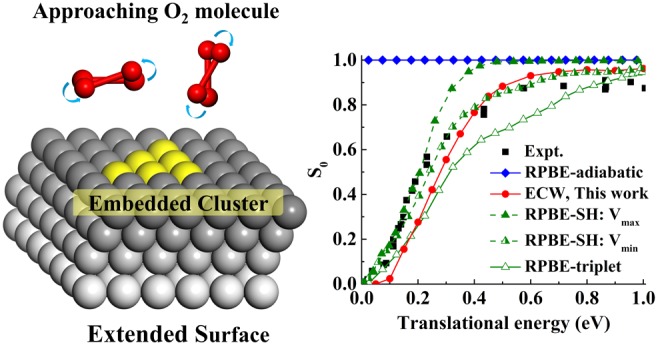
The details of ECW theory, PES representation, as well as quasi-classical trajectory calculations can be found in the Supporting Information (SI). In brief, we put the O2 molecule above a small cluster of 10 to 14 atoms embedded in an Al(111) slab composed of a periodic 5 × 5 supercell and four metal layers27,31 and first treat the entire system with DFT (EtotDET). An embedding potential (Vemb) mediates the interaction between the cluster and its environment following density-functional embedding theory.32 The energy of the cluster itself is computed by second-order multireference many-body perturbation theory33 as well as DFT, both in the presence of Vemb, yielding Ecluster and EclusterDEF,emb, respectively. The ECW total energy thus is expressed as

graphic file with name jz-2018-01470g_m001.jpg 1

To construct the PES, we collect over 700 single points above three high-symmetry sites: top, bridge, and fcc. These data were mainly used to generate the two-dimensional (2D) cuts reported in refs (27) and (31) with the O2 molecule lying either parallel or perpendicular to the surface. Because of the limited number of data points, we took advantage of the physically inspired flexible periodic London–Eyring–Polanyi–Sato (FPLEPS) function34,35 to represent the 6D PES. This FPLEPS approach has been validated in describing the reaction dynamics of both dissociative chemisorption and Eley–Rideal reactions for N2 and H2 interacting with tungsten surfaces.34−36

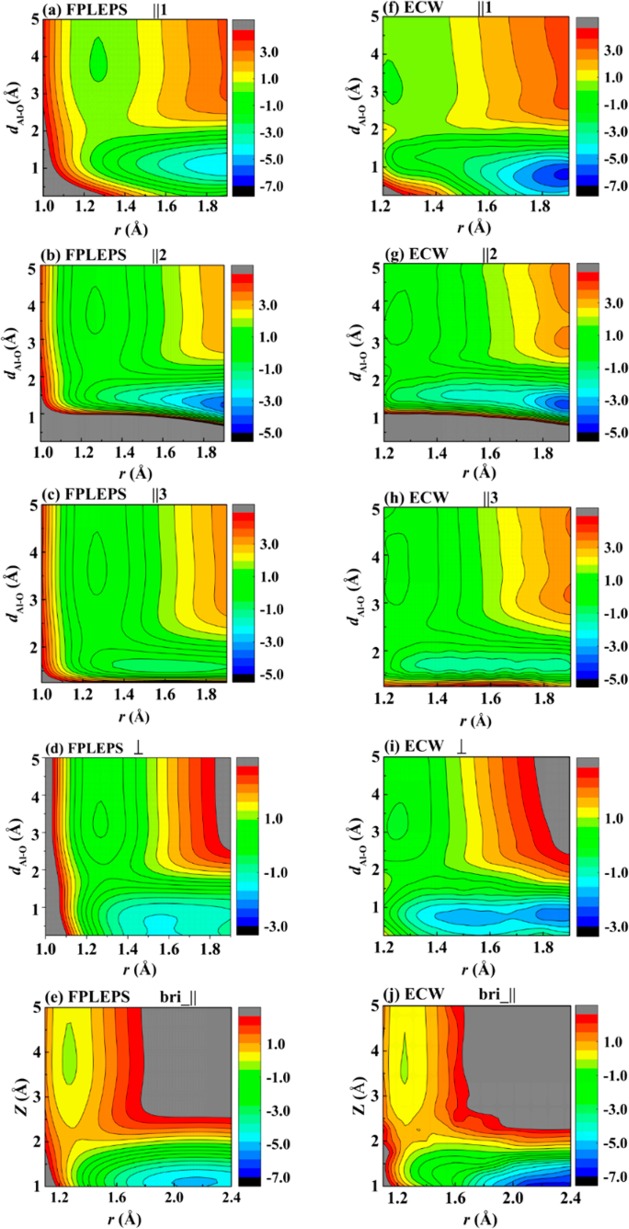
As a first consistency check, we use our analytical FPLEPS approach to reproduce the 2D elbow plots of the O2/Al (111) PES reported in refs (27) and (31) (Figure 1). Importantly, the raw ECW data contain systematic small-scale fluctuations27 in the final energies due to the nonvariational nature of many-body perturbation theory, resulting in unphysical wrinkles in the PES. These wrinkles are absent in the analytical FPLEPS PES, providing a much smoother representation that allows for dynamical calculations. The shallow physisorption wells and dissociation barriers in the entrance channel are all qualitatively reproduced in the FPLEPS PES as well as the deep wells after dissociation representing the coadsorbed oxygen atoms. In addition, despite the lack of ECW data with r smaller than 1.2 Å, the FPLEPS PES correctly predicts the repulsive feature in this short-range region thanks to its physically inspired analytical form. By contrast, the more widely used corrugation reducing procedure (CRP)9,37 and neural-network-based (NN)38−41 PESs could run into problems here because they rely on ab initio data exclusively.

Figure 1.

Figure 1

Open in a new tab

Comparison of 2D (elbow) contour plots for the dissociative chemisorption of O2 on Al(111) generated by the FPLEPS PES (left column) and the raw ECW data (right column), with O2 oriented parallel at the fcc site with //1 (a,f), //2 (b,g), and //3 (c,h), perpendicular at the fcc site (d,i) as a function of Al–O (dAl–O) and O–O distances (r), and parallel at the bridge site (e,j) as a function of molecular height above surface (z) and r. Energies are in electronvolts. The zero of energy corresponds to that of O2 at its equilibrium geometry (r = 1.25 Å) at a distance of 6 Å above the surface.

More quantitatively, the barrier locations and heights obtained from the raw ECW data and the FPLEPS PES are compared in Table 1 for different surface sites and molecular orientations. By removing the unphysical wrinkles, the analytical form of the FPLEPS function allows for a more precise extraction of stationary points of the PES. The FPLEPS PES largely captures the site-specific and orientation-dependent features provided by the ECW data, although it does not reproduce all numbers exactly. For example, the minimum energy pathway at the fcc site with a specific parallel orientation along the [1̅21̅] direction (labeled as //3 here and in ref (31)) is quantitatively reproduced with merely the same barrier height and 0.07 Å difference in the vertical position of O2 at the saddle point. This guarantees an adequate description of the reaction dynamics at lowest energies. In addition, the FPLEPS PES also reproduces the incremental increase in the barrier height by varying the molecular orientation along the azimuthal direction from [1̅21̅] to [011̅] (//2) and [112̅] (//1), although the barriers are lower than the estimated ECW values for the [011̅] and [112̅] by ∼0.17 eV. The minimum energy barrier for the //3 orientation has been ascribed to the largest amount of orbital overlap of the outer O atom and a surface Al atom, which facilitates the charge-transfer process.31

Table 1. Location of O2 and Energy at the Site-Specific Barriers for Dissociative Chemisorption Optimized on the FPLEPS PES and Estimated with Raw ECW Dataa.

    barrier height (eV)
 zTS/dAl–OTS (Å)
site O–O orientation FPLEPS ECW FPLEPS ECW
fccb //1 0.48 0.62 2.23 1.9
//2 0.28 0.45 2.25 2.2
//3 0.19 0.19 2.33 2.4
⊥ 0.36 0.43 1.90 1.9
topc // 0.19 0.66 2.00 2.6
⊥   0.66d   2.8
bridgec // 0.55 0.56 2.20 2.4
⊥ 0.72 0.45 2.40 2.7
Open in a new tab
a

Bold numbers indicate that these data have been included in fitting.

b

Ref (31).

c

Ref (27).

d

This number corresponds to a saddle point before the steep rise of the potential but not to dissociation.

More importantly, the perpendicular orientation (⊥) at the fcc site is found to have an intermediate barrier (0.36 eV), which is higher than that of //3 but lower than that of //1, again in good agreement with the original ECW data. The preference of certain parallel orientation over the perpendicular one could serve as the origin of the experimentally observed steric effect, as discussed in more detail below. At the bridge site, we have used only one set of data with parallel orientation //1 in the fitting, for which the barrier height (0.55 vs 0.56 eV) and location (dAl–O2barrier = 2.2 vs 2.4 Å) are well reproduced. The FPLEPS PES, however, presents a higher barrier than the estimated ECW value for the perpendicular orientation apparently due to the smaller number of ECW data points for the bridge site. Similarly, we have only ∼50 points on the top site, with the O2 molecule lying along the //3 orientation. As a result, the FPLEPS description on the top site may be less certain. Whereas both ECW data and the FPLEPS PES present a consistent picture that the perpendicular configuration at the top site results in no dissociative product with O–O bond broken, the FPLEPS barrier height is much lower than the estimated ECW value for the //3 orientation. Parameters yielding a barrier height more comparable to the ECW results would, in turn, be inconsistent with the ECW data on the angular degrees of freedom. Interestingly, the top site potential is somewhat similar to that in the triplet DFT PES.19 We emphasize that the parameters we obtain are fit from hundreds of ECW values, while we compare here only a very limited set determining the barrier heights, most of which agree very well between the FPLEPS and ECW data. To check the robustness of our predictions, we have nevertheless calculated dissociation probability curves for several parametrizations, emphasizing the agreement of the FPLEPS model with the ECW data in different regions, and found no qualitative change. We thus conclude that the deviations at the top site only affect the quantitative agreement with experiment but not the qualitative conclusions of the present work. As detailed in the SI, our FPLEPS PES 2D cuts also demonstrate a strong dependence of the barrier on the angular coordinates, which are in general accord with the previous analyses based on the original ECW data.31

After benchmarking our analytical FPLEPS PES against the original ECW data, we can now perform dynamics simulations to evaluate the normal incidence sticking probability (S0) of the ground ro-vibrational state O2 on the Al(111) surface (Figure 2). We compare our results with previous ones from DFT-based PESs18 using the revised Perdew–Burke–Ernzerhof (RPBE) functional,42 as well as with the experimental data of Österlund et al.,13 as a function of translational energy (Et) from 0.02 to 1.0 eV. Conventional DFT results in an unphysical, near-unit S0 that is independent of translational energy due to the absence of a barrier to dissociation.27 The sticking probability calculated on the triplet DFT PES alone qualitatively reproduces the measured translational dependence and yields a translational energy threshold that agrees with the experimental one (∼0.024 eV) well.18,19 However, the sticking probability is too small over most incident translational energies, especially in the middle range 0.2 ≤ Et ≤ 0.7 eV, with a slower increase with increasing Et compared with experiment. Given that the final state in dissociative chemisorption will be a singlet (two chemisorbs oxygen atoms), the restriction to a triplet surface is unphysical. The inclusion of nonadiabatic transitions from the triplet state to a singlet state using the SH method increases S0, but its effect depends on the coupling of the two states.21 Although the maximal coupling (Vmax) was argued to be closer to the true coupling, it yields too large a sticking probability compared with experiment.21 In comparison, the calculated S0 on our ECW-based FPLEPS PES, which contains no tunable coupling parameters, also captures the activated nature of O2 dissociative chemisorption on Al(111) and predicts the translational dependence in better agreement with the experiment for Et ≥ ∼0.2 eV, albeit with a slightly higher threshold than measured (by ∼0.05 eV). A slightly higher saturated S0 value than experiment is as expected given that we neglect the energy dissipation to the surface phonons and electron–hole pairs, either of which could reduce the reactivity.43−45 This result provides dynamical evidence in support of an activation barrier naturally originating from an abrupt charge transfer from metal to O2, which cannot be treated correctly using standard DFT functionals.27,28 The discrepancy in the threshold in S0 may stem from the remaining errors in the barrier height due to the finite cluster size and the non-self-consistent Vemb in the ECW calculations,28 since the FPLEPS PES describes the minimum energy pathway fairly well.

Figure 2.

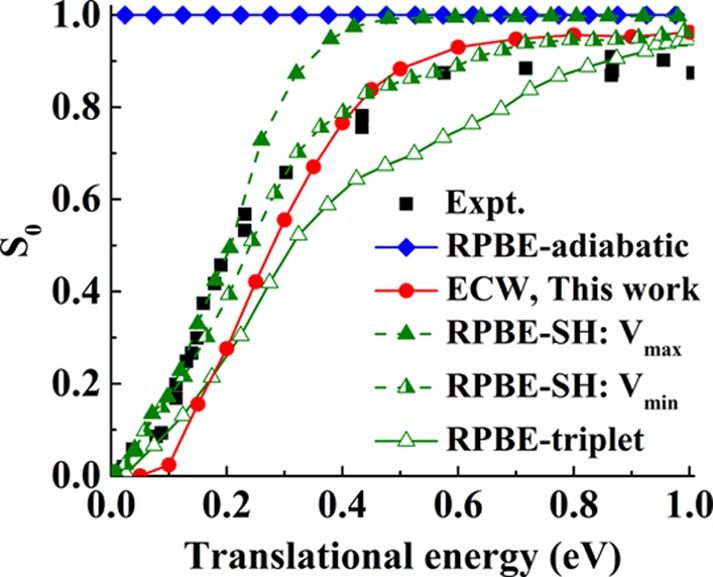
Figure 2

Open in a new tab

Comparison of dissociative sticking probability (S0) of O2 on Al(111) obtained with the RPBE adiabatic PES (blue diamonds),19 RPBE-triplet PES (green open triangles),19 surface-hopping (SH) method with a maximal (Vmax, green filled triangles) and a minimal coupling (Vmin, green half-filled triangles) between the triplet and singlet states,21 and ECW FPLEPS PES (red circles) with experiment13 (black squares) as a function of translational energy.

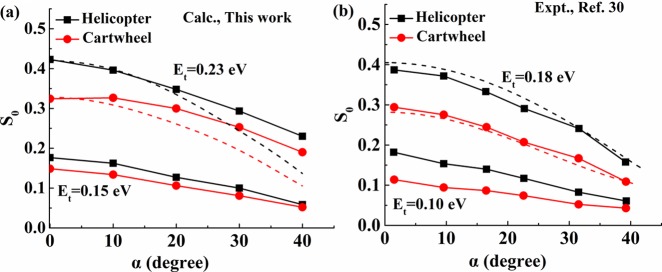
Next, we turn to the steric effect, which reflects the dependence of the reactivity on the initial alignment of the O2 molecule. In Figure 3, we compare the calculated sticking probabilities of O2 for helicopter [S0(H)], perpendicular [S0(P)], as well as random [S0(R)] orientations to their experimental counterparts.30 As already suggested by the normal incidence sticking probability (Figure 2), the predicted minimum barrier height is too high by ∼0.05 eV, resulting in a corresponding shift of the calculated S0 curves for all molecular orientations to higher Et. Still, the ECW-based FPLEPS PES correctly reproduces the strong preference of reactivity for the helicopter geometry, except at the lowest energies (Et < 0.15 eV). In good agreement with experiment, our results show that the translational energy difference between the helicopter and perpendicular geometries for the same S0 is roughly 0.1 eV. This steric effect can certainly be attributed to a lower barrier height for the //3 orientation than for the perpendicular orientation. To the best of our knowledge, no comparable dynamical studies on orientation effects have been reported for the DFT PES.

Figure 3.

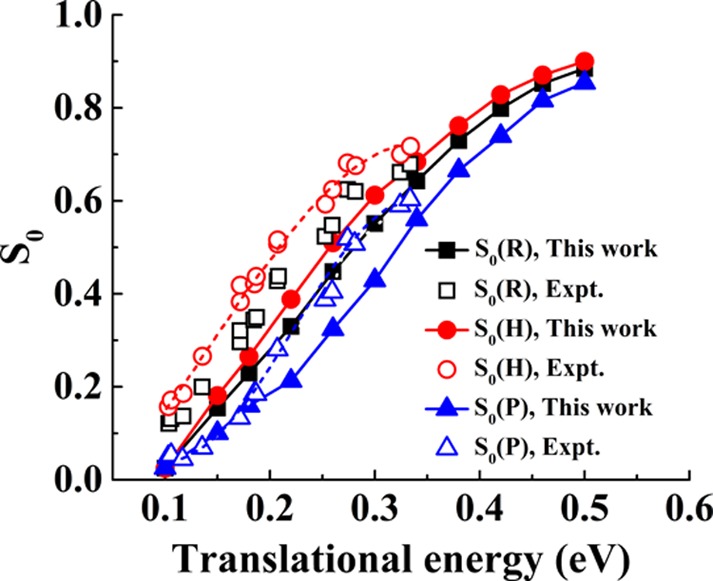
Figure 3

Open in a new tab

Translational energy dependence of the O2 sticking probability (S0) on Al (111) for three different orientations (helicopter (H), random (R), and perpendicular (P)). Solid and open symbols correspond to theoretical (this work) and experimental30 results, respectively. Solid and dashed lines are meant to guide the eyes.

In general, decreasing Et would weaken the steric effect, as observed, for example, in H2 adsorption on Cu(111)46 and NO adsorption on Al(111).47 This phenomenon usually results from a steering effect, which redirects the incoming molecule to a more favorable orientation and is operative at low energies where the molecule has sufficient time to reorient. In our calculations, the steric effect indeed disappears at very low energies. However, the preference for the parallel geometry is still very strong in experiment, even when Et is as low as 0.06 eV.30 This discrepancy indicates that the current PES may predict a too strong steering effect.

We finally discuss the dependence of the sticking probability on the incident angle (α) for helicopter [S0(H)] and cartwheel [S0(C)] orientations (Figure 4). In experiment,30 Kurahashi and Yamauchi showed at Et = 0.1 and 0.18 eV that the α-dependent sticking probability scales with the translational energy normal to the surface (En), representing the normal energy scaling behavior. Because our PES predicts a higher barrier height by ∼0.05 eV compared with experiment, we present in Figure 4 the calculated results at Et = 0.15 and 0.23 eV, respectively. Both S0(H) and S0(C) decrease monotonically with decreasing incident angle, and the preference for the helicopter geometry never changes, in qualitative agreement with experiment. However, the calculated S0 curves deviate from the normal energy scaling with increasing α, indicating that the PES is highly corrugated so that the parallel momentum can promote dissociative sticking. Such a strong corrugation also may be responsible for the steering effect at low energies seen in Figure 3. The remaining discrepancies between theory and experiment suggest that the current FPLEPS PES is still not quantitatively accurate and further improvement is required, perhaps by adding more points at low-symmetry sites and with various molecular orientations and by employing more accurate NN-based or CRP methods.

Figure 4.

Figure 4

Open in a new tab

Comparison of the O2 dissociative sticking probability as a function of incident angle (α) for helicopter and cartwheel orientations obtained from this work (left panel, Et = 0.15 and 0.23 eV) and experiment30 (right panel, Et = 0.10 and 0.18 eV). The difference between experimental and theoretical translational energies accounts for the overestimation of the barrier by roughly 0.05 eV by theory. The incident plane is directed to the [111] (112̅]) direction of the Al(111) surface. The dashed lines correspond to the normal energy scaling curves derived from the translational dependence of S0 with normal incidence.

In summary, we investigated the reaction dynamics of dissociative chemisorption of O2 on Al(111) with a newly developed full-dimensional PES based on accurate ECW calculations. Taking advantage of the flexible and analytical FPLEPS function, we were able to construct a global 6D PES with just 700 previously computed ECW points, largely reproducing the site-specific and orientation-dependent activation barriers and the anisotropy in angular degrees of freedom found in the original ECW studies.27,31 Dynamics based on this new PES semiquantitatively reproduce the translational energy dependence in the experimental data, capturing the activated nature suggested in experimental work.13,30 In addition, O2 initially aligned parallel to the surface is more reactive than the perpendicular one as a result of an overall lower barrier by ∼0.1 eV for the parallel orientation, again in good agreement with experiment.30 Such a steric effect is always present as the incident angle varies from 0 to 40° with respect to surface normal, while the sticking probability decreases monotonically, in qualitative agreement with experiment.30 Despite these successes, quantitatively, the onset of sticking is shifted to higher energies by roughly ∼0.05 eV compared with experiment13,30 and does not obey the normal energy scaling law,30 presumably due to the uncertainty of the barrier heights in the ECW calculations and approximation in the FPLEPS function.

We emphasize that this work reports the first global multidimensional PES for a gas-surface reaction using points generated from an embedded approach based on a high-level, ab initio treatment of the reaction zone. The move beyond conventional DFT, which is known to suffer from many weaknesses due to intrinsic approximations, is expected to encourage the development of more accurate electronic structure methods for describing molecule–surface interactions. Further improvement of the ECW-based PES can be done with more ECW points, which will allow us to apply more accurate NN-based or CRP methods to gain a more quantitative understanding for this important gas-surface reaction.

Acknowledgments

This work was supported by National Key R&D Program of China (2017YFA0303500 to B.J.), National Natural Science Foundation of China (21722306, 91645202, and 21573203 to B.J.), and U.S. National Science Foundation (CHE-1462109 to H.G.). B.J. also appreciates support from Anhui Initiative in Quantum Information Technologies. F.L. acknowledges support by the Austrian Science Fund, FWF SFB-041 ViCoM. E.A.C. is grateful for support from the National Science Foundation under award no. 1265700. We thank Dr. Jin Cheng for sending us part of the ab initio data and for helpful discussion in the beginning of this project.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.8b01470.

  • Details of ECW theory, PES representation, as well as the quasi-classical trajectory calculations. (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz8b01470_si_001.pdf (1.5MB, pdf)

References

  1. Juurlink L. B. F.; Killelea D. R.; Utz A. L. State-resolved probes of methane dissociation dynamics. Prog. Surf. Sci. 2009, 84, 69–134. 10.1016/j.progsurf.2009.01.001. [DOI] [Google Scholar]
  2. Beck R. D.; Utz A. L.. Quantum-State Resolved Gas/Surface Reaction Dynamics Experiments. In Dynamics of Gas-Surface Interactions; Muiño R. D., Busnengo H. F., Eds.; Springer: Heidelberg, 2013. [Google Scholar]
  3. Chadwick H.; Beck R. D. Quantum state resolved gas-surface reaction dynamics experiments: a tutorial review. Chem. Soc. Rev. 2016, 45, 3576–3594. 10.1039/C5CS00476D. [DOI] [PubMed] [Google Scholar]
  4. Gross A. Reactions at surfaces studied by ab initio dynamics calculations. Surf. Sci. Rep. 1998, 32, 291–340. 10.1016/S0167-5729(98)00008-9. [DOI] [Google Scholar]
  5. Kroes G.-J. Six-dimensional quantum dynamics of dissociative chemisorption of H2 on metal surfaces. Prog. Surf. Sci. 1999, 60, 1–85. 10.1016/S0079-6816(99)00006-4. [DOI] [Google Scholar]
  6. Kroes G.-J. Towards chemically accurate simulation of molecule–surface reactions. Phys. Chem. Chem. Phys. 2012, 14, 14966–14981. 10.1039/c2cp42471a. [DOI] [PubMed] [Google Scholar]
  7. Jiang B.; Yang M.; Xie D.; Guo H. Quantum dynamics of polyatomic dissociative chemisorption on transition metal surfaces: Mode specificity and bond selectivity. Chem. Soc. Rev. 2016, 45, 3621–3640. 10.1039/C5CS00360A. [DOI] [PubMed] [Google Scholar]
  8. Guo H.; Farjamnia A.; Jackson B. Effects of lattice motion on dissociative chemisorption: Toward a rigorous comparison of theory with molecular beam experiments. J. Phys. Chem. Lett. 2016, 7, 4576–4584. 10.1021/acs.jpclett.6b01948. [DOI] [PubMed] [Google Scholar]
  9. Díaz C.; Pijper E.; Olsen R. A.; Busnengo H. F.; Auerbach D. J.; Kroes G.-J. Chemically accurate simulation of a prototypical surface reaction: H2 dissociation on Cu(111). Science 2009, 326, 832–834. 10.1126/science.1178722. [DOI] [PubMed] [Google Scholar]
  10. Kroes G.-J. Frontiers in surface scattering simulations. Science 2008, 321, 794–797. 10.1126/science.1157717. [DOI] [PubMed] [Google Scholar]
  11. Carbogno C.; Gross A.; Meyer J.; Reuter K.. O2 Adsorption Dynamics at Metal Surfaces: Non-Adiabatic Effects, Dissociation and Dissipation. In Dynamics of Gas-Surface Interactions; Díez Muiño R., Busnengo H. F., Eds.; Springer: Heidelberg, 2013. [Google Scholar]
  12. Brune H.; Wintterlin J.; Behm R. J.; Ertl G. Surface migration of “hot” adatoms in the course of dissociative chemisorption of oxygen on Al(111). Phys. Rev. Lett. 1992, 68, 624–626. 10.1103/PhysRevLett.68.624. [DOI] [PubMed] [Google Scholar]
  13. Österlund L.; Zoric-acute I.; Kasemo B. Dissociative sticking of O2 on Al(111). Phys. Rev. B: Condens. Matter Mater. Phys. 1997, 55, 15452–15455. 10.1103/PhysRevB.55.15452. [DOI] [Google Scholar]
  14. Komrowski A. J.; Sexton J. Z.; Kummel A. C.; Binetti M.; Weiße O.; Hasselbrink E. Oxygen abstraction from dioxygen on the Al(111) surface. Phys. Rev. Lett. 2001, 87, 246103. 10.1103/PhysRevLett.87.246103. [DOI] [PubMed] [Google Scholar]
  15. Sasaki T.; Ohno T. Dissociation process of O2 on the Al(111) surface. Surf. Sci. 1999, 433–435, 172–175. 10.1016/S0039-6028(99)00056-4. [DOI] [Google Scholar]
  16. Honkala K.; Laasonen K. Oxygen molecule dissociation on the Al(111) surface. Phys. Rev. Lett. 2000, 84, 705–708. 10.1103/PhysRevLett.84.705. [DOI] [PubMed] [Google Scholar]
  17. Yourdshahyan Y.; Razaznejad B.; Lundqvist B. I. Adiabatic potential-energy surfaces for oxygen on Al(111). Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 65, 075416. 10.1103/PhysRevB.65.075416. [DOI] [Google Scholar]
  18. Behler J.; Delley B.; Lorenz S.; Reuter K.; Scheffler M. Dissociation of O2 at Al(111): The role of spin selection rules. Phys. Rev. Lett. 2005, 94, 036104. 10.1103/PhysRevLett.94.036104. [DOI] [PubMed] [Google Scholar]
  19. Behler J.; Reuter K.; Scheffler M. Nonadiabatic effects in the dissociation of oxygen molecules at the Al(111) surface. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 115421. 10.1103/PhysRevB.77.115421. [DOI] [Google Scholar]
  20. Carbogno C.; Behler J.; Groß A.; Reuter K. Fingerprints for Spin-Selection Rules in the Interaction Dynamics of O2 at Al(111). Phys. Rev. Lett. 2008, 101, 096104. 10.1103/PhysRevLett.101.096104. [DOI] [PubMed] [Google Scholar]
  21. Carbogno C.; Behler J.; Reuter K.; Gross A. Signatures of nonadiabatic O-2 dissociation at Al(111): First-principles fewest-switches study. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 035410. 10.1103/PhysRevB.81.035410. [DOI] [Google Scholar]
  22. Fan X. L.; Lau W. M.; Liu Z. F. Comment on ″Dissociation of O2 at Al(111): The role of spin selection rules″. Phys. Rev. Lett. 2006, 96, 079801. 10.1103/PhysRevLett.96.079801. [DOI] [PubMed] [Google Scholar]
  23. Mosch C.; Koukounas C.; Bacalis N.; Metropoulos A.; Gross A.; Mavridis A. Interaction of dioxygen with Al clusters and Al(111): A comparative theoretical study. J. Phys. Chem. C 2008, 112, 6924–6932. 10.1021/jp711991b. [DOI] [Google Scholar]
  24. Livshits E.; Baer R.; Kosloff R. Deleterious effects of long-range self-repulsion on the density functional description of O2 sticking on aluminum. J. Phys. Chem. A 2009, 113, 7521–7527. 10.1021/jp900892r. [DOI] [PubMed] [Google Scholar]
  25. Bacalis N. C.; Metropoulos A.; Gross A. Theoretical study of the O2 interaction with a tetrahedral Al4 cluster. J. Phys. Chem. A 2010, 114, 11746–11750. 10.1021/jp1052198. [DOI] [PubMed] [Google Scholar]
  26. Liu H.-R.; Xiang H.; Gong X. G. First principles study of adsorption of O2 on Al surface with hybrid functionals. J. Chem. Phys. 2011, 135, 214702. 10.1063/1.3665032. [DOI] [PubMed] [Google Scholar]
  27. Libisch F.; Huang C.; Liao P.; Pavone M.; Carter E. A. Origin of the energy barrier to chemical reactions of O2 on Al(111): Evidence for charge transfer, not spin selection. Phys. Rev. Lett. 2012, 109, 198303. 10.1103/PhysRevLett.109.198303. [DOI] [PubMed] [Google Scholar]
  28. Libisch F.; Huang C.; Carter E. A. Embedded correlated wavefunction schemes: Theory and applications. Acc. Chem. Res. 2014, 47, 2768–2775. 10.1021/ar500086h. [DOI] [PubMed] [Google Scholar]
  29. Katz G.; Kosloff R.; Zeiri Y. Abstractive dissociation of oxygen over Al(111): A nonadiabatic quantum model. J. Chem. Phys. 2004, 120, 3931–3948. 10.1063/1.1635360. [DOI] [PubMed] [Google Scholar]
  30. Kurahashi M.; Yamauchi Y. Steric effect in O2 sticking on Al(111): Preference for parallel geometry. Phys. Rev. Lett. 2013, 110, 246102. 10.1103/PhysRevLett.110.246102. [DOI] [PubMed] [Google Scholar]
  31. Cheng J.; Libisch F.; Carter E. A. Dissociative adsorption of O2 on Al(111): The role of orientational degrees of freedom. J. Phys. Chem. Lett. 2015, 6, 1661–1665. 10.1021/acs.jpclett.5b00597. [DOI] [PubMed] [Google Scholar]
  32. Huang C.; Pavone M.; Carter E. A. Quantum mechanical embedding theory based on a unique embedding potential. J. Chem. Phys. 2011, 134, 154110. 10.1063/1.3577516. [DOI] [PubMed] [Google Scholar]
  33. Andersson K.; Malmqvist P. Å.; Roos B. O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  34. Martin-Gondre L.; Crespos C.; Larregaray P.; Rayez J. C.; van Ootegem B.; Conte D. Is the LEPS potential accurate enough to investigate the dissociation of diatomic molecules on surfaces?. Chem. Phys. Lett. 2009, 471, 136–142. 10.1016/j.cplett.2009.01.046. [DOI] [Google Scholar]
  35. Martin-Gondre L.; Crespos C.; Larregaray P.; Rayez J. C.; Conte D.; van Ootegem B. Detailed description of the flexible periodic London-Eyring-Polanyi-Sato potential energy function. Chem. Phys. 2010, 367, 136–147. 10.1016/j.chemphys.2009.11.012. [DOI] [PubMed] [Google Scholar]
  36. Pétuya R.; Larrégaray P.; Crespos C.; Busnengo H. F.; Martínez A. E. Dynamics of H2 Eley-Rideal abstraction from W(110): Sensitivity to the representation of the molecule-surface potential. J. Chem. Phys. 2014, 141, 024701. 10.1063/1.4885139. [DOI] [PubMed] [Google Scholar]
  37. Busnengo H. F.; Salin A.; Dong W. Representation of the 6D potential energy surface for a diatomic molecule near a solid surface. J. Chem. Phys. 2000, 112, 7641–7651. 10.1063/1.481377. [DOI] [Google Scholar]
  38. Lorenz S.; Scheffler M.; Gross A. Descriptions of surface chemical reactions using a neural network representation of the potential-energy surface. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 115431. 10.1103/PhysRevB.73.115431. [DOI] [Google Scholar]
  39. Jiang B.; Guo H. Permutation invariant polynomial neural network approach to fitting potential energy surfaces. III. Molecule-surface interactions. J. Chem. Phys. 2014, 141, 034109. 10.1063/1.4887363. [DOI] [PubMed] [Google Scholar]
  40. Jiang B.; Hu X.; Lin S.; Xie D.; Guo H. Six-dimensional quantum dynamics of dissociative chemisorption of H2 on Co(0001) on an accurate global potential energy surface. Phys. Chem. Chem. Phys. 2015, 17, 23346–23355. 10.1039/C5CP03324A. [DOI] [PubMed] [Google Scholar]
  41. Liu T. H.; Fu B. N.; Zhang D. H. Six-dimensional potential energy surface of the dissociative chemisorption of HCl on Au(111) using neural networks. Sci. China: Chem. 2014, 57, 147–155. 10.1007/s11426-013-5005-7. [DOI] [Google Scholar]
  42. Hammer B.; Hansen L. B.; Nørskov J. K. Improved adsorption energetics within density functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 7413–7421. 10.1103/PhysRevB.59.7413. [DOI] [Google Scholar]
  43. Nave S.; Jackson B. Methane dissociation on Ni(111): The role of lattice reconstruction. Phys. Rev. Lett. 2007, 98, 173003. 10.1103/PhysRevLett.98.173003. [DOI] [PubMed] [Google Scholar]
  44. Jiang B.; Alducin M.; Guo H. Electron–hole pair effects in polyatomic dissociative chemisorption: Water on Ni(111). J. Phys. Chem. Lett. 2016, 7, 327–331. 10.1021/acs.jpclett.5b02737. [DOI] [PubMed] [Google Scholar]
  45. Luo X.; Zhou X.; Jiang B. Effects of surface motion and electron-hole pair excitations in CO2 dissociation and scattering on Ni(100). J. Chem. Phys. 2018, 148, 174702. 10.1063/1.5025029. [DOI] [PubMed] [Google Scholar]
  46. Hou H.; Gulding S. J.; Rettner C. T.; Wodtke A. M.; Auerbach D. J. The stereodynamics of a gas-surface reaction. Science 1997, 277, 80–82. 10.1126/science.277.5322.80. [DOI] [Google Scholar]
  47. Komrowski A. J.; Ternow H. k.; Razaznejad B.; Berenbak B.; Sexton J. Z.; Zoric I.; Kasemo B.; Lundqvist B. I.; Stolte S.; Kleyn A. W.; et al. Dissociative adsorption of NO upon Al(111): Orientation dependent charge transfer and chemisorption reaction dynamics. J. Chem. Phys. 2002, 117, 8185–8189. 10.1063/1.1519107. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz8b01470_si_001.pdf (1.5MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES