Dynamic Sparse Sampling for Confocal Raman Microscopy

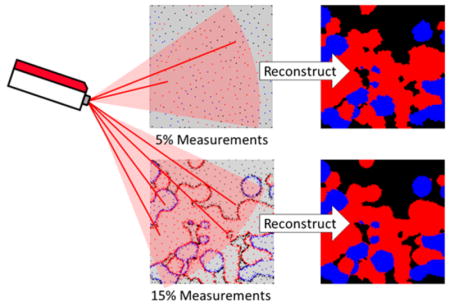
Abstract

The total number of data points required for image generation in Raman microscopy was greatly reduced using sparse sampling strategies, in which the preceding set of measurements informed the next most information-rich sampling location. Using this approach, chemical images of pharmaceutical materials were obtained with >99% accuracy from 15.8% sampling, representing an ~6-fold reduction in measurement time relative to full field of view rastering with comparable image quality. This supervised learning approach to dynamic sampling (SLADS) has the distinct advantage of being directly compatible with standard confocal Raman instrumentation. Furthermore, SLADS is not limited to Raman imaging, potentially providing time-savings in image reconstruction whenever the single-pixel measurement time is the limiting factor in image generation.

Graphical Abstract

Raman microscopy, which combines Raman spectroscopy with optical imaging, is a powerful tool to provide detailed chemical information in multiple dimensions (spatial and spectral).¹ Because of its high chemical specificity and requirement for minimal sample preparation, Raman imaging has found broad adoption in both chemical and biological sample analysis, with applications ranging from the screening of pharmaceutical formulations,^2–5 to characterization of semiconductors,^6,7 to cancer diagnosis,^8–10 to forensic analysis.^11,12 Specifically, in the pharmaceutical industry, spontaneous Raman spectroscopy and microscopy have been established as a standard method for polymorphic characterization of active pharmaceutical ingredients (APIs).^2,13 Previous studies show that more than 80% of APIs have multiple polymorphic forms,¹⁴ and polymorphic transition of APIs can significantly impact their chemical and physical properties, including stability, apparent solubility, morphology, and bioavailability. Polymorphism is a critical issue in the industry, and there is increasing need for fast and reliable analytical methods for API polymorphic characterization. However, the spontaneous Raman cross section is weak (on the order of 10⁻³⁰ cm²/sr).¹⁵ As a result, imaging based on spontaneous Raman typically requires relatively long integration times to obtain suficient signal-to-noise, which in turn limits the applications of Raman imaging.¹⁶

Several strategies have been adopted to reduce the measurement time in Raman imaging. Some techniques, such as stimulated Raman scattering (SRS)¹⁷ and coherent antistokes Raman scattering (CARS),¹⁸ dramatically improve the speed of Raman imaging with significantly shorter exposure times (up to video-rate frame rates). However, these approaches typically require ultrafast laser sources, which can limit the rate of adoption. Furthermore, it can be challenging to recover complete high-resolution spectra at each location by SRS and CARS.⁸ Alternatively, several illumination strategies have been applied to improve the speed of spontaneous Raman imaging, which are mainly classified as wide-field, line-illumination, and confocal scanning methods.¹⁹ In wide-field Raman microscopy, the entire field of view is illuminated, and the Raman spectra are collected by spectral filtering to select discrete frequencies. This approach recovers highly efficient spatial information but inefficient spectral collection. Incorporation of acousto-optic tunable filters, liquid-crystal tunable filters (LCTFs), fiber array assemblies, and integrated light sheet illumination can improve the signal-to-noise ratio and the efficiency of spatial and spectral collections.²⁰ However, wide-field strategies such as these reject much of the Raman signal, as measurements are typically acquired by serially scanning through wavelengths. In addition, illumination of the entire field of view reduces the intensity at each individual pixel, with the corresponding signal scaling proportionally. Line-illumination (or push-broom) methods using a hemicylindrical lens circumvent this complication by allowing full spectral acquisition in one dimension of an array-detector and spatial information on the orthogonal axis. By sweeping a line of illumination across the sample (or translating the sample), spectra images are produced one line at a time.²¹ However, similar to wide-field strategies, line-illumination also suffers from reduced intensity at each individual pixel, resulting in extended measurement time.

Point scanning has the distinct advantage of enabling confocal sectioning, which can greatly reduce background and interference from out-of-plane contributions. However, the traditional approach to point-mapping Raman imaging utilizes raster scanning to sample all pixels in the field of view, which often results in prohibitively long imaging times for practical applications. Raster scanning always samples locations immediately adjacent to those previously sampled, which typically are among the least informative pixels for sampling in order to perform image reconstruction. In brief, sampling adjacent pixels interrogates the highest spatial frequency achievable by the instrument hardware for all locations in the image, regardless of the frequency components actually present.

To improve the speed of point mapping Raman imaging, several selective sampling algorithms have been employed to determine the optimal positions of measurement locations and reduce the numbers of sampling points. Rowlands et al. developed a sampling method, in which a score assigned to each unmeasured pixel was used to determine the next sampling location.^22,23 This score is equal to the difference between the interpolated values for a pixel, computed using two different interpolation algorithms (e.g., a cubic spline and a Kriging interpolation). The pixel location where the reconstruction algorithms differed the most was deemed the most informative pixel and then measured. While an improvement over random sampling, it is not clear from a fundamental perspective that the location where the difference is largest with two interpolation approaches corresponds to the pixel with the most information about the underlying object. Another approach for selective sampling is to use the information from a much faster alternative imaging tool, such as second harmonic generation (SHG) microscopy²⁴ and/or confocal fluorescence microscopy.²⁵ However, such hyphenated methods add complexity to the instrument and have specific requirements for samples (e.g., SHG-guided Raman spectroscopy is only applicable for sample systems whose components are symmetry-allowed for SHG).

In the present study, a supervised learning approach for dynamic sampling (SLADS) is demonstrated for hyperspectral imaging, which allows rapid determination of optimal sampling locations in real-time during image acquisition. In contrast to previous methods for sparse-sampling in Raman imaging, SLADS is based on a machine learning approach that incorporates training data for sample selection. Furthermore, SLADS allows the use of labeled images (i.e., pixels classified according to spectra), as opposed to being limited to continuously valued images, which could result in the adverse effects described in previously discussed method by Rowlands et al. and in the original SLADS publication.²⁶ On the basis of the training results and the SLADS algorithm, the error of dynamic image reconstruction was less than 0.5% with 15% sampling points, with resolution negligibly different from full raster scanning. The stopping condition was determined by training data to optimize the number of sampling points and the quality of reconstructed image. By using SLADS guided Raman imaging, polymorphic discrimination of active pharmaceutical ingredients (APIs) shown in this study was accelerated by ~6 times.

1. THEORETICAL METHODS

1.1. Classifying Raman Spectra for Discretized Imaging

Classification of acquired Raman spectra was performed to identify the chemical composition of the sample measured at specific locations. The Raman spectroscopic image was thus converted to a discrete valued image, in which the value of each pixel is its corresponding class label, to inform the SLADS algorithm. Raman spectral classification was achieved by a combination of linear discriminant analysis (LDA) for initial dimension reduction and support vector machine (SVM) classification. In brief, LDA constructs the N-1-dimensional space for N classes of data that maximizes the Fisher linear discriminant, which in turn maximizes the resolution between classes. SVM is a complementary machine-learning algorithm specifically designed for classification, in which optimal hyperplanes are constructed in the data space to separate different clusters of data points. With linearly inseparable data, SVM utilizes a predefined kernel function to draw nonlinear decision boundaries, which is a more computationally economical equivalent of projecting data into a higher dimensional space, in which the data become linearly separable.

SVM is not inherently designed to work with N-class problems, such that additional steps were taken to enable classification. In the present work, a 1-vs-1 SVM approach was adopted to enable SVM analysis with N > 2: one decision boundary was made for each pair of classes, generating $\left(\begin{array}{c}n\\ 2\end{array}\right)$ decision boundaries. Classification of a data point is achieved using this procedure:²⁷ all the $\left(\begin{array}{c}n\\ 2\end{array}\right)$ decision boundaries were applied to the unseen data point, and each decision boundary returns one prediction for a class label. Then a polling procedure is conducted, in which the class that obtains the highest number of prediction votes is used as the classification result. If the polling results in a tie, a tie-breaking algorithm is implemented to make a final classification decision.

1.2. Dynamic Sampling

In this section, we describe the theoretical framework underpinning SLADS for identifying a sparse set of sampling locations, which allows for a high fidelity reconstruction of the underlying object.^26,28,29 Let us assume that we have previously measured k locations, S = {s⁽¹⁾, s⁽²⁾,··· s^(k)}, of some sample, X ∈ ℛ^N, and we want to find the next location, s^(k+1), to measure. The measurements can be described by a matrix,

$$Y^{(k)}=\left(\begin{array}{c}{s}^{(1)},X_{s^{(1)}}\\ ⋮\\ s^{(k)},X_{s^{(k)}}\end{array}\right)$$ (1)

After these measurements are acquired, one can perform a reconstruction to form X̂^(k) ∈ ℛ^N. In SLADS, the goal is to find the pixel location that maximizes the expected reduction in distortion.

$$s^{(k+1)}=arg\underset{s\in \{\mathrm{\Omega }\backslash \mathrm{S}\}}{max}\{E[R^{(k;s)}\mid Y^{(k)}]\}$$ (2)

In eq 2, Ω is the set of all pixel locations in X, and the reduction in distortion R resulting from measuring pixel s is given by the following expression.

$$R^{(k;s)}=D(X,{\widehat{X}}^{(k)})-D(X,{\widehat{X}}^{(k;s)})$$ (3)

In eq 3, X̂^(k;s) is the reconstruction made with Y^(k) and X_s, and D(A, B) is the distortion between two images A and B. In SLADS it is assumed that the expectation value for the reduction in distortion can be written as a function of Y.

$$E[R^{(k;s)}\mid Y^{(k)}]=f_{\theta }^s(Y)$$ (4)

In eq 4, the function $f_{\theta }^s(Y)$ is learned using a supervised learning approach, where θ is a parameter vector.

In this implementation of SLADS, the distortion D between two images A and B is defined as,

$$D(A,B)=\sum _{i=1}^{N}I(A_i,B_i)$$ (5)

Here, I is an indicator function defined as,

$$I(A_i,B_i)=\{\begin{array}{ll}0\hfill & \text{if}{A}_i=B_i\hfill \\ 1\hfill & \text{if}{A}_i\ne B_i\hfill \end{array}$$ (6)

In eq 6, A_i is the ith element of the image A. However, in this implementation, since we measure a spectrum from each pixel location, we have an l-dimensional vector at each pixel location. Hence, we label each measured spectrum, as it is measured (i.e., on-the-fly), using the classification method described in the previous section.

1.3. Stopping Condition for SLADS

The SLADS framework includes a stopping condition that allows us to stop sampling when the expected total distortion (ETD) is smaller than a threshold T;

$${\mathit{ETD}}_k=E\left[\frac{1}{\mid \mathrm{\Omega }\mid }D(X,{\widehat{X}}^{(k)})\right]<T$$ (7)

Since this quantity cannot be computed without foreknowledge of the ground truth image, another function ε^(k), is used in SLADS instead to identify the stopping condition.

$${\mathrm{\epsilon }}^{(k)}=(1-\beta ){\mathrm{\epsilon }}^{(k-1)}+\beta D(X_{s^{(k)}},{\widehat{X}}_{s^{(k)}}^{(k-1)})$$ (8)

Here, k > 1, β is a user selected parameter that determines the amount of temporal smoothing, X_s^(k) is the measured value of the pixel at step k, and ${\widehat{X}}_{s^{(k)}}^{(k-1)}$ is the reconstructed value of the same pixel at step k − 1. The threshold to place on this function, T̃(T), to stop sampling when ETD_k is below T, is computed as follows.

First, M training images are measured using the SLADS algorithm and stopped when the total distortion is below the desired threshold T. For example,

$${TD}_k=\frac{1}{\mid \mathrm{\Omega }\mid }D(X,{\widehat{X}}^{(k)})<T$$ (9)

Then the value of ε^(K_m) for each experiment is recorded. Here ε^(K_m) is the value of ε^(k) when SLADS is stopped for the mth image. Then the threshold to place on ε^(k) in the SLADS experiment is computed as,

$$\stackrel{\sim }{T}(T)=\sum _{m=1}^M{\mathrm{\epsilon }}^{(K_m(T))}$$ (10)

2. EXPERIMENTAL METHODS

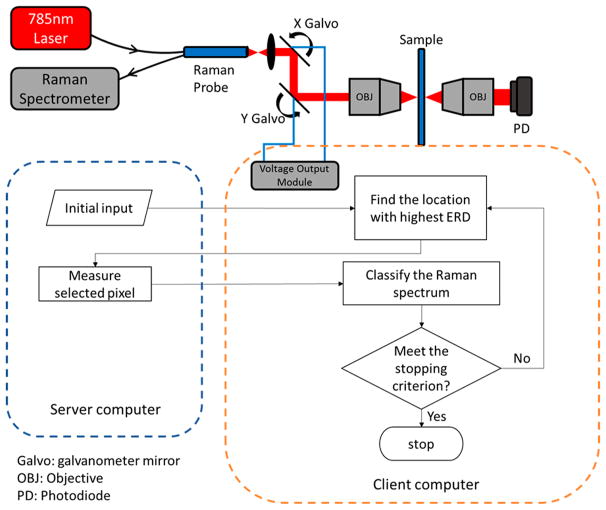
Instrumentation for dynamic sampling Raman imaging is shown in Figure 1. A continuous wave diode laser (Toptica, 785 nm wavelength) was coupled into a Raman probe (InPhotonics, RPS785/24). The light was then collimated by a 1/2 in. fused silica lens and directed through an X-Y scan head composed of two galvanometer scanning mirrors. Two additional 1 in. diameter fused silica lenses formed a 4f configuration to deliver a collimated beam on the back of a 10× objective (Nikon). The Raman signal from the sample was collected in epi direction and sent back through the same beam path into the Raman probe, and a photodiode was set behind the sample to collect the laser transmittance signal for bright field imaging. A notch filter was built in the Raman probe to reject the laser signal. Raman spectra were acquired using an Acton SP-300i spectrometer with a 100 × 1340 CCD array and controlled by a computer running WinSpec32. Another computer was used to control the galvanometer scanning mirrors with a digital to analog converter (DAC, NI 9263, National Instruments) coupled with a programmable USB interface (NI USB-9162, National Instruments). MATLAB R2014a (MathWorks, Inc.) software written in-house was used to output analog voltages to the galvanometer mirrors and direct the laser beam to the desired locations. To achieve automation of dynamic sampling, network communication programs based on WinSock application programming interface were designed (a client/server network) in house using Visual C++ 6.0 (Microsoft Corporation) in combination with MATLAB to allow remote control of the Raman spectrometer vendor computer (server computer) as well as data transfer between the two computers. During the experiment, the client computer used the SLADS algorithm (coded in MATLAB) to determine the next measurement location, calculated the corresponding voltages needed at the galvanometer mirrors, output voltages via the DAC to direct the laser, and sent request to the server computer for Raman spectrum acquisition. After receiving the acquired Raman spectrum file from the server computer, the client computer used pretrained classifier to identify the sample at the point of measurement and continued SLADS algorithm to decide the next measurement point.

Figure 1.

Schematic of the random access Raman microscope, with the dynamic sampling Raman imaging workflow described in the flowchart. The server computer (outlined in blue to the left) controlled the Raman spectrometer, and the client computer (outlined in orange to the right) controlled the laser beam location, operated the SLADS algorithm, and performed Raman spectral classification.

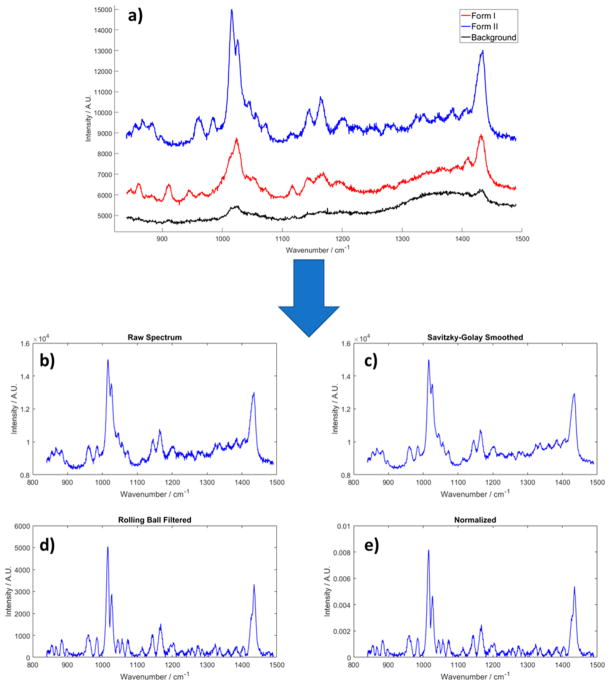
Pure clopidogrel bisulfate form I and form II were produced in-house at Dr. Reddy’s Laboratories. Both the form I and form II particles were spherical with similar particle size distributions (diameter: ~25 μm). The sample prepared for Raman imaging was a mixture of clopidogrel bisulfate form I and form II, which consisted of 50% form I and 50% form II by mass. The powder sample was placed on a fused quartz microscope slide to collect Raman spectrum. The laser power measured at the sample place was ~30 mW. The exposure time was 0.5 s per spectral frame. To achieve higher signal-to-noise ratio for high quality training data for classification, 30 consecutive frames were averaged for each pixel. A Savitzky-Golay filter was applied to smooth the spectra,³⁰ and a rolling ball filter was used to remove the fluorescence background.³¹ Finally, the spectra were normalized to their integrated intensities (i.e., the area under the curves). The integrated intensity information on every spectrum was recorded so it can be retrieved when intensity information within each spectrum was needed for subsequent analysis. The spectral processing procedures are shown in Figure 2.

Figure 2.

(a) Sample raw Raman spectra of form I, form II clopidogrel bisulfate polymorphs, and background signal, and (b–e) the spectral processing procedure illustrated using a spectrum of form II clopidogrel bisulfate measurement, including Savizhky-Golay filtering, rolling ball filtering, and normalization to the area under the curve.

Ground Truth Data Acquisition

Ground truth data were acquired using a raster scan sampling pattern in order to allow evaluation of the performance of dynamic sampling. Raman spectra of the 50%/50% (w/w) clopidogrel bisulfate form I/form II were taken at every pixel of a 128 pixel × 128 pixel field of view. Classification algorithms were developed using the information and knowledge obtained from this data set.

Classification of Raman Spectra

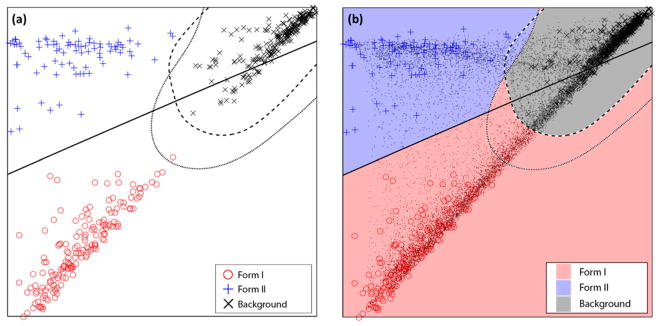
LDA and SVM both being supervised learning algorithms, Raman classifiers were constructed using 500 training spectra, which were randomly picked from the 16384 ground truth spectra and then manually classified by inspection as either form I clopidogrel, form II clopidogrel, or background. During this process, if a selected spectrum was ambiguous for manual classification (e.g., if a spectrum was taken at the boundary between a form I and a form II particle and exhibited spectral features of both polymorphs), it was excluded from training. Then, LDA was used to reduce the dimensionality of the training data, and spectra in the data set were projected into the two-dimensional space formed by the two LDA axes. An SVM algorithm with a Gaussian kernel was then used to define the classification decision boundaries for form I, form II, and background Raman spectra. A 5-fold cross-validation was applied during training to optimize the parameters and ensure the robustness of the classifiers. Using SVM to construct classification boundaries enabled both discrimination of different classes and maximization of the probability of correct classification. Figure 3a shows the constructed decision boundaries in the two-dimensional space, with all 500 training data points overlaid.

Figure 3.

(a) Training spectra projected onto the two-dimensional space generated from the two principal eigenvectors produced by LDA, and three decision boundaries constructed using 1-vs-1 SVM, in which the solid curve separates form I and form II clopidogrel data points, the dashed line curve separates form II and background data points, and the dotted curve separates form I and background data points. (b) Visual representation of Raman spectral classification decision making. All 16384 spectra collected by the ground truth Raman imaging experiment are projected to the same LDA space as gray dots. Shaded areas that these dots fall into indicate corresponding classification results.

The constructed classifiers were then applied to the Raman ground truth data previously acquired. During the 1-vs-1 SVM polling process, a tie in votes will typically occur when the signal measured at the location is a mixture of form I, form II clopidogrel, and background spectra. A simplified tie-breaking algorithm was implemented that all voting ties (30 out of 16384) are resolved as a form I clopidogrel spectrum. With 16384 classified Raman spectra, the Raman spectral image was converted into a discrete valued 128 × 128 image, in which pixels valued 1, 2, and 3 correspond to form I, form II, and background, respectively. This classified image was used as the ground truth data for subsequent simulation studies. Figure 3b shows all 16384 data points overlaid in the two-dimensional space. Color-shaded regions mark how data points within corresponding areas were classified.

Experimental Implementation of Dynamic Sampling

Dynamic sampling Raman imaging was conducted using the aforementioned instrument, with SLADS algorithm and Raman classifiers trained for clopidogrel bisulfate samples. Another replicate of clopidogrel bisulfate sample was prepared for Raman imaging, with 50% form I and 50% form II by mass. The SLADS stopping condition was set such that experimental measurements automatically ended when the estimated image reconstruction error was less than 1%. More measurements (to 35% of all pixels sampled) were conducted after the SLADS stopping condition to evaluate and validate the trained stopping condition.

RESULTS AND DISCUSSION

Simulation Results

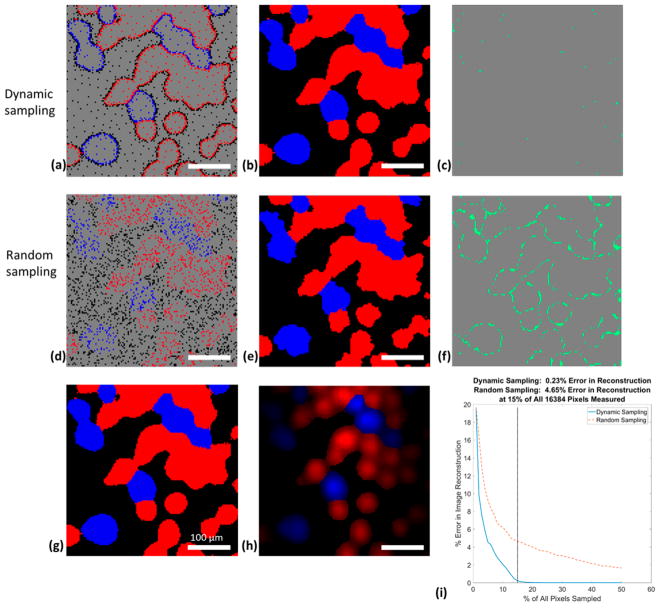
Prior to implementation, the SLADS algorithm was characterized through a series of studies in which the ground truth results were measured at each pixel. Simulated dynamic sampling was conducted on the 128 × 128 ground truth image, the results of which are provided in Figure 4g. Before each measurement, the SLADS algorithm used an average of 71.5 μs to determine the next measurement location. Image reconstruction was done each time an additional 1% of all 16384 pixels was measured. The measured pixel locations, reconstructed images, and errors in image reconstruction when 15% of all 16384 pixels were measured are shown in Figure 4 (panels a–c). The image reconstruction error with dynamic sampling was 0.23%. At 35% of all pixels sampled, all 16384 pixels in the reconstructed image are identical to those in the ground truth image. Previously recorded integrated intensity of each spectrum was used to rescale the discrete valued Raman image in order to reconstruct a grayscale Raman spectroscopic image with classification information, shown as Figure 4h. Video S1 is demonstrates the simulation process.

Figure 4.

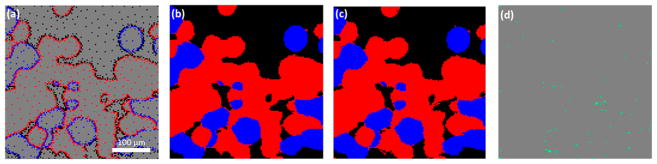
Simulated dynamic sampling (first row) and random sampling (second row) reconstruction with a known ground truth image. Results shown in the figure are both at 15% sampling percentage (i.e., 2458 out of 16384 pixels are measured). (a) Measured locations of simulated dynamic sampling. (b) Reconstructed image of dynamic sampling. (c) Dynamic sampling image reconstruction error map. (d) Measured locations of simulated random sampling. (e) Reconstructed image of random sampling. (f) Random sampling image reconstruction error map. (g) The ground truth image in which all 16384 pixels are sampled. (h) Grayscale image with classification information by rescaling every pixel in the discrete valued image by the integrated intensity of the Raman spectrum measured at the pixel. (i) Comparison of image reconstruction error using dynamic sampling (blue solid line) and random sampling (orange dotted line) as a function of sampling percentage. In (a), (b), (d), (e), (g), and (h) red pixels correspond to form I polymorph, blue pixels correspond to form II polymorph, black pixels correspond to background, and gray pixels correspond to unmeasured locations. In (c) and (f), gray pixels correspond to locations where the reconstructed image is the same as the ground truth image, and cyan pixels correspond to locations where reconstructed image difiers from the ground truth image.

Comparison with Random Sampling

In order to compare the performance of dynamic sampling to other alternative sampling strategies, simulated random sampling experiments were also conducted. The first simulated random sampling imaging was conducted using the ground truth image acquired in a simulated dynamic sampling experiment. The measured pixel locations, reconstructed images, and errors in image reconstruction corresponding to measurements of 15% of all 16384 pixels are shown in Figure 4 (panels d–f). The image reconstruction error with dynamic sampling was 0.23%, while with random sampling it was 4.65%. It can be seen that most of the errors in random sampling were located at the edges of the sample particles of different species (i.e., the boundaries between classes). This edge ambiguity can be easily rationalized; boundaries have high spatial frequency information compared to other areas in the image. Random sampling does not adjust its measurement density according to the different spatial frequency accessed in different locations. In contrast, dynamic sampling adjusts the measurement density accordingly, selectively interrogating more pixels at areas with higher spatial frequency information and measures fewer pixels at areas with lower spatial frequency information.

Experimental Implementation of SLADS for Dynamic Raman Imaging

The experimental dynamic Raman imaging stopping condition of <1% expected distortion was reached for a sampling of 15.8%; the sampled pixel locations and the reconstructed image are shown in Figure 5 (panels a and b). Consistent with the preceding analysis with a known ground truth, the SLADS reconstruction converged quickly to a low relative reconstruction error. Also consistent with the evaluation of simulated results, the SLADS approach preferentially sampled the edges in the images, at which the composition changes abruptly. This preferential sampling retained the high spatial-frequency information content at the boundaries in the image reconstruction, enabling high-edge resolution in the classification.

Figure 5.

Dynamic sampling Raman imaging experimental results. (a) Measurement locations correspond to the stopping criterion (15.8% sampling percentage). (b) Reconstructed Raman image. (c) Reference image reconstructed after 35% of all pixels locations are measured. (d) Difference between reconstructed image at 15.8% sampling percentage and the reference image. 67 pixels are different, corresponding to 0.41% difference. In (a, b, and c), red pixels correspond to form I polymorph, blue pixels correspond to form II polymorph, black pixels correspond to background, and gray pixels correspond to unmeasured locations. In (d), gray pixels correspond to locations where reconstructed image is the same as the ground truth image, and cyan pixels correspond to locations where reconstructed image is different from the ground truth image.

In order to assess the merits of the SLADS algorithm at this stopping condition, additional subsequent measurements were made for up to 35% of all pixels sampled, shown in Figure 5c. No additional changes were observed in the reconstructed images after 29% of all pixels were sampled. Video S2 demonstrates the experiment measurement process. The difference between the reconstructed image at SLADS algorithm stopping condition and at 35% of all pixels sampled is 67 pixels, or 0.41% of all 16384 pixels in the image. Details of images used for training the SLADS stopping condition are included in Supporting Information.

Performance Analysis and Potential Applications of Dynamic Sampling

The benefit of reduced measurement time delivered by SLADS is most pronounced in Raman imaging, where the data acquisition time for each measurement is over 10 times longer than the time required for laser beam relocation, data transfer, spectra analysis, and SLADS computation. Comparable advantages are reasonable to expect in other imaging applications, in which the random access time can be significantly faster than the single-pixel measurement time, such as energy dispersive spectroscopy,³² photoacoustic imaging,^33,34 and infrared hyperspectral imaging.³⁵

Previous analysis using images of different pixel resolution suggests that the sampling benefits of SLADS increase significantly as the number of pixels in the image increases.³⁶ In SLADS simulations based on X-ray diffraction imaging, an 80-fold increase in resolution (from 40 × 80 to 512 × 512 pixels) yielded a 6-fold reduction in the fraction of pixels sampled for similar distortions. This result suggests that substantial improvements over the current design could be anticipated with higher resolution of sampling but at the expense of increased overall measurement time.

It is interesting to compare the results of SLADS with the previously described sampling strategy by Rowlands et al.,²³ based on comparisons between spline and Kriging interpolations. Quantitative comparisons are challenging, as the previous work did not include assessment of the reliability of the algorithm (e.g., by using model calculations with known ground truth results). In Rowlands et al., the boundaries between phases appear qualitatively to be significantly blurred in the reconstructed images, and as a result, the misclassification rate along the boundaries and in the whole image is anticipated to be relatively large. One possible reason for this effect is that the difference between two interpolations of a pixel is generally not proportional to the information that the pixel would provide upon measurement. For example, consider three features with different gray scale values in proximity. The Rowlands et al. algorithm will preferentially sample between the features with the greatest differences, rather than the locations that will optimize reconstruction. Furthermore, the algorithm operates on continuously valued images and uses the difference between pixel values directly to select the next measurement. However, the difference between continuously valued pixels is a different question than posed in the present reconstruction, which focused on properly classifying composition. The algorithm proposed by Rowlands et al. cannot readily be extended to labeled images; all pixels in labeled interpolations would either be identical using the two methods or differ by a score of 1 because of the discrete nature of the classification.

In practice, the discrete classification boundaries identified by SLADS are not representative of the smoothly varying changes in composition expected for realistic three-dimensional objects. Two strategies were considered for recovering the intrinsic gradient in intensities associated with geometric objects (in this case, spheroidal particles). First, the SLADS algorithm can be applied for images in which each pixel is allowed to have continuous amplitudes of all components (e.g., form I, form II, and background). SLADS imaging has been demonstrated using continuously valued images (continuous-SLADS), in which different regions have either hard boundaries or soft gradient edges.²⁹ Since gradients in continuously valued images are smoother, SLADS will sample along this smoother more spread out boundary. As a result, the misclassification rate of the reconstruction, if calculated with only one label allowed per pixel, will decrease slower than when SLADS trained on labeled images is applied to the same image after labeling it. However, if the RMSE was computed as the error metric, continuous-SLADS will decrease the error faster because it is trained to find the pixel that reduces the RMSE the most. However, continuous-SLADS, just as the method proposed by Rowland et al., suffers from the inaccuracy of using the difference between continuously valued pixels to quantify how different the pixels are. An alternative strategy illustrated in Figure 4h was adopted herein, in which the original classified images were subsequently weighted by the ground-truth vector magnitudes of the filtered spectra. While the primary focus of the present study was centered on quantitatively and accurately classifying composition, the general strategies described above demonstrate possible strategies for recovering gradient information in discretized SLADS images.

Although the central focus of the present work is the reduction in measurement time afforded by dynamic sampling, the SLADS algorithm has the added benefit of reducing the total optical dose to the sample. Phototoxicity is routinely observed in Raman imaging of live cells, in which local heating and/or photochemical reactions significantly perturb the system under investigation during the process of data acquisition.^37,38 In addition, significant laser-induced local heating could potentially lead to phase transformation between crystal forms in analyses of pharmaceutical materials.³⁹ In a previous application of dynamic sampling in synchrotron X-ray diffraction for crystal positioning, the reduced number of measurement points significantly reduced the X-ray dosage used for crystal identification and avoided excessive X-ray damage.³⁶ Similarly, in other imaging applications where sample overheating or damage caused by extended exposure to light source is a major concern, such as four-wave mixing microscopy for living cell imaging, using dynamic sampling to reduce the number of sampling points can be potentially beneficial.

While the measurements presented herein were all acquired using a dedicated prototype instrument, the SLADS approach is expected to be directly compatible with broad classes of point-scanning instruments for Raman imaging. Assessment of compatibility can be made by comparisons between the random access time within the field of view relative to the sampling period per-pixel. In many practical commercially available confocal Raman systems supporting imaging applications, the single-pixel measurement time dictates the overall frame rate, such that SLADS is expected to be advantageous. Given the quality of the reconstructions produced with ~16% of pixels sampled, the time-reductions associated with SLADS is highly attractive.

CONCLUSIONS

An integrated Raman imaging system utilizing dynamic sampling with SLADS was demonstrated for clopidogrel bisulfate polymorphism discrimination. This approach significantly reduced the number of sampling points required for image reconstruction. For a three-component system consisting of form I clopidogrel/form II clopidogrel/background, the implementation of dynamic sampling was found to increase the imaging speed by over 6 times without significantly sacrificing image fidelity relative to traditional raster scanning. Simulation results also support a 1 order of magnitude improvement of image reconstruction accuracy by dynamic sampling over random sampling. Dynamic sampling capabilities have the potential to be easily retrofitted into existing imaging systems, with few requirements beyond those inherently already present in point-scanning Raman microscopy instrumentation. The flexibility of the sampling architecture enables compatibility with a variety of applications, providing benefits including increased imaging speed and reduced sample damage.