Microscopy with a single-molecule scanning electrometer

The single-molecule limit in electromechanical sensing is realized through TERS-relayed molecular force microscopy.

Abstract

The vibrational spectrum of a single carbon monoxide molecule, adsorbed on the tip apex of a scanning tunneling microscope, is used to image electrostatic fields with submolecular spatial resolution. The method takes advantage of the vibrational Stark effect to image local electrostatic fields and the single-molecule sensitivity of tip-enhanced Raman scattering (TERS) to optically relay the signal. We apply the method to single metalloporphyrins adsorbed on Au(111) to image molecular charges, intramolecular polarization, local photoconductivity, atomically resolved hydrogen bonds, and surface electron density waves.

INTRODUCTION

Shapes of molecules are ultimately determined by how one molecule sees another. This forms the working principle of the highest resolution scanning probe microscopes, which rely on a small test molecule attached to the probe to image another through the sensed intermolecular forces (1–5). The concept is most closely realized in atomic force microscopy using cantilevers terminated with a single carbon monoxide molecule (CO-AFM) (2), where interaction potentials due to electrostatic, dispersive, and Pauli repulsion forces acting on successively shorter range are sampled as a function of approach between CO and targeted molecules. At closest approach, the repulsive wall of interaction potentials images the ball-and-stick structure of molecules (6), with resolution sufficient to make structural assignments of unknown molecules (7). At a longer range, electrostatic forces are interrogated, and CO-AFM operating in the Kelvin probe force mode (8) has been used to image intramolecular charge distributions (9). Forces localized on one molecule are contrasted with a mechanical cantilever, although the measurement entails the sum over all interactions between tip and substrate. A stiff cantilever, with high-quality factor and 0.2 Å oscillation amplitude, is used to localize the sampled forces (10). With the demonstration that the vibrations of a single tip-attached CO can be detected through tip-enhanced Raman scattering (TERS), we suggested TERS-relayed molecular force microscopy (TERS-mfm) as a direct application of single-molecule vibrational spectroscopy (11). Here, we present the realization of the concept. Dispensing entirely with cantilevers, we use the molecular spring of CO attached to the tip apex of a scanning tunneling microscope (STM) as a force sensor and transducer. We implement TERS-mfm in the range where electrostatics dominate the intermolecular forces. In addition, by taking advantage of the vibrational Stark effect on the CO stretch (12), we interrogate electrostatic fields within single metalloporphyrin molecules adsorbed on Au(111). Molecule-metal charge transfer, structure-specific intramolecular polarization, counter polarization of surface electrons, and atomically resolved hydrogen bonds are among the unique observables that are imaged and quantified.

TERS-mfm may be recognized as the single-molecule limit of microelectromechanical sensors (MEMS). Among the notable operating specifications in this limit are extreme localization of the sensor to the 1.1 Å bond length of CO, amplitude of motion limited to single quantum excitation Δr = |〈1|r|0〉| = 0.034 Å, high stiffness k = 1.7 × 10³ N/m, and optical operating frequency ν = 10¹⁴ Hz, whereby the measurements are transferred to the spectral domain, with practically instantaneous response and multiplexing advantage. The already demonstrated resolvable frequency shift of the molecular oscillator, $\mathrm{\Delta }\overline{\mathrm{\nu }}$ ~ 0.1 cm⁻¹, establishes the detectable force $\mathit{F}=2\mathit{k}\mathrm{\Delta }\mathit{r}\mathrm{\Delta }\overline{\mathrm{\nu }}/\overline{\mathrm{\nu }}$ ~ 0.5 pN (11), which competes favorably with the advanced quartz cantilevers used in CO-AFM (10). The key development that enables TERS-mfm is the ~12 orders of magnitude signal enhancement necessary to raise the feeble Raman signal from a single CO molecule to levels useful for force microscopy. Detection of Raman scattering on single CO molecules was demonstrated previously at the plasmonic junction of fusing silver nanospheres, with large enhancement ascribed to tunneling charge transfer plasmons (13). A formal treatment of the scattering process in this regime (14) and explicit time-dependent density functional simulations of the photofield-driven tunneling current at the CO-STM junction (15) provide the background for the present development.

Despite the simplicity of a diatomic molecule, the electronic structure of CO is unusual. The free molecule carries 0.12-D dipole, with negative pole on carbon and negative charge density dangling from both oxygen and carbon ends (16). The sign of its apparent dipole upon adsorption on metals has led to ambiguity, necessitating explicit electronic structure calculations to interpret images obtained with CO-terminated tips (17). As the diatomic with the largest bond energy, the C–O stretch is stiff. Therefore, mechanical stresses are principally transmitted to the soft, frustrated rotation and translation modes (4, 18). However, because of its combined electric and mechanical anharmonicity, the CO stretch has a large Stark tuning rate (STR), ∂ν/∂E (12), which makes it an effective molecular transducer of electrostatic fields E = −∂V_es/∂r generated by local charge distributions

$${\mathit{V}}_{\text{es}}(\mathit{r})={\displaystyle \int }\frac{\mathrm{\rho }(\mathit{r}\prime )}{|\mathit{r}-\mathit{r}\prime |}\mathit{d}\mathit{r}\prime$$ (1)

In this context CO has been used to probe electrostatic potentials at surfaces and interfaces (19) and plasmonic junctions (20, 21) in proteins and enzymes (22). We use it here as a scanning electrometer. Because of its weak binding to silver, CO preferentially attaches to the apex of silver tips. The same consideration limits the measurements to long-range intermolecular interactions governed by electrostatics. As we show, the vibrational frequency shift maps out the E-field along the tip axis, while the pendular motion manifested through the linewidth probes lateral electrostatic forces. Since the bond order, bond energy, and therefore STR of CO depend on binding site and geometry, it is useful to calibrate the molecular electrometer before its use. The measurements are carried out in an ultrahigh vacuum (UHV) STM operating at 6 K (see Materials and Methods).

RESULTS

Calibration of the molecular electrometer

The inset of Fig. 1 shows the TERS spectrum of ¹²C¹⁸O attached to the silver tip apex. It consists of a single line, with center frequency that shifts upon varying the junction bias. Figure 1 illustrates this for tunneling gap fixed at g = 5.5 Å. The curve fits the quadratic form

$$\overline{\mathrm{\nu }}({\mathit{V}}_{\mathit{b}};\mathit{g})=\overline{\mathrm{\nu }}(0;\mathit{g})-\mathit{a}{\mathit{V}}_{\mathit{b}}-\frac{1}{2}\mathit{b}{\mathit{V}}_{\mathit{b}}^2$$ (2)

with linear and quadratic coefficients, a = 19.3 cm⁻¹/V and b = 0.73 cm⁻¹/V². To obtain absolute values, it is necessary to relate the spectral shift to the local field, and the necessary information can be extracted from the gap dependence of the frequency shown in Fig. 1 (A and C). The data can be fit to

$$\overline{\mathrm{\nu }}({\mathit{V}}_{\mathit{b}};\mathit{g})={\overline{\mathrm{\nu }}}_{\mathit{g}\to \infty }-\mathit{c}\frac{{\mathit{V}}_{\mathit{b}}-\mathrm{\Delta }\mathrm{\phi }}{\mathit{g}+\mathit{d}}$$ (3)

where g + d defines the effective length over which the applied bias drops, and Δφ = φ_Au − φ_Ag is the contact potential between the gold substrate and silver tip. The latter is directly determined by the crossing point between the asymptotic limit ${\overline{\mathrm{\nu }}}_{\mathit{g}\to \infty }$ of the gap dependence and the bias dependence (see Fig. 1A). The extracted value Δφ = 0.78 V is larger than the difference in work functions of Au(111) and Ag(111) of 0.57 V (23), which is rationalized by the positive charge on protruding Ag atoms (24). The obtained value of d = 2.8 Å is a good fraction of what may be estimated (d₀ ~3.5 Å) as the physical distance between the O atom terminus and the image plane on the silver tip (25). Along the voltage drop between the gold and silver electrodes, CO acts as a capacitor, with relative dielectric constant ε_r = d₀/d ~ 1.2 (see fig. S2), as expected when molecular orbitals are not aligned with the Fermi level (26). Converting the applied bias to local field E_L = V_b/(g + d) generates the calibration curve of the molecular field meter, which is cast in more transparent notation

$$\overline{\mathrm{\nu }}({\mathit{E}}_{\mathit{L}})=\overline{\mathrm{\nu }}(0)-\mathrm{\Delta }\mathrm{\mu }{\mathit{E}}_{\mathit{L}}-\frac{\mathrm{\Delta }\mathrm{\alpha }}{2}{\mathit{E}}_{\mathit{L}}^2$$ (4)

The magnitude of the linear coefficient Δμ = 〈1|μ|0〉 = a(g + d) = 160 cm⁻¹ V⁻¹ Å⁻¹ (0.095 D) is in excellent agreement with the prediction of the density functional theory (DFT) calculations for CO adsorbed on tipped silver (15). The sign of effective dipole flips upon adsorption (15), and the linear STR is nearly three times that of the free molecule (see fig. S3). While contact potentials change upon reshaping the tip apex and quadratic coefficients vary on different tips, the linear Stark coefficients show little tip-to-tip variation (see fig. S4). It may be useful to note that the frequency shift, $\mathrm{\Delta }\overline{\mathrm{\nu }}=\overline{\mathrm{\nu }}(\mathit{E})-\overline{\mathrm{\nu }}(0)$, is a direct measure of mechanical force, F_m, with a conversion factor of 5.8 pN cm⁻¹ given by the vibrational constants of CO.

Fig. 1. Calibration of the molecular electrometer.

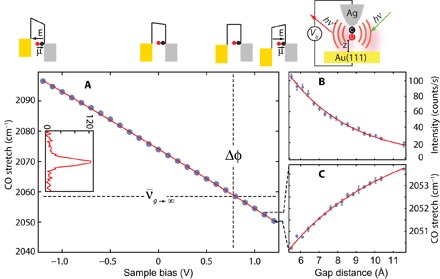
(A) Bias dependence with a gap fixed at 5.5 Å (set at 0.1 nA, +1.2 V). The inset shows the CO line spectrum. (B) Gap dependence of Raman intensity and (C) C–O stretching frequency. All data are recorded with an excitation at λ = 634 nm and an incident intensity of ~5 μW/μm².

TERS intensity as optical field meter

The line intensity determined by the TERS mechanism gives an additional imaging principle. We can extract the Raman scattering cross section of the tip-adsorbed CO from the quadratic Stark tuning coefficient in Eq. 4, Δα = 〈1|α|0〉 = −50 cm⁻¹ V⁻² Å⁻² (8.8 × 10⁻²⁶ cm³)

$$\frac{\mathit{d}\mathrm{\sigma }}{\mathit{d}\mathrm{\Omega }}=\frac{{(2\mathrm{\pi })}^4}{{\mathrm{\lambda }}_{\mathit{i}}{\mathrm{\lambda }}_{\mathit{s}}^3}{|\langle 1|\mathrm{\alpha }|0\rangle |}^2=4.8\times {10}^{-31}{\text{cm}}^2/\text{sr}$$ (5)

where λ_i and λ_s are the wavelengths of incident and scattered photons. The measured value is 50% larger than that of the free molecule. Under the experimental conditions (I = 5 μW/μm²; ∫dΩ = 2.7 sr), we would expect a scattering rate of Iσ = 5 × 10⁻¹⁰ s⁻¹ from one molecule. The observed count rates of 5 × 10² s⁻¹ imply enhancement by a factor of 10¹². These large factors are associated with the combined effects of electromagnetic and chemical (CM) enhancement mechanisms (27), associated with the displacement field D = E + 4πP confined between tip plasmon and its image in the metal substrate. The displacement current, dD/dt, is common to the series capacitors consisting of the vibrating CO, vacuum gap, and targeted molecule. In the hardwired CO, the CM arises from the charge transfer photocurrent through the projected density of <CO(2π*)|Ag(5s)> states (15). Modeling shows the light field to be confined to ~3 Å in the vacuum capacitor by the CO-terminated tip (28). Consistent with this, the TERS intensity can be seen in Fig. 1B to decay on a scale of 3.6 Å as a function of the gap. While TERS of CO is used to image the porphyrins, Raman of the interrogated molecules remains silent. Given their larger Raman cross section, the absence of the molecular spectra underscores the role charge transfer resonances can play (29), which are evidently absent in the physisorbed molecules. On the imaged molecules, the TERS intensity can be recognized to probe the local capacitive reactance, 1/ωC, to the displacement current, due to spatial variations in polarizability, C ∝ (1 + α(ω))/d, at optical frequencies.

Peering inside molecules

To illustrate the method, we consider two members of the porphyrin family: cobalt(II)-tetraphenylporphyrin (CoTPP) and zinc(II)-etioporphyrin (ZnEtio), evaporated on an atomically flat Au(111) substrate. Given their ubiquity in nature and importance of their applications in catalysis and molecular optoelectronics, researchers extensively investigated metalloporphyrins on metal surfaces (30–32). It is known that CoTPP saddles upon adsorption on coinage metals (33, 34), while ZnEtio remains fairly flat (35). TERS-mfm reveals very different intramolecular charge distributions for these seemingly similar molecules. Figure 2 summarizes the measurements and simulations carried out on ZnEtio. The data consist of simultaneously recorded STM- and TERS-relayed images extracted from TERS spectra recorded on every 0.5 Å × 0.5 Å pixel with an acquisition time of 1 s/pixel. We then fit the vibrational line (Fig. 2A) to a Gaussian to map out the three observables: integrated line intensity, line shift, and full width at half maximum (FWHM). Two sets of images, obtained under constant current (CC) and constant height (CH) scan modes, are displayed along with results of DFT calculations. The experimental and theoretical methods are expanded in the Supplementary Materials.

Fig. 2. ZnEtio on Au(111): Imaging principles of TERS-mfm are illustrated in the header.

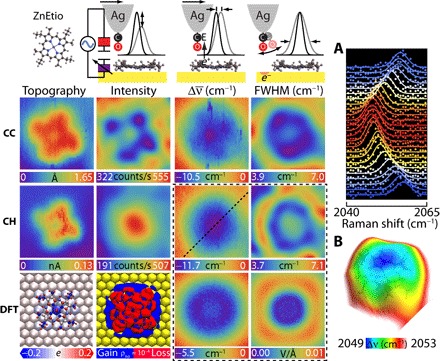
Simultaneously recorded STM topography and TERS-relayed images of intensity, frequency shift ($\mathrm{\Delta }\overline{\mathrm{\nu }}$), and linewidth recorded under CC and CH scan mode. We low pass–filtered the intensity and linewidth maps for clarity. The $\mathrm{\Delta }\overline{\mathrm{\nu }}$ maps in CC and CH mode are referenced to 2058.6 and 2059.5 cm⁻¹, respectively. The DFT results consist of the Löwdin projected atomic charges, deformation charge density, and vertical and lateral electric fields. (A) Stark tuning of the CO vibration along the dashed line in the CH $\mathrm{\Delta }\overline{\mathrm{\nu }}$ map. (B) Electrostatic field surface obtained by color-coding the Stark shift on the STM CH topography. The common image size is 23 Å × 23 Å. The set point is 0.1 nA, 1.2 V.

In its CC topography, ZnEtio appears as a pinwheel with a depression at the central metal atom. The frontier orbital is on the aromatic macrocycle, and unlike the free molecule, the ethyl groups are coplanar in this instance. The CH topography additionally identifies that the scanning plane is slightly tilted relative to the substrate. The TERS CC intensity map images the tetrapyrrole. The metal center and gold surface show similar polarizability, while the signal drops on the pyrroles. Convoluted in the CC intensity map is the effect of tip height variation: The tip rises on the pyrroles and descends on the central Zn atom, as seen in the CC topography. In molecular circuit terms (Fig. 2, header), the spatial variation in capacitance, C ∝ ε_r/d, controls the displacement current. The CH intensity image, recorded 5.5 Å above the molecule, shows the effect of filling the vacuum between CO and Au with a dielectric: Adding a polarizable molecule increases the total capacitance and, with it, the displacement current.

The STM topography does not contain direct information about charges. The down-shift of the CO vibrational frequency on the molecule establishes that it carries a net positive charge. Relative to gold, the CO frequency shifts by as much as $\mathrm{\Delta }\overline{\mathrm{\nu }}$ = −10 cm⁻¹, equal to a potential drop of ΔV = 0.5 V. Evidently, the highest occupied molecular orbital (HOMO) on the macrocycle transfers charge to gold by aligning with the metal Fermi level, and it is the partially empty HOMO that is imaged by the STM. The charge is angularly isotropic, as seen in the CH $\mathrm{\Delta }\overline{\mathrm{\nu }}$ map and the electrostatic field surface obtained by color-coding the Stark shift on the CH topography (Fig. 2B). Rather than a charged disk, the radial structure in the CH FWHM map betrays charge on a ring. Evidently, and consistent with theory (36), the occupied d-electrons on Zn are significantly below the Fermi level such that the central Zn atom does not share the macrocycle charge. Under the constraint of charge on a ring, we can quantify the net charge and its spatial distribution through approach curves. Figure S5 provides such an analysis, where we show that a net charge of +0.67e, distributed on a ring with inner and outer radii of 3.3 and 7.1 Å, respectively, adequately reproduces the data, including CH $\mathrm{\Delta }\overline{\mathrm{\nu }}$ and CC $\mathrm{\Delta }\overline{\mathrm{\nu }}$ maps. The analysis verifies that the anticorrelation between the CC $\mathrm{\Delta }\overline{\mathrm{\nu }}$ image and the CC topography, which appears as a rotation of the image, is the result of varying tip height from the charged plane of the molecule.

The DFT calculations show a net charge of 0.92e transferred from porphyrin to gold. The associated vertical component of the electrostatic field E_z is calculated at different heights and scaled by the experimental linear Stark coefficient Δμ to generate the CH $\mathrm{\Delta }\overline{\mathrm{\nu }}$ image. The computed image at a height of 7 Å above the molecular plane is in fairly good agreement with the experiment, although the predicted magnitude of the shift is nearly half of what is seen. The magnitudes agree when the field is computed at a height of 4 Å; however, the image develops a depression at the center instead of the maximum seen in the experiment (see fig. S10). The general agreement validates the assumptions that the Stark effect dominates the $\mathrm{\Delta }\overline{\mathrm{\nu }}$ map, CO is vertically aligned at this bias (1.2 V), and in the range of measurements, electrostatics dominates the intermolecular forces between CO and ZnEtio. However, the computed charge distribution appears to be more strongly localized on the periphery than in the experiment. Whether in theory or experiment, forces are the observables. Their inversion to extract charge distributions is generally not unique. With that in mind, we provide in Fig. 2 the Löwdin projection and the charge deformation obtained as the density difference between the free and adsorbed molecule. The former localizes charges on atoms, with positive charge mostly carried by the hydrogens. The latter shows delocalized charge with radially polarized periphery. The experiment suggests that the aromatic HOMO carries the charge. The latter is consistent with a previous analysis of the ZnEtio⁻ radical anion prepared on a thin oxide, where it has been shown that, because of the high symmetry of the planar molecule, the dynamic Jahn-Teller effect imposes a ring current (35). This vibronic effect is absent in the DFT calculations.

The linewidth of CO serves as a sensitive probe of lateral electrostatic fields. The observed width on the macrocycle ring is near the instrument limit (FWHM = 4.5 cm⁻¹). It broadens on the central atom and nearly doubles in width on a ring outside the molecule. The observed break in the outer ring is due to interference from another nearby ZnEtio. Consistent with the conservative nature of electrostatic forces, the lack of correlation between width and intensity maps establishes that the broadening is not due to dissipation. The close correspondence between the linewidth map and the computed in-plane electrostatic field, |E_x + E_y|, which reaches ~10 meV/Å on a ring outside the molecule, establishes that the spatial variation in linewidth arises from lateral forces. We can associate the spectral width with the angular distribution of CO sampled by the pendular (frustrated translation) motion, which, at 2 meV (4), is the only accessible state at 6 K. We subject the pendular motion of a dipole in an electrostatic field to torque that we can sense through its modified angular frequency $\mathrm{\omega }=\sqrt{(\mathrm{\kappa }+\mathrm{\mu }\mathit{E})/\mathit{I}}$. When the field is aligned with the dipole, the motion stiffens, and its angular distribution narrows; therefore, the spectral width of the stretch sharpens. This explains the observed line narrowing on the positively charged ring, where the requirement of a vertical field E ~ κ/μ can be satisfied if we assume the dipole to arise from the dangling 0.2e⁻ charge on oxygen (for μ = 3.5 D and κ/μ = 0.24 V/Å; see fig. S5). Upon falling off the molecule, the mode softens, and its thermal occupation increases; therefore, the line broadens. While this explains the principle of imaging contrast through linewidths, larger area scans clarify that, both here and in the case of CoTPP, Friedel oscillations of surface electrons, known to be induced by charged adsorbates (37), are being imaged (see below).

Figure 3 shows the equivalent set of images for a CoTPP molecule. In the STM topography, the C₄ symmetry of the free molecule is reduced to C₂ because of the saddling distortion, which can be more clearly seen in the TERS relayed images. The CC intensity map shows the inequivalent dim (up) and bright (down) pyrroles. The polarization associated with the distortion is relayed in the CC $\mathrm{\Delta }\overline{\mathrm{\nu }}$ map, where a potential drop of ~1 V is seen to extend along the edges of the lower pyrroles. The CC $\mathrm{\Delta }\overline{\mathrm{\nu }}$ image is reproduced by the computed E_z field calculated at a height of 4 Å above the molecular plane, and the linewidth images are adequately reproduced by the computed lateral field, |E_x + E_y|. The agreement between experiment and theory validates the scanning molecular electrometer and gives confidence to the dissection of previously unknown charge distributions in what may be considered a weakly bound molecule on gold.

Fig. 3. Results for CoTPP on Au(111): The $\mathbf{\Delta }\overline{\mathbf{\nu }}$ maps in CH and CC mode are referenced to 2048.1 and 2046.9 cm⁻¹, respectively.

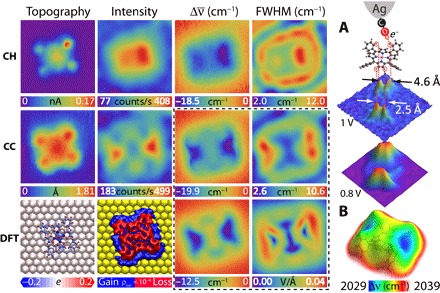
(A) Atomically resolved forces due to hydrogen bonding between CO and the indicated H atoms. The indicated voltages are the potential differences relative to the gold substrate, as measured by the Stark shift of CO of 19.3 cm⁻¹/V according to the calibration of Fig. 1A. (B) Electrostatic field mapped on the isosurface of local density of states (LDOS). The common image size is 27 Å × 27 Å. The set point is 0.1 nA, 1.2 V.

Contrary to previous x-ray photoelectron spectroscopy analysis, which assigns the charge transfer from gold to Co (38), and consistent with a previous DFT analysis (34), we find that nearly a unit charge is transferred from CoTPP to Au. This is extracted from the present DFT calculations and separately established by modeling the Stark shift maps and approach curves recorded on Co and pyrroles using a charged rectangular plate decorated with two line charges (fig. S6). The charge transfer is from the macrocycle, rather than Co. We corroborated this by observing the Kondo resonance of Co(II), which establishes that cobalt retains its unpaired ${\mathrm{d}}_{{\mathit{z}}^2}^1$ electron configuration (see fig. S7). Once again, the Löwdin projection localizes the positive charge on the peripheral hydrogens, and we directly verified this by the experiment in this case. We show in Fig. 3A that the contours of the largest spectral shift in the CH $\mathrm{\Delta }\overline{\mathrm{\nu }}$ image, at a potential of 1 V ($\mathrm{\Delta }\overline{\mathrm{\nu }}~-20{\text{cm}}^{-1}$) relative to gold, are sharply localized on two pairs of atoms separated by 2.5 and 4.6 Å, respectively. The former aligns with the hydrogens of the lower pyrrole, while the latter aligns with the nearby hydrogen atoms on the phenyl groups (circled in red in Fig. 3A). The four atomically resolved distributions highlight the spatial resolving power of the method, when such features exist. Here, they suggest hydrogen bonding between CO and the positively charged H atoms governed by electrostatic bonding between the dangling electron charge on oxygen and acidic hydrogens. The same bonding motif was recently reported in CO-AFM measurements (39). As we stepped up the potential to 0.8 V relative to gold, the distributions merge and appear as the line charge of acidic hydrogens on the lower pyrroles (Fig. 3A), followed by the trace of the H atoms decorating the pocket between the pyrroles and phenyl rings. In effect, the hydrogens are polarized through induction due to the charge transferred from the physisorbed molecule to gold, which is apparent in the DFT-computed deformation density. The theory and experiment agree that there is ~0.3 V difference between the lower and upper pair of the saddled pyrroles, and Fig. 3B visualizes this in the electrostatic field surface. This intramolecular polarization was separately recognized through TERS imaging of CoTPP with bare silver tips, where the Stark shift of a normal mode could be seen within the molecule (28).

The CH FWHM map of CoTPP appears as a stadium with two foci bounded by the molecular frame. We can also see partial edges of the recursion of the stadium at an inter-ring separation of ~9 Å, which, at V_b = 1.2 V, is consistent with the momentum of the surface Shockley state sustained on Au(111) (37, 40). We can see the secondary rings around both ZnEtio and CoTPP in expanded area scans (fig. S8). The ripples represent the dielectric response of the two-dimensional (2D) gas to the charge on the molecular adsorbates. This exquisite sensitivity to small fluctuations in surface charge density may be reconciled by the coulombic force exerted on the dangling charge on oxygen, sensed by motional instability of a very soft mode (κ → 0), such as the azimuthal component of the 2D pendular motion. Such a motion would carry a magnetic field and could, in principle, serve as a molecular magnetometer.

DISCUSSION

The presented deployment of a single CO molecule as a sensor and transducer may be recognized as a leap into the ultimate limit in miniaturization of MEMS in current use. In effect, TERS-enabled single-molecule vibrational spectroscopy directly accesses the electromechanical machinery of individual molecules. Under the more general framework of mfm, the present implementation has emphasized the scanning electrometer as a probe of electrostatic fields with submolecular spatial resolution. It gives access to electrostatic potential surfaces that define molecular shapes of greatest functional relevance, which, to date, have been mainly theoretical constructs. Electrostatic potentials distinguish the activity of surfaces and interfaces that control processes ranging from heterogeneous catalysis to optoelectronic devices, and to the extent that charge transfer drives the fundamental molecular processes, charge distributions on the nanoscale provide the structural information of functional relevance. Yet, for the most part, quantitative probes of electrostatics on the nanoscale have been lacking. The challenge is addressed with the single-molecule electrometer. The demonstrated quantitative measurement of charge on a physisorbed molecule, its intramolecular distribution and associated structural deformation, and surface dielectric response are fundamental to understanding interfaces, where the predictability of current theory remains questionable. Beyond probing fundamental science of interfaces, it is not too difficult to surmise that TERS-relayed single-molecule vibrational spectroscopy may serve as the essential, missing multimeter required to advance the field of molecular electronics.

MATERIALS AND METHODS

Experimental

STM-TERS measurements were performed under UHV (base pressure = 4 × 10⁻¹¹ torr) at 6 K. A parabolic mirror installed inside the homebuilt STM system was aligned to the tip apex by imaging electroluminescence from the tunneling junction (41). For Raman measurements, the tip-sample junction was illuminated at 45° with a single-mode 634-nm diode laser (CrystaLaser) focused at the tunneling junction through an aspheric lens. The Raman spectra were acquired using a 0.3-m spectrograph (SpectraPro 2300i, Princeton Instruments) equipped with a liquid nitrogen-cooled charge-coupled device (Spec-10). The nanoscopically smooth silver tip was prepared by ex situ Ar⁺ field-directed sputter sharpening (FDSS) and finalized by Ne⁺ ion FDSS in situ (11). The cone radius of the tip before in situ processing was 16 nm. We dosed ¹²C¹⁸O, CoTPP, and ZnEtio onto the Au(111) surface, as shown in fig. S1. The Ag tip was terminated by a single CO molecule through field emission on a CO lattice gas on Au(111), and the functionalization was directly verified through the CO stretch Raman spectrum and enhanced resolution in STM topographic images. The CO Raman maps were acquired in constant current and constant height modes.

Theoretical calculations

The geometry optimizations were performed using DFT at the Generalized Gradient Approximation (GGA)–Perdew-Burke-Ernzerhof (PBE) level, with the dispersion correction (DFT-D3) (42) on the ADF-BAND package (43, 44). The Slater-type orbitals represented by double zeta basis sets without polarization functions with small frozen cores were used. The relativistic effects were taken into account by means of the scalar zero-order regular approximation (45–47). The spin-unrestricted approach was used for the open shell system of CoTPP adsorbed on the Au(111) surface. During the structural minimizations, the Au slab was constrained to the bulk with the experimental lattice parameter of 4.08 Å to be consistent with the experimental adsorbate ordering (34). The CoTPP was placed on the top side with the orientation of 39.5° between N-Co-N axis and (110) direction of the face-centered cubic (111) surface.

To reduce the interplay effects arising from the molecules on the adjacent unit cells, the size of the unit cell was extended to 28.8 × 29.9 × 22.7 Å in the electronic state calculations. The Au slab model consisted of 360 atoms in three layers. The plane-wave DFT calculations were carried out using the Quantum ESPRESSO package (48) to reduce the computational cost. The GGA-PBE functional incorporated with dispersion correction (DFT-D2) was used. We found that the combination of wave function cutoff of 80 rydberg (Ry) and charge density cutoff of 800 Ry, together with ultrasoft pseudopotentials, provided a reliable electron densities for the electrostatic field calculations. The spin-polarization calculations with the initial guess of 0.05 static magnetization were used for the CoTPP system.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaat5472/DC1

Supplementary Materials and Methods

Supplementary Text

fig S1. Topographic image of CoTPP, ZnEtio, and CO islands adsorbed on the Au(111) surface at 6 K.

fig. S2. Schematic diagram and equivalent circuit.

fig. S3. The vibrational Stark effect on CO.

fig. S4. Stark tuning of two differently terminated CO tips.

fig. S5. Equivalent charge model for ZnEtio.

fig. S6. Equivalent charge model for CoTPP.

fig. S7. Variation of Kondo resonance peaks.

fig. S8. Detection of standing waves through the linewidth of CO stretch peak.

fig. S9. Optimized geometries of ZnEtio and CoTPP adsorbed on Au(111) surfaces.

fig. S10. Electrostatic potential, field, and CO frequency shift mapping of ZnEtio on the Au(111) surface.

fig. S11. Electrostatic potential, field, and CO frequency shift mapping of the CoTPP on the Au(111) surface.

References (49–57)