Permselectivity limits of biomimetic desalination membranes

Biomimetic desalination membranes could achieve ultraselectivity for water over ions, but not over neutral solutes.

Abstract

Water scarcity and inadequate membrane selectivity have spurred interest in biomimetic desalination membranes, in which biological or synthetic water channels are incorporated in an amphiphilic bilayer. As low channel densities (0.1 to 10%) are required for sufficient water permeability, the amphiphilic bilayer matrix will play a critical role in separation performance. We determine selectivity limits for biomimetic membranes by studying the transport behavior of water, neutral solutes, and ions through the bilayers of lipid and block-copolymer vesicles and projecting performance for varying water channel densities. We report that defect-free biomimetic membranes would have water/salt permselectivities ~10⁸-fold greater than current desalination membranes. In contrast, the solubility-based permeability of lipid and block-copolymer bilayers (extending Overton’s rule) will result in poor rejection of hydrophobic solutes. Defect-free biomimetic membranes thus offer great potential for seawater desalination and ultrapure water production, but would perform poorly in wastewater reuse. Potential strategies to limit neutral solute permeation are discussed.

INTRODUCTION

Water scarcity affects 4 billion people globally and will be severely exacerbated in the coming century by rising population growth and climate change (1). While improved water management is important, sustainable technologies to augment drinking water supplies from unconventional sources are just as crucial. One of the most important tools is reverse osmosis (RO), in which hydraulic pressure is applied to drive water through a water-selective membrane (2, 3). Because of its high energy efficiency, low cost, and modularity, RO will likely remain the premier technology for desalination of saline sources such as seawater, brackish groundwater, and industrial wastewaters (for example, oil-and-gas produced water) (2). RO additionally plays a central role in advanced wastewater treatment processes, which allow for the potable reuse of municipal wastewater. Reuse of coastal wastewater effluent, which currently drains to the sea, could provide 27% of the drinking water supply in the United States (4).

Despite the importance of RO, improvements in performance have been marginal for conventional polyamide reverse osmosis (PA-RO) membranes over the past three decades. The lack of significant progress comes despite a practical need for improved membrane selectivity, as inadequate rejection by PA-RO membranes of ions and small neutral solutes can necessitate extensive posttreatment (5). For example, in seawater RO, the inability of PA-RO membranes to meet stringent chloride and boron standards in one RO pass often requires a second RO pass, in which a second RO train (pumps, piping, membranes) is used to further purify a portion of the permeate from the first pass. In wastewater RO, small carcinogens such as N-nitrosodimethylamine (NDMA) and 1,4-dioxane are poorly removed by PA-RO membranes during potable wastewater reuse. Their permeation necessitates an advanced oxidation step (typically H₂O₂/ultraviolet irradiation) to chemically degrade recalcitrant species (5).

Because of the growing challenges related to water scarcity, there has been extensive interest recently in so-called biomimetic desalination membranes (3, 6). In this class of materials, biological or synthetic water channels are incorporated within a fluid-like lipid or amphiphilic block-copolymer (BCP) bilayer to form a composite selective layer (Fig. 1A). A diverse array of channels have been fundamentally explored, including aquaporins (7), carbon nanotubes (8), supramolecular water channels (9–11), and single-molecular synthetic channels (12). In addition, extensive academic and industrial work has sought to fabricate functional biomimetic desalination membranes, particularly using aquaporin, for use in RO (6). However, such efforts have been critically hindered by the presence of macroscopic defects within the selective layer, which have led to anomalously low salt rejections (20 to 65%), despite the near-perfect water/solute selectivity of some aquaporin variants. These low rejections obscure the expected performance of biomimetic membranes, and the attainable performance and potential impact of defect-free biomimetic desalination membranes remain unclear.

Fig. 1. Projecting performance of biomimetic desalination membranes.

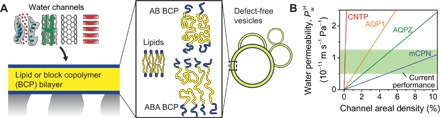
(A) To make a composite biomimetic selective layer, biological or synthetic water channels are incorporated into a fluid-like lipid or amphiphilic BCP bilayer that is supported by a porous substrate. The same materials can form defect-free LUVs, for which intrinsic permeabilities can be measured. (B) Hydraulic water permeability ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$ of a composite selective layer for given channel densities based on published single-channel permeabilities (8, 32, 50). Permeabilities were experimentally determined for all but modified cyclic peptide nanotube (mCPN), for which simulations were used (50). Depending on the channel type, densities of 0.1 to 10% will yield sufficient water permeability. CNTP, carbon nanotube porin; AQP1, aquaporin-1; AQPZ, aquaporin-Z.

Extensive characterization of transport behavior within water channels allows for ready comparison with conventional PA-RO membranes. In particular, relatively low channel densities of 0.1 to 10% would enable water permeabilities within the range attained by current PA-RO membranes (Fig. 1B and table S1). Since increased water permeability above current levels would have minimal practical impact in RO (5), this range of hydraulic water permeabilities ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$ (0.5 to 1.2 × 10⁻¹¹ m s⁻¹ Pa⁻¹) is an appropriate target for biomimetic membranes. In contrast to channels, very little attention has been paid to the amphiphilic channel matrix, which is critical for channel insertion, alignment, stability, and functionality (6, 13, 14). Given the near-perfect selectivity of some channels (for example, aquaporin) and expected matrix surface areas exceeding 90%, the amphiphilic matrix will strongly impact the separation performance. In addition, because similar matrices could be used for any channel type, study of the permeability behavior of amphiphilic bilayers can provide insight into the performance of biomimetic desalination membranes as a general class of materials.

To this end, we investigated the transport of water, neutral solutes, and ions through the lipid and BCP bilayers that have been most commonly explored as matrices in biomimetic selective layers. As model membranes, we used large unilamellar vesicles (LUVs), which intrinsically self-assemble to form bilayer structures that are free of macroscopic defects. Thus, permeabilities measured for LUVs are the expected values for defect-free planar membrane selective layers using similar amphiphilic materials. Using the measured permeabilities, we project the performance limits of biomimetic desalination membranes in water treatment applications, with particular emphasis on membranes using a perfectly selective water channel (for example, aquaporin). Our work shows that ultraselectivity can be attained for some solutes (ions), but not others (hydrophobic solutes), suggesting areas where materials design research will be needed to produce high-performance biomimetic membranes.

RESULTS

LUVs were formed from a synthetic lipid with two monounsaturated aliphatic chains [1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)], an ABA-type BCP comprising poly(2-methyloxazoline)₁₁-b-poly(dimethylsiloxane)₆₅-b-poly(2-methyloxazoline)₁₁ (MDM), and an AB-type BCP comprising poly(1,2-butadiene)₄₆-b-poly(ethylene oxide)₂₀ (PB-PEO). All three materials readily form vesicles (also called liposomes or polymersomes) upon hydration and have been used in the past to stably incorporate aquaporin and synthetic channels (6, 7, 13, 15). The study of BCPs is particularly important, as the industrial application of biomimetic membranes will almost certainly require polymeric matrices due to their enhanced chemical and mechanical robustness compared with lipid bilayers (7, 16). To control LUV size, vesicles were extruded through a 200-nm pore size polycarbonate membrane. Resulting LUV solutions had average hydrodynamic diameters of 188 to 224 nm with polydispersities of 0.04 to 0.14, as determined by dynamic light scattering. Cryo–electron microscopy (cryo-EM) confirmed the major presence of ~200-nm LUVs for MDM and PB-PEO (Fig. 2A and fig. S1). Other aggregate structures (for example, worm-like micelles) were not observed for PB-PEO but were observed at low levels for MDM (fig. S1). Membrane core thicknesses were estimated using cryo-EM to be 15 ± 2 nm for MDM and 13 ± 2 nm for PB-PEO. DOPC has a published hydrocarbon core thickness of 2.68 nm (17).

Fig. 2. Permeability measurements using lipid and BCP vesicles.

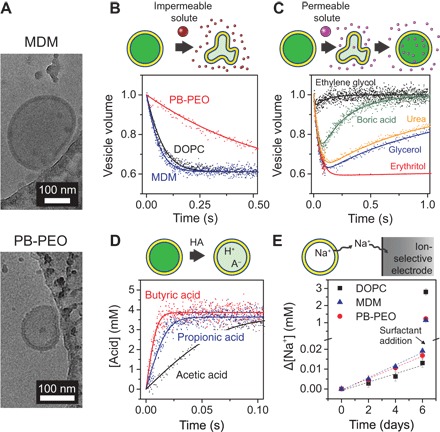
(A) Cryo-EM images of MDM and PB-PEO LUVs prepared by extrusion through 200-nm pores. The vesicles are located near the edge of a carbon-coated copper microscopy grid. Small, irregular structures are artifacts of the ice structure and the carbon coating. From these and more images (fig. S1), the nonpolar core thicknesses of the MDM and PB-PEO bilayers were estimated to be 15 ± 2 and 13 ± 2 nm, respectively. (B) Water and (C) solute permeability measurements using osmolarity differences. Normalized LUV volume was determined via the self-quenching of encapsulated fluorophore upon exposure at 25°C to osmotic gradients induced by (B) relatively impermeable NaCl and (C) relatively permeable solutes. The data are averaged from 3 to 10 time traces and fitted (solid curves) using Eqs. 1 and 2 to determine water and solute permeabilities. LUV volumes change because of water transport that balances the osmotic pressures inside and outside of the vesicles. Solute permeability measurements in (C) are shown for MDM. (D) Acid influx measurements for DOPC at 6.4°C, showing intravesicular acid concentration based on decreased intravesicular pH and the pH sensitivity of encapsulated fluorophore. Data are averaged from 6 to 10 time traces and fitted (solid curves) using Eq. 5 to determine acid permeability. (E) Sodium efflux from LUVs at 25°C, shown as the cumulative change in extravesicular sodium concentration, as determined using a sodium-selective electrode (n = 3). Dashed lines are linear fits used in Eq. 6 to determine the sodium permeability. After 6 days, a surfactant (Triton X-100) was added to solubilize the vesicles and determine the total vesicle volume.

Permeabilities of model solutes were measured using a range of techniques (Fig. 2, B to E). All techniques relied on encapsulated solutes and were therefore only affected by aggregate structures that encapsulate aqueous solutions (that is, vesicles). Using a stopped-flow apparatus to enable rapid kinetic measurements, we first performed vesicle shrinkage experiments to measure the osmotic water permeability P_w (Fig. 2B) and solute permeability P_s (Fig. 2C) for neutral, nondissociative solutes. During experiments, LUVs were rapidly mixed with a solution made hyperosmotic by the solute of interest. Initially, fast water efflux due to the osmotic pressure difference causes the vesicle volume to shrink. Subsequently, relatively slow solute influx induces water influx to balance osmotic pressures, eventually resulting in vesicles returning to their original volume. Water and solute permeabilities were related to the rate of LUV volume change. Vesicle shrinkage experiments exploited the self-quenching property of an encapsulated fluorophore, carboxyfluorescein (CF), to linearly relate measured fluorescence with vesicle volume (fig. S2) (18). Fluorescence self-quenching is less susceptible than light scattering to measurement artifacts, such as scattering by nonvesicular aggregates or changes in the refractive index with concentration that can occur for some solutes (for example, urea) (18–20). Measured water permeabilities were consistent over a range of osmotic driving forces (fig. S3). Permeability measurements for rapidly permeating carboxylic acids (Fig. 2D) utilized the pH sensitivity of CF (fig. S2). Only neutral acid molecules permeate on a relevant time scale, causing the intravesicular pH and the corresponding fluorescence to decrease (fig. S4). Experiments were conducted at pH 7.5, well above the solute pK_a, to have an excess of conjugate base and thus eliminate boundary-layer (also called unstirred layer) effects (21). Last, for Na⁺ permeability measurements, an ion-selective electrode was used to measure slow sodium efflux from Na⁺-containing vesicles (Fig. 2E). Na⁺ serves as a model for dissolved salt and other ionic species. Measured solute permeabilities for DOPC were comparable to literature values for similar lipid materials (table S2).

The measured permeabilities (Fig. 3 and table S3) can be directly related to expected desalination membrane performance. First, permeabilities measured for LUVs should be identical to the permeabilities of planar membrane selective layers comprising the same materials. Second, the biophysical models used to calculate P_w and P_s in vesicle experiments (Eqs. 1 and 2) are identical to the performance equations that are commonly used to characterize RO membranes, particularly ${\mathit{J}}_{\mathrm{w}}={\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}(\mathrm{\Delta }\mathit{p}-\mathrm{\Delta }\mathrm{\pi })$, where J_w, ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$, Δp, and Δπ are the water flux, hydraulic water permeability, applied pressure, and osmotic pressure difference across the membrane, respectively, and J_s = P_sΔC, where J_s and ΔC are the solute flux and solute concentration difference across the membrane, respectively. In these relations, the same solute permeability is used for both vesicular and planar membrane systems, and the hydraulic water permeability ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$ can be directly calculated from the osmotic water permeability P_w as ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}={\mathit{P}}_{\mathrm{w}}{\mathit{V}}_{\mathrm{w}}/{\mathit{R}}_{\mathrm{g}}\mathit{T}$, where R_g, T, and V_w are the gas constant, absolute temperature, and molar volume of water, respectively (3, 22).

Fig. 3. Permeability trends of lipid bilayers, BCP bilayers, and conventional desalination membranes.

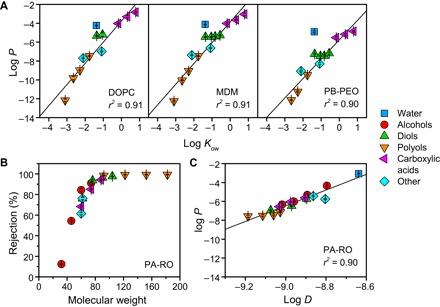
(A) Solubility-based permeability of fluid-like lipid and amphiphilic BCP bilayers. Water and solute permeabilities P (in m/s) were measured at 25°C (n = 3) and are compared with the octanol-water partition coefficient K_ow, a commonly used measure of solute hydrophobicity. Regression lines consider all species except for water because of its anomalously rapid permeation stemming from its small size (21, 51). The strong correlation between solute permeability and hydrophobicity matches and extends Overton’s rule, which was originally formulated for lipid bilayers (21). (B) Solute rejection, defined as 1 − C_permeate/C_feed, for a commercial PA-RO membrane (SW30XLE, Dow), measured at 15.5 bar and 25°C (n = 6). Rejection is size-based, with a molecular weight cutoff of ~80 Da, which leads to (C) a strong dependence of permeability (in m/s) on the solute diffusivity in water D (in m²/s), which decreases with increasing solute size.

The two membrane performance equations above stem from the solution–diffusion model. This model, which is widely accepted for passive transport in lipid bilayers (21, 23) and transport through PA-RO membranes (22, 24), separates molecular transport across a membrane into three steps: sorption into the membrane, diffusion across the membrane, and desorption on the other side of the membrane. The permeability P is predicted to be proportional to the partition coefficient K_mem and the diffusivity within the membrane D_mem and inversely proportional to membrane thickness δ (that is, P = K_memD_mem/δ). In classical application of the solution–diffusion model, the lipid bilayer is depicted as a homogeneous slab of hydrocarbon to circumvent the substantial challenge of accurately measuring K_mem and D_mem. While this simplification does not capture important effects such as membrane fluidity (25–27), heterogeneous bilayer structure (28), and steric resistance from polar headgroups (23), it enables comparison of P with molecular diffusivities in solution and bulk liquid/liquid partition coefficients such as the hexadecane/water partition coefficient K_hdw and the octanol/water partition coefficient K_ow (21). For lipid bilayers, the correlation between P and solute partitioning is typically remarkably strong. For example, the logarithms of P and K_hdw have been found to strongly correlate over six orders of magnitude for egg lecithin (21). This solubility-based permeability of lipid bilayers, traditionally called Overton’s rule, stems from large variability in solute solubility in hydrocarbons. Size-based selectivity can be important (26), but typically has a relatively minor impact on the overall permeability (21, 25).

We analyzed the measured solute permeabilities according to the solution–diffusion model. Following the example of classic biophysical studies, permeabilities were compared with bulk liquid/liquid partition coefficients and molecular diffusivity in water D (21). As expected, permeability for DOPC is solubility-dependent; P was strongly correlated with K_ow (Fig. 3A) and K_hdw (fig. S5) over 5 to 10 orders of magnitude, and poorly correlated with D (fig. S5). Permeability for the two BCPs was similarly found to be solubility-dependent (Fig. 3A and fig. S5). Considering the physical similarities between the two BCP bilayers and DOPC bilayers (particularly the fluid-like, nonpolar core), the similarity in transport behavior is perhaps unsurprising. However, permeability analyses for amphiphilic BCPs are scarce (29, 30), and the extension of Overton’s rule to amphiphilic BCPs has not been reported in the literature, despite the importance of polymersomes in drug delivery and analytical chemistry (14). Furthermore, permeability for MDM was very similar to DOPC, whereas permeabilities for PB-PEO were 5- to 200-fold lower than for DOPC. Decreased permeability for PB-PEO largely stems from increased size-based selectivity (fig. S5), likely due to decreased fluidity within the PB core compared with that of DOPC and MDM (16, 29). Decreased fluidity has been shown to decrease the permeability of lipid bilayers through enhanced size-based discrimination of both partitioning and diffusion (22, 25–27).

For comparison with the three bilayers, transport through a commercial seawater PA-RO membrane was characterized for the same solutes. Sharply contrasting with the three bilayers, PA-RO permeability is strongly size-dependent with a molecular weight cutoff (corresponding to 90% rejection) of ~80 Da (Fig. 3B). The size-dependent rejection leads to a strong dependence of P on diffusivity in water D (Fig. 3C), which is inversely related with molecular size by the Stokes-Einstein relation. P did not correlate with K_ow (fig. S5), showing limited effect of solute hydrophobicity on transport within PA-RO membranes. The size-based permeability of PA-RO membranes stems from steric resistance to solute partitioning into and diffusion between molecular voids present within the highly cross-linked PA selective layer (22, 31). While chemical effects such as hydrogen bonding can affect permeability (31), the ratio of solute size to the size of molecular voids within the PA film is the dominant factor (22).

Using published single-channel permeabilities and our measured bilayer permeabilities, we can project the performance in water treatment applications of defect-free biomimetic desalination membranes with varying channel areal densities. The water permeability for AQPZ (32) is used for our calculations. Because of its near-perfect water/solute selectivity and relative stability (33, 34), AQPZ has been the biological channel of choice for desalination research (6). The superlative selectivity of AQPZ allows channel-driven solute permeation to be neglected. This assumption of course is not valid for all channels, and solute permeabilities characteristic of individual channels must be taken into account when considering other channel types. For example, small neutral solutes such as urea would likely permeate carbon nanotubes that reject salt. Channel water permeability has been reported to be similar when channels were incorporated within different matrices (13). Thus, the same channel water permeability was used for all calculations.

We first consider seawater desalination, for which the removal of ions (salinity) and boron (boric acid) is the biggest need to produce potable water and water for irrigation. Sodium permeability was measured as a surrogate for salt (NaCl) permeability. Chloride is more permeable than sodium through lipid bilayers (35), and during RO, the need to maintain electroneutrality means the less permeable ion determines the overall salt permeability. Sodium permeability ${\mathit{P}}_{{\text{Na}}^{+}}$ was comparable (10⁻¹⁵ to 10⁻¹⁶ m/s) for the three bilayers, with slightly higher values for the BCPs than for DOPC. These extremely low permeabilities largely stem from the enormous solvation energies needed to move an ion from a medium with a high dielectric constant (water) to a medium with a low dielectric constant, such as hydrocarbon or poly(dimethylsiloxane) (35). Figure 4 shows the expected water/salt permselectivities (defined as the ratio of the respective permeabilities ${\mathit{P}}_{\mathrm{w}}/{\mathit{P}}_{{\text{Na}}^{+}}$) for the three materials with increasing AQPZ channel densities. With channel densities of 1 to 5%, comparable water permeability to seawater PA-RO membranes is achieved, but with water/salt permselectivities that are 10⁷ to 10⁸ times greater. Such extreme permselectivities would yield salt passage values <10⁻⁷% under standard seawater RO conditions (~0.5% is typical for PA-RO) (2, 3). In other words, a defect-free biomimetic membrane would provide near-perfect salt rejection. Analysis of water/boron permselectivity (Fig. 4) shows a similar, if less dramatic, story. Defect-free biomimetic desalination membranes using the least permeable matrix (PB-PEO) are projected to have boron passage of ~0.1%, compared to ~10% for PA-RO (36). All three materials would have water/boron permselectivities that are sufficient to meet boron standards in one-pass RO, which would result in major efficiency gains in seawater desalination.

Fig. 4. Projected performance of biomimetic membranes in seawater desalination.

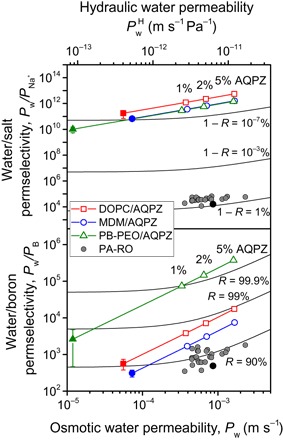
Water/salt (top) and water/boron (bottom) permselectivities are calculated from measured bilayer permeabilities (solid symbols), bilayer permeabilities assuming increasing incorporation densities of AQPZ (lines and open symbols), and measured permeabilities (black circles) and manufacturer specifications (gray circles) (5, 52) for commercial PA-RO membranes. AQPZ is shown because of its frequent usage in biomimetic desalination membrane research. A single-channel water permeability of 2.9 × 10⁻¹³ cm³/s was used (table S1), adjusted from recently measured values (1.8 × 10⁻¹³ cm³/s at 5°C) (32) using an activation energy of 4 kcal/mol (42). Black isorejection lines are displayed to indicate the expected performance of the various materials and are calculated for salt (top) and boron (bottom) assuming standard seawater RO test conditions of 32,000–parts per million (ppm) NaCl, 5-ppm boron, and 55.2-bar applied pressure. R, observed rejection.

For potable reuse of wastewater, RO is used to reduce not only salinity but also, more importantly, the concentrations of a wide variety of organic and inorganic pollutants. To assess the suitability of biomimetic desalination membranes in wastewater RO, we compare water/solute permselectivities for PB-PEO with 3% AQPZ incorporation (Fig. 5A) with the physicochemical properties of micropollutants that are relevant to wastewater reuse (Fig. 5B and table S4) (37–40). Micropollutants are species that can adversely affect human or ecological health at very low concentrations (41); their removal is therefore crucial for safe potable reuse of wastewater. The solubility-based permeability of amphiphilic bilayers results in a corresponding solubility-based selectivity for biomimetic membranes. Calculating expected rejections from permselectivity yields a “hydrophobicity cutoff” of approximately log K_ow = −0.2. Comparison with micropollutant properties shows that the vast majority of micropollutants have log K_ow >> −0.2 and would therefore rapidly permeate a biomimetic membrane (fig. S6). In other words, a biomimetic desalination membrane using a fluid-like matrix would perform poorly in wastewater RO, even if the membrane is defect-free and the channel is perfectly selective for water. In contrast, nearly all of the micropollutants are larger than 80 Da, the approximate molecular weight cutoff of the tested PA-RO membrane (Fig. 3B). PA-RO membranes would thus be expected to yield high rejections of most micropollutants, matching what has been observed in practice (39, 40).

Fig. 5. Projected performance of biomimetic membranes in wastewater reuse.

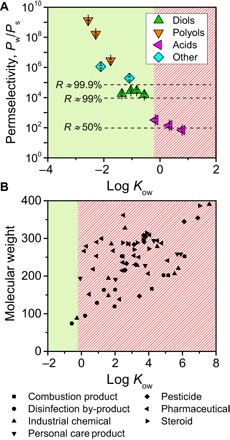
(A) Calculated permselectivities for a PB-PEO–based biomimetic selective layer, assuming 3% incorporation of AQPZ. Because PB-PEO is the least permeable material considered, water/solute permselectivities are correspondingly the greatest. Permselectivities that correspond to the displayed approximate rejections (dashed lines) were calculated for 2000-ppm solute and 15.5-bar applied pressure. The approximate hydrophobicity cutoff of log K_ow = −0.2 is depicted by solid green and diagonal red shadings. (B) Physicochemical properties of various micropollutants (species that can adversely affect human or ecological health at low concentrations) that are relevant to wastewater reuse (37–40). Nearly all of the micropollutants are relatively hydrophobic and are expected to be poorly rejected by a fluid-like biomimetic membrane. Conversely, almost all have molecular weights that exceed the molecular weight cutoff (80 Da) of the tested PA-RO membrane. Micropollutants shown are listed in table S4.

DISCUSSION

The goal of this study was to provide general performance limits for biomimetic desalination membranes, which can comprise a variety of water channels and essentially infinite possibilities (for example, polymer chemistry and length) for the amphiphilic matrix. Hence, while the general trends in performance demonstrated in this study—solubility-based solute permeability with extremely low ion permeability—will hold for most matrices, the quantitative results apply specifically to the polymers chosen in this study. For example, lower–molecular weight PB-PEO, which may be more effective for reconstitution of aquaporin (15), will likely be slightly more permeable than the PB-PEO used here due to reduced thickness of the nonpolar core. In addition, the projected performance assumes key technical hurdles can be overcome. These include (i) sufficient incorporation of functional water channels (for example, 1 to 5% AQPZ) to achieve target water permeabilities, (ii) lack of defects at the channel/matrix interface, and (iii) lack of macroscopic defects when forming the biomimetic selective layer. Engineered two-dimensional crystals of biological and artificial channels (12, 15) and high reported water permeabilities (${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$ ~3 × 10⁻¹¹ m s⁻¹ Pa⁻¹) for AQPZ in a BCP membrane (20) suggest that sufficient channel reconstitution will be possible. Defects at the channel/matrix interface still require study for BCPs and are most relevant for ion permeation. With optimized BCP chemistry and structure, channel/matrix defects using fluid-like BCPs will likely be minimal, especially considering that aquaporin incorporation in model lipid bilayers causes no change in ion permeation (42). As for the last challenge, complete elimination of macroscopic defects during formation of large-area membrane selective layers will be extremely difficult, if not impossible. Thus, performance levels projected in this study can serve as the benchmark for a truly defect-free membrane.

With these qualifications in mind, the results of this study offer important implications for the prospects and research needs for biomimetic desalination membranes. Extraordinary water/ion selectivities are within reach for these materials and are likely orders of magnitude above what is possible for not only current PA-RO membranes but also other “next-generation” membrane materials such as nanoporous graphene and graphene-based frameworks (3). Extreme water/ion selectivities would be highly beneficial in applications where exceptional ion rejections are needed, such as seawater RO and ultrapure water production. However, if membranes are used with the currently-envisioned design (a fluid-like biomimetic selective layer on a porous support), then posttreatment would often be needed to account for the poor rejection of hydrophobic species. For example, in the production of ultrapure water, a critical and high-volume reagent for the semiconductor, pharmaceutical, and power industries (5), the need for low levels of total organic carbon (TOC) would necessitate a complementary separation technique such as activated-carbon adsorption or a second RO step with PA-RO membranes.

Instead of extra process steps, a more preferred route would be to confer the selective layer with features that decrease solute permeation. The most obvious solution would be to use an amphiphilic matrix with lower permeability. Some lessons may be learned from low-permeability biological membranes, which through tailored lipid compositions have low permeability while still allowing for protein function (25, 43). For example, urea permeability through 60% sphingomyelin/40% cholesterol is 28-fold lower than we found for PB-PEO (25). More radical synthetic approaches may be necessary, as low-permeability bilayers still retain solubility-based selectivity (21). Some possible avenues include direct channel incorporation within a glassy, nearly impermeable polymeric matrix (44), or perhaps chemical modification (for example, cross-linking) of a fluid-like matrix after channel insertion. However, highly non-native environments may disrupt channel alignment, structure, and function and may introduce defects at the channel/matrix interface. A second, relatively feasible approach would be a composite membrane with two selective layers in series: A fluid-like biomimetic selective layer would first remove ions and polar solutes, and a second layer (for example, high-permeability PA) would remove species based on size. Such a membrane would retain the ultrahigh water/ion selectivity of the biomimetic layer without compromising water/organic selectivity and could be beneficial in all desalination and water treatment applications that use RO.

MATERIALS AND METHODS

Materials and chemicals

DOPC was obtained from Avanti Polar Lipids. MDM with block molecular weights of 900-4800-900 Da and M_w/M_n of 1.23, and PB-PEO with block molecular weights of 2500-900 Da and M_w/M_n of 1.09 were obtained from Polymer Source Inc. 5(6)-CF, propionic acid, and butyric acid were obtained from Acros. Methanol, 1-propanol, boric acid, magnesium sulfate heptahydrate, magnesium chloride hexahydrate, and hydrochloric acid were obtained from J.T. Baker. Ethanol, 1-butanol, 1,2-ethanediol, 1,3-propanediol, 1,4-butanediol, 1,5-pentanediol, erythritol, xylitol, mannitol, urea, sodium chloride, Hepes, and acetic acid were obtained from Sigma-Aldrich. Glycerol and tris were obtained from American Bioanalytical. Triton X-100 was obtained from Thermo Fisher Scientific. Sodium hydroxide was obtained from Macron.

LUV preparation and characterization

Multilamellar vesicles were first prepared for DOPC and MDM using the film rehydration method. Ten to fifteen milligrams of DOPC and MDM were dissolved in chloroform and ethanol, respectively, dried in a glass test tube under a stream of nitrogen, and then placed under vacuum overnight to remove residual solvent. Films were then rehydrated in buffer through magnetic stirring at room temperature for 2 hours. PB-PEO was rehydrated directly to form vesicles by probe sonication in buffer for 15 min on ice (5 kW/liter, Misonix 3000, Misonix Inc.). Vesicles were then extruded 21 times at room temperature through 200-nm pore size polycarbonate track-etched membranes (GE Whatman) to form LUVs. PB-PEO was pre-extruded 11 times through 400-nm pore size membranes. After extrusion and just before permeability experiments, LUVs were buffer-exchanged to remove extravesicular CF or sodium using a HiTrap Desalting column (GE Healthcare). Average vesicle hydrodynamic radius was determined to be 94 to 112 nm with polydispersity indices of 0.04 to 0.14 by dynamic light scattering (DLS) using an ALV-5000 instrument (Langen) with a 532-nm laser and the scattering angle set to 90°. For cryo-EM analysis, vesicle solutions were prepared in 20 mM Hepes, 100 mM NaCl (pH 7.5), and diluted to approximately 0.2 weight % (wt %). Quantifoil carbon-coated copper EM grids (Electron Microscopy Sciences) were first treated in a PELCO easiGlow system, after which 5 μl of the vesicle solution was added to the grid surface. After 45-s incubation, grids were blotted and plunged into liquid ethane for rapid vitrification. Cryo-EM was performed at liquid nitrogen temperature using an FEI Talos L120C operating at 120 kV.

Permeability measurements using osmolarity differences

Vesicle size change through rapid mixture with hyperosmotic solutions was used to measure water permeability and the permeability of nondissociative neutral solutes and boric acid, which is predominantly uncharged at pH 7.5. Prior to the experiments, LUVs were prepared with an intravesicular solution of 20 mM Hepes, 72 mM NaCl, 15 mM CF (pH 7.5), and buffer-exchanged into an isosmotic solution of 20 mM Hepes, 100 mM NaCl (pH 7.5). For permeability measurements of relatively permeable solutes, LUV solutions at approximately 0.1 wt % were rapidly mixed 1:4 with a hyperosmotic solution [20 mM Hepes, 100 mM NaCl + 200 mM solute (pH 7.5)] at 25.0° ± 0.2°C using an SX20 stopped-flow fluorometer (Applied Photophysics) with a mixing dead time of 1 ms, excitation wavelength of 492 nm, bandwidth of 3 nm, and emission wavelength of 512 nm. Data were averaged from 3 to 10 time traces. Fluorescence intensity changed due to self-quenching of CF at high concentrations, a method which is less sensitive than light scattering to measurement artifacts (18, 19). For LUV solutions in each experiment, a series of solutions with increasing levels of NaCl was used to linearly relate fluorescence intensity with normalized vesicle volume (fig. S2). For each solute except boric acid, the calibrated slope was used with a normalized vesicle volume of 1 corresponding to the final stabilized fluorescence. Boric acid influx slightly decreased the intravesicular pH, which decreased the rebound in fluorescence by ~30%. The part of the curve corresponding to boric acid influx was normalized independently to yield a final normalized vesicle volume of 1.

Water permeability P_w and solute permeability P_s were determined by fitting the vesicle volume data to the following relations (19, 32, 33) using custom code that used built-in numerical integration and least-squares optimization functions in Python 2.7 (Python Software Foundation)

$$\frac{{\mathit{V}}_0}{{\mathit{A}}_{\mathrm{s}}}\frac{\mathit{d}\overline{\mathit{V}}(\mathit{t})}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathrm{w}}{\mathit{V}}_{\mathrm{w}}[\frac{{\mathit{C}}_{\mathrm{I}}^{\mathrm{i}}+{\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})}{\overline{\mathit{V}}(\mathit{t})}-({\mathit{C}}_{\mathrm{I}}^{\mathrm{o}}+{\mathit{C}}_{\mathrm{S}}^{\mathrm{o}})]$$ (1)

$$\frac{{\mathit{V}}_0}{{\mathit{A}}_{\mathrm{s}}}\frac{\mathit{d}{\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathrm{s}}({\mathit{C}}_{\mathrm{S}}^{\mathrm{o}}-\frac{{\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})}{\overline{\mathit{V}}(\mathit{t})})$$ (2)

where V₀, A_s, and $\overline{\mathit{V}}(\mathit{t})$ are the initial vesicle volume, vesicle surface area, and vesicle volume normalized to the initial volume, respectively. ${\mathit{C}}_{\mathrm{I}}^{\mathrm{i}}$ and ${\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})$ are the intravesicular osmolarities of impermeable (for example, Hepes and NaCl) and permeable solutes, respectively, relative to the initial vesicle volume. ${\mathit{C}}_{\mathrm{I}}^{\mathrm{o}}$ and ${\mathit{C}}_{\mathrm{S}}^{\mathrm{o}}$ are the extravesicular osmolarities (after mixing) of impermeable and permeable solutes, respectively, and are assumed to remain constant due to the low volume (~0.1%) of vesicles in solution. The average vesicle radius from DLS was used to calculate V₀ and A_s during fitting. Fitted water permeabilities were consistent (within ~20%) for different solution conditions. Water permeability values are reported for vesicles mixed 1:4 with 20 mM Hepes and 200 mM NaCl (pH 7.5; 70% increase in osmotic strength). For osmolarity and osmotic pressure estimations, a van’t Hoff factor of 1 was used for each discrete species (for example, urea and Na⁺) in solution.

For slowly permeating solutes (xylitol for PB-PEO and mannitol for DOPC and MDM), vesicles were mixed 1:1 with solutions containing 200 mM of the solute of interest and assessed using a plate fluorometer (Synergy HT, Bio-Tek) with excitation and emission wavelengths of 485 and 528 nm, respectively, and bandwidths of 20 nm. Samples were kept at ambient temperature (24° ± 1°C). Because the initial water efflux occurs rapidly (<1 s), fluorescence signal monotonically increased during the experiments due to solute and water influx. Normalized vesicle volume was determined from fluorescence using a linear relationship. The intravesicular solute concentration ${\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})$ was then determined from the normalized vesicle volume, which is the ratio of the solution osmolarities

$$\overline{\mathit{V}}(\mathit{t})=({\mathit{C}}_{\mathrm{S}}^{\mathrm{i}}(\mathit{t})+{\mathit{C}}_{\mathrm{I}}^{\mathrm{i}})/({\mathit{C}}_{\mathrm{S}}^{\mathrm{o}}+{\mathit{C}}_{\mathrm{I}}^{\mathrm{o}})$$ (3)

The solute concentration data were fitted using a combination of Eqs. 2 and 3 to determine the solute permeability.

Permeability measurements using pH sensitivity

The pH sensitivity of CF was used to measure the permeability of model carboxylic acids (acetic acid, propionic acid, and butyric acid) that were too permeable to be measured using vesicle shrinkage experiments. Methodology was adapted from a previous study on the ammonia permeability of lipid vesicles (25). Prior to the experiments, LUVs were prepared with an intravesicular solution of 10 mM MES, 10 mM MOPS, 100 mM NaCl, 1 mM CF (pH 6.8), and buffer-exchanged into 10 mM MES, 10 mM MOPS, and 100 mM NaCl (pH 6.8) to remove extravesicular CF. For permeability measurements, vesicles were rapidly mixed 1:4 in a stopped-flow fluorometer with 20 mM MOPS and 50 mM NaCl + 50 mM carboxylic acid (pH 7.5). Data were averaged from 6 to 10 time traces. The extravesicular pH was kept well above the solute pK_a to ensure a large excess of the relatively impermeable conjugate base and thus eliminate unstirred layer effects (that is, concentration polarization) (21, 45). Rapid acid/base reactions allow for permeating acid species to be replaced, thus maintaining the undissociated acid concentration at the membrane surface. Fluorescence decreased rapidly due to acid permeation into the vesicles, which decreased the intravesicular pH and the resulting fluorescence. Normalized fluorescence was fitted using a linear calibration curve (fig. S2) to yield the intravesicular pH, pHⁱ(t). The total (dissociated and undissociated) intravesicular acid concentration ${\mathit{C}}_{\mathrm{A}}^{\mathrm{i}}(\mathit{t})$ was taken to vary linearly with the change in intravesicular pH. To determine the slope of this relationship, the total intravesicular acid concentration at pseudo-equilibrium ${\mathit{C}}_{\mathrm{A},\text{eq}}^{\mathrm{i}}$ (that is, when fluorescence stabilized) was calculated from the Henderson-Hasselbalch relation such that the concentration of uncharged (undissociated) acid was the same across the membrane

$${\mathit{C}}_{\mathrm{A},\text{eq}}^{\mathrm{i}}={\mathit{C}}_{\mathrm{A}}^{\mathrm{o}}\left(\frac{{10}^{{\text{pH}}_{\text{eq}}^{\mathrm{i}}-\mathrm{p}{\mathit{K}}_{\mathrm{a}}}+1}{{10}^{{\text{pH}}^{\mathrm{o}}-\mathrm{p}{\mathit{K}}_{\mathrm{a}}}+1}\right)$$ (4)

where ${\mathit{C}}_{\mathrm{A}}^{\mathrm{o}}$ and pH^o are the extravesicular total acid concentration (40 mM after mixing) and pH (~7.4 after mixing), respectively, and ${\text{pH}}_{\text{eq}}^{\mathrm{i}}$ is the intravesicular pH at pseudo-equilibrium. To determine the solute permeability, data were fitted to the following relation

$$\frac{{\mathit{V}}_0}{{\mathit{A}}_{\mathrm{s}}}\frac{\mathit{d}{\mathit{C}}_{\mathrm{A}}^{\mathrm{i}}(\mathit{t})}{\mathit{d}\mathit{t}}={\mathit{P}}_{\mathrm{s}}(\frac{{\mathit{C}}_{\mathrm{A}}^{\mathrm{o}}}{{10}^{{\text{pH}}^{\mathrm{o}}-\mathrm{p}{\mathit{K}}_{\mathrm{a}}}+1}-\frac{{\mathit{C}}_{\mathrm{A}}^{\mathrm{i}}(\mathit{t})}{{10}^{{\text{pH}}^{\mathrm{i}}(\mathit{t})-\mathrm{p}{\mathit{K}}_{\mathrm{a}}}+1})$$ (5)

Equation 5 is a modification of the solute flux equation (Eq. 2), assuming that permeation is driven solely by undissociated acid (25, 45). In addition, changes in vesicle volume were neglected due to limited self-quenching at this CF concentration (1 mM) and the nearly equivalent osmolarities of the internal and external solutions. Permeabilities were directly measured at 25.0° ± 0.2°C for all acids for PB-PEO and for acetic acid for DOPC and MDM. Permeation of propionic acid and butyric acid was too rapid for accurate measurement at 25°C using DOPC and MDM vesicles. Permeabilities were therefore measured at a series of temperatures between 6° and 12°C, and the permeability at 25°C was calculated using Arrhenius relationships (fig. S4). Fluorescence was measured using an excitation wavelength of 492 nm, bandwidth of 6 nm, and emission wavelength of 512 nm.

Sodium permeability measurements

Sodium permeation was assessed by measuring the slow efflux of sodium entrapped in vesicles into a sodium-free extravesicular solution (46). Extravesicular sodium concentration was measured using a sodium-selective electrode (Cole-Parmer) and an Orion A324 pH meter (Thermo Fisher Scientific). LUVs were prepared at 1.0 to 1.5 wt % with an intravesicular solution of 20 mM tris and 300 mM NaCl (pH 7.5), and buffer-exchanged into 20 mM tris, 150 mM MgCl₂, and 75 mM MgSO₄ (pH 7.5). Samples were stored in a water bath at 25.0° ± 0.5°C and assessed every 2 days for 6 days. As only a small amount (<2%) of the entrapped sodium permeated during experiments, sodium permeability ${\mathit{P}}_{{\text{Na}}^{+}}$ was calculated from the solute flux equation using the linear rate of extravesicular sodium concentration change ($\mathrm{\Delta }{\mathit{C}}_{{\text{Na}}^{+}}/\mathrm{\Delta }\mathit{t}$) (46)

$${\mathit{P}}_{{\text{Na}}^{+}}=\frac{\mathit{V}}{{\mathit{A}}_{\mathrm{s}}{\mathit{C}}_{{\text{Na}}^{+}}^{\mathrm{i}}}\left(\frac{\mathrm{\Delta }{\mathit{C}}_{{\text{Na}}^{+}}}{\mathrm{\Delta }\mathit{t}}\right)=\frac{{\mathit{V}}_0}{{\mathit{A}}_{\mathrm{s}}\mathrm{\Delta }{\mathit{C}}_{{\text{Na}}^{+}}^{\text{TX}}}\left(\frac{\mathrm{\Delta }{\mathit{C}}_{{\text{Na}}^{+}}}{\mathrm{\Delta }\mathit{t}}\right)$$ (6)

where V is the total solution volume, A_s is the total vesicle area, and ${\mathit{C}}_{{\text{Na}}^{+}}^{\mathrm{i}}$ is the internal sodium concentration (300 mM) and the overall driving force, neglecting the small amount of extravesicular sodium (<0.04 mM). Unlike the methods using fluorescence, the rate of extravesicular sodium concentration change is dependent on the quantity of vesicles. Therefore, after 6 days, vesicles were solubilized to release entrapped sodium through a 10-fold dilution and addition of Triton X-100 to 1 wt %. The initially turbid solutions became clear upon Triton X-100 addition, and the maximum sodium concentration $\mathrm{\Delta }{\mathit{C}}_{{\text{Na}}^{+}}^{\text{TX}}$ was measured and used to determine the total vesicle volume V₀ via a material balance. The ratio V₀/A_s is simply a function of the vesicle radius, which was measured by DLS. Sodium concentrations were obtained from measured electrode potentials using freshly assessed calibration standards in the same background buffer. Intravesicular and extravesicular solutions were chosen so as to balance osmotic pressures across the membrane to minimize vesicle volume change. Concentrations of chloride, which is typically more permeable than sodium through lipid bilayers (35), were also balanced to minimize the formation of electrical potentials across the membrane.

RO characterization

Commercial PA thin-film composite seawater RO membranes (SW30XLE, Dow Water & Process Solutions) were characterized in a custom, laboratory-scale crossflow RO system, with methods adapted from previously established procedures (47). Membranes were first wetted in 25% isopropanol for 30 min, rinsed in deionized water, and stored in water at 4°C prior to testing. Membrane coupons with 20.0-cm² active surface area were tested at a crossflow velocity of 0.21 m/s and 25.0° ± 0.5°C. Flux was first stabilized by running the system in deionized water overnight with an applied pressure Δp of 17 bar. Hydraulic water permeability ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}$ was measured using deionized water at 15.5 bar, with ${\mathit{P}}_{\mathrm{w}}^{\mathrm{H}}={\mathit{J}}_{\mathrm{w}}/\mathrm{\Delta }\mathit{p}$, where J_w here is the pure water flux. Individual observed solute rejections, defined as R = 1 − C_permeate/C_feed, were then measured at 15.5 bar using 2 g/liter feed solute concentrations and pH 7.0 for all solutes except for the carboxylic acids, which were assessed at 1 g/liter solute and pH 3.0 to ensure that nearly all of the solute was uncharged. NaCl concentrations were measured using a calibrated electrical conductivity meter (Oakton Instruments). Concentrations of organic species were determined using a TOC analyzer (TOC-V, Shimadzu). Boric acid concentration was determined using inductively coupled plasma–atomic emission spectroscopy (Optima 3000, Perkin Elmer). P_s was determined from R by accounting for mass transfer effects (that is, concentration polarization) using film theory (48)

$${\mathit{P}}_{\mathrm{s}}={\mathit{J}}_{\mathrm{w}}\left(\frac{1-\mathit{R}}{\mathit{R}}\right)\text{exp}\left(\frac{-{\mathit{J}}_{\mathrm{w}}}{{\mathit{k}}_{\mathrm{s}}}\right)$$ (7)

The mass transfer coefficient k_s for each solute was calculated from the solute diffusivity (table S3) and the Sherwood number for laminar flow in a rectangular channel (49). k_s varied from 11 to 20 μm/s, depending on the solute diffusivity.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/6/eaar8266/DC1

Supplementary Text

fig. S1. Cryo-EM images of MDM and PB-PEO polymer vesicles.

fig. S2. Relating measured fluorescence to vesicle volume and pH.

fig. S3. Effect of fitting methodology on water permeability.

fig. S4. Permeability measurements of carboxylic acids.

fig. S5. Permeability relationships.

fig. S6. Projected water flux and organic solute rejection of a defect-free biomimetic desalination membrane.

table S1. Water permeabilities of selected biological and synthetic water channels that have been considered for use in biomimetic desalination membranes.

table S2. Comparison of measured water and solute permeabilities for DOPC with published permeabilities for similar lipid bilayers.

table S3. Water and solute permeabilities measured in this study for lipid and BCP bilayers and PA-RO membranes.

table S4. Physicochemical characteristics of micropollutants displayed in Fig. 5.

References (53–70)