Using convolutional neural networks for enhanced capture of breast parenchymal complexity patterns associated with breast cancer risk

Abstract

Rationale and Objectives

We evaluate utilizing convolutional neural networks (CNNs) to optimally fuse parenchymal complexity measurements generated by texture analysis into discriminative meta-features relevant for breast cancer risk prediction.

Materials and Methods

With IRB approval and HIPAA compliance, we retrospectively analyzed “For Processing” contralateral digital mammograms (GE Healthcare 2000D/DS) from 106 women with unilateral invasive breast cancer and 318 age-matched controls. We coupled established texture features (histogram, co-occurrence, run-length, structural), extracted using a previously validated lattice-based strategy, with a multi-channel CNN into a hybrid framework in which a multitude of texture feature maps are reduced to meta-features predicting the case or control status. We evaluated the framework in a randomized split-sample setting, using the area under the curve (AUC) of the receiver operating characteristic (ROC) to assess case-control discriminatory capacity. We also compared to CNNs directly fed with mammographic images, as well as to conventional texture analysis, where texture feature maps are summarized via simple statistical measures which are then used as inputs to a logistic regression model.

Results

Strong case-control discriminatory capacity was demonstrated on the basis of the meta-features generated by the hybrid framework (AUC=0.90), outperforming both CNNs applied directly to raw image data (AUC=0.63, p<0.05) and conventional texture analysis (AUC=0.79, p<0.05).

Conclusion

Our results suggest that informative interactions between patterns exist in texture feature maps derived from mammographic images, and can be extracted and summarized via a multi-channel CNN architecture toward leveraging the associations of textural measurements to breast cancer risk.

Introduction

The stratification of breast cancer risk levels is becoming increasingly important and is rapidly evolving beyond the “one-size-fits-all” approach in breast cancer screening to personalized regimens tailored by individual risk profiling^{1, 2}. Starting from the pioneering work of Wolfe³, studies have consistently shown an association of the breast parenchymal complexity (i.e., the distribution of fatty and dense tissues) on breast images with levels of breast cancer risk. In particular, full-field digital mammography, which is routinely used for breast cancer screening⁴, has demonstrated substantial potential in providing novel quantitative imaging biomarkers related to breast cancer risk. Mammographic density is one of the strongest risk factors for breast cancer^{5, 6}, while studies increasingly support significant associations of breast cancer risk with mammographic texture descriptors^7–9, which reflect more refined, localized characteristics of the breast parenchymal pattern.

In early studies investigating the role of mammographic texture in breast cancer risk assessment^10–14, textural measurements have been estimated within a single region of interest (ROI) in the breast. In an attempt to provide more granular texture estimates, more recent studies have proposed sampling the parenchymal tissue through the entire breast for subsequent texture analysis^15–17. For instance, in a recently proposed lattice-based strategy¹⁵, each texture descriptor is calculated within multiple non-overlapping local square ROIs through the breast and texture measurements are then averaged over the breast regions sampled by the lattice. In a preliminary case-control evaluation¹⁵, the lattice-based texture features were shown to outperform state-of-the-art features extracted from the retroareolar or central breast region, thereby suggesting that enhanced capture of the heterogeneity in the parenchymal texture within the breast may also improve the associations of texture measures with breast cancer risk. However, by averaging regional texture values, important information about the overall parenchymal tissue complexity might be still missed and, therefore, an improved fusion approach, which retains richer information about texture variability over the breast, might leverage the potential of such granular texture measurements provided by multiple ROIs.

Convolutional neural networks (CNNs) and “Deep Learning” technology^{18, 19} are able to automatically generate hierarchical representations useful for a particular learning task via neural networks with multiple hidden layers. In the last few years, CNNs have demonstrated a remarkable impact on medical image analysis^{20, 21} and they are now gaining increasing attention in applications with digital mammography, including primarily mass or lesion detection and characterization^22–25. However, their potential in breast cancer risk prediction remains largely unexplored with only a few studies having used CNNs to relate mammographic patterns to breast cancer risk^{26, 27} or breast density²⁸. Moreover, although CNNs have been primarily applied to raw imaging data, they may also have value as efficient feature-fusion techniques, especially in cases that conventional feature summarization approaches may have limitations.

In this study, we employ a multi-channel CNN architecture to fuse parenchymal texture feature maps into discriminative meta-features relevant for breast cancer risk prediction. The rationale is that CNNs can also be used as a high-level approach to effectively summarize high-dimensional patterns resulting from handcrafted features such as texture descriptors, for which conventional feature summarization and/or dimensionality reduction approaches may be limited in capturing the available rich information. Our hypothesis, therefore, is that by capturing sparse, subtle interactions between localized patterns present in texture feature maps derived from mammographic images, a multitude of textural measurements can be optimally reduced to meta-features capable of improving associations with breast cancer. We assess our hypothesis by evaluating these meta-features in a case-control study with digital mammograms, and we also compare their performance to the performances of conventional texture analysis and CNNs when fed directly with raw mammographic images.

Materials & Methods

Study Dataset

In this IRB-approved, HIPAA-compliant study under a waiver of consent, we retrospectively analyzed a case-control dataset of raw (i.e., ‘FOR PROCESSING’) mediolateral-oblique (MLO)-view digital mammograms previously reported^{15, 29}. Briefly, the cases included women diagnosed with biopsy-proven unilateral primary invasive breast cancer (n = 106) at age 40 years or older, recruited by a previously-completed, IRB-approved, multimodality breast imaging trial (2002–2006; NIH CAXXXXX), in which all women had provided informed consent. For cases the contralateral images were analyzed (i.e., images from the unaffected breast) as a surrogate for inherent breast tissue properties associated with high breast cancer risk, as done in prior case-control studies of mammographic pattern analysis^{15, 29–31}. Controls were randomly selected from the eligible population of women seen for routine screening over the closest possible overlapping time period at the same institution, and had negative breast cancer screening and confirmed negative one-year follow-up. Controls were age-matched to cases on 5-year intervals at a 3:1 ratio (n = 318), yielding a total sample size of 424.

Image Acquisition

All images were acquired using either a GE Senographe 2000D or Senographe DS full-field digital mammography (FFDM) system (image size: 2294×1914 pixels; image spatial resolution: 10 pixels/mm in both dimensions). Prior to further analysis, images were log-transformed, then inverted, and, finally, intensity-normalized by a z-score transformation within the breast region which was automatically segmented in each image using the publicly available “Laboratory for Individualized Breast Radiodensity Assessment” (LIBRA)^{29, 32}. These common preprocessing steps help to alleviate differences between studies via intensity histogram alignment, while also maintaining the overall pattern of the breast parenchyma¹⁷. Additionally, we flipped horizontally the images of right MLO views so that the breast is always on the same side of the image.

Revealing Meta-features of Breast Parenchymal Complexity

We developed a hybrid framework which coupled state-of-the-art texture analysis with CNNs (Fig. 1). In the first step which follows the previously validated lattice-based strategy for parenchymal texture analysis¹⁵, a regular lattice was virtually overlaid on the mammographic image and a set of texture descriptors were computed on 6.3×6.3 mm² (63×63 pixels²) local square ROIs centered on each lattice point within the breast. For each image, this step generated a set of 36×30 pixels² texture feature maps (each pixel corresponds to an ROI defined by the lattice), one for each texture descriptor, that represent the spatial distribution of the corresponding textural measurements as sampled by the lattice over the entire breast.

Fig. 1.

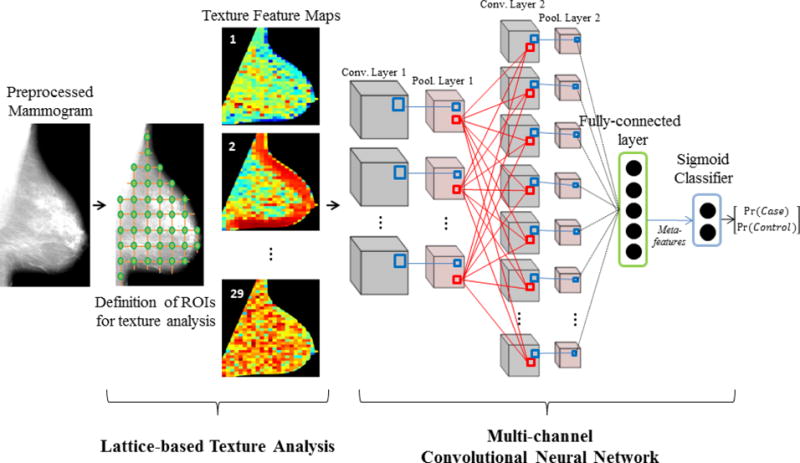
Hybrid framework workflow: Employing multi-channel convolutional neural networks to fuse texture feature maps into case-control discriminative meta-features.

Our texture feature set included a total of 29 established texture descriptors (Table 1 and Appendix for detailed feature descriptions), including gray-level histogram, co-occurrence, run-length, and structural features, all of which have been previously used for mammographic pattern analysis and breast cancer risk assessment⁷. Briefly, gray-level histogram features are common first-order statistics which describe the distribution of gray-level intensity. The co-occurrence features also consider the spatial relationships of pixel intensities in specified directions and are based on the gray-level co-occurrence matrix (GLCM) which encodes the relative frequency of neighboring intensity values. Run-length features capture the coarseness of texture in specified directions by measuring strings of consecutive pixels which have the same gray-level intensity along specific linear orientations. Finally, structural features capture the architectural composition of the parenchyma by characterizing the tissue complexity, the directionality of flow-like structures in the breast, and intensity variations between central and neighboring pixels.

Table 1.

Parenchymal texture feature maps (TFMs) extracted from each digital mammogram of the study dataset.

	Gray-level Histogram
TFM1	5th Percentile
TFM2	5th Mean
TFM3	95th Percentile
TFM4	95th Mean
TFM5	Entropy
TFM6	Kurtosis
TFM7	Max
TFM8	Mean
TFM9	Min
TFM10	Sigma
TFM11	Skewness
TFM12	Sum
	Co-occurrence
TFM13	Contrast
TFM14	Correlation
TFM15	Homogeneity
TFM16	Energy
TFM17	Entropy
TFM18	Inverse Difference Moment
TFM19	Cluster Shade
	Run-length
TFM20	Short Run Emphasis
TFM21	Long Run Emphasis
TFM22	Gray Level Non-uniformity
TFM23	Run Length Non-uniformity
TFM24	Run Percentage
TFM25	Low Gray Level Run Emphasis
TFM26	High Gray Level Run Emphasis
	Structural
TFM27	Edge-enhancing index
TFM28	Box-Counting Fractal Dimension
TFM29	Local Binary Pattern

The set of 29 texture feature maps generated for each mammogram were then fed as separate “channels” of breast parenchymal complexity into a multi-channel CNN with a LeNet-like design, a pioneering CNN architecture suitable for small input images³³. The multi-channel CNN consisted of two hidden convolutional/down-sampling layers (2×2 max-pool) and each convolutional layer contained 10 convolutional maps with 5×5 and 4×3 kernels for the first and second hidden layers, respectively. The second hidden layer fed into a fully-connected layer with five nodes, which in turn outputs five meta-features used as inputs to a final logistic regression layer (LR) predicting the case or control status. The hyperbolic tangent activation function was utilized in all but the LR layer, which utilized the sigmoid activation.

The multi-channel CNN was trained via training (n=200) and validation (n=100) sets, with the final model tested on 124 women; membership assignment into each set was carried out by stratified random sampling. Training occurred by sequentially feeding the CNN with the training image data (forward pass) and updating the weights (backward pass) via stochastic gradient descent (batch-size = 1 and learning rate = 0.01) so as to minimize the difference between the LR classification and the ground-truth case-control status³⁴. Then, the trained model was applied to the validation set and the validation error was measured as the mean difference between the LR outputs and the ground-truth information. To better train our model while also avoiding over-fitting, this process was repeated 200 times (epochs) maximum, until the validation error got higher than it was in the previous epoch³⁵. The final trained CNN was applied to the “unseen” images of the test set, via a single forward pass of all the test image data and the case-control discriminatory capacity was assessed via the area under the curve (AUC) of the receiver operator characteristic (ROC).

The multi-channel CNN was implemented using Theano v.0.8.2 on Python v.2.7 and parameters involved in the CNN architecture and training were empirically set.

Comparative Evaluation

To investigate the potential advantage of the proposed hybrid framework, we compared with the case-control discriminatory capacity of 1) conventional texture feature analysis and 2) CNNs applied directly to the original mammographic images (Fig. 2). DeLong’s tests³⁶ were used to test for AUC differences between our hybrid framework and each of these two approaches.

Fig. 2.

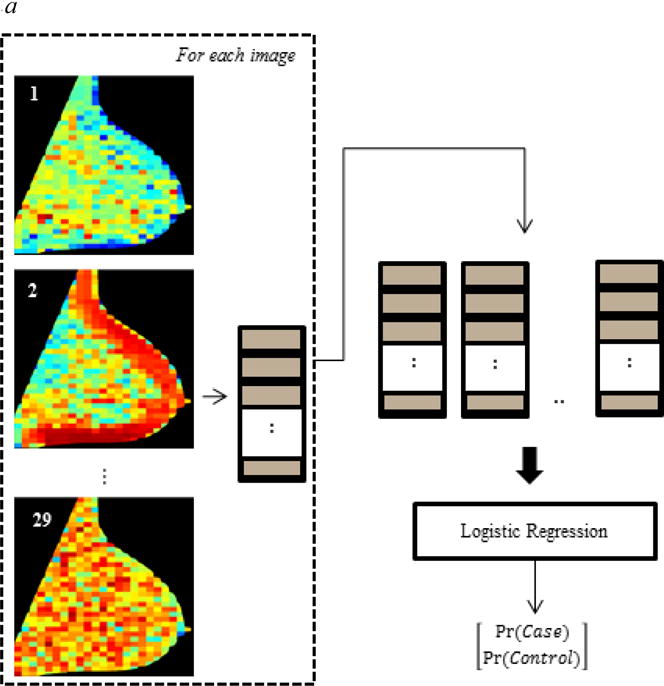
Design of comparative evaluation experiments: Evaluating the case-control discriminatory capacity of (a) conventional texture analysis and (b) convolutional neural networks applied directly to the original images.

Briefly, to evaluate conventional parenchymal texture analysis, each lattice-based texture feature map was summarized by the mean and the standard deviation of the corresponding feature across all the ROIs defined by the lattice¹⁵, thereby generating a 58-element feature vector for each breast (Fig. 2 (a)). To build a logistic regression model (similar in principle to the final layer of the CNN) while also limiting potential over-fitting, the texture feature vectors of subjects belonging to the training and validation sets were processed with elastic net regression³⁷, a regularized technique suitable for strongly correlated features which assigns zero coefficients to weak covariates during model construction. The model was then fed with the texture feature vectors of the test set to obtain an estimate of its discriminatory capacity (AUC) which was compared to the AUC of the hybrid framework.

To assess the performance of CNNs when fed directly with the mammographic images, we developed a single-channel CNN with input the pre-processed image downscaled by a factor of four, as typically done in the field to address the computational issues of handling full-resolution images²⁸. Our network was developed using the Lasagne library (Release 0.2.dev1)³⁸ built on top of Theano, with an overall architecture as shown in Fig. 2 (b). The CNN consisted of five hidden convolutional/down-sampling layers, feeding into a pair of fully-connected layers and a logistic regression classifier. The parameters of the network were initialized using the recipe of Glorot & Bengio³⁹ and, similarly to the multi-channel CNN, the CNN was trained and tested via distinct training, validation and test phases, now using the pre-processed mammograms of the same training, validation and test sets, respectively.

Results

Strong linear separability of cancer cases from controls was demonstrated on the basis of the five meta-features generated by the proposed hybrid framework. Figure 3 shows the predicted probabilities, along with the ground-truth labels of the test set. The corresponding case-control classification performance was AUC = 0.90 (95% CI: 0.82–0.98), with sensitivity and specificity equal to 0.81 and 0.98, respectively.

Fig. 3.

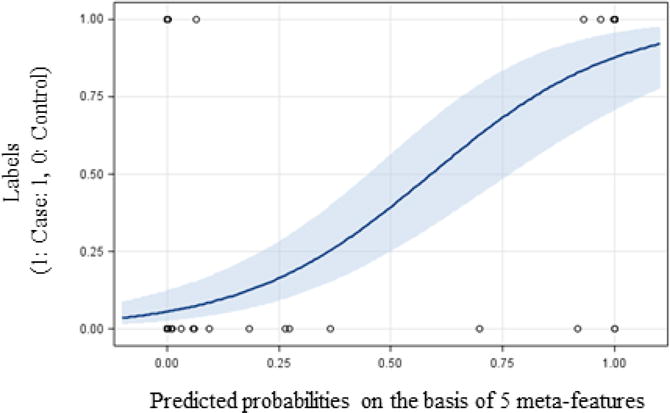
Case-control classification outcomes of the hybrid framework: Probabilities (with 95% confidence limits) of test images to belong to a cancer case as predicted by the hybrid approach versus corresponding ground-truth labels (1: Case, 0: Control).

When the texture feature maps were summarized into simple statistical measures (i.e., average and standard deviation), the discriminative performance was significantly lower (DeLong’s test, p = 0.03). Specifically, 12 texture features were selected by elastic net regression for inclusion in the logistic regression model, including one gray-level histogram feature, four co-occurrence, four run-length, and three structural features; among these, eight represented mean values and four the variability in the texture feature maps (Table 2). With these features, the lattice-based strategy demonstrated an AUC = 0.79 (95% CI: 0.69-0.89). The hybrid framework outperformed also the single-channel CNN (DeLong’s test, p = 0.0004) which showed an AUC = 0.63 (95% CI: 0.57–0.81) in the same case-control dataset (Fig. 4).

Table 2.

Texture features selected by elastic net regression. For each feature, the logistic regression coefficient (b), the p-value and 95% confidence interval (CI) for b are provided.

	b	p-value	95% CI
TFM13_mean	−0.59	0.013	[−1.05 −0.12]
TFM17_mean	0.03	0.897	[−0.44 0.50]
TFM19_mean	−0.69	0.001	[−1.08 −0.29]
TFM22_mean	−1.31	0.395	[−4.34 1.71]
TFM23_mean	0.76	0.582	[−1.96 3.48]
TFM24_mean	−0.14	0.602	[−0.64 0.37]
TFM28_mean	1.07	0.437	[−1.62 3.75]
TFM29_mean	0.05	0.944	[−1.34 1.44]
TFM11_std	0.24	0.642	[−0.79 1.28]
TFM15_std	0.52	0.031	[0.05 1.00]
TFM22_std	0.14	0.483	[−0.25 0.53]
TFM28_std	−0.54	0.002	[−0.87 −0.20]

Fig. 4.

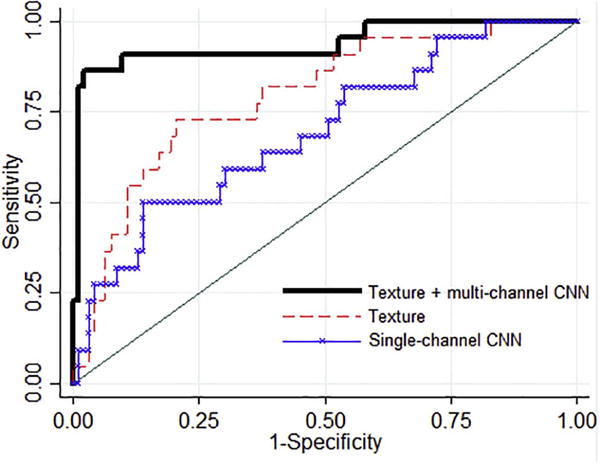
Comparative evaluation results: The hybrid approach,, i.e., texture analysis followed by multi-channel CNNs, (AUC = 0.90) compared to conventional parenchymal texture analysis (AUC = 0.79) or single-channel CNNs applied directly to the original images (AUC = 0.63). CNNs: convolutional neural networks.

Discussion

We assessed the feasibility of a texture-feature fusion approach, utilizing a CNN architecture able to capture sparse, subtle, yet relevant interactions between localized patterns present in texture feature maps derived from mammographic images. This approach may also be interpreted as a methodology for non-linear feature reduction, in which an entire ensemble of parenchymal texture feature maps is reduced down to a small number of meta-features which may serve as a basis for separating cases from controls via a simple linear classifier such as the logistic regression classifier implemented in the last layer of our CNN architecture.

Our hybrid framework demonstrated a promising case-control classification performance. Moreover, it outperformed standard texture analysis (AUC = 0.90 vs. AUC = 0.79), providing preliminary evidence that coupling texture analysis with this CNN-based texture-feature fusion approach can leverage textural features in breast cancer risk assessment. Additionally, the proposed hybrid framework also outperformed CNNs fed directly with raw mammograms. Our results from the single-channel CNN are in line with the few reported similar analyses with raw mammographic images²⁶, in which comparable case-control classification performance (AUC = 0.57 – 0.61) was demonstrated by features learned with a multilayer convolutional architecture in multiscale patches of film and digital mammograms. However, given the relatively small size of our dataset, and considering that no data augmentation was applied in our study which might increase the performance of CNNs especially when deeper networks are used, a more extensive comparison between our hybrid approach and CNNs fed directly with raw image data is warranted.

Limitations of our study must also be noted. First, we evaluated our framework using as “case” images the contralateral mammograms of cancer cases, rather than prior unaffected screening mammograms of women in whom breast cancer was later detected. This is a common first-step approach in this field⁷, based on the premise that the contralateral unaffected breasts of cancer cases share inherent breast tissue properties that may predispose to a higher breast cancer risk. In future studies, we aim to test our hybrid framework on larger datasets in which prior negative screening mammograms for cancer cases will be analyzed. Larger datasets, combined with data augmentation techniques to further increase the volume of training data, may also allow us to develop deeper networks and to boost the performance of our CNNs, as well as to consider established demographic and clinical risk factors (e.g., body-mass-index, parity, family history of breast cancer) in our logistic regression models. Moreover, this study used only images from two FFDM devices, both of which were from the same vendor. Considering the reported substantial differences in textural measurements across image acquisition settings¹⁷, FFDM representations, and vendors⁴⁰, in our future analyses we will also test the performance of our method by incorporating data from multiple FFDM vendors. Additionally, because of limited computational resources, we had to heavily rely on our experience in the choice of learning CNN hyper-parameters. Given the promising results obtained, in a future step, we will perform a systematic search for optimal hyper-parameters following grid or random search optimization⁴¹, which might further improve the performance of our CNNs.

In conclusion, this work introduced a texture feature fusion method, implemented via convolutional neural networks, designed for the detection of interactions among a multitude of hand-designed features, and optimized for the assessment of breast cancer risk. Our results suggest that informative interactions between localized patterns exist in feature maps derived from mammographic images, and can be extracted and summarized via a multi-channel CNN architecture toward leveraging textural measurements in breast cancer risk prediction. Upon further optimization and validation, such tools might be useful in routine breast cancer screening to provide each woman a breast cancer risk score, as well as to visualize parenchymal complexity patterns and breast locations associated with increased levels of breast cancer risk, towards assisting radiologists’ recommendations for supplemental breast cancer screening or breast cancer prevention treatments.

Appendix

Descriptions of texture features

Gray-level histogram features are 13 well-established first-order statistics⁴², which were calculated from the gray-level intensity histogram of the image using 128 histogram bins^{17, 40}.

The co-occurrence features reflect the spatial relationship between pixels and summarize the information encoded by the gray-level co-occurrence matrix (GLCM)⁴³ which corresponds to the relative frequency with which two neighboring pixels, one with gray level i and the other with gray level j, occur in the image. Such matrices are a function of the distance (d) and the orientation (ϑ) between the neighboring pixels. In this study, the M × M GLCM matrices were estimated using M = 128 gray levels to balance computational precision with efficiency, d = 11 pixels^{17, 40}, and the co-occurrence features were computed by averaging over four orientations.

Run-length features capture the coarseness of a texture in specified directions^{44, 45}. A run is defined as a string of consecutive pixels with the same gray-level intensity along a specific linear orientation. Fine textures tend to contain more short runs with similar gray-level intensities, while coarse textures have more long runs with different gray-level intensities. Similarly to the GLCM, a M × N run-length matrix is defined, representing the number of runs with pixels of gray-level intensity equal to i and length of run equal to j along a specific orientation. In correspondence with the co-occurrence features, the run-length statistics were estimated for M = 128 gray levels, N = 11 pixels^{17, 40}, and averaged over four polar-grid-driven orientations.

The structural features include (a) the edge-enhancing index, which is based on edge enhancing diffusion and it describes the directionality of flow-like structures within the image⁴⁶, (b) the local binary pattern (LBP), which captures intensity variations between central and neighboring pixels⁴⁷ and (c) the fractal dimension (FD), which reflects the degree of complexity and was estimated using the box-counting method⁴⁸.