Thermodynamics of Conformational Transitions in a Disordered Protein Backbone Model

Abstract

Conformational entropy is expected to contribute significantly to the thermodynamics of structural transitions in intrinsically disordered proteins or regions in response to protein/ligand binding, posttranslational modifications, and environmental changes. We calculated the backbone (dihedral) conformational entropy of oligoglycine $\left({\text{Gly}}_N\right)$, a protein backbone mimic and model intrinsically disordered region, as a function of chain length ($N=3$, 4, 5, 10, and 15) from simulations using three different approaches. The backbone conformational entropy scales linearly with chain length with a slope consistent with the entropy of folding of well-structured proteins. The entropic contributions of second-order dihedral correlations are predominantly through intraresidue ϕ-ψ pairs, suggesting that oligoglycine may be thermodynamically modeled as a system of independent glycine residues. We find the backbone conformational entropy to be largely independent of global structural parameters, like the end-to-end distance and radius of gyration. We introduce a framework referred to herein as “ensemble confinement” to estimate the loss (gain) of conformational free energy and its entropic component when individual residues are constrained to (released from) particular regions of the ϕ-ψ map. Quantitatively, we show that our protein backbone model resists ordering/folding with a significant, unfavorable ensemble confinement free energy because of the loss of a substantial portion of the absolute backbone entropy. Proteins can couple this free-energy reservoir to distal binding events as a regulatory mechanism to promote or suppress binding.

Introduction

Over the past 20 years, it has become clear that the classical structure-function paradigm is not a universal property of the eukaryotic proteome (1, 2, 3). Although structure dictates function for a large class of proteins like enzymes, a vast array of proteins employ highly dynamic, intrinsically disordered regions (IDRs) to carry out diverse functions, many of which are involved in regulation and control of signaling networks (1, 2, 3, 4, 5). Modular proteins, like nuclear transcription factors, rely on a combination of order and disorder to function, and a coupling between these regions provides additional regulatory mechanisms to fine tune binding affinity and downstream signal cascades (6, 7, 8, 9, 10). Mutations in IDRs can abrogate control of signaling networks, eventually leading to disease onset (3, 11, 12). A seemingly ubiquitous and functionally necessary property of IDRs is their ability to undergo structural transitions in response to a number of factors, including protein/ligand binding, posttranslational modifications, and environmental changes (3, 5, 10, 13, 14, 15, 16, 17). These transitions may proceed to more ordered or disordered states but can also result in a redistribution of the disordered, structural ensemble (3, 10, 15, 16). To successfully target drugs to IDRs or genetically engineer IDRs with certain therapeutic properties to treat various diseases, we need a more complete understanding of the thermodynamics associated with IDR conformational transitions.

IDRs directly responsible for facilitating protein interactions primarily do so with relatively short, contiguous amino acid sequences that become more ordered or structured upon binding. These functional elements or sequence motifs have been referred to as short linear motifs, eukaryotic linear motifs, and molecular recognition features (MoRFs) (3, 12, 18, 19, 20). Short linear motifs are typically around 3–10 amino acids (19), whereas MoRFs are longer at 10–70 amino acids and, by definition, form secondary structures upon binding (18). Transcription factors are enriched with these motifs (21). p53, for example, contains multiple MoRFs with individual MoRFs being able to bind many partners by forming different secondary structures (22), thus allowing it to serve as a hub protein or master regulator in signaling.

Protein, DNA, and small-molecule binding can also induce structural transitions or a redistribution of the structural ensemble in regions distal to the binding interface. For example, Amemiya et al. (23) and Zea et al. (17) found that ligand binding increased or decreased disorder in regions that were typically less than 10 amino acids long from analyses of protein structure databases. There are also numerous examples in which proteins use conformational transitions in IDRs (or simply disorder in general) in an allosteric or cooperative mechanism to effect downstream signaling (7, 10, 15, 24). These observations prompted the development of new allostery models based on the ensemble nature (i.e., structural diversity) of IDRs (10, 15, 25, 26). Propagation of the allosteric signal does not necessarily require the folding or unfolding of an IDR; rather, it can also be achieved through the remodeling of the disordered ensemble (10).

Of particular interest is the potential thermodynamic coupling between effector and allosteric sites facilitated by IDR structural transitions. Conformational entropy is a critical property to describe or understand the thermodynamic origin of IDR structural transitions and how such transitions can modulate protein binding at distal sites (10, 14, 15). Recently, nuclear magnetic resonance methods have been developed to probe binding-induced conformational entropy changes in structured proteins. This so-called “entropy meter” (27, 28), which relates changes in backbone and side-chain motions to changes in conformational entropy, has highlighted the importance of conformational entropy in suppressing or driving ligand binding (27, 29, 30, 31). As a result, one emerging concept is that protein structural plasticity, or the capacity of a protein to alter its internal structural fluctuations, provides a reservoir of entropy and thus free energy that is available to the protein to carry out its function (32). So we consider IDRs as significant conformational entropy reservoirs from which free energy may be withdrawn or deposited via structural transitions (e.g., due to binding). With respect to protein or ligand binding, these transitions would mediate the thermodynamic connection between allosteric and effector sites. Qualitatively, our understanding of how proteins can tune conformational entropy to modulate IDR function continues to improve (10, 14, 15), yet a complete, quantitative description is lacking.

In this article, we are primarily interested in the thermodynamics underlying structural transitions of short IDRs, which we expect will provide insight into the numerous biological processes that rely on order-disorder transitions of IDRs of varying lengths and establish a framework to develop a more quantitative theory of IDRs as free-energy reservoirs. We use oligoglycine (${\text{Gly}}_N$, where N is the chain length) as a protein backbone mimic and model IDR (33, 34, 35, 36). IDRs are often enriched in glycine residues (13, 37); a high glycine content has been associated with more compact IDRs (38), and stretches of oligoglycine can be found in large disordered domains (7, 39). We begin first by calculating the conformational entropy of oligoglycine from backbone ϕ and ψ dihedral angles sampled by molecular dynamics (MD) as a function of chain length ($N=3\text{to}15$ residues) comparing the quasi-harmonic analysis (QHA) (40, 41), Boltzmann quasi-harmonic (BQH) (42, 43, 44), and mutual information expansion (MIE) methods (45). Because proteins containing IDRs likely impose structural constraints on the disordered region and order-disorder transitions may alter the global structural properties of an IDR, we calculate the backbone conformational entropy of ${\text{Gly}}_{15}$ as a function of end-to-end distance and radius of gyration. Then, we consider how much conformational entropy is lost or gained as free energy when oligoglycine is constrained to or released from particular conformational states.

Theory

We briefly review the theory underlying the approaches we use to calculate the conformational entropy of various glycine polypeptides. We refer to conformational entropy as the contribution to the system entropy that depends only on the spatial coordinates of the solute molecule. Although this article primarily focuses on the dihedral angle contributions to conformational entropy (discussed in detail in Materials and Methods), the theories presented below are general and may be used with any coordinate system and any number of coordinates. Where appropriate, we refer the reader to more detailed discussions, and for consistency, we follow the notation of (44, 45, 46).

Solute entropy and coordinate system

The entropy of a solute can be expressed in terms of the probability density, $\rho (\mathbf{p},\mathbf{r})$, of Cartesian coordinates $\left(\mathit{r}\right)$ and conjugate momenta $\left(\mathit{p}\right)$ as follows:

$$S^{\text{solute}}=-k_B\iint \rho \left(\mathbf{p},\mathbf{r}\right)\text{ln}\left[h^s\rho \left(\mathbf{p},\mathbf{r}\right)\right]\text{d}\mathbf{p}\text{d}\mathbf{r},$$ (1)

where $k_B$ is Boltzmann’s constant, h is Planck’s constant, and s is the number of coordinate-momenta pairs that define solute phase space. In Cartesian coordinates, $s=3N$, where N is the number of solute atoms. Because of independence, $\rho (\mathbf{p},\mathbf{r})$ can be factored into marginal distributions of p and r, which upon expanding Eq. 1 gives the following:

$$S^{\text{solute}}=-k_B\int \rho \left(\mathbf{p}\right)\text{ln}\left[h^s\rho \left(\mathbf{p}\right)\right]\text{d}\mathbf{p}-k_B\int \rho \left(\mathbf{r}\right)\text{ln}\left[\rho \left(\mathbf{r}\right)\right]\text{d}\mathbf{r}=S_p+S_r,$$ (2)

with $S_p$ and $S_r$ being the momentum and conformational contributions to $S^{\text{solute}}$, respectively. By separating $S^{\text{solute}}$, neither $S_p$ nor $S_r$ is correctly dimensioned because of the factor $h^s$, and only upon their addition or considering changes in entropy will $S^{\text{solute}}$ have the correct units (46).

It is often more convenient or appropriate to describe the conformation of a protein or polypeptide in an internal coordinate system, for example, using bonds, angles, and torsions (i.e., BAT coordinates) (47, 48, 49). Under a transformation of Cartesian coordinates to internal coordinates $\left(\mathit{q}\right)$, the conformational entropy becomes

$$S_r=S^{\text{int}}+S^{\text{ext}}+k_B\text{ln}\langle J\rangle ,$$ (3)

where $S^{\text{int}}$ is the conformational entropy associated with the $3N-6$ internal coordinates that specify the relative atomic positions and is given by

$$S^{\text{int}}=-k_B\int \rho \left(\mathbf{q}\right)\ln \rho \left(\mathbf{q}\right)\text{d}\mathbf{q}.$$ (4)

$S^{\text{ext}}$ is the entropic contribution of the remaining six coordinates associated with the overall translation and rotation of the molecule that specify the absolute positions of the atoms. $\langle J\rangle$ is the ensemble average of the Jacobian of the coordinate transformation, $\mathit{r}\to \mathit{q}$. Expressions for $S^{\text{ext}}$ and the Jacobian in the BAT coordinate system can be found in (46). In BAT coordinates, the “hard” bond and angle coordinates may be treated essentially independent of or separable from the “soft” torsions/dihedrals (47, 48, 50), and therefore, their contributions to $S^{\text{int}}$ are additive. Depending on the system, it may be reasonable to assume that an isothermal process (e.g., protein binding) does not significantly perturb the bond and angle vibrations, which may be approximated at their equilibrium positions. Then, from Eqs. 2 to 4, the change in solute entropy can be approximated as $\mathit{\Delta }{S}^{\text{solute}}=\mathit{\Delta }{S}_r\approx \mathit{\Delta }{S}^{\text{int}}\approx \mathit{\Delta }{S}^{\text{dihed}}$.

A number of methods have been developed to estimate $S^{\text{int}}$ or $\mathit{\Delta }{S}^{\text{int}}$ (44, 51). Below, we briefly sketch the QHA (40, 41), BQH (42, 43, 44), and MIE (45) methods used in this article.

QHA and BQH analysis

In the QHA method, the distribution of internal coordinates, $\rho \left(\mathit{q}\right)$, around an average conformation is assumed to be multivariate Gaussian. This allows the entropy integral in Eq. 4 to be evaluated analytically, giving

$$S^{\text{int}}\approx S^{\text{QHA}}=\frac{1}{2}{k}_B\text{ln}\left[{\left(2\pi e\right)}^s\left|\mathit{\sigma }\right|\right],$$ (5)

where $\left|\mathit{\sigma }\right|$ is the determinant of the variance-covariance matrix of q about $\langle \mathit{q}\rangle$, and $s=3N-6$ is the number of internal coordinates or perhaps some subset of coordinates. Equation 5 can be expressed in terms of a correlation matrix, $\mathit{C}$, by factoring out the diagonal terms from $\mathit{\sigma }$ (42, 43, 44) as follows:

$$S^{\text{QHA}}=\frac{1}{2}{k}_B\sum _{i=1}^s\text{ln}\left(2\pi e{\sigma }_i\right)+\frac{1}{2}{k}_B\text{ln}\left|\mathbf{C}\right|.$$ (6)

The first term involves a sum over the variance $\left({\sigma }_i\equiv {\sigma }_{ii}\right)$ of each internal coordinate, whereas the second term accounts for correlations among coordinates through the determinant, $\left|\mathit{C}\right|$. Each element of the $s\times s$ matrix $\mathit{C}$ is ${\sigma }_{ij}/\sqrt{{\sigma }_i{\sigma }_j}$, where ${\sigma }_{ij}$ is the covariance of coordinates i and j. Coordinate variances and the correlation matrix can be calculated from the trajectories of atomic positions from an MD simulation.

Assuming Gaussian distributions of q can produce a poor approximation of $S^{\text{int}}$ when, for example, BAT coordinates are used because torsion/dihedral angle probability distributions are typically multimodal (52). To improve estimates of $S^{\text{int}}$ and account for non-Gaussian distributions, Di Nola et al. (42) proposed replacing the first term in Eq. 6 with the Boltzmann entropy, such that

$$S^{\text{int}}\approx S^{\text{BQH}}=-k_B\sum _{i=1}^s\int \rho \left(q_i\right)\text{ln}\rho \left(q_i\right)\text{d}{q}_i+\frac{1}{2}{k}_B\text{ln}\left|\mathbf{C}\right|,$$ (7)

where i indexes one of the internal coordinates $\left(q_i\right)$. The probability distribution, $\rho \left(q_i\right)$, and associated entropy integral (Eq. 4) can be numerically approximated from one-dimensional histograms collected over an MD trajectory. In QHA and BQH, the first terms in Eqs. 6 and 7 represent a first-order approximation of conformational entropy under the assumption of independent coordinates, whereas the second term contributes a negative correction because of second-order correlations among coordinates.

MIE

MIE (45) is a nonparametric approach that approximates the probability density of all coordinates in terms of a set of lower-order density distributions using the generalized Kirkwood superposition approximation from liquid theory. As a simple example, the second-order approximation of a three-dimensional density function of coordinates $q_1$, $q_2$, and $q_3$ is

$${\rho }^{\left(2\right)}\left(q_1,q_2,q_3\right)=\frac{{\rho }_2\left(q_1,q_2\right){\rho }_2\left(q_1,q_3\right){\rho }_2\left(q_2,q_3\right)}{{\rho }_1\left(q_1\right){\rho }_1\left(q_2\right){\rho }_1\left(q_3\right)},$$ (8)

where the numerator includes joint distributions $\left({\rho }_2\right)$ of all possible pairs of coordinates, and the denominator includes the marginal distributions $\left({\rho }_1\right)$ of each coordinate. Unlike liquid theory, the marginal and joint distributions are treated as unique and depend on the coordinates or coordinate pairs, respectively. Substituting Eq. 8 into Eq. 4 and expanding the logarithm gives the second-order MIE approximation of $S^{\text{int}}$:

$$S^{\text{int}}\approx S_2^{\text{MIE}}=S_1\left(q_1\right)+S_1\left(q_2\right)+S_1\left(q_3\right)-I_2\left(q_1,q_2\right)-I_2\left(q_1,q_3\right)-I_2\left(q_2,q_3\right),$$ (9)

where the mutual information (MI) term is defined as $I_2\left(q_i,q_j\right)=S_1\left(q_i\right)+S_1\left(q_j\right)-S_2\left(q_i,q_j\right)$. The general functional forms of $S_1$ and $S_2$ are given by Eq. 4 but with their subscripts indicating that the entropy integral is over a marginal or joint distribution, respectively. Note that the sum over the $S_1$ terms in Eq. 9, which we will refer to as $S_1^{\text{MIE}}$, is equivalent to the first term in Eq. 7. Whereas the QHA and BQH methods account for correlations among coordinates via a harmonic approximation, MIE estimates the entropic contribution to $S^{\text{int}}$ due to correlations directly from the joint distributions that define the MI terms. For a more complete discussion of MIE, its application to a number of molecular systems, and its generalization to higher-order approximations with any number of internal coordinates, we refer to (45). In this article, we will at most consider a third-order approximation of $\rho \left(\mathit{q}\right)$ with the corresponding estimate of $S^{\text{int}}$ given by

$$S^{\text{int}}\approx S_3^{\text{MIE}}=S_2^{\text{MIE}}+I_3\left(q_1,q_2,q_3\right).$$ (10)

For a system with more internal coordinates, Eq. 10 will include an $I_3$ term for each coordinate triplet. The various marginal and joint distributions of internal coordinates can be estimated by constructing the necessary histograms from MD simulation trajectories. Although in principle $\rho \left(\mathit{q}\right)$ may be approximated at higher orders, practically it may become computationally prohibitive to achieve the necessary conformational sampling required to converge estimates of $S_3^{\text{MIE}}$ even for small systems because of the sparseness of the three-dimensional histograms. This problem may be mitigated to a certain extent by using coarser histogram bins or alternative binning strategies.

We next present a general framework to estimate the change in free energy and conformational entropy when an ensemble of disordered polypeptide structures is restricted or confined to particular conformational states. We use this process, hereafter referred to as ensemble confinement, to study the backbone contributions to the thermodynamics associated with order-disorder transitions of short IDRs.

Ensemble confinement free energy

We start by assuming that there are M states defined through a partition of conformation space. The probability of observing a conformation in state j is $p_j$. Each state has an internal energy $\left(U_j\right)$ and intrastate entropy $\left(S_j^{\text{intra}}\right)$, with the latter accounting for the degeneracy of state j. The conformational entropy, or entropy of the ensemble excluding rotation and translation, may be decomposed into two terms (53, 54) as follows:

$$S^{\text{ens}}=\sum _{j=1}^M{p}_j{S}_j^{\text{intra}}-k_B\sum _{j=1}^M{p}_j\text{ln}{p}_j=S^{\text{intra}}+S^{\text{state}},$$ (11)

where $S^{\text{state}}$ is the entropy arising from the partition of conformation space into the M predefined states. The free energy of restricting or confining the ensemble to a single state i is $\mathit{\Delta }{A}_i=\mathit{\Delta }{U}_i-T\mathit{\Delta }{S}_i$, where $\mathit{\Delta }{U}_i=U_i-\langle U\rangle$ and $\mathit{\Delta }{S}_i=S_i^{\text{intra}}-S^{\text{ens}}$. Substituting Eq. 11 into the expression for $\mathit{\Delta }{A}_i$ and rearranging the terms gives the following:

$$\mathit{\Delta }{A}_i=U_i-T{S}_i^{\text{intra}}+\sum _{j=1}^M{p}_j\left(-U_j+T{S}_j^{\text{intra}}-k_{B}T\text{ln}{p}_j\right)$$ (12)

Using the fact that

$$p_j=\frac{{\text{e}}^{S_j^{\text{intra}}/k_B-\beta U_j}}{Z},$$ (13)

where Z is the partition function that normalizes $p_j$, Eq. 12 simplifies to

$$\mathit{\Delta }{A}_i=-k_{B}T\text{ln}{p}_i.$$ (14)

Equation 14 indicates that the (ensemble) confinement free energy, $\mathit{\Delta }{A}_i$, is almost always positive or unfavorable because $p_i\le 1$. The average confinement free energy across the possible states is

$$\langle \mathit{\Delta }A\rangle =\sum _{i=1}^M{p}_i\mathit{\Delta }{A}_i=-k_{B}T\sum _{i=1}^M{p}_i\text{ln}{p}_i=T{S}^{\text{state}},$$ (15)

which highlights the entropic nature of the confinement free energy. Although any collective variable may be used to define state i, we follow the approaches of (54, 55) by defining the conformational state of oligoglycine in terms of backbone dihedral angles. As detailed in the Materials and Methods, we calculate the dihedral angle contribution to the conformational entropy $\left(S^{\text{int}}\right)$ of successively longer oligoglycines using the QHA, BQH, and MIE approaches, and using the framework presented above, we quantify the extent of conformational entropy lost or free energy gained upon confining the ensemble of oligoglycine structures to particular conformational states.

Materials and Methods

We use oligoglycine as a model to study the backbone contributions to the thermodynamics associated with order-disorder transitions of short IDRs. Oligoglycine (${\text{Gly}}_N$, where N is the number of residues or chain length) is a protein backbone mimic and model disordered polypeptide (33, 35, 36, 56, 57, 58). Tracts of oligoglycine can be found in IDRs (59), and high glycine content has been associated with compact IDRs (38). Using MD simulations, we sample the structural ensemble of successively longer oligoglycines and calculate the dihedral angle contributions to the absolute conformational entropy as a function of chain length. Units of entropy (eu) are cal/mol/K. Because a protein containing an IDR may impose some structural constraints on the disordered region, we consider these entropy estimates as a function of end-to-end distance and radius of gyration. Using the ensemble confinement framework presented in Theory, we determine the extent of backbone entropy lost or gained when oligoglycine is constrained to or released from particular conformational states. Below, we provide details on the oligoglycine model, MD simulation parameters/protocol, and the application of the various methods discussed in Theory to calculate the backbone dihedral conformational entropy. Data, analysis scripts, and simulation input files are available upon request.

System and simulations

${\text{Gly}}_3$, ${\text{Gly}}_4$, ${\text{Gly}}_5$, ${\text{Gly}}_{10}$, and ${\text{Gly}}_{15}$ were built in an extended conformation with neutral acetyl and N-methylamide caps using XLeap in AmberTools (60). Each oligoglycine was solvated in a box of transferable intermolecular potential with three points water molecules with at least a 10 Å padding to the walls of the box. Simulations were performed with nanoscale molecular dynamics 2.9 and 2.10 (61) with Amber (Assisted Model Building with Energy Refinement) ff12SB (60) at constant temperature (300 K) and pressure (1 atm). MD trajectories of ${\text{Gly}}_3$ and ${\text{Gly}}_{10}$ were taken from a previous study (62), and the same parameters were used here to simulate the remaining oligoglycines. Briefly, a steepest descent minimization was performed for each system followed by production simulations with a 2 fs time step using the velocity Verlet algorithm. A Langevin thermostat and barostat were used to maintain temperature and pressure, respectively. A cutoff of 12 Å was used for nonbonded interactions, and the van der Waals interactions were attenuated with a switching function beginning at 10 Å. Full electrostatic interactions were calculated every two steps using particle mesh Ewald method with a 1 Å grid spacing. To be consistent with Amber’s nonbonded exclusion policy, the 1–4 scaling was set to 0.8333. Bonds involving hydrogen atoms were fixed with SHAKE. ${\text{Gly}}_3$, ${\text{Gly}}_4$, ${\text{Gly}}_5$, ${\text{Gly}}_{10}$, and ${\text{Gly}}_{15}$ were simulated for 300, 550, 995, 950, and 1150 ns, respectively, after dropping at least 20 ns for equilibration. Coordinates were saved for analysis every 1 ps.

Dihedral angle conformational entropy

From simulations of each oligoglycine, we construct trajectories of the ϕ and ψ backbone dihedral angles, neglecting the nearly rigid ω angles, and calculate the backbone conformational entropy (Theory). We refer to the entropy estimates from QHA, BQH, and MIE as $S^{\text{QHA}}$, $S^{\text{BQH}}$, and $S^{\text{MIE}}$, respectively. By considering only dihedral angles, we are assuming that they, as a set, contribute to the conformational entropy, $S^{\text{int}}$ (Eq. 4), independent of the bonds and angles that define the BAT coordinate system. That is, we assume any changes in the entropic contributions of dihedral-bond and dihedral-angle correlations are negligible. $S^{\text{QHA}}$, $S^{\text{BQH}}$, and $S^{\text{MIE}}$ were calculated as a function of oligoglycine length.

To calculate $S^{\text{QHA}}$ and $S^{\text{BQH}}$ using Eqs. 6 and 7, dihedral angles were represented on the unit circle in the complex plane, which is convenient for constructing the variance-covariance $\left(\mathit{\sigma }\right)$ matrix and subsequently the correlation matrix $\left(\mathit{C}\right)$ for angular coordinates (63). Each element of $\mathit{\sigma }$ is computed as ${\sigma }_{ij}=\langle Z_i{Z}_j^{\text{∗}}\rangle -\langle Z_i\rangle \langle Z_j^{\text{∗}}\rangle$, where Z is the complex representation of dihedral i or j, and $Z^{\text{∗}}$ is the complex conjugate. The diagonal terms were factored out of $\mathit{\sigma }$ to give $\mathit{C}$ (see Theory), which can then be directly used in Eqs. 6 and 7 to calculate $S^{\text{QHA}}$ and $S^{\text{BQH}}$, respectively. For $S^{\text{BQH}}$, histograms of each dihedral angle were constructed on the range $\left[-\pi ,\pi \right]$ using 180 bins to evaluate the exact Boltzmann entropy expression in Eq. 7. Note that the summations in Eqs. 6 and 7 are over the $2N_{\text{res}}$ dihedral angles, where $N_{\text{res}}$ is the number of glycine residues, and that the correlation matrix has dimensions of $2N_{\text{res}}\times 2N_{\text{res}}$.

With Eqs. 9 and 10, the second- $\left(S_2^{\text{MIE}}\right)$ and third- $\left(S_3^{\text{MIE}}\right)$ order MIE approximations of the full entropy were calculated from the marginal and joint distributions of the $2N_{\text{res}}$ dihedral angles using the program Algorithm for Computing Configurational ENTropy (45). Marginal and two-dimensional probability distributions were approximated with histograms using 120 bins over the range $\left[-\pi ,\pi \right]$. An analysis of $S_2^{\text{MIE}}$ versus bin size suggested that 120 bins in each dimension were sufficient to converge $S_2^{\text{MIE}}$ to within $\sim 1$–2 eu of those calculated with 110 and 130 bins for all oligoglycines. However, $S_3^{\text{MIE}}$ is much more sensitive with respect to the number of bins, and due to the sparseness of the 3D histograms, 20 bins were used in each dimension to calculate $S_3^{\text{MIE}}$. We also explored the use of an alternative, second-order MIE truncation strategy in which each residue in oligoglycine is assumed independent of one another. Here, $S_{\text{res}}^{\text{MIE}}$ is calculated using only the MI terms for the ϕ and ψ angles within each residue and ignoring those terms that include dihedrals from different residues. $S_{\text{res}}^{\text{MIE}}$ will always be greater than or equal to $S_2^{\text{MIE}}$ because the latter includes more MI terms that may potentially reduce $S_{\text{res}}^{\text{MIE}}$. Equality is achieved only when each residue represents an independent subsystem. However, depending on the strength of correlated dihedral motions and the desired accuracy, $S_{\text{res}}^{\text{MIE}}$ may be a reasonable and less computationally demanding approximation of $S_2^{\text{MIE}}$ because histograms of all pairs of dihedrals are not needed. In a similar fashion, if no third or higher-order correlations exist between dihedrals, then $S_2^{\text{MIE}}=S_3^{\text{MIE}}$ and so on.

To assess convergence, all entropy estimates were monitored as a function of simulation time. $S_2^{\text{MIE}}$ and to a greater extent $S_3^{\text{MIE}}$ showed poorer convergence than $S^{\text{QHA}}$, $S^{\text{BQH}}$, and $S_{\text{res}}^{\text{MIE}}$, especially for ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$. To improve accuracy, functions of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ with respect to time (t) were individually fit to a hyperbolic function, $f\left(t\right)=a-b/t$, for all oligoglycines in a manner similar to the approaches of (45, 64). The asymptotes (a) were used as an additional approximation of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ and are referred to as $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$, respectively. To estimate statistical uncertainty, simulation trajectories for each oligoglycine were split into five contiguous blocks, and the various entropy estimates were calculated for each block with the exception of the third-order MIE entropy estimates, which showed poor convergence. We take the SD of each entropy estimate across the blocks as a conservative error estimate. This approach was similarly taken for subsequent thermodynamic analyses.

Effects of structural constraints on entropy estimates

A preliminary analysis of the ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$ MD trajectories suggested that constraints on the end-to-end distance (R), which is defined between carbons in the acetyl and N-methylamide caps, and on the radius of gyration $\left(R_g\right)$ only weakly affected the dihedral angle populations and therefore likely the dihedral conformational entropy. Because of a lack of conformational sampling from the explicit solvent MD simulation, particularly at values of R and $R_g$ far from average, eight implicit solvent simulations of ${\text{Gly}}_{15}$ were performed with end-to-end distances restrained to 5, 10, 15, 20, 25, 30, 35, and 40 Å using a harmonic bias potential and the Amber ff12SB force field. Simulations were conducted at constant temperature (300 K) and volume with nanoscale molecular dynamics 2.11 (61) using the default Generalized Born implicit solvent model (65, 66) and a descreening cutoff of 12 Å.

A force constant of 25 kcal/mol/Ų was used for the harmonic bias potential to restrain R. Simulations were run for 1 $\mathit{\mu }$s each with 10 ns dropped for equilibration. The trajectories were further partitioned by selecting conformations with an $R_g$ centered at 6, 7, 8, 9, 10, 11, 12, and $13\pm 0.5$ Å. $S_{\text{res}}^{\text{MIE}}$, $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$ were calculated as a function of R and $R_g$. Additionally, we compute the one-dimensional entropy $\left(S_1^{\text{MIE}}\right)$ from the marginal distributions of each dihedral angle (i.e., ${\sum }_{i=1}^{2N_{\text{res}}}{S}_1\left(q_i\right)$ in Eq. 9).

Ensemble confinement free energy

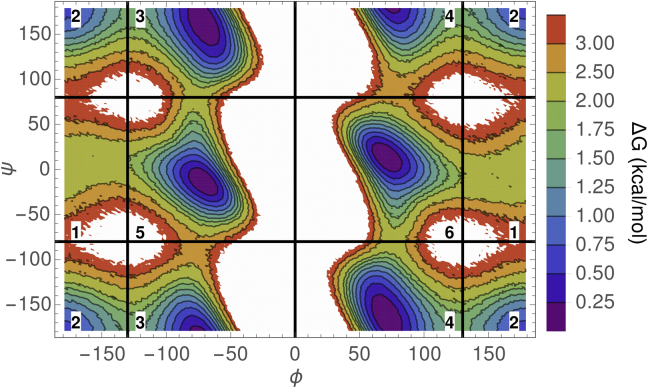
We use the ensemble confinement framework presented in Theory to estimate the change in free energy $\left(\mathit{\Delta }{A}_i\right)$ upon limiting the ensemble of oligoglycine structures to some conformational state, i. To define the reference state, we follow an approach similar to that in (54, 55, 67). We begin by partitioning the two-dimensional ϕ-ψ map (Fig. 1) of a glycine residue into six regions, labeled 1–6, that correspond to a high-energy region (1), β-sheet (2), right (3) and left (4) ppII, and right (5) and left (6) α-helix regions. For a given oligoglycine conformation sampled from an MD simulation, each residue, $j\in \left[1\dots N_{\text{res}}\right]$, is assigned to one of these six regions given its ϕ-ψ pair. The conformational state (i) is then defined as $i=\left\{d_1,d_2,\dots ,d_{N_{\text{res}}}\right\}$, where $d_j$ takes on values of 1–6. The free-energy change of confining oligoglycine to state i is calculated using Eq. 14 as $\mathit{\Delta }{A}_i=-k_{B}T\text{ln}{p}_i$. For ${\text{Gly}}_{3-5}$, $p_i$ was calculated as $p_i=h_i/n_f$, where $h_i$ is the number of times oligoglycine visited conformational state i, and $n_f$ is the total number of observations or simulation frames.

Figure 1.

ϕ-ψ free-energy map. For illustrative purposes, a two-dimensional histogram of ϕ,ψ dihedral angles was constructed across all residues from an MD trajectory of ${\text{Gly}}_{15}$. The histogram was converted to a free-energy map relative to the most populated bin. Regions with values greater than 3.5 kcal/mol are colored white. The map is partitioned into six regions that are used to define a conformational state of oligoglycine. States 2, 3, 4, 5, and 6 correspond to the β, ${\text{ppII}}_R$, ${\text{ppII}}_L$, ${\alpha }_R$, and ${\alpha }_L$ regions, respectively. State 1 corresponds to a high-energy region (Hi).

Although $p_i$ may be accurately estimated for the short oligoglycines, it is much more challenging to obtain a statistically meaningful or physically representative estimate of $p_i$ for long oligoglycines because, for example, there are $6^{15}$ possible conformational states of ${\text{Gly}}_{15}$, most of which are transiently populated. Therefore, we treated ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$ as being composed of two and three independent yet connected systems of ${\text{Gly}}_5$, respectively. $p_i$ can then be factored into joint probability distributions of the ${\text{Gly}}_5$ blocks, and approximated as follows:

$$p_i\approx {\tilde{p}}_i=\{\begin{array}{cc}p\left(\left\{d_{1-5}\right\}\right)p\left(\left\{d_{6-10}\right\}\right),& \text{for }{\text{Gly}}_{10}\\ p\left(\left\{d_{1-5}\right\}\right)p\left(\left\{d_{6-10}\right\}\right)p\left(\left\{d_{11-15}\right\}\right)& \text{for }{\text{Gly}}_{15}.\end{array}$$

For ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$, $\mathit{\Delta }{A}_i$ is evaluated using the approximate distribution, $\widetilde{p_i}$, with Eq. 14. The average confinement free energy over all observed conformational states is given by Eq. 15 as $\langle \mathit{\Delta }A\rangle ={\sum }_{i=1}^M{p}_i\mathit{\Delta }{A}_i$. Although ${\tilde{p}}_i$ was used to estimate $\mathit{\Delta }{A}_i$ for ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$, we use the observed probabilities, $p_i=h_i/n_f$, to calculate the weighted average, $\langle \mathit{\Delta }A\rangle$, in Eq. 15 to limit any systematic error introduced by assuming that they can be decomposed into independent blocks of ${\text{Gly}}_5$. Additionally, to study the effects of interresidue correlations, we computed $\langle \mathit{\Delta }A\rangle$ for all oligoglycines assuming each residue is independent of the others [i.e., $p_i\approx p\left(d_1\right)p\left(d_2\right)\cdots p\left(d_{N_{\text{res}}}\right)$]. We refer to these estimates as ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ and those based on the joint-probability distributions $\left(p_i\text{ or }{\tilde{p}}_i\right)$ as ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$.

Results

We wish to better understand the thermodynamics associated with conformational transitions of short IDRs and in particular the free energy afforded to such transitions in the form of backbone conformational entropy. We begin by calculating the dihedral angle contribution to the absolute conformational entropy (hereafter simply referred to as conformational entropy) of successively longer oligoglycine polypeptides (${\text{Gly}}_{3-5}$, ${\text{Gly}}_{10}$, and ${\text{Gly}}_{15}$). Comparing the QHA, BQH, and MIE methods, we calculated the conformational entropy (S) from the ϕ and ψ backbone dihedral angles sampled from MD simulations. Superscripts are used to denote the method used to calculate the conformational entropy, and for the MIE approach, subscripts indicate the order of approximation or truncation strategy (see Materials and Methods). Entropy units (eu) are cal/mol/K. Then, we investigate the conformational entropy as a function of end-to-end distance (R) and radius of gyration $\left(R_g\right)$ of ${\text{Gly}}_{15}$ using restrained, implicit solvent simulations because IDR-containing proteins likely impose global, structural constraints on the disordered region, and order-disorder transitions may alter R and $R_g$. Lastly, we consider the extent of conformational entropy lost or gained as free energy when oligoglycine is constrained to or released from particular conformational states.

Conformational entropy scaling with chain length

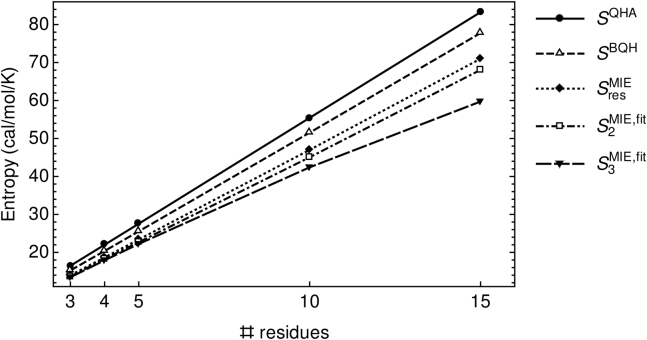
Fig. 2 shows the scaling of $S^{\text{QHA}}$, $S^{\text{BQH}}$, $S_{\text{res}}^{\text{MIE}}$, $S_2^{\text{MIE},\text{fit}}$, and $S_3^{\text{MIE},\text{fit}}$ as a function of oligoglycine chain length. $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$ are taken as the asymptotes of hyperbolic fits of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$, respectively, as functions of simulation time for each oligoglycine individually. As discussed in Materials and Methods, $S_{\text{res}}^{\text{MIE}}$ is an alternative, second-order MIE approximation in which each glycine residue is treated as independent of the others by ignoring MI terms that include dihedrals from two different residues. The data plotted in Fig. 2 are provided in Table S1. The various entropy estimates in Fig. 2 all scale linearly with the number of residues or chain length, with slopes ranging from $3.86\mathrm{–}5.57$ eu/res or $1.16\mathrm{–}1.67$ kcal/mol/res at 300 K. Slopes were estimated from least-square fits, all of which yielded values of $R^2\ge 0.99$.

Figure 2.

Backbone conformational entropy scaling with oligoglycine chain length or number of glycine residues. Superscripts indicate the method used. For the MIE entropy estimates, subscripts denote the order of approximation or truncation strategy. $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$ are taken as the asymptotes of hyperbolic fits of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$, respectively, as functions of time (see Materials and Methods for more details).

The difference or range in slopes can be attributed to the assumptions or approximations underlying each method used to calculate conformational entropy (Theory). Here, $S^{\text{QHA}}$ provides an upper bound on the true conformational entropy, as it effectively merges conformational states (52). As expected, $S^{\text{QHA}}>S^{\text{BQH}}>S_{\text{res}}^{\text{MIE}}>S_2^{\text{MIE},\text{fit}}>S_3^{\text{MIE},\text{fit}}$ across chain lengths because each method in the given order more accurately captures the multimodal distributions of and/or correlations among dihedral angles than those preceding. With respect to the MIE approach, MI terms may effectively reduce the entropy if there are substantial correlations among dihedrals along the oligoglycine backbone. We find that differences among $S_{\text{res}}^{\text{MIE}}$, $S_2^{\text{MIE},\text{fit}}$, and $S_3^{\text{MIE},\text{fit}}$ are at most $\sim 1.1$ eu for ${\text{Gly}}_3$, ${\text{Gly}}_4$, and ${\text{Gly}}_5$, suggesting that the most significant correlations exist between ϕ and ψ dihedrals within each residue and that $S_{\text{res}}^{\text{MIE}}$ largely accounts for the entropic contributions of these correlations. For ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$, differences between $S_{\text{res}}^{\text{MIE}}$ and $S_2^{\text{MIE},\text{fit}}$ increase slightly to $\sim 2$ eu, whereas a much greater difference is observed between $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$. This large difference between the latter two is likely due to insufficient conformational sampling and the large bin widths required to estimate $S_3^{\text{MIE}}$. All second-order MI terms or entropies were less than 0.02 eu for pairs of dihedrals separated by two or more residues in ${\text{Gly}}_{15}$, suggesting that long-range correlations are minimal in ${\text{Gly}}_N$ systems even at this longer chain length (data not shown). That significant correlations do not span multiple glycine residues is consistent with various estimates of the persistence length being on the order of 1–2 residues for denatured or unfolded proteins (34, 68, 69, 70). When excluding $S_3^{\text{MIE},\text{fit}}$ for ${\text{Gly}}_{15}$, linear fits of $S_{\text{res}}^{\text{MIE}}$, $S_2^{\text{MIE},\text{fit}}$, and $S_3^{\text{MIE},\text{fit}}$ yielded slopes of 4.73, 4.52, and 4.11 eu/res, respectively.

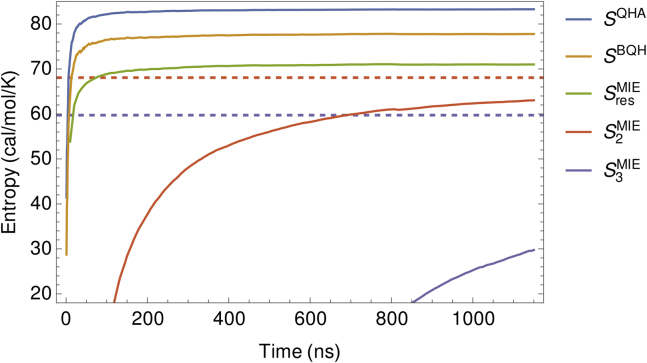
For the oligoglycine systems considered here, we find that $S^{\text{QHA}}$, $S^{\text{BQH}}$, and $S_{\text{res}}^{\text{MIE}}$ converge considerably faster with respect to time than $S_2^{\text{MIE}}$ and, to a greater extent, $S_3^{\text{MIE}}$. As an example, Fig. 3 shows the trajectories of these entropy estimates for ${\text{Gly}}_{15}$. We also provide trajectories of the MIE entropies for all oligoglycines in Fig. S1. Hyperbolic fits of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ with respect to simulation time yielded $R^2\ge 0.99$ for all oligoglycines, allowing us to probe the convergence properties of these entropy estimates. For ${\text{Gly}}_{3-5}$, sampling was sufficient to converge $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ to within less than 1 eu of their asymptotic values ($S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$, respectively). However, for ${\text{Gly}}_{15}$, we estimate that it would take $\sim 5.9$ and $\sim 34.6$ $\mathit{\mu }$s of simulation time to converge $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ to within 1 eu of their asymptotes (Table S1). The hyperbolic nature of the $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ trajectories may only be relevant for the oligoglycine systems considered here, in which the residues are highly uncoupled. However, future work is warranted to determine if $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$ follow hyperbolic trajectories for other short, disordered polypeptides, as relatively short simulations could be run to establish the initial scaling of the hyperbola after which a least-square fit could be performed to conveniently extract the asymptotes of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$. Error estimates of $S^{\text{QHA}}$, $S^{\text{BQH}}$, and the various first- and second-order MIE entropies were all less than 1 eu with the exception of $S_2^{\text{MIE},\text{fit}}$ for ${\text{Gly}}_{15}$ which was $\sim 2$ eu (Table S1).

Figure 3.

Trajectories of ${\text{Gly}}_{15}$ conformational entropy estimates with respect to simulation time. The dashed lines indicate the asymptotes, $S_2^{\text{MIE},\text{fit}}$ and $S_3^{\text{MIE},\text{fit}}$, of the hyperbolic fits of $S_2^{\text{MIE}}$ and $S_3^{\text{MIE}}$, respectively, and are colored accordingly.

Effects of structural constraints on dihedral conformational entropy

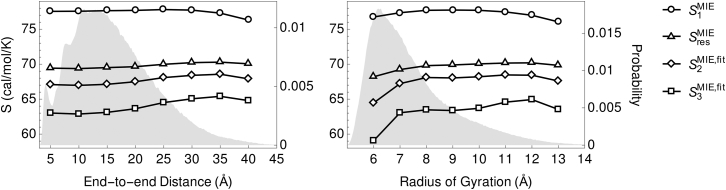
To determine if structural transitions altering the end-to-end distance (R) or radius of gyration $\left(R_g\right)$ of an IDR elicit a significant entropic change, we performed microsecond implicit solvent simulations of ${\text{Gly}}_{15}$ constrained to eight different values of R. We further partitioned conformations by $R_g$ as described in Materials and Methods. Then, we calculated the conformational entropy using the MIE approach as a function of R and $R_g$. We find that $S_1^{\text{MIE}}$ (one-dimensional entropy), $S_{\text{res}}^{\text{MIE}}$, $S_2^{\text{MIE},\text{fit}}$, and $S_3^{\text{MIE},\text{fit}}$ are largely independent of R and $R_g$ (Fig. 4; Tables S2 and S3) with the greatest effects observed at their extreme values. Furthermore, these entropy estimates are also very consistent with those obtained from the unconstrained, explicit solvent simulations (Table S1). It appears, then, that global, structural changes in R or $R_g$ produce only a minimal change in backbone entropy when compared to the absolute conformational entropy that could potentially be lost or gained up such structural transitions. In the following section, we explore the extent of conformational entropy lost as free energy when individual residues are constrained to particular regions of the ϕ-ψ map (i.e., local versus global constraints).

Figure 4.

MIE conformational entropy estimates of ${\text{Gly}}_{15}$ as a function of end-to-end distance (left) and radius of gyration (right). Implicit solvent simulations of ${\text{Gly}}_{15}$ were performed with the distance between terminal carbons constrained to eight different values with a harmonic bias potential. Trajectories were then partitioned by radius of gyration. The first-order MIE approximation is given as ${\sum }_{i=1}^{2N_{\text{res}}}{S}_1\left(q_i\right)$ (i.e., the sum over one-dimensional terms in Eq. 9). Probability distributions of end-to-end distance and radius of gyration from explicit solvent simulations of ${\text{Gly}}_{15}$ are shaded in gray.

Ensemble confinement free energy

The ensemble confinement free energy $\left(\mathit{\Delta }{A}_i\right)$ presented in Theory and Materials and Methods estimates the gain (loss) of conformational free energy when oligoglycine is constrained to (released from) a conformational state (i), which is defined by assigning each glycine residue to one of six regions of the ϕ-ψ map (Fig. 1). Equation 14 gives $\mathit{\Delta }{A}_i=-k_{B}T\text{ln}{p}_i$, where $p_i$ is the probability of observing oligoglycine in state i. For ${\text{Gly}}_{3-5}$, $p_i$ is calculated directly from the observed frequencies of state i from simulation, whereas for ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$, $p_i$ is approximated by assuming that they are composed of two and three independent, contiguous blocks of ${\text{Gly}}_5$, respectively. $\mathit{\Delta }{A}_i$ calculated in this manner is denoted as $\mathit{\Delta }{A}_i^{\text{oligo}}$. Additionally, to study the effects of correlations among residues, we calculate $\mathit{\Delta }{A}_i$ by factorizing $p_i$ as the product of the probabilities of each residue being in one of the six predefined regions of the ϕ-ψ map. These estimates carry the superscript “res.” An ensemble average of $\mathit{\Delta }{A}_i^{\text{oligo}}$ and $\mathit{\Delta }{A}_i^{\text{res}}$ across observed conformational states (Eq. 15) gives ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}=T{S}_{\text{oligo}}^{\text{state}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{res}}=T{S}_{\text{res}}^{\text{state}}$, respectively, where $S^{\text{state}}$ is the entropy related to the number of possible oligoglycine conformers.

We find that both ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ scale linearly with oligoglycine chain length (Table 1). Least-square fits of ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ yielded similar slopes of 0.95 and 0.99 kcal/mol/res, respectively. The corresponding slopes of $S_{\text{oligo}}^{\text{state}}$ and $S_{\text{res}}^{\text{state}}$ are 3.15 and 3.28 eu/res, which represent a significant fraction of the absolute conformational entropy per residue (Table S1). In other words, a large portion of the conformational entropy, on average, is lost as free energy when the structural ensemble is confined to particular states. For example, the slope of $S_{\text{res}}^{\text{state}}$ is roughly $69\text{\%}$ of that estimated for $S_{\text{res}}^{\text{MIE}}$, and the remaining entropy can be attributed to the internal entropy within the conformational states, which is often referred to as vibrational entropy (53, 54). The slope of $S_{\text{oligo}}^{\text{state}}$ is $85\text{\%}$ of that measured for $S_3^{\text{MIE},\text{fit}}$ and $80\text{\%}$ when excluding ${\text{Gly}}_{15}$. Whereas for well-structured proteins the loss of backbone vibrational entropy upon binding may dominate that associated with the loss of the number of rotamers, the opposite may be true for IDRs. That ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ exhibit similar scaling profiles with respect to oligoglycine length again suggests that oligoglycine can be reasonably modeled as a system of uncoupled glycine residues over the length scale considered here. These results were also independently confirmed using the program CENCALC (71).

Table 1.

Average Confinement Free Energy and Corresponding Conformational Entropy as a Function of Oligoglycine Chain Length

Gly	${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$	${\langle \mathit{\Delta }A\rangle }^{\text{res}}$	$S_{\text{oligo}}^{\text{state}}$	$S_{\text{res}}^{\text{state}}$
3	$2.87\left(0.01\right)$	$2.89\left(0.02\right)$	9.57	9.63
4	$3.80\left(0.02\right)$	$3.85\left(0.03\right)$	12.67	12.83
5	$4.72\left(0.01\right)$	$4.82\left(0.02\right)$	15.73	16.07
10	$9.44\left(0.03\right)$	$9.74\left(0.03\right)$	31.47	32.47
15	$14.20\left(0.11\right)$	$14.70\left(0.04\right)$	47.33	49.00
Slope	0.95	0.99	3.15	3.28
$R^2$	0.99	0.99

Free energies are reported in kcal/mol and entropy is measured in cal/mol/K. Slopes were estimated from linear least-squares fit. For ${\text{Gly}}_{3-5}$, ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ was calculated from the joint distributions of ϕ-ψ dihedral state assignments across residues, whereas those for ${\text{Gly}}_{10}$ and ${\text{Gly}}_{15}$ were approximated using the joint distributions of two and three consecutive segments of ${\text{Gly}}_5$, respectively. ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ is estimated from the product of the marginal distributions of the per residue state assignments (see Materials and Methods). Errors in the ensemble confinement free energy were approximated as the SD of ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ or ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ calculated from five equally sized blocks of the MD trajectory. These are provided in parentheses. $S_{\text{oligo}}^{\text{state}}$ and $S_{\text{res}}^{\text{state}}$ are calculated from ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$, respectively, with Eq. 15.

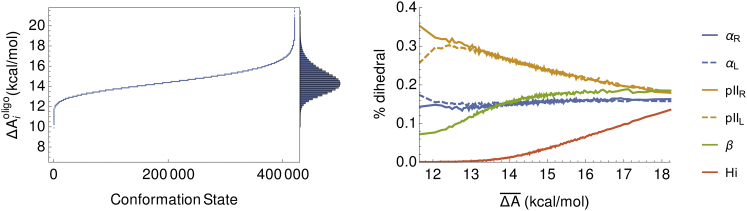
Next, we provide more detail on the results for ${\text{Gly}}_{15}$. Over the $\sim 1.1$ $\mathit{\mu }$s simulation, ${\text{Gly}}_{15}$ visited roughly 400,000 unique conformational states. Fig. 5 (left) shows a plot of $\mathit{\Delta }{A}_i^{\text{oligo}}$ across the visited states, i, which are arbitrarily numbered and ordered by increasing values of $\mathit{\Delta }{A}_i^{\text{oligo}}$. $\mathit{\Delta }{A}_i^{\text{oligo}}$ is large and unfavorable and spans a range of $\sim 10$–20 kcal/mol, corresponding to the most and least energetically favorable or probable states, respectively. The characteristic sigmoidal shape of $\mathit{\Delta }{A}_i^{\text{oligo}}$ shows that there are a large number of somewhat energetically degenerate conformational states with very similar values of $\mathit{\Delta }{A}_i^{\text{oligo}}$. Conformational states with the lowest values of $\mathit{\Delta }{A}_i^{\text{oligo}}$ are characterized by a higher polyproline II content (Fig. 5, right), whereas those states with the highest values are composed of residues more equally proportioned across the six major regions of the ϕ-ψ map (Fig. 1). Interestingly, the confinement free energy is insensitive to α-helical content.

Figure 5.

(Left) ${\text{Gly}}_{15}$ confinement free energy as a function of conformational states (i). The vertical bar chart is a histogram of $\mathit{\Delta }{A}_i^{\text{oligo}}$ values. (Right) A fraction of residues falling within the six partitions of the ϕ-ψ map (see Fig. 1) are shown as a function of the average confinement free energy $\left(\overline{\mathit{\Delta }A}\right)$ taken over a sliding, nonoverlapping window of 100 conformational states, ordered by increasing values of $\mathit{\Delta }{A}_i^{\text{oligo}}$. A windowing average was taken to reduce noise and is different than the weighted average, ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$, which is taken across all conformations.

Discussion

The ability of an IDR to undergo structural transitions is key to disorder-mediated recognition and allostery (10, 14, 15). Toward providing bounds on the thermodynamics associated with such transitions, we consider the conformational entropy and free energy of oligoglycine, a model IDR and protein backbone model. We began first by calculating the absolute backbone conformational entropy of oligoglycine as a function of chain length over a biologically relevant range using the QHA, BQH, and MIE methods. The conformational entropy is significant, and all methods consistently report a linear scaling of backbone conformational entropy with chain length (Fig. 2), yet with different slopes. Recently, Towse et al. observed a linear scaling of backbone conformational entropy with chain length (up to ∼400 residues), albeit with considerable spread, from a large-scale analysis of 807 structured proteins in the Dynameomics MD data set (72), suggesting that this linear relationship may be robust with respect to chain length and sequence space. We find that $S_{\text{res}}^{\text{MIE}}$, which scales at $\sim 1.4$ kcal/mol/res, captures the most significant entropic contributions from pairwise dihedral correlations along the oligoglycine backbone.

Disorder-to-order transitions, commonly observed in short IDRs on the order of $\sim 10$ amino acids that bind target proteins, necessitate a significant loss of conformational entropy (or gain of free energy). We estimate the loss of conformational entropy $\left(\mathit{\Delta }S\right)$ from the absolute conformational entropy scaling profiles in Fig. 2. The MIE estimates yield $T\mathit{\Delta }S=1.16$–1.42 kcal/mol/res at 300 K, which is consistent with the loss of entropy upon folding of well-structured proteins reported from a number of different experimental and computational studies (67, 72, 73). The ensemble confinement free energies, ${\langle \mathit{\Delta }A\rangle }^{\text{res}}$ and ${\langle \mathit{\Delta }A\rangle }^{\text{oligo}}$, which implicitly account for intrachain and chain-solvent enthalpic interactions, also scale linearly with chain length with slopes of 0.94 and 0.99 kcal/mol/res, respectively. Although of similar magnitude, these slopes are slightly less than those based on the absolute backbone entropy because, by definition, each conformational state retains internal entropy. From an analysis of 103 polypeptide-protein complexes, London et al. (74) found that polypeptide-protein interfaces use significantly more main-chain/main-chain hydrogen bonds than larger protein-protein interfaces. The protein backbone appears equipped to provide, at least partially, compensating enthalpic interactions to promote folding upon binding or recognition.

Conversely, order-to-disorder transitions, which occur in response to allosteric effector binding and environmental changes (13, 16, 17, 23), permit the protein backbone access to the disordered ensemble with a concomitant, substantial increase in conformational entropy ($-{\langle \mathit{\Delta }A\rangle }^{\text{oligo}}\approx -14$ kcal/mol for ${\text{Gly}}_{15}$) and change in functional state. The entropic expansion of conformation space resulting from local protein unfolding has been proposed as a general allosteric mechanism (10, 15, 16, 75) and a possible mode of targeting IDRs with small molecules (76). Lastly, protein/ligand binding and changes in cellular environment can remodel the disordered structural ensemble of an IDR (10) (e.g., extended versus collapsed disorder). We found that the conformational entropy of ${\text{Gly}}_{15}$ is largely independent of end-to-end distance and radius of gyration, suggesting that backbone conformational entropy does not oppose ensemble remodeling—a property that may be necessary for certain types of disorder-mediated allostery.

IDRs as entropic reservoirs

Wand and co-workers proposed that the residual conformational entropy of proteins provides an entropic reservoir that may be energetically coupled to ligand binding (32, 77). Evidence continues to mount that supports this idea (29, 30, 31, 32, 77). Changes in conformational entropy primarily attributed to changes in side-chain dynamics or fluctuations have been shown to promote or suppress the binding of structured proteins to their targets. The ability of zinc to allosterically inhibit homodimeric CzrA (chromosomal zinc-regulated repressor) binding to DNA is a particularly interesting example (30). Upon binding DNA, there is an increase in side-chain motion in CzrA that was estimated to be a significant contribution to the total favorable change in entropy. When bound, zinc appears to prevent this favorable change in entropy by preventing an increase in side-chain dynamics when binding to DNA, thus decreasing CzrA:DNA binding affinity.

In well-structured proteins, the protein backbone may not have the structural plasticity or capacity to alter its dynamics to the extent observed for side chains (31, 77). That is, in well-structured proteins, side chains may represent an entropic (energetic) reservoir. Analogously, extending this concept to IDRs, we may consider the protein backbone as an entropic reservoir from which free energy may be extracted or deposited through IDR order-disorder transitions that alter the backbone conformational entropy.

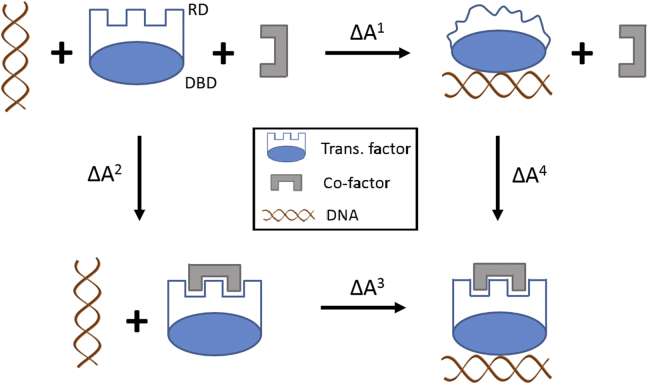
To illustrate, we consider an idealized, disorder-mediated model of allostery (Fig. 6) that parallels the zinc-binding negative regulation of CzrA discussed above. In this example, a transcription factor (TF) composed of a DNA-binding domain and a regulatory domain (RD) binds to DNA, resulting in an order-to-disorder transition in the RD. The entropic expansion associated with the unfolding of RD contributes favorably to binding $\left(\mathit{\Delta }{A}^1\right)$. A cofactor (CF) can decrease the affinity of the transcription factor for DNA (i.e., $\mathit{\Delta \Delta }A=\mathit{\Delta }{A}^3-\mathit{\Delta }{A}^1=\mathit{\Delta }{A}^4-\mathit{\Delta }{A}^2>0$) either by binding to and stabilizing the RD $\left(\mathit{\Delta }{A}^2\right)$, thus preventing the entropically favorable structural transition of RD, or by destabilizing the TF:DNA complex by reducing the conformational entropy of RD $\left(\mathit{\Delta }{A}^4\right)$. In either case, the increase in the free energy or chemical potential of the CF:TF:DNA complex shifts the equilibrium to favor the state in which the transcription factor is not bound to DNA (Fig. 6, bottom left) in a manner dependent on the concentration of CF. Taking ${\text{Gly}}_{15}$ as a model for RD, we can approximate a bound on the decrease in the affinity across the possible confined states of ${\text{Gly}}_{15}$, as $0<\mathit{\Delta \Delta }A<{\langle A\rangle }^{\text{oligo}}=T{S}_{\text{oligo}}^{\text{state}}\approx -14$ kcal/mol (Eq. 15). Although we have clearly neglected a number of (compensatory) thermodynamic contributions needed for a more physically representative model, our goal with this example is to illustrate the concept of the protein backbone as a free-energy reservoir and the potentially significant energetic/entropic contribution of IDR order-disorder transitions to binding.

Figure 6.

Thermodynamic cycle of an idealized transcription factor composed of a DNA-binding domain and regulatory domain (RD), exhibiting disorder-mediated, negative allostery. Upon binding DNA, the RD undergoes an order-to-disorder transition that entropically promotes binding. A cofactor may bind to the RD and prevent the favorable increase in conformational entropy (bottom right), thus decreasing the binding affinity of the transcription factor for its target DNA sequence. To see this figure in color, go online.

Conclusions

In this article, our goal is to illustrate that the conformational entropy of the protein backbone represents a significant source of free energy that proteins may exploit through conformational transitions of IDRs as a means to regulate protein binding and, ultimately, function. We believe that our oligoglycine model provides an upper bound on the amount of conformational entropy potentially gained or lost as free energy when folding or unfolding of IDRs is coupled to binding. Lastly, we note that the development of force fields for simulations of intrinsically disordered proteins is an active field, as such systems continue to challenge the accuracy of existing force fields (78). Previously, we found that the solvation thermodynamics of ${\text{Gly}}_{2-5}$ calculated from simulations with the CHARMM (Chemistry at Harvard Macromolecular Mechanics) 36 (79) and Amber ff12SB (60) force fields were very consistent (62) despite the two generating markedly different structural ensembles. In the future, we plan to investigate whether the conformational entropy estimates studied in this article are similarly insensitive to differences or perturbations in the structural ensemble of the same disordered polypeptide model.

Author Contributions

J.A.D. performed all calculations and wrote the initial manuscript draft. Both authors conceptualized and planned the project and worked on the analysis of the results and the final manuscript.

Editor: Alemayehu Gorfe.