The Effects of Statistical Multiplicity of Infection on Virus Quantification and Infectivity Assays

Abstract

Many biological assays are employed in virology to quantify parameters of interest. Two such classes of assays, virus quantification assays (VQAs) and infectivity assays (IAs), aim to estimate the number of viruses present in a solution and the ability of a viral strain to successfully infect a host cell, respectively. VQAs operate at extremely dilute concentrations, and results can be subject to stochastic variability in virus-cell interactions. At the other extreme, high viral-particle concentrations are used in IAs, resulting in large numbers of viruses infecting each cell, enough for measurable change in total transcription activity. Furthermore, host cells can be infected at any concentration regime by multiple particles, resulting in a statistical multiplicity of infection and yielding potentially significant variability in the assay signal and parameter estimates. We develop probabilistic models for statistical multiplicity of infection at low and high viral-particle-concentration limits and apply them to the plaque (VQA), endpoint dilution (VQA), and luciferase reporter (IA) assays. A web-based tool implementing our models and analysis is also developed and presented. We test our proposed new methods for inferring experimental parameters from data using numerical simulations and show improvement on existing procedures in all limits.

Introduction

Understanding viral dynamics is an important task in medicine, epidemiology, public health, and, in particular, for the development of antiviral therapies and vaccines. Drugs that hinder viral infection include blockers of viral entry into the host cell (1, 2, 3, 4, 5, 6) and inhibitors of genetic activity and protein assembly inside the cytoplasm and nucleus (7, 8, 9). Mechanistic models of drug action have recently emerged as useful tools in helping design ad hoc experiments to study drug efficacy and in interpreting results (10, 11, 12, 13). Mathematical models typically assume prior knowledge of given physical quantities pertaining to the virus, host cell, or the biological assay being studied. Once these parameters are assigned, viral and cell population dynamics and their statistical properties can be predicted. Among the different experimental assays, one often seeks to evaluate the number of virus particles in a stock solution or the number of viruses that have successfully infected host cells (6, 14, 15, 16, 17, 18, 19).

In the case of virus quantification assays (VQAs), performing repeated controlled experiments on viral dynamics or comparing results across multiple studies requires knowing how many viruses are present in the initial stock solution of each experiment (4, 5). Furthermore, antigens that induce immune responses against viral infections may be engineered from viral components such as capsid proteins, viral enzymes, and genetic vectors (20) and may be used in the development of vaccines. Being able to determine the exact number of virus-derived antigens helps control the efficacy of vaccines and optimize yield (21, 22, 23).

Given the central role of VQAs, several assays have been designed to estimate viral particle counts. These include plaque (24) and endpoint dilution (23, 25) assays, which will be discussed in more detail in the remainder of this work. For now, we note that these assays involve repeatedly diluting an initial solution of virus particles in the presence of a layer of plated cells until viral concentrations are low enough that the dynamics of an individual virus can be extrapolated. At these low particle counts, however, the discrete nature of the infection process cannot be neglected and can cause substantial discrepancies when replicating experiments. Average quantities are not necessarily representative, and a more in-depth approach in quantifying virus-cell interactions is necessary.

Infectivity assays (IAs), on the other hand, aim to quantify the number of viruses that have successfully infected host cells under varying antiviral drug environments (14, 15, 16). IAs may measure the total transcription activity across all cells, such as the luciferase reporter assay (15, 26), or may count the number of host cells that were successfully infected, such as the enzyme-linked immunosorbent assay and the immunofluorescence assay with fluorescence-activated cell sorting (4, 14, 15, 18). These assays are performed using undiluted solutions with large numbers of viral particles, reducing stochastic variability. The average number of viruses that infect a cell is estimated as the ratio of the number of viruses in solution to the number of plated cells, a quantity known as the multiplicity of infection (MOI) (19). However, each cell may be infected by different numbers of viruses distributed around the average given by the MOI. In these cases, one may be interested in the complete probability distribution for the number of virus infections in each plated cell and in the related statistical variance.

In this work, we derive a probability model for the distribution of viral infections per host cell, which we call the statistical multiplicity of infection (SMOI). The SMOI can be used as a starting point to help estimate the number of viral particles in solution in VQAs and to determine a viral strain’s ability to successfully infect host cells in IAs. In Probabilistic Models of Statistical Multiplicity of Infection, we present the mathematical foundations for the SMOI in the two experimentally relevant parameter regimes of small and large viral particle counts and derive a probability model for the total number of infected cells under any dilution level. In Plaque Assay, we apply our models to the plaque assay and, to our knowledge, formulate a new method of analyzing plaque count data. In Endpoint Dilution Assay, we employ a special case of the derived probability distribution to the endpoint dilution assays and compare our results to those arising from traditional titration techniques such as the Reed and Muench (RM) (27) and Spearman-Karber (SK) methods (28). In Luciferase Reporter Assay, we use the large particle limit of our model to describe the luciferase reporter assay. Lastly, a discussion of our results, a side-by-side comparison with existing methods, and a link to web-based data analysis tools are provided in Conclusions. Mathematical appendices and further discussion of experimental attributes such as cell-size variability, coinfection, viral interference, and optimal experimental design using parameter-sensitivity analysis are presented in the Supporting Materials and Methods.

Methods

Probabilistic models of statistical multiplicity of infection

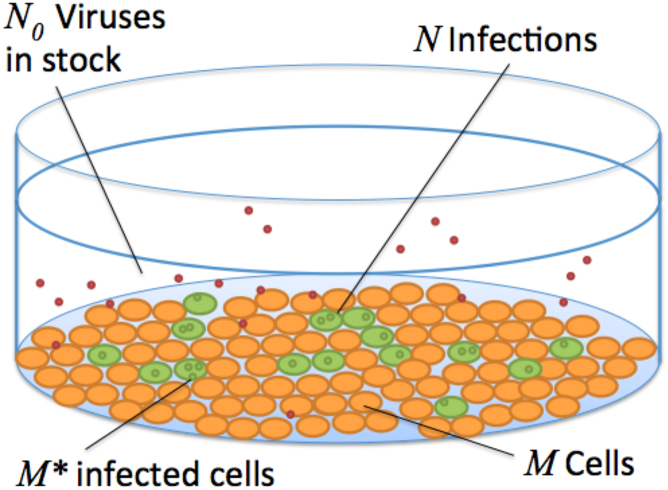
A typical viral assay is initiated by laying a monolayer of M cells on the bottom of a microtiter well, as illustrated in Fig. 1 (17, 24, 25). Although variability exists among experiments, M is often set within the range of 10⁴–10⁵ (14, 26) and is assumed to be a known experimental parameter. A supernatant containing N₀ virus particles in the range of 10⁵–10⁷ (24, 25, 26) is then added to the microtiter well. Although, theoretically, all N₀ particles are capable of infection, not all will successfully infect a cell. Because infection of a host cell requires a complex sequence of biochemical processes that may include receptor binding, membrane fusion, reverse transcription, nuclear pore transport, and DNA integration (10, 19), virus particles that fail at one or several of these sequential steps lead to abortive infections. To differentiate, the particles that do succeed are called infectious units (IU) or plaque-forming units (PFU). We will denote the number of IUs as N ≤ N₀. Depending on the strain of virus, the particular experimental protocol used, and specific conditions of the assay, the random quantity N is distributed according to N₀ and the overall effective probability that an arbitrary viral particle successfully infects a host cell. A proxy that is typically used in place of this effective probability is the “particle to PFU ratio” Q, an experimentally determined parameter that quantifies, on average, the minimal number of particles required to ensure at least one infected cell (29, 30). Q is often treated as an a priori measured quantity, primarily associated with the particular strain of virus being studied. Low values of Q, such as with poliovirus (Q = 30) (30), have a high likelihood of successful infection compared to viruses with large Q, such as human immunodeficiency virus type 1 (HIV-1) (Q = 10⁷) (31). Thus, the reciprocal Q⁻¹ can be interpreted as the probability for a single virus to infect a host cell. Assuming an initial stock of N₀ particles, the discrete probability density function of N is

$$\text{Pr}\left(N=n|N_0,Q\right)=\left(\frac{N_0}{n}\right){\left(Q^{-1}\right)}^n{\left(1-Q^{-1}\right)}^{N_0-n},$$ (1)

which defines a binomial distribution with parameters N₀ and Q⁻¹. Although we assume Q to be a priori known, in actuality, the probability of a virus successfully infecting a host is highly dependent on the methods used to harvest the virus stock, the experimental parameters of the assay, the host receptor concentrations and binding rates, and the dynamics of the physiological processes leading to infection (29, 32). A thorough investigation into these processes would be necessary to mechanistically model Q and is outside of the scope of this work. However, we will discuss in Conclusions how, with direct measurements of certain other parameters, especially N₀, our derived methods may also be used to infer Q.

Figure 1.

A typical assay includes a plate of M host cells inoculated with a solution of N₀ viruses. Each viral particle has some probability of infection, and the total number N of infections are distributed to the M^∗ infected cells. The probability of infection is roughly estimated with the reciprocal of the a priori measured particle to PFU ratio Q. To see this figure in color, go online.

We assume each viral particle in solution acts independently of others and that host cell infection attempts are random events. At high ratios N₀/M of particles to cells, a quantity referred to as the MOI, it becomes increasingly probable for more than one IU to infect the same host cell. We define M₀ as the count of cells not infected by any IU, M₁ as the count of cells infected by exactly one IU, and so on, up to M_N, the number of cells infected by all N IUs. The SMOI is defined as the ensemble of cell counts $\left\{M_0,M_1,\cdots ,M_N\right\}$. Note that two constraints must hold: ${\sum }_{r=0}^N{M}_r=M$ to account for all infected and uninfected cells and ${\sum }_{r=0}^{N}r{M}_r=N$ for conservation of the total number of IUs. If we assume all M cells are of identical size and volume, they carry equal probability of being infected by a particular virus. Thus, evaluating the probability distribution that M_r takes on the value m_r reduces to the well-known occupancy problem of randomly placing balls into identical urns (33), and we derive

$$\text{Pr}\left(M_r=m_r|M,N\right)=\sum _{j=m_r}^M\left(\begin{array}{c}j\\ m_r\end{array}\right)\left(\begin{array}{c}M\\ j\end{array}\right)\left(\begin{array}{c}N\\ r,\cdots ,r,\left(N-rj\right)\end{array}\right)\frac{{\left(-1\right)}^{j-m_r}{\left(M-j\right)}^{N-rj}}{M^N},$$ (2)

where the r term is repeated j times in the lower argument of the multinomial coefficient. The derivation of Eq. 2 is detailed in Appendix A in the Supporting Materials and Methods, and an investigation into the effects of inhomogeneous cell sizes is presented in Appendix B. Furthermore, in Appendix A, we derive the expected value and variance of M_r as

$$\text{E}\left[M_r\right]=M\left(\begin{array}{c}N\\ r\end{array}\right){\left(\frac{1}{M}\right)}^r{\left(1-\frac{1}{M}\right)}^{N-r}$$ (3)

and

$$\text{Var}\left[M_r\right]=M\left(\begin{array}{c}N\\ r\end{array}\right){\left(\frac{1}{M}\right)}^r{\left(1-\frac{1}{M}\right)}^{N-r}+\frac{M\left(M-1\right)N!{\left(M-2\right)}^{N-2r}}{{\left(r!\right)}^2\left(N-2r\right)!M^N}-\frac{M^2{\left(N!\right)}^2{\left(M-1\right)}^{2N-2r}}{{\left(r!\right)}^2{\left[\left(N-r\right)!\right]}^2{M}^{2N}}.$$ (4)

Note that the variance is equal to the expected value with two additional correction terms that cancel each other as N and M increase, indicating the probability distribution of M_r is Poisson-like for large N and M. A plot of a representative probability distribution and a test of agreement between our analytical result and numerical simulation is provided in Fig. 2.

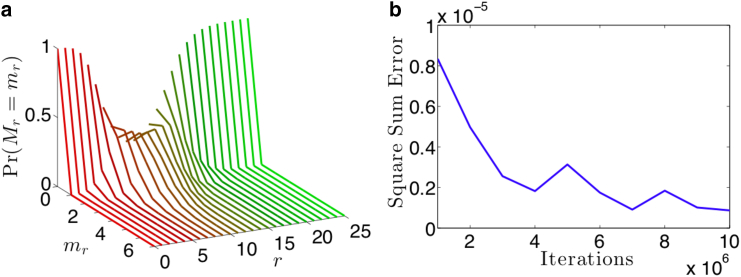
Figure 2.

(a) A collection of curves of the probability of finding m_r cells that have been infected by exactly r IUs, given a total number of IUs N = 100 and a total number of cells M = 10, using Eq. 2. With N/M = 10, we expect very few cells to be uninfected, resulting in the probability distribution concentrated close to 0 for low values of r. Similarly, we expect few cells to be infected by a very large number of IUs, accumulating the probability distribution close to 0 for large r. Only at intermediate values of $r\approx N/M=10$ do we observe a Poisson-like distribution. (b) We perform a numerical study to show empirically that our analytical result in Eq. 2 matches the statistical frequency of virus cell counts from a simulation of N = 100 IUs being randomly assigned to M = 10 cells. The square sum error between the simulated proportions and the analytical result was calculated with increasing numbers of iterations of the simulation. For iterations around 10⁶, our square sum error is on the order of 10⁻⁶, indicating strong agreement between our model and simulation. To see this figure in color, go online.

We also derive the joint probability $\text{Pr}\left(M_0=m_0,\cdots ,M_N=m_N|M,N\right)$ that the SMOI $\left\{M_0,M_1,\cdots ,M_N\right\}$ takes on the set of values $\left\{m_0,m_1,\cdots ,m_N\right\}$ as

$$\begin{array}{c}\text{Pr}\left(M_0=m_0,\cdots ,M_N=m_N|M,N\right)=\frac{1}{M^N}\left(\begin{array}{c}M\\ m_0,m_1,\cdots ,m_N\end{array}\right)\left(\begin{array}{c}N\\ 0,\cdots ,\mathrm{0,1},\cdots ,1,\cdots ,N,\cdots ,N\end{array}\right)\\ =\frac{M!N!}{M^N}\prod _{r=0}^N\frac{1}{m_r!{\left(r!\right)}^{m_r}}.\end{array}$$ (5)

The first and second multinomial expressions enumerate the degeneracy of how the M identical cells are distributed across the configuration $\left\{m_0,\cdots ,m_N\right\}$ and how the N identical IUs are chosen for those cells, respectively. Although the second expression in Eq. 5 is more succinct, it must be explicitly conditioned on the constraints ${\sum }_{r=0}^N{m}_r=M$ and ${\sum }_{r=0}^{N}r{m}_r=N$.

The expressions in Eqs. 2 and 5 provide an exact discrete description of the stochasticity of the MOI but are computationally expensive to evaluate for large values of N and M. In a typical virology experiment, the number of viral particles N₀ and host cells M are large enough for certain asymptotic methods to be applicable. Furthermore, for intermediate values of Q and based on Eq. 1, the expected number of IUs N would be similarly large. We can thus take the mathematical limit $N,M\to \infty$ while keeping the ratio $\mu =N/M$ fixed and approximate Eq. 2 as

$$\text{Pr}\left(M_r=m_r|M,N\right)\approx \frac{1}{m_r!}{\left[\frac{M{\mu }^r{e}^{-\mu }}{r!}\right]}^{m_r}\text{exp}\left[-\frac{M{\mu }^r{e}^{-\mu }}{r!}\right].$$ (6)

Equation 6 implies that M_r is Poisson-distributed, with mean and variance

$$\text{E}\left[M_r\right]=\text{Var}\left[M_r\right]\approx \frac{M{\mu }^r{e}^{-\mu }}{r!}.$$ (7)

A mathematical justification of Eq. 6 is given in Appendix A, and comparisons of Eq. 6 and the analytical result in Eq. 2 to simulations are shown in Fig. 3.

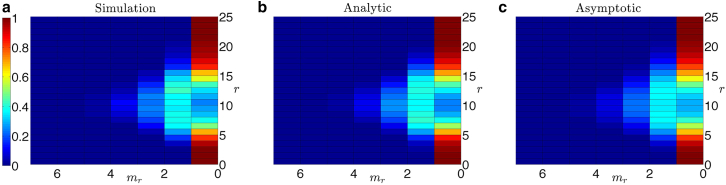
Figure 3.

Heat maps of the probability distribution Pr(M_r = m_r | M,N) of finding m_r cells that have been infected by exactly r IUs given a total number of viruses N = 100 and M = 10 cells. (a) The statistical frequency of virus cell counts after simulating IUs randomly distributing to the M cells is shown, averaged over 1000 iterations. (b) The analytical result obtained from Eq. 2 is shown. (c) The asymptotic approximation with M = 10 and $\mu =\left(N/M\right)=10$ is shown, using the expression in Eq. 6. There is close agreement between the simulated and analytical results. The relatively low values of M and N make the asymptotic formula in Eq. 6 inappropriate for this parameter regime, explaining the discrepancy between the asymptotic result and the exact analytical result. However, it is noteworthy how qualitatively small that deviation is, which will continue to vanish as M and N increase in value. To see this figure in color, go online.

Under the same large M,N limit and using Eq. 6, we show in Appendix A

$$\text{Pr}\left(M_0=m_0,\cdots ,M_N=m_N|M,N\right)\approx \prod _{r=0}^N\text{Pr}\left(M_r=m_r|M,N\right),$$ (8)

which implies that as $M,N\to \infty$, the random variables $M_0$,$\cdots$, $M_N$ are independently distributed. In the next section, we will apply results of our probability model of SMOI to the case of a repeatedly diluted solution of virus particles, a procedure used in many VQAs.

Serial dilution

Low viral-particle concentrations in assays are typically obtained via serial dilution processes to increase the sensitivity to individual viral infections (4, 24, 25). The initial viral stock containing N₀ particles is diluted by a fixed factor of D, and the process is repeated d_max times. At each dilution number d, an assay can be performed to determine if the concentration of virus particles in the diluted solution is sufficient to generate a qualitative signal of infection, known as a “cytopathic effect” (CE). For example, the diluted stock can be administered in vivo to a model organism such as a mouse. The mouse’s death would indicate that at least one lethal unit of the virus was present at that dilution level. Alternatively, an in vitro assay can be carried out to measure a signal that, for example, quantifies the exact number of plated cells that were successfully infected. To model these assays, we first define M^∗ as the number of host cells infected by at least one IU and that are capable of producing new viruses. In Appendix A we derive the discrete probability density function for finding M^∗ = m infected cells at a given dilution number d and find

$$\text{Pr}\left(M^{\ast }=m\right)=\left(\begin{array}{c}M\\ m\end{array}\right){\left[1-\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)\right]}^m\text{exp}{\left(-\frac{N_0}{QM{D}^d}\right)}^{M-m}.$$ (9)

Equation 9 shows that the number of infected cells M^∗ is binomially distributed with expected value

$$\text{E}\left[M^{\ast }\right]=M\left[1-\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)\right]$$ (10)

and variance

$$\text{Var}\left[M^{\ast }\right]=M\left[1-\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)\right]\text{exp}\left(-\frac{N_0}{QM{D}^d}\right).$$ (11)

We can define the probability of observing a CE at dilution number d as the probability of finding one or more infected cells:

$$\begin{array}{c}\text{Pr}\left(\text{“}\text{Cytopathic}\text{effect}\text{”}\right)\equiv \sum _{m=1}^M\text{Pr}\left(M^{\ast }=m\right)\\ =1-\text{exp}\left(-\frac{N_0}{Q{D}^d}\right).\end{array}$$ (12)

The definition we use in Eq. 12 assumes an in vitro assay that can exhibit a cytopathic signal after a single cell infection or more. For in vivo assays, the probability that m infected cells are sufficient for a CE will depend on many complex physiological factors such as immune pressure, in-host viral evolution, and virion burst size (34). A plot of how the initial particle count N₀ and dilution factor D effect the characteristic functional form of Eq. 12 is shown in Fig. 4. Although both Eqs. 9 and 12 assume each IU contains all viral genes required for in-host replication, an extended probability model that factors in genetic mutation and degradation is provided in Appendix C. Furthermore, for the case of retroviruses, infectious processes inside the host cytoplasm may be suppressed by previous infections, known as viral interference, and is explored in Appendix D. In Plaque Assay, we will use Eq. 9 to analyze the plaque assay. Equation 12 will be used for “binary” assays that are only concerned with the presence or absence of a CE, such as the endpoint dilution assay, which we will explore in Endpoint Dilution Assay.

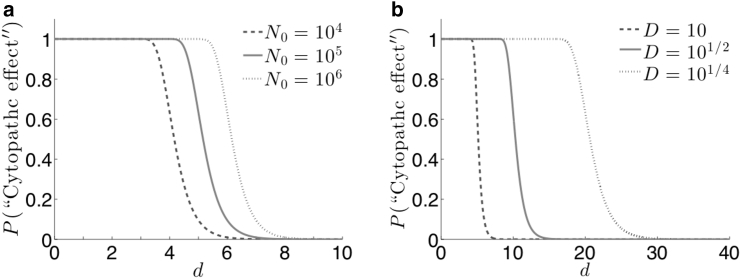
Figure 4.

The probability of observing a cytopathic effect (CE) given in Eq. 12 as a function of the dilution number d and with Q = 1. (a) For D = 10, as the initial particle count N₀ increases, the critical dilution moves toward higher d. (b) Common dilution factors include logarithmic dilution (D = 10), half-logarithmic dilution (D = 10^1/2), and quarter-logarithmic dilution (D = 10^1/4). Logarithmic dilution requires a lower number of dilutions to cause the characteristic decrease in probability, requiring less individual assays to perform. Quarter-logarithmic dilution, though requiring more dilutions, has a slower transition from high to low probability across d, making the assay less sensitive to experimental error or noise. The plot above can be used to quantify the tradeoffs between the choices of D.

Results and Discussion

Plaque assay

The plaque assay is an example of a VQA in which the objective is to infer the total number of viruses N₀ present in a solution, assuming the PFU to particle ratio Q has been independently measured and estimated (24, 25, 35). After d serial dilutions, the viral stock is added to a monolayer of M cells, and a layer of agar gel is added to the well to inhibit the diffusion of virus particles in the plate. If a virus successfully infects a host cell, the agar will limit the range of new infections to the most adjacent cells. Viral infection thus spreads out radially from the initial nucleation infection and forms a visible discoloration in the plate called a “plaque.” For high particle concentrations, the number of plaques formed may be large enough to cover the entire plate surface. After a sufficient critical dilution number d_c, however, the number of plaques formed are low enough to be visibly distinct and countable. For each dilution number d, the assay can be performed for T number of trials. The “signal” data arising from the plaque assay P_d,t is defined as the number of visible plaques counted, where $t=1,\cdots ,T$ is the trial number. The standard method of obtaining an estimate ${\hat{N}}_0$ of the true particle count N₀ is to apply the sample mean of the data $P_{d_c,t}$ at the critical dilution level d_c to the formula

$${\hat{N}}_0=D^{d_c}\left(\frac{1}{T}\sum _{t=1}^T{P}_{d_c,t}\right),$$ (13)

which posits that the average number of plaques is directly proportional to the particle count N₀. Equation 13 assumes that each infected cell corresponds to one IU, which is not necessarily true in the context of SMOI. Furthermore, although data corresponding to dilution numbers d < d_c are unusable, data for d > d_c corresponding to countable plaques are not used at all in Eq. 13.

To improve on Eq. 13 by using the entire set of plaque counts P_d,t for our estimate of N₀, we propose a maximal likelihood estimation (MLE) scheme. Using the mathematical models derived above, we can construct an expression $\mathcal{L}\left(P_{d,t}|N_0\right)$ of the probability that the observed data P_d,t can be generated assuming a particular value for N₀, known as a likelihood function. A value for N₀ that maximizes $\mathcal{L}\left(P_{d,t}|N_0\right)$ corresponds to the most probable estimate ${\hat{N}}_0$ that could have generated the data. As each nucleation of a plaque corresponds to a distinct infected cell (and assuming that overlapping lesions of necrotic cells are still discernible as distinct plaques), we can equate P_d,t to the total number of successfully infected cells M^∗. We will ignore the dynamics of coinfection and viral interference. Using Eq. 9, we propose the following likelihood function of the data given N₀:

$$\mathcal{L}\left(P_{d,t}|N_0\right)=\mathit{\prod }_{d=d_c}^{d_{\text{max}}}\mathit{\prod }_{t=1}^T\left(\begin{array}{c}M\\ P_{d,t}\end{array}\right){\left[1-\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)\right]}^{P_{d,t}}\text{exp}{\left(-\frac{N_0}{QM{D}^d}\right)}^{M-P_{d,t}}.$$ (14)

To obtain the MLE ${\hat{N}}_0$, we take the derivative of the natural log of Eq. 14 with respect to N₀ and set the result to zero to obtain

$$0=\sum _{d=d_c}^{d_{\text{max}}}\sum _{t=1}^T\frac{M\text{exp}\left(-\frac{{\hat{N}}_0}{QM{D}^d}\right)-M+P_{d,t}}{QM{D}^d\left[1-\text{exp}\left(-\frac{{\hat{N}}_0}{QM{D}^d}\right)\right]}.$$ (15)

We can solve Eq. 15 for ${\hat{N}}_0$ using numerical methods such as Newton-Raphson (36), an iterative scheme that approaches the solution of an equation asymptotically starting from an initial guess ${\hat{N}}_0^{\text{init}}$. To increase the stability of convergence to the solution, we choose ${\hat{N}}_0^{\text{init}}$ by equating the sample average of plaque counts $\left(1/T\right)\sum P_{d_c,t}$ with the expected number of infected cells E[M^∗] in Eq. 10 at the critical dilution d_c to derive

$${\hat{N}}_0^{\text{init}}=-QM{D}^{d_c}\text{ln}\left[1-\frac{1}{M}\left(\frac{1}{T}\sum _{t=1}^T{P}_{d_c,t}\right)\right].$$ (16)

An example of raw plaque-count data and the resulting estimates for N₀ are given in Fig. 5. To quantify the relative improvement of the MLE of N₀ over the standard method in Eq. 13, we simulate plaque assay data assuming a fixed, known N₀ value. In our simulation, we use the models established in Probabilistic Models of Statistical Multiplicity of Infection to sample the N₀ particles according to Eq. S9 in Appendix A to account for serial dilution and sample again the resulting particles according to Eq. 1 to obtain the number of IUs N. The IUs are distributed randomly to the M cells with equal probability, and the resulting number of infected cells M^∗ is recorded. Because plates of cells with too many infections render the number of plaques uncountable, a “countable plaque threshold” renders the data unusable when the number of infected cells exceed the threshold. Thus, the resulting plaque data P_d,t for a given dilution d and trial t is assigned the number of simulated infected cells if the latter is less than the given threshold. A scatter plot of the data P_d,t of one such simulation is shown in Fig. 6 a, and the corresponding likelihood function from Eq. 14 is plotted in Fig. 6 b. Because the MLE method utilizes a full probabilistic model of the plaque count distribution instead of relying only on the expected value at the single critical dilution d_c, it produces an estimate consistently closer to the original N₀ that generated the data. To better quantify this property, in Appendix E, we derive an asymptotic approximation of the variance of ${\hat{N}}_0$ as

$$\text{Var}\left[{\hat{N}}_0\right]\approx {\left[\sum _{d=d_{\text{c}}}^{d_{\text{max}}}\frac{T\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)}{Q^{2}M{D}^{2d}\left[1-\text{exp}\left(-\frac{N_0}{QM{D}^d}\right)\right]}\right]}^{-1}.$$ (17)

Figure 5.

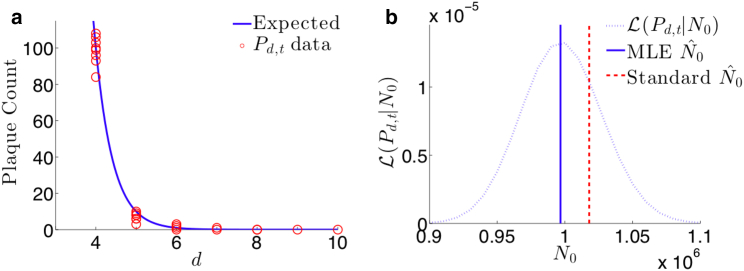
An example of raw plaque count data taken from Sloutskin et al. (35). A viral solution was assayed in a plate of M = 3 × 10⁵ cells at dilution numbers d = 2, 3, 4, 5, 6, and 7 at a dilution factor of D = 10. The particle to PFU ratio is assumed to be Q = 1. For T = 3 separate trials, the number of plaques were counted at each dilution level. The bottom row of plates used as a control is ignored. For dilution numbers d = 2 and 3, the entire plate of cells shows cytotoxicity so that the numbers of plaques were undiscernible and, thus, the countable data starts at d_c = 4. For the old method featured in Eq. 13, the estimate for N₀ is ${\hat{N}}_0=1.19\times {10}^6$, and for the MLE derived from Eq. 15, ${\hat{N}}_0=1.26\times {10}^6$. This results in a relative difference of 5.5%. Furthermore, when applying these parameters and the ${\hat{N}}_0$ estimate to Eq. 17, we observe a 10.7% decrease in the estimate variation using the MLE technique. To see this figure in color, go online.

Figure 6.

Results of plaque assay simulation for parameters N₀ = 10⁶, M = 10⁵, Q = 1, D = 10, d_max = 10, and T = 10. (a) The scatter plot of simulated data P_d,t (circles) and the expected value of plaque counts as given by Eq. 10 show close agreement. (b) The likelihood function $\mathcal{L}\left(P_{d,t}|N_0\right)$ with respect to N₀ using the same simulated data. The MLE obtained by iteratively solving Eq. 15 is ${\hat{N}}_0=9.97\times {10}^5$ and is relatively closer to the true value of N₀ than the estimate calculated from the standard method in Eq. 13, ${\hat{N}}_0=1.02\times {10}^6$. To see this figure in color, go online.

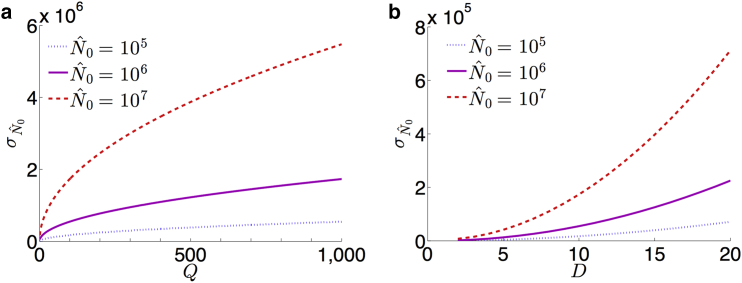
The variance is an explicit function of Q, which is assumed to be a priori known. If there is uncertainty in the value of Q, Eq. 17 can quantify how sensitive the distribution of ${\hat{N}}_0$ is to variation in Q, as shown in Fig. 7 a. We can see that for small assumed Q, such as in poliovirus (30), error in this measurement can cause a large relative change in the accuracy of ${\hat{N}}_0$. This type of sensitivity analysis on estimation variance can be done with any experimental parameter included in the likelihood function in Eq. 14. Furthermore, for directly controllable parameters, such as the serial dilution factor D, Eq. 17 can provide insight into optimizing the assay protocol, as shown in Fig. 7 b. Although it is evident that small D would increase the accuracy of the ${\hat{N}}_0$ estimate, doing so requires more serial dilutions, which increases the time and expense of the assay. Thus, our sensitivity analysis provides a quantitative method for making experimental design choices between minimizing uncertainty versus the cost of an assay protocol. Lastly, if we compute the variance of the standard method in Eq. 13 due to the known variance in the data P_d,t and compare with Eq. 17, we find, when using realistic parameter values from Fig. 5, the standard method results in a 10.7% higher variance than that of our method. Although the significance of the relative increase in precision of estimating N₀ found using our method is highly dependent on the context of the experimental study for which the assay was performed, similar sensitivity analysis can be used to determine such tolerances.

Figure 7.

Approximations of the standard deviation ${\sigma }_{{\hat{N}}_0}=\text{Var}{\left[{\hat{N}}_0\right]}^{1/2}$ of MLEs for the plaque assay using Eq. 17 and parameters ${\hat{N}}_0={10}^5$, 10⁶, and 10⁷, M = 3 × 10⁵, d_c = 4, d_max = 7, and T = 3, corresponding to the assay displayed in Fig. 5. (a) For D = 10, the standard deviation increases proportional to the square root of Q. (b) For Q = 1, we can see a low dilution factor D will increase the accuracy of the estimate ${\hat{N}}_0$. To see this figure in color, go online.

Endpoint dilution assay

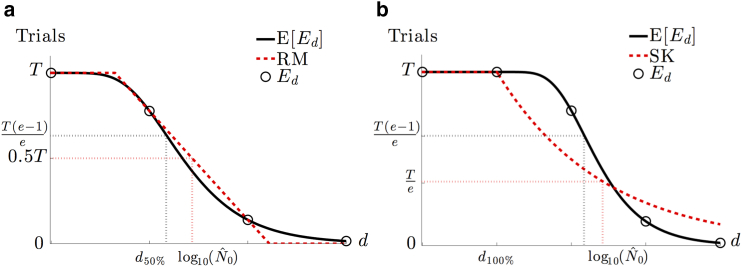
Another widely used assay for quantifying the initial viral particle count N₀ is the endpoint dilution or endpoint titration assay (23, 25, 37). It is often used in place of the plaque assay, as it can be more rapidly performed and is useful for viral strains that are unable to form plaques. Here, serial dilutions at a factor of D are employed, and at every dilution number d, an assay is performed T times to test for a successful CE. The number E_d of observed CEs among the T trials at a given dilution number d is recorded as the signal. For low dilution, we expect many cells to be infected, and the probability of observing a CE, as shown in Eq. 12, is close to 1. If every trial of the assay is likely to display a CE, then E_d is expected to be close to T. However, at high dilution, the probability in Eq. 12 rapidly decreases to 0, as shown in Fig. 4, and E_d will be similarly small. For a large initial stock of viral particles N₀, a larger dilution number d is needed to ensure the dramatic change in probability in Eq. 12. Thus, the critical dilution at which E_d most rapidly decreases from T can be used to estimate the particle count N₀. This occurs at the point of inflection when d = log_D(N₀Q⁻¹) and corresponds to when the expected number of successful trials E[E_d] = T (1 − e⁻¹), as shown in Fig. 8.

Figure 8.

An illustration of the consistent overestimation of the Reed and Muench (RM) and Spearman-Karber (SK) methods using the expected curve E[E_d] of CEs given T trials as a function of the dilution number d derived from Eq. 12. (a) The RM method approximates the steepest decent of the expectation curve with a line connecting the two data points $E_{d_{50\text{\%}}}\le 0.5T<E_{d_{50\text{\%}}+1}$. Because of the relative convexity of the expected curve, the linear approximation consistently rests above the curve and results in an overestimate of ${\text{log}}_{10}\left({\hat{N}}_0\right)$. (b) From the last dilution $d_{100\text{\%}}$ such that all trials exhibit a CE, the SK method assumes an exponential decay of the expectation. Obtaining the characteristic decay rate of the exponential involves calculating the area under the curve, which is done numerically using the data E_d. However, according to our model, many of the expected values of E_d exist above the exponential, causing the numerical integration to overestimate the area and, thus, decay too slowly. This gradual decrease in the exponential curve results in a larger estimate of ${\text{log}}_{10}\left({\hat{N}}_0\right)$. To see this figure in color, go online.

One commonly used way to estimate N₀ is the RM method, which utilizes the two dilution numbers that capture the greatest change in the data E_d (27). We first define a critical dilution number $d_{50\text{\%}}$ to be the largest dilution such that at least 50% of the trials exhibit a CE. The estimate ${\hat{N}}_0$ for the particle count N₀ is given by

$${\text{log}}_{10}\left({\hat{N}}_0\right)=d_{50\text{\%}}+\frac{E_{d_{50\text{\%}}}-0.5T}{E_{d_{50\text{\%}}}-E_{d_{50\text{\%}}+1}}.$$ (18)

The RM method effectively attempts to approximate the steepest descent of the CE probability given in Eq. 12 with a line connecting the assay data at dilutions $d_{50\text{\%}}$ and $d_{50\text{\%}+1}$, as displayed in Fig. 8 a. Unfortunately, this line always rests above the actual expectation curve of E_d, so any estimate ${\hat{N}}_0$ obtained from this method will overestimate the true N₀. Another commonly used estimation scheme is the SK method, which uses the critical dilution number $d_{100\text{\%}}$, the largest dilution such that 100% of trials exhibit a CE (28, 37). The SK estimate ${\hat{N}}_0$ is given by

$${\text{log}}_{10}\left({\hat{N}}_0\right)=d_{100\text{\%}}-\frac{1}{2}{\text{log}}_{10}\left(D\right)+{\text{log}}_{10}\left(D\right)\sum _{d=d_{100\text{\%}}}^{d_{\text{max}}}\frac{E_d}{T}.$$ (19)

In this method, the downward slope for the expectation of E_d is assumed to follow a decaying exponential starting at dilution $d_{100\text{\%}}$, as shown in Fig. 8 b. The intention is to find the dilution at which Te⁻¹ CEs are expected by calculating the area under the exponential curve, given by the summation term in Eq. 19. However, the actual values of E_d will follow the expected curve from our model, leading to an overestimate of the area and, by extension, a larger value for ${\hat{N}}_0$. Both standard methods were derived from the heuristic observation that E_d exhibits sigmoidal behavior as a function of the dilution number d, but an underlying probabilistic model was missing, resulting in consistent overestimation of the true N₀. Furthermore, neither method uses the “particle to PFU ratio” Q, accounts for the stochasticity of serial diluting viral samples, considers the dynamics of SMOI, or employs the entire set of data E_d.

We present an alternative way to infer N₀, using Eq. 12 to establish an MLE scheme. We restrict ourselves to in vitro assays in which a single infected cell is sufficient to display a CE. Then each cytopathic count is binomially distributed with parameters T and the probability given in Eq. 12. Thus, for a set of data $\left\{E_1,E_2,\cdots ,E_{d_{\text{max}}}\right\}$, we propose the likelihood function

$$\mathcal{L}\left(E_d|N_0\right)=\prod _{d=1}^{d_{\text{max}}}\left(\begin{array}{c}T\\ E_d\end{array}\right){\left[1-\text{exp}\left(-\frac{N_0}{Q{D}^d}\right)\right]}^{E_d}\text{exp}{\left(-\frac{N_0}{Q{D}^d}\right)}^{T-E_d}.$$ (20)

Equation 20 is an expression of the probability of the data $\left\{E_1,\cdots ,E_{d_{\text{max}}}\right\}$ given the current assumed value of N₀. To obtain the best estimate ${\hat{N}}_0$ of N₀, we maximize the likelihood function by taking the log and derivative of $\mathcal{L}\left(E_d|N_0\right)$ with respect to N₀ and set it equal to zero to obtain

$$0=\sum _{d=1}^{d_{\text{max}}}\frac{E_d-T+T\text{exp}\left(-\frac{{\hat{N}}_0}{Q{D}^d}\right)}{Q{D}^d\left[1-\text{exp}\left(-\frac{{\hat{N}}_0}{Q{D}^d}\right)\right]}.$$ (21)

As with Eq. 15, solving Eq. 21 for ${\hat{N}}_0$ requires a numerical method such as Newton-Raphson. As an appropriate initial estimate for ${\hat{N}}_0$, the formula

$${\hat{N}}_0^{\text{init}}=-0.5Q{D}^{d_c}\left[\text{ln}\left(1-\frac{E_{d_c}}{T}\right)+D\text{ln}\left(1-\frac{E_{d_c+1}}{T}\right)\right]$$ (22)

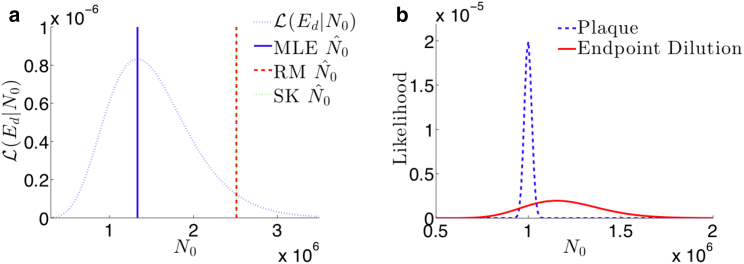
can be used, where d_c is the largest dilution number such that at least half of the trials exhibit a CE. Equation 22 is the average of the N₀ estimates at dilutions d_c and d_c+1 when setting the CE probability in Eq. 12 to 1/2. For a comparison of our MLE method with the RM and SK methods, we simulate data similar to that described in Plaque Assay. Here, we take the number of trials such that the simulated count of infected cells is greater than zero as the values of E_d for a given dilution number d. We plot the likelihood from Eq. 20 and compare the MLE of N₀ with those derived by the RM and SK methods in Fig. 9 a. Although both RM and SK estimate very similar values of ${\hat{N}}_0$, they both consistently overestimate the a priori set N₀ relative to the MLE method. This demonstrates the advantage of a probabilistic model for parameter inference over heuristically determined formulas.

Figure 9.

(a) The likelihood function $\mathcal{L}\left(E_d|N_0\right)$ in Eq. 20 for the endpoint dilution assay and the corresponding maximal likelihood, RM, and SK estimates given simulated data generated with N₀ = 10⁶, Q = 1, D = 10, and d_max = 10. The estimates for maximal likelihood $\left({\hat{N}}_0=1.33\times {10}^6\right)$, RM $\left({\hat{N}}_0=2.51\times {10}^6\right)$, and SK $\left({\hat{N}}_0=2.51\times {10}^6\right)$ all overestimate N₀, but the smaller relative error of the MLE is an improvement on the errors of the existing two methods. (b) The likelihood functions $\mathcal{L}\left(P_{d,t}|N_0\right)$ and $\mathcal{L}\left(E_d|N_0\right)$ for the plaque and endpoint dilution assays, respectively, are shown, given simulated data. The data were generated with the parameters N₀ = 10⁶, M = 10⁵, Q = 1, D = 10^1/4, d_max = 30, and a “countable plaque threshold” of 150. The plaque assay likelihood is concentrated close to the true N₀ value, whereas the endpoint dilution likelihood is far more spread out and overestimates N₀. This direct quantitative comparison can inform an experimentalist when choosing between the two methods. To see this figure in color, go online.

The expressions we derived in Eqs. 14 and 20, applied to simulated data, can also help quantify tradeoffs in experimental design. As discussed above, there exist viruses that cannot form plaques, restricting the options of VQAs to endpoint dilution. However, for many cases, the choice between using one assay over the other can be one of convenience. More specifically, endpoint dilution assays can often be performed more rapidly than plaque assays. Using the same simulated data for both assays, we plot Eqs. 14 and 20 together in Fig. 9 b. The plots clearly show the superiority of the plaque assay for estimating the viral stock number N₀ in respect to both how close the MLE infers the true N₀ value and the amount of variance in that estimate. Although the amount of variability and error that is tolerable for an experiment may be context dependent, the plots in Fig. 9 b provide a quantitative way to differentiate between the two methods.

Luciferase reporter assay

The luciferase reporter assay is commonly used to measure the infectivity of a viral strain. Here, the ratio μ = N/M of total infections over the number of plated cells is estimated by measuring the transcription activity of viral proteins (14, 15, 16). The reporter employs an oxidative enzyme luciferase that facilitates a reaction when introduced to the substrate luciferin, resulting in bioluminescence. The protocol begins with attaching the luciferase gene to the viral genome. The altered viral strain is cloned to a total particle count N₀, which, in this case, is assumed to be fixed and known. The solution of viruses is added to a plated monolayer of M host cells. An incubation time is allowed for transcription of viral proteins and, incidentally, the luciferase enzyme. Subsequently, all cells are lysed to release all cytoplasmic contents into the solution, upon which luciferin is added. The oxidation of luciferin is facilitated by the luciferase enzyme, and the resulting bioluminescence yields a measurable signal (38). The light intensity is thus a measure of total transcription activity of the viral genome in all infected cells and can be used as a proxy for the total number of viruses N that successfully infected host cells.

Although there is stochasticity in transcription-factor binding and, in the case of retroviruses, the number of integration sites on the host DNA, we will assume that each successful virus infection contributes one viral genome to be transcribed and each transcription occurs at a constant rate proportional to the total number of integrated viral genomes. Note that the limited number of transcription factors, ribosomes, and other cell machinery necessary to produce viral proteins and the luciferase reporter causes the production rate to saturate as the number of infecting viruses r per cell increases. Thus, transcription activity saturates with increasing number of infections r. We can model this effect by defining a monotonically increasing function f(r) representing the number of transcribed viral proteins when a cell is infected by r viruses over the course of the assay. Thus, for a given SMOI $\left\{M_0,\cdots ,M_N\right\}$, we will model the intensity signal L of the total luciferase reporter luminescence with

$$L=\sum _{r=0}^N{L}_{0}f\left(r\right)M_r,$$ (23)

where L₀ is the fluorescence intensity arising from a single luciferase reporter present in the solution. Although f(r) may take on many functional forms, a commonly used model for transcription-factor kinetics is the Hill function (39) given by

$$f\left(r\right)=\frac{f_{\text{max}}{r}^h}{K+r^h},$$ (24)

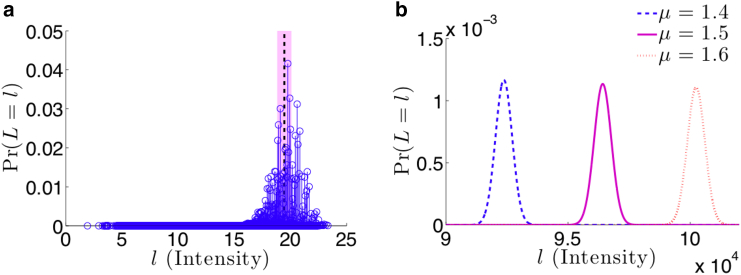
where $f_{\text{max}}$ is the maximal transcription activity of luciferase, h is the Hill coefficient that effectively describes cooperative binding of multiple transcription factors at a promoter region, and K is an effective dissociation constant relating the binding and unbinding rates of transcription factor. The functional form of Eq. 24 accounts for the limited transcription machinery available for the multiple copies of viral genome present in the cell. In Fig. 10 a, we calculate the discrete probability distribution $\text{Pr}\left(L=\ell \right)$ by considering the cumulative weight of every allowable configuration of N viruses infecting M cells through Eq. 23.

Figure 10.

Probability distributions of the luciferase assay fluorescence intensity L from Eq. 23. (a) A toy example of a discrete probability distribution of allowable fluorescence intensities for N = 30 viruses infecting M = 20 cells is shown. Due to the M^N finite number of allowable configurations of the SMOI, there are a corresponding finite number of intensities with specific probabilities determined by Eq. 5 and represented by a unique circle. The parameters used for the reporter kinetics are f_max = 2, h = 1, K = 1, and L₀ = 1. The mean intensity of the fluorescence signal is E[L] = 19.5, represented by the vertical dotted line, and variance is Var[L] = 1.49, represented by the shaded region. (b) The normally distributed approximation of fluorescence intensity using M = 1 × 10⁵, f_max = 2, h = 1, K = 1, and L₀ = 1 is shown. The distributions are plotted for μ = 1.4, 1.5, and 1.6 by computing the expected values E[L] = 9.23 × 10⁴, 9.64 × 10⁴, and 1 × 10⁵ and the variances Var[L] = 1.7 × 10⁵, 1.24 × 10⁵, and 1.3 × 10⁵ respectively. To see this figure in color, go online.

Because luciferase reporter assays typically involve large values of initial virus count N₀ and cell count M, we can use the asymptotic approximations in Eqs. 6 and 7 along with the central limit theorem (40) to assume L is normally distributed with expected value

$$\text{E}\left[L\right]=L_0{f}_{\text{max}}M{e}^{-\mu }\sum _{r=0}^N\frac{r^h{\mu }^r}{\left(K+r^h\right)r!}$$ (25)

and variance

$$\text{Var}\left[L\right]=L_0^2{f}_{\text{max}}^{2}M{e}^{-\mu }\sum _{r=0}^N\frac{r^{2h}{\mu }^r}{{\left(K+r^h\right)}^{2}r!}.$$ (26)

A visualization of the normal approximation of the probability distribution of L is shown in Fig. 10 b. Furthermore, with Eqs. 25 and 26, we can derive the likelihood function $\mathcal{L}\left(L_t^{\text{data}}|\mu \right)$ of the data $L_t^{\text{data}}$, given μ:

$$\mathcal{L}\left(L_t^{\text{data}}|\mu \right)=\prod _{t=0}^T\frac{1}{\sqrt{2\pi \text{Var}\left[L\right]}}\text{exp}\left[-\frac{{\left(L_t^{\text{data}}-\text{E}\left[L\right]\right)}^2}{2\text{Var}\left[L\right]}\right],$$ (27)

where 1 ≤ t ≤ T is the trial number. Because of the complicated functional form of the mean and variance of L, creating a maximal likelihood scheme to estimate μ from experimental data is intractable, so we use Eq. 25 by replacing the expected value with the experimental average of measurements $L_t^{\text{data}}$. If we assume no cooperative transcription binding (h = 1), we solve for the estimate $\hat{\mu }$ by applying the Newton-Raphson iterative method to the equation

$$0=\frac{1}{T}\sum _{t=0}^T{L}_t^{\text{data}}-L_0{f}_{\text{max}}M{e}^{-\hat{\mu }}\sum _{r=0}^{N_0}\frac{r{\hat{\mu }}^r}{\left(K+r\right)r!}.$$ (28)

The typical method, under the assumption that luminescent intensity is proportional to the number of IUs N, is to use the sample mean via the formula ${\hat{\mu }}^{\text{init}}=\left(1/L_{0}MT\right){\sum }_{t=0}^T{L}_t^{\text{data}}$. This standard approach fails to account for the effects of SMOI, but can be used to generate an initial guess for solving Eq. 28 iteratively. To compare the two estimates, we simulate data similar the descriptions in the previous two sections. Here, we do not dilute the initial particle count and, after distributing the N IUs to the M cells with equal probability, we compile the SMOI configuration and calculate $L_t^{\text{data}}$ using Eq. 23. The results are shown in Fig. 11. The iterative method produces an estimate $\hat{\mu }$ far closer to the true value of μ than the former method. A similar approach can be used to compare methods for alternative functional forms of the viral protein transcription dynamics described in Eq. 24.

Figure 11.

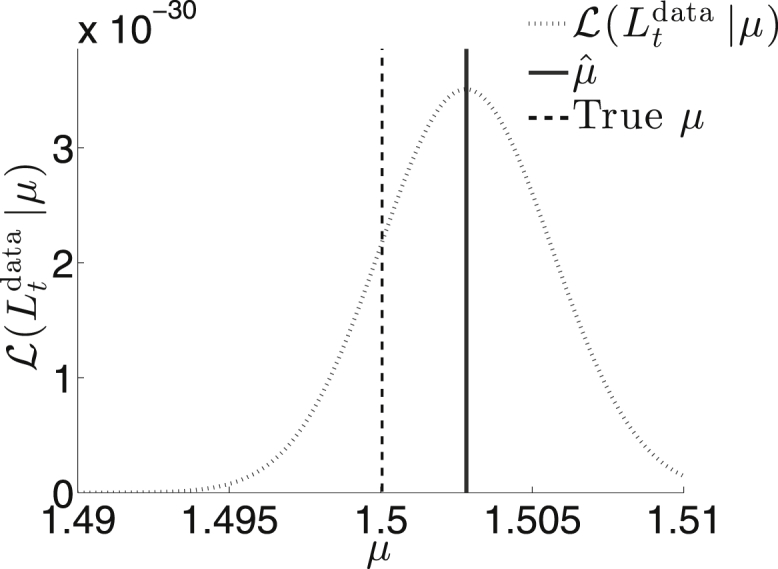
The likelihood function $\mathcal{L}\left(L_t^{\text{data}}|\mu \right)$ using Eq. 27 and simulated data. We set μ = 1.5 and assign other parameters with M = 1 × 10⁵, f_max = 2, h = 1, K = 1, and L₀ = 1. The estimate derived from solving Eq. 28 is $\hat{\mu }=1.502$, whereas the standard method based on the sample mean yields $\hat{\mu }=0.97$, far lower than what is displayed in the plot.

Conclusions

In this work, we derived probability models that quantify the viral infectivity of host cells in an in vitro environment. By factoring in the stochastic nature of virus-host engagement, defective and/or abortive events, and the possibility of multiple infections of a single host, we defined the SMOI and determined related probabilistic models. We analyzed two limiting regimes: small numbers of infecting viruses N and large N. For the low N regime, Eqs. 2 and 5 model how the limited number of IUs are distributed among the M host cells. Alternatively, for large N, we showed that the cell counts of the SMOI become statistically independent, as displayed in Eq. 8, and that they display a Poisson distribution (Eq. 6). Lastly, we explored the effects of serial dilution on the total number of infected cells and the probability of observing an infectious signal in Eq. 9.

Using our probability models along with reasonable assumptions of applied combinatorics and nonlinear inference, we analytically derived expressions for several virus assays to improve on existing methods of experimental data analysis. For virus quantification assays, serial dilution results in low numbers of viral particles. Using the appropriate probability model, we created to our knowledge new methods of estimating the particle count N₀ in the initial viral stock for the plaque assay and the endpoint dilution assay. For measuring infectivity of a viral strain, the objective is to determine the effective multiplicity of infection μ = N/M as the ratio of successfully infecting viruses N and the total number of cells M included in the assay. As these assays operate under no dilution, we employed the large N limit probability model to analytically derive expressions for the luciferase reporter assay to estimate μ. A summary of each estimation method along with the most commonly used counterpart is displayed in Table 1.

Table 1.

A Summary of the Analytically Derived Expressions Used to Analyze Experimental Results

Comparison of Virological Assay Analyses
Assay (parameter)	Standard Method	New Method
Plaque (N0)	${\hat{N}}_0=D^{d_c}\left(\frac{1}{T}\sum _{t=1}^T{P}_{d_c,t}\right)$	$0=\sum _{d=d_c}^{d_{\text{max}}}\sum _{t=1}^T\frac{M\text{exp}\left(-\frac{{\hat{N}}_0}{QM{D}^d}\right)-M+P_{d,t}}{QM{D}^d\left[1-\text{exp}\left(-\frac{{\hat{N}}_0}{QM{D}^d}\right)\right]}$
		Initial guess: ${\hat{N}}_0^{\text{init}}=-QM{D}^d\text{ln}\left(1-\frac{1}{MT}\sum _{t=1}^T{P}_{d_c,t}\right)$
Endpoint dilution (N0)	RM: ${\text{log}}_{10}\left({\hat{N}}_0\right)=d_{50\text{\%}}+\frac{E_{d_{50\text{\%}}}-0.5T}{E_{d_{50\text{\%}}}-E_{d_{50\text{\%}}+1}}$	$0=\sum _{d=1}^{d_{\text{max}}}\frac{E_d-T+T\text{exp}\left(-\frac{{\hat{N}}_0}{Q{D}^d}\right)}{Q{D}^d\left[1-\text{exp}\left(-\frac{{\hat{N}}_0}{Q{D}^d}\right)\right]}$
	SK: ${\text{log}}_{10}\left({\hat{N}}_0\right)=d_{100\text{\%}}-\left[\frac{1}{2}-\sum _{d=d_{100\text{\%}}}^{d_{\text{max}}}\frac{E_d}{T}\right]{\text{log}}_{10}D$	Initial guess: ${\hat{N}}_0^{\text{init}}=\frac{-Q{D}^{d_c}}{2}\text{ln}\left[\left(1-\frac{E_{d_c}}{T}\right){\left(1-\frac{E_{d_c+1}}{T}\right)}^D\right]$
Luciferase reporter $\left(\mu =\frac{N}{M}\right)$	$\hat{\mu }=\frac{1}{L_{0}MT}\sum _{t=0}^T{L}_t^{\text{data}}$	$0=\frac{1}{T}\sum _{t=0}^T{L}_t^{\text{data}}-L_0{f}_{\text{max}}M{e}^{-\hat{\mu }}\sum _{r=0}^{N_0}\frac{r{\hat{\mu }}^r}{\left(K+r\right)r!}$
		Initial guess: ${\hat{\mu }}^{\text{init}}=\frac{1}{L_{0}MT}\sum _{t=0}^T{L}_t^{\text{data}}$

For virus quantification assays, such as the plaque and endpoint dilution assays, one typically wishes to estimate the number of initial viral particles N₀. For luciferase reporter infectivity assay, the ratio μ = N/M is desired. Our improved parameter estimation methods are listed next to standard methods currently used.

VQAs are primarily concerned with inferring N₀ and assume a priori knowledge of M and the particle to PFU ratio Q. In actuality, there can be variability in the number of cells present in the microtiter well, and, as discussed in Probabilistic Models of Statistical Multiplicity of Infection, the true value of Q is dependent on the particular protocol and particular conditions under which an assay was performed. If an alternative assay (RNA tagging, spectroscopy, super-resolution imaging, etc.) not using cell infection can accurately measure N₀, then, in theory, a subsequent infection assay can be used to infer a more reliable measure of Q. In fact, in our analysis of the plaque assay presented in Appendix E of the Supporting Materials and Methods, we show that one can determine a significantly higher amount of information about Q with the same assay protocol if N₀ is a priori known rather than the reverse case. Thus, one may argue that assays that employ serial dilution, such as plaque and endpoint dilution assays, may be better utilized to infer Q. Because the underlying likelihood of the data in all assays would be the same, the same derivation techniques would follow with respect to Q to formulate its MLE. This analysis shows the robust utility of a full probabilistic model and data likelihood function.

Although the derived assay models provide explicit equations for inference, many of the expressions are analytically unsolvable and require numerical solutions. To improve the accessibility of some of our results, we have created a web-based tool (available at https://bamistry.github.io/SMOI/) that can accept data from plaque, endpoint dilution, or luciferase reporter assays and automatically estimate the parameter of interest. Ultimately, these tools can be used for analysis of future virological studies but may also be useful when revisiting the results of studies that stress quantifying viral infectivity (15, 41). For studies that use serial dilution assays, our approach stresses the advantages of using information in the data associated with all dilution numbers rather than just that of the critical dilution.

Our probabilistic models of viral infection can be further generalized to include, for example, the effects of cell size inhomogeneity, coinfection, and viral interference. In the Supporting Materials and Methods, we provide a framework that would allow one to explore how these confounding factors can further alter the signal of a virus assay. Future refinement of these extensions can help to ultimately derive a mechanistic model for the probability of a single virus successfully infecting a host cell, which we defined as Q⁻¹. Understanding this probability of infection can help aid further experimental design and allow better quantification and resolution of the infection dynamics of particular viral strains.

Author Contributions

B.A.M. derived mathematical formulae, developed statistical inference framework, performed simulations, generated plots, and wrote the initial draft. B.A.M. (bamistry@ucla.edu) also developed the web-based analysis tool at https://bamistry.github.io/SMOI/. M.R.D. and T.C. verified the mathematical results, contributed to their analyses, and edited the manuscript. T.C. conceptualized, designed, and supervised the research.

Editor: Ruth Baker.