Principles for Optimal Cooperativity in Allosteric Materials

Abstract

Allosteric proteins transmit a mechanical signal induced by binding a ligand. However, understanding the nature of the information transmitted and the architectures optimizing such transmission remains a challenge. Here we show, using an in silico evolution scheme and theoretical arguments, that architectures optimized to be cooperative, which efficiently propagate energy, qualitatively differ from previously investigated materials optimized to propagate strain. Although we observe a large diversity of functioning cooperative architectures (including shear, hinge, and twist designs), they all obey the same principle of displaying a mechanism, i.e., an extended soft mode. We show that its optimal frequency decreases with the spatial extension L of the system as $L^{-d/2}$, where d is the spatial dimension. For these optimal designs, cooperativity decays logarithmically with L for d = 2 and does not decay for d = 3. Overall, our approach leads to a natural explanation for several observations in allosteric proteins and indicates an experimental path to test if allosteric proteins lie close to optimality.

Introduction

Many proteins are allosteric: binding a ligand at an allosteric site can affect the properties of a distant active site, sometimes located on the other side of the protein (1, 2). Predicting the existence of such allosteric pathways from protein structure alone would be of great interest (3, 4), because they can be used as targets for drug design (5). Solving this challenge requires making progress on both physical and biological questions. First, how can such disordered materials (6) be designed to carry mechanical information specifically over long distances? Are there fundamental limits to what can be achieved? Second, what are allosteric pathways really optimized for? What kind of elastic information do they carry? A physical theory of allostery should address these points. It should also explain the following empirical facts. 1) Some allosteric proteins (7), including hemoglobin (8, 9), essentially function as hinges, whereas others display a “shear” design, in which two rigid parts are connected by a weak plane (10). This classification is, however, not exhaustive, as in various cases, the response to binding a ligand cannot be described in terms of a simple shear or hinge motion (11, 12, 13). 2) The response to binding often corresponds mostly to motion along a few soft normal modes of the protein (14, 15). These modes tend to be conserved during evolution (16). 3) In some cases, the allosteric functional effect at the active site is significant, whereas the physical mean displacement induced by binding the ligand is small. It has been proposed that for these proteins, binding can affect how particles near the active site fluctuate around their mean position, while changing the mean itself little (17, 18, 19, 20).

Recently, allostery was investigated using in silico evolution schemes, in which a system evolves to perform a given function (21, 22, 23, 24, 25). Most relevant here are schemes developed to solve inverse elastic problems (23, 24, 25), in a spirit similar to the topology optimization used in engineering to design functional tools from compliant materials (26, 27, 28). The task studied in (23, 24, 25) was to design a material whose response to a specific local strain applied on one of its sides (the allosteric site) leads to a displacement whose geometry is prescribed on the opposite side (the active site). Under broad conditions, these algorithms find solutions that achieve such “geometric” tasks essentially perfectly. The corresponding architectures turn out to have surprising properties: their response almost vanishes in the bulk of the material and reappears near the active site (23). This amplification of the elastic signal is caused by the emergence of a powerful lever, made of a soft elastic region surrounding the active site, where the system is just constrained enough to act as a solid (23, 29). Although there is great interest in finding whether such architectures exist in nature, an intriguing aspect of this approach is that it does not generate the well-known allosteric architectures such as the simple shear and hinge designs, in which the response remains of similar magnitude between the allosteric and the active sites.

Here, we show that a simple modification of the task, in which materials are optimized such that the binding at the allosteric site lowers the binding energy of another ligand at the active site, leads to different design principles. In the context of proteins, this task corresponds to maximizing the cooperativity of binding two ligands, a central feature of various allosteric proteins (1). We find that there is a zoology of architectures achieving such cooperativity, but they always display a stiff structure (embedded in a softer elastic matrix) with a single very soft extended elastic mode or “mechanism.” We lay out the principles behind such designs and show theoretically that the soft mode frequency should be neither too large nor too small to optimize function: its optimal value decreases with the material size, and scales as $L^{-d/2}$ in spatial dimension d. We prove that cooperativity then decays as ln⁻¹(L/c) for d = 2 and is even independent of L in larger spatial dimensions d ≥ 3, where L is the linear extension of the system and c the length scale on which binding takes place. This result is very different from a normal continuous elastic medium, in which cooperativity rapidly decays with distance as L^−d. Overall, the classification we provide leads to a natural explanation for the key aspects of allostery described in (1, 2, 3). It also shows that a path of large strain values connecting the allosteric and active site and induced by binding is not necessary for cooperativity to occur, and it makes further testable predictions, including the locations where a shear or hinge design would be mostly affected by a mutation and conserved during evolution.

Methods

In silico evolution scheme

Elastic networks

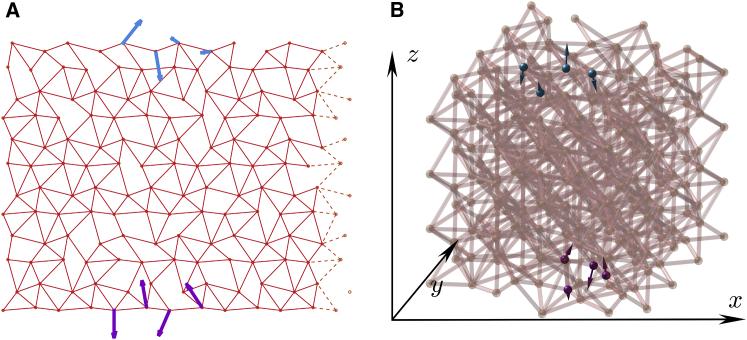
To model allosteric materials, we consider elastic networks, often used to describe proteins (14, 15, 16). Specifically, N = L^d nodes are located on a lattice (slightly distorted periodically to avoid straight lines, as discussed in Supporting Materials and Methods, Section A and (30, 31)), and among all N_c links of nearest nodes, a subset of N_s pairs are connected by harmonic springs of stiffness k = 1, as indicated by lines in Fig. 1. We declare that ${\sigma }_{\alpha }=1$ if a spring is present in the link α and ${\sigma }_{\alpha }=0$ otherwise. Thus, the network is entirely described by a connection vector $|\sigma \rangle$ made of zeros and ones, whose dimension is the number of links N_c. We define the average coordination number $z\equiv 2N_{\text{s}}/N$ and average connection $\overline{\sigma }=N_{\text{s}}/N_c$ and keep them fixed during evolution. We find that our results do not depend qualitatively on z as long as z > z_c = 2d, the rigidity limit derived by Maxwell (32).

Figure 1.

Examples of on-lattice elastic networks. (A) A hexagonal lattice (d = 2) with periodic boundary conditions along the horizontal axis (springs crossing the periodic boundary are shown in dashed lines and are not present when open boundary conditions are used), mimicking a cylindrical geometry. (B) For d = 3, we use a face-centered cubic lattice with open boundaries. In all cases, occupied links displaying a spring of stiffness unity are indicated by lines. The stimulus displacement is shown in purple arrows, and the target displacement is shown in blue arrows; each are applied on four nodes. All data are presented for L = 20 and z = 5.0 in d = 2 and L = 12 and z = 8.4 in d = 3. To see this figure in color, go online.

Binding

Binding a ligand exerts forces locally that leads to an imposed local strain. To model this effect at the allosteric site, we choose four adjacent nodes on one side of the system (shown in purple in Fig. 1) and consider that binding at that site imposes a displacement $|\delta {\mathbf{R}}^{\mathcal{A}l}\rangle$ on these nodes, as indicated by purple arrows. (Strictly speaking, this description of binding assumes that the ligands are rigid. However, we expect our results to hold true qualitatively as long as the ligands are not significantly softer than the protein itself.) Minimizing the elastic energy in the entire system with these constraints then leads to a response $|\delta \mathbf{R}{\left(\sigma \right)}_r^{\mathcal{A}l}\rangle$ that can be extended (see a formal expression for this response in Supporting Materials and Methods, Section B and (23)). The corresponding energy cost associated with binding is written as follows:

$$E^{\mathcal{A}l}\left(\sigma \right)=\frac{1}{2}\langle \delta {\mathbf{R}}_r^{\mathcal{A}l}\left|\mathcal{M}\right|\delta {\mathbf{R}}_r^{\mathcal{A}l}\rangle ,$$ (1)

where $\mathcal{M}$ is the stiffness matrix of the network (whose definition is recalled in Supporting Materials and Methods, Section B) of dimension Nd × Nd, which depends on the network considered. The same procedure is used to model the binding of another ligand at the active site (indicated in blue in Fig. 1), allowing us to define a binding energy $E^{\mathcal{A}c}\left(\sigma \right)$. If the two binding events take place simultaneously, the same procedure leads to the derivation of a joint binding energy $E^{\mathcal{A}c,\mathcal{A}l}\left(\sigma \right)$.

Cooperativity

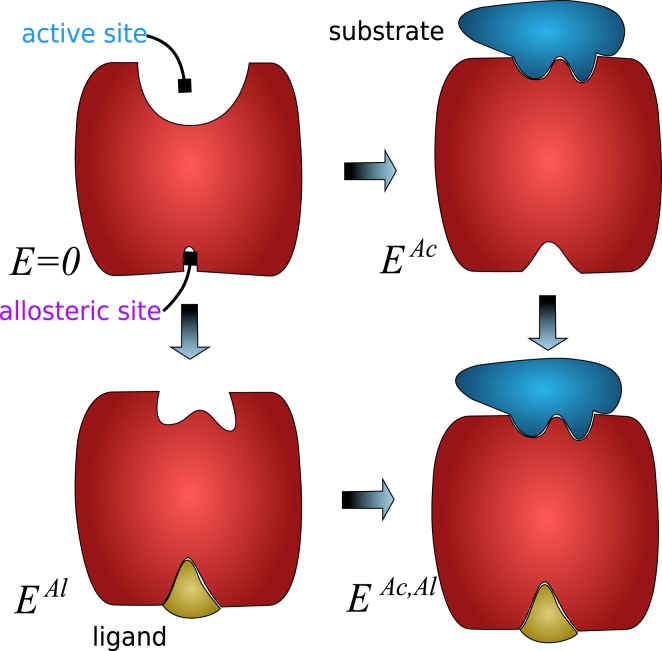
We seek to engineer materials in which binding at the allosteric site lowers the binding energy at the active site as much as possible, as illustrated in Fig. 2. In the absence of the ligand at the allosteric site, the binding energy at the active site is simply $E^{\mathcal{A}c}\left(\sigma \right)$, whereas if present, it is $E^{\mathcal{A}c,\mathcal{A}l}\left(\sigma \right)-E^{\mathcal{A}l}\left(\sigma \right)$. We seek to maximize the cooperative energy, simply defined as the difference between these terms:

$$E_{\text{coop}}=E^{\mathcal{A}c}\left(\sigma \right)+E^{\mathcal{A}l}\left(\sigma \right)-E^{\mathcal{A}c,\mathcal{A}l}\left(\sigma \right)\equiv \mathcal{F},$$ (2)

which also defines our fitness function.

Figure 2.

Illustration of cooperativity. With two binding sites, a protein displays four states. Cooperativity is high if binding a substrate molecule at its active site is difficult when the allosteric site is empty (i.e., $E^{\mathcal{A}c}$ is large), whereas it is much simpler when the allosteric site is occupied (i.e., $E^{\mathcal{A}c,\mathcal{A}l}-E^{\mathcal{A}l}$ is small). To see this figure in color, go online.

Cooperativity turns out to differ greatly from the geometric task in which a displacement imposed at one end of the material must elicit a given displacement at the other end (23, 24, 25) (see below and Supporting Materials and Methods for a detailed comparison). The architectures associated with the latter task are very asymmetric; in particular, they are much softer near the active site than near the allosteric site (23). By contrast, it is clear from our definition of cooperativity that both active and allosteric sites play a symmetric role. At an intuitive level, the difference can be understood by considering the limit of weak elastic coupling between allosteric and active sites, for which one finds $E_{\text{coop}}\approx \langle F^{\mathcal{A}c}|\delta R^{\mathcal{A}l\to \mathcal{A}c}\rangle$, where $|F^{\mathcal{A}c}\rangle$ is the external force field generated by the substrate when it binds to the active site and $|\delta R^{\mathcal{A}l\to \mathcal{A}c}\rangle$ is the displacement field induced at the active site by binding a ligand at the allosteric site. Maximizing cooperativity thus requires having a large and specific response $|\delta R^{\mathcal{A}l\to \mathcal{A}c}\rangle$ (which is essentially what the geometric task accomplishes) and a large force scale $|F^{\mathcal{A}c}\rangle$, which requires the material to be stiff near the active site. This additional constraint makes the cooperative task harder than the geometric one.

Evolutionary dynamics

To generate cooperative architectures, we implement an evolution scheme that selects preferably networks with high fitness. Specifically, we use a Monte Carlo algorithm in which the relocation of individual springs is considered, i.e., $|\sigma \rangle \to |{\sigma }^{\prime }\rangle$, where a randomly chosen vacant link γ becomes occupied $\left({\sigma }_{\gamma }=0\to {\sigma }_{\gamma }^{\prime }=1\right)$ and a randomly occupied link α becomes empty $\left({\sigma }_{\alpha }=1\to {\sigma }_{\alpha }^{\prime }=0\right)$. The new structure is selected with the probability $p=\min \left[1,\text{exp}\left(\mathcal{F}\left({\sigma }^{\prime }\right)-\mathcal{F}\left(\sigma \right)/T_e\right)\right]$, where 1/T_e is inverse evolutionary “temperature” characterizing the selection pressure.

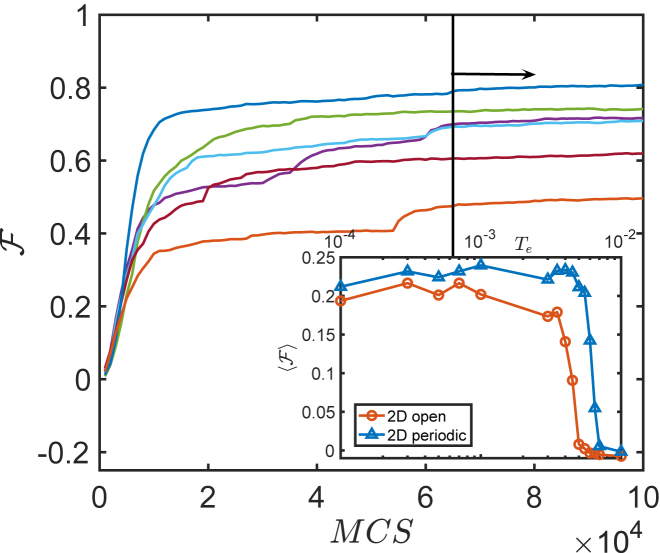
We find that as the selection pressures increases and T_e decreases, there is a rather sudden transition from nonworking networks with zero fitness to cooperative ones, as illustrated in the inset of Fig. 3. The fitness then appears to plateau, and in what follows, we choose T_e = 10⁻⁴, where this plateau is reached. Interestingly, in this plateau region, we find that the fitness landscape is glassy: there are many families of solutions that are not dynamically connected on the timescale of our runs, implying the presence of large fitness barriers. The families obtained in a given run are defined by the respective initial conditions and do not display exactly the same fitness as shown in Fig. 3. We checked that sequences are much more similar within a family than between different families. Indeed, in a single family, the mean overlap between distinct configurations i and j, $q\equiv \langle {\overline{{\sigma }_{\alpha }^i{\sigma }_{\alpha }^j}}^{\alpha }\rangle -{\overline{\sigma }}^2$, is high (with $q\approx 0.36$), whereas it is small $\left(q\approx 0.03\right)$ for different families (${\overline{•}}^{\alpha }$ averages over links and $\langle •\rangle$ averages over configurations). Glassiness also implies that the architectures slowly evolve in time, but less and less so as time goes on. In what follows, we study architectures only in the last third of the run, when transient effects are weaker and fitness is nearly stationary. In total, we generated 25 families in d = 2 and 10 families in d = 3.

Figure 3.

Evolution of the fitness $\mathcal{F}$ versus the number of Monte Carlo steps MCS. Different initial conditions resulted in different architectures, which are analyzed at a sufficiently long time to avoid significant transient effects (keeping only the data from the last 3.5 × 10⁴ steps out of the 10⁵MCS in each run, as delineated by the black vertical line in the plot). The inset shows the fitness $\mathcal{F}$ averaged over 25 initial conditions as a function of the evolution temperature T_e for the two-dimensional network with both open and periodic boundaries. To see this figure in color, go online.

Analysis toolbox

In this section, we review useful observables characterizing allosteric architectures. Most of them are known in the protein literature; others are novel to the best of our knowledge.

Geometry of allosteric response

By computing the structure of proteins crystallized with and without the ligand bound on their allosteric site, one gets access to the internal response of the protein induced by binding, $|\delta {\mathbf{R}}_r^{\mathcal{A}l}\rangle$ in our notations. As recently emphasized in this context (10), a key aspect of this response is its strain, which must be zero in parts of the proteins moving as rigid blocks. The strain thus captures where deformation is actually taking place. The strain tensor $\overleftrightarrow{\mathrm{ϵ}}\left(i\right)$ can be directly computed from any displacement $|\delta \mathbf{R}\rangle =\left\{\delta R_i\right\}$ where i labels particles or nodes, as shown in Supporting Materials and Methods, Section C or (33). Removing the trace leads to a local shear tensor $\overleftrightarrow{\gamma }\left(i\right)=\overleftrightarrow{\mathrm{ϵ}}\left(i\right)-\left(1/d\right)\text{tr}\left[\overleftrightarrow{\mathrm{ϵ}}\left(i\right)\right]$1, where 1 is a d × d identity matrix. It’s useful to define scalar observables to visualize the strain, in particular the shear intensity $E_{\text{shear}}\left(i\right)$ (not sensitive to compression or dilation) and the bulk intensity $E_{\text{bulk}}\left(i\right)$ (sensitive to it) as follows (10):

$$\begin{array}{c}{E}_{\text{shear}}\left(i\right)=\frac{1}{2}\stackrel{d}{\sum _{l,m=1}}{\left[{\gamma }_{lm}\left(i\right)\right]}^2;\\ E_{\text{bulk}}\left(i\right)=\frac{1}{2}\stackrel{d}{\sum _{l=1}}{\left[{\mathrm{ϵ}}_{ll}\left(i\right)\right]}^2.\end{array}$$ (3)

Rigidity of the structure

For elastic networks, as understood by Maxwell, an important aspect of rigidity is the coordination number z(i), counting the local connectivity (number of springs) attached to a node i. This notion, sufficient in our model, can be extended to interactions relevant in proteins as discussed in (34).

Another commonly used observable is the B-factor or Debye-Waller factor (35). It characterizes the mean square thermal fluctuations of the particle positions. In a harmonic approximation, it can be expressed in terms of the vibrational modes (neglecting a temperature-dependent prefactor):

$$B\left(i\right)=\sum _{\omega >0}\frac{1}{{\omega }^2}\delta {\mathbf{R}}_{\omega }\left(i\right)\cdot \delta {\mathbf{R}}_{\omega }\left(i\right),$$ (4)

where the ωs and $\delta {\mathbf{R}}_{\omega }$ are frequencies and the corresponding vibrational modes that are obtained from the diagonalization of the stiffness matrix.

B-factors, however, may not pick up the interesting flexibility of the structure. For example, if a hinge connects two rigid parts, B-factors may be large in the rigid parts, too, as they are sensitive to rigid motions as well. Here, we introduce an observable that would reveal the presence of a hinge, as it characterizes the thermal fluctuations of the strain (which is therefore zero by construction for a rigid body). We call it the strain B-factor, which for harmonic dynamics follows

$$SB\left(i\right)=\sum _{\omega >0}\frac{2}{{\omega }^2}\left[E_{\text{shear},\omega }\left(i\right)+E_{\text{bulk},\omega }\left(i\right)\right],$$ (5)

where $E_{\text{shear},\omega }$ and $E_{\text{bulk},\omega }$ are the shear and bulk intensities for a given mode $\delta {\mathbf{R}}_{\omega }\left(i\right)$, as defined from Eq. 3.

Spectral analysis

The response to binding can be decomposed into the vibrational modes (16), which form a complete orthogonal basis. We define the overlap

$$q_{\omega }={\Vert \langle \delta {\mathbf{R}}_r^{\mathcal{A}l}|\delta {\mathbf{R}}_{\omega }\rangle \Vert }^2/{\Vert \delta {\mathbf{R}}_r^{\mathcal{A}l}\Vert }^2$$ (6)

that satisfies ${\sum }_{\omega }{q}_{\omega }=1$.

The extendedness of the vibrational modes is characterized by the participation ratio, defined as

$$P_{\omega }={\left(N\sum _i{\left(\delta {\mathbf{R}}_{\omega }\left(i\right)\cdot \delta {\mathbf{R}}_{\omega }\left(i\right)\right)}^2\right)}^{-1}$$ (7)

for normalized modes ${\sum }_i\delta {\mathbf{R}}_{\omega }{\left(i\right)}^2=1$. Translations have a unity participation ratio. By contrast, if a mode only involves the motion of ∼N₀ particles, then $P_{\omega }\sim N_0/N$.

Conservation

We quantify the local conservation of the structure by considering the mean occupancy, defined over a period of observation τ:

$$\langle {\sigma }_{\alpha }\rangle \equiv \frac{1}{\tau }\sum _{t=1}^{\tau }{\sigma }_{\alpha }\left(t\right).$$ (8)

If there is no selection pressure on that link, we expect $\overline{\sigma }$. We thus define the conservation ∑ to quantify the deviation from this average (23):

$${\text{Σ}}_{\alpha }=\langle {\sigma }_{\alpha }\rangle \text{ln}\frac{\langle {\sigma }_{\alpha }\rangle }{\overline{\sigma }}+\left(1-\langle {\sigma }_{\alpha }\rangle \right)\text{ln}\frac{1-\langle {\sigma }_{\alpha }\rangle }{1-\overline{\sigma }}.$$ (9)

Results

We now document examples of architectures generated by our scheme, focusing on shear, hinge, and twist designs. We consider individual families: when average quantities are presented, they always correspond to a time average over the last third of our Monte Carlo algorithm, as previously described. We then emphasize the features common to all these designs, to be explained in the next section.

Shear design

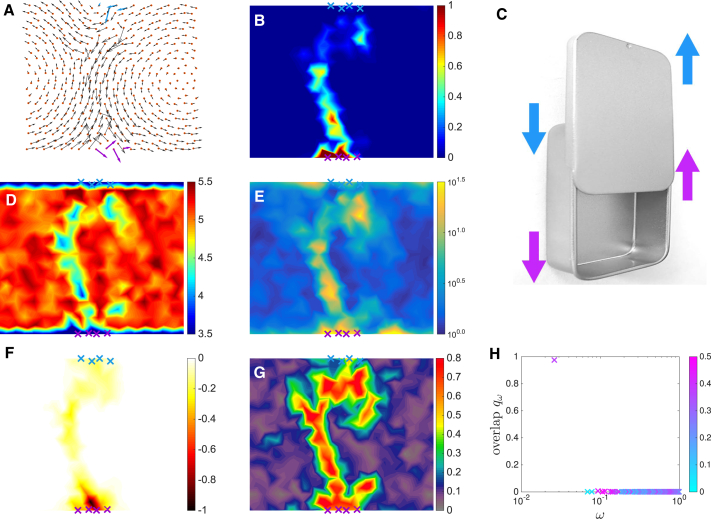
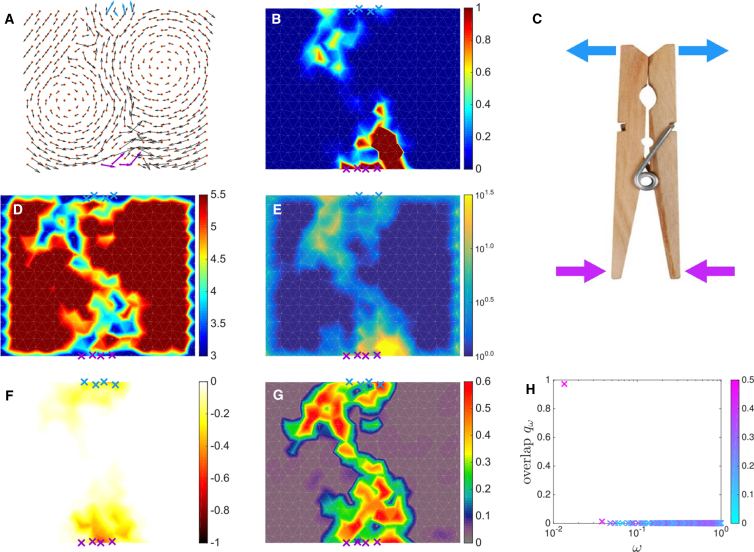
We start by the two-dimensional case in which visualization is easier. If periodic boundary conditions are considered on the horizontal axis (cylindrical geometry), we find that all 25 architectures correspond to a shear design. This is illustrated in Fig. 4 A, showing the response to binding: except for a linear path connecting the allosteric and active sites, the motion is essentially that of a rigid body (pure rotations and translations). This is most obvious when plotting the map of the shear intensity $E_{shear}$ in Fig. 4 B, which is essentially zero except along that path. Overall, the design is similar to that of the mint box illustrated in Fig. 4 C, in which strain also localizes on a hyperplane (a line for d = 2 and a plane for d = 3). At the structural level, we find that the strain path corresponds to a softer region with lower coordination, as shown in Fig. 4 D, and a larger strain B-factor, as illustrated in Fig. 4 E.

Figure 4.

Shear design. (A) The average cooperative response $\delta {\mathbf{R}}_r^{\mathcal{A}l}$ induced by binding at the allosteric site is shown in black arrows. (B) The average shear intensity map $E_{\text{shear}}$ reveals strain localization along a path. (C) A mint box that opens by sliding illustrates the shear mechanism. (D) A map of the average coordination number z is shown. (E) A map of the average strain B-factor SB is shown. (F) A map of the fitness cost of single-site mutation normalized by its absolute value $\mathit{\Delta }\mathcal{F}/\mathcal{F}$ is shown. (G) A map of the conservation $\text{Σ}$ in the evolution simulation is shown. (H) The overlap q_ω between the response and the vibrational modes, colored as a function of the participation ratio P_ω, shows that a single extended mode dominates the response to binding. To see this figure in color, go online.

Hinge design

When open boundaries (instead of periodic ones) are used, we find that ∼40–50 percent of the families lead to hinge architectures, and the rest display a shear design. In the former case, the response exemplified in Fig. 5 A can be decomposed into the motion of two rigid bodies connected by a hinge. Again, this is most apparent in the map of the shear intensity in Fig. 5 B, showing that there is little strain excepted for two disconnected regions near the allosteric and active sites. There is thus no connecting path of high strain between these sites. This design is common in our daily life, as illustrated by the clothespin in Fig. 5 C. At the structural level, the map of coordination shown in Fig. 5 D and that of strain B-factor shown in Fig. 5 E display an “H” shape with two rather disconnected regions being weakly coordinated with a high strain B-factor.

Figure 5.

Hinge design. (A) The averaged cooperative response $\delta {\mathbf{R}}_r^{\mathcal{A}l}$ induced by binding at the allosteric site is shown in black arrows. (B) The shear intensity $E_{\text{shear}}$ of the response is given. (C) A clothespin illustrates the hinge mechanism. (D) A map of the average coordination number z is shown. (E) A map of the average strain B-factor SB is shown. (F) A map of the fitness cost of single-site mutation normalized by its absolute value $\mathit{\Delta }\mathcal{F}/\mathcal{F}$ is shown. (G) A map of the conservation $\text{Σ}$ is shown. (H) The decomposition q_ω of the response on the vibrational modes ω, colored as a function of the participation ratio P_ω, is shown. To see this figure in color, go online.

Twist design

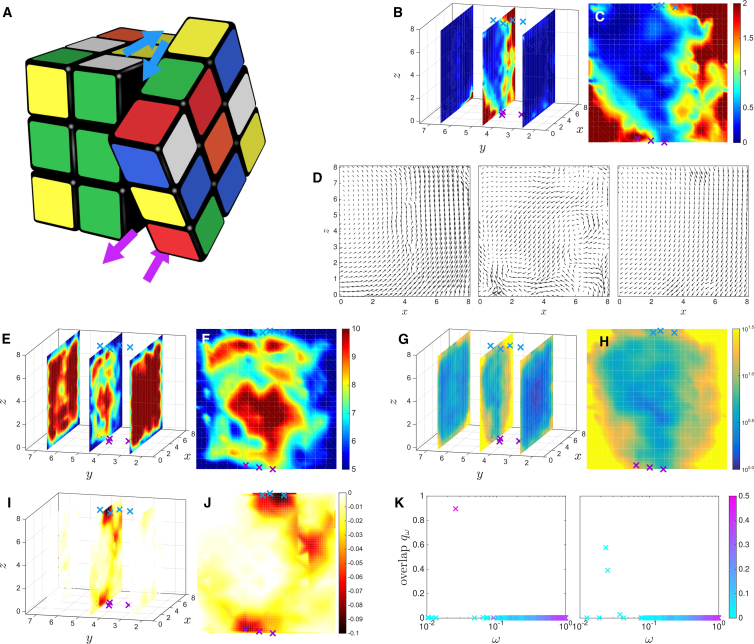
In three dimensions, we find a rich variety of architectures whose structures and responses are sometimes hard to describe. Here, we present the simple case of a twist architecture, as illustrated in Fig. 6 A with the Rubik Cube. To visualize this design, we consider the shear intensity in three sections parallel to the x-z plane as illustrated in Fig. 6 B. We find that there is little strain except on the central plane connecting the allosteric (purple) and active (blue) sites shown in Fig. 6 C. There is not, however, a homogeneous shear on that plane: instead, the strain is low at its center and larger near the boundaries. Further evidence for the twist design appears in the allosteric response itself, shown in Fig. 6 D with the same slicing geometry: the two side planes show reverse rotating motions, whereas the middle plane shows a more complex displacement pattern. Once again, the structural analysis confirms this view: we find that the coordination is large and the strain B-factor is small except near the boundaries of the central plane, as shown in Fig. 6, E–H. The middle of the central plane thus acts as a well-connected joint around which two quite rigid bodies can rotate.

Figure 6.

Twist design. (A) An illustration of a Rubik Cube and its twist mechanism is shown. (B) Two-dimensional sections of the shear strain intensity are shown. The allosteric and active sites are shown in purple and blue, respectively. (C) The shear intensity $E_{\text{shear}}$ in the central section is shown. (D) The response $\delta {\mathbf{R}}_r^{\mathcal{A}l}$ to binding in the same three distinct sections, organized from left to right as in (B), is shown. Maps of the average coordination number z on (E) the three sections and (F) the central section are shown. The strain B-factor SB is shown on the three sections (G) and the central one (H). The fitness cost of single-site mutation normalized by its absolute value $\mathit{\Delta }\mathcal{F}/\mathcal{F}$ on (I) the three sections and (J) the central one is shown. (K) The decomposition q_ω of the response on the vibrational modes versus the mode frequency ω, colored as a function of their participation ratios P_ω, is shown at two different time points during the run. In three dimensions, most of the spectral decomposition resembles the right panel, in which several vibrational modes project on the response, although we can always identify time points at which a single mode contributes, as shown on the left panel. To see this figure in color, go online.

Universal features of cooperative designs

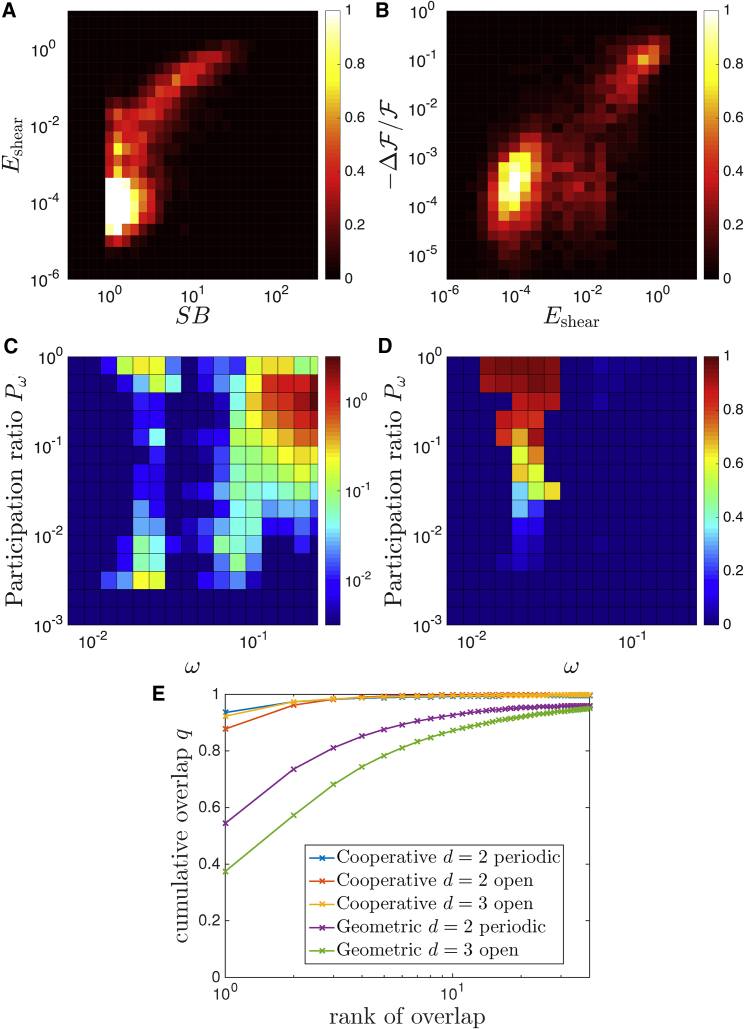
Our in silico evolution scheme generates different designs, as illustrated with the examples above. However, all these designed architectures follow the same principles, which we list in the following. These principles are systematically tested by averaging on the 25 families found in two dimensions with periodic boundaries in Fig. 7. The same analysis holds for other boundary conditions and in three dimensions as well, as documented in Supporting Materials and Methods, Section E:

• 1)The system separates into a rigid and a soft manifold, as observed in a class of proteins (36) and in protein models (20).
• 2)The strain associated with the allosteric response is small in the rigid manifold (indicating rigid-body or long-wavelength motion), whereas it is large in the soft manifold. Both properties are apparent in Fig. 7 A, showing the two-dimensional density of nodes found with a given strain B-factor (reflecting the local rigidity) and strain intensity (reflecting the strain induced by the allosteric response). This histogram displays a branch of soft nodes, where the strain B-factor is large and positively correlated to the strain intensity.
• 3)In all cases, the mutation cost is high precisely in these locations where the system is soft and the strain intensity is large, as illustrated in Fig. 7 B.
• 4)Most importantly, the daily-life examples we provided all have a common point: they display a single mechanism, i.e., a very soft elastic mode. We observe that this is also true in our cooperative architectures: there is always a single soft and extended mode along which most of the response projects. This fact is already apparent in the decomposition of the response on vibrational modes shown in Figs. 4 H, 5 H, and 6 K. It is studied systematically in Fig. 7, C and D, showing respectively the density of vibrational modes D(ω, P_ω) and the overlap q(ω, P_ω) as a function of both frequency ω and participation ratio P_ω. Fig. 7 C shows a peak of extended (large P_ω) modes at low ω, and Fig. 7 D shows that most of the response projects precisely on these modes. We find that essentially one mode governs the response. This result can also be visualized by classifying modes for each system by decreasing overlap q and by representing the cumulative overlap (the sum of q_ω for the r modes with the largest overlap) as a function of the rank r, as illustrated in Fig. 7 E. On average, the first mode captures more than 90% of the response.

Figure 7.

Histogram of network nodes displaying (A) a given strain B-factor SB and shear intensity $E_{\text{shear}}$ (showing that most of the strain induced by the response to binding occurs in regions where the material is soft) and (B) a given shear intensity $E_{\text{shear}}$ and normalized fitness cost $-\mathit{\Delta }\mathcal{F}/F$ (showing that mutations are costly where the response strain is localized). The color bar indicates the relative abundance of the data points. (C) The density of vibrational modes D(ω, P_ω) and (D) the overlap q(ω, P_ω) is shown as a function of both frequency ω and participation ratio P_ω, revealing the presence of a soft extended mode on which most of the response projects. For (A–D), the statistics is done over all 25 families of solutions found in the cooperative task in two dimensions with a periodic boundary. (E) The cumulative overlap on the first r modes with strongest overlap, where r is denoted the rank, is shown. Results are shown both for the cooperative and the geometric tasks, for all dimensions and boundary conditions. To see this figure in color, go online.

It is interesting to note that many properties of materials optimized to be cooperative, whose specific property is to display a single soft elastic mode controlling function, differ from materials studied previously optimized to propagate a given strain—below, we will refer to both cases as “cooperative” and “geometric” designs. An extensive comparison is performed in Supporting Materials and Methods, Sections F and G. Salient differences include that 1) the magnitude of the response is essentially constant in space in cooperative designs (it decays by fivefold or more in geometric designs); 2) the cooperative design is symmetric: binding at the allosteric or at the active site leads to a very similar response (whereas elastic information cannot propagate from the active site to the allosteric site in geometric designs); 3) the cooperative design responds much more specifically than the geometric ones (in the latter case, imposing a strain anywhere in the material typically leads to a strong displacement at the active site); and 4) for geometric designs, the response does not correspond to a single soft elastic mode but to a few of them, as already apparent in Fig. 7 E.

To explain the universal features of cooperative designs and to predict the frequency of the soft extended mode controlling the response, we now investigate the optimality of designs.

Discussion

Absence of design

We now argue that in a continuous elastic medium—where no design is involved—cooperativity decreases very rapidly with the distance L between the allosteric and active sites. Any imposed local strain can be decomposed into multipole moments (dipole and higher), and the slower decaying response in the far field—sufficiently distant from the source—is dipolar, because higher multipoles decay faster. To model the perturbation induced by ligand binding, we may thus consider without loss of generality two dipoles each of magnitude fc, where f is the applied force and c the distance over which these are exerted. Here we give a simple scaling argument for a medium with elastic modulus G. As mentioned earlier, for $L\gg c$, we have $E_{\text{coop}}\sim \langle dR|F\rangle$, where $|dR\rangle$ is now the dipolar response induced by the first dipole of magnitude $dR\left(r\right)\sim \left(fc/r^{d-1}G\right)$, and $|F\rangle$ the force field of the second dipole. Because $|F\rangle$ is dipolar, its scalar product on $|dR\rangle$ acts as a derivative taken at r = L, and one obtains $E_{\text{coop}}\sim \left(f^2{c}^2/G{L}^d\right)\sim L^{-d}$, i.e., a very rapid decay with distance. This result is confirmed numerically for the case of a crystalline network in the Supporting Materials and Methods, Section D.

Illustration of optimal cooperativity: shear architecture

We now show that cooperativity can be greatly improved if the material presents a very soft extended mode. For illustration, we consider the geometry of Fig. 8, in which a cylinder of elastic modulus G is cut on its length L, by a band of width c. This generates a zero mode corresponding to the rotation of a square. If displacements at the active or allosteric sites of size δ are imposed, as illustrated in Fig. 8, they will only couple to that mode (because it costs no energy) and lead to the same response. This statement will be true even if the band of width c is filled up with soft material of elastic modulus G_w, as long as it is small enough (see below). Thus, we have $E^{\mathcal{A}c}\approx E^{\mathcal{A}l}\approx E^{\mathcal{A}c,\mathcal{A}l}$ implying $E_{\text{coop}}\approx E^{\mathcal{A}l}$, which can be readily estimated as the amount of elastic energy stored in the soft band, i.e., $E_{\text{coop}}\sim \left(L/c\right)G_{\text{w}}{\delta }^2$.

Figure 8.

In a cylindrical geometry, a mechanism—or zero mode—can be constructed by slicing the cylinder, as can be achieved by creating a cut of length L and width c. One then obtains an object with the topology of a square, which now displays an additional zero mode corresponding to a rigid rotation. If the cut is filled up with a soft elastic material, the mode gets a finite frequency. As long as it is small, imposing a local displacement as indicated in the figure at the allosteric or at the active site will be dominated by this mode and will lead to essentially the same response. Thus $E^{\mathcal{A}c}\approx E^{\mathcal{A}l}\approx E^{\mathcal{A}c,\mathcal{A}l}$ and $E_{\text{coop}}\approx E^{\mathcal{A}l}$. To see this figure in color, go online.

This result implies that $E_{\text{coop}}=0$ when the material presents a mechanism (i.e., G_w = 0) but increases with G_w. This argument eventually breaks down, however, when it becomes more favorable to deform the rigid material and to couple to other modes in the system. This takes place when the energy of deforming a continuous medium of modulus G, $E_{cont}\sim G{\delta }^2/\text{ln}\left(L/c\right)$, becomes smaller than the energy associated with the soft mode $\left(L/c\right)G_{\text{w}}{\delta }^2$. Comparing these two expressions, we get a crossover for $G_{\text{w}}=G_{\text{w}}^{\text{∗}}$ with

$$G_{\text{w}}^{\text{∗}}\sim \frac{cG}{L\ln \left(L/c\right)}.$$ (10)

For $G_{\text{w}}\gg G_{\text{w}}^{\text{∗}}$, the role of the soft mode becomes negligible, and the system will respond as a homogeneous elastic material (whose cooperativity is small, as described above). Thus, cooperativity will be maximal for $G_{\text{w}}\approx G_{\text{w}}^{\text{∗}}$, leading to an optimal cooperativity of order

$$E_{\text{coop}}^{\text{∗}}\sim \frac{G{\delta }^2}{\ln \left(L/c\right)}.$$ (11)

This result is confirmed numerically in the Supporting Materials and Methods, Section D.

The small energy of the response to binding for large L described by Eq. 11 implies the presence of a soft elastic mode, which is relevant experimentally. It can be detected in the vibrational spectrum of the protein and implies large thermal fluctuations. Such fluctuations, in a harmonic approximation, are inversely proportional to the corresponding eigenvalue of the stiffness matrix of order ${\lambda }^{\text{∗}}\approx E_{\text{coop}}^{\text{∗}}/{\Vert \delta R\Vert }^2$, where ${\Vert \delta R\Vert }^2$ is the square norm of the allosteric response. For the shear mode considered, the following relation holds ${\Vert \delta R\Vert }^2\sim L^2{\delta }^2$ because all particles are moving by a distance of order δ, leading to ${\lambda }^{\text{∗}}\sim 1/\left(L^2\ln \left(L/c\right)\right)$. For the vibrational spectrum, such a small eigenvalue will lead to a low frequency ${\omega }^{\text{∗}}$. Assuming for simplicity that all the particles have identical mass leads to

$${\omega }^{\text{∗}}\sim \sqrt{{\lambda }^{\text{∗}}/m}\sim \frac{1}{L{\ln }^{1/2}\left(L/c\right)},$$ (12)

which is thus much softer than the lowest-frequency plane wave modes, of frequency 1/L. We expect this result to hold both for the vibrational spectrum of the protein, or for that of the protein-ligand complex, for which the frequency of the soft mode is higher but of similar magnitude in our framework.

It is straightforward to extend these results to three dimensions in the geometry of a shear plane, where we find $E_{\text{coop}}^{\text{∗}}\sim Gc{\delta }^2$, which does not decay with distance, and ${\omega }^{\text{∗}}\sim L^{-3/2}$, which is now even much smaller than plane wave modes, thus justifying why the spectrum of our materials show an isolated soft extend mode at low frequency. These results are tested in Fig. 9 for d = 2, which confirms that cooperativity is optimal for a finite frequency of the soft extended mode.

Figure 9.

(A) We build a shear architecture using a triangular lattice with a soft band, where the springs have a stiffness $k_{\text{w}}\ll k=1$ such that the network modulus is proportional to the spring stiffness G_w/G = k_w/k. The imposed displacement at the allosteric site is shown in purple arrows and the associated response in black. Here k_w = 0.05, L = 16, and c = L/10. (B) The energy of simultaneous binding $E^{\mathcal{A}c,\mathcal{A}l}$ and cooperative energy $E_{\text{coop}}$ versus k_w for L = 32 is shown. We confirm that $E_{\text{coop}}$ depends nonmonotonically on k_w. (C) The overlap between the response and the eigenmodes q_ω versus mode frequency ω at optimal $k_{\text{w}}^{\text{∗}}=0.036$ for L =32 and c = L/10, colored as a function of their participation ratio P_ω, is shown. To see this figure in color, go online.

Principles of optimal cooperativity

Overall, the common principle emerging from this study is that optimal cooperativity results from the following antagonist effects. On the one hand, the architectures are such that they nearly present an extended mechanism. Because this mode is much softer than others, an imposed strain strongly couples to it, thus allowing the transfer of the elastic information over long distances. On the other hand, if this extended soft mode is too soft, the elastic costs associated with binding become too small, leading to a small cooperative energy. As a result, there is an optimal frequency scale for cooperativity.

This idea leads to a natural explanation for the empirical facts listed in the introduction. Indeed, shear and hinge designs (observation 1) are clear realizations of this principle, which implies the presence of a soft extended modes at low frequency, consistent with observation 2.

We expect that our main result, i.e., the existence of an optimal vibrational frequency for cooperativity, will hold true when nonlinearities are taken into account. This prediction can be tested using a combination of molecular dynamics and experiments. Molecular dynamics can be used to measure the effect of point mutations on the thermal fluctuations along the relevant normal mode, and experiments can measure the effect of the same mutation on cooperativity. In the spirit of Fig. 9 B, we predict that there is an optimal magnitude of fluctuations for cooperativity to function properly. It would be very interesting to test if proteins function close to this optimum.

Fluctuation-driven cooperativity

Finally, as pointed out in (18, 20), the existence of a soft extended mode of frequency ${\omega }^{\text{∗}}$ leads to the possibility of a cooperative effect with no mean displacement at play once thermal effects are accounted for (observation 3). Indeed, binding at the active site will hinder motion and increase the soft mode frequency, leading to an entropic cost that can be diminished if binding already took place at the allosteric site. Let us define ${\omega }_{\mathcal{A}l}$, ${\omega }_{\mathcal{A}c}$, and ${\omega }_{\mathcal{A}c,\mathcal{A}l}$ as the frequencies of the soft mode after binding at the allosteric site, active site, and both, respectively. We can estimate these quantities as ${\omega }_{\mathcal{A}l}^2={\omega }^{\text{∗}2}+e_{\mathcal{A}l}$, ${\omega }_{\mathcal{A}c}^2={\omega }^{\text{∗}2}+e_{\mathcal{A}c}$, and ${\omega }_{\mathcal{A}c,\mathcal{A}l}^2={\omega }^{\text{∗}2}+e_{\mathcal{A}l}+e_{\mathcal{A}c}$, where $e_{\mathcal{A}l}$ $\left(e_{\mathcal{A}c}\right)$ characterizes the additional energy required for the mode to move when a ligand is bound at the allosteric (active) site. Assuming harmonic dynamics, the entropy of a normal mode of frequency ω reads $S=k_B\text{ln}\left(k_{B}T/\hslash \omega \right)$. Using this expression, one can now estimate the cooperative free energy $\mathit{\Delta \Delta }F=-T\mathit{\Delta \Delta }S=k_{B}T\ln \left({\omega }_{\mathcal{A}c,\mathcal{A}l}{\omega }^{\text{∗}}/{\omega }_{\mathcal{A}l}{\omega }_{\mathcal{A}c}\right)=-k_{B}T\ln \left(1-e_{\mathcal{A}c}{e}_{\mathcal{A}l}/\left({\omega }^{\text{∗}2}+e_{\mathcal{A}l}\right)\left({\omega }^{\text{∗}2}+e_{\mathcal{A}c}\right)\right)$, which can indeed be large if ${\omega }^{\text{∗}2}$ is small compared to both $e_{\mathcal{A}l}$ and $e_{\mathcal{A}c}$.

Conclusions

We have used in silico evolution to design materials which are highly cooperative. Strikingly, the architectures found differ greatly from materials optimized to propagate a geometrical information over long distances. The latter architectures are based on the emergence of a lever that amplifies the mechanical signal where it is desired, which may be relevant in proteins whose task is to trigger large motions when a ligand binds—e.g., to close an ion channel. By contrast, we predict that proteins optimized to be cooperative should display different architectures, including shear and hinge designs, which are well known in the literature. Intriguingly, we find that there is a great variety of possible functioning architectures, especially in the three-dimensional case. However, they all function along the same principle: they nearly display an extended mechanism, whose frequency should be neither too large nor too small for optimal function to occur.

Our approach rationalizes several empirical observations on allosteric proteins and also makes testable predictions. In particular, we predict that a single soft extended mode, whose frequency should decrease with protein size, contributes to function. We find that this prediction is hard to test stringently from a spectral decomposition of the allosteric response alone, because localized soft modes (typically near the surface of the system) can hybridize with the relevant mode if they lie at similar frequencies. As a result, the response appears to project on a few modes (despite the localized modes being irrelevant for function) instead of one.

Recent methods have been developed in computer science to clean up spectra of localized modes—see, e.g., (37)—in the field of community detection. An exciting path forward is to adapt these methods to proteins, allowing one to test if a single extended mode indeed contributes to allostery. Ultimately, this suggests a mechanical approach to discover de novo allosteric proteins, such as those in which a single extended mode lies at low frequency in the cleaned-up spectrum. Such an analysis would further predict where mutations would affect function: we have observed that most damaging mutations hinder the allosteric response and take place where the extended mode generates high shear.

Author Contributions

L.Y. and M.W. conceived the project, and M.W. supervised research. L.Y., R.R., and M.W. developed the theory. L.Y., R.R., and C.B. performed the computations and developed the numerical methods. All authors analyzed the results and wrote the final manuscript. L.Y. and R.R. contributed equally to this work.

Editor: Enrique De La Cruz.

Supporting Citations

Reference (38) appears in the Supporting Material.