FSCS Reveals the Complexity of Lipid Domain Dynamics in the Plasma Membrane of Live Cells

Abstract

The coexistence of lipid domains with different degrees of lipid packing in the plasma membrane of mammalian cells has been postulated, but direct evidence has so far been challenging to obtain because of the small size and short lifetime of these domains in live cells. Here, we use fluorescence spectral correlation spectroscopy in conjunction with a probe sensitive to the membrane environment to quantify spectral fluctuations associated with dynamics of membrane domains in live cells. With this method, we show that membrane domains are present in live COS-7 cells and have a lifetime lower bound of 5.90 and 14.69 ms for the ordered and disordered phases, respectively. Comparisons to simulations indicate that the underlying mechanism of these fluctuations is complex but qualitatively described by a combination of dye diffusion between membrane domains as well as the motion of domains within the membrane.

Introduction

The biophysical properties of the cell plasma membrane are thought to arise from the diversity of lipids and their interactions. For example, the lipid raft hypothesis suggests that membrane heterogeneity is caused by the associations of saturated phospholipids such as sphingomyelin with cholesterol to form a highly ordered lipid domain that diffuses in a sea of less ordered and more fluid phospholipids (1, 2). Further, the hypothesis postulates that a distinct subset of membrane proteins partition preferentially in the raft-like lipid environments, affecting protein clustering, interactions, and diffusion dynamics. An alternative theory is the picket-fence model, which proposes that the plasma membrane is segregated into compartments by underlying cortical actin filaments that are associated with the membrane (3). In this model, membrane lipids and proteins exhibit random diffusion within the compartments but require hop diffusion to cross the membrane-actin barriers. Other studies have proposed that glycosylphosphatidylinositol-anchored proteins are directly coupled to cortical actin in an ATP-dependent manner, resulting in the formation of cholesterol-enriched nanoclusters (4, 5). It should be noted that these models do not exclude each other so that different organizing principles could yield coexisting membrane domains within the plasma membrane (6).

We and others have previously used environment-sensitive fluorescent probes such as Laurdan, di-4-ANEPPDHQ, and NR12S (7, 8, 9), to visualize differences in membrane order in intact and living cells (10, 11). For example, we showed that the plasma membrane at T cell activation sites (12) and focal adhesions (13, 14) is more ordered than the unstimulated regions in the same cell and that membrane condensation contributes to the formation of clathrin-independent endocytic invagination (15, 16, 17). Environment-sensitive fluorescent probes have the advantage that they are often only fluorescent in the hydrophobic environment of the membrane (i.e., minimal background fluorescence from the aqueous media), are not required to partition preferentially into a particular lipid phase, and report the biophysical state of the membrane via spectral shifts or intensity changes. For example, the membrane-order-sensitive dye NR12S displays a large blue shift in the emission maxima in liquid-ordered (L_o) lipid vesicles composed of sphingomyelin and cholesterol compared to liquid-disordered (L_d) vesicles composed of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) (8). This probe inserts itself exclusively into the outer leaflet of both model and cell membranes, avoiding issues with internalization and labeling of internal membranes (8). In phase-separated liposomes, NR12S exhibits no preference for L_o or L_d phases (8).

Because individual membrane domains in cell membranes cannot be resolved with diffraction-limited microscopy (18, 19), most of our biophysical understanding of lipid phase separation and phase coexistence comes from model membranes (20, 21, 22). Researchers have used various techniques to map the phase diagrams of ternary lipid mixtures (23) and four-component bilayers (24) and observed cholesterol-rich L_o-like nanodomains of ∼10 nm in one-component lipid membranes and DOPC-sphingomyelin mixtures with high cholesterol content (21, 22). In an attempt to provide evidence of L_o-like nanodomains in cell membranes that are below the resolution limit of conventional microscopes, we previously unmixed the fluorescence lifetime signal from Laurdan membranes (19). We found that the plasma membrane is better described as a mixture of two lipid environments of low and high membrane order than as a single membrane environment of intermediate order (19). Interestingly, the oxysterol 7-ketocholesterol (7KC), which increases the overall fluidity of the membrane (25), reduced the relative abundance of the ordered membrane but retained the coexistence of two distinct membrane environments (19). Other aspects of lipid phase separation, such as the fluctuations near the critical point, have so far only been observed in model membranes (26, 27).

A technique that has the required temporal resolution to detect even short-lived membrane domains is fluorescence correlation spectroscopy (FCS). By performing FCS measurements at different spatial scales (variable-spot FCS), Wawrezinieck et al. established the so-called FCS diffusion law, in which spot size is plotted against diffusion time through the spot size (28). The FCS diffusion law can distinguish between free diffusion and diffusion impacted by confinement in domains and membrane compartments. Superresolution techniques, such as stimulated emission depletion, dramatically improve the resolution of FCS (29) and reveal the confinement times of different lipids. For example, fluorescently labeled phosphoethanolamine, a putative nonraft lipid, diffused across the detection spot in ∼1 ms, whereas sphingomyelin or raft-associated glycosylphosphatidylinositol-anchored proteins took ∼10 ms (30, 31) and appeared to be trapped in domains of ∼20 nm in diameter (31).

In this article, we combined the high temporal resolution of FCS with the environmentally sensitive probe NR12S in a spectral unmixing approach called fluorescence spectral correlation spectroscopy (FSCS) (32). When FSCS is applied to environment-sensitive fluorescent probes such as NR12S, the fluorescence emitted from more ordered and more fluid membranes can be distinguished by spectral channels. The subsequent analysis essentially treats signals from the separate environments as separate emissive species. This yields timescales of NR12S signal fluctuations originating from the two lipid environments independently. FSCS is analogous to fluorescence lifetime correlation spectroscopy (33, 34), in which the fluorescence lifetime is used to segregate fluorescent signals with overlapping spectra so that correlation curves can be calculated for different signals. FSCS too can separate simultaneous signals arising from multiple fluorophores with overlapping spectra (32). FSCS has the advantage that recording spectra with multiple spectrally resolved detectors is technically simpler than using lifetime measurements and can utilize dyes that show a spectral, but not lifetime, shift in response to the environment, which is the case with NR12S. We applied FSCS to NR12S-stained live cells and found evidence for two coexisting lipid environments, even in cells that have been treated with an oxysterol, 7KC, that increases the overall fluidity of cell membranes. To understand the origin of the fluorescence fluctuation arising from these domains and their dynamic coexistence, we performed a series of simulations and qualitatively compared them to the experimental FSCS data.

Methods

Lipid vesicles were formed by extrusion of the desired lipid mixture (Lo, 70:30 n-palmitoyl-sphingomyelin:cholesterol; Ld 80:20 DOPC:cholesterol; Avanti Polar Lipids, Alabaster, AL) through 100 nm pores at 55°C. Supported lipid bilayers (SLBs) were prepared by diluting extruded and stained vesicles in Ca²⁺ buffer (10 mM HEPES, 150 mM NaCl, 1 mM CaCl₂ (pH 7.4)) and incubated on glass coverslips for 30 min. The formed bilayer was gently flushed three times with HEPES buffer (pH 7.4) to remove remaining vesicles. Samples were stained with NR12S (N-[3-[[9-(diethylamino)-5-oxo-5H-benzo[α]phenoxazin-2-yl]oxy]-propyl-N-methyl-N-(3-sulfopropyl)-1-dodecanaminium; obtained from Dr. Andrey Klymchenko) at a concentration of 0.7 μM for 15 min at room temperature.

COS-7 live cells were stained with NR12S by adding dye solution to the growth medium at a final concentration of 105 nM for 30 min at 37°C. Where indicated, cells were additionally treated with 30 μM oxysterol 7KC (C6970-000; Steraloids, Newport, RI) complexed to 38 mM methyl-β-cyclodextrin (C4555; Sigma, St. Louis, MO) at a concentration of 30 μM simultaneously with the NR12S staining. Cells were treated with latrunculin B (LatB) (L5288; Sigma) by adding LatB to the growth medium at a concentration of 5 μM in the final 5 min of NR12S staining. Cells were then washed three times with phosphate-buffered saline and imaged in Dulbecco’s modified eagle medium.

Data were acquired on a Zeiss LSM 780 confocal microscope using a C-Apochromat 40× 1.20 NA water-immersion objective with 514 nm excitation (7 μW at objective back aperture). Emission was separated by a dichroic mirror and emission filter before passing through a 36.3 μm pinhole. The emission signal was split by a prism before reaching a 32-channel gallium arsenide phosphide photodetector operating in single-photon counting mode. The detector signal was binned into six spectral channels with centers/bandwidths of 552.9/35.6, 579.6/17.8, 597.4/17.8, 615.2/17.8, 637.5/26.7, and 673.1/44.5 nm, respectively. These ranges yield more even count rates across the spectral channels than are obtained from channels with equal spectral widths. The proper z-position of the focus during the acquisition of single point data was confirmed by subsequent line scan FCS acquisition, which provides the actual illuminated area radius.

Spectral analysis and correlations were calculated using home-written LabVIEW and MATLAB (The MathWorks, Natick, MA) code, including an implementation of the multi-τ algorithm for correlation of time-tagged single photon counting data, which accepted double-precision weights for each photon based on the spectra of the two emissive species (see Supporting Materials and Methods).

Fluorophores (n = 200) were simulated as noninteracting particles experiencing two-dimensional Brownian motion within the simulated area (5 × 5 μm) with periodic boundary conditions. The magnitude of motion of the particle between time step t − 1 to t was defined by the identity of the particle, assigned as existing in either the L_o or L_d state. This identity was either assigned at the beginning of the simulation and not varied (the “independent” simulation condition) or evaluated at each time step. In these cases, the particle identity was assigned based on the particle’s location within a two-dimensional (2D) binary domain-containing lattice (“static domains” or “motile domains”) or by a two-state hidden Markov simulation (“switching domains”). The particle identity of L_o was assigned a value equal to 1 and the identity of L_d was assigned a value of 0. Cross talk was introduced by biasing these binary values toward the mean of 0.5, either by a multiplicative factor (in the “independent” case) or by blurring the binary lattice with a Gaussian spatial filter.

The domain-containing lattice was generated as a partially relaxed binary 2D Ising spin lattice in which the input temperature and number of relaxation cycles were used to generate domains of various sizes (here, interaction strength = k_B; temperature = 50, 0.5, 0.01, or 0.001 K for small (1.1 ± 0.05 pixels), medium (25.9 ± 0.51 pixels), and large domains (49.6 ± 1.8 pixels); either 50 (small and medium domains) or 100 (large domains) relaxation iterations). These domain sizes were evaluated through pair correlation and approximation of the resulting curve with a Gaussian domain model (fullwidth at half-maximum values are reported). This Ising lattice was simulated at a 1 nm pixel size with total dimensions of 2 × 2 μm placed at the center of the particle simulation area. The remainder of the area was filled with randomly assigned binary values. In the “static domains” case, this lattice was held fixed and only the particles diffused; in the “motile domains” case, the lattice was also allowed to diffuse randomly within the 2D field. This was accomplished by simulating a single diffusing particle of a defined diffusion constant and shifting the position of all diffusing particles by this position when determining the particle identity at that time step.

Diffusion constants were set at 0.1 μm²/s for the L_o phase and 0.3 μm²/s for the L_d phase (35) for the data presented here in the “independent,” “static domain,” “eroded,” or “blended” cases (Fig. 2; Figs. S6–S8). These values give a reasonable qualitative match to the experimental data under the simulation conditions and fall within an order of magnitude of diffusion constants found in other works (36). In the “motile domain” case (Fig. 3 A), the domains were given a diffusion constant of 5.0 μm²/s and probes diffusion constants of 0 μm²/s. For the “switching domains” case (Fig. 3 C), the switching rate was set to 5 s⁻¹ for the L_o → L_d transition and 15 s⁻¹ for the L_d → L_o rate, and both L_o and L_d diffusion constants were set to 0.01 μm²/s (setting these diffusion constants to 0 μm²/s produced anomalous results). When combining both domain and particle diffusion (Fig. 4), these diffusion constants were set to 0.05, 0.3, and 0.1 μm²/s for the domain, L_o particle, and L_d particle diffusion, respectively.

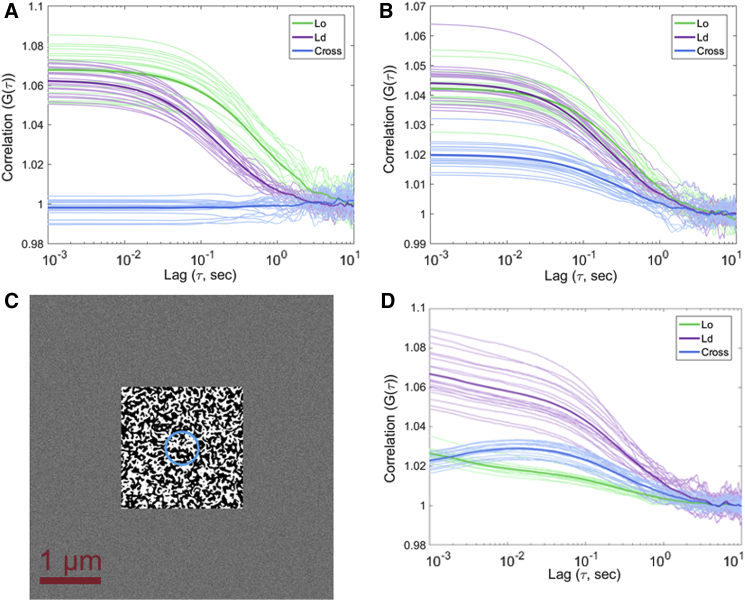
Figure 2.

Simulations of freely diffusing probes in static modeled membranes. (A) Correlations are shown from simulations in which the diffusion rate of the probe differs by environment, but the probes do not change spectral identity after the initial assignment. (B) Correlations from the same simulations are shown, but now with cross talk between spectral channels. (C) A heterogeneous 2D membrane environment is simulated as a 2 × 2 μm semirelaxed binary Ising lattice within a 5 × 5 μm box. The 1/e² diameter of the simulated Gaussian focal spot is shown in blue. (D) Correlations from simulations in which probes are allowed to diffuse and probe identity at a given time is determined by the lattice identity at the probe’s location. Data are processed as for experimental FSCS data sets, resulting in autocorrelation curves shown in (A), (B), and (D) for the L_o (green) and L_d (purple) components and their cross correlation curves (blue) under the respective simulation conditions. To see this figure in color, go online.

Figure 3.

Simulation results from dynamic domain environments. (A) Correlations from simulations in which dyes are fixed relative to the lattice are shown, but the lattice and probes diffuse through the static observational volume. (B) A representative result from LatB-treated cells shows anticorrelation behavior at short timescales (for experimental details, see Fig. 1). Dashed lines indicate the t_1/2 timescales. (C) Correlations from simulations in which probes are additionally allowed to slowly diffuse in addition to switching identities are shown via a hidden Markov model. In (B) and (C), autocorrelation curves for the L_o (green) and L_d (purple) components and cross correlation curves (blue) are shown. To see this figure in color, go online.

Figure 4.

Correlation results from simulations with simultaneous probe diffusion through the modeled domain lattice and diffusion of the underlying domain lattice relative to the observational volume. Autocorrelation curves for the L_o (green) and L_d (purple) components and cross correlation curves (blue) are shown. To see this figure in color, go online.

Simulations were prerun for 10,000 time steps of 1 ms to allow the system to approach the steady state. The simulation was then recorded for an additional 10,000 time steps (10 s). The generated position of each particle was then converted into intensity within the simulated focal spot by evaluating a Gaussian of defined width (1/e² radius of 230 nm) and centered in the simulation box at each particle’s position. This intensity was multiplied either by the particle’s identity or by 1 minus the particle’s identity to generate L_o- and L_d-specific intensity traces. Matrix multiplication of each of these traces by the respective L_o and L_d reference spectra generated identity-specific spectral intensity traces, the sum of which represented the simulated six-channel intensity trace for the simulation. This, along with the generating reference spectra, was passed to an unmixing and correlation function (via fast Fourier transform) to generate the resulting simulated auto- and cross correlation curves. Twenty runs of each simulation were accumulated, and averages for each of the correlation curves were generated before plotting.

Statistical analysis was performed where indicated using the two-sample t-test using the provided MATLAB function ttest2.

Analysis and simulation codes are available through the author’s GitHub repository (https://github.com/PRNicovich/FSCS.git).

Results and Discussion

FSCS in live cells with the polarity-sensitive membrane dye NR12S

In FSCS, the fluorescence intensity of NR12S emitted from live cells is spectrally split or “unmixed” into “ordered” and “fluid” membranes with 16 μs temporal resolution (Fig. S1). It is assumed that the observed spectra originate from at least two fluorescent species that coexist within the observation volume (∼200 nm in diameter) at any given time. The linear spectral unmixing calculation (28) reconstitutes the contributions from a given number of species to the overall spectra. This is done with so-called filter coefficients that are applied to the total mixed spectrum on a per photon basis. This generates the contributions of a signal photon in a given spectral channel at a given time to one of the decomposed signals. It is this decomposition that allows retention of the dynamics to generate the correlation curves.

In our study, we assume the coexistence of only two NR12S species: one residing in “L_o” membranes and the other in “L_d” membranes. Please note that this assumption only allows us to address whether membrane domains of different orders dynamically coexist in cells; it does not allow us to draw conclusions about the similarity or difference between these two membrane environments. Thus, we could use model membranes as reference data that represent membranes in L_o and L_d environments that are vastly different from each other. The use of such simple model systems does not presume that the “L_o” and “L_d” membranes unmixed from our experimental data are indeed L_o and L_d environments; the two cellular membrane environments could be much more similar in their degree of membrane order than the two reference model systems. To ensure that the brightness and diffusion constant of the environmentally sensitive dye has no impact on the FSCS auto- and cross correlation curves, we conducted simulations (Fig. S6) that illustrate the suitability of NR12S as a probe in our work. Additional semiempirical modeling indicates that the chosen reference spectra drawn from model membrane systems are at or near the optimum basis spectra to describe the experimentally observed NR12S emission spectra (Supporting Materials and Methods and Fig. S8).

We recorded spectra and intensity fluctuations of NR12S-labeled COS-7 cells and in model membranes in six spectral channels with 16 μs temporal resolution. Autocorrelations from the fluctuation of NR12S signal as it transited through the detection volume centered on SLBs, which are characteristic of the L_o phase, showed an average diffusion time of 3.55 ± 0.79 ms (±SD, n = 8, Fig. S1) using a 2D free diffusion model. Within this model environment, we can assume that dye motion is the only cause of fluorescence fluctuations on the 10⁻⁴–10⁰ s timescale.

The spectrum acquired from NR12S in these SLB experiments was used as the reference for the pure L_o environment. A similar measurement was performed in single-phase vesicles characteristic of the L_d phase (Figs. 1, A–C and S1). Spectra obtained in cells could be then decomposed into a linear combination of these reference spectra, producing a scaled sum spectrum that reasonably matched the original observed spectrum. Furthermore, the decomposition of the observed spectrum into scaled reference spectra provided FSCS filter coefficients for each of the six spectral channels.

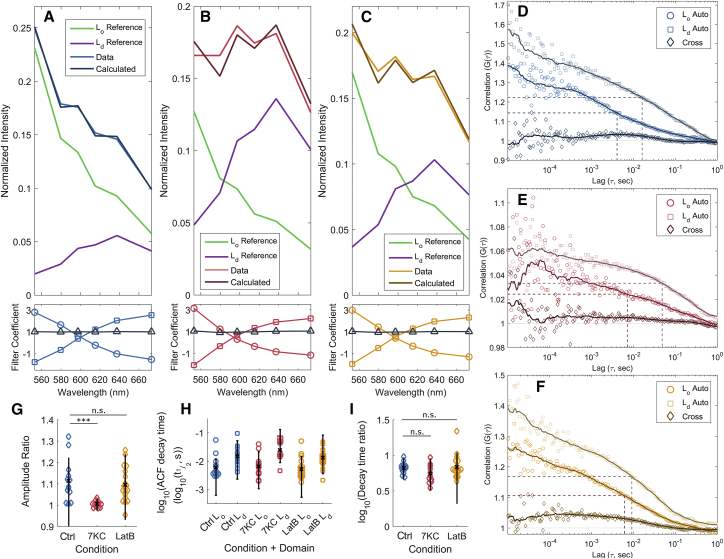
Figure 1.

FSCS in live COS-7 cells. (A–C) Representative measured and fitted spectra of NR12S in control (A), 7KC-treated (B), and LatB-treated (C) cells are shown as well as reference data from model membranes in L_o (green) and L_d (purple) phases. NR12S was excited at 514 nm, and emission was collected in channels with centers/bandwidths of 552.9/35.6, 579.6/17.8, 597.4/17.8, 615.2/17.8, 637.5/26.7, and 673.1/44.5 nm, respectively. Using the reference data from the model membranes, filter coefficients (A–C, bottom) were calculated so that the cellular spectra could be described as a two-component system (calculated, top). Filter coefficients (bottom) represent the relative weighting for each channel for the L_o (circles) and L_d (squares) spectra, with sums that should equal unity (triangles). Data are representative of at least 12 independent measurements. (D–F) Representative correlations for control (D), 7KC-treated (E), and LatB-treated (F) cells were calculated by applying extracted filter coefficients as in (A)–(C) to yield autocorrelations for the L_o (circle) and L_d (square) components of the cellular data and the corresponding cross correlation (diamonds). Dashed lines indicate autocorrelation decay timescales (t_1/2 values). (G) Ratio of autocorrelation amplitudes is shown. (G) A summary of autocorrelation decay timescales is shown. (I) Ratio of autocorrelation decay times is shown. In (G)–(I), each colored symbol is one measurement (n = 13, 12, and 19 for control, 7KC, and LatB conditions, respectively) with mean (black cross) and error bars (black lines) corresponding to 5–95% confidence interval. ^∗∗∗p ≤ 0.001 by two-sample t-test. To see this figure in color, go online.

That the sum of filter coefficients at each spectral channel did not significantly deviate from unity further indicates that the observed spectrum could be adequately described by two components (Fig. 1, A–C, bottom). This does not contradict the presence of “in between” membrane environments or those in which the dye exhibits behavior indicative of an environment somewhere between the extremes of the L_o and L_d reference environments; rather, it shows that a linear combination of these two environments is sufficient to explain the observed behavior.

Untreated cells showed a preference for the ordered phase and enrichment with 7KC, which acts as a spacer in the membrane, greatly increasing the contribution of the disordered phase (19) (Fig. 1 B). LatB treatment, which depolymerizes actin, shows a similar enhancement of the disordered phase in the bulk spectrum but to a lesser extent than 7KC treatment (Fig. 1 C).

These filter coefficients were applied to the measured photon arrival stream to produce the FSCS curves for the two observed spectral components, corresponding to the L_o and L_d contributions. Representative correlation results appear in Fig. 1, D–F, with all measured correlation curves appearing in Figs. S2–S4.

Autocorrelation FSCS curves have a total amplitude approximately equal to the inverse of the average number of molecules in the focal volume. Within this amplitude, the respective curves are divided proportionally to the intensity of the signal from a given NR12S spectral signal and the square of the diffusing entity brightness. The resulting FSCS autocorrelations in live cells show that NR12S in the L_d phase resulted in a stronger correlation signal than in the L_o phase across all conditions (Fig. 1 G). The ratio of amplitudes between L_d and L_o autocorrelations was reduced under 7KC treatment (p = 0.0010) but did not significantly vary under LatB treatment (p = 0.59, Fig. 1 G). This could represent a difference in prevalence of a given membrane environment, of the probe’s preference for one environment over the other, or of a change in diffusing entity brightness in each environment.

All autocorrelation curves show a decrease from a maximum near zero lag (τ = 0) to a value close to 1 signifying no correlation at times approaching τ = ∞, as is typical for aperiodic motion of probes through a single focal volume. The intervening curve shape is complex and not readily fitted to a multicomponent 2D or three-dimensional diffusion model. To compare timescales, the model-free half-amplitude autocorrelation decay time (t_1/2) was used. For cases of single-component 2D diffusion, this value is equal to the diffusion time (τ_D), but for more complex (or unknown) sources of fluorescence fluctuations, it provides a means to compare timescales without fitting to an explicit model.

Mean decay lifetimes were 5.90, 6.48, and 5.15 ms for the L_o component and 14.69, 24.38, and 13.13 ms for the L_d component in control, 7KC-treated, and LatB-treated cells, respectively (Fig. 1 H; Table S1). Previous work indicated that lipid molecules are trapped or confined on timescales of 10–11 ms (31, 37); our results show similar timescales are associated with changes in lipid environment for the probe and that each environment is associated with a distinct timescale.

Autocorrelation decay times showed a similar trend to the amplitude results wherein the L_d autocorrelation decayed to the half amplitude point in a longer time than the L_o phase. This trend carried across treatments, whereas the difference in autocorrelation decay times between the two phases did not vary significantly with treatment (p = 0.075 for 7KC, p = 0.50 for LatB) (Fig. 1 I). As the autocorrelation times are longer than diffusion times observed within SLBs (3.55 ± 0.79 ms in L_d model membranes vs. 13.13–24.37 ms for the L_d component in live cells, ±SD), this means that the diffusion in cell membranes was greatly hindered to constrain the dye molecules within a region smaller than the focal volume. Such constrained motion is a known feature of molecules in plasma membranes; the cause is attributed to multiscale confinement of the lipids to regions 20–750 nm in size (31, 37).

Weighting detected photons with filters for the two spectral components respectively further allows the calculation of an FSCS cross correlation curve. This curve represents the timescale and magnitude of similarities (or dissimilarities) in the fluctuations between the two spectral channels. Representative cross correlations appear in the correlation curves in Fig. 1, D–F, with the full set of measured correlations in Figs. S2–S4. As with the autocorrelation curves, the observed cross correlation signals are complex and not readily fitted to an a priori model of membrane behavior. Still, it is possible to describe commonalities observed in the results.

In all cases, observed cross correlations were of lower amplitude than were the autocorrelations. A common motif in the cross correlation curve is a peak occurring at or near the timescale of the autocorrelation decays (see Fig. 1 D). Such a peak was observed in 11/13 control cells, 4/12 7KC-treated cells, and 9/19 LatB-treated cells over the timescale of the autocorrelation decays (10⁻⁴–10⁻¹ s). These peaks were at timescales comparable to the L_o and L_d autocorrelation decays in the control cell case (Fig. S2), and where present, this moves to faster timescales when cells were treated with 7KC or LatB (Figs. S3 and S4). The reduction in cross correlation peak timescale upon treatment is consistent with a reduction in domain size or reduction in confinement strength of the dye within a single domain.

Other cross correlation curves show anticorrelation (values below 1) at short timescales (τ < 10⁻⁴ s). This feature is observed in 2/13 control cells, 0/12 7KC-treated cells, and 5/19 of the LatB-treated cells. An additional 5/19 cells showed persistent anti-cross-correlation at all measured (10⁻⁵–10⁰ s) timescales.

Simulations of NR12S fluctuations in a heterogeneous membrane environment

Three mechanisms are proposed to potentially give rise to the observed fluorescence fluctuations: 1) the transit of probe through a static, if heterogeneous, membrane; 2) the transit of membrane domains relative to the focal volume; and 3) fluctuation of domain order identity in each location in the membrane. The true process could be a combination of all three hypothesized mechanisms, but the FSCS signal will be dominated by the fastest process, which yields a change in intensity of a single probe species with other processes occurring at longer timescales and lower magnitudes masked.

Simulations provide a means to investigate the implications of these proposed mechanisms on the observable auto- and cross correlation curves. These simulations assume a heterogeneous 2D membrane of a binary mixture of L_o and L_d domains, generated as a semirelaxed Ising lattice. This model is a reasonable approximation of observed membrane behavior on the nanometer scale (26, 38). The degree of relaxation (and resulting size of membrane domains) is held as a variable, as is the membrane viscosity within each environment, degree of motion of the domains, and other potential transition rates. The focal volume is matched to the experimental point-spread function (approximated as a Gaussian with width σ = 230 nm) and centered in a much larger simulated area (5 × 5 μm). Dye intensity is assumed to be equal in both environments. Dye abundance is held constant at 8 dyes/μm² in the simulated membrane, and L_o and L_d spectra are those measured experimentally. Simulations were run 20 times in each condition for 10⁵ ms in 1 ms steps, and the correlation curves were averaged.

As a control, dyes were assigned an environmental and corresponding spectral identity at the start of the simulation and allowed to diffuse. These simulations are not sufficient to yield the observed correlation behavior (Fig. 2). Without switching of dye spectral identity, there is no significant average cross correlation signal, and individual simulation runs show small deviations around 1 that do not change with timescale (Fig. 2 A). Introducing cross talk between channels does add a cross correlation decay as essentially a scaled replica of the average autocorrelation curves (Fig. 2 B; Fig. S5). Importantly, this curve does not show a peak but rather a monotonic decay. These results show that dye switching spectral identity is required for the observed auto- and cross correlation signals. It is not sufficient to have two populations of dye that do not alter their spectral properties through the course of the experiment to recapitulate the experimental observations.

If instead the dyes diffuse within a heterogeneous environment, many of the features are observed in the experimental results (Fig. 2, C and D). Here, a binary membrane lattice domain environment with equal proportion of the two environments was generated, and dyes were allowed to diffuse within this environment. The spectral identity of a given dye was assigned by the value of the binary lattice at the dye’s position at that time point. An additional parameter was added to allow the dye diffusion rate to vary along with the lattice environment. The simulation progressed for 10⁴ time steps to relax to a steady state before the recording of the simulated fluorescence output began.

These simulations produce two key features in the experimental correlations. First, the autocorrelation curves show a deviation in amplitude along with timescale. In all cases with equal probe intensity and domain abundance, the faster diffusional component shows a lower amplitude and faster decay timescale than the slower diffusional component. This occurs even with the two membrane environments being present in equal amounts and without any thermodynamic effects on the preference of the probe for a given environment. The difference in amplitude points to kinetic trapping within an environment of higher effective viscosity as a possible mechanism for the observed difference in autocorrelation amplitude. The observed autocorrelation curves nearly always have the ordered phase autocorrelation curve at higher amplitude, which, given that this phase is of higher viscosity, is consistent with this explanation.

The cross correlation curves under these conditions are also qualitatively consistent with the broad peak near the autocorrelation decay timescale observed in the experimental data. This peak is present in all simulated data sets and represents the motion of dye from one membrane environment to another. The peak position varies linearly with simulated domain size, being at a longer timescale for larger domains. Here, an increase in simulated domain size from 25.93 ± 0.51 nm (±SD, n = 120) to 49.61 ± 1.78 nm (±SD, n = 40) results in an increase in the peak position from 12.15 ± 3.4 ms (±SD) to 25.5 ± 5.0 ms (±SD). If domain size is exceedingly small, approaching the 1 nm pixel size of the simulated area, then three identical correlation curves are observed. Together, these results indicate that the domains must be on the same size scale but smaller than the focal spot for the observed experimental behavior. If they are too small, then the differential correlation behavior is not observed, whereas if they are too large, the domains would be visible in diffraction-limited imaging. Ultimately, previous work indicating a domain size of tens of nanometers (19, 31) is consistent with the observations here.

Kinetic trapping as the primary mechanism for autocorrelation amplitude differences assumes that the two phases are present in near-equal amounts. Manipulating the prevalence of environments in the lattice additionally alters this difference in autocorrelation amplitude, with the ratio of autocorrelation amplitudes being switched when the prevalence of the faster diffusional environment is sufficient to overcome the kinetic trapping effects (Fig. S6). For simulated probes with diffusion constants of 0.1 and 0.3 μm²/s for the L_o and L_d phases, respectively, this crossover occurs when the abundance of the L_d domain increases from 50% to between 44% (Fig. S6, A and B) and 31% (Fig. S6, C and D). In these trials, the cross correlation always shows a peak at a timescale approximately equal to the autocorrelation decays and with an amplitude between the two autocorrelation curves at the peak position. The experimental data are qualitatively consistent with a near-equal distribution of domain abundance.

Intensity differences between probes in the L_o or L_d environment have an additional compounding effect. It has been previously shown that NR12S can vary by a factor of ∼2 in fluorescence quantum yield based on the polarizability of the surrounding environment (8). We ran simulations in equivalent environments while varying the diffusion constant and relative intensity of the probe in different environments (Fig. S7). The autocorrelation amplitude did vary with probe brightness; an increase in brightness yielded an increase in autocorrelation amplitude for that phase.

The effect of different diffusion coefficients in the two phases worked in concert with the brightness effect on autocorrelation amplitude. In the experimental data, we observe that the autocorrelation in the ordered channel is always at a longer timescale than in the fluid channel. All experimental systems show an autocorrelation amplitude ratio of the fluid to the ordered phase greater than 1 (Fig. 1 G). We expect the fluid channel autocorrelation to have a greater amplitude than the ordered channel autocorrelation, given equal probe brightness.

Varying the simulated probe brightness by a factor of two away from equal is sufficient to reach the crossover point such that the brighter ordered channel shows greater autocorrelation amplitude than the dimmer fluid phase (simulated diffusion constants of 0.3 and 0.1 μm2/s and relative brightness of 2:1 for the ordered and fluid environment, respectively). The converse brightness ratio with the same diffusion constants yields simulated amplitudes in the proper sign but with ordered/fluid autocorrelation amplitudes greater than most of the observed experimental data. Although it is difficult to extract an experimental diffusion constant given the complex membrane environment, these data together suggest that the relative brightness of the NR12S probe in the experimental membrane environments is within a factor of 2 or equivalent.

Introducing an intermediate membrane environment state (one between the binary L_o or L_d extreme) by blurring the binary lattice does not alter the qualitative features of the correlation curves (Fig. S8). Modeling domain boundaries as gradients rather than as discrete binary transitions resulted in correlation curves that retained the qualitative features of the curves from the binary condition. The only effect is a reduction in contrast between the three correlation curves with reduced discrete binary character. As with the spectral data, it is not possible to discern if there are truly two distinct membrane environments in the experimental data or if a continuum of environments exists between the two extremes. However, the data observed requires membrane heterogeneity and is not inconsistent with a binary lattice of two distinct membrane states. Additionally, this loss of correlation contrast may provide a route to experimentally quantify the level of discrete character in the membrane, especially if this can be varied by temperature or drug treatment.

Together, these coupled effects of domain abundance, size, and viscosity in the membrane environment on the correlation curves are challenging to disentangle. However, the qualitative features of the correlation curves remain consistent. As such, it is reasonable to continue to compare simulated results against the experimental data to determine parameters that describe the qualitative correlation features observed. From these, we can determine that the experimental behavior is consistent with membrane domains in near-equal abundance with approximately discrete transitions while differing in viscosity. Further, the NR12S probe brightness in the two environments is nearly equivalent.

Simulating mobile domains and domain formation and disassembly

On their own, the cross correlation curves from these simulations are in good agreement with many of the cross correlation curves in the experimental data. However, the experimental data do not always show the same peak as that in the simulations, but in some cases, no peak or a negative anticorrelation signal is shown. Additionally, the cross correlation curve is always at a lower amplitude than both autocorrelation curves rather than crossing the lower-amplitude autocorrelation curve, as seen in these simulations. Whereas this simulated mechanism does explain much of the data, it is not sufficient to explain all qualitative features.

Rather than holding the domain lattice position constant and allowing probes to move, the probes can be held static relative to the lattice while the lattice is allowed to move as a single unit (Fig. 3 A). This would represent a case in which domains moving through a cell membrane carry relatively fixed membrane constituents along with them. Under these conditions, no difference in autocorrelation amplitude or timescale is seen between the two spectral components. The cross correlation curve, however, can recapitulate the observed anticorrelation behavior seen in many of the experimental data sets. This anticorrelation would represent a case in which the presence of one environment excludes the signal from the other being present. In previous work, this was observed with a mixed population of vesicles, each of either L_o or L_d environment, in which the size of the vesicle was sufficient to exclude others from the focal volume (32). Here, the mosaic of the domain lattice accomplishes the same effect.

Anti-cross-correlation behavior was primarily observed in the LatB condition (Fig. 3 B), suggesting the role of the actin meshwork in domain formation and diffusion confinement within the membrane (37, 39). Removal of this confinement through actin depolymerization could yield more motile domains and subsequently the observed correlation behavior.

Notably, the conditions that can yield this anti-cross-correlation are also likely to yield positive cross correlation of the same amplitude and timescale across the measurement window (Fig. 3 A). Such variability in cross correlation in the simulated results helps explain the variability observed in the experimental results, especially under LatB treatment conditions.

A change in domain identity around the dye molecules is the third possibility. Such behavior could be attributed to that of a membrane at or near its critical temperature. Emergent from these conditions are domains similar to the Ising-like regions invoked above but with domain identity at a given point evolving over time as domains percolate within the membrane environment (38, 40). Simulations for this mechanism modeled each dye using a hidden Markov model switching between L_o and L_d identity at a specified rate. There was no spatial connection between simulated probe molecules, but this should not affect the results, as switching entire domains would be equivalent to switching individual probes at the probe densities characteristic of these experiments.

Allowing for both probe identity switching and diffusion (slower than that in the diffusion-only case), it was possible to observe some general parallels between the simulated and observed curves (Fig. 3 C). Interestingly, without additionally allowing for diffusion of the probe, the autocorrelation results for both phases were identical, with the cross correlation being equal in opposite magnitude regardless of specified switching timescale. Like with the diffusion-only case, the autocorrelation curve amplitudes diverge with the longer-lived state, resulting in a greater amplitude. A peak in the cross correlation is observed at a similar timescale to that of the autocorrelation decay. However, the shape of this peak differs from that observed in the diffusion-only case. Rather than a broad peak with positive signal at τ = 0 and increasing to a maximum, the peak here is very close to 1 (uncorrelated) at τ = 0 and rises to a relatively sharp peak at the maximal value. The former diffusion-only peak shape is a much closer fit to the experimental cross correlation curves than that generated by Markov switching of dye identity.

It remains that no one mechanism simulated is sufficient to describe the observed correlation curves. Dye diffusion through a heterogeneous membrane can capture the difference in autocorrelation amplitudes and the shape and presence of the common cross correlation peak motif. Membrane domain translation alternatively can explain the anti-cross-correlation seen in the experimental data. Although a single mechanism may be a simpler explanation, it is fully possible that a more complex set of mechanisms underlies the behavior of probe molecules in the cell membrane.

Combining mechanisms of dye molecules diffusing in and out of mobile domains

To test one such set of combination of mechanisms, we allowed both dye diffusion in and out of domains and lattice motion during the simulation. The result yielded a set of curves well-approximating much of the experimental data (Fig. 4). The amplitude of the correlation curves is correct, with the autocorrelation of the slower-diffusing environment yielding the greatest amplitude, followed by the autocorrelation of the slower environment and finally the cross correlation curve. The cross correlation curve maintains the broad peak with a positive signal at τ = 0.

The match between these simulations and the observed data implies that the dynamics in the cell membrane environment is complex and not well described by a single mechanism. Two separate and plausible mechanisms operating on similar timescales describe the experimental data better (Fig. 4) than any single simulated mechanism alone (Fig. 3). It is therefore likely that multiple mechanisms are involved, and any experiment biased to show only one is present in driving membrane dynamics may well be confirmed. These results show that care should be taken in the interpretation of these results to not unduly exclude other mechanisms. The ability of FSCS does allow for extra information in the form of the cross correlation that is not present in conventional FCS. These crossing events prove exceptionally useful in distinguishing between possible mechanisms, enforcing the utility of this approach to investigate lipid dynamics in live cells.

Conclusions

We demonstrate that FSCS is an appropriate tool for monitoring the dynamics of an environmentally sensitive lipid probe within a dynamic membrane environment. Mechanisms underlying the fluorescence fluctuations are proposed, and we find no single mechanism is sufficient to describe the observed fluctuations; at minimum, a combination of two mechanisms—probe motion through distinct membrane domain environments and motion of domains through the membrane—is necessary to qualitatively recapitulate the correlation behavior observed.

Regardless of mechanism, these experiments show that domains must exist as distinct environments to yield the observed spectrally separable dye signals. Further, these environments are likely to exist on the length scale of tens of nanometers and persist for at least the timescale of the autocorrelation decay i.e., 5.90 and 14.69 ms for the ordered and disordered phases, respectively (Fig. 1 G). These results confirm the presence of distinct lipid phases in live cells and that these domains can fluctuate on biologically relevant timescales.

Author Contributions

J.M.K. and A.B. designed and performed the experiments and initial analysis. P.R.N. performed the analysis and simulation, wrote the manuscript, and generated the figures. K.G. conceived the study and wrote the manuscript. Y.M. contributed to the manuscript preparation.