A Three-Dimensional Region-Growing Motion Tracking Method For Ultrasound Elasticity Imaging

Abstract

A three-dimensional (3D) region-growing motion tracking (RGMT) method for ultrasound elasticity imaging is described. This 3D RGMT method first estimates the displacements at a sparse subset of points, called seeds, uses an objective measure to determine, among those seeds, which displacement estimates to trust, and then performs RGMT in 3D to estimate displacements for the remaining points in the field. During the growing process in 3D, the displacement estimate at one grid point is employed to guide the displacement estimation of its neighboring points using a 3D small search region. To test this algorithm, volumetric ultrasound radiofrequency echo data was acquired from a phantom and five in vivo human breasts. Displacement estimates obtained with the 3D RGMT method were compared with a published two-dimensional (2D) RGMT method via the motion-compensated cross correlation (MCCC) of pre- and post-deformation radiofrequency echo signals. For data from experiments with the phantom, the average MCCC values in the entire tracking region of interest (ROI) were approximately 0.95 and the contrast to noise ratios were 4.6 for both tracking methods. For all 5 human subjects, the average MCCC values within the ROI obtained with the 3D RGMT were consistently higher than those obtained with the 2D RGMT method. These results demonstrated that the 3D RGMT algorithm has the ability to track displacements with increased accuracy and generate higher-quality 3D elasticity images than the 2D RGMT method.

Introduction

Ultrasound strain elastography (Hall, et al. 2003, Odonnell, et al. 1994, Ophir, et al. 1991) (SE) is a noninvasive method to estimate the relative stiffness of biological tissues. Changes in tissue elasticity often correlate to pathological evolution of many diseases (Fung 1993). SE has been successfully applied to noninvasive differentiation of breast lesions (Barr, et al. 2015, Burnside, et al. 2007, Hall, et al. 2003) and is now available on most commercial ultrasound imaging systems using one-dimensional (1D) or 1.25D linear array transducers to form two-dimensional (2D) strain images. Block matching is a common approach to track displacements between pairs of RF echo signal frames (Jiang and Hall 2009, Odonnell, et al. 1994, Zhu and Hall 2002). To obtain displacement (and strain) estimates within a region of interest (ROI), the simplest approach is to perform an exhaustive (block-matching) search.

Since breast tissues can roughly be assumed to be a continuum, internal displacement fields due to an external load should be reasonably continuous. Because of this tissue continuity assumption, a cohort of guided-search motion tracking methods have been reported in the literature (Jiang and Hall 2007, Zahiri-Azar and Salcudean 2006, Zhu and Hall 2002). More specifically, a guided-search motion tracking method assumes that a displacement vector at one location can be used to guide the block-matching search in its immediate neighboring points. This strategy reduces the computational cost by limiting the search range. The guided-search strategy also makes large (“peak hopping” (Walker and Trahey 1995)) tracking errors less likely (given good initial displacement estimates). Early guided-search motion-tracking algorithms had preferred guidance directions, e.g. axial guidance (Zhu and Hall 2002), lateral guidance (Jiang and Hall 2007), and diagonal guidance (Zahiri-Azar and Salcudean 2006). The problem with these guidance strategies is displacement estimate error accumulation due to those errors providing bad guidance during the guided-search process. Chen et al. (Chen, et al. 2009) suggested that, instead of a systematic directional search, the priority of search guidance should depend on the quality of echo signal matching, and this strategy has significantly reduced displacement estimate error accumulation (Zhu and Hall 2002). However, this strategy can also be influenced by the accuracy of the initial displacement estimates (known as the seeds). Fleming and Hassan proposed a robust regularized displacment estimation method in which displacement was first estimated for one most robust RF-line (called seed RF-line) by optimizing a cost function that incorporates the RF amplitude similarity and displacement smoothness via dymamic programming, and then propagated in others directions throughout the entire image (Fleming, et al. 2012, Rivaz, et al. 2008, Rivaz, et al. 2008). Jiang and Hall improved the quality-guided search by setting strict criteria for seed selection, thereby improving the tracking outcome (Jiang and Hall 2011).

Although those studies showed that the guided search can effectively eliminate some large tracking errors using two-dimensional ultrasound data, improved motion tracking alone cannot completely overcome echo signal decorrelation induced by out-of-plane motion (perpendicular to the 2D imaging plane). (Bharat, et al. 2008, Bilgen and Insana 1997) The three-dimensional (3D) volumetric whole breast ultrasound systems (e.g. Siemens Acuson ABVS and GE Invenia ABUS) now available present an excellent opportunity for performing 3D volumetric SE. The perceived advantages of a 3D breast SE systems include: (1) motion tracking errors due to the presence of out-of-plane motion can be reduced; and (2) viewing the full breast lesion in 3D (multiple parallel planes, perpendicular, or arbitrary planes; not just the easiest plane to obtain a strain image) may further aid diagnostic accuracy. To track 3D displacements, a 2D region-growing motion tracking (RGMT) method was previously reported (Wang, et al. 2017), in which high-quality seed selection and subsequent region growing were limited to a single plane while the motion tracking was performed in 3D. In other words, region-growing motion tracking was first performed in one plane to obtain 3D displacement vector fields and then the displacement estimates in that plane were used to guide displacement estimation of its adjacent plane(s).

The 2D region growing used in the 2D RGMT method is constrained within an imaging plane and therefore, may be “sub-optimal” in the practical sense. The primary goals of this study were twofold. First, a framework/strategy termed 3D RGMT is described that extends the quality guided search (Chen, et al. 2009) into 3D search in arbitrary directions (not limited by the direction of acquisition of consecutive 2D planes). Second, the performance of 3D RGMT was compared to the 2D RGMT approach using 3D ultrasound data acquired from a tissue-mimicking phantom and in vivo breast tissues containing lesions. Given signal decorrelation and anatomical discontinuities presented in the breast, we expect that some large tracking errors may be avoided if high-quality 3D motion tracking guidance can be provided.

Methods and Materials

The core concept of this motion tracking method is built on several previously published guided-search algorithms in 2D (Chen, et al. 2009, Jiang and Hall 2011, Wang, et al. 2017). Hence, emphasis here was given to new developments in 3D. 3D RGMT was performed on a pair (a pre-deformation and a post-deformation) of volume radiofrequency (RF) echo signal data. In the pre-deformation data, a sparsely and evenly-distributed set of RF sample points within a 3D region of interest (ROI) was selected as the tracking ROI. The aim of the 3D RGMT was to estimate displacements of the points within the tracking ROI.

Our description below starts with some basic definitions used in the motion tracking algorithm, followed by implementation details. These basic definitions include the neighboring point (NP), known-displacement point set, interior point (IP) set and boundary point (BP) set. More details can be found in the Appendix. In the framework of motion tracking, our goal was to make the known-displacement point set include the entire tracking ROI. In this sense, mathematically, the motion-tracking task converts members of the unknown-displacement point set to members of the known-displacement point set.

Algorithm overview

Similar to other guided-search algorithms (Fleming, et al. 2012, Jiang and Hall 2011), the 3D RGMT algorithm is a two-step process. It starts with a set of highly-reliable displacement estimates, called “seeds”. Then, similar to other region-growing algorithms (Wang, et al. 2017), motion tracking proceeds by a guided-search in the neighborhood of those seeds.

Step1 - Finding seeds

To initiate this algorithm, some highly reliable seeds need to be identified by meeting a set of pre-determined acceptance criteria described below. First, a sparse set of points (typically 1-2mm apart) in the tracking ROI are randomly selected as candidates for seed centers. For each selected center point, its 6 NPs are also included in the test for that seed. An exhaustive block matching search is performed (using normalized cross correlation for the block-matching metric) for each of the 7-points for each candidate seed using a large 3D search region that accommodates at least 5% local strain. The maximum (tracking) cross correlation sum (MCCS) (Wang, et al. 2017) of all the 7 points is one metric for the quality of motion tracking for that seed. The maximum absolute displacement difference (MADD) (Wang, et al. 2017) between the NPs and the center point (i.e. the displacement difference between the square and the solid round point in Fig. 1) provides a measure of the continuity among displacement estimates for that seed.

Fig 1.

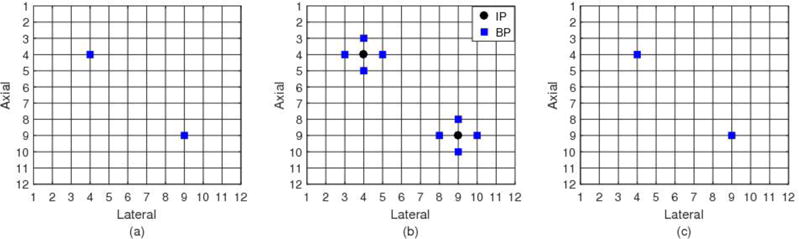
An example of guided-search motion tracking seeds. Subfigures (a), (b) and (c) show the three successive slices of the motion tracking grid. Two 7-point neighborhoods (14 points), represented by both the round and square makers, are selected seeds, which comprise the initial known-displacement set. Among them, the solid round points compose the initial interior point set, and square points constitute the initial boundary point set.

The combination of high correlation and continuity in the neighborhood of a seed candidate center point are used to assess the reliability of those initial displacement vectors. More specifically, one 7-point neighborhood will be accepted as trusted seeds only if the MCCS of those 7 points is higher than a threshold and the MADD is lower than a threshold. Those two thresholds are selected empirically for specific experiments. Fig. 1 shows an example of trusted seeds.

Step 2 - 3D region growing displacement estimation

Once initial seeds are determined (in Step 1), those seeds comprise initial known-displacement point set. The subsequent guided-search 3D region-growing motion tracking process is described as follows:

1. The interior point set and boundary point set of the known-displacement point set are determined, as shown in Fig. 1.

2. In the BP set, the BP that has the highest (tracking) correlation value will be selected as the current active growing point (AGP). In Fig. A.1(b), the diamond marker (6, 8) represents the active growing point.

3. Region-growing displacement estimation is performed in the neighborhood of this AGP. Briefly, displacements of the NPs of this AGP will be estimated guided by the displacement of this AGP. Using the displacement of the AGP as the initial guess, the displacements of the neighboring points are estimated by searching the maximum normalized cross correlation within a small search region (1 RF sample in each direction).

   Subsample displacement is estimated by quadratic interpolation (Chen, et al. 2005, Jiang and Hall 2009). In Fig. A.1, the open circles (with or without a solid point in it) are the neighboring points of the AGP. Because the tracking ROI can be uniquely divided into three sets (the IP set of the known-displacement set, the BP set of the known-displacement set, and unknown-displacement point set), every neighboring point of the AGP must belong to one and only one of those three sets. Consequently, the algorithm will distinguish the following three conditions:

   • If the AGP’s NP belongs to the IP set, its displacement is known and there will be no change in its displacement estimate. In Fig. A.1(b), the solid round point with an outer open circle whose coordinate is (6, 7) is this type of the NP.
   • If the AGP’s NP belongs to the unknown-displacement point set, its displacement will be estimated with guidance from the displacement of AGP. In Fig. A.1, all the open circles without any solid point in it, i.e. (6, 9) and (7, 8) in Fig. A.1(b), are this type of NP.
   • If the AGP’s NP belongs to the BP set, its displacement has been already estimated, but it will be re-estimated using guidance from the current AGP. If the newly-obtained correlation coefficient of this BP estimated by the current AGP is larger than its previous (tracking) correlation value, the displacement of this BP will be replaced by the newly-obtained value. If not, its previously-estimated displacement will not be changed. In Fig. A.1(b), the square point with an outer open circle (5, 8) is this type of NP. Its displacement was previously estimated by the point (5, 7) and now will be estimated again by the current AGP (6, 8). Thereafter, its displacements may be updated further by its other NPs. The displacement estimate with the highest correlation value will be taken as the ‘best’ displacement estimate of this point.

4. After completion of region-growing displacement estimation in the neighborhood of AGP, among the AGP’s neighboring points, those points whose displacements were initially unknown now have known displacements and now become new boundary points of the updated known-displacement set. Hence, these points will be added into the known-displacement point set and boundary point set. The open circle points without any round or square inside it, such as points (6, 9) and (7, 8) in Fig. A.1(b), are these points.

5. The AGP now becomes a member of the IP set because displacements have been estimated for all its NPs.

6. The known-displacement set, the IP set and the BP set have been updated (Step 1 repeated). The BP that has the highest (tracking) correlation value is selected as the current AGP (Step 2 is repeated). The rest of the above process is repeated until the IP set covers the whole tracking ROI.

The 3D RGMT algorithm can use the number of elements in the IP set to track progress of the region-growing loop because that number increases by one after one loop. The loop terminates when the number of elements in the IP set reaches the total number of points in the ROI. The algorithm flowchart is shown in Fig. 2.

Fig 2.

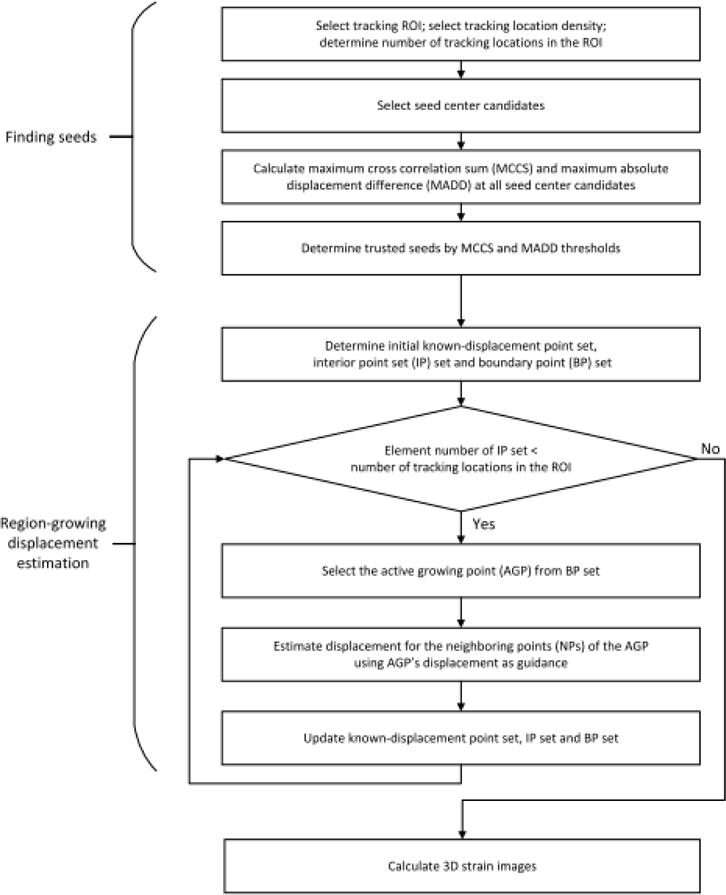
The flowchart for the 3D RGMT method.

Comparison with the 2D region-growing motion tracking method

The performance of the 3D RGMT method was compared with a plane-by-plane 2D RGMT method (Wang, et al. 2017) using motion compensated cross-correlation (MCCC) (Jiang, et al. 2006) between pre-deformation RF echo signals and the motion-compensated post-deformation RF echo signals in the tracking ROI as a metric of displacement estimate accuracy. Recall that both 2D RGMT and 3D RGMT can produce a 3D displacement vector field. However, the growing strategy between these two methods is different. The 2D RGMT grows only in an image plane and then uses the displacement estimates in that plane to guide displacement estimation of its immediate adjacent plane, whereas the 3D RGMT has no constrained growth direction and thus, is expected to better cope with known detrimental factors of motion tracking such as signal decorrelation and anatomical discontinuities.

The target in an image was segmented from its background using a gray level threshold method. Small connected regions outside the inclusion were removed and the gaps inside the inclusion, if they existed, were filled using morphologic operations, like dilation and erosion. The target contrast-to-noise ratio (CNR) (Fisher, et al. 2010, Song, et al. 2004) was used as a metric of image quality for comparing motion tracking algorithms, as shown in Eqn (1). S_TG and S_BK are the average strain of the target and background region respectively. σ_TG and σ_BK are the standard deviation (SD) of strain estimates in the target and background, respectively. The CNR is weighted by the relative area contributions of the target (w_TG) and the background (w_BK); the summation of w_TG and w_BK equals 1. Both 2D and 3D CNR were calculated. For the 3D CNR, the entire 3D inclusion was selected as the target and the rest of the tracking ROI was the background.

$$\mathit{CNR}=\frac{\left|S_{TG}-S_{BK}\right|}{\sqrt{\left[w_{TG}{\sigma }_{TG}^2+w_{BK}{\sigma }_{BK}^2\right]}}$$ (1)

Experiments

The 3D volumetric ultrasound (RF) echo data was collected using a modified (Wang, et al. 2017) Siemens S2000 automated breast volume scanning system (ABVS; Siemens Medical (USA) Solution Inc., Mountain View, California). The ABVS was equipped with a high-frequency 1D array ultrasound transducer (14L5BV), controlled by two motors. One stepper motor moved the ultrasound transducer along the elevational direction to obtain a sequence of 2D ultrasound echo frames. The second motor controlled vertical movement of the transducer, thus allowing contact between the probe and the breast surface to be adjusted. The second motor enabled different levels of deformation in consecutive automated whole breast scans. The center frequency of the ultrasound transducer was 11MHz and the sampling rate was 40 MHz (Brunke, et al. 2007). The full width at half-max of the pulse-echo autocorrelation functions were 0.2mm, 0.7mm, and 1.4mm in the axial, lateral, and elevational directions, respectively (Wang, et al. 2017). More details about this system and the scanning procedure were described in (Wang, et al. 2017).

In this paper, when we describe a 3D parameter, the first, second, and third elements are always the axial, lateral, and elevational directions, respectively.

Phantom experiment

A 10cm×10cm×7cm (axial×lateral×elevational) tissue-mimicking (TM) phantom containing two hard 1cm diameter spherical inclusions (Fisher, et al. 2010, Madsen, et al. 2003, Madsen, et al. 2006) was scanned with the ABVS. To obtain a volume-average strain of about 2%, the ABVS arm was lowered about 1.5mm between volume scans. A 3D RF echo data set, spanning 6cm×7.6cm×4.4cm, was scanned resulting in 3116×512×220 RF samples with the spatial sampling interval of 0.02mm×0.15mm×0.2mm. The pre- and post-deformation volumes of RF echo data were recorded for off-line processing.

A sub-volume approximately centered on one of the two inclusions (1.7cm×2.4cm×1.9cm) was selected as the motion tracking ROI. Motion tracking was performed on a grid separated by 8×1×1 RF samples (every 8 samples along the axial direction and no decimation along the other two directions). A sparse set of grid points with spacing of 7×7×5 points in the ROI was selected as seed candidate centers. The MCCS and MADD thresholds for seed acceptance were 5.6 (=0.8×7) and 1×1×1 RF sample, respectively. Overall, these correlation thresholds were empirically determined, in order to make sure that a reasonable number of seeds were obtained. The motion tracking correlation kernel size for the seed selection and region growing was 19×3×5 RF samples. The search region for seed selection and region growing were 41×9×9 and 1×1×1 RF samples, respectively.

For comparison, the 2D RGMT method was also conducted on the same data set and same ROI for motion tracking. The middle slice was arbitrarily selected as the initial slice for the convenience of programming considerations. The correlation threshold for elevational guiding point selection was 0.8. To give a fair comparison, it was selected in accordance with the MCCS threshold in 3D RGMT, which equals 5.6 (=0.8×7), meaning that every point in this neighborhood has, on average, a correlation higher than 0.8. Other motion tracking parameters, including the distribution of seed center candidates, the MCCS and MADD for seed selection (with adjustments for 2D), seed selection and region-growing tracking kernel and search region sizes (with adjustments for 2D), were all the same as those in the 3D RGMT method.

Human subjects experiment

Human breasts were also scanned in vivo. We recruited 15 human subjects. Seven of those subjects were volunteers with normal tissue (no evidence of breast abnormality in screening mammography) and five had a biopsy-confirmed fibroadenoma. Three additional subjects were recruited from a pool of subjects scheduled for core biopsy. The protocol used in the study was approved by the Health Sciences Institutional Review Board of University of Wisconsin and was compliant with the Health Insurance Portability and Accountability Act. Written informed consents were obtained from all subjects.

Each subject was in the supine position on a scanning bed with the ABVS pod placed over her breast. A series of RF echo signal volumes were acquired with sequential lowering of the ABVS scan head. The subject was asked to not breathe during individual volume scans. After each volume scan was completed, the subject was allowed to take several breaths and the ABVS arm was lowered to generate a strain of about 1-2%. Then, another volume scan was performed. A total of about 20 RF echo signal volumes were acquired for each subject.

Among the 15 subjects, some had significant body movement, and some breathed, during the scan. Some data were acquired with bad coupling between the scan head and the breast which wasn’t discovered until late into the study. These data were not suitable for motion tracking and were excluded. Among the well-acquired data, five subjects whose B-mode image demonstrated a suspected tumor were selected to test the performance to the motion tracking method. Motion tracking was performed on three volume pairs for each of those five subjects.

For each subject, a rectangular volume around the suspected tumor observed in the B-mode image was chosen for the tracking ROI. The tracking ROI sizes for the five subjects are shown in Table 1. Among the five subjects, the other motion tracking parameters (correlation kernel size, search region, MCCS, MADD etc.) were all the same for both 3D RGMT and 2D RGMT methods. The 3D RGMT parameter settings of a representative woman are described in the result section.

Table 1.

The tracking ROI size, average MCCC obtained, and computation times for the 2D and 3D RGMT methods for each of the five subjects included in this study and for three volume pairs for each subject. The standard deviations in MCCC and computation time represent the variation among three volume pairs among each of the five subjects.

Subject Number	1	2	3	4	5
ROI Size (cm3) for 2D and 3D RGMT	2.0×3.3×1.5	1.7×3.6×1.6	1.9×5.8×1.1	2.2×4.8×1.4	2.1×4.6×1.8
MCCC for 2D RGMT	0.71±0.08	0.80±0.04	0.79±0.02	0.72±0.16	0.87±0.06
MCCC for 3D RGMT	0.79±0.03	0.87± 0.03	0.83±0.03	0.87±0.03	0.90±0.03
Execution time (min) for 2D RGMT	10.2±0.4	7.8±0.4	9.1±0.5	11.4±0.7	12.1±1.0
Execution time (min) for 3D RGMT	27.7±1.5	18.8±1.1	22.2±0.6	35.7±0.3	36.1±1.7

For the 2D RGMT method the middle slice was selected as the initial slice. The MCCS threshold for seed acceptance was 3.8 (=0.76×5). The correlation threshold for elevational guiding point selection was 0.76. All other motion tracking parameters were set to the same as these used the 3D RGMT method.

Both 2D RGMT and 3D RGMT methods were written in C++ as MEX functions which were compiled and called by MATLAB. Both algorithms ran on a computer with Intel Core i7-4790k CPU and 32GB memory. The execution time for both methods was measured in MATLAB (version 2016b Mathworks Inc., MA, USA) and therefore includes both the runtime of the C++ function and the MATLAB scripts using the same data and comparable parameters.

Results

Phantom experiment

Fig. 3 shows the results from the phantom experiment for one slice through the inclusion. The inclusion is not apparent in the B-mode image (Fig. 3(a)). In Fig. 3(b), white points represent the seeds in this slice. Each 5-point white cross, together with one point in each of the two adjacent slices (not shown in this figure) compose the 7-point neighborhood of one seed center. In Fig. 3(c), the axial displacement is brighter at top-left corner and darker at the bottom-right corner, suggesting the right side might be subjected to a slightly higher stress possibly due to the transducer scanning plane being not exactly horizontal during the compression process. Lateral expansion is seen in the lateral displacement field (Fig. 3(d)). Fig. 3(f) shows the elevational displacement field. In axial strain image (Fig. 3(e)), an obvious round inclusion stiffer than its background can be seen. The average strain of the inclusion and the background are 1.3% and 2.7% respectively. Fig. 3(g) shows the segmentation result from the axial strain image used to calculate the CNR. The white area represents the target (the spherical inclusion). The black area represents the background. The 2D CNR of this slice is 4.5. The MCCC image shown in Fig. 3(h) has an average value of 0.95.

Fig. 3.

Motion tracking results for one plane through the phantom using the 3D region-growing motion tracking method. The subfigures show: (a) one plane through the B-mode image, (b) location of trusted seeds in that plane, (c) the resulting axial displacement field, (d) lateral displacement field, (e) axial strain, (f) elevational displacement field, (g) image segmentation result, and (h) image of motion compensated cross correlation coefficient values. The location and size of the round inclusion in the axial strain image can be clearly observed. The axial displacement is smoothly varying. The average MCCC for this slice (0.95) is high.

Three perpendicular slices through the inclusion were selected from the 3D axial displacement field and shown in Fig. 4(a), (b) and (c), respectively. The horizontal and vertical lines in each image show the positions of the other 2 images. The stiff spherical inclusion is clearly seen in all the three images. Fig. 4(d) shows the composite view of the three slices. For the whole 3D tracking ROI, the average (± SD) elevational displacement is −0.33±0.16 mm (about −1.7±0.8 planes) and 96% of the elevational displacements are between −0.6 to 0 mm (about −3 to 0 planes).

Fig. 4.

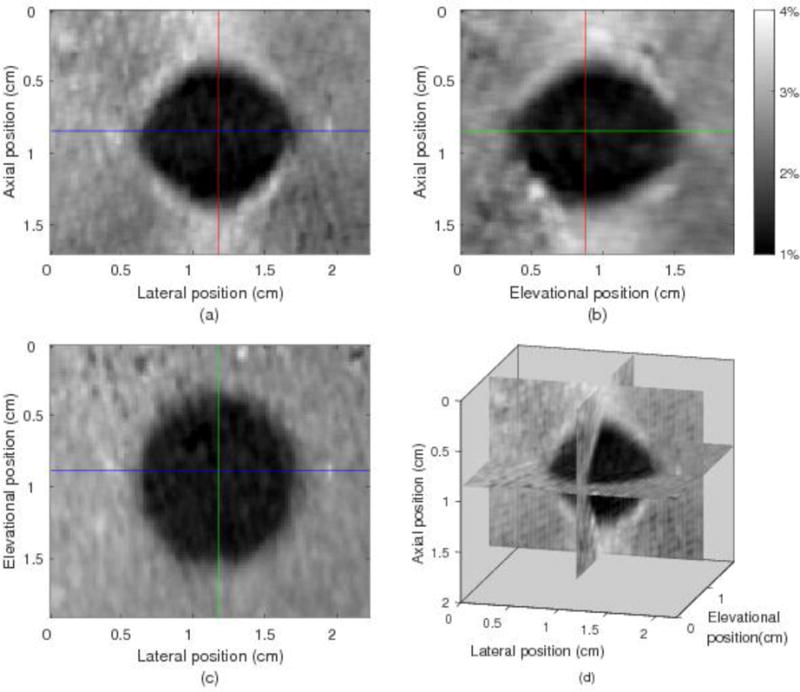
Three orthogonal views and a composite view of the 3D axial strain field from the 3D region-growing motion tracking in the phantom. (a) Axial-lateral view, (b) Axial-elevational view, (c) Elevational-lateral view, (d) composite 3D view. The spherical inclusion is apparent in this figure.

Through three-dimensional visualization and objective performance metrics, we found that both 2D and 3D RGMT methods led to high-quality strain images for the phantom data. More specifically, the 3D CNR for the phantom experiment obtained by the 2D and 3D RGMT methods were both 4.6. The averages of MCCC for the whole 3D tracking ROI using the 3D RGMT was slightly better than that obtained using the 2D RGMT (0.95 vs. 0.94). These results imply that both methods produced comparable performance for the phantom data (phantom experiments are too easy to distinguish among high-quality tracking algorithms).

The execution times for the 2D RGMT was shorter than that needed by 3D RGMT algorithms (8min vs. 17min).

In vivo human breast

The tracking result of a representative woman whose breast has an obvious abnormality (fibroadenoma) is shown in Fig. 5 for illustration. For this subject, a 3D region 6cm×7.6cm×4cm was scanned with the sampling interval of 0.02mm×0.15mm×0.17mm. A 2.0cm×3.3cm×1.5cm cuboid region enclosing the fibroadenoma with displacement grid points separated by 8×1×1 RF samples was selected as the motion tracking ROI. A more sparse grid with spacing of 7×5×5 samples in the ROI was selected for seed candidate centers. The threshold MCCS and MADD for seed acceptance were 5.32 (=0.76×7) and 1×1×1 RF sample, respectively. The correlation kernel sizes (19×3×5 RF samples) were the same as those in the phantom experiment. The search region for seed acceptance and region growing were 41×11×11 and 1×1×1 RF samples, respectively.

Fig. 5.

Motion tracking results for one plane through the human breast using the 3D region-growing motion tracking method. The subfigures show: (a) one plane through the B-mode image, (b) axial strain, (c) candidate seed centers, (d) trusted seeds (e) axial displacement, (f) lateral displacement, (g) elevational displacement, and (h) MCCC image. The lesion location and size in the axial strain image (b) correspond to those in the B-mode image (a). The average MCCC (0.85) for this slice (h) is high.

Fig. 5 shows an example of the motion tracking results for one volume pair and one slice passing through a lesion from that subject. Fig. 5(a) shows the B-mode image with a hypoechoic fibroadenoma (see arrows). The bright reflector near the center of the fibroadenoma (see double arrows) is a surgical clip used to identify the lesion for future reference. Fig. 5(b) shows the axial strain image where the frame average strain is 1.6%. The white points in Fig. 5(c) represent the candidates for seed center points. In Fig. 5(d), the six white crosses are the locations of trusted seeds in this slice. Fig. 5(e) shows the axial displacement field with the estimated displacement being relatively small at the top and larger at the bottom. Fig. 5(f) and (g) show the lateral and elevational displacement fields, respectively. The MCCC image (Fig. 5(h)) displays local MCCC values and the MCCC average of this slice is 0.85.

Figure 6 shows the three orthogonal views of the 3D axial strain field from the in vivo breast data shown in Fig. 5. In Fig. 6, the dark area indicating low strain in the tumor can be clearly seen. For the scan on this subject, the tumor was close to the edge of the elevational scan range and only a little more than half of the tumor was scanned in the elevation direction as shown in Fig. 6(b) and (c). The boundary of the tumor looks brighter, representing higher strain. This might be due to the surrounding tissue sliding along the tumor boundary during compression. The average (±SD) MCCC (among three volume pairs) for the whole 3D tracking ROI is 0.79±0.03. For the whole 3D tracking ROI, the average elevational displacement (±SD) is 0.34±0.28 mm (about 2±1.6 image planes), and 96% elevational displacements are located between −0.34 and 0.84 mm (about −2 to +5 image planes).

Fig. 6.

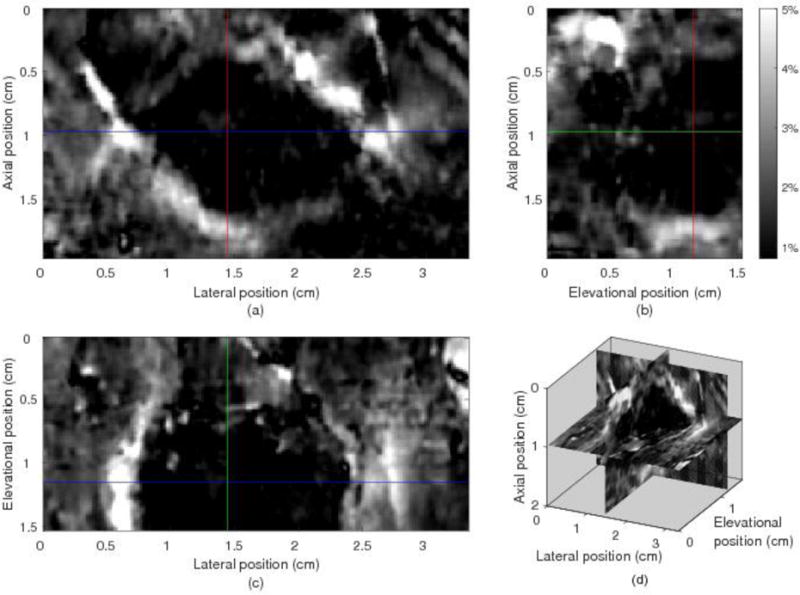
Three orthogonal and composite views of the 3D axial strain filed from 3D region growing motion tracking in the 3D ROI of the in vivo human breast. The dark area, indicating increased local stiffness, represent the lesion. The 3D location and structure of this lesion can be observed.

Figs. 7 and 8 show comparisons of motion tracking results in two example slices obtained using the 2D RGMT algorithm (left column) and 3D RGMT algorithm (right column), respectively. For the slice of Fig. 7, both algorithms provide similar motion tracking results in these images. Comparing rows 1 and 3, the location and size of the lesion corresponds well between the B-mode and axial strain. The average MCCC using the 3D RGMT algorithm (Fig. 7(h)) was 0.85, which is slightly higher than the value (0.83) obtained using the 2D RGMT algorithm (Fig. 7(g)). Comparable motion tracking performance among these two algorithms was generally the case. However, there were examples where the 2D RGMT produced noticeably large displacement estimate errors and the 3D RGMT demonstrated considerable improvement, as illustrated in Fig. 8. There the 2D RGMT produced large motion tracking errors at the bottom left corner of this slice (see rectangular in Fig. 8(c) and (e)) where the corresponding MCCC values (Fig. 8(g)) were low with local average value in the rectangular being 0.44, while the 3D RGMT (Fig. 8(h)) performs better at that corner with local average MCCC in the rectangular being 0.76. The average MCCC of this slice for the 3D RGMT is 0.79, higher than that for the 2D RGMT which is 0.73.

Fig. 7.

Motion tracking results for a plane (elevation position=1.2cm) through the in vivo human breast shown in Figs. 5 and 6 comparing displacement estimates obtained by 2D RGMT (left column) and 3D (right column) RGMT methods. Shown in the subfigures are: (a) pre-deformation B-mode image, (b) post-deformation B-mode image, (c and d) axial displacement, (e and f) axial strain, (g and h) MCCC image. For both methods, the axial displacement fields are smooth and the axial strain images show the clearly-defined lesion that is consistent with that in the B-mode images. In this image plane, the average MCCC obtained using the 3D RGMT method (0.85 in (h)) is only slightly higher than that by the 2D RGMT (0.83 in (g)).

Fig. 8.

Motion tracking results for a plane (elevation position=0.8cm) through the in vivo human breast shown in Figs. 5–7 comparing displacement estimates obtained by 2D RGMT (left column) and 3D RGMT (right column) methods. For this slice, the 2D RGMT produced significant motion tracking errors at the bottom-left corner shown in (c) and (e). The MCCC values are low at this corner shown in (g). However, the 3D RGMT performs better here. The average MCCC of this slice by the 3D RGMT method (0.79 in (h)) is slightly higher than that by the 2D RGMT (0.73 in (g)).

Table 1 shows the average (for 3 volume pairs) tracking ROI size, MCCC for the whole 3D tracking ROI, and the execution time for one volume pair, for each of the five subjects using the 2D and 3D RGMT algorithms. For all five subjects, 3D RGMT algorithm produced slightly higher average MCCC than the 2D RGMT algorithm indicating somewhat better motion tracking performance is achieved by the 3D RGMT method compared to the 2D RGMT. That improvement in motion tracking performance comes with an increase in computational cost. The execution times for the 3D RGMT algorithm for one volume pair is approximately 2-3 times of that of the 2D RGMT algorithm.

To understand how the seed location might influence tracking results obtained with the 3D RGMT method, motion tracking was performed on one volume pair for each of the 5 human breast data sets using all the same motion tracking parameters except that a coarser grid of 9×7×5 samples for seed candidate centers was used (as opposed to the 7×5×5 initial grid used throughout the rest of this study). Fig. 9 shows a comparison of the 3D RGMT results for the two seed candidate center grids for the same breast data and image plane shown in Figure 5. For those data, the average absolute fractional error (the absolute difference of the two results divided by the mean of the two results over the entire tracking ROI) of the axial displacement, lateral displacement, elevational displacement, and axial strain are 0.004%, 0.59%, 0.64% and 0.19%, respectively. Summarizing analogous re sults for all the 5 subjects, the average (±SD) fractional error of the axial displacement, lateral displacement, elevational displacement, and axial strain are 0.02%±0.02%, 1.1%±1.5%, 2.2%±3.2%, and 0.46%±0.34%, respectively. These small differences imply that the outcome of the 3D RGMT method is not sensitive to different seed locations, as long as a reasonably large number of trusted seeds can be found.

Fig. 9.

Motion tracking results for the same image plane shown in Fig. 5 through the in vivo human breast comparing displacement estimates obtained by the 3D RGMT with the spacing of seed candidate centers being 7×5×5 (left column) and 9×7×5 (right column). Comparing the images in the two columns, although the locations of the seed candidate centers and trusted seeds from which 3D RGMT start are different, similar motion tracking results are obtained, suggesting that the 3D RGMT is less dependent on the seed locations.

Discussion

The 3D RGMT algorithm provided improved motion tracking and strain image quality compared to the 2D (consecutive image plane) RGMT algorithm. Compared with other guided motion tracking methods, the 3D RGMT algorithm has some advantages, which might account for its good performance. Specifically, like some other region-growing motion tracking algorithms (Fleming, et al. 2012, Jiang and Hall 2011, Wang, et al. 2017), the 3D RGMT method selects seeds by stricter criteria, instead of an exhaustive search (Chen, et al. 2009).

The direction of guidance in the displacement estimation process is completely free in 3D space; it is not restricted to some fixed direction (Jiang and Hall 2007, Wang, et al. 2017, Zahiri-Azar and Salcudean 2006, Zhu and Hall 2002). Previous studies have demonstrated the displacement estimate errors lead to poor displacement estimate guidance which result in increasingly large displacement errors (through error accumulation) and poor-quality strain images. (Zhu and Hall 2002)

The 3D RGMT strategy has advantages over the quality-guided approach reported by Chen, et al (Chen, et al. 2009), and its variations. First, when selecting the next AGP, the 3D RGMT algorithm estimates displacement at each BP and uses those tracking cross correlation values for ranking quality, whereas, in Chen’s method the displacement of a point in the BP set (called ‘set S’) was not estimated and the motion tracking quality of a point in ‘set S’ was assigned from its NP’s correlation. Using the tracking cross correlation of a BP itself, rather than assigning the value from a NP, can more accurately reflect the motion tracking quality at that BP and is more suitable for choosing which BP to use for region-growing, even though estimation of the displacement for all BP increases computational load.

Second, the displacement of a BP is replaceable for the 3D RGMT method, whereas it is not in the 2D RGMT method (Wang, et al. 2017). The displacement estimate for a BP can be estimated with guidance from several of its neighboring points. The displacement for which the highest correlation value is obtained will be taken as the final displacement of this BP. However, for the 2D RGMT the displacement of a BP will be estimated only once. This replacement strategy obviously can increase the computation time but it can also increase the final cross correlation between pre- and motion-compensated post-deformation RF echo fields as demonstrated in the Results section.

Third, in terms of algorithmic implementation, separating the known-displacement set into an interior point set and boundary point set gives a clear description of the displacement estimation process and hence facilitates the implementation of the algorithm. In one region-growing loop, an AGP point will be found and the region-growing displacement estimation in the AGP’s neighborhood will be performed once. After one loop, the number of elements in the known-displacement set will typically increase by 1 to 6, the number of elements in the interior point set increase by one, and the number of elements in the boundary point set will increase early in the motion tracking process and then decrease as tracking nears completion.

The runtime of the 3D RGMT algorithm is longer than that of the 2D RGMT algorithm. The known-displacement set, inner point set, and boundary point set for 3D RGMT contain many more elements than those for the 2D RGMT algorithm. Finding and ranking/sorting element points in larger sets require more time to complete. Additionally, the potential for replacement of BP displacement estimates also increases the computational cost. However, our results show that the improved performance of the 3D RGMT method in some cases justified the higher computational demands. The availability of graphic processing units (GPUs) makes massive parallel processing possible (Peng, et al. 2017), which might mitigate the computational demands.

Previous studies (Jiang and Hall 2011, Rivaz, et al. 2008) used a cost function to combine the similarity of RF data and displacement continuity and then optimized this function to obtain reliable displacements. Those methods require determination of an appropriate regularization weighting coefficient for the sum of those two components of tracking quality. In this study, an alternate approach tested motion tracking performance in a small region (e.g. a 7-point neighborhood – instead of testing at a single location or along an RF-line). Specifically, the combined RF echo signal correlation (MCCS) among displacement estimates in that 7-point neighborhood was tested separately from the continuity (MADD) among those displacement estimates in that 7-point neighborhood. MCCS and MADD were tested separately against independent thresholds instead of combined in a single regularization optimization. This approach guarantees that both motion tracking performance metrics are met (instead of a combined metric). The initial testing in in vivo human data presented in this study demonstrated that this alternate approach was effective. Figure 5 (c) shows the seed candidate centers and Figure 5 (d) shows the seed selection result via the MCCS and MADD thresholds. The candidate seed centers were selected in every 5th image plane within the tracking ROI. Therefore, about 1-in-5 center images were selected to calculate MCCC and MADD. In the slice shown in Figure 5, several seeds were selected. The smooth displacement fields and axial strain image demonstrated that these seeds provided good guidance for displacement estimation of other regions.

Conclusion

The 3D RGMT method has the ability to produce better 3D axial strain images than the 2D RGMT method. Compared with 2D RGMT, the 3D RGMT method can provide 3D displacement fields with higher MCCC but requires more computational time. Our initial results suggested that the improved motion tracking accuracy outweights the increased computational demands, particularly, given the readily available GPU technology that could mitigate this increased computational load.

Appendices

A. Basic definitions used in the motion tracking algorithm

Definition 1

A point set is defined here as a collection of n points (P₁., P₂, …, P_n) which are RF echo signal sample locations in the tracking ROI. The attributes of the set include their spatial coordinates and displacement estimates associated with each and every point.

Definition 2

A known-displacement point (at a given time during the displacement estimation process) is a point in tracking ROI for which displacement has been established through previous displacement estimation (up to that time). Furthermore, the known-displacement point set is composed of all points for which displacement has been estimated. On the other hand, the unknown-displacement point set (at a given time) is the collection of points for which displacement has not been estimated (up to that time).

Definition 3

A center point (CP) is the location of an RF echo sample that identifies the center of a motion tracking kernel. Neighboring points (NP) of a center point are defined as a set of 6-connected points of the center point, following the typical definition in computational geometry. The NP number of a CP could be less than 6, if the CP is at the edge of the tracking ROI.

Definition 4

An interior point (IP) of a point set (PS) is defined as an element of this point set for which all of its neighboring points also belong to this point set. If the point set is the known-displacement set and a point in this PS is an IP, this is equivalent to stating that displacement has been estimated for this point and all of its NPs.

Definition 5

A boundary point (BP) of a point set is defined as an element of the point set for which at least one neighboring point does not belong to this point set. If, for example, the point set is the known-displacement point set and one element is a BP, displacement of that point has been estimated, but displacement has not been estimated for at least one neighboring points.

A simple illustrative example of the IP and BP sets is shown in Fig. A.1. Suppose the tracking ROI in the pre-deformation RF echo volume contains 5 slices, each of which has 12×12 points. Consequently, the cubic ROI contains 12×12×5 points. Inside this ROI, there are some points whose displacements are known. All of those known-displacement points are located in three consecutive slices, e.g., slices 2, 3 and 4 (see Figs. 1a-c). In Figs. A.1(a-c), all known-displacement points are represented by the solid points, including both the round and square points. The other grid points are the unknown-displacement points, including all points in slices 1 and 5 which are not shown in Fig. A.1. Given this known-displacement point set, its IP set and BP set can be determined, indicated by the solid round points and square points, respectively. Note that the edge point (12, 8) in Fig. A.1(b) is also considered as the interior point in this algorithm, because it has only 5 neighboring points, not 6, and all their displacements are known.

By the definitions above, during the process of motion tracking, the known-displacement point set is always the union of its IP set and its BP set. In contrast, the intersection of its IP set and its BP set is the empty set. The union of the known-displacement point set and unknown-displacement point set is tracking ROI, and the intersection of those two sets is the empty set.

Fig. A.1.

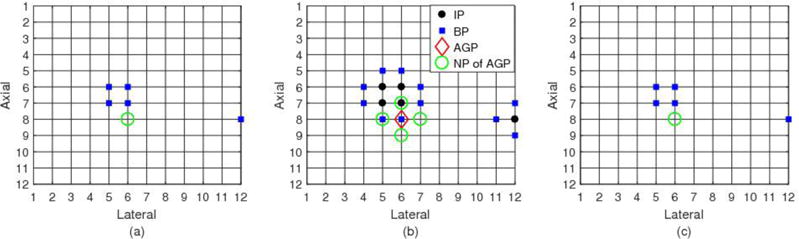
An example of the interior point set and boundary point set of a given known-displacement point set. (a), (b) and (c) show three successive slices respectively. The solid (round and square) points are the known-displacement point set. The solid round points are the interior point set. The square points are the boundary point set. The diamond marker is the active growing point (the boundary point with highest tracking correlation value). The open circles are the neighboring points of this active growing point, for which displacement estimation is guided by the active growing point.