Small Bottleneck Size in a Highly Multipartite Virus during a Complete Infection Cycle

ABSTRACT

Multipartite viruses package their genomic segments independently and thus incur the risk of being unable to transmit their entire genome during host-to-host transmission if they undergo severe bottlenecks. In this paper, we estimated the bottleneck size during one infection cycle of Faba bean necrotic stunt virus (FBNSV), an octopartite nanovirus whose segments have been previously shown to converge to particular and unequal relative frequencies within host plants and aphid vectors. Two methods were used to derive this estimate, one based on the probability of transmission of the virus and the other based on the temporal evolution of the relative frequency of markers for two genomic segments, one frequent and one rare (segment N and S, respectively), both in plants and vectors. Our results show that FBNSV undergoes severe bottlenecks during aphid transmission. Further, even though the bottlenecks are always narrow under our experimental conditions, they slightly widen with the number of transmitting aphids. In particular, when several aphids are used for transmission, the bottleneck size of the segments is also affected by within-plant processes and, importantly, significantly differs across segments. These results indicate that genetic drift not only must be an important process affecting the evolution of these viruses but also that these effects vary across genomic segments and, thus, across viral genes, a rather unique and intriguing situation. We further discuss the potential consequences of our findings for the transmission of multipartite viruses.

IMPORTANCE Multipartite viruses package their genomic segments in independent capsids. The most obvious cost of such genomic structure is the risk of losing at least one segment during host-to-host transmission. A theoretical study has shown that for nanoviruses, composed of 6 to 8 segments, hundreds of copies of each segment need to be transmitted to ensure that at least one copy of each segment was present in the host. These estimations seem to be very high compared to the size of the bottlenecks measured with other viruses. Here, we estimated the bottleneck size during one infection cycle of FBNSV, an octopartite nanovirus. We show that these bottlenecks are always narrow (few viral particles) and slightly widen with the number of transmitting aphids. These results contrast with theoretical predictions and illustrate the fact that a new conceptual framework is probably needed to understand the transmission of highly multipartite viruses.

INTRODUCTION

Since their discovery, the evolutionary reasons for why the genome of multipartite viruses is divided into several nucleic acid segments encapsidated independently have not received a satisfactory explanation. Most of the potential advantages proposed so far, e.g., that shorter genome segments allow faster replication (1) or have a higher chance to produce error-free genome copies (2), are not specific to multipartite viruses; they are shared with segmented viruses which package all their genomic segments together. The only specific advantage in favor of a multipartite genome structure (separate packaging of genomic segments) over a segmented genome structure (all segments packaged together within a single capsid) is rather idiosyncratic: Ojosnegros et al. (3) witnessed, under specific conditions, the evolution of a bipartite virus from an originally monopartite ancestor and ascribed the evolutionary advantage of the bipartite virus over its monopartite ancestor to higher virion stability conferring higher infectivity and longer life span. It is unclear how general such an advantage might be (4).

The potential loss of at least one segment during transmission (resulting in an unsuccessful infection) constitutes the most obvious cost of the multipartite genome architecture. If segments are transmitted independently, this cost increases with the number of segments constituting the viral genome. Thus, the number of viral particles (multiplicity of infection [MOI] in their work) entering the infected cells must increase with the number of segments constituting the genome of a multipartite virus, as shown by Iranzo and Manrubia (5) in a theoretical study. For example, while an MOI of ≤30 viral particles should select for multipartitism in viruses with three segments, an MOI of >100 would be required for viruses with four segments, and MOIs of >1,000 would be necessary for multipartite viruses composed of more segments, like members of the Nanoviridae family (6 to 8 segments). These calculations assume an intrinsic selective advantage of the multipartite architecture over the nonsegmented architecture of 0.5, inspired from reference 3; in the absence of any selective advantage the multipartite architecture would never be selected, as it would only confer costs. The estimations made by Iranzo and Manrubia (5) suppose that all segments occur a priori at equal frequency in the viral population. However, three recent studies performed with the multipartite nanovirus Faba bean necrotic stunt virus (6), alfamovirus Alfalfa mosaic virus (7), and bidensovirus Bombyx mori bidensovirus (8) showed that genomic segments converge to different relative frequencies within hosts. Thus, the probability of transmitting all segments when some are rare would be even smaller than formerly considered by Iranzo and Manrubia (5). The multipartite architecture may incur this additional cost upon transmission, and relatively large numbers of transmitted particles are expected to ensure genomic integrity.

The estimation of the number of virus particles (or genomes) transmitted has recently received a lot of attention under the name “bottlenecks,” because viruses typically reach huge population sizes within their hosts, and it appears intuitive that only a very small portion will participate in transmission of the infection to the next host. A few studies measured the bottleneck (or founder) size during transmission of distinct viral species (see references 9 and 10, among others, for reviews) and revealed important variations. Although these variations can be partly explained by a dose-dependent effect within each biological system (10), they likely also relate to virus-specific transmission mechanisms. For many monopartite viruses the bottleneck size is quite small, varying between one and four individuals (Potato virus Y [11], Tobacco mosaic virus [TMV] [12], Human immunodeficiency virus [HIV] [13], and Hepatitis C virus [HCV] [14]). However, for some other animal viruses, like Dengue virus (15) or Equine influenza virus (16), the sizes of bottlenecks undergone by the viral populations seem to be much higher than the figures cited above. To our knowledge, only one article reported the bottleneck size of a multipartite virus after aphid transmission: Betancourt et al. (17) estimated that the tripartite Cucumber mosaic virus (CMV), a noncirculative plant virus, undergoes a narrow bottleneck on the order of one or two founders only. As a point of comparison, Iranzo and Manrubia (5) predicted that multipartitism could evolve in a tripartite virus with a 2-fold disadvantage of monopartite viruses if about 30 viral particles entered each host cell, equivalent to about 10 copies for each segment. Our calculations extending Iranzo and Manrubia's work (see “Calculating the critical MOI,” below) indicate that with a smaller disadvantage of monopartite viruses (10%), these numbers would increase to approximately 900 for the total number of viral particles and to ∼300 per segment.

In the present article, we estimated the bottleneck size of FBNSV, a multipartite virus belonging to the family Nanoviridae and composed of eight genomic segments (18). As previously mentioned, the different FBNSV segments reproducibly accumulate within infected host plants at different relative frequencies (6). In faba bean, the host plants we used in this study, the relative frequency of the different genomic segments is given by the formula 3^C 3^M 9^N 2^R 1^S 6^U1 11^U2 15^U4, meaning, for example, that for one S segment there are 9 N segments in an infected faba bean. Further, this formula was shown to change in the aphids transmitting these viruses, with a reproducible trend corresponding to a sharp drop and increase in the frequency of the segment N and U2, respectively (19). Plant viruses transmitted by aphid vectors could experience bottlenecks during aphid transmission, during plant colonization, or at both stages of their life cycle (Fig. 1). We used two approaches to investigate at which stage(s) the bottleneck occurs and to estimate its size. We first used the transmission rate obtained in our experiments to estimate the number of viral particles efficiently transmitted by aphids, i.e., generating a systemic infection after transmission, and hence characterize the bottleneck size at this stage of the virus life cycle. Second, we used the variation of the relative frequency of marked FBNSV segments over an entire infection cycle (from apex to apex) to estimate the effective population size (N_e) of a rare (S) and a frequent (N) segment in the host plants. The effective population size (N_e) assesses the importance of genetic drift relative to other evolutionary forces (typically selection). Because effective population size strongly affects the amount of genetic diversity that populations can maintain, it also strongly impacts the potential for complementation and recombination to affect the evolutionary trajectories of viruses. In the context of our experiment, N_e could reflect bottlenecks occurring during aphid transmission or plant colonization or during both stages.

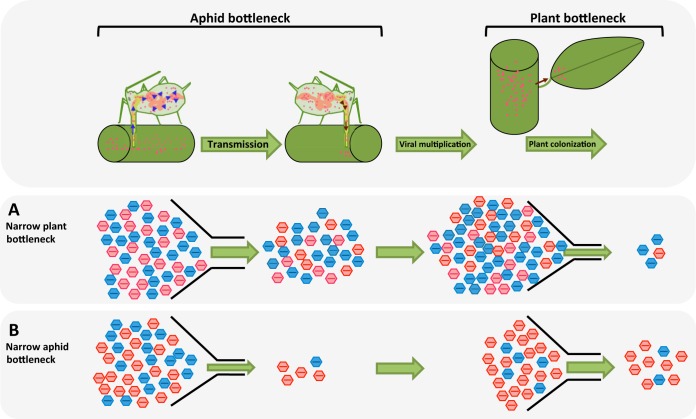
FIG 1.

Illustration of potential population bottlenecks occurring during FBNSV life cycle from apex to apex. (Upper) In our experiment, bottlenecks can impact viral populations during the transmission step or during plant colonization. (A and B, lower) Effect of population bottlenecks on the viral population, when the bottleneck occurring during plant colonization is narrower than the one occurring during transmission (A) or when the transmission bottleneck is narrower than the one occurring during plant colonization (B). Blue and red capsids represent two alleles of the same FBNSV segment.

RESULTS

To estimate the bottleneck size of the octopartite FBNSV, we first agroinoculated the virus in faba bean plants, which subsequently served as donors, and later attempted to transmit the virus from donor to recipient plants by using 1 or 10 aphid vectors. The experiment was replicated twice.

The first approach to estimate bottleneck size consisted of using the proportion of recipient infected plants as a way to infer the number of transmitted segments. It is currently not known how multipartite viruses are transmitted from one host individual to the next. We thus considered the following two extremes. The first, here called the packing hypothesis, consisted of packing several viral particles together, each containing a different segment, through some sorting mechanism such that all genomic segments are represented in the pack propagule. The other extreme, here called the random hypothesis, would consist of the transmission of each segment in proportion to its frequency in the aphids. Bottleneck size was estimated under both the random and the packing hypotheses.

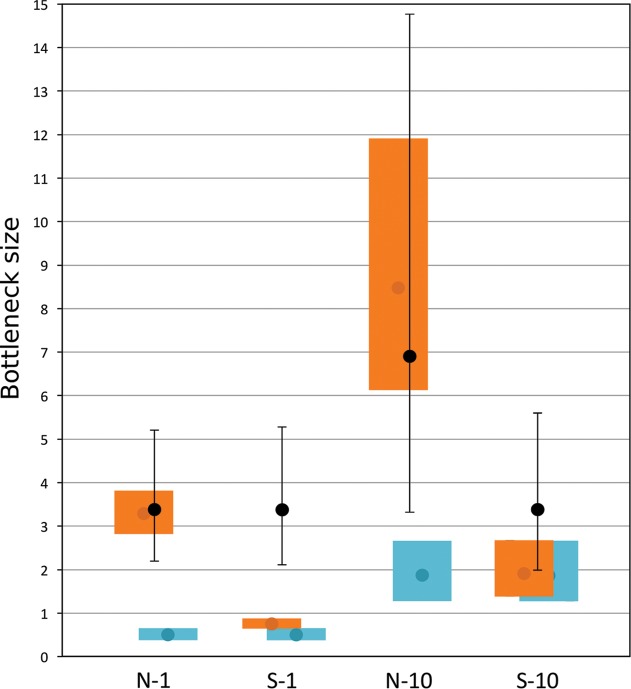
The transmission rate of FBNSV from donor to recipient faba bean plants was equal to 0.37 and 0.38 with one aphid and equal to 0.91 and 0.84 with 10 aphids for replicates 1 and 2, respectively (see Materials and Methods for an overview of the experiment and detailed descriptions of the estimation methods). Based on these transmission rates, we could estimate the number of N and S segments transmitted by 1 (N-1 and S-1) or 10 aphids (N-10 and S-10) (Fig. 2, orange and blue squares). These results indicate that (i) the bottleneck size of FBNSV segments is always surprisingly small: the largest value within 95% confidence intervals (CI) of an estimate was lower than 15; all estimated bottleneck sizes thus are within the same order of magnitude, whatever the segment (frequent [N] or rare [S] in the aphids) or number of transmitting aphids; (ii) the bottleneck sizes estimated under the packing hypothesis are narrower than those estimated under the random hypothesis; and (iii) under both hypotheses the bottleneck size is wider when transmission is performed by 10 aphids rather than a single one. It is worth recalling here that under the packing hypothesis the two segments have equal bottleneck sizes by construction, since we assume that each pack contains one copy of each segment. For the random hypothesis we assume that segments are transmitted following their relative frequency within aphids, i.e., according to the aphid-specific formula, and this is reflected in their relative estimated bottleneck sizes. Therefore, the comparisons of bottleneck sizes across segments obtained through this method result directly from our assumptions and should not be interpreted without confronting them with the results of the second approach.

FIG 2.

Estimations of FBNSV bottleneck sizes with two approaches. Black dots show the effective population sizes (N_e) estimated from variations in the relative frequency of marked N and S segments after transmission with 1 or 10 aphids (values shown in Table 1). Error bars correspond to the 95% credibility intervals of these estimates. Colored rectangles show the mean (dot) and 95% confidence intervals of bottleneck size predictions based on transmission rates under the random (orange) and packing (blue) hypotheses.

The second approach used the frequency variation of marked segments to estimate the bottleneck sizes. Bottlenecks are demographic events during which the size of a population can be drastically reduced. Such events impose random fluctuations in the frequency of alleles present in the fraction of the population that survives the bottleneck. The narrower the bottleneck, the more variable the relative allele frequencies among replicate populations. We thus estimated the relative allelic frequencies of marked segments in the apical part of faba bean plants and compared the variance of relative allelic frequencies in donor and recipient plants. In this study, effective population sizes (N_e), as defined in population genetics, i.e., the size of an ideal population drifting at the same rate as the population under study (see reference 20 for a review), of the N and S segments were estimated. To this end, we measured the variations in the relative frequency of two marker alleles (mys2 and mys7 for the N segment and mys1 and mys8 for the S segment; see reference 21 for a full description of the markers) after an aphid transmission episode between donor and recipient plants.

The statistical methods used to estimate N_e value from the temporal variation of allele frequencies typically assume that the markers are neutral (22, 23). However, we detected selection for specific variants of the markers that we used for both the N and S segments during our experiments. We thus adapted a recently developed statistical method (24) to jointly estimate selection coefficients (s) and N_e (Table 1). The results revealed selection in favor of the mys2 over the mys7 marker for segment N and in favor of the mys8 over the mys1 marker for segment S. The statistical analysis also showed that the N_e values of the N and S segments of FBNSV were small, varying from 3.4 to 6.9 individual segments (Table 1 and Fig. 2). Unsurprisingly, the number of aphids used in the experiment also affected the N_e estimates. While the estimated N_e values were very similar for the N and S segments when 1 aphid was used for transmission, N_e for the N segment was twice that of the S segment when 10 aphids were used for transmission (Fig. 2). This observation is supported by the comparison of five competing models that we considered (see “Statistical analyses,” below), revealing that the model with the highest posterior probability considers similar N_e for combinations N-1, S-1, and S-10 and a different N_e value for combination N-10 (Table 2).

TABLE 1.

Selection coefficients of the mys genetic markers and effective population sizes^a

Model	Parameter	Exptl conditions	Mean	CI
M1	sN	N1, N10	0.78	0.25–1.38
M1	sS	S1, S10	0.86	0.29–1.54
M1	NeN,1	N1	3.37	2.16–5.2
M1	NeS,1	S1	3.36	2.08–5.27
M1	NeN,10	N10	6.87	3.29–14.78
M1	NeS,10	S10	3.38	2.06–5.58
M5	sN	N1, N10	0.71	0.3–1.21
M5	sS	S1, S10	0.8	0.31–1.36
M5	NeN1,S1,S10	N1, S1, S10	3.26	2.63–3.99
M5	NeN,10	N10	5.77	3.58–9.17

^aSelection coefficients (s) of the mys genetic markers and effective population sizes (N_e) were estimated with model M₁ and M₅ from the relative frequency variations of marked N and S segments after a transmission episode with 1 or 10 aphids (CI, 95% credibility intervals). Selection coefficients show the relative fitness of the mys2 over mys7 markers for the N segment and of the mys8 over mys1 markers for the S segment. The values reported for N_e correspond to the mean of the zero-truncated Poisson distribution (using the λ parameter of the ZTP yields very close results).

TABLE 2.

Posterior probabilities of the five models^a

Tolerance	Posterior probability for model:
	M1	M2	M3	M4	M5
0.001	0.1	0.24	0.11	0.14	0.41
0.0005	0.09	0.23	0.08	0.14	0.46
0.0001	0.05	0.2	0.04	0.12	0.59

^aPosterior probabilities of the five models were considered while evaluating whether effective population sizes varied between genomic segments or the number of aphids used for donor-to-recipient transmission. The boldface values correspond to the model that is best supported by the data. The multinomial logistic regression method implemented in the ABC package was used for model selection. Three tolerance parameters were tested.

The N_e values presented in Table 1 are also shown in Fig. 2 to allow a direct comparison with the estimates of the bottleneck sizes obtained by the first method. The estimates obtained by the two methods are of the same order of magnitude. In particular, the estimated N_e values for the N segment match well the estimated bottleneck sizes under the random hypothesis and are significantly larger than the estimates under the packing hypothesis for this segment. For the S segment, the N_e value is larger than the estimates under both hypotheses when transmission is performed by a single aphid and is compatible with both hypotheses when transmission is performed by 10 aphids. The implications of these results are discussed below.

DISCUSSION

Effective population sizes of FBNSV are small.

As explained in Results, an estimation of N_e typically requires the use of neutral markers. Despite the fact that we used short genetic markers of equal length (22 nucleotides) inserted at the exact same location between the end of the coding regions and the poly(A) signal sequences of the N and S segments, we detected deviations from neutrality for both marker couples (N_mys2/N_mys7 and S_mys1/S_mys8) (see significant s values in Table 1). Several hypotheses may explain this observation: (i) markers were inserted in undiscovered regulatory regions, (ii) the presence of these markers differentially modified the folding of the DNA segment, potentially impacting its replication or degradation rate, and (iii) markers impacted the stability of transcribed mRNA.

A statistical method adapted from Rousseau et al. (24) (see “Statistical analyses,” below) permitted the joint estimation of both s and N_e (Table 1). Our estimations of bottlenecks undergone by FBNSV populations during transmission by the vector and plant colonization from apex to apex (i.e., during transmission by the vector followed by plant colonization; Fig. 2) indicate that, during its life cycle, FBSNV undergoes narrow bottlenecks ranging, on average, from 3.4 to 6.9 viral particles for the N segment, depending on the number of transmitting aphids, and equal to approximately 3 particles for the S segment, whatever the number of aphids (Table 1 and Fig. 2). The fact that N_e estimates are similar for both segments when only one aphid could transmit the virus probably results from a very small number of viral particles being transmitted by a single aphid. This is reflected by the relatively low transmission rates observed under this condition (see Results). When 10 aphids potentially transmit the virus, the effect of the transmission bottleneck is probably weaker, and within-plant processes may contribute via, e.g., the FBNSV within-plant genome formula to differentially affect the N_e of FBNSV segments. We discuss the relative influence of bottlenecks occurring at different stages of the FBNSV life cycle in more detail below.

Interestingly, for both N and S segments, these N_e values are of the same order of magnitude as those observed for monopartite viruses (9) or for the tripartite CMV (17) and are remarkably lower than those theoretically predicted to be necessary for the evolution of multipartitism (5). Indeed, extending the calculations of Iranzo and Manrubia (5) to account for the fact that FBNSV is octopartite and that the different segments occur at unequal frequencies within infected plants and aphids, the lowest MOI allowing the evolution of multipartitism would need to be larger than 130 for segment S and larger than 1,800 for segment N (these specific calculations assume a 2-fold disadvantage of monopartite viruses, following Irranzo and Manrubia [5], and the faba bean genome formula; see “Calculating the critical MOI,” below, for a description of the calculations and critical values for other cases).

Small effective population sizes imply that genetic drift is important for FBNSV evolution. Importantly, the fact that N_e significantly differs across segments under at least one condition (the 10-aphid transmission treatment) suggests that the evolution of the different segments of FBNSV genome is not equally affected by genetic drift. This could in turn affect the interpretation of sequence variation patterns. For example, typically the variation of dN/dS across genomic regions of an organism is interpreted as variation in selection, because all genomic regions are supposedly experiencing the same demographic processes. Our results indicate, however, that the relative influence of genetic drift varies across FBNSV segments (genes), and therefore variations in dN/dS between segments may be due to differential patterns of selection and/or differential patterns of drift. Given that a genome formula, i.e., the accumulation of segments at different relative frequencies within hosts, has been documented in the two other multipartite viruses where it has been looked for (7, 8), this variation in the influence of genetic drift across segments could be a general feature of the multipartite life style.

How does FBNSV ensure the transmission of all its segments?

The main objective of this study was to investigate whether a multipartite virus such as FBNSV can overcome the a priori cost due to multipartitism and ensure its transmission by massively transmitting its segments, as assumed by Iranzo and Manrubia (5). We performed two independent estimations on the N and S segments, present at different relative frequencies in the aphid (relative frequency, N/S, of 4.5 [19]) and in faba bean plants (relative frequency, N/S, of 9 [6]). Both methods indicate that FBNSV undergoes rather severe bottlenecks during aphid transmission. This is observed even when the number of aphids used is sufficient to attain high transmission rates, such as 80 to 90%, as in our ten-aphid treatment.

It is interesting that the number of aphids used for transmission does not have the same effect on the N_e of the N and S segments. This indicates that segment-specific bottlenecks occur in the plant: in the case of the S segment, such processes could mask the effect of the bottleneck occurring in aphids. Therefore, bottlenecks likely affect FBSNV both during plant-to-plant transmission and during plant colonization (Fig. 1), although the effect of plant-to-plant transmission appears much stronger. This is compatible with the reported exponential growth of FBNSV population size within host plants (see Fig. 4a in reference 6), which suggests that only demographic processes occurring early during plant infection, and thus shortly after transmission, can significantly impact N_e. The importance of demographic stochasticity mostly during the initial steps of viral infections has been shown in the theoretical and empirical work of Kennedy et al. (25).

Interestingly, segment N has both a higher relative frequency in the genomic formula and a higher N_e in the ten-aphid treatment than the segment S. This suggests a function of the genomic formula in these segment-specific bottlenecks. However, since we only measured the bottleneck of two segments of FBNSV, we cannot draw any firm conclusion on this.

We do not have a way to contrast the plausibility of the random versus packing hypotheses. For segment N, the bottleneck size estimates of the random hypothesis match the estimated N_e values, while those of the packing hypothesis lie below the 95% CI (Fig. 2). For segment S the situation appears to be more complex: estimates of the bottleneck size following both hypotheses lie below the 95% CI for N_e in the one-aphid treatment, while they are both within the 95% CI for N_e in the ten-aphid treatment (Fig. 2). It would be tempting to compare the results obtained by the two methods used here. However, we currently have no way to assess whether the differences in the N_e estimates between segments are due to processes occurring during aphid transmission, during plant colonization posttransmission, or both.

Previous studies comparing the dose responses of monopartite versus multipartite RNA viruses have led to the rejection of the packing hypothesis (26, 27). However, as these dose-response experiments were performed using mechanical inoculations, it is not obvious that their results would hold for the aphid-transmitted FBNSV. Thus, even if RNA viruses seem to be transmitted according to the random hypothesis, we currently cannot reject the packing hypothesis for FBNSV. More detailed and specific investigations are needed to evaluate whether FBNSV uses a specific sorting mechanism for the aphid transmission of its segments.

Iranzo and Manrubia (5) investigated on a theoretical level the number of viral particles of multipartite viruses that need to enter a given host cell to offset the cost of infection failure due to the loss of one segment. They found that this number needed to be large, with its specific value depending on the number of genomic segments of the virus and the putative selective benefit of multipartitism. When considering highly multipartite viruses, such as the octopartite FBNSV, they concluded their study by stating that “other conceptual frameworks are needed in order to explain the origin of these highly multipartite viruses” (5). Our results on the bottleneck size experienced by FBNSV during an infection cycle reinforce this view and are consistent with previous results on the tripartite CMV (17), which was also reported to experience severe bottlenecks. As our results show that the bottleneck size gets wider when the number of aphids increases, one possibility to resolve the apparent paradox between Iranzo and Manrubia's (5) predictions and measured bottlenecks would be to invoke transmission by a much larger number of aphids than those typically used in laboratory experiments. We note that in our experiments a 10-fold increase in the number of aphids leads to approximately a doubling of the bottleneck size. It is difficult to extrapolate to, e.g., a hundredfold increase in the number of aphids. Our current knowledge on the ecology of multipartite viruses is extremely fragmentary and incomplete. In particular, to properly evaluate this hypothesis we would need to know the number of viruliferous aphids circulating in the field. This information is typically lacking for any kind of virus, although the few investigations reporting on this indicate that only very few aphids are viruliferous. For example, Schwinghamer et al. (28) reported that only 10 out of 447 aphids field trapped on faba beans were able to transmit a virus. Therefore, even though this possibility cannot be excluded at present, it does not appear very plausible.

Another possibility, at least for host-to-host transmission, would be the packing hypothesis that we consider. Indeed, if a sorting mechanism of segments exists, then any successful transmission event would be sufficient to ensure that all segments are transmitted from one host to the next. This could in principle resolve the paradox at least at this level, and as we previously wrote we do not have adequate data to evaluate this possibility. We note, however, that the paradox would not be entirely resolved, as the cost presumably exists at the host cell level: it supposes that all segments need to enter a given host cell for an infection to be successful, and the existence of the genomic formula renders this more problematic than a situation where all segments are equally frequent. How this virus overcomes this cost at the host cell level remains a mystery, but large bottleneck sizes and high MOI are unlikely to be the adopted solution.

Conclusion.

Betancourt et al. (17) showed that the tripartite CMV undergoes severe bottlenecks and concluded that genetic drift must be an important process in the evolution of these viruses. Our results on the octopartite FBNSV confirm this view. Moreover, we show that the bottlenecks mostly occur during aphid transmission while within-host processes have a smaller influence. Interestingly, the different FBNSV segments appear to drift at different rates, and therefore their evolution may be differentially impacted by selection and demographic processes. This may apply to all multipartite viruses, making this genomic architecture even more intriguing.

MATERIALS AND METHODS

Experiment overview.

Effective population sizes (N_e) were estimated by measuring the variations in the relative frequency of two alleles of the N and S genomic segments after aphid transmission between donor and recipient plants. Two supposedly neutral genetic markers were inserted in the N (mys2 and mys7 markers) and S (mys1 and mys8 markers) segments (see “DNA marker introduction,” below, for more information).

Faba bean plants (Vicia faba cv. Seville) were agroinoculated at equimolar concentration with 10 different Agrobacterium tumefaciens strains (each containing a plasmid vector carrying one of the six unmodified segments or one of the marked segments N_mys2, N_mys7, S_mys1, and S_mys8). Infected plants carrying all markers were used as sources to feed Acyrthosiphon pisum for a 3-day acquisition access period (AAP). After the AAP, aphids were mixed and redistributed on one hundred susceptible 9-day-old faba bean plants for a 3-day inoculation access period (IAP). Three weeks postinfection, symptomatic faba bean plants were tested for the presence of the N and S marked segments, and their relative frequencies were measured by quantitative PCR (qPCR; see “qPCR,” below, for more information). Plants with polymorphic markers (relative frequency between 0.99 and 0.01) were kept for the transmission assay as source plants, here called donor plants. Thirty aphids were caged with nets on each donor plant and left for a 3-day AAP. After the AAP, aphids from donor plants were collected and caged on 9-day-old faba bean recipient plants during a 3-day IAP. Either 1 or 10 aphids were used for the transmission assay. Under these experimental conditions, 100% of aphids became viruliferous (19). Recipient plants receiving aphids from donor plant x were named recipient plant x in order to always associate each recipient plant with its respective donor. Three weeks postinfection, symptomatic faba bean plants were tested for the presence of the marked segments, whose relative frequencies were measured by qPCR.

The experiment was replicated twice independently. In the first replicate, 20 and 13 donor plants were polymorphic for the N and S segments, respectively (10 plants were polymorphic for both markers at the same time), and subsequently used in the transmission assay. To make sure we would have at least one infected recipient plant per donor plant in the one-aphid treatment (given that the transmission rate with one aphid was equal to 0.37), we used four replicated recipient plants in this treatment. Two recipient plants were used in the ten-aphid treatment.

In the second replicate, 36 and 38 donor plants were polymorphic for the N and S segments, respectively (36 plants were polymorphic for both markers at the same time), and used in the transmission assay. Since we had a lot of donor plants and a limited number of recipient plants in this second trial, each donor plant was used to infect a single recipient plant in the ten-aphid treatment and three in the one-aphid treatment. In total, the whole data set gathered 277 virus lineages (paired donor and recipient plants) distributed as 77 and 70 pairs for the segment N with 1 and 10 aphids, respectively, and 68 and 62 pairs for the segment S with 1 and 10 aphids, respectively.

DNA marker introduction.

Genetic markers (22 nucleotides; sequences available upon request) were inserted between the end of the coding regions and the poly(A) signal sequences of the N and S segments. Markers mys2 and mys7 were introduced in the N segment, while markers mys1 and mys8 were introduced in the S segment (21).

Viral strain and agroinoculation.

We used the FBNSV strain provided by Gronenborn's laboratory and described in reference 18. Agrobacterium tumefaciens COR308 strains carrying the different viral segments on pbin19 plasmids were grown for 24 h at 28°C and 200-rpm agitation in 500-ml Erlenmeyer flasks containing 50 ml of NZY (10 g NZ amine, 5 g yeast extract, 5 g NaCl, 2.5 g MgCl₂, 3 g MgSO₄²⁻, 4 g glucose, 1,000 ml H₂O) supplemented with 10 mM morpholineethanesulfonic acid (MES), pH 5.5, 5 μg/ml tetracycline, 50 μg/ml kanamycin, 20 μg/ml gentamicin, 50 μM acetosyringone. After growth, cultures were transferred in 50-ml Falcon tubes and centrifuged at 1,000 × g at 18°C for 30 min in a 5810R Eppendorf centrifuge. Pellets were resuspended in 5 ml MS½ (2.17 g of Murshige and Skoog basal mixture [M-5524; Sigma] in 1,000 ml H₂O) supplemented with 50 μl of MES, pH 5.5 (1 M), and 150 μM acetosyringone. In total, 10 A. tumefaciens cultures were performed in parallel, each containing one of the six unmodified segments or one of the marked segments N_mys2, N_mys7, S_mys1, and S_mys8. All suspensions were mixed together (1, 1, 1, 1, 1, 1, 0.5, 0.5, 0.5, and 0.5 volumes of C, M, R, U1, U2, U4, N_mys2, N_mys7, S_mys1, and S_mys8, respectively, in order to inoculate all eight segments composing the FBNSV in equal proportions). The mixture was left in the dark for 90 min at room temperature and finally injected in 9-day-old faba bean plants. The infected status of agroinoculated plants was established 3 weeks postinoculation.

Sampling and DNA extraction.

To study a full infection cycle, plant samples were collected on the apical leaves both in donor and recipient plants. Apical leaves were chosen because this is where the viral concentration is maximal and because, as shown by Sicard et al. (6), FBNSV reaches its genome formula in the youngest leaves of infected faba beans. Total DNA from these samples was extracted according to a modified Edwards protocol (29) with an additional washing step with 70% ethanol. DNA was resuspended in 100 μl of water.

qPCR.

All qPCRs (40 cycles at 95°C for 10 s, 60°C for 10 s, and 72°C for 10 s) were carried out using a LightCycler 480 thermocycler (Roche), by following the manufacturer's instructions, and the LightCycler FastStart DNA master plus SYBR green I kit (Roche). Sample DNA (1.2 μl of a 10-fold dilution) was added to the qPCR mix (5 μl of Roche 2× qPCR master mix, 3.5 μl of H₂O, 0.3 μl of primer mix, 8.8 μl total) after distribution in 384-well microtiter plates. Primers (Table 1) were used at a final concentration of 0.3 μM.

Analysis of qPCR results.

In this work, we were interested in measuring relative frequencies of genomic FBNSV segments tagged with different markers. To do so, we analyzed our qPCR results by following Rutledge and Stewart (30). To summarize, this method considers that fluorescence intensity depends on two parameters: N₀, i.e., the number of target DNA molecules prior to amplification, and the optical calibration factor (OCF), i.e., the number of fluorescence units per nanogram of double-stranded DNA (FU/ng dsDNA). This technique offers a useful alternative to the use of standard curves to perform the conversion of a fluorescent signal into nanograms of double-stranded DNA.

As we were not interested in absolute quantification per se but in a precise measure of relative frequencies of segments tagged with different genetic markers, we adapted this protocol. We assumed that the amount of fluorescence produced per nucleotide of amplicon was constant and simply considered that the fluorescence intensity, F₀, depends on two parameters: N₀, the number of copies of the targeted DNA molecule, and L, the length of the amplicon:

$$F_0\propto N_0\times L$$ (1)

Thus, we calculated the relative frequencies of tagged segments as

$$f_{\text{mysA}}=\frac{\frac{F_0^A}{L^A}}{\frac{F_0^A}{L^A}+\frac{F_0^B}{L^B}}$$ (2)

where f_mysA is the relative frequency of the mysA marker, F₀^A and F₀^B are the estimated fluorescence values of the mysA and mysB amplicons prior to amplification, and L^A and L^B are the lengths of the mysA and mysB amplicons.

To verify if our method was able to estimate relative frequencies of tagged segments with precision, we created relative frequency control scales for the N and S segments. To do so, plitmus28 plasmids carrying the tagged segments N_mys2, N_mys7, S_mys1, and S_mys8 were purified with a miniprep kit (Qiagen). The concentrations of each miniprep were measured with a Quant-iT PicoGreen dsDNA assay kit (Thermo Fisher Scientific) in order to calibrate the concentration of all minipreps (40 ng/μl). Minipreps of plasmids carrying the same segment but different markers (plitmus28 N_mys2/plitmus28 N_mys7 and plitmus28 S_mys1/plitmus28 S_mys8) were mixed at 11 different relative frequencies (frequencies of marker mys2 [for the N segment] and mys1 [for the S segment] in each of the 11 mixes composing the control scales for relative frequencies: 0, 0.01, 0.1, 0.25, 0.4, 0.5, 0.6, 0.75, 0.9, 0.99, and 1). These relative frequency scales were added to all qPCR microplates to verify for each qPCR run that we could measure relative frequencies of tagged segments with precision. Figure 3 illustrates an example of the correlation between theoretical versus observed relative frequencies obtained with our relative frequency control scales in our experiments. This correlation demonstrates that we could accurately measure relative frequencies of marked segments with the protocol and analysis described above. Regressions obtained with relative frequency control scales were always of very high quality both for N and S (R² > 0.99 in all cases; data not shown).

FIG 3.

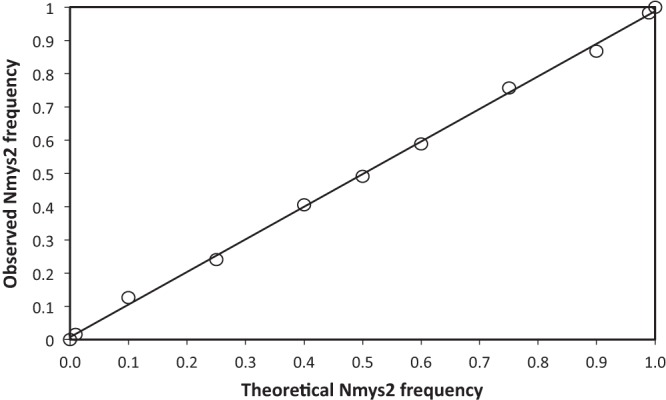
Example of theoretical versus observed relative frequencies of the N_mys2 segment obtained with the relative frequency control scale. This plot confronts the theoretical relative frequencies of the plitmus28 N_mys2 plasmid in the control scale N, with relative frequency estimations from qPCR performed on the control scale samples. The regression formula is the following: y = 0.9807x + 0.0072. R² = 0.9988.

Calculating the critical MOI.

Iranzo and Manrubia (5) showed that for a given relative degradation rate of the monopartite particles, σ (with respect to single segment particles), there is a critical MOI above which the single segment classes are able to outcompete other classes with longer genomes and, in consequence, a fully multipartite population is established.

One can generalize the stability analysis of paragraph 1.2.1 from the supplemental material of Iranzo and Manrubia (5) to the case of a multipartite equilibrium of N separated segments (instead of 2) perturbed by the introduction of a double-segment class (which, for N > 2, does not correspond to the monopartite version of the virus). If the investigated MOI (over all segments) is not too small (i.e., >50 for N up to 8, but a correction factor can be applied to recover the exact value, although it is difficult to calculate it in the case of formulas where segment frequencies are unequal), it can be shown that the leading eigenvalue of the generalized version of the Jacobian matrix in equation 13 of the supplemental material of Iranzo and Manrubia (5) ensures the stability of the multipartite equilibrium if

$$\frac{(\text{differential\hspace{0.17em}degradation})\times (\text{MOI})}{\left(\text{total\hspace{0.17em}number\hspace{0.17em}of\hspace{0.17em}segments\hspace{0.17em}produced\hspace{0.17em}in\hspace{0.17em}one\hspace{0.17em}generation,\hspace{0.17em}at\hspace{0.17em}equilibrium}\right)}<1$$ (3)

With notations inspired from their work, this formally translates to

$${\sigma }_2{m}_{\text{crit}}{\left(N{\displaystyle \sum _{a_1\text{,\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}.,}{a}_N}\mathrm{Pr}\left(a_1\text{,\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}.,}{a}_N,0|\frac{1}{N}\text{,\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}.,}\frac{1}{N},0\right)\min \left\{a_1\text{,\hspace{0.17em}.\hspace{0.17em}.\hspace{0.17em}.,}{a}_N\right\}}\right)}^{-1}=1$$ (4)

in which m_crit is the lowest MOI that ensures the fixation of the multipartite class for a given differential degradation of the double-segment classes, σ₂.

Following Iranzo and Manrubia (5), intermediate combinations of segments have a differential degradation that is only a fraction of the full coefficient, σ, that applies for the monopartite class. More precisely, they assume that the differential degradation, σ_s, of a class consisting of the concatenation of s segments out of N possible segments is

$${\sigma }_s=\frac{1-\sigma }{N-1}(1-s)+1$$ (5)

hence, in the case of double segments, we have σ₂ = 1 − [(1 − σ)/(N − 1)]. It follows that one can rewrite equation 4 as

$$F_{\sigma }(m_{\text{crit}})=\left(1-\frac{1-\sigma }{N-1}\right)m_{\text{crit}}{\left(N{\displaystyle \sum _{\mathbf{a}:{\Vert \mathbf{a}\Vert }_1=m_{\text{crit}}}{P}_{\mathbf{a}}}(m_{\text{crit}},{\mathbf{p}}^{*})\text{min(}\mathbf{a}\text{)}\right)}^{-1}-1=0$$ (6)

where a denotes the (truncated) infection configuration (a₁, … , a_N) and P_a(m,p*) the probability factor occurring in equation 4 that also depends on the N + 1 stationary frequencies p* = {1/N, … , 1/N, 0}. Consequently, m_crit can be determined as the root of F_σ for a given σ. When N and m_crit are large, it can take time to sum all convenient a (infection configurations) values, but one can easily estimate ∑_{a:∣∣a∣∣1=mcrit} P_a(m_crit, p*)min(a) with the Monte-Carlo method (that is, sampling in a multinomial distribution). We can thus numerically recover (though poorly for N = 2, because the difference between the Poisson and multinomial distributions is not negligible in this specific case) and extrapolate from Fig. 4b from Iranzo and Manrubia (5) for N > 6 and any other values of σ. These results are shown in Table 3 and supported by stochastic simulations of the full dynamic system (with 2^N − 1 classes).

TABLE 3.

m_crit for two to eight segments and two degradation coefficients

σ	mcrit for segment:
	2	3	4	5	6	7	8
0.5	4	38	1.5 × 102	4.2 × 102	9.5 × 102	1.8 × 103	3.1 × 103
0.9	71	8.8 × 102	3.8 × 103	1.1 × 104	2.4 × 104	4.5 × 104	7.9 × 104

In the case of FBNSV, it has been shown that the different segments occur in different frequencies in infected plants (6) and aphids (19). The critical MOI might therefore be different, as the distribution of unequal segment frequencies alters the probability distribution of the infection configurations. This affects the way we calculate the denominator in equation 3. The number of segments produced by a cell infected by a given configuration, a (of single segments only), is governed by the rarest segment but with respect to its genome formula relative frequency. More precisely, at equilibrium, there is a complete set of segments produced by the infected cell for each set of segments that satisfies the genome formula frequency distribution that have entered the cell.

Let us define c := (c₁, … , c_N) as the genome formula, following Sicard et al. (6), of the multipartite virus. The number of genome formula sets of segments contained in an infection configuration is thus min(a⊙c⁻¹) := min{a₁/c₁, … , a_N/c_N}, that is, the number of replicates of the rarest segment normalized by its genome formula coefficient. For each of the min{a₁/c₁, … , a_N/c_N} segment sets, now there is a full set of ∣∣c∣∣₁ := c₁ + … + c_N segments produced. One can indeed view ∣∣c∣∣₁ as the effective segment number of the virus, rather than N, which does not take into account the relative utility of each segment (in particular, ∣∣c∣∣₁ > N, as soon as one segment is very frequent in the formula compared to the others).

Considering a given formula, c, the critical MOI can thus be numerically estimated by calculating the root of

$$F_{\sigma ,\mathbf{c}}(m):=\left(1-\frac{1-\sigma }{N-1}\right)m{\left({\Vert \mathbf{c}\Vert }_1{\displaystyle \sum _{\mathbf{a}:{\Vert \mathbf{a}\Vert }_1=m}{P}_{\mathbf{a}}}(m,{\mathbf{p}}^{*})\text{min(}\mathbf{a}\odot {\mathbf{c}}^{-1}\text{)}\right)}^{-1}-1$$ (7)

where the frequencies at equilibrium here are p* := {c₁/∣∣c∣∣₁, … , c_N/∣∣c∣∣₁, 0} (the fact that this point is the attractor has been checked by stochastic simulations). It is straightforward that the homogeneous case is recovered for c = 1_N.

The results of critical MOI for the genome formulas found in the case of FBNSV are given in Table 4. It is interesting that these MOI values are approximately two times higher than their equivalents for formulas with equal frequencies for all segments.

TABLE 4.

m_crit for the genome formulas of FBNSV and different degradation coefficients

Formula	C	M	N	R	S	U1	U2	U4	σ	mcrit
Faba bean	3	3	9	2	1	6	11	15	0.5	6.6 × 103
									0.9	1.7 × 105
Aphid	6	13	9	6	2	8	22	34	0.5	6.2 × 103
									0.9	1.6 × 105

Shown are m_crit for the genome formulas of FBNSV and different degradation coefficients to obtain the critical MOI per segment one needs to multiply the total critical MOI by the relative frequency of the segment in the genome formula. See Sicard et al. 2013 (6) for the faba bean formula and Sicard et al. 2015 (19) for the aphid formula.

Statistical analyses. (i) Prediction of the number of transmitted segments.

Let n be the number of effectively transmitted viral particles (or packs), i.e., the number of inoculated particles (or packs) that contribute to the colonization of the recipient plant. We assume that n has a Poisson distribution with mean λ_A and that the probability for a plant to be infected is equal to the probability that at least one copy of each of the 6 indispensable genomic segments of FBNSV (C, M, R, S, U1, and U2) is inoculated by the A aphids (A ∈ {1, 10}). On this basis, λ_A (and the corresponding 95% confidence intervals) were inferred from the observed proportion of infected plants (p_i,A), using the following maximum likelihood approach (and the profile likelihood method for the confidence intervals) under two hypotheses on the transmission process.

Under the packing hypothesis, the absence of any indispensable segment means that no pack has been effectively transmitted. Thus, the maximum likelihood estimate for λ_A was derived from the null class of the Poisson distribution, p_i,A = 1 − P(n = 0) = 1 − e^−λ_A, hence

$${\lambda }_A=-\ln (1-p_{i,A})$$ (8)

Under the random hypothesis, the absence of the i^th indispensable segment corresponds to the null class of the Poisson distribution with parameter λ_Af_i, where f_i is the relative frequency of the i^th segment according to the FBNSV genome formula in aphids (6^C 13^M 9^N 6^R 2^S 8^U1 22^U2 34^U4 [19]). The maximum likelihood estimate of λ_A then was obtained by numerically solving the equation ∏_{i = 1}⁶(1 − e^−λ_Af_i). The estimates for the two genomic segments under study then were obtained as λ_N,A = λ_Af_N and λ_S,A = λ_Af_S.

(ii) Estimation of N_e in the presence of selection.

This estimation method is adapted from reference 24. Let us denote by f_p,G,A^init (and f_p,G,A^end) the observed marker frequency in the paired donor and recipient plants p at the beginning (init) or the end of the experiment with genomic segment G ∈ {N, S} and aphid number A ∈ {1,10}. The index, p (1 ≤ p ≤ 277), is over all 277 pairs of donor and recipient plants of the data set (77 and 70 pairs for segment N with 1 and 10 aphids, respectively; 68 and 62 pairs for segment S with 1 and 10 aphids, respectively).

We modeled the life cycle of the FBNSV from the apex of the donor to the apex of the recipient plants (including aphid transmission and subsequent plant colonization) as a binomial sampling process. The model writes as

$$n_p|{\lambda }_{G,A}\sim ZTP({\lambda }_{G,A})$$ (9)

$$m_p|f_{p,G,A}^{\text{init}},n_p,s_G\sim \text{Bin}\left(\text{size}=n_p,\text{prob\hspace{0.17em}=\hspace{0.17em}}\frac{(1+s_G)\cdot f_{p,G,A}^{\text{init}}}{(1+s_G)\cdot f_{p,G,A}^{\text{init}}+(1-f_{p,G,A}^{\text{init}})}\right)$$ (10)

$$f_{p,G,A}^{\text{end}}=m_p/n_p$$ (11)

The size parameter of the binomial process, n_p, corresponds to the effective population size during the apex-to-apex life cycle of the FBNSV genomic segment involved in the paired donor and recipient plants, p. It varies as a result of a zero-truncated Poisson (ZTP) process of unknown parameter λ_G,A. We use a zero-truncated Poisson distribution because it ensures that n_p cannot be zero. This means that N_e^G,A = λ_G,A/[1 − exp(−λ_G,A)] corresponds to the effective population size. For a given genomic segment, G, the mean frequency, prob, of the marker of interest after the bottlenecks depends on its initial frequency, f_p,G,A^init, and on S_G, an unknown selection coefficient of the marker during the entire life cycle (i.e., from apex to apex). If S_G = 0, the final mean frequency of the marker of interest will be equal to its initial frequency (i.e., prob = f_p,G,A^init). If S_G > 0, the final mean frequency of the marker of interest will be higher than its initial frequency (i.e., prob > f_p,G,A^init) due to selection in favor of this marker during the entire life cycle. The m_p variable corresponds to the number of copies of the marker that have been sampled during the life cycle in the recipient plant, p, given the effective population size, n_p, and the final mean frequency, prob. Finally, we also assumed that the uncertainty on the measures of f_p,G,A^init and f_p,G,A^end is negligible.

The vector of parameters of the full model (M₁) is θ_M1 = (s_N, s_G, λ_N,1, λ_N,10, λ_S,1, λ_S,10). θ includes one selection coefficient for each genomic segment (s_N, s_S). We assumed that the intensity of selection was the same regardless of the number of aphids used in the transmission episode. Model M₁ (six parameters) assumes that effective population sizes depend on both the genomic segment and aphid number (λ_N,1, λ_N,10, λ_S,1, λ_S,10). Four alternative models having from four to five parameters were also considered to explore the dependence of effective population sizes on the genomic segment or the number of aphids used for transmission. Model M₂ [five parameters, θ_M2 = (s_N, s_G, λ₁, λ_N,10, λ_S,10)] states that effective population sizes are the same for both segments with one aphid (i.e., λ_N,1 = λ_S,1) but different with 10 aphids (i.e., λ_N,10 ≠ λ_S,10). Model M₃ (five parameters, θ_M3 = (s_N, s_G, λ_N,1, λ_S,1, λ₁₀)) states that effective population sizes are the same for both segments with 10 aphids (i.e., λ_N,10 = λ_S,10) but different with one aphid (i.e., λ_N,1 ≠ λ_S,1). Model M₄ [four parameters, θ_M4 = (s_N, s_G, λ₁, λ₁₀)] states that effective population sizes are the same for both segments and depend on aphid number (i.e., λ_N,1 = λ_S,1 and λ_N,10 = λ_S,10). Finally, model M₅ [four parameters, θ_M5 = (s_N, s_G, λ_N1,S1,S10, λ_N,10)] states that effective population sizes are the same for three experimental conditions, (N, 1), (S, 1), and (S, 10) (i.e., λ_N,1 = λ_S,1 = λ_S,10), but are different for the genomic segment N with 10 aphids. Model selection was used to identify the model (and underlying hypotheses) that is best supported by the observations.

The parameters were estimated using approximate Bayesian computation (ABC) with eight summary statistics (two summary statistics × four experimental conditions). For a given experimental condition (G, A), the first summary statistic, S_{G, A}¹ = mean(f_p,G,A^init − f_p,G,A^end), averaged over the pair of plants, p, was the difference between the frequency of the marker of interest at the beginning and the end of the experiment. The second summary statistic, $S_{G,A}^2=mean[{(f_{p,G,A}^{\text{init}}-f_{p,G,A}^{\text{end}})}^2/(z_{p,G,A}·(1-z_{p,G,A}))]$, where $z_{p,G,A}=(f_{p,G,A}^{\text{init}}+f_{p,G,A}^{\text{end}})/2$ averaged over the pair of plants, p, was an unbiased estimator of genetic drift (31). Estimations were performed with the adaptive ABC algorithm of reference 32 implemented in the package EasyABC with tuning parameters nb_simul = 5000, p_acc_min = 0.04, and alpha = 0.5. Uniform priors on the range [−0.9, 5] were used for the parameters related to selection coefficients. Log-uniform priors on the range [0.2, 100] were used for the parameters related to effective population sizes. For the latter parameters, estimations were also performed by setting the upper bound of the log-uniform priors to 500. Additionally, a model selection among models, M_j (1 ≤ j ≤ 5), was conducted to identify the impact on effective population sizes of the genomic segment and the number of aphids (Table 2). The multinomial logistic regression method implemented in the ABC package was used for this purpose, with 3 × 10⁶ simulations used for each model and three tolerance values tested (10⁻³, 5 × 10⁻⁴, and 10⁻⁴). All statistical analyses were performed with R software (R 3.1.3).

We checked (for the genomic segment N only) if a data set with 147 samples (77 [respectively 70] pairs of plants with 1 [respectively 10] aphid), as in our experiment, was informative enough to efficiently estimate the parameters θ = (s_N, λ_N,1, λ_N,10). We proceeded in 3 steps. First, θ_true parameters were drawn from dedicated distributions: s_N^true ∼ Unif(−0.5, 1.5), λ_N,1^true ∼ log − unif(2, 20), and λ_N,10^true ∼ log − unif(λ_N,1^true, 20). Second, a data set (consisting of 147 frequencies of the marker of interest at the end of the experiment) was simulated given θ_true and the frequencies truly observed initially. Steps one and two were iterated until acceptance of 200 simulated data sets. Data sets were accepted if the two markers were detected in at least 70% of the plants at the end of the experiment. Third, for each accepted data set, θ was reestimated using the ABC method detailed above. The practical identifiability was assessed through the best linear model fit between estimated and true parameter values. Overall, the practical identifiability was very satisfactory. For s_N, the R² of the best-fit line was 0.95, the slope 1.05, and the intercept 0.001. For parameters λ_N,1 and λ_N,10, log-transformed values were used. The R² of the best-fit line was 0.92, the slope 1.05, and the intercept −0.01. Finally, the credibility intervals were also satisfactory, with 91% of the true values of λ_N,1 and λ_N,10 (resp. 85% of the true values of s_N) included in 90% credibility intervals.

A final cautionary remark is due here. In line with all other studies using similar methods that we know of, we assumed that the changes in marker frequencies occur in a single time step. This allows a direct comparison of our estimates to what has been previously reported in the relevant literature. However, strictly speaking, N_e is defined per generation. A more rigorous estimation, here and in the literature, would thus require knowing the number of viral generations separating the two successive samples. Not only is this information currently unknown, but even defining what is a viral generation is a conceptual challenge. In general, in methods based on the temporal variation of marker frequencies, the estimate of N_e increases linearly with the number of generations elapsed between the two sampling points (see, e.g., reference 33), while the estimate of selection coefficients would decrease linearly. For example, with our data for N-10, assuming that 5 generations elapsed between the two time points would correspond to an N_e of ∼35, and 10 generations would correspond to an N_e of ∼70. We note that these estimates, although based on the larger N_e that we observe, are much smaller than those predicted to favor multipartitism for an octopartite virus.