Taming the Strength of Interfacial Interactions via Nanoconfinement

Abstract

The interaction between two immiscible materials is related to the number of contacts per unit area formed by the two materials. For practical reasons, this information is often parametrized by the interfacial free energy, which is commonly derived via rather cumbersome approaches, where properties of the interface are described by combining surface parameters of the single materials. These combining rules, however, neglect any effect that geometry might have on the strength of the interfacial interaction. In this Article, we demonstrate that the number of contacts at the interface between a thin polymer coating and its supporting substrate is altered upon confinement at the nanoscale level. We show that explicitly considering the effect of nanoconfinement on the interfacial potential allows a quantitative prediction of how sample geometry affects the number of contacts formed at the interface between two materials.

Short abstract

Interaction between polymer films and their supporting substrates decreases upon nanoconfinement or by addition of a capping layer, because of a geometrical perturbation in the interfacial potential.

The performance of multiphase systems, as nanocomposites and hybrid nanomaterials, depends on the work of adhesion, ΔW, necessary to separate the different phases to an infinite distance in vacuum.¹ This quantity, whose estimation is a major requirement in several engineering applications, is proportional to the number of contacts, n, formed at the interface.² Because the determination of n requires a microscopic description of the interface, approximate macroscopic methods are adopted in practice. For example, the Good–Girifalco–Fowkes equation, one of the most known among the combining relations present in the literature,³⁻⁵ describes the interfacial free energy between two immiscible materials A and B, γ_AB(≡ −1/2 ΔW), as a function of dispersive (van der Waals) and polar components; the latter term is further parametrized in terms of the electron-donor and the electron-acceptor contributions. For each phase, three parameters are determined by an experimental procedure in which contact angles of three (or more) reference liquids are measured. These parameters are then used to solve a (overdetermined) system of equations, leading to results too often depending on the chosen triad of liquids.^4,6 In the case of thin polymer films^7,8 deposited onto solid substrates⁹⁻¹³—systems widely employed in a large number of everyday life applications, e.g., as antifouling coatings,¹⁴ dielectric¹⁵ and conducting media,¹² lubricating layers,¹⁶ etc.—combining methods^3−5,17 provide a thickness-independent value of γ_AB. The outcome of these approaches^14,18,19 commonly used at both the academic and industrial level, hence, implies that the interaction strength between two materials placed in intimate contact is not affected by confinement at the nanoscale level. In neat disagreement with this assumption, in this Article, by measuring the equilibrium adsorbed amount of thin polymer films deposited onto a solid substrate, we prove that the number of contacts between polymer and substrate, a quantity directly proportional to the work of adhesion, is actually correlated to sample geometry. A substantial drop in adsorbed amount—and in turn in ΔW—is observed upon reduction of the polymer film thickness below 5–10-fold the macromolecular size, R_g, that is ≲30–300 nm (see Figure 1), or when the adsorbing coating is capped by another polymer layer (see Figure 2). We explain these effects considering how interfacial interactions are tamed by nanoconfinement.

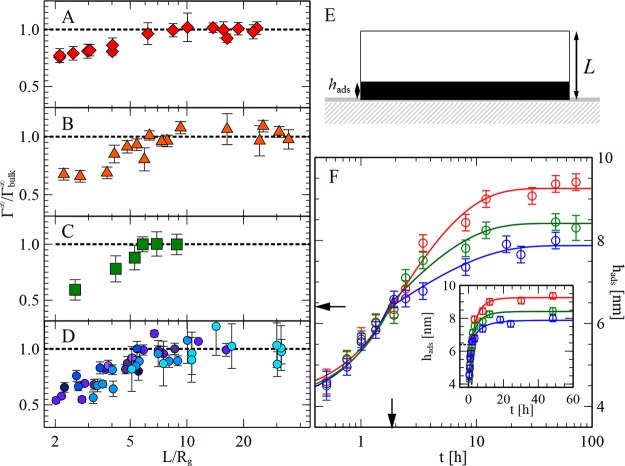
Figure 1.

Thickness dependence of the equilibrium adsorbed amount. (A – D) Equilibrium adsorbed amount (Γ^∞) normalized to the value measured in bulk samples [Γ_bulk^∞ = Γ^∞(L > 7R_g)] as a function of the spin-coated film thickness (L) normalized to the macromolecular size (R_g), for PtBS74, where 74 is the molecular weight in kg/mol (A, red diamonds), PMMA320 (B, orange triangles), P4MS72 (C, green squares), and PS (D, circles) of molecular weight 49, 99, 325, 488, 560, 1000, and 1460 kg/mol (ordered respectively to the molecular weight from light blue to dark purple, see Table S1). The black dashed lines mark the bulk value of the equilibrium adsorbed amount. (E) Sketch of a substrate/polymer monolayer system of spin-coated thickness L and adsorbed layer thickness h_ads. (F) Kinetics of adsorption for PS1000 at 433 K, the thickness of the adsorbed layer is plotted as a function of annealing time for spincoated monolayer samples of varying thickness L (130 nm blue circles, 235 nm green circles, and 325 nm red circles). Data superimpose in the linear growth regime, indicating a constant value of the adsorption rate. After the crossover point, marked by the arrows, the adsorption kinetics transitions from linear to logarithmic growth, and the effect of nanoconfinement becomes relevant: the equilibrium adsorbed amount, Γ^∞, decreases with L. The inset shows the same data set on a linear time scale.

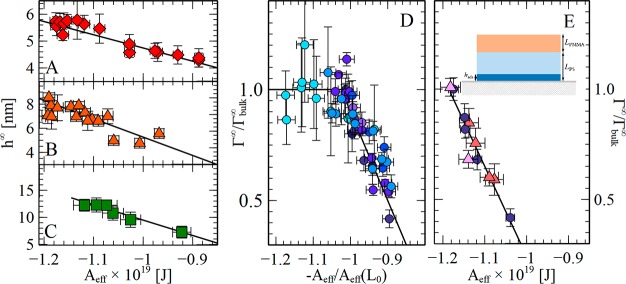
Figure 2.

Correlation between equilibrium adsorbed amount and effective Hamaker constant. (A–C) Equilibrium adsorbed thickness for single-layer systems (see sketch in Figure 1E) of PtBS74 (A, red diamonds), PMMA350 (B, orange triangles), and P4MS72 (C, green squares) as a function of the effective Hamaker constant (A_eff) acting at the polymer/substrate interface. (D) Equilibrium adsorbed amount normalized to bulk value as a function of the ratio A_eff(L)/A_eff (L₀ = 7R_g) for thin films of PS of different molecular weight (same symbols as in Figure 1D). We remark that data sets of Γ^∞/Γ_bulk^∞ vs A_eff(L/L₀) for different molecular weights do not collapse in a master plot, because A_eff(L) is not a linear function of L. Moreover, while for data sets A–C discriminating a constant value of the adsorbed amount at more negative Hamaker constants is hindered by experimental errors, for data in panel D a regime where the adsorbed amount is independent of A_eff is clearly visible. (E) Bilayer systems (see sketch in the top right corner of the same panel): normalized adsorbed amount for layers PS1000 (320 nm pink triangles, 140 nm orange triangles) capped by thin layers of PMMA. In these experiments A_eff is controlled by changing the PMMA layer thickness. For example, the Hamaker constant of the polymer bilayer system air/PMMA(150 nm)/PS(320 nm)/SiO₂(2 nm)/Si equals that of the monolayer system air/PS(103 nm)/SiO₂(2 nm)/Si. The adsorption kinetics for these bilayer systems are presented in Figure S12. Data for (uncapped) single layer of PS of the same molecular weight (purple circles) have been added for comparison.

In our experiments, we spin-coat ultrathin polymer films of different film thickness L (corresponding to the range 2–30 R_g(20)) onto Si substrates, covered by a native oxide layer (≈2 nm). Samples are annealed over time under isothermal conditions above the glass transition temperature to favor adsorption of chains onto the supporting substrate;²¹ the nonadsorbed material is washed away in a good solvent, following Guiselin’s experiment.²² The adsorbed layer thickness, an operational parameter directly proportional to the number of chains adsorbed per unit area, Γ, is measured via ellipsometry and atomic force microscopy (Materials and Methods section in the Supporting Information (SI)). For a given polymer and a given molecular weight, Γ is strictly proportional to the number of directly adsorbed monomers, and thus to the number of contacts between macromolecules and substrate (see eqs S1–S6).

Figure 1F shows the adsorption kinetics for films of polystyrene (PS) of three different spin-coated thicknesses. At short times, the growth of the adsorbed layer proceeds irrespectively of the film thickness, which implies the lack of nanoconfinement effects on the monomer adsorption rate.²³ At later times, a pronounced reduction in Γ^∞, the equilibrium adsorbed amount corresponding to the value reached after prolonged annealing, is observed as the film thickness decreases. This quantity is directly related to the depth of the interfacial potential (see the SI for additional details on the kinetics of adsorption). Nanoconfinement, therefore, mitigates the strength of interfacial interactions, without affecting the mechanisms of adsorption (see Figure 1F, and Figures S1, S2, S10, and S12). This observation is in line with our previous work,^23,24 showing that adsorption originates from the perpetuated repetition of fluctuations in the density of chains located in the layer in direct contact with the substrate. The monomer adsorption rate is, hence, not affected by the global dynamics of the whole film nor by the peculiar relaxation mode active at the free surface.²⁵

To understand the origin of the trends in Figure 1, we searched for a material property connected to the polymer/substrate potential and having a similar thickness dependence as Γ^∞. We discarded those components of the interfacial potential acting only on short-range, e.g., electronic and polar interactions, since those vanish at distances from the interface 1–2 orders of magnitude smaller than those observed here.² We have noticed that a change in polymer thickness yields a variation in the effective Hamaker constant of the system,²⁶A_eff (see the supplementary text in the SI). This parameter, indicating the strength of the long-ranged interactions at the polymer/substrate interface, is directly proportional to the depth of the interfacial potential^27,28 and, consequently, to the equilibrium number of molecules in direct contact with the adsorbing medium after long annealing time.²⁹ We have, hence, tested if the changes in Γ^∞ upon reduction of L could be ascribed to the thickness dependence of A_eff.

Our results confirm a linear correlation between the equilibrium thickness of the absorbed layer h^∞ (and therefore Γ^∞, see eq S6) and the effective Hamaker constant (see Figure 2A–D) of single-layer systems (i.e., air/polymer/SiO₂/Si). In line with our hypothesis, smaller adsorbed amounts are measured in thinner films, which are characterized by less negative values of the Hamaker constant (see the SI for details on the determination of A_eff). In our analysis, we considered unretarded Hamaker constants; we verified that our findings are not affected by retardation effects—arising from the London component of van der Waals interactions—which would require a nonzero time to cover the layer thickness (see Figures S7–S9).

To discard that the trend in Γ^∞(L) could be ascribed to finite size effects or any other unknown or uncontrolled parameter which could arise from sample preparation, we designed a second type of experiment where we modified the effective Hamaker constant without altering the thickness of the adsorbing layer. This condition was achieved by preparing bilayer polymer systems³⁰⁻³² (i.e., air/PMMA/PS/SiO₂/Si) in which the thickness of PS, L, is kept constant, while the thickness of the capping PMMA layer is varied from 0.1- to 1-fold L. Importantly, a reduction in A_eff can be obtained upon either increasing the thickness of the PMMA layer in bilayer systems or upon reduction of the thickness of the PS layers in the monolayer system (see Figure S6). Results (see Figure 2E) show that the number of chains of PS adsorbed onto SiO₂ decreases with increasing the thickness of the PMMA layer (see Figure S5), as expected for less negative values of A_eff.

The correlation between Γ^∞ and A_eff in bilayer samples of constant PS film thickness proves that sample preparation and the presence of free surfaces in contact with air are not responsible for the observed trend in the monolayer systems. By changing the thickness of the capping PMMA layer, while keeping constant that of PS, we were able to modify Γ^∞ in an identical manner as when reducing the thickness of PS in monolayers (see Figure S12). Importantly, in Figure 2E data of different PMMA/PS bilayers overlap with those of single layers of PS. This observation corroborates that the number of contacts at the PS/SiO₂ interface depends on the value of A_eff only and not on the thickness of the single spin-coated layers.

Finally, we have extended our investigation to thin films of monodisperse PS samples of different polymerization degree, N, covering a broad range of molecular weights (≈50–1500 kg/mol). A linear relation between Γ^∞ and A_eff was verified for all samples, regardless of chain length (see Figure S11). We remark that, while the thickness dependence of the Hamaker constant does not depend on the molecular weight, the number of chains necessary to cover a surface of unit area does. Because the number of contacts a polymer chain makes with a flat substrate scales as N^–1/2 (∼R_g^–1), all data collapse in a master plot where the normalized adsorbed amount is presented as a function of L/R_g, see Figure 1D.

Such a plot reveals that a size-independent value of Γ^∞(L) is reached at thicknesses L > L₀ ∼ 7R_g. In our reasoning L₀ indicates the thickness at which the number of polymer/substrate contacts reaches a given value, ensuring bulk work of adhesion. Remarkably, the onset of confinement effects on the adsorbed amount (∼7R_g) is in line with the length scale within which properties of the air/polymer surface are affected by the substrate.³³ While it seems unrealistic to rationalize such unexpectedly large molecular length scale via mechanisms involving adsorbed chains having at least one monomer in the polymer/surface layer,³⁴ our results indicate that confinement effects are directly ascribable to changes in work of adhesion, in agreement with the outcome of recent in silico experiments.³⁵

In view of the results in Figure 2, we conclude that in thin polymer coatings the equilibrium adsorbed amount deviates from bulk value, following the modification in the strength of the interaction potential induced by confinement in nanoscopic geometries. We remark that the trend observed for the impact of nanoconfinement on the kinetics of adsorption, see Figure 1F, is shared by other nonequilibrium phenomena, e.g., physical aging,³⁶ where the kinetics of equilibration (in our case the monomer adsorption rate) are not affected by a change in thermodynamic driving force (the depth of the interfacial potential).

At a fundamental level, determination and modeling of the interaction of two materials placed in intimate contact should take into account this experimental evidence. On a more applied side, the method described in this Article allows tuning the equilibrium adsorbed amount—a quantity permitting control of glass transition temperature,^19,37,38 crystallization ability,³⁹ viscosity,⁴⁰ etc.—without modification of the polymer/substrate pair, even without altering the thickness of the spin-coated film (L), which has never been accomplished before.

Methods

Thin films of polystyrene(PS), poly(methyl methacrylate) (PMMA), poly(4-tert butylstyrene) (PtBS), and poly(4-methylstyrene) (P4MS) were prepared by spin-coating dilute solutions of the polymers in good solvents (benzene for PMMA, toluene otherwise) onto silicon wafer substrates. Details on molecular weight, polydispersity, and source of the polymers used in this study are presented in Table S1; further information on sample preparation is provided in the SI; no unexpected or unusually high safety hazards were encountered. Film thickness, L (from 10 to 500 nm, corresponding to the interval 2R_g < L < 30R_g), was varied by changing the concentration of the polymer solution. Spin-coated films were dried in vacuum and preannealed above the glass transition temperature, to allow structural relaxation without altering the adsorbed amount. The value of the spin-coated thickness was determined after drying, via ellipsometry.^41,42 For the experiments in Figure 2E, we fabricated a series of multilayers of the type air/PMMA/PS/SiO₂/Si. First, we prepared single polymer layers of the type air/PS/SiO₂/Si following the procedure described above; then we spin-coated solutions of PMMA in acetic acid directly onto the PS films—as polystyrene is not soluble in acetic acid, the previously spin-coated films of PS are not affected by the deposition of the upper layer. The samples were again dried in vacuum for 20 min and preannealed as described above. For the adsorption experiments, spin-coated films of thickness L were annealed on a hot plate for different times to allow for adsorption of polymer chains onto the substrate. After annealing, nonadsorbed polymer chains are washed off reproducing Guiselin’s experiment:²² samples were rinsed and soaked for a fixed time in the same good solvent used to prepare the spin-coated solutions, in a one-step protocol for the monolayer samples and a two-step (first in acetic acid, then in toluene) protocol for the bilayer samples. The thickness of the adsorbed layer, h_ads, a direct measurement of the adsorbed amount Γ, was measured using ellipsometry (MM-16, Horiba),^41,42 using a bulk optical method, validated by independent measurements via atomic force microscopy.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00240.

• Methods for the preparation of single-polymer-layer and polymer-bilayer systems; determination of spin-coated thicknesses and the adsorbed amount via ellipsometry; data handling and fitting to the kinetic model of irreversible adsorption; the effect of nanoconfinement on the kinetics of irreversible adsorption, on the calculation of the effective Hamaker constant, including the role of retardation forces; and figures on the role of finite size effects on the kinetics of adsorption, on the impact of molecular weight on the adsorbed amount and a comparison of adsorption kinetics of single and bilayer systems having the same Hamaker constant (PDF)

The authors declare no competing financial interest.