Mechanism of Chemical and Electrochemical N₂ Splitting by a Rhenium Pincer Complex

Abstract

A comprehensive mechanistic study of N₂ activation and splitting into terminal nitride ligands upon reduction of the rhenium dichloride complex [ReCl₂(PNP)] is presented (PNP^– = N(CH₂CH₂PtBu₂)₂^–). Low-temperature studies using chemical reductants enabled full characterization of the N₂-bridged intermediate [{(PNP)ClRe}₂(N₂)] and kinetic analysis of the N–N bond scission process. Controlled potential electrolysis at room temperature also resulted in formation of the nitride product [Re(N)Cl(PNP)]. This first example of molecular electrochemical N₂ splitting into nitride complexes enabled the use of cyclic voltammetry (CV) methods to establish the mechanism of reductive N₂ activation to form the N₂-bridged intermediate. CV data was acquired under Ar and N₂, and with varying chloride concentration, rhenium concentration, and N₂ pressure. A series of kinetic models was vetted against the CV data using digital simulations, leading to the assignment of an ECCEC mechanism (where “E” is an electrochemical step and “C” is a chemical step) for N₂ activation that proceeds via initial reduction to Re^II, N₂ binding, chloride dissociation, and further reduction to Re^I before formation of the N₂-bridged, dinuclear intermediate by comproportionation with the Re^III precursor. Experimental kinetic data for all individual steps could be obtained. The mechanism is supported by density functional theory computations, which provide further insight into the electronic structure requirements for N₂ splitting in the tetragonal frameworks enforced by rigid pincer ligands.

1. Introduction

Industrial ammonia synthesis produces more than 150 Mt/a of fixed nitrogen, securing the nutrition of about half of Earth’s population with synthetic fertilizers, and serving as the feedstock for most nitrogen-containing organic chemicals.¹ The Haber–Bosch process fixes N₂ using the chemical reductant H₂, and thus relies on energy-intensive steam reforming of fossil fuels, leading the overall process to consume about 1–2% of the global energy supply. More sustainable approaches to ammonia production, such as electrochemical N₂ fixation, would therefore be highly desirable.² Examples of the use of electrochemical methods to achieve catalysis, or even key individual steps relevant to N₂ functionalization, are deeply limited. Heterogeneous electrode materials capable of the nitrogen reduction reaction (NRR) to ammonia have been reported, with recent advances tending toward ambient temperature and pressure conditions.³⁻⁵ However, Faradaic yields of the challenging 6e^–/6H⁺ NRR are low, usually due to the competitive hydrogen evolution reaction (HER), a 2e^–/2H⁺ process with a comparable standard reduction potential.⁶ Molecular catalysts typically exhibit much higher ammonia selectivities,⁷ but mainly rely on chemical reductants. Importantly, despite some early examples over 30 years ago, electrochemical NRR with molecular (pre)catalysts is still in its infancy.⁸

Advances in electrochemical nitrogen fixation with molecular catalyst platforms will rely on establishing detailed mechanistic insights. Almost all well-defined molecular catalysts have been proposed to follow sequential N₂ protonation/reduction mechanisms⁹ that are related to that of the [Fe,Mo]-nitrogenase enzyme, which is still under investigation.¹⁰ This pathway contrasts with the mechanism of the heterogeneously catalyzed Haber–Bosch process that passes through initial, turnover-limiting dissociative N₂ chemisorption to surface-bound nitrides on the way to ammonia formation. A well-defined molecular model for the challenging N₂ splitting step was first reported by Laplaza and Cummins in 1995 starting from a three-coordinate molybdenum(III) tris-anilide (Scheme 1).¹¹ This platform binds N₂ to form a dinuclear, linearly N₂-bridged complex that directly cleaves the extremely strong N–N bond (225 kcal/mol) into molybdenum(VI) nitrides at room temperature.¹² Several other examples of N₂ splitting into molecular nitrides with group 4–8 transition metals and uranium have since been reported,^13,14 and further employed to directly utilize N₂ in the synthesis of organic amines, nitriles, or isocyanates.¹⁵ However, for most of these systems the reactive intermediates that activate N₂ and the mechanistic details of splitting are not known. Furthermore, electrochemically driven N₂ cleavage into nitrides remains unknown.¹⁶

Scheme 1. N₂ Splitting into Terminal Nitrides with Molybdenum Tris-anilides and Transition Metal Pincer Halide Platforms Reported in the Literature^11,15d,17,19.

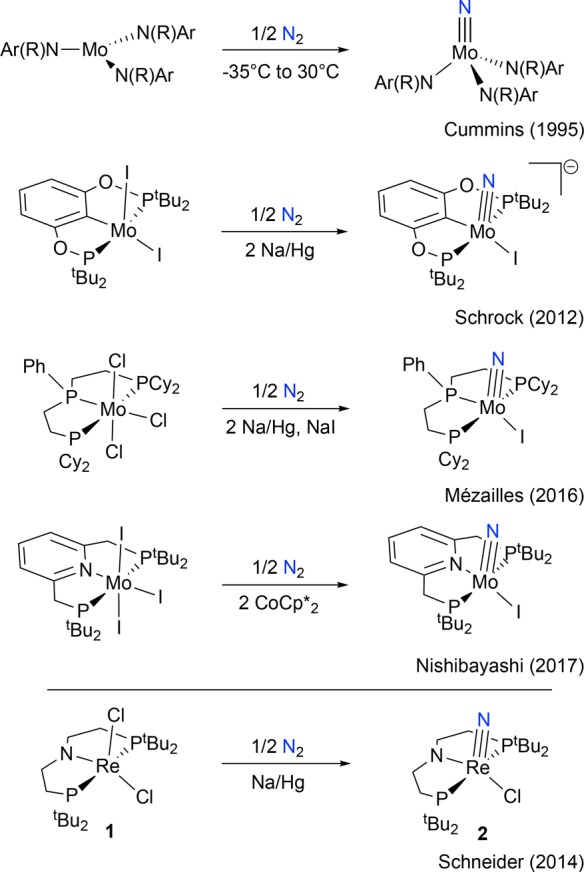
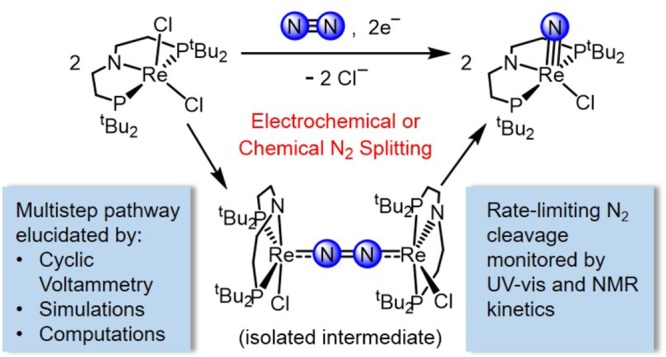
The groups of Schrock, Mézailles, and Nishibayashi independently reported stoichiometric N₂ activation and splitting into terminal nitrides upon reduction of pincer supported Mo halide complexes (Scheme 1).^15d,17 Nishibayashi’s nitride is also an active catalyst for ammonia synthesis,^17b providing early evidence that N₂ splitting into nitrides might in fact be relevant to N₂ fixation. Experimental information regarding the nature and reactivity patterns of the key intermediates in these pincer supported N₂ splitting reactions remains highly limited, particularly for pathways that proceed via in situ reduction of transition metal halide precursors. Dinuclear N₂-bridged species are possible intermediates in these reactions, and in fact, starting from a Mo^IV halide precursor, Schneider and co-workers isolated the N₂-bridged complex [{(PNP)ClMo}₂(N₂)] (PNP^– = N(CH₂CH₂PtBu₂)₂^–), which splits into Mo^V nitrides upon protonation (Scheme 2).¹⁸ This group also expanded N₂ splitting reactivity to group 7 precursors.¹⁹ Chemical reduction of a rhenium(III) pincer complex [ReCl₂(PNP)] (1) under 1 atm N₂ affords the terminal nitride [Re(N)Cl(PNP)] (2) in over 80% yield (Scheme 1). The N₂-bridged dinuclear complex [{(PNP)ClRe}₂(N₂)] (3) was proposed as an intermediate based on density functional theory (DFT) computations. Like most of the pincer complexes capable of splitting N₂, experimental data regarding the mechanism of formation and structure of polynuclear intermediates remains elusive. In contrast to the molybdenum pincer platforms, reduction of the rhenium system requires only one electron equivalent per metal ion. We therefore chose this system to examine the full mechanism of N₂ splitting starting from 1 as an archetypal pincer halide precursor utilized in N₂ cleavage. In this article, we present a comprehensive mechanistic picture that evolved from a combined synthetic, spectroscopic, crystallographic, kinetic, electrochemical, and computational study. We also report the first example of electrochemically driven N₂ splitting into well-defined molecular nitrides.

Scheme 2. N₂ Splitting upon Protonation of an N₂-Bridged PNP Pincer Complex¹⁸.

2. Results

2.1. Chemical N₂ Splitting

The mechanism of N₂ splitting was first examined by spectroscopic monitoring of the chemical reduction of 1 under N₂. Our previous DFT model predicted a sizable kinetic barrier for the N–N splitting step that forms the final nitride product 2,¹⁹ suggesting that an intermediate might be observable. In fact, the presence of a relatively long-lived intermediate was indicated by a temporary red coloration of the mixture during the reduction of violet 1 with Na/Hg to yellow nitride 2 at room temperature.

In an attempt to characterize the intermediate, Na/Hg reduction was carried out in tetrahydrofuran (THF) at −30 °C, leading to a persistent red solution with two new bands at 375 and 533 nm in the electronic absorption spectrum (Figure S4). NMR spectroscopic monitoring at −30 °C gave further insights. The decay of 1 upon reduction was accompanied by the formation of two doublets (δ −120 and +18 ppm) in the ³¹P{¹H} NMR spectrum (Figure 1). The doublets are correlated in a ³¹P–³¹P correlation spectroscopy (COSY) experiment (Figure S11) and feature a typical trans P–M–P coupling constant (²J_PP = 235 Hz), indicating chemically inequivalent phosphine substituents at a single Re(PNP) fragment. The ¹H NMR spectrum of the Re intermediate features sharp resonances covering a wide range of chemical shifts (−16 to +12 ppm, Figure S5) that correlate to the two ³¹P signals in a ¹H–³¹P heteronuclear multiple-bond correlation spectroscopy (HMBC) experiment (Figure S10). The number and multiplicity of the NMR signals resemble the N₂-bridged dimolybdenum complex [{(PNP)ClMo}₂(N₂)], which also features two doublets in the ³¹P{¹H} NMR spectrum and 12 ¹H NMR signals for the ligand tert-butyl (4) and backbone ethylene linker protons (8), respectively.¹⁸ This NMR pattern is attributed to a rigid, C₂-symmetric conformation enforced by the bulky phosphine substituents. Reduction of 1 under ¹⁵N₂ at −30 °C revealed a single new ¹⁵N{¹H} NMR signal at 211 ppm (besides the nitride signal of product 2 at 369 ppm; Figure S12), fully consistent with a symmetrically N₂-bridged intermediate (and inconsistent with a terminal N₂ ligand). The chemical shift lies in the typical range for coordinated N₂,²⁰ but the value notably differs from the isostructural Mo complex [{(PNP)ClMo}₂(N₂)] (δ = 69 ppm). The combined spectroscopic data identify the intermediate as the N₂-bridged dimer [{(PNP)ClRe}₂(N₂)] (3, Scheme 3). The characterization of the dinuclear intermediate 3 (∼75% yield at −30 °C based on ¹H NMR integration, Figure S6) substantiates our previous computational proposal.¹⁹

Figure 1.

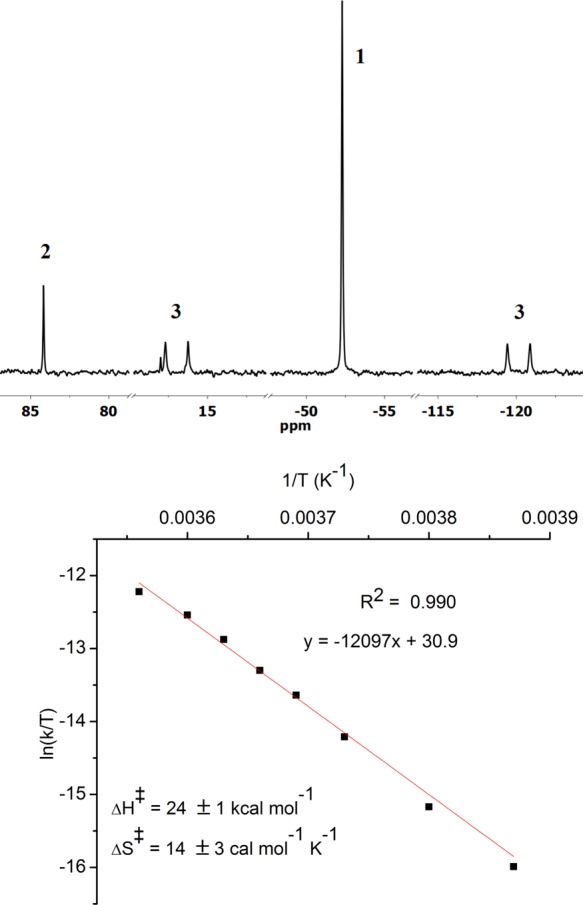
(top) ³¹P{¹H} NMR spectrum during reduction of 1 at −30 °C under N₂. (bottom) Eyring plot for the conversion of 3 to 2 in the temperature range −15 to +7.5 °C.

Scheme 3. N₂ Splitting upon Chemical Reduction of Rhenium(III) Complex 1 via N₂-Bridged Dirhenium Complex 3.

The unusual chemical shift ranges found for the ¹H, ³¹P, and ¹⁵N NMR spectra of 3 require an additional comment. These strongly shifted, yet narrow, NMR lines are tentatively attributed to an expression of temperature independent paramagnetism (TIP).²¹ Unusual chemical shift parameters of rhenium(III) phosphine complexes that were attributed to TIP are well-documented.²² TIP arises from an open-shell electronic structure with a thermally isolated ground state (≫k_BT) that results from strong mixing with excited states via spin–orbit coupling, as was found for the related square-planar complex [Os^IICl{N(CHCHPtBu₂)₂}].²³ Variable-temperature NMR (VT-NMR) spectra of 3 between −55 and −5 °C feature signals that are almost all temperature independent, supporting TIP. Only the ³¹P peak at −120 ppm (Δδ = 8 ppm) and one ¹H signal of the pincer backbone at 0.4 ppm (Δδ = 1.5 ppm) show some temperature dependence (Figures S13–S15). However, these signals scale linearly with T^–1, which would not be expected for the thermal population of a higher lying electronic state (Figures S16 and S17). Furthermore, the tBu ¹H NMR signals exhibit significant broadening at lower temperatures, suggesting that an additional dynamic process, such as freezing rotation of the tBu groups at low temperatures, is responsible for the temperature dependence of these two signals. Unfortunately, the low chemical stability of 3 in solution precluded the isolation of samples suitable for SQUID magnetometric characterization to confirm TIP.

The structure of 3 was confirmed through an X-ray diffraction study (Figure 2) of single crystals grown at −80 °C from a THF solution layered with pentane. The asymmetric unit contains one dinuclear molecule of 3 and one mononuclear molecule (comprised of a 50/50 mix of cocrystallized parent 1 and nitride 2). The molecular structure features a μ²:η¹:η¹-N₂ ligand that bridges the apical positions of square-pyramidal rhenium ions (τ₅ = 0.18 on Re1 and τ₅ = 0.16 on Re2).²⁴ The {ReCl(PNP)} fragments are twisted with respect to each other (Cl1–Re1–Re2–Cl2: 112.1°), which interlocks the bulky PtBu₂ groups. This rigid conformation is in agreement with the C₂-symmetric structure observed in solution. A moderate degree of activation is indicated by the N₂ bond length (1.202(10) Å), which is intermediate between free dinitrogen (1.10 Å)²⁵ and diazene (1.25 Å).²⁶ In turn, the short Re–NN–Re bonds (1.861(6) and 1.886(8) Å) support considerable metal-to-N₂ π-backbonding. The conformation and the other structural features are in excellent agreement with the prior computational model.¹⁹

Figure 2.

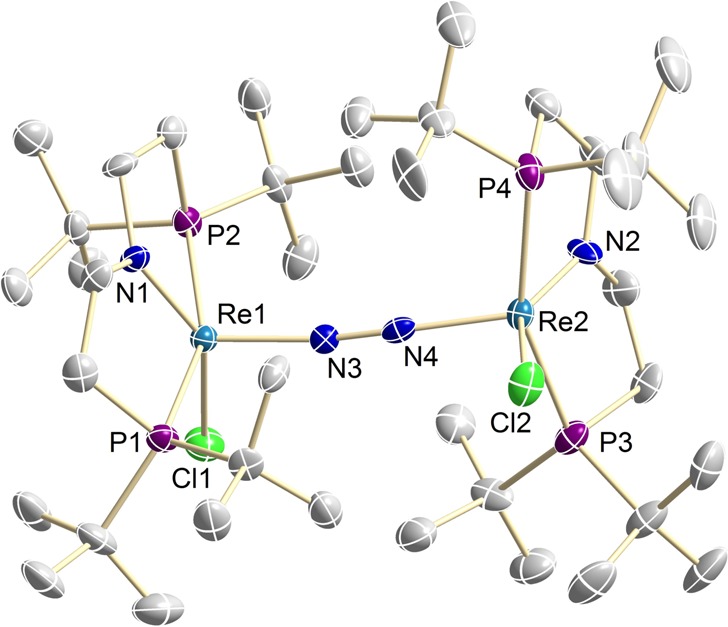
Molecular structure of 3 from single-crystal X-ray diffraction with anisotropic displacement parameters drawn at the 50% probability level. Hydrogen atoms and cocrystallized 1 and 2 are omitted for clarity. Selected bond lengths (Å) and angles (deg): Re1–N3 1.861(8), Re1–N1 1.937(7), N3–N4 1.202(10), Re2–N4 1.886(8), Re2–N4 1.949(8), N1–Re1–Cl2 146.30(2), P1–Re1–P2 157.38(9), P3–Re2–P4 156.28(9), N2–Re2–Cl2 146.6(3), Cl1–Re1–Re2–Cl2 112.0(6).

The direct observation of 3 in high spectroscopic yields at low temperatures allowed for kinetic examination of the N₂ splitting reaction. Warming a solution of 3 to room temperature resulted in selective formation of nitride 2 according to ³¹P and ¹H NMR spectroscopies. Monitoring the decay of 3 by ¹H NMR spectroscopy at a particular temperature revealed clean first-order kinetics over more than two half-lives (Figure S1). An Eyring analysis within the temperature range −15 to +7.5 °C (Figure 1) provides activation parameters for N₂ splitting: ΔH^‡ = +24 ± 1 kcal·mol^–1; ΔS^‡ = 14 ± 3 cal·mol^–1·K^–1. These experimental activation parameters compare well with the previously computed free energy of activation (+20.2 kcal/mol)¹⁹ and the values obtained for a slightly refined computational model (see section 2.3).

After identifying 3 as the pivotal intermediate that splits N₂ in the formation of nitride 2, reactivity relevant to the assembly of the N₂-bridged species was examined. Dinitrogen binding and chloride dissociation were considered likely initial chemical processes. The possibility of N₂ binding to 1 was investigated using infrared (IR) spectroscopy, but a solution of 1 in THF under 1 atm N₂ gave no indication of end-on binding of dinitrogen (Figure S25). Furthermore, UV–vis spectra obtained under Ar and N₂ were identical, even upon cooling from room temperature to −78 °C (Figures S26 and S27). Finally, ³¹P{¹H} NMR spectra of 1 showed no perceptible difference when recorded under Ar or N₂ (1 or 5 atm), even upon cooling to −95 °C (Figures S20–S22). On the basis of these experiments, a limiting binding constant for N₂ binding to 1 can be estimated (K_eq < 1 M^–1, Supporting Information, section 5). The interaction of 1 with chloride, which is released during the N₂ splitting reaction, was also assessed. NMR spectroscopic monitoring of a solution of 1 under N₂ in the presence of excess [ⁿBu₄N]Cl indicated chemical stability and no chloride association over more than 48 h (Figure S24). These binding studies indicate an alternative initial step, such as reduction of rhenium(III). Therefore, electrochemical methods were employed to interrogate formation of 3.

2.2. Electrochemical N₂ Splitting

2.2.1. Electrochemical Synthesis of Nitrides from N₂

To probe whether N₂ splitting can be driven electrochemically, controlled potential electrolysis (CPE) of 1 was explored. Electrolysis of 1 in THF containing 0.2 M [ⁿBu₄N][PF₆] was carried out at −1.90 V vs Fc^+/0 under 1 atm N₂,²⁷ based on the CV data for 1 (see section 2.2.4) and the successful use of Co(Cp*)₂ (E° = −1.9 V)²⁸ as a chemical reductant for this reaction. During electrolysis at room temperature, the color of the solution changed from purple to yellow as charge amounting to 1.2 electrons per Re was passed. Analysis of the product mixture by ³¹P{¹H} NMR spectroscopy showed that 2 was produced in 58% yield (Scheme 4, Figure S19). An analogous CPE experiment of 1 under 1 atm Ar instead of N₂ gave an intractable mixture of unidentified products. Notably, the conversion of 1 to 2 under N₂ represents the first synthesis of a nitride complex via electrochemically driven dinitrogen cleavage.

Scheme 4. Electrochemical Conversion of 1 to Rhenium(V) Nitride Complex 2.

2.2.2. UV–Vis Spectroelectrochemical Examination

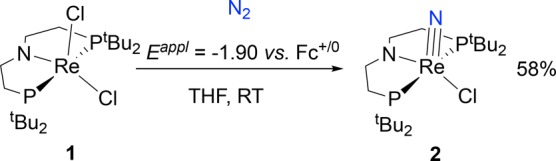
UV–visible spectroelectrochemistry (SEC) was utilized to probe for the buildup of intermediates during electrolysis. Electrolysis resulted in conversion of 1 (λ_max = 530 nm) to a new species with strong absorbances at 384 and 537 nm within 60 s (Figure 3). This intermediate was not observed when the corresponding UV–vis SEC experiment was conducted under Ar (Figure S28), clearly indicating the role of N₂ in its formation. The intermediate is assigned as N₂-bridged dimer 3, based on the close agreement of the spectral features with a solution of 3 obtained by chemical reduction at −30 °C (λ_max = 375 and 533 nm, see section 2.1) and the time-dependent (TD) DFT computed UV–vis spectrum for 3 (see section 2.3 and Figure S4). Upon continued electrolysis, the intermediate converted to product 2 (λ_max = 393 nm) over the course of about 2 min (Figure 3, inset). Kinetic data for the N₂ splitting chemical reaction was obtained by fitting the decay of 3 in the time period after a minimum in electrolytic current was reached (approximately 100 s) to avoid significant impact by diffusion or competing electrochemical processes. The half-life obtained under these conditions for the conversion of 3 into 2, t_1/2 = 28 s at 298 K (Figure S2), is in close agreement with the rate constant derived for splitting of 3 into 2 after chemical reduction of 1 under N₂ (k^298 K = 0.018 s^–1, t_1/2 = 38 s, see section 2.1).

Figure 3.

UV–vis spectroelectrochemistry (SEC) electrolysis of 1, showing the absorption profile during conversion of 1 to intermediate 3. (inset) Time course tracking absorbance at 540 nm for formation and decay of 3. Conditions: 2 mM 1, 0.2 M [ⁿBu₄N][PF₆] in THF at 25 °C, −1.45 V vs Ag wire pseudoreference constant applied potential over 10 min, Au working and counter electrodes, Ag wire pseudoreference electrode in a “honeycomb” cell arrangement.

2.2.3. Cyclic Voltammetry under Ar

Several elementary steps must be involved on the pathway from complex 1 to the N₂-bridged dimer and ultimately to the nitride products of N₂ cleavage. We therefore turned to cyclic voltammetry (CV) to build a deeper understanding of the initial steps of reductive N₂ cleavage. Reduction under Ar was examined first in order to rationalize the redox behavior of the rhenium platform in the absence of N₂; the electrochemical behavior under N₂ is described in the subsequent section.

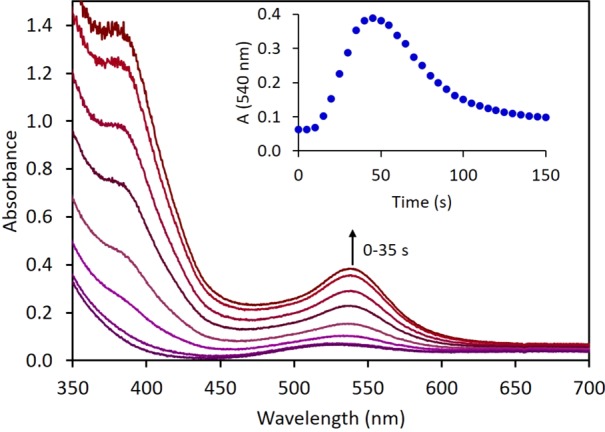
CV of 1 under Ar shows two reduction processes at −1.96 and −2.24 V, respectively (Figure S33). The peak current of the first reduction wave (i_p,c,1) increases linearly with the square root of the scan rate, indicating a diffusion-controlled process. Increased scan rates lead to a large cathodic shift in the peak potential of the first reduction of 1, which suggests that the first reduction is followed by a chemical reaction. Considering chloride dissociation a plausible reduction-triggered chemical step, the influence of chloride ion concentration on the first reduction process was examined. The peak potential of the first reduction shifts cathodically by ΔE = −0.04 V upon addition of 20 equiv of [ⁿBu₄N]Cl (Figure 4). This cathodic shift is accompanied by an increase in reversibility (i_p,c,1/i_p,a,1 = 1.4 with 20 equiv of Cl^– and 0.1 V·s^–1) when sweeping through only the initial reduction event. The second reduction process remains irreversible at all examined scan rates and is essentially unaffected by chloride addition. Varying the concentration of 1 from 0.5 to 4 mM has a negligible effect on the overall features of the CV and the peak current ratio of the two reductive features is virtually unaffected. These observations are consistent with an ECE mechanism (electrochemical–chemical–electrochemical reaction sequence). Initial reduction of 1 forms [ReCl₂(PNP)]⁻, which undergoes reversible chloride ligand dissociation forming [ReCl(PNP)]. The second feature is assigned to irreversible reduction of [ReCl(PNP)].

Figure 4.

CV data of 1 in THF containing 0.2 M [ⁿBu₄N][PF₆] under Ar with varying amounts of [ⁿBu₄N]Cl, ν = 0.1 V·s^–1.

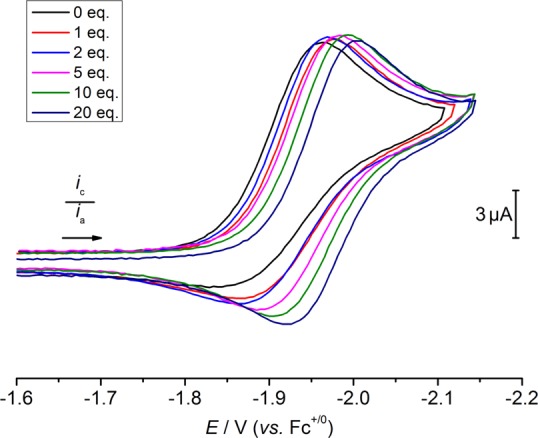
The proposed ECE mechanistic model was probed by digital simulation of the electrochemical data. The simulation parameters (formal potentials, rate constants, and electron transfer parameters) for the best fit are given in Table 1. Figure 5 compares the experimental and simulated CV data with 0–20 equiv of added chloride ion across a wide range of scan rates (see the Supporting Information for more details). The peak current of the second reduction process and the reversibility of the first process cannot be modeled satisfactorily by a simple ECE mechanism (i.e., reduction, chloride ion loss, reduction). In order to achieve good agreement of the simulated and experimental CV data, unimolecular (k₂) decay of [ReCl(PNP)] had to be considered in addition to reduction of [ReCl₂(PNP)] (E₁) and [ReCl(PNP)] (E₂), which are connected by reversible chloride dissociation from [ReCl₂(PNP)]⁻ (k₁, K₁; Scheme 5).

Table 1. Thermodynamic and Kinetic Parameters Obtained from Simulation of CV Data under Ar.

Parameter	Value
K1 (M)	0.05
k1 (s–1)	1000
k2 (s–1)	0.11
E1 (V)	–2.00
α1	0.5
ks,1 (cm/s)	0.05
E2 (V)	–2.29
α2	0.8
ks,2 (cm/s)	0.05
E1 – E2 (V)	0.29

Figure 5.

Overlay of experimental (black lines) and simulated (red dashed lines) CV data (I = 0.2 M [Bu₄N][PF₆] in THF at room temperature, ν = 0.1 V·s^–1) for 1 at different concentrations (top) and with various amounts of Cl^– ions (bottom). Simulations according to the mechanism in Scheme 5 with the thermodynamic and kinetic parameters given in Table 1.

Scheme 5. Minimum Mechanistic Models for Electrochemical Reduction of 1 under Ar (Orange Box) and under N₂ (Gray Box), Respectively.

The PNP ligand is omitted for all species for clarity.

A sensitivity analysis was carried out to provide insight into the accuracy of the parameters derived from the simulation. Doubling/halving of k₂ leads to substantially worse fits for the second reduction peak, which cannot be compensated satisfactorily by changing any other rate constant. The rate and equilibrium constants of chloride loss (k₁ and K₁) were extracted from the chloride titration experiments, and doubling/halving of the values leads to considerably worse fits.

2.2.4. Cyclic Voltammetry under N₂

The CV data of 1 under N₂ (1 atm) is dramatically different than under Ar (Figure 6). The peak potential of the first reduction process shifts anodically by 60 mV under N₂ with respect to Ar (E_p,c = −1.90 V, ν = 0.1 V·s^–1) and exhibits a substantial increase in the current response indicative of a multielectron reduction. The feature that is assigned to the reduction of [ReCl(PNP)] near −2.2 V under Ar is absent under N₂; a new minor reduction feature is observed near E_p,c = −2.4 V (ν = 0.1 V·s^–1).

Figure 6.

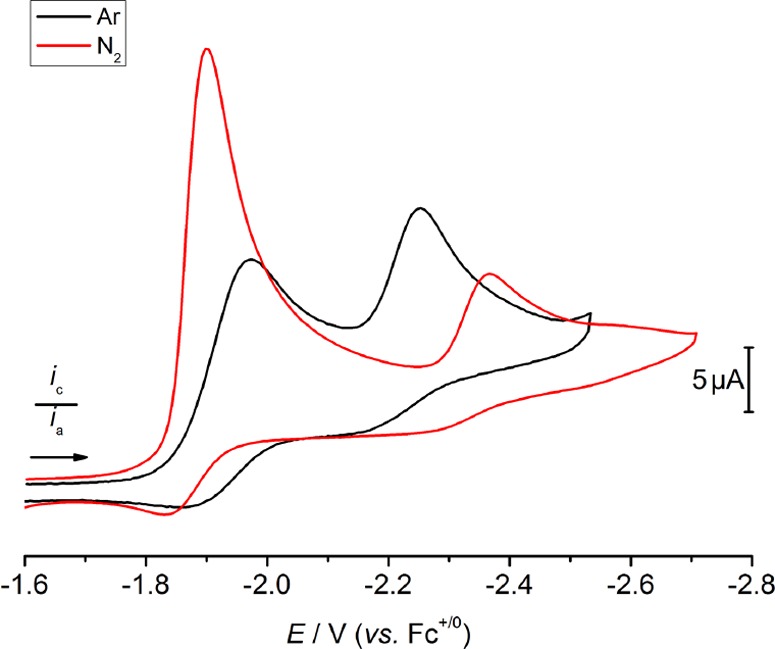
CV data of 1 in THF containing 0.2 M [ⁿBu₄N][PF₆] under 1 atm N₂ (red) and Ar (black). Conditions: 1 (0.8 mM) in 0.2 M [ⁿBu₄N][PF₆] measured at 0.1 V·s^–1.

Upon increasing scan rate, the peak potential of the first reduction process of 1 shifts cathodically and exhibits increasing reversibility, which indicates a coupled chemical reaction following initial reduction (Figure S40). This chemical reaction must involve N₂, because the reduction feature assigned to [ReCl(PNP)] in the CV data under Ar is not present. The characteristic reversible Re^VI/Re^V redox couple (E_1/2 = −0.09 V) of the nitride complex 2 is not observed among the several oxidation features in the return sweep, indicating that the nitride is not produced at the electrode in significant quantities within the time scale of a single CV experiment, which is in line with the rate constant for the decay of 3 (see section 2.1). The smaller second reduction feature observed at a 0.1 V·s^–1 scan rate decreases in current and then disappears altogether as the scan rate is increased, which is consistent with the formation of an intermediate that is electrochemically detectable by subsequent reduction. It remains unclear whether this species corresponds to the N₂-bridged intermediate 3 observed in NMR and SEC experiments. However, the potential of this reduction is far too negative to play a significant role in electrolytic N₂ splitting, so further characterization of this feature has not been pursued.

Increasing the concentration of free chloride ions leads to a cathodic shift of the peak potential of the initial reduction of 1, and a slight increase in reversibility (Figure 7). In the presence of 20 equiv of [ⁿBu₄N]Cl, E_p,c shifts from −1.90 to −1.94 V (ν = 0.1 V·s^–1). The ratio of cathodic and anodic peak currents is 1.9 at a scan rate of 0.1 V·s^–1, indicating less reversibility than was achieved under the same conditions but under an Ar atmosphere. More current passes at higher concentrations of 1, as expected, and the peak potential of the initial reduction is essentially unchanged in the range of 0.5–4 mM 1 (Figure S36).

Figure 7.

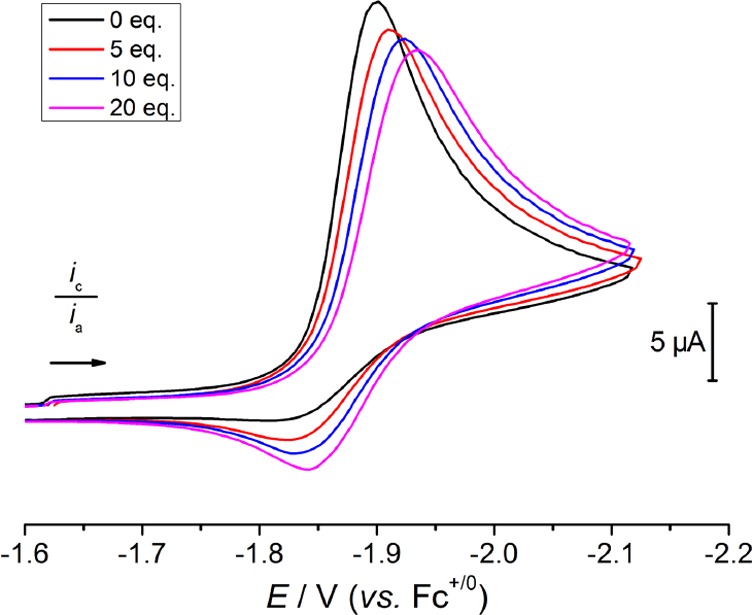
CV of 0.8 mM 1 in THF containing 0.2 M [ⁿBu₄N][PF₆] and 0–20 equiv [ⁿBu₄N]Cl under N₂ at 0.1 V·s^–1.

Finally, the N₂ binding step of the reaction was evaluated by variation of the N₂ concentration. Upon increasing the pressure to 10 atm, the first cathodic process rises in current and seems to reach a plateau in this pressure range, while the potential remains unchanged (Figures S37 and S38). The second reduction feature near E_p,c = −2.4 V (ν = 0.1 V·s^–1) decreases in intensity with increasing N₂ pressure. CV data measured at 1 atm before and after pressurization are almost unchanged.

Simulation of the CV data was pursued to identify the N₂ activating species and derive a comprehensive, quantitative picture of the formation of the N₂-bridged intermediate that splits into nitrides. Several mechanisms that involve the necessary N₂ binding (C^N₂), chloride ion dissociation (C^Cl), and dimerization (C^dim) chemical steps were considered (Scheme S1). The multielectron transfer character of the reduction peak is consistent with rapid 2e^– reduction of complex 1 to a rhenium(I) species before formation of a bridging N₂ intermediate with parent 1 in the diffusion layer. In contrast, lower current similar to a 1e^– reduction would be expected for a pathway involving a mixed-valent N₂-bridged rhenium(II)/rhenium(III) intermediate, as confirmed by digital simulations (Figure S45). The pronounced peak potential shift and current increase of the first cathodic process observed moving from Ar to N₂ suggest fast chemical reactions and a potential inversion of the subsequent reduction process. The increased reversibility in the presence of added chloride suggests reversible chloride ion dissociation (C^Cl). Irreversible dimerization (C^dim) is taken to be the last step of the reaction sequence based on the SEC studies above in which N₂-bridged dimer 3 builds up before N₂ splitting and the multielectron nature of the first reduction process.

Three conceivable pathways involve pre-equilibrium N₂ binding (Scheme S1). The N₂ coordination step could be followed by (a) two-electron reduction, chloride ion loss, and dimerization (C^N₂E^2eC^ClC^dim), (b) two successive one-electron reductions, chloride ion loss, and dimerization (C^N₂EEC^ClC^dim), or (c) successive steps of reduction, chloride ion loss, reduction, and dimerization (C^N₂EC^ClEC^dim). Such pre-equilibrium pathways are unlikely due to the lack of NMR, UV–vis, and IR spectroscopic evidence for a dinitrogen adduct of 1 under various conditions (see section 2.1). These pathways were further excluded by electrochemical simulations (Figures S45–S47) using the spectroscopically estimated upper limit for initial N₂ binding (K_eq < 1 M^–1, Supporting Information, section 5). Most importantly, a pre-equilibrium should lead to a dramatic shift of the peak potential with increasing N₂ pressure, which has not been observed experimentally.

Alternative pathways all involve the initial electrochemical reduction of 1, followed by various orders of the N₂ binding, chloride ion loss, and second reduction preceding the final dimerization step. An EC^ClC^N₂EC^dim sequence would follow the kinetics of reduction and chloride ion loss, just as observed under argon, with subsequent N₂ binding to the monochloride intermediate [ReCl(PNP)]. In this situation, the formal potential of the first reduction and the chemical kinetics of chloride dissociation must be the same under N₂ and Ar. The observed anodic shift of the peak potential moving from Ar to N₂ immediately casts doubt on [ReCl(PNP)] being involved in N₂ binding. Indeed, even with diffusion-controlled N₂ binding, the simulation could not account for the large peak potential shift observed under N₂ (Figure S48). The EC^N₂EC^ClC^dim scenario features initial reduction of 1 followed by N₂ binding to form [ReCl₂(N₂)(PNP)]⁻, which would be subsequently reduced. It would be surprising for the reduction potential of this anionic dinitrogen complex to be in a similar range to neutral complex 1. In fact, for this species, a reduction potential E = −3.26 V was computed by DFT (see section 2.3). Even if taking an unrealistic reduction potential of −1.89 V for the intermediate, the current dependence on chloride addition could not be sufficiently modeled for this pathway, which makes the EC^N₂EC^ClC^dim scenario also unlikely (Figure S49).

The minimum scenario that could adequately simulate the CV data is the EC^N₂C^ClEC^dim pathway (Scheme 5): reduction of 1 is followed by N₂ binding to form [ReCl₂(N₂)(PNP)]⁻. This rhenium(II) species undergoes chloride loss to neutral [ReCl(N₂)(PNP)], which can be reduced at a less negative potential (ΔE ≈ 0.4 V) than [ReCl(PNP)] due to the π-acceptor ligand N₂. Resultant rhenium(I) species [ReCl(N₂)(PNP)]⁻ ultimately comproportionates with parent 1. Subsequent or simultaneous chloride loss would form N₂-bridged dimer 3, but for simplicity this process was not included in the simulations. The simulated and experimental CV data are in excellent agreement over a wide scan rate and chloride ion concentration range (Figure 8 and Figures S50 and S51) for this highly complex reaction sequence. The simulation parameters were chosen to maximize conserved parameters from the Ar data (E₁, E₂, k₁, k₂), and to minimize the number of variables in the simulation; other processes such as redox disproportionation and competing concurrent pathways were not considered for the sake of simplicity.²⁹ The numerical ranges of the fit parameters under N₂ (E₃, k₃, K₃, k₄, K₄, k₅) lead to fits within the experimental error of the measurements as judged by the standard deviations of the peak currents and potential shifts obtained from multiple experiments (Tables S1 and S2; see the Supporting Information for further information).

Figure 8.

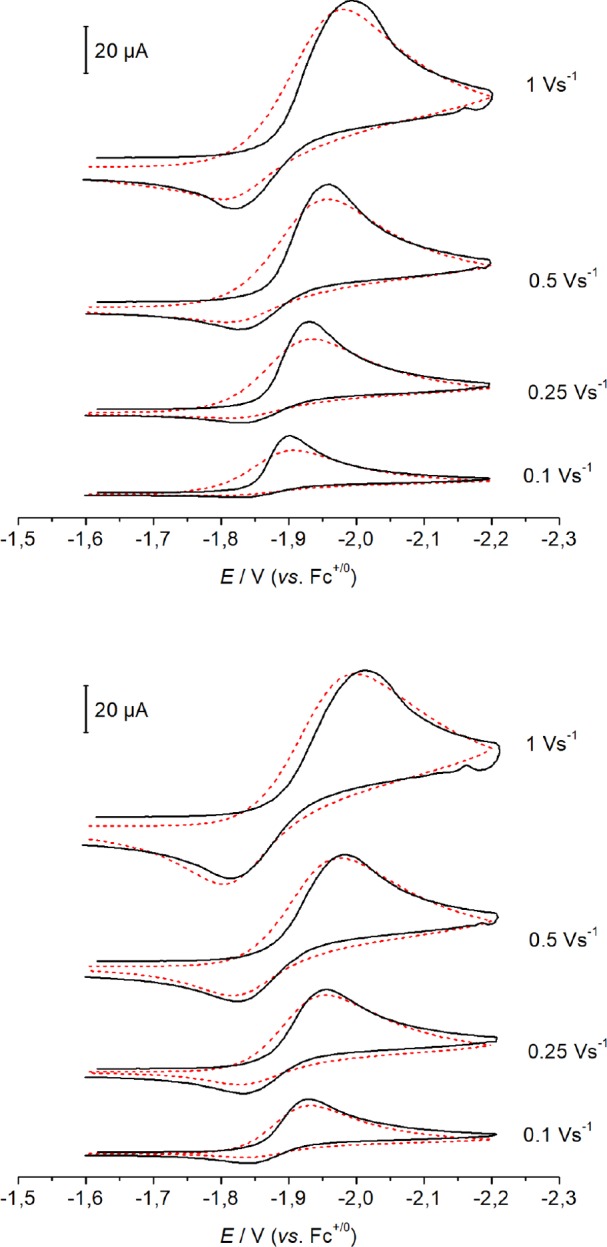
Overlay of experimental (black lines) and simulated (red dashed lines) CV data (I = 0.2 M [ⁿBu₄N][PF₆] in THF at room temperature) for 1 (top) and 1 with 10 equiv [ⁿBu₄N]Cl (bottom). Simulation according to Scheme 5 with the thermodynamic and kinetic parameters given in Tables 1 and 2.

Key results of the simulations (Table 2) include the following: (1) trapping of the electron-rich and coordinatively unsaturated rhenium(II) species [ReCl₂(PNP)]⁻ by the π-acceptor ligand N₂ is both thermodynamically favorable (K₃ ≈ 10⁴ M^–1) and kinetically rapid (k₃ > 5 × 10⁷ M^–1 s^–1); (2) chloride ion loss from [Re^IICl₂(N₂)(PNP)]⁻ is thermodynamically not favored (K₄ ≈ 10^–2 M) but rapid (k₄ > 5 × 10² s^–1); (3) reduction of [Re^IICl(N₂)(PNP)] to rhenium(I) (E₃ = −1.86 V) is at a more positive potential than parent 1, resulting in the characteristic peak shape. The potential value E₃ is somewhat less well-defined by the simulations, given that changes of ±20 mV did not have a dramatic influence on the simulation quality. This simple minimum model does not reproduce the increasing peak current with N₂ pressure (Figure S52). The conversion of [Re^ICl(N₂)(PNP)]⁻ to bis-dinitrogen complex [Re^ICl(N₂)₂(PNP)]⁻ through an additional N₂ binding equilibrium could account for this trend. Stabilization of Re(I) might slow the rate of dimerization to 3 and therefore the depletion of parent 1 in the diffusion layer resulting in higher currents at higher N₂ pressure. Furthermore, computational analysis suggests reversible formation of a rhenium(I) bis-dinitrogen compound (see section 2.3). With K₆ ∼ 50 M^–1 and k₆ ∼ 1000 M^–1 s^–1 for this equilibrium, the simulations for ambient pressure are virtually unchanged while the current increase for the high pressure data is well resembled (Figure S53).

Table 2. Estimated Ranges for Rate and Equilibrium Constants of the Best Model for Electrochemical Reduction of 1 under N₂ Atmosphere^a.

Parameter	Range	Value
K3 (M–1)	5 × 103–5 × 104	(1 × 104)
k3 (M–1 s–1)	>5 × 107	(5 × 109)
K4 (M)	2 × 10–2–2 × 10–3	(5 × 10–3)
k4 (s–1)	>5 × 102	(1 × 105)
k5 (M–1 s–1)	4 × 103–1 × 104	(7 × 103)
E3 (V)	–1.84 to −1.88	(−1.86 V)

^aThe values in parentheses were used to plot the simulation in Figures 8 and Figures S50–S53.

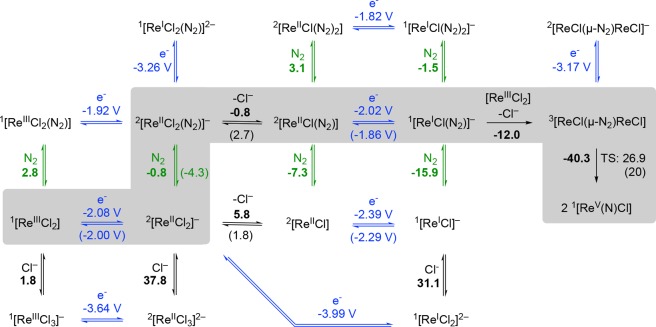
2.3. Computational Analysis

Density functional theory (DFT) computations were carried out to evaluate the N₂ splitting mechanism presented in the preceding sections. The calculations were mainly restricted to reaction steps directly supported by experimental data. This study expands upon the previous report that focused on the splitting of dinuclear complex 3 into nitrides.¹⁹ This N₂ splitting step was also revisited in light of the additional experimental results presented above that include ample structural, spectroscopic, electrochemical, and kinetic data for benchmarking.

Electrochemical potentials were anchored with the experimental [Re(N)Cl(PNP)] (2⁺/2) redox couple (E_1/2 = −0.086 V).^30,31 Several functionals were evaluated by comparison with (a) the experimental/simulated redox potentials and equilibrium constants E₁, E₂, E₃, K₁, K₃, and K₄ and (b) DLPNO-CCSD(T)³² calculations of truncated model complexes (see Supporting Information, section 7, and Tables S6–S8). Best agreement was obtained with the M06 functional³³ for the thermochemistry of both redox (E°_M06 – E°_exp = 0.1–0.2 V) and chemical steps (Scheme 6; see also the Supporting Information, section 7). Reaction free energies in THF were estimated by application of Truhlar’s SMD solvation model,^34,35 including structural relaxation of gas-phase optimized geometries in solution.

Scheme 6. Computed (M06/def2-TZVP(SMD(THF))//D3BJ-RIJ-PBE/def2-SVP) Formal Reduction Potentials and Reaction Free Energies (kcal·mol^–1) of Electrochemical and Chemical Steps That Connect 1 with Nitride 2.

The proposed mechanism is highlighted in gray. Experimentally derived potentials and free energies are given in parentheses. Irreversible decomposition routes under Ar were not considered in the computational model.

Binding of N₂ (ΔG°_M06 = +2.8 kcal·mol^–1) or chloride (ΔG°_M06 = +1.8 kcal·mol^–1) to parent 1 are both calculated to be endergonic, in accord with the experimental stability of 1 in the presence of N₂ and chloride. An initial reduction process from 1 to [Re^IICl₂(PNP)]⁻ was considered next, with the computed potential in excellent agreement with experiment (E°_M06 = −2.1 V; E°_exp = −2.0 V).²⁷ Further reduction of all anionic intermediates to dianionic species is computed at reduction potentials well beyond −3.0 V, and can therefore be safely discarded. In the absence of N₂, chloride dissociation, which is slightly overestimated in endergonicity (ΔG°_M06 = +5.8 kcal·mol^–1; ΔG°_exp = +1.8 kcal·mol^–1), and subsequent reduction of [Re^IICl(PNP)] (E°_M06 = −2.4 V; E°_exp = −2.3 V) represent the preferred pathway, fully supporting the experimental CV simulations. For both redox couples [ReCl₂(PNP)]^0/– and [ReCl(PNP)]^0/–, respectively, small structural rearrangements were computed suggesting fast and electrochemically reversible electron transfer.

Coordination of N₂ to the initial reduction product [Re^IICl₂(PNP)]⁻ is considerably more favorable than chloride dissociation (ΔΔG°_M06 = 6.6 kcal·mol^–1; Scheme 6). The product of N₂ binding is predicted to be most stable as the cis-dichloro isomer. The chloride ligand in octahedral cis-[Re^IICl₂(N₂)(PNP)]⁻ was computed to be labilized relative to [Re^IICl₂(PNP)]⁻ (ΔΔG°_M06 = 6.6 kcal·mol^–1), rendering Cl^– dissociation slightly exergonic. Electrochemical simulations actually point to slightly less favorable Cl^– dissociation from the N₂ adduct, which might be explained by computational underestimation of the stability of [Re^IICl₂(N₂)(PNP)]⁻. Reduction is reflected by a shift of the computed N₂ stretching vibration and slight elongation of the N–N bond relative to hypothetical cis-[Re^IIICl₂(N₂)(PNP)] (Table 3), indicating a moderate degree of N₂ activation at rhenium(II)³⁶ with less than 20% of the computed spin density located at the N₂ ligand.

Table 3. Computed Structural and Electronic Parameters of Selected Dinitrogen Intermediates in the Most Stable Configuration.

	[ReIIICl2(N2)(PNP)]	[ReIICl2(N2)(PNP)]−	[ReIICl(N2)(PNP)]	[ReICl(N2)(PNP)]−	3
dRe–Na (Å)	1.969	1.892	1.892	1.877	1.875
dN–Na (Å)	1.141	1.162	1.158	1.170	1.200
υN–Na (cm–1)	2105	1975	1955	1935	1771
ρReb	0.36	0.24 (0.50)	0.42 (0.59)	0.13	0.37 (0.91)
ρNαb	–0.05	–0.09 (−0.01)	–0.13 (−0.03)	–0.13	–0.22 (0.00)
ρNβb	–0.08	–0.28 (0.18)	–0.15 (0.30)	–0.42	–

^aGas phase structures.

^bCalculated NPA charges with natural spin densities in parentheses.

Subsequent reduction of [Re^IICl(N₂)(PNP)] after chloride loss was computed to occur at E° = −2.0 V, i.e., about the same potential as the initial reduction and thus consistent with an ECCE-type mechanism. A closely related pathway, in which N₂ binding is followed by reduction of the bis-dinitrogen complex to rhenium(I) at slightly less negative reduction potential, cannot be ruled out computationally (Scheme 6). For each of these pathways, the key finding of potential inversion upon N₂ addition and chloride loss is preserved. As expected, reduction of rhenium(II) is accompanied by an additional bathochromic shift of the N₂ stretching vibration and N–N bond elongation (Table 3). Furthermore, natural population analysis (NPA) shows an accumulation of negative charge at the terminal N atom of [Re^ICl(N₂)(PNP)]⁻. However, natural bond orbital (NBO) analysis (Figure S57) and the computed N₂ stretching vibration (1935 cm^–1) clearly favor formulation as a Re^I dinitrogen over Re^III diazenido complex. In comparison, Cummins’ anionic diazenido complex [Mo(N₂)(NtBuAr)₃]⁻ (Ar = C₆H₃-3,5-Me₂) exhibits an N₂ stretching vibration at 1761 cm^–1.³⁷

Structural comparison of the range of computed mononuclear rhenium structures (Supporting Information, section 7.7) shows that the octahedral rhenium(II) and rhenium(I) species exhibit distorted minimum conformations of the pincer backbone that involve either a considerable tilt around the Re–N_PNP bond or pyramidalization of the pincer nitrogen atom. Both structural distortions would help minimize a π-mismatch of filled rhenium d-orbitals with the amide lone pair. This observation suggests that the strong π-donating ability of the dialkylamide ligand works in concert with the steric bulk to facilitate halide loss.

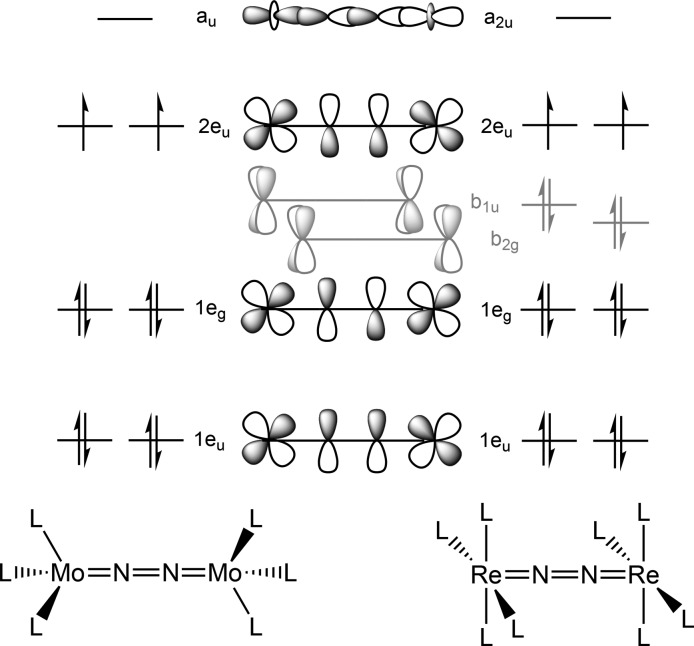
Comproportionation of the rhenium(I) dinitrogen intermediate with parent rhenium(III) complex 1 and concomitant chloride loss to form the dinuclear compound 3 was computed to be exergonic (ΔG°_M06 = −12.0 kcal·mol^–1). Consequently, the formation of 3 is the first irreversible reaction within the lowest energy EC^N₂C^ClEC^dim pathway, in support of the electrochemical model. In the previous model, using the PBE functional, an antiferromagnetically coupled electronic singlet ground state was computed to be energetically almost degenerate with a triplet state for 3.¹⁹ In contrast, the M06 functional favors the triplet state by 4.6 kcal·mol^–1, with the spin density mainly centered on the Re ions (Table 3). However, the shifted, yet sharp NMR signals of 3 (see section 2.1) indicate an energetically well-separated ground state presumably due to further splitting by spin–orbit coupling. Despite the obvious inability of DFT to properly describe the multireference character of 3, the molecular structure is excellently reproduced. Furthermore, TD-DFT computations predict an absorption spectrum for 3 (Figure S4) that is in excellent agreement with the spectra obtained in SEC experiments. In comparison with the mononuclear N₂ complexes discussed above, the computed N–N bond distance (1.20 Å) and stretching frequency (1771 cm^–1) range between typical values for a moderately activated N₂ ligand and a diazenido (N₂^2–) bridge.³⁶ Within a localized description of the core, the rhenium-centered spin density is in agreement with a Re^II(N₂)Re^II formulation or alternatively Re^III(N₂^2–)Re^III with intermediate-spin rhenium(III) (S = 1) antiferromagnetically coupled to (triplet) N₂^2–. However, oxidation states can be physically meaningless in the case of highly covalent metal–ligand multiple bonding as was pointed out, e.g., for nitrosyl or nitride complexes.³⁸ Within a more covalent bonding picture, diazenido (formal N–N double bonding) character of the N₂ bridge is reflected by the occupation of two Re–N–N–Re π_ReN–π*_NN–π_ReN molecular orbitals (MO236/237; Figure 9) with four electrons and two electrons in the π*_ReN–π_NN–π*_ReN MOs (MO240/241), respectively.

Figure 9.

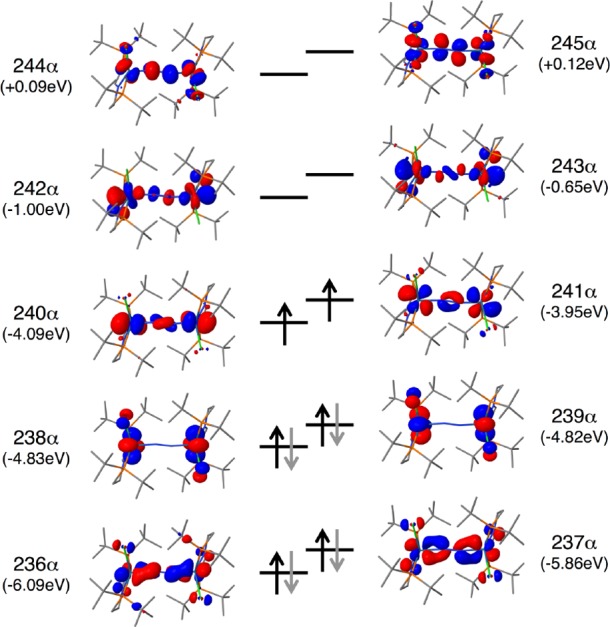
DFT computed frontier molecular orbital (FMO) diagram of 3.

As in the previous computational model,¹⁹ the transition state (TS) for splitting of 3 into nitrides exhibits a Re–N–N–Re in-plane zigzag structure³⁹ with an N–N distance (1.59 Å) that is considerable longer than the N–N single bond in hydrazine (1.45 Å). Upon approaching the TS, MO242 (Figure 9), which is essentially Re–N–N–Re nonbonding, gains considerable σ_Re–N and σ*_N–N character and is gradually stabilized with respect to the π-MO manifold (Figure S59). Population of this MO from the π*_ReN–π_NN–π*_ReN level leads to both N–N bond weakening and Re–N strengthening and ultimately full N–N bond cleavage. The computed free energy of activation at 298 K (ΔG^‡_M06 = +26.9 kcal/mol) is slightly higher than the experimental value (ΔG^‡_exp = +19.8 kcal/mol) and the previously computed values (ΔG^‡_PBE = +20.2 kcal/mol). However, the enthalpy of activation (ΔH^‡_M06 = 26.2 kcal·mol^–1) is in excellent agreement with experiment (ΔH^‡_exp = 24 kcal·mol^–1). The considerable deviation of the entropy of activation (ΔS^‡_M06 = −3 cal·mol^–1 K^–1; ΔS^‡_exp = 14 cal·mol^–1 K^–1) can in part be attributed to an underestimated contribution of the electronic partition function, which arises from the inability of DFT to describe the multireference character of 3. With that notion, the better agreement of ΔG^‡_PBE with experiment might be a consequence of error compensation.

3. Discussion

3.1. Chemical vs Electrochemical N₂ Splitting

The transition metal mediated reduction of N₂ to two nitrides formally requires the transfer of six electrons and the cooperative action of at least two metal ions. As the closest analogues of our rhenium platform, Schrock, Mézailles, and Nishibayashi have reported N₂ splitting upon 2e^– reduction of either Mo^III or Mo^IV pincer halides under dinitrogen.^15d,17 For all of these systems, experimental information about the nature of the key species and kinetics of the elementary steps remains unknown. A complex reaction mechanism can be expected that is composed of several steps, such as reduction, N₂ binding, halide dissociation, formation of N₂-bridged species, and N–N bond cleavage. Consequently, the kinetics of the elementary steps need to be aligned to obtain the desired reactivity, specifically if reactive intermediates with short lifetimes under the experimental conditions are involved.

In many systems that were shown to fully split N₂, the nature of the chemical reductant has a strong influence on the nitride yield. For example, Holland and co-workers have shown that alkali metal reductants facilitate N₂ splitting in Fe(nacnac) complexes by producing alkali metal cations that stabilize the products of N₂ activation and cleavage through contact ion-pair formation.^14,40 However, in most cases the origin of reductant effects is not well understood. In the case of parent 1, the N₂ splitting yield is slightly higher with Na/Hg (>85%) than with Co(Cp*)₂ (up to 75%).¹⁹ A productive role for Na⁺ in removing chloride after dissociation (K₄ = 10^–3 M, Table 2) could be envisioned in this case. Our mechanistic model also reveals that the rhenium(II) species formed upon initial reduction (E₁ = −2.0 V) is the N₂ binding state, followed by reduction to rhenium(I) at a slightly less negative potential (E₃ = −1.9 V) and Re^I/Re^III comproportionation leading to productive nitride synthesis (Scheme 5). If N₂ does not bind, the rhenium(II) intermediate can undergo reductive decomposition (E₂ = −2.3 V), as seen in the Ar CV data. Very strong reductants (E° < – 2.3 V) could introduce the possibility of over-reduction of the rhenium(II) species competing with productive N₂ binding, which might lead to unproductive decomposition pathways.

As judged from the complexity of our mechanistic model, it is obvious that molecular platforms for N₂ splitting with chemical reductants are not necessarily transferable to electrochemical approaches. Electrochemical methods also have inherent speciation and concentration gradients from the electrode surface through the diffusion/reaction layer to the bulk solution, which give rise to different kinetic profiles compared with both molecular and solid chemical reductants, respectively. However, in contrast to the other pincer halide precursors that have been used for N₂ splitting, our rhenium platform 1 only requires one reduction equivalent per metal ion. It therefore is the simplest candidate to directly initiate N₂ activation by electrochemical electron transfer and obtain mechanistic information from the voltammetric response. In fact, the rhenium pincer system represents the first example of electrochemical N₂ splitting into well-defined molecular nitride complexes. Other electrochemical nitride syntheses have started from ammonia, such as Meyer and co-workers’ electrochemical oxidation of osmium(III) ammine complexes to terminal osmium(VI) nitrides.⁴¹ In the present reductive N₂ splitting reaction, the same N₂-bridged intermediate is formed in both chemical and electrochemical reductions, as evidenced by UV–vis absorption spectroscopy (λ_max = 533 nm). This mechanistic connection and the relatively high Faradaic yield offer, for the first time, the possibility of electrochemical examination of a full N₂ splitting sequence triggered by reduction of a transition metal halide complex.

3.2. Formation of the N₂-Bridged Intermediate

The accumulation of N₂-bridged complex 3 as the only observable intermediate, within seconds of electrolysis, indicates rapid kinetics for all elementary steps prior to dinitrogen cleavage. Simulations of the electrochemical data under a broad range of experimental conditions and scan rates are supported by DFT computations to provide compelling evidence for a EC^N₂C^ClEC^dim mechanism. The process begins with electrochemical reduction immediately followed by coordination of N₂. The kinetic model reveals two key findings about the initial steps: (1) the N₂ binding step occurs in the Re(II) formal oxidation state; (2) N₂ binding occurs before chloride dissociation. According to experimental data, N₂ binding to [Re^IICl₂(PNP)]⁻ is strongly favorable (K₃ > 5 × 10³ M^–1) and rapid (k₃ > 5 × 10⁷ M^–1 s^–1), in sharp contrast to the unobserved binding to the rhenium(III) complex 1 (K_eq < 1 M^–1). This increased affinity for the π-acid N₂ is anticipated for the more electron-rich, anionic rhenium(II) complex. The DFT computations qualitatively align with this trend, as reflected by the large computed bathochromic shift of the N₂ stretching vibration for [ReCl₂(N₂)(PNP)]^0/– (Δν = 130 cm^–1). Peters and co-workers observed an increase in N₂ binding affinity by 6 orders of magnitude upon reduction of a low valent bimetallic iron complex.⁴² The rate of N₂ binding for this Fe system (7 × 10⁸ M^–1 s^–1) is similar to that found for rhenium(II) intermediate [ReCl₂(PNP)]⁻. An alternative pathway involving N₂ activation by a rhenium(I) species (EC^ClE-type mechanism) was irreconcilable with the distinct current increase observed for the first reduction feature under N₂ relative to Ar and the missing reduction feature E₂ of [ReCl(PNP)] under N₂. The rapid N₂ binding to rhenium(II) is a prerequisite to avoid unimolecular decay after chloride loss (k₂). We therefore hypothesize that the bulky pincer ligand, which enforces a five-coordinate geometry in the starting complex 1, might be instrumental for productive N₂ activation and splitting.

The next step is chloride dissociation from the anionic dinitrogen complex, [Re^IICl₂(N₂)(PNP)]⁻. The rate constant for chloride dissociation from [Re^IICl₂(N₂)(PNP)]⁻ (k₄ > 5 × 10² s^–1) is comparable to or faster than that of [Re^IICl₂(PNP)]⁻ under Ar (k₁ = 1 × 10³ s^–1). Chloride dissociation is likely facilitated by the bulky tert-butyl substituents and the strong amide π-donating ability of the PNP ligand framework. In comparison, chloride loss from another rhenium(II) complex, [Re^II(PMe₂Ph)₃Cl₃]⁻, was reported to be several orders of magnitude slower (k = 0.91 s^–1).⁴³ On the other hand, chloride dissociation from isoelectronic [Mo^ICl₂(dppe)₂]⁻ (k = 2.5 × 10² s^–1; dppe = bis(diphenylphosphino)ethane) proceeds with a comparable rate constant to the present system.⁴⁴ The net result of the two chemical steps that follow reduction is an associative substitution at five-coordinate [Re^IICl₂(PNP)]⁻.

Substantial evidence has been collected that the neutral dinitrogen complex [Re^IICl(N₂)(PNP)] undergoes reduction to the corresponding anionic Re^I complex at a potential less negative than the reduction potential of parent 1. Compared with the CV under argon, the current amplification and the potential shift of the first reduction feature under N₂ is indicative of potential inversion; i.e., reduction of this intermediate is more facile than reduction of 1. The presence of a π-accepting N₂ ligand should shift the reduction of [Re^IICl(N₂)(PNP)] to more anodic potentials relative to 1, and computations bear out this hypothesis. Similar potential inversion has been observed with [Re^IIICl₂(dppe)₂]⁺, which is reduced at a more cathodic potential relative to the reduction of [Re^IICl(N₂)(dppe)₂]⁺ (−0.81 and −0.27 V, respectively), despite the lower formal oxidation state for the latter.⁴⁵ [Re^IICl₂(N₂)(PNP)]⁻ was also considered a candidate for this second electron transfer process, but as expected the reduction potential was computed at a much more negative potential.

Formation of the bridging dinitrogen complex 3 requires a bimolecular reaction step. Since the transformation involves one electron per rhenium, and Re^II is easily reduced to Re^I, a reasonable hypothesis involves the comproportionation of Re^III and Re^I through the reaction of 1 with [Re^ICl(N₂)(PNP)]⁻. The two species would react as the anionic Re(I) complex diffuses away from the electrode and 1 diffuses from the bulk solution toward the electrode (Figure S54). This is taken to be the rate-limiting process in the electrochemical reduction of 1, on the basis of the observed accumulation of N₂-bridged 3 in UV–visible SEC experiments. For the sake of simplicity, CV simulations only include the bimetallic dimer formation process, and chloride dissociation is not directly considered. Chloride dissociation does occur, either in a concerted fashion or in a separate dissociation process, to form 3. DFT calculations suggest that the net dimerization and chloride dissociation process is in fact strongly exergonic (ΔG° = −12.0 kcal·mol^–1) and thus irreversible.

At least five steps occur during the sweep of a cyclic voltammogram to form the N₂-bridged intermediate 3 from molecular nitrogen. The complexity of the ECCEC-type reaction sequence adds some degree of uncertainty to the quantitative rate and equilibrium constants, and a sensitivity analysis provides a range of viable values. However, DFT calculations provide strong support for the proposed mechanism. As an additional key finding, the computational results indicate that considerable N₂ activation, as judged by the stretching vibrations, is not obtained prior to Re^I/Re^III comproportionation to dinuclear complex 3, thereby avoiding the unfavorable one-electron reduction of N₂.⁴⁶

3.3. Splitting of the N₂-Bridged Intermediate into Nitrides

The final step of nitride formation is the rate-determining cleavage of dirhenium complex 3. Dinitrogen splitting with molecular platforms has recently been comprehensively reviewed.¹³ Within a simple, covalent bonding model, the degree of N₂ activation in linearly N₂-bridged dinuclear complexes can be predicted based on the occupation of the π-manifold that is constructed by linear combination of metal d-orbitals and nitrogen p-orbitals of the {M–N–N–M} core.⁴⁷ Splitting of such compounds into terminal nitride complexes has been associated with π¹⁰–{M–N–N–M} electronic configurations to reach stable nitrides with filled M–N π and vacant π* MOs.^13,48,49 These simple considerations are showcased by Cummins’ S₆-symmetric intermediate [{(tBuArN)₃Mo}₂(N₂)]^12,50 (Scheme 7) and other examples.^18,51 The electronic structure computations for 3 are in full agreement with this picture (Figure 9). In the current case, the square-pyramidal ligand field renders nonbonding, metal d-orbital based MOs with δ-symmetry (Figure 9, MO238/239) energetically accessible to host the four additional valence electrons in the dirhenium complex, i.e., {ReN₂Re}⁴⁺ (π¹⁰δ⁴) vs {MoN₂Mo}⁶⁺ (π¹⁰) (Scheme 7). The similar degree of N₂ activation is expressed by the N–N bond distances found for 3 (1.202(10) Å) and [{(tBuArN)₃Mo}₂(N₂)] (1.212(2) Å),⁵⁰ respectively. These values are considerably shorter than related compounds with π⁸ ([{(tBuArN)₃Mo}₂(N₂)]²⁺, 1.265(5) Å)) or π⁸δ⁴ ([{(PNP)ClMo}₂(N₂)], 1.258(9) Å) configurations.^18,50

Scheme 7. Qualitative Comparison of the Electronic Configurations of L₃Mo^III(N₂)Mo^IIIL₃ in S₆-Symmetric (left) and of L₄Re^II(N₂)Re^IIL₄ in D_4h-Symmetric (right) Ligand Fields, Respectively.

The simple analogy of the trigonal- and square-pyramidal platforms suggests that the success with group 7 metal rhenium is facilitated by the square-pyramidal coordination geometry with apical N₂ coordination, enforced by the bulky pincer ligand. Schneider and co-workers showed that the stable (π⁸δ⁴)-complex [{(PNP)ClMo}₂(N₂)] (S = 0) also splits into nitrides upon protonation of the pincer backbone, which is associated with a transition to a π¹⁰δ² (S = 2) configuration.¹⁸ Hence, besides coordination geometry, the spin state seems to have a subtle influence on N₂ splitting. In this context, the Mo pincer halides that are overall reduced by 2e^–/Mo are particularly interesting (Scheme 1). There, several redox and spin states are conceivable for binuclear N₂-bridged intermediates that split into nitrides. Applying the simple considerations discussed above, e.g., to Schrock’s POCOP complex,^17a low-spin [{(POCOP)(I)Mo}₂(N₂)]^2– (π¹⁰δ⁴, S = 0; POCOP = C₆H₃-2,6-(OPtBu₂)₂) or high-spin [{(POCOP)(I)Mo}₂(N₂)] (π¹⁰δ², S = 2) might be the preferred states for N₂ splitting.

DFT studies for the splitting of [{(RR′N)₃Mo}₂(N₂)] suggest a distortion of the {Mo–N–N–Mo}-core from linearity toward a zigzag shaped transition state prior to full cleavage into nitrides.⁵² Krewald and González recently examined the photochemical splitting of [{(H₃N)₅Os}₂(N₂)]⁵⁺ using multireference computations with perturbative treatment of spin–orbit splittings (SO-CASPT2) for a defined linear trajectory of the two separating {(H₃N)₅OsN}ⁿ⁺ fragments.⁵³ However, as a general picture that evolves for the different pathways, N₂ bond cleavage can be correlated with the population of N–N σ* orbitals at the expense of M–N π*-MOs. This electronic rearrangement weakens the N–N and strengthens the M–N bonds. These considerations also hold true for the computational model for splitting of 3, which nicely reproduces the experimental activation enthalpy. In the transition state, the MO with σ*_N–N character (Figure 9, MO242; Scheme 7, a_2u) is populated. Notably, this MO would be destabilized by an additional ligand (e.g., N₂) trans to the bridging N₂-ligand. For example, in contrast to Cummins’ tris-anilides with trigonal-pyramidally coordinated Mo, Schrock’s five-coordinate triamidoamine complex [{(tBuMe₂SiNCH₂CH₂)₃NMo}₂(N₂)], which exhibits the same spin states, formal oxidation states, and similar degrees of N₂ activation, does not split into nitrides. In this context, it is tempting to speculate that the square-pyramidal (rather than octahedral) geometries enforced by the bulky PtBu₂-containing pincer ligands utilized in Re- and Mo-mediated N₂ splitting are a prerequisite for facile kinetics.

4. Concluding Remarks

The pincer-supported rhenium complex described here is, to date, the only group 7 transition metal complex reported to split N₂ into nitrides. It is also a representative example of a high-valent metal halide that produces nitrides upon reduction under N₂ at ambient conditions. The nitride is formed rapidly and in high yield, both using chemical reductants and, for the first time, electrochemical reduction. These traits are prerequisites for successful incorporation into future (electro)catalytic cycles. Furthermore, this system is amenable to detailed mechanistic analysis that has provided unprecedented insight into the elementary steps from reduction and N₂ activation all the way to splitting. The electrochemical data, chemical kinetics, and supporting computational treatment give a comprehensive mechanistic picture that involves initial, extremely rapid assembly of the dinuclear intermediate 3, followed by slightly slower N–N bond scission to furnish nitrides. Key findings for this sequence are the following: (1) the N₂binding state is a mononuclear Re^IIspecies with dramatically increased dinitrogen affinity after reduction of precursor 1, (2) binding of the π-accepting N₂ ligand leads to immediate further reduction of the Re^IIN₂adduct to Re^Idue to potential inversion, followed by comproportionation with the Re^IIIprecursor to reach the N₂-bridged dimer, and (3) considerable N₂activation is not achieved prior to formation and subsequent splitting of this dimer. It is reasonable to assume that the accessibility of more stable Re^I is instrumental to avoiding Re^II decay pathways. Furthermore, it allows for storage of two reduction equivalents at the metal, thereby avoiding thermodynamically unfavorable one-electron N₂ reduction. This chain of events is facilitated by the bulky, π-donating pincer ligand, which stabilizes the coordinatively unsaturated precursor and low-valent, transient intermediates.

This Re^I/Re^III comproportionation defines the first irreversible step in the electrochemically driven reaction sequence. The steric bulk of the pincer ligand might also be advantageous in stabilizing coordinatively unsaturated 1 in this step. Trapping of the Re^I dinitrogen intermediate in the diffusion layer by parent 1, which is fully depleted at the cathode surface, emphasizes the importance of mass transport for electrochemical N₂ functionalization. The electronic configuration of N₂-bridged 3 resembles that of Cummins’ prototypical N₂ splitting intermediate [{(RR′N)₃Mo}₂(N₂)], with the square-pyramidal geometry proving crucial to accommodating the additional electrons of Re^II relative to Mo^III. The mechanistic insight gained in this Re system offers guidance for the future development of additional platforms for chemical and electrochemical N₂ splitting.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b03755.

• Full experimental details, including synthetic procedures and characterization details, cyclic voltammetry and other electrochemical data, details of voltammetric simulations, crystallographic and computational details (PDF)

• Crystallographic information for 3·0.51·0.52·0.5C₅H₁₂ (CIF)

Author Contributions

^∥ B.M.L. and R.S.v.A.: These authors contributed equally.

The authors declare no competing financial interest.

Notes

CCDC-1832925 (3·0.51·0.52·0.5C₅H₁₂) contains the supplementary crystallographic data for this paper. This data can be obtained free of charge via http://www.ccdc.cam.ac.uk/products/csd/request/ (or from Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge, CB2 1EZ, U.K. Fax: + 44-1223-336-033. E-mail: deposit@ccdc.cam.ac.uk).