Plasmonic Surface Lattice Resonances: A Review of Properties and Applications

Abstract

When metal nanoparticles are arranged in an ordered array, they may scatter light to produce diffracted waves. If one of the diffracted waves then propagates in the plane of the array, it may couple the localized plasmon resonances associated with individual nanoparticles together, leading to an exciting phenomenon, the drastic narrowing of plasmon resonances, down to 1–2 nm in spectral width. This presents a dramatic improvement compared to a typical single particle resonance line width of >80 nm. The very high quality factors of these diffractively coupled plasmon resonances, often referred to as plasmonic surface lattice resonances, and related effects have made this topic a very active and exciting field for fundamental research, and increasingly, these resonances have been investigated for their potential in the development of practical devices for communications, optoelectronics, photovoltaics, data storage, biosensing, and other applications. In the present review article, we describe the basic physical principles and properties of plasmonic surface lattice resonances: the width and quality of the resonances, singularities of the light phase, electric field enhancement, etc. We pay special attention to the conditions of their excitation in different experimental architectures by considering the following: in-plane and out-of-plane polarizations of the incident light, symmetric and asymmetric optical (refractive index) environments, the presence of substrate conductivity, and the presence of an active or magnetic medium. Finally, we review recent progress in applications of plasmonic surface lattice resonances in various fields.

1. Introduction

1.1. What Is Plasmonics and Why Is It Interesting/Important?

Plasmonics is a field that has emerged at the interface of photonics, electronics, and nanotechnology.¹ It has seen spectacular progress in recent years that promises dramatic advances and new developments in nano-optics, nanophotonics, and metamaterials.²⁻⁷ Plasmonics exploits the collective motion of conduction electrons in metals (plasmons), making possible the coupling of light with nano-objects and the generation of a range of new optical effects at the nanoscale. The excitation of plasmons is accompanied by a dramatic localization and enhancement of the electric field associated with light at optical frequencies. Field localization and enhancement are central to a variety of novel applications in nanoelectronics, optical imaging, biomedicine, telecommunications, photovoltaics, photocatalysis, etc.

1.2. Types of Plasmon Modes

Plasmon modes can be subdivided into two classes: propagating surface plasmons and localized surface plasmons.

1.2.1. Propagating Surface Plasmons (PSP)

PSPs have been extensively studied (for reviews see, e.g., refs (2 and 7)) and are still the focus of interest for numerous research groups, for example, owing to their importance for biosensing/biorecognition applications. PSPs are surface electromagnetic waves which may be supported at a metal/dielectric interface. They comprise an electromagnetic wave that is coherently bound with the collective motion of mobile charges in the surface of the metal; this coherent interaction leads to the PSP having greater momentum than that of a free photon of the same frequency. The excitation of PSPs thus requires some kind of momentum matching technique, these include prism coupling^8,9 and grating coupling,¹⁰ of which nanohole array couplers are an important example.^11,12 The Turbadar–Kretschmann–Raether prism geometry,^8,13 also referred to as surface plasmon resonance (SPR), is a prominent example of PSP excitation in which p-polarized light is directed into a glass prism and subsequently reflected from a thin (∼50 nm) metal film that has been deposited on one of the prism’s faces. Light incident in this way leads to the generation of PSPs on the far (opposite to the metal/prism) side of the metal film and occurs for a specific combination of angle of incidence and wavelength.² For a fixed angle of incidence, the excitation of PSPs is accompanied by the appearance of a minimum in the reflectance spectrum. The spectral width of this reflectance dip is typically ∼50 nm full-width at half-maximum (fwhm) for Au films⁷ and is accompanied by a clear change in the phase of the reflected light near the minimum of the resonance.^14,15 Based on the extremely high sensitivity of SPR to variations in the refractive index (RI) of the dielectric medium close to the SPP-supporting metal surface,^16,17 SPR have led to a major advance in the development of biosensing methods; indeed, they provide a leading state-of-the-art label-free technology for the detection and study of biomolecular binding events involving a target analyte (protein, DNA, drug, etc.) from a solution and its corresponding receptor (ligand, DNA capture, etc.) immobilized on the liquid/metal interface.^18,19

1.2.2. Localized Surface Plasmons (LSPs)

LSPs involve the combined oscillation of the free electrons in a metallic nanoparticle and associated oscillations of the electromagnetic field. The resonance frequency depends on the size, shape, composition, and local optical environment of the particle,^20,21 and typically occurs in the visible to near-infrared part of the spectrum for nanostructures of noble metals (Au, Ag, Cu). LSPs have emerged as an attractive alternative to PSPs in a range of applications, primarily because momentum matching is not required to excite LSPs owing to their lack of translational symmetry; they also benefit from simple fabrication routes for the metal nanoparticles (e.g., by colloidal chemistry based on reduction of metal salts²²) and nanoparticle arrays (e.g., by nanosphere lithography²³) and a series of unique properties and functionalities, including the possibility of light manipulation and transformation at the nanoscale level,²⁴⁻²⁹ subwavelength imaging,³⁰⁻³² nanolensing^25,30 and nanolasing,^33,34 field concentrators,³⁵ nanotweezers,³⁶ supersensitive plasmonic nanosensors,³⁷⁻⁴⁰ improved photovoltaic devices,⁴¹ active optical elements,⁴² etc. However, localized surface plasmons are generally of greater spectral width when compared to propagating surface plasmons; as an example, the resonance width typically exceeds ∼80–100 nm fwhm for LSPs for Au nanostructures, compared to a spectral width of ∼50 nm for PSP. This increased width significantly limits the potential of LSPs for many applications. Though not within the noble metal list, aluminum can also be used as viable plasmonic material supporting resonances in the UV–visible region.⁴³⁻⁴⁵

1.3. Width of Plasmon Resonances

The spectral width of localized surface plasmon resonances (LSPRs) can be appreciated from the general properties of LSP excitation of a metal nanostructure, or indeed an ensemble of such nanostructures. For a single metallic nanosphere placed in vacuum, the applied electromagnetic field induces a dipole moment p in the sphere whose magnitude is proportional to |E₀|, the strength of the applied electric field. The polarizability, α, is then defined through p = αE₀ and can be derived in the quasistatic approach, where the particles are assumed to be smaller than the wavelength of the light involved, as⁴⁶

1

where ε(ω) is the relative permittivity (dielectric constant) of the sphere and a is the particle radius. (In the quasistatic approach, the analysis is performed as in the static case but the material parameters of the nanoparticles are taken to be frequency dependent. This approach is found to work well in many experimental situations, even at optical frequencies.) The localized surface plasmon resonance is associated with a dramatic increase in the polarizability α, when the denominator of the right-hand side of (1) approaches zero. Hence, the spectral position of the LSPR can be found from the condition Re[ε(ω)] = −2. The quality factor of the resonance Q, which is intrinsically linked to the ratio of energy stored to the energy lost by an oscillator, can be estimated as Q = λ_min/Δλ (λ_min is the resonance wavelength, and Δλ is the width of the resonance) and is large when Im[ε(ω) + 2] is small. For metals, the dielectric constant is a complex value so that it is not possible to have a zero value for the denominator in (1); Q-factors of ∼10–20 are found to be typical for most LSPRs.

1.3.1. Limitations for Simple Nanostructures

An improvement in the quality factor of LSPRs was originally expected from appropriate engineering of the shape and size of nanostructures. However, studies involving various geometries, including nanotriangles,^47,48 nanorods,⁴⁹ nanostars,^50,51 and nanocrosses,⁵² did not lead to the anticipated remarkable narrowing of the LSP resonances associated with these particles. Wang and Shen⁵³ showed, in the quasi-static approximation, that there is an underlying reason for this behavior. They showed that the quality factor of the plasmon resonance, Q, depends only on the dielectric function of the metal at the plasmon frequency 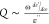(where ε = ε^′ + iε^′′). Thus, while the shape and environment do influence the LSPR frequency, Wang and Shen’s analysis showed that, to a first order approximation, the quality factor Q is independent of the geometric form of the nanostructure and independent of the dielectric medium that surrounds the nanostructure. A typical LSPR is broader than this simple formula predicts owing to radiative damping and dynamic depolarization (the effect of retardation within the particle). As a result, LSPRs typically have quality factors of order 10, well below that desired for many applications.

1.3.2. Beyond Single Nanostructure

Fortunately, and at first sight rather surprisingly, the limitations on the Q-factor of LSPs associated with individual nanostructures discussed above can be largely overcome when nanostructures are arranged in arrays. The electromagnetic fields related to the LSP mode of one nanoparticle may then act to influence the response of neighboring nanoparticles. This electromagnetic coupling can take several forms: via near-fields and via far-fields.

Near-Field Coupling

Particles interact via near-field coupling when they are relatively densely packed, leading to significant spectral shifts of the plasmonic resonances and a modification and splitting of their line-shapes due to the hybridization of the plasmonic modes.⁵⁴⁻⁵⁸ In particular, such hybridization can lead to the generation of antisymmetric modes,⁵⁹ which provide slightly narrower resonances (full width half-maximum (fwhm) ∼ 50 nm). However, these modes are typically dark; that is, they cannot easily be excited by incident light.

Far-Field Coupling

A significant improvement in the quality of localized plasmon resonances becomes possible with the involvement of far-field coupling of LSPs, i.e. via their scattered radiation fields. When a number of particles are randomly distributed, the scattered fields impinging on a given particle have no particular phase relationship and the effects of the scattered fields are relatively minor.⁶⁰ However, when metal nanoparticles (nanoantennas) are arranged in a periodic array, where the period is comparable to the wavelength of the incident light, then under appropriate conditions the scattered fields impinging on a given particle can arrive in phase with the incident light. The scattered fields correspond to diffraction of the incident light in the plane of the array. By using the right combination of nanoparticle size and shape, together with an appropriate array period, one can arrange for the light scattered by each nanoparticle into the plane of the array to be in phase with the plasmon resonance induced in its neighbor by the incident light, thereby reinforcing the resonance in the neighboring particle. Thus, by appropriate tuning of the array period one can significantly increase the quality factor of the resonance. This is possible because the scattered fields can act to counter the damping of the single particle response. When extended over a large array of nanoparticles,⁶¹ such plasmonic surface lattice resonances (diffractively coupled localized surface plasmon resonances) can lead to a remarkable narrowing of the resonance width (down to a few nm), as well as to related phenomena such as a dramatic enhancement of both absorption and the local electric fields near the nanostructures; all of these phenomena are important for a variety of projected applications.

1.4. Overview of Early History of Concept of Collective Resonances

The fundamental ideas behind diffractive coupling of particle resonances were explored in theoretical works by several research groups starting in the 1960s, but the path to their experimental realization was a long one. DeVoe gave the first theoretical description of an electric dipole model for quasi-stationary aggregations of molecules,^62,63 while Purcell and Pennypacker⁶⁴ completed this description by including phase retardation effects based on the consideration of propagation of electromagnetic waves. Laor and Schatz⁶⁵ were the first to consider the coupled dipole approximation (CDA) for aggregations of nanoparticles and to obtain Mie solutions of the dipole sum (for finite size of nanoparticles), while Meier and co-workers^66,67 extended the CDA description to structures where retardation effects due to wave propagation should be taken into account. It is interesting to note that the idea of using coupled dipoles to calculate the mean polarizability of a molecule in liquids and gases was introduced by Silberstein as early as 1917.⁶⁸

1.4.1. Some Details of Early Work

Markel developed a CDA-based model for a one-dimensional chain of nanoparticles and gave the first rigorous mathematical description of diffraction-based coupling,⁶⁹ while Schatz and co-workers^70,71 clearly explained the physical essence of diffractively coupled effects and described conditions for the generation of ultranarrow resonances. However, despite a well-developed mathematical description of ultranarrow resonances and clarification of the physical mechanism, the experimental observation of these resonances was not straightforward. Early works recorded a slight narrowing of the resonances,⁷²⁻⁷⁵ but this narrowing was far from that expected from theory.^69,70,76,77 The main problem was related to the high numerical aperture (NA > 0.5) of the focusing optics used in these works. Such high numerical apertures resulted in low spatial coherence of the incident light and thus limited the number of dipoles that could interact in phase with each other. There were other factors that contributed to the lack of observation of narrow resonances in early experiments. The high NA of the focusing optics also meant that light was collected over a range of angles leading to broadening of the observed modes due to the dispersive properties of the SLRs. Additionally, nanofabrication techniques in early work often led to a large amount of disorder leading to further broadening. (Subsequent improvements in nanofabrication techniques made it possible to produce metal NP arrays with a uniform period and controlled sizes over patterned areas as large as cm², resulting in stronger coherent coupling between NPs and measurements which could be performed without the use of an objective lens.) The breakthrough in the experimental observation of ultranarrow collective plasmon resonances was obtained using optics that provided high spatial coherence to illuminate large arrays of Au nanoparticles.⁷⁸⁻⁸⁰ Kravets et al.⁷⁸ reported the first observation of ultranarrow plasmonic resonances (resonant widths down to 2–5 nm fwhm, resonances with Q ∼ 100) by illuminating, at a certain angle, a large array (30 × 60 μm) of glass substrate-supported ∼100 nm Au nanopillars. Auguié and Barnes⁷⁹ observed similar resonances using normal incidence light transmitted through arrays of 50–120 nm Au nanorods, although the resonance features were generated only by placing the nanostructures in a uniform refractive index environment; very similar results were obtained at the same time by Chu et al.⁸⁰ Later studies led to an improved understanding of the properties and conditions necessary for the excitation of ultranarrow plasmonic resonances, as well exploring a variety of applications of these resonances. During the past decade, studies of diffractively coupled ultranarrow resonances have evolved into a separate, rapidly expanding research area with many tens of groups involved. One result of this expanding community has been the use of different names for the coupled resonances, these include the following: diffractively coupled localized surface plasmon resonances, collective plasmon resonances, lattice resonances, etc. For simplicity, we refer to them in this article as plasmonic surface lattice resonances (SLRs).

1.5. Aim of this Review

The aim of this review is to describe the physical phenomena leading to the appearance of ultranarrow diffractively coupled resonances and contextualize recent works in the field of narrow plasmon resonances. We also consider different manifestations and applications of these resonances, including the generation of an optomagnetic response at visible-light and near-infrared frequencies, extremely sensitive bio- and chemical sensing, and strong electromagnetic field enhancement in composite plasmonic nanostructures for laser and LED applications.

1.5.1. An Example—To Convey What Is Involved in Plasmonic Surface Lattice Resonances

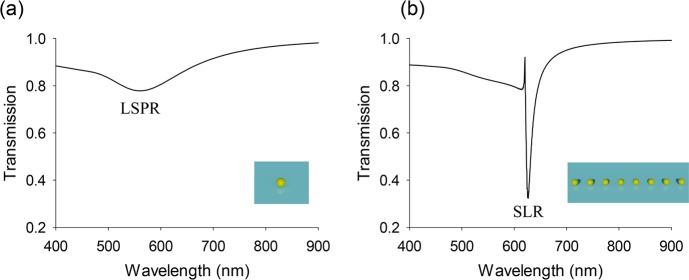
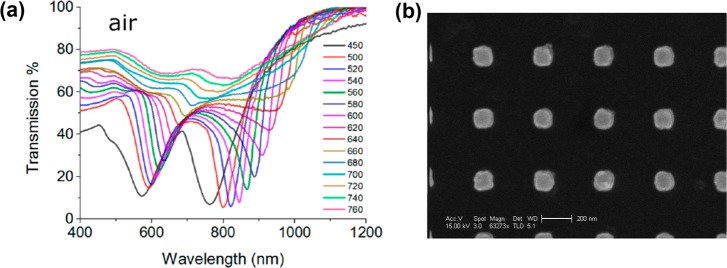
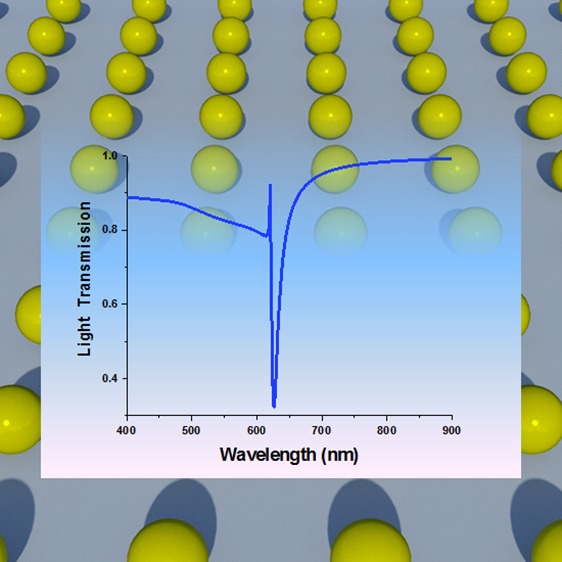
To give an idea of the structures that we consider, Figure 1 shows a schematic of (a) a single particle, and (b) a 1D periodic chain of particles, together with their computed normal incidence transmission spectra (the single particle spectrum was renormalized by the same number of individual particles as in the chain). These spectra represent the essence of the described phenomenon: the plasmonic SLR observed in the chain of nanoparticles is much stronger than that of individual nanoparticles (the drop in transmission at the resonance position is 70% compared to 20%) and much narrower (HWFM is 14 nm compared to 130 nm, which corresponds to an almost 10-fold improvement of resonance quality).

Figure 1.

Comparison of LSPR and SLR in transmission spectra. Schematic of structures considered: (a) single particle, (b) a periodic 1D chain. For both systems the transmission observed at normal incidence is plotted as a function of wavelength; the inset shows a schematic of the particle arrangement. The electric field of the incident wave was perpendicular to the direction of the chain. The gold particles were 80 nm in radius made in air environment. The period in the chain was 620 nm and the total number of particles in the chain was 1000. The calculations were performed using Doyle’s approximation, see section 2 below.

1.6. Structure of the Review

This review is structured as follows. In section 2 we discuss the early theoretical work in more detail. Early experimental work will be described in section 3. Section 4 is devoted to the important role played by the substrate on which the array is fabricated. Section 5 describes the importance of out-of-plane modes for excitation of plasmonic SLR, and we discuss what limits the Q-factor of the surface lattice resonances. The production of SLR is accompanied by generation of singularities of phase of light that is important for sensing applications. This phenomenon is described in section 6. The addition of gain can dramatically alter the optical response associated with SLRs and, e.g., offers the prospect of lasing, which is discussed in section 7. Section 8 describes combination of SLRs with various 2D materials while other applications of SLRs are discussed in section 9. Finally, general conclusions are given.

2. Early Theoretical Studies of Diffractively Coupled Localized Plasmon Resonances—SLRS

In this section we review the early theoretical work that launched this research field. As noted above, the theoretical approaches that were adopted, such as the coupled dipole model, had already been established ahead of their application to plasmonic resonances. Here we look specifically at how those models were harnessed, and how the early theoretical investigations were followed up.

2.1. The Coupled Dipole Approximation

The coupled dipole approximation (CDA)^{62−67,69−71,81} was instrumental in the prediction of diffraction coupled resonances and the elucidation of their basic properties. In this approximation, an array of N nanoparticles (NPs) is replaced by an array of electric dipoles. Consider an array of N particles whose polarizabilities and positions are denoted α_i and r_i. A dipole P_i will be induced in each particle, given by P_i = α_iE_loc,i, where E_loc,i is the local field at the nanoparticle position r_i. The local field E_loc,i is then the sum of the incident field E_inc,i, and the retarded fields produced by the other N – 1 dipoles E_dipole,i. For a given wavelength, λ, this field may be written as

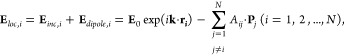2

where E₀ and k = 2π/λ are respectively the amplitude and wavenumber of the incident plane wave. (The choice of a minus sign in front of the sum is simply a matter of convention.) The dipole interaction matrix A_ij may be expressed as

3

(i = 1, 2, ..., N, j = 1, 2, ..., N, i ≠ j), where r_i j is a vector from dipole i to dipole j. To obtain the polarization vectors, the 3N equations of the form A_i,jP_i = E_j need to be solved. For an infinite array of identical particles with polarizability α_s, an analytical solution of eq 3 can be readily found by assuming that in each particle the induced polarization is the same. Doing so one finds the polarization, P, of each particle to be,

4

where S is the dipole sum (see below). The extinction cross-section produced by one particle in such an array can be written as

4*

For the case when the wavevector is perpendicular to the plane of the array, the retarded dipole sum S can be found as follows,⁸²

5

where the angle θ_ij is between r_ij and the direction of the polarization (induced by the incident electric field).

2.1.1. Importance of the Dipole Sum

For a given array of nanostructures of a particular choice, the extinction cross section of the particles within the array can be determined using the equations given above. First, the polarizability α_s of a single nanostructure (a particle) should be calculated using electromagnetic theory (see below). Second, the dipole sum S can be calculated using eq 5. The dipole moment associated with each particle in the array is then found from eq 4 while eq 4* yields the extinction cross section of a single particle in the array. We see that when the real parts of 1/α_s and S are equal, then the real part of the denominator in eq 4 goes to zero and the polarization of a particle in the array becomes large. This is exactly the condition of excitation of surface lattice resonances. Therefore, excitation of plasmonic SLR has some analogy with excitation of LSPR (which happens when the real part of the denominator describing polarization of a particle becomes zero; see above). The main difference between SLR and LSPR lies in the presence of the dipole sum in the former case. The dipole sum depends on array parameters (the period, size of a particle, etc.) and provides an additional degree of freedom to improve the quality of plasmonic SLRs as compared to LSPRs. Indeed, the width of plasmonic SLRs is governed by Im(1/α_s – S) and can be made small by compensating Im(1/α_s) with Im(S). Calculations show that the dipole sum S becomes large (and comparable with α_s) only at conditions when some diffracted wave propagates along the surface of the array which explains the term diffraction coupled localized plasmons as an alternative to plasmonic SLRs.⁷²Figure 2 compares the extinction cross section per particle, as calculated using the dipole sum procedure adopted from ref (83), to that of a single particle.

Figure 2.

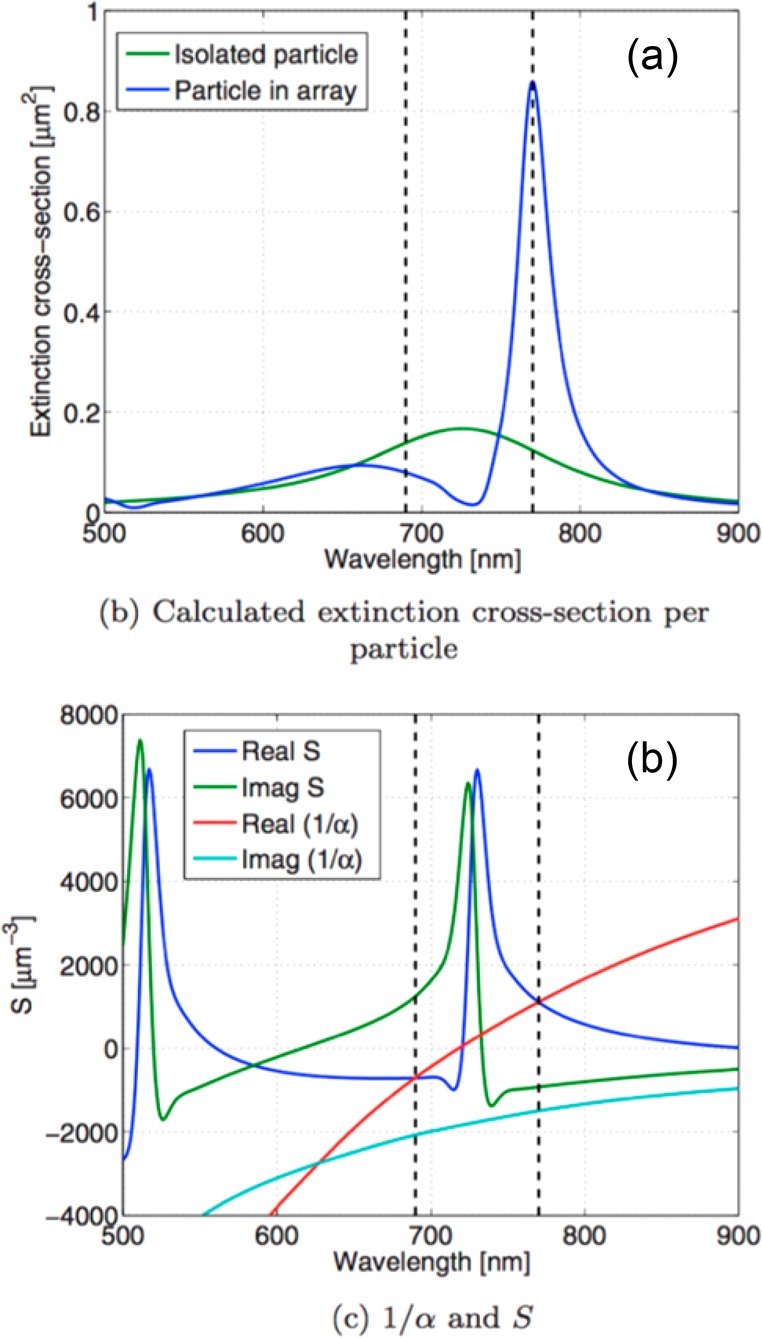
Comparison of SLR with LSPR. (a) Extinction cross section calculated per particle. (b) Dipole sum for a square array (having period 480 nm) of silver disks (h = 30 nm, d = 120 nm). Light is incident normally, using linearly polarized light where the electric field is parallel to the array’s y-axis. Index matching was used, with an immersion oil having n = 1.515; thus, the diffraction edge occurs at 727 nm. The intersection of the real parts of 1/α and S is indicated by dashed lines in (a) and (b). Reproduced and adapted with permission from ref (83). Copyright 2014 American Physical Society.

The calculations were performed for a square array (period 480 nm); the particles were silver disks (diameter = 120 nm, height = 30 nm) immersed in a medium of refractive index 1.515. The SLR resonance is clearly observed at a wavelength of ∼760 nm. It shows a ∼5 times increase of extinction cross section per particle (compared to LSPR of an isolated particle) and demonstrates a ∼7 times improvement of resonance quality.

2.1.2. Response of an Array Calculated Using CDA

The first thing to notice in Figure 2(a) is that the response of the array is very different from that of the single particle. The array resonance is much stronger, is much shaper, and has a longer wavelength. To help understand these changes, we show in Figure 2(b) the real and imaginary parts of both 1/α and S. There are two wavelengths at which the real parts of 1/α and S are equal, each suggesting the possibility of an SLR; they are shown by the vertical dashed black lines. The long-wavelength crossing point corresponds to the SLR seen in Figure 2(a). At this point the imaginary parts of 1/α and S are both negative and nearly equal in magnitude. This means that the imaginary part of the polarizability in eq 4 is small, thereby yielding the strong resonance. In contrast, at the short wavelength crossing point for the real parts of 1/α and S, the imaginary parts of 1/α and S are of the opposite signs; they contribute additively to the polarizability so that damping is increased cf. the single particle case and no SLR is seen at this wavelength.

2.2. Beyond the Dipole Approximation

For the calculations shown in Figure 2(a) slightly extended version of the approach indicated above has been adopted, this is so that effects arising from the finite size (radius ∼60 nm) of the particles may be accounted for; details are given in ref (83). The two key effects that have to be accounted for are (i) radiation damping and (ii) dynamic depolarization, i.e. the role of retardation across the particle. In some cases it is convenient to use an approach that is known as the modified long-wavelength approximation,⁸⁴ in which extra terms are incorporated into the polarizability to account both for the radiative damping and the retardation. The dielectric constants for the silver were taken from Palik.⁸⁵ As an alternative, a numerical approach was successfully adopted by Kuwata that achieved a similar result.⁸⁶ Doyle also explored how to modify the polarizability to take account of dynamic (retardation) effects⁸⁷ by making an approximation that made partial use of the complete electromagnetic solution for spherical particles in Mie theory.⁸⁸ These approximations allow one to include particles which are not small when compared with the incident wavelength λ while still staying within the simple dipole approximation. Figure 1 was calculated using Doyle’s approximation. Frequently, although not always,⁸⁹ higher multipole effects can be ignored.

Swiecicki and Sipe⁹⁰ recently presented an extensive analytic model of SLRs in 2D arrays of gold spheres that takes into account electric dipole, electric quadrupole, and magnetic dipole moments of the spheres. They identified “ideal” surface-lattice modes of the array which are characterized by strong interaction between different moments of the nanoparticles and possess interesting spectral properties.⁹⁰

2.3. Effect of Array Period

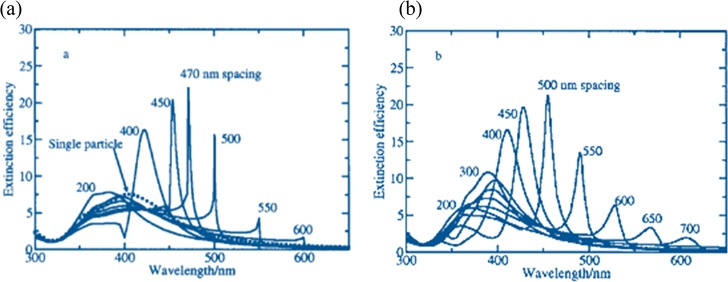
A primary focus of the early work by Zou et al.⁷⁰ was to examine the effect of the array period for chains and square arrays of particles using the dipole sum approach, and some of their results are reproduced below. They calculated the extinction efficiency (the ratio of the extinction cross section compared to the geometrical area) of the array of particles for array periods in the range 200–700 nm, for arrays containing 400 particles. Their results are reproduced in Figure 3, which shows the results of calculations for a 1D chain (a) and for a 2D hexagonal array (b). For comparison, the spectrum of an isolated particle is shown in Figure 3(a) as a dotted line.

Figure 3.

Extinction spectra (calculated) of 100 nm (diameter) silver nanoparticles for (a) a 1D chain of 400 particles and (b) a 2D hexagonal array of 400 particles. Data are shown over a range of array periods, as indicated. For the chain, both the polarization vector and the wave vector are perpendicular to the chain. For the array, the wave vector is perpendicular to the plane, while the polarization vector is in the plane. These results are reproduced and adapted with permission from ref (70). Copyright 2004 American Institute of Physics.

Zou et al.⁷⁰ found a remarkable narrowing and shift to the red of the plasmonic SLR when compared to the single particle response as the particle separation was increased for both 1D and 2D array types. They established that the linear chain gives the sharpest SLR. For the chain of 470 nm period, the calculated resonance wavelength was 471.4 nm while the calculated HWFM was 3.7 nm, yielding a Q-factor of ∼135, which represents at least a 10-fold improvement over LSPR of a single particle. The line width narrowed further on increasing the period, giving Q > 300, but the strength of the response for these longer periods, where the SLR is further from the peak position of the single particle response, is also reduced. Figure 3(a) refers to the case when the light wavevector is perpendicular to the chain axis. At the same time, calculations in the parallel situation also indicate narrow resonances, albeit slightly wider.⁹¹ The results in Figure 3(b) indicate that for a 2D array the spectral position of the resonance scales as the particle separation rises in a manner that is similar to that for the 1D chains, albeit with resonances that are slightly broader. Zou et al. also found that other wavevector and polarization choices led, for a given spacing, to broader line-shapes.⁷⁰ Gomez et al.⁹² theoretically considered the effect of array period on the formation of SLR and presented a simple nearest-neighbor approximation to describe the collective resonances in terms of superposition of the eigenmodes of uncoupled nanostructures that exhibit a standing-wave character delocalized across the entire periodic structure of the array. The formalism they developed allows one to describe plasmonic edge states.⁹²

2.4. Holes Rather Than Particles

Nanoholes in thin metal films may also support localized plasmon resonances, as one might expect from Babinet’s principle, in which the diffraction pattern produced by an opaque body is identical to that produced by a hole of the same shape and size, except for the overall intensity of the forward beam.⁹³ There are thus similarities between the modes supported by arrays of metallic nanoparticles, as discussed above, and arrays of holes in thin metallic films. Ebbesen and colleagues showed enhanced transmission of light through metallic thin films perforated with periodic arrays of holes; this remarkable result was a key step in the very significant expansion of plasmonics research toward the end of the last century.¹¹ A detailed discussion of the interaction of light with 2D periodic arrays of holes can be found in the review of García-Vidal et al.⁹⁴ and that of particles and holes in the review by García de Abajo.⁹⁵ García de Abajo noted that some of the collective effects in nanohole arrays have the same origin as for particle arrays; that is, that resonances associated with individual elements (hole, particle) are coherently coupled by scattered fields. Parsons et al., demonstrated the presence of the thin metallic film to be responsible for changes in the interaction between adjacent resonators, due to the propagating surface plasmon mode that the thin metal film supported;⁹⁶ hole arrays will not be considered further in the present article since they do not provide a significant increase in the resonance quality. It is worth noting that hole arrays can also demonstrate a different type of collective plasmon resonance where individual hole resonances are coupled together by propagating surface plasmon waves. These resonances are normally wider than typical SLRs.

2.5. 3D Arrays

Schatz et al.⁹⁷ described the theoretical methods to calculate the optical properties of 1D, 2D, and 3D arrays of plasmonic nanostructures. They showed that three-dimensional arrays can exhibit unique effective-medium properties, such as a negative permittivity that leads to metallic optical response even when there is less than 1% metal content in the array. Thus, the collective plasmonic effect in three-dimensional arrays is a promising means for the continued development of visible-light metamaterials and for the creation of optoelectronic plasmonic devices and sensors. These authors also showed that simple theoretical methods may be used to describe complex media with deliberately designed properties.⁹⁷

2.6. Section Summary

To summarize, early theoretical investigations provided the following insights:

• 1.1D arrays of metallic nanoparticles may support very narrow surface lattice resonances.
• 2.Narrow SLR features having spectral widths less than 1 nm may occur when the array spacing is somewhat greater than the resonance wavelength of the isolated particle plasmon.
• 3.The narrow plasmonic SLRs occur because of the interaction between the localized plasmons associated with the nanoparticles and light diffracted by the array.
• 4.SLRs can be derived within the electric dipole approximation when the imaginary part of the dipole field (retarded) cancels the effect of resonance damping of a single particle.
• 5.The SLR may disappear either if the particles are too small or if the array size is too small. In both cases, the dipole sum, S, is insufficient to offset the effect of single particle relaxation (decay) effects.
• 6.2D arrays also show narrow plasmonic modes; indeed, it is only for the 2D arrays that SLRs have thus-far been seen through experiment.

3. Experimental Observations of SLRs and Clarification of Their Properties

Early attempts to observe SLRs were not very successful.⁷²⁻⁷⁵ One of the main obstacles in detecting SLRs was the high numerical aperture optics (NA > 0.5) used. Observation of SLRs requires the incident light to be spatially coherent over a large area (i.e., a sufficient number of particles) to ensure useful interference of light scattered by different nanoparticles in an array. Focused light of wavelength λ has a lateral spatial coherence of order λ/NA. This means that the number of particles in a 2D array, N, that may interact coherently and thus be involved in a collective resonance is given by N ∼ (λ_R/(NA·a))²¸ where λ_R is the wavelength at which the collective resonance is excited and a is the array period. Thus, only focusing optics with a small NA (NA < 0.1) are suitable for the excitation of SLRs.

3.1. First Report of Experimental Observation of Plasmonic SLRs

Probably the first report of an experiment in which SLRs were observed came in 2008.⁷⁸ The necessary conditions for sufficient spatial coherence of the incident light were achieved by using the focusing optics of an ellipsometer (NA = 0.1), thereby providing sufficient spatial coherence over the ∼30 × 30 μm focal spot on the sample surface. Arrays of Au nanopillars (200 μm × 200 μm, containing ≈10⁶ pillars) were fabricated by electron-beam lithography on top of a glass substrate. A number of arrays with lattice period, a, in the range 270–400 nm were examined. The pillar dimensions were as follows: height h ≈ 90 nm (first 3 nm Cr, then 90 nm of Au), diameter d ≈ 100 nm; these dimensions were picked so that the LSPR of an individual pillar appeared in the visible spectrum, specifically the red part.

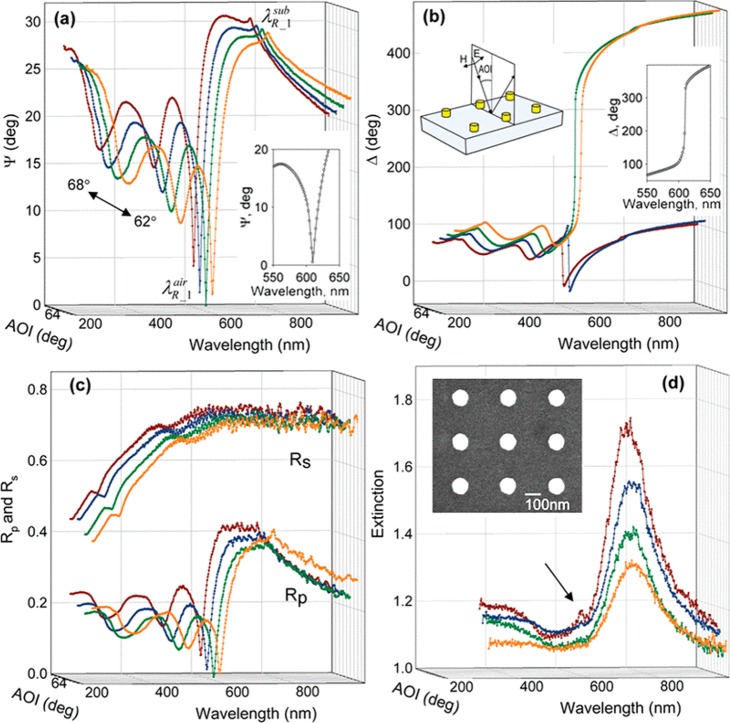
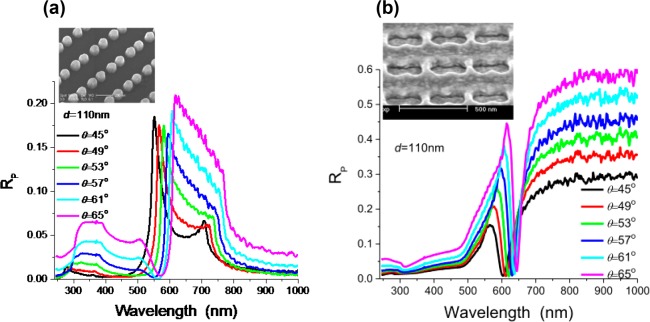
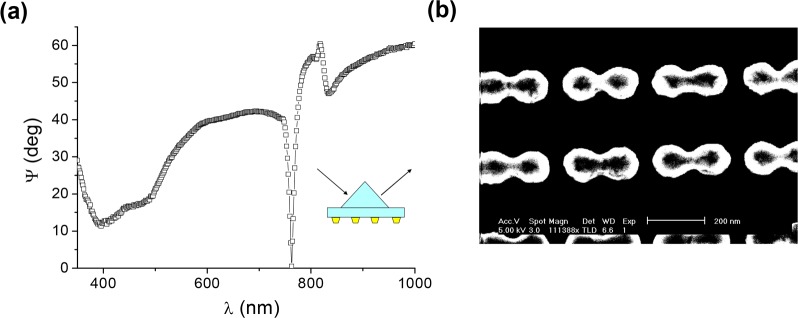
Figure 4(a) shows some typical very narrow SLRs observed in experiment near λ_R ≈ 600 nm at angles of incidence, θ, of 62–68° for a square array of period a = 320 nm.

Figure 4.

Surface lattice resonances for an array of Au nanoparticles. Experimentally measured spectra of ellipsometric parameters, reflection, and extinction for the studied 2D arrays. (a) The ellipsometric parameter Ψ. The inset provides a zoom-in of the minimum at θ = 64°. λ_{R_1}^air and λ_{R_1}^sub are given by eq 6 (using the + sign). (b) The phase Δ. The left inset shows the geometry for the p-polarized incident light. The right inset provides a zoom-in of the jump in phase at θ = 64°. (c) Reflection spectra for p polarization, R_p, and for s polarization, R_s. (d) Extinction spectra for p polarization. An SEM image is shown in the inset, while the arrow marks the location of the weak and narrow resonance in absorption. Data have been plotted for θ = 62° (orange), 64° (green), 66° (blue), and 68° (brown). The array period was a = 320 nm, the dot diameter d = 100 nm, while the dot height was h = 90 nm. Reproduced and adapted with permission from ref (78). Copyright 2008 American Physical Society.

3.1.1. Use of Ellipsometry

Greater insight can be gained by looking at other parameters that can be determined using a spectroscopic ellipsometer. Ellipsometry routinely provides amplitude (Ψ) and phase (Δ) parameters for light reflected from a sample object, which are related to the reflected field amplitudes E_p (p-polarization) and E_s (s-polarizations) of the incident light (E_i), in the following equation E_P/E_S = tan(Ψ) exp(iΔ).⁹⁸ In addition, the ellipsometer allows one to measure the intensity reflection and transmission coefficients (R_p, T_p) for p- and (R_s, T_s) for s-polarized light at various incident angles. The advantages of using spectroscopic ellipsometry for characterization of plasmonic materials are described in ref (99). Figure 4(b) shows the behavior of Δ (the relative phase) at the same values of θ while Figure 4(c) shows the spectral dependence of the polarization specific reflection coefficients R_p and R_s. A very deep and narrow SLR with a half-width of 5 nm is seen in reflection for p-polarization when the first-order diffraction in air is in the plane of the array. In the presence of a substrate, two types of lattice coupling are possible differentiated by whether the diffraction takes place in the substrate medium (typically glass) or in the superstrate (sometimes air). For the experimental conditions studied in ref (78), two subsets of these conditions are given by

6

where n_s is the substrate’s refractive index. These conditions (eq 6) are sometimes known as “diffraction edges”. The extinction only showed a weak feature at the wavelength of interest, λ_R ≈ 600 nm, and then only at large angles; see Figure 4(d) where the arrow marks a weak and narrow feature at θ = 68°. This was because in-plane diffraction occurs at wavelengths too far from the spectral position of LSPR of nanoparticles; see Figure 4(d).

3.1.2. SLRs in Extinction

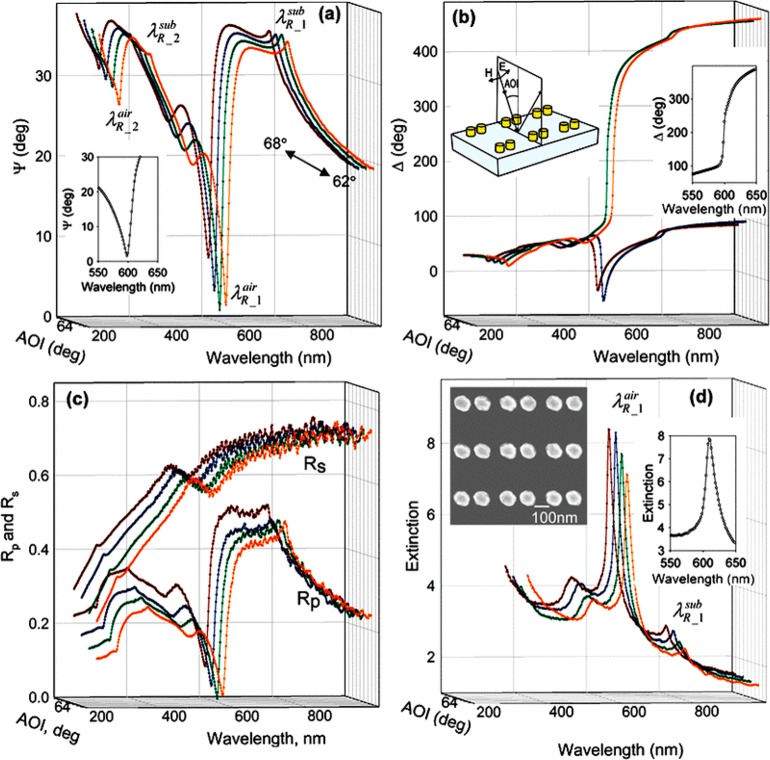
Although the data in Figure 4 show clear evidence of SLRs, they do not show the strong signature expected in extinction; see Figure 4(d). As noted in the previous paragraph, this is because the spectral position of the SLR was too far from the position of LSPR of a single particle. There are several ways to match the LSPR of a nanoparticle with SLRs: (i) to increase the period of the array, (ii) to decrease the particle size, or (iii) to select a different geometry for the array unit cell and use it to tune the SLR resonance. The authors of ref (78) selected the third method and designed a two nanoparticle (dimer) basis, shown in the inset of Figure 5(d) to match LSPR wavelength with SLR.

Figure 5.

SLRs for the Au dimer array. Experimentally measured spectra of ellipsometric parameters, reflection, and extinction for the studied 2D arrays. (a) The ellipsometric parameter Ψ. Shown in the inset is a zoom-in of the reflection minimum at θ = 64°; λ_{R_1}^air and λ_{R_1}^sub are given by eq 6 with using the “+” sign. (b) The phase Δ. Left inset shows the geometry for the p-polarized incident light. Right inset shows a zoom-in of the jump in phase at θ = 64°. (c) Reflection spectra for p polarization, R_p, and for s polarization, R_s. (d) Extinction for p-polarized light, the incident electric field is perpendicular to the dimer axis. The inset at left shows an SEM of the array. The inset at right shows a zoom-in of the maximum in extinction for θ = 64°. Data are shown for θ = 62° (orange), 64° (green), 66° (blue), and 68° (brown). The period of the dimer array was a = 320 nm, the diameter of the particles was d = 108 nm, the height of the particles was h = 90 nm, the separation of the dimer particles was 140 nm (center-to-center). Reproduced and adapted with permission from ref (78). Copyright 2008 American Physical Society.

For small separations of the nanoparticles in the dimer, the electromagnetic interaction between neighboring particles splits the observed LSPR, producing 4 in-plane and 2 out-of-plane modes.⁵⁸ Some resonant modes are red-shifted compared to the single particle LSPR (e.g., a symmetric mode for incident waves where the electric field is along the direction that connects neighboring particles) while some are blue-shifted (e.g., a symmetric mode for waves where the electric field is perpendicular to the dimer axis) as a result of the dipole–dipole interactions.^26,100 As a consequence, the electromagnetic interaction can shift the LSPR from 700 nm for a single particle (d ≈ 100 nm) to around 600 nm for the dimer having center-to-center separation of s = 140 nm. Figure 5(a) shows very narrow resonances near λ_R ≈ 600 nm for an angle of incidence θ = 62–68° for the Au dimer square array of the same period a = 320 nm and for d = 108 nm, s = 140 nm. Note the pronounced and narrow resonance features that occur both for the phase of the reflected light, Figure 5(b), and for the reflection amplitudes, Figure 5(c). In contrast to the single particle array (Figure 4), the in-plane diffraction for the dimer array is well coupled with the LSPR of the Au dimer so that extinction, Figure 5(d), now shows a remarkably narrow peak near λ_R=a[1 + sin(θ)]. Both Figures 4 and 5 demonstrate extremely narrow SLRs for predioic arrays of Au NPs yielding high quality factors of Q ≈ 40 for the dimer array, as measured using extinction, and of Q ≈ 60 measured using ellipsometry/reflection data from the single particle arrays. This presents a significant improvement when compared with standard LSPR in analogous Au nanodots.²⁶

3.2. SLR Optimization

As noted above, another method to modify the response of the array so that in-plane diffraction coincides spectrally with the LSPR is to tune the period of the array. This method was chosen by Auguié and Barnes,⁷⁹ who reported the observation of sharp spectral features in light transmitted (at normal incidence) through 2D arrays of substrate-supported gold nanorods; see Figures 6 and 7. Their extinction data (Figure 6) show the features one expects on the basis of the coupled dipole model.^70,71 (Note, the areas under the extinction curves appear to be constant, indicating the possibility of an extinction sum rule.⁶⁴) A strong dependence of the intensity, width, and position of the sharp spectral feature was found on three factors: size of particle, particle aspect ratio, and interparticle separation. Electron beam lithography was used to make these samples on fused silica (n = 1.46), the size of the arrays was 35 μm × 35 μm, while nanorods were produced in the range 50–120 nm that had aspect ratios that ranged from 1:1 to 2:1. The data presented are in the form of extinction spectra, obtained from the transmittance per particle T using σ_ext = h²(1 – T), where h is the pitch value (the array period). Several features may be seen in the data shown in Figure 6: (i) As the period is altered, a complex response pattern moves through a broad resonance (LSPR of an isolated particle, with a width typically of ∼ 100 nm, located at λ ∼ 710 nm); (ii) there is a correlation between the array period and the sharp transmission dip.

Figure 6.

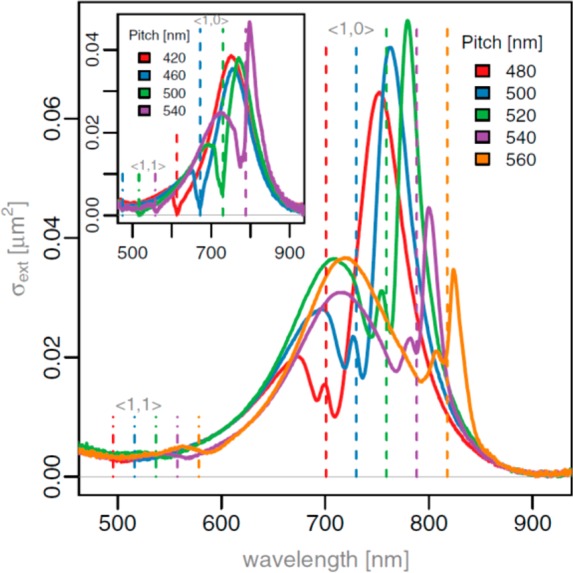
Extinction spectra for a number of gold nanoparticle arrays (per particle). The average particle size was 123 nm × 85 nm × 35 nm. For the inset the nominal particle size was 120 nm × 90 nm × 35 nm. When the diffraction edge is located on the blue side of the LSP resonance, then a considerably weaker effect is seen. Of interest we note that complete transmission can occur near the diffraction edge; see particularly the data for the 420 nm period (inset). Vertical lines mark the positions of the ⟨1,0⟩ and ⟨1,1⟩ diffraction edges for the various arrays measured. Reproduced and adapted with permission from ref (79). Copyright 2008 American Physical Society.

Figure 7.

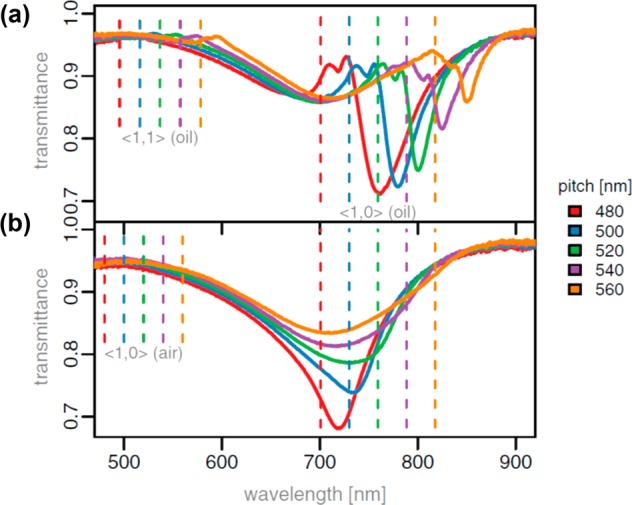
Transmittance spectra for light incident on arrays of gold nanorods in a homogeneous index environment (upper panel, light incident through immersion oil n = 1.46) and an asymmetric refractive index configuration (lower panel, incident light through air), for five array periods. Nominal particle sizes were 100 nm × 90 nm × 35 nm (upper), 120 nm × 90 nm × 35 nm (lower). Vertical lines mark the positions of the ⟨1,0⟩ and ⟨1,1⟩ diffraction edges for the two environments (refractive index configurations). Reproduced and adapted with permission from ref (79). Copyright 2008 American Physical Society.

The data in Figure 6, including the inset, show the effect of varying the array period and reveal two regimes. With the diffraction edge located on the high-energy side of the main LSPR, the radiative coupling is very weak because the allowed diffracted orders are all of higher energy than the plasmon resonance, and it is not possible to match the real part of 1/α and S (they both have the same sign). In the second regime, with the diffraction edge located on the low-energy side of the main resonance, then the long wavelength tail of the main resonance is found to have a very sharp and intense peak; the intensity and width of this resonance both become smaller for spectral positions that are further from the main resonance.

3.3. Refractive Index of the Environment

A key feature of the system studied by Auguié and Barnes⁷⁹ was the need for an homogeneous (symmetric) index environment for observation of SLRs at the normal angle of incidence which is in contrast to the study discussed above.⁷⁸ In Figure 7 data from a homogeneous environment, upper panel, are compared with an inhomogeneous (asymmetric) one, lower panel; the homogeneous environment was achieved by replacing the air superstrate with an index matching oil.

The strong asymmetry between superstrate and substrate acts to spoil the radiative coupling between the nanorods at normal angle of light incidence; see the lower panel of Figure 7. (It is interesting to note that in this case SLR spectral positions are clearly not matched with the LSPR of the nanorods; see above.) Several earlier studies recorded a strong impact of the asymmetry of the environment on the line shape of the resonances observed.^75,77

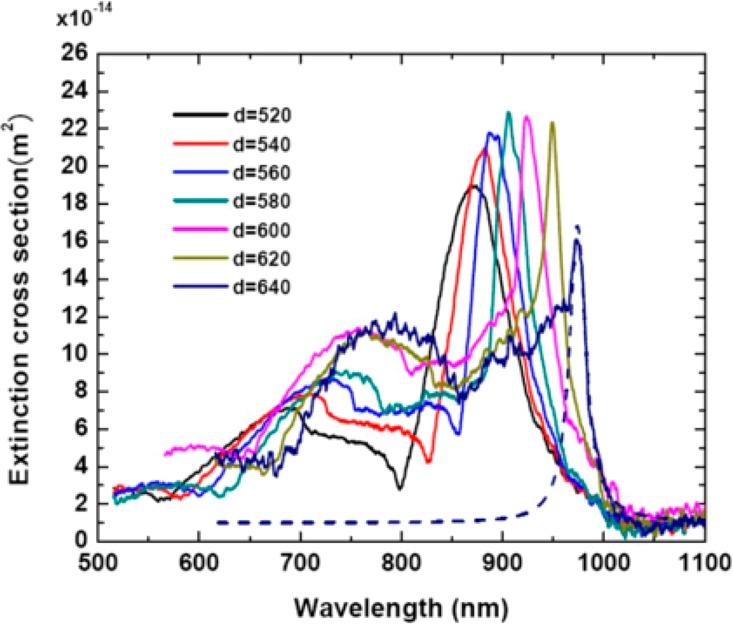
Chu et al.⁸⁰ also showed that diffractive coupling between LSPRs in 2D gold nanoparticle arrays with a superstrate of water could lead to narrow near-IR resonance peaks in the far-field extinction spectra. Arrays of gold nanoparticles were made using e-beam lithography and indium tin oxide (ITO)-coated glass substrates. The arrays were square lattices of Au disks with array periods in the range 520 to 640 nm, and the gold disks were 40 nm thick and 180 nm in diameter. The use of water as the superstrate was sufficient to allow the observation of surface lattice resonances, Figure 8; the measured extinction spectra are shown for arrays of Au disks having different periods, labeled here as d. One can see that, as for Figures 6 and 7, the array period determines both the strength of the peak and the spectral position of the extinction. We will return to the question of the refractive index environment necessary to observe SLRs below. Before doing so we next look at two other key requirements: What size of array is required, i.e. how many particles are needed for SLRs to be supported? And to what extent does disorder matter?

Figure 8.

Measured extinction spectra of arrays of gold disks on a glass substrate immersed in water (indicated by solid lines) and the associated peak of a Lorentzian fit to the extinction data from the 640 nm period array (indicated by the dashed line). Figure reproduced with permission from ref (80). Copyright 2008 American Institute of Physics.

3.4. Effect of Array Size

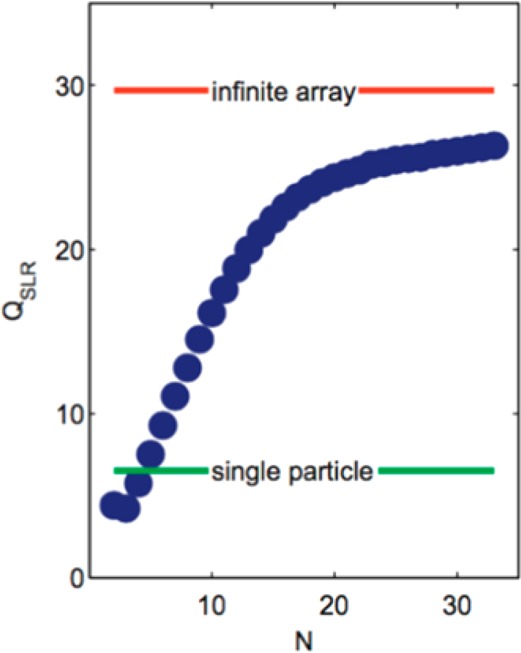
The question of array size was perhaps first discussed by Zou et al., who found that narrow plasmon line-shapes may be produced by chains of ∼50 particles; however, the observation of narrow resonances with Q > 10 requires a substantially larger number of particles.⁷⁶ A comprehensive investigation into the effect of array size for 2D arrays was carried out by Rodriguez et al.⁶¹ using both experiments and numerical modeling. Using the coupled dipole model outlined above, they showed that the quality factor of SLRs increases with array size; see Figure 9. The response saturates for arrays of a few hundred particles.

Figure 9.

Calculated Q-factor of the surface lattice resonance for arrays of gold nanodiscs as a function of the number of particles N along the side of the square array. Disc dimensions are diameter 120 nm and height 50 nm. Arrays were of N × N particles in size and were situated in a homogeneous environment. Figure reproduced with permission from ref (61). Copyright 2012 American Physical Society.

3.5. Effect of Disorder in the Array

The effect of disorder on the appearance of narrow peaks in the extinction spectra of silver nanoparticle arrays was considered in several early theoretical investigations.^77,101 Disorder in a 1D array was investigated, and a narrow resonance still found, even when the maximum displacement of a particle was half the array period.⁷⁷ Markel et al.¹⁰¹ studied the propagation of plasmon modes in both long ordered and long disordered chains of nanospheres, and two possible types of mode were predicted: ordinary (quasistatic) modes and extraordinary (nonquasistatic) modes.¹⁰¹ The ordinary mode has short-range interactions between nanospheres along a chain; retardation effects were not found to be important. The ordinary mode is not able to radiate into the far-zone in the case of perfectly periodic chains because its wavenumber is larger than the free-space wavenumber k = ω/c of electromagnetic waves. By contrast the extraordinary mode propagates along the chain due to radiative interactions. Simulations¹⁰¹ have suggested that even a relatively small degree of positional disorder or disorder in the properties of the nanoparticles leads to localization of the ordinary mode. However, the extraordinary mode was seen to remain delocalized even for modest levels of disorder of a few percent.

3.5.1. Positional Disorder

Auguié and Barnes¹⁰² investigated the effect of disorder in 2D nanoparticle arrays on their spectral properties by carrying out experiments where the distribution of particle position and particle size was well controlled. The nanorods (nominal size 120 nm × 80 nm × 35 nm) were fabricated by thermal deposition on fused silica substrates, as for ref (79). The particles were immersed in an index matching fluid, held between two substrates so as to provide a homogeneous environment (n = 1.46). Figure 10(a) shows extinction spectra obtained from 2D square arrays having different degrees of disorder in particle position. An ordered (nominally) array yielded a narrow extinction peak toward the low-energy side of the LSP as expected. Increasing random displacements of the particles from their regular locations led to an evolution of the shape of the spectra in the vicinity of the diffraction edge (Figure 10(a)). In particular, the narrow peak weakened and blue-shifted, while the extinction feature due to the LSPRs regained its full strength. Figure 10(b) presents results of calculations using a coupled dipole model for 441 dipoles that were arranged in a 2D configuration to simulate the experiment. The calculations are generally in agreement with the results of experiment and help to reinforce the view that the narrow spectral feature results from coherent coupling between the particles that takes place via dipolar interactions.

Figure 10.

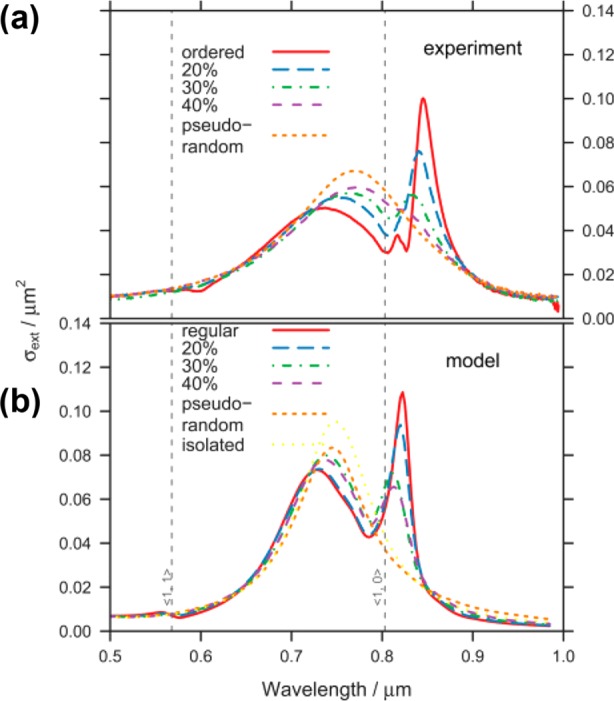
An effect of positional disorder on SLRs. (a) Measured extinction spectra obtained using five nanoparticle arrays having different amounts of positional disorder but having constant average occupancy. The legend indicates the deviation from the ordered array, shown as a percentage of the nominal regular separation of the particles (550 nm). Vertical lines (dashed) mark the ⟨1,0⟩ and ⟨1,1⟩ diffraction edges of the periodic array in an homogeneous environment (n = 1.46). The nominal sizes of the particles were 120 nm × 80 nm × 35 nm. (b) Calculated extinction spectra from a coupled dipole model using the same parameters. Reproduced and adapted from ref (102). Copyright 2009 The Optical Society.

De Zouani et al.¹⁰³ also studied the effects of positional disorder on SLR and discussed it in terms of plasmonic metacrystals and metaglasses. They performed experiments on high quality arrays of nanoparticles supported by theoretical calculations based on CDA. They identified the role of the particle density, the local density of nearest neighbors, and the global particle density at long distances, on the shape, position, and dispersion of SLRs. In particular, they found that an increase in the long-range density of particles leads to a reduction in the extinction per particle and attributed this reduction to an increase in the collective radiative coupling.¹⁰³

3.5.2. Size Disorder

A different kind of disorder, that of a random dispersion in particle size, was explored by Auguié and Barnes and is shown in Figure 11.¹⁰² Note that compared to the situation for positional disorder (Figure 10), here the minimum in the extinction curve related to the diffraction edge remains visible as the extent of disorder rises. All spectral features become wider as the dispersion in particle size increases. Some of the particles possess LSPRs that are not matched to the period of the array, they thus make a smaller contribution to coherent coupling.^78,79

Figure 11.

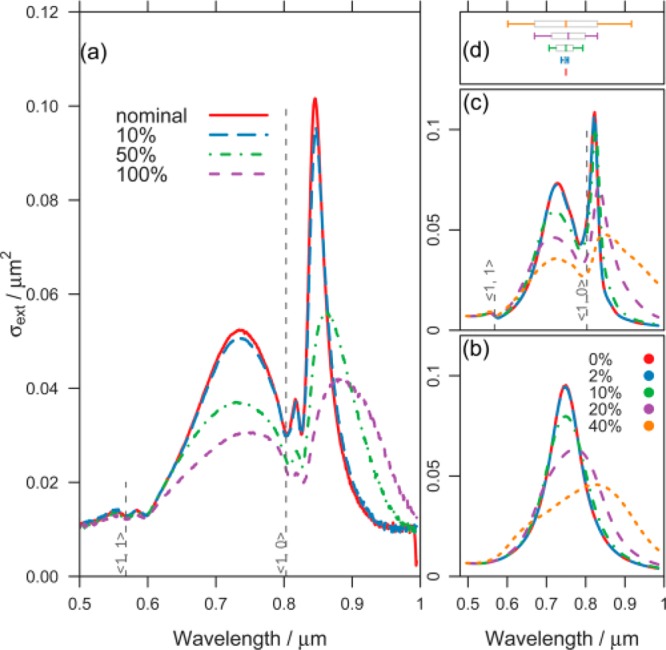
Effect of size disorder on SLRs. (a) Measured extinction spectra from arrays of nanoparticles that have regular positions but that have a variation in particle size. The legend shown indicates the level of disorder in the length of the nanorods’ long-axis. Vertical lines (dashed) mark the ⟨1,0⟩ and ⟨1,1⟩ diffraction edges for the 550 nm periodic array for a homogeneous environment of refractive index equal to 1.46. The nominal sizes of the particles were 120 nm × 80 nm × 35 nm. (b) Calculated extinction spectra based on five distributions of 441 ellipsoids. (c) Calculated extinction spectra for a regular array of dipoles (pitch 550 nm) based on the distribution of individual LSPR frequencies that are shown in (d). Reproduced and adapted with permission from ref (102). Copyright 2009 The Optical Society.

3.6. Interlude on Fabrication Techniques

In the works described above^{78,79,102,104} the arrays of particles studied were made by electron beam lithography, a powerful technique for exploring the underlying science, but it is not suitable for making the large-area structures needed for applications. A number of authors have looked at the surface lattice resonances supported by large arrays made by alternative techniques. These include the following: conformal imprint lithography, Vecchi et al.,¹⁰⁵ direct imprinting, Buzzi et al.,¹⁰⁶ and laser assisted fabrication, Aristov et al.,¹⁰⁷ and soft lithography methods such as phase-shifting lithography and solvent-assisted nanoscale embossing.^108,109 Next we examine some of the work by Vecchi et al.,¹⁰⁵ who used large area arrays to measure transmittance and reflectance (as was done in the early work⁷⁶), which allowed them to provide some extra evidence for the plasmonic nature of SLRs.

3.7. SLRs in Absorption

Vecchi et al.¹⁰⁵ conducted experiments on large area (3 × 3 mm²) arrays of Au nanoantennas fabricated by conformal imprint lithography. The lattice constants were a_x = 600 nm along the x-axis and a_y = 300 nm along the y-axis, and the size of the nanoantennas was 415 nm × 85 nm × 38 nm; some of their data are reproduced in Figure 12. The strong and broad feature centered at ∼650 nm is the LSPR of the individual nanoantennas. Superimposed on this individual nanoantenna response are two sharper surface lattice resonances that disperse with incident angle. Importantly these authors measured transmittance as well as reflectance spectra from their samples. This enabled them to determine the absorption, as shown in Figure 12(b), where it can be seen that absorption peaks can be associated with the SLRs, a clear signature of plasmonic resonances.¹² The vertical lines in Figure 12 corresponded to the (−1,0) and (+1,0) diffraction edges, calculated at θ = 6° using the period a_x = 600 nm and taking the refractive index of both the substrate and superstrate to be n = 1.45, thereby representing the conditions at which these diffracted orders become evanescent. As discussed above, the surface lattice resonances arise on the long-wavelength side of their associated diffraction edge provided the dipole sum is large enough.

Figure 12.

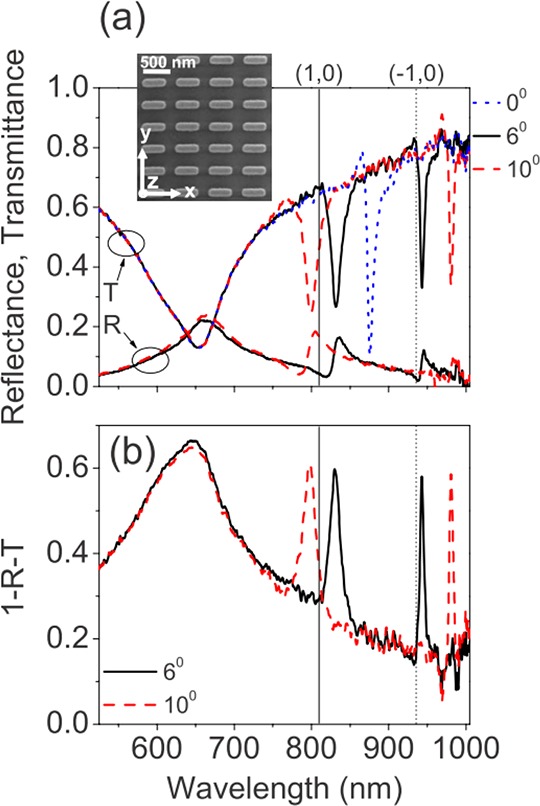
SLRs in absorption. (a) Measured zero-order transmittance, T, through, and specular reflectance, R, from a plasmonic array of nanoantennas. Data are shown as a function of wavelength for angles of incidence, θ = 6° (black, solid), θ = 10° (red, dashed); transmittance at normal incidence is also shown (blue, dotted). The light was polarized in the y direction, and the wave vector component of the incident wave that was parallel to the array surface is in the x direction. Vertical lines (solid) mark the (+1,0) and (−1,0) diffraction edges at 6°. The inset shows the SEM image of an array of plasmonic nanoantennas. (b) The absorption, as determined using A = 1 – R – T, shown as a function of wavelength for the angles 6° (black, solid) and 10° (red, dashed). Reproduced and adapted with permission from ref (105). Copyright 2009 American Physical Society.

The narrowest measured resonance had a spectral width 6 nm fwhm, corresponding to a quality factor of Q ≈ 160 for wavelengths near 950 nm, more than an order of magnitude greater than the Q of the individual nanoantenna resonance.

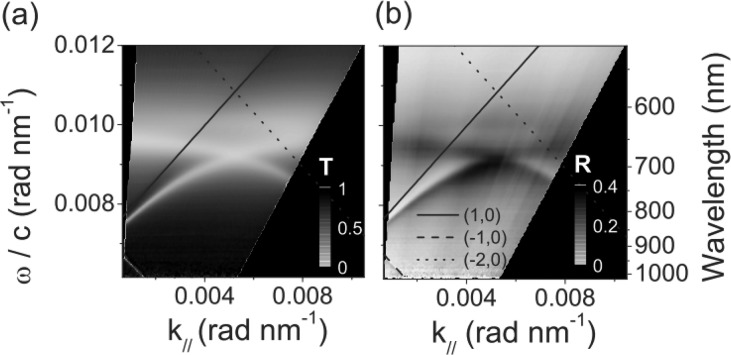
3.8. SLR Dispersion Diagrams

The first dispersion diagram of SLRs was obtained in ref (78), where the SLRs extinction was plotted as a function of the angle of incidence (representing in-plane wave-vector) and wavelength (representing energy). The LSPR did not change in position with the angle of incidence while the SLRs closely followed the diffraction edges (Rayleigh cutoff wavelengths) for the experimental conditions discussed in the paper. Vecchi et al.¹⁰⁵ also acquired data for a considerable range of incident angles and used them to construct the dispersion diagram shown in Figure 13, where the measured zero-order transmittance/reflectance spectra are displayed as a function of the in-plane wavevector, k_II = k₀sin(θ), and the energy expressed as k₀ = ω/c. Again, the LSPR remained nearly unchanged with angle of incidence. Further analysis by Vecchi et al.¹⁰⁵ showed the hybrid (polaritonic) nature of the surface lattice resonances; they also found that SLRs propagate across a number of unit cells of the array.

Figure 13.

(a) Transmittance (zero-order) as a function of the in-plane wave vector k_II and a function of normalized frequency ω/c. (b) Reflectance (specular) as a function of k_II and wavelength. The added lines mark the diffraction edges. Reproduced and adapted with permission from ref (105). Copyright 2009 American Physical Society.

The same group examined the way these plasmonic arrays modified the emission from dye molecules placed close to the array.^105,110 They showed an enhanced directional emission associated with the SLRs and associated this with an increased local density of optical states that the dye molecules may couple into.

3.9. Effect of Array Geometry

Humphrey and Barnes⁸³ studied surface lattice resonances in silver nanoparticle arrays for several array geometries. They showed that square, honeycomb, and hexagonal arrays can support similar SLRs; no particular geometry showed a clear advantage over the other geometries in terms of the resonance line width. As noted above for square arrays, these authors found that in general the precise position of the SLR was governed by the intersection point of the real part of the array factor S and the real part of the inverse single particle polarizability 1/α (eq 5). The strength as well as the width of the SLRs depended on the difference between the imaginary part of S and the imaginary part of α. Finally, by studying rectangular arrays⁸³ Humphrey and Barnes showed that particles in wavelength-scale arrays couple together in the direction that is perpendicular to the applied electric field. This point had been made before¹¹¹ and was investigated further by Guo et al.,¹¹² who looked at square, hexagonal, honecomb rectangular, and Lieb lattices. Particular attention was paid to the important role that the different diffracted orders play in determining the SLR phenomena.¹¹² These authors also discussed a nice model for interpreting SLR features and made connection with the Dirac physics possible with some of these structures. Giessen and co-workers investigated the transition between near- to far-field coupling in a plasmonic dimer system in a 3D arrangement.¹¹³ The structure consisted of two stacked gold nanowires with the vertical distance d_z varied over a considerable range, from small distances where the limit of near-field coupling applies, to distances with a spacing greater than the LSPR wavelength. It was demonstrated¹¹³ that such systems can be considered to be coupled ensembles of plasmonic oscillators that also exhibit Fabry–Perot modes. Special attention was given to stacking distances that corresponded to half-integer multiples of the resonance wavelength of the particle plasmon, where matching the resonance wavelength to the spatial arrangement of the plasmonic oscillators produces superradiant coupling. Such results might be useful in controlling the optical properties of plasmonic nanostructures, perhaps allowing emitters to be incorporated so as to yield a strong collective resonance with enhanced radiative properties.¹¹³

3.10. Field Distributions at SLR

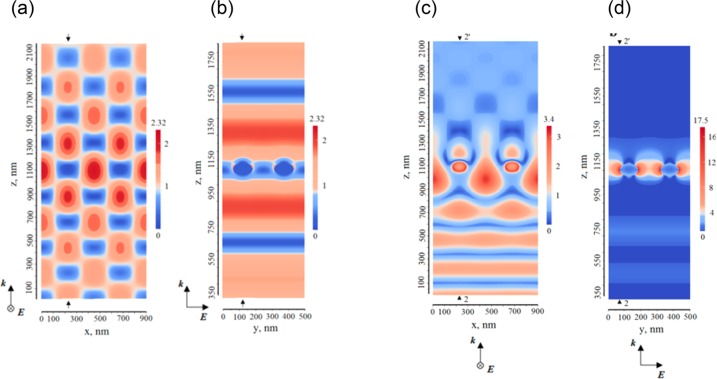
In some applications (e.g., sensing) it is important to know the near-field distributions associated with surface lattice resonances, how the field is distributed across a unit cell of the array. Nikitin et al.¹¹⁴ examined regimes of excitation of SLRs under normal illumination of an array of Au nanoparticles located in a homogeneous refractive index environment, and they determined electric near-field distributions using numerical simulations. They identified two clear regimes of response from lattices under normal incidence. The first is characterized by a localization of the electric field between nanoparticles for the excitation wavelength close to the diffraction edge, leading to nearly complete transparency of the array, Figure 14(a, b), (something which was previously discussed by Abajo⁹⁵).

Figure 14.

Electric field distributions (amplitude) |Ey| for the structure with lattice constants a_x = 450 nm, a_y = 250 nm at the condition of SLRs for two cases: near the diffraction edge where the field is distributed between nanoparticles (a) and (b) at the SLR condition where the field is distributed on the nanoparticles (c) and (d). The pictures show two unit cells. Reproduced and adapted with permission from ref (114). Copyright 2012 The Optical Society.

The second regime corresponds to a SLR for which there is a localization of the electric field on the nanoparticles, combined with a strong absorption/scattering, Figure 14(c, d). All these features have a natural explanation in terms of the SLR theory described above. Finally, the authors in ref (114) optimized the lattice parameters so as to maximize the electric field enhancement on the nanoparticles. It is worth noting that SLRs observed under oblique incidence could often be characterized by the fact that SLRs and the diffraction edge coincide; for this case (in contrast to the normal angle of incidence) the field enhancement is observed at a diffraction edge condition; see below. Recently, a finite-element analysis was implemented to determine the distribution of electromagnetic fields under conditions that support SLRs with an emphasis on near-field and far-field interference.¹¹⁵ The study confirmed that constructive and destructive interferences are possible near SLRs and that SLRs can indeed lead to strongly enhanced local electric fields near the nanoparticles.

3.11. Two Types of SLRs

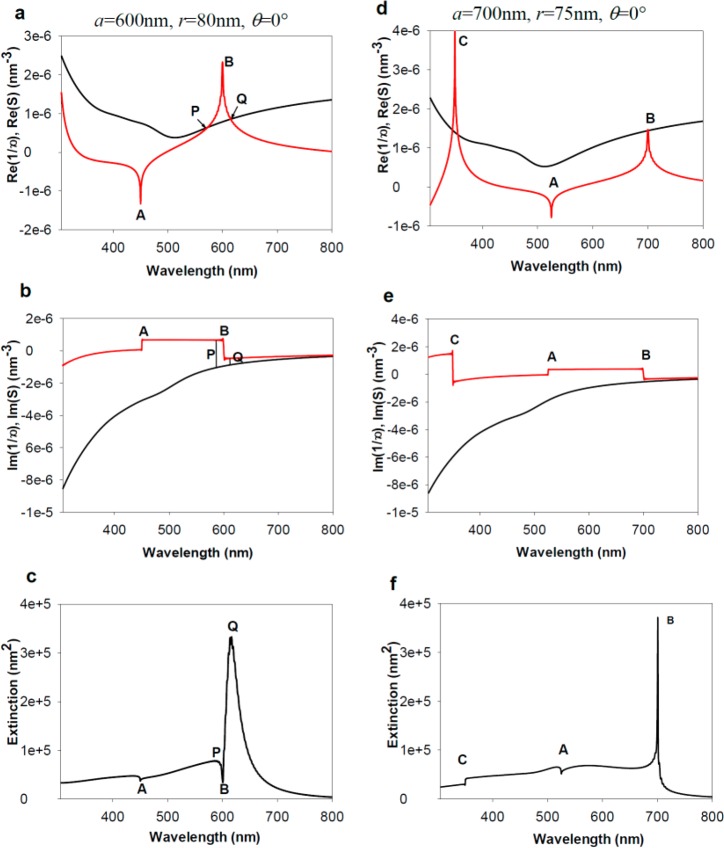
The question of how the diffraction edge relates to the spectral position of plasmonic SLR is quite important. Thackray et al.¹¹⁶ considered in detail the properties of SLRs excited by light of normal and oblique angles of incidence and showed that there are two generic types of SLRs distinguished by the behavior of the inverse polarizability, 1/α, and the dipole sum S near the resonance; see Figure 15.

Figure 15.

Spectral behavior of the real and imaginary components of the inverse polarizability 1/α (black) and dipole sum S (red) for a square array of gold nanospheres on a substrate of glass, and the resulting normal incidence extinction spectra (in air). (a to c) are for period a = 600 nm, and radius r = 80 nm, and (d to f) are for a = 700 nm and r = 75 nm at normal incidence. Figure reproduced with permission from ref (116). Copyright 2014 American Chemical Society.

The first type of SLR is observed when the dipole sum is large and the curve Re(S) intersects the curve Re(1/α), Figure 15(a–c). In this case, two unequal resonances are observed (P and Q) while the location of the diffraction edge corresponds to the minimum of extinction—the situation discussed in ref (114). One of the resonances (Q in Figure 15) is much larger than the other (P in Figure 15) due to a much smaller value of Im(1/α – S) which defines the strength of the resonance. (Note that Im(S) changes sign near the diffraction edge and combines with Im(1/α) either in phase or in antiphase.) This is exactly the case discussed in section 2 above. It is important to note that the location of the stronger resonance is shifted from that of the diffraction edge.

The second type of SLR is observed when Re(S) does not intersect the curve Re(1/α) but comes close to it; see Figure 15(d–f). In this case, a single, extremely narrow Fano-type, resonance is observed at the location of the diffraction edge and the diffraction edge corresponds to a significant field enhancement. This SLR normally yields SLRs of the highest resonance quality due to the fact that the imaginary part of Im(1/α – S) is smaller in this case. Since the spectral position of this single-peak SLR coincides with the diffraction edge position, the task of interpreting chemical and biosensing events becomes much simpler for SLRs of this second type (there exists an analytical expression which gives the spectral position of the diffraction edge.) It is worth noting that the first type of SLR is more often observed at normal incidence while the second type is typically observed at oblique angles.

3.12. Section Summary

To summarize, early experimental investigations provided the following insights:

• 1.SLRs may be observed in reflection, transmission, extinction, and absorption.
• 2.As few as 50 particles in an array are enough to observe SLR.
• 3.The effects of disorder were as follows: positional array disorder suppresses SLRs while particle size disorder makes SLRs wider.
• 4.SLRs can be observed in a variety of arrays with no array geometry showing a distinct advantage.
• 5.Field distributions inside the array can radically change as one sweeps the frequency of the incident light through the condition of SLR excitation.
• 6.For normal incidence SLRs are usually detuned from the diffraction edge while for oblique incidence SLRs are usually observed close to the diffraction edge.

4. Factors Influencing the Properties and Excitation of Surface Lattice Resonances

Here we discuss the role of various factors that affect the properties and excitation of surface lattice resonances; these include the following: the optical environment (refractive index), the illumination conditions, and the shape and size of the nanoparticles from which the array is made.

4.1. Optical Environment (Refractive Index)

We begin by looking at the refractive index of the medium surrounding the particles, and especially whether the refractive index of the substrate and superstrate need to be matched. In the early stages of experimental investigation into plasmonic surface lattice resonance phenomena there was initially some confusion about the need for a homogeneous (symmetric) refractive index environment. The first report⁷⁸ of ultranarrow SLRs involved substrate and superstrate having markedly different refractive indices, Chu et al.⁸⁰ observed SLRs in the case of less pronounced asymmetry between substrate and superstrate, while Auguié et al.⁷⁹ made use of an homogeneous environment; indeed Auguié et al.⁷⁹ showed that a homogeneous environment was a “soft” requirement to observe SLRs at normal angles of incidence. We note that this requirement is not necessary for light of oblique incidence as SLRs can be easily excited by such light in inhomogeneous conditions; see ref (78). The following works also showed that the requirement of homogeneous conditions for the observation of SLRs at normal angle of incidence can be lifted for arrays of larger and composite particles; see below.

Auguié et al.¹¹⁷ explored the symmetry/asymmetry problem in a detailed theoretical investigation. They found that excitation of SLRs under normal incidence is facilitated by the placement of metal nanoparticles into the symmetric environment, for example by adding matching oil in order to remove the refractive index contrast between substrate and superstrate. Using rigorous electromagnetic simulations they showed that the asymmetric environment can suppress long-range interactions between the particles and thus inhibit lattice resonances for normal incidence (Figure 16). It was shown that the superstrate-to-substrate index contrast together with the distance of the array from the interface are the key parameters that determine the strength of diffractive coupling.

Figure 16.

(a) Two-dimensional square array (schematic) of nanoparticles (gold) situated in a homogeneous semi-infinite medium having refractive index n₁ at a distance d above a substrate that has refractive index n₂. The array period is a. Normally incident light is polarized along one of the lattice vectors (x). (b) Cross section (scattering) of a single gold sphere in water (n = 1.33) and in glass (n = 1.46), as calculated using Mie theory. (c) Same as (b) but now for an array having period a = 500 nm, as opposed to that of an individual particle; also included is the asymmetric configuration for which now the spheres are in water and have their surfaces positioned 1 nm away from a glass substrate. Dashed lines (vertical) mark the position of the ⟨0,1⟩ and ⟨1,1⟩ diffraction edges in the various media. Notice how the sharp SLR features adjacent to the ⟨0,1⟩ diffraction edges are absent for the asymmetric environment (red line). All gold nanospheres were supposed to be of radius 35 nm. Reproduced and adapted with permission from ref (117). Copyright 2010 American Physical Society.

The effect of a dielectric substrate in terms of the excitation of SLRs can be understood as follows. The substrate affects both the polarizability of an individual nanoparticle α (by changing its environment) and the dipole sum S. These changes, however, can be compensated for by a change in array period and/or a size of the nanoparticle. The main cause for suppressing SLRs in an asymmetric environment is then the additional reflection produced by the substrate. For a dielectric substrate, this additional reflection is purely real and should be combined with Re(1/α – S), producing no contribution to Im(1/α – S). Therefore, the cancellation of the inverse polarizability (real part) happens at the spectral position where there is no cancellation of the imaginary part and SLRs become suppressed. For large nanoparticles, the contribution of the substrate reflection to the total array reflection becomes small and SLRs can again be observed. Also, when oblique light of p-polarization is used, the reflection from the substrate becomes small near the Brewster angle and SLRs can be observed again. It is worth noting that particles of large sizes (or in denser arrays) restore SLRs in asymmetric environments for light of both s- and p-polarizations (exciting either in-plane or out-of-plane resonances), while oblique incidence (and the Brewster phenomenon) works only for p-polarization (for out-of-plane resonances).

Mahi et al.¹¹⁸ looked at the dispersion curves of SLRs as a function of both the angle of incidence and the polarization direction for 2D square arrays of monomers and dimers for gold nanocylinder substrates. They used a Green’s tensor method and compared it to simulations based on the CDA approach. They confirmed that the substrate interface greatly modifies the shape of the dipole sum around the Rayleigh wavelength, compared to a grating embedded in a homogeneous environment.

4.2. In-Plane vs Out-of-Plane LSPRs

Understanding the differing conclusions reached by different authors is possible by considering the different relevant aspects involved. In particular, the simple view that an homogeneous medium is a “must” is a view that only strictly applies to arrays of particles where the particle height is relatively small (e.g., 35 nm in⁷⁹ and 38 nm in¹⁰⁵). In this case the dipole moment of the plasmon resonance of the particle that is used is in the plane defined by the array. As a consequence of the close proximity of the dipole moment to the interface between the substrate and the superstrate, the fields by which neighboring particles interact span both substrate and superstrate. If these two media have differing refractive indices then constructive interference is not possible. If however taller particles are used and light made incident at an oblique angle then a dipole moment may be excited perpendicular to the plane of the array. In this case, the electric fields associated with the interaction between neighboring particles are primarily in the superstrate and a refractive index mismatch between substrate and superstrate is less important. Odom et al.^119,120 introduced the terms “in-plane” and “out-of-plane” resonances in order to characterize excitations of plasmon oscillations in the plane of the array and perpendicular to the array plane. Another way to promote the interaction via fields in just one medium is to bury the particles in the (higher index) substrate. This approach was adopted by Adato et al.¹²¹ who demonstrated strong near-field enhancement and long plasmon lifetimes by embedding nanoantenna arrays into a dielectric substrate. Far-field extinction measurements confirmed the strong diffractive coupling between the particles and the resulting narrow plasmonic line shapes.

The properties (optical) of in-plane and out-of-plane SLRs for hexagonal and square lattices as determined with the discrete-dipole approximation were studied by Huttenen et al.¹²² These authors concluded that out-of-plane SLRs show much stronger polarization dependence as compared to in-plane SLRs. This comes from the fact that out-of-plane oscillations are able to couple in all directions within the array plane.

4.3. SLRs at Normal Incidence

Significant effort was expended to find ways to employ normally incident light and yet still observe sharp surface lattice resonances for asymmetric water/glass or air/glass environments. The motivation to do this stems from the fact that normal incidence observation requires only simple equipment readily based on a standard optical microscope, and an asymmetric environment makes the pursuit of applications, such as biosensing, much easier.³⁷⁻⁴⁰ It was found that it is possible; the key idea is that one has to use either composite¹¹⁶ or large¹¹⁹ nanostructures as the elementary element in the unit cell of the array so as to enable the excitation of out-of-plane dipole moments.⁷⁸ Several studies reported success in accomplishing this, albeit the narrowing effect was not as pronounced as in a symmetric, homogeneous environment.^80,123,124 However, narrow SLRs were achieved for normally incident light.

Zhou et al.¹²⁰ later showed that out-of-plane SLR modes may be thought of as a surface Bloch mode that comprises many Bloch harmonics. The out-of-plane dispersion evolves from a stationary state as the in-plane wavevector increases to become a propagating state, and as this happens, the nonradiative loss falls since a smaller fraction of the optical energy is stored by the nanoparticles; in contrast, the radiative loss rises since better coupling between higher-order Bloch harmonics and the leaky zero-order harmonics takes place. Such a system provides a nice conceptual framework for the dispersive properties of delocalized plasmon resonances that may be supported by other kinds of plasmonic nanostructures.¹²⁵

4.3.1. Complex Particle Geometries

An example of using a complex particle geometry to achieve SLRs under normal incidence for an inhomogeneous environment is the specially designed L-shaped and also rather tall nanostructures employed by Thackray et al.,¹¹⁶ for use with air/glass and water/glass interfaces. For these L-shaped (and tall) nanostructures light that is normally incident may excite the oscillation of in-plane electrons in the base of the structure, which is electrically connected to the out-of-plane plasmon, thereby inducing an out-of-plane dipole moment. Tall nanostructures were found to be more effective in generating narrow resonances under normal incidence than L-shaped ones. Q-factors of ∼45 for a water/substrate and Q ∼ 85 for a glycerol/substrate were achieved.¹¹⁶ SLRs excitation in a strongly inhomogeneous situation (air/glass) was also possible; see Figure 17.

Figure 17.

(a) Transmission of arrays of large, 200 nm tall, square nanostructures 200 nm × 200 nm, with periods that vary from 450 to 760 nm. SLRs are excited in an air environment. (b) SEM image of one array. Figure reproduced with permission from ref (116). Copyright 2014 American Chemical Society.

4.3.2. Importance of Substrate Conductivity

The presence of substrate conductivity can strongly influence SLRs by (i) introducing coupling between nanoparticles due to substrate conductivity and suppressing both LSPRs and SLRs and by (ii) absorbing electromagnetic waves propagating near the substrate at grazing angles and hence suppressing diffractive coupling (this is relevant when the electric field is parallel to the surface of substrate). The substrate conductivity is important since nanofabrication often requires the presence of a thin metallic layer (or ITO sublayer) to avoid charging during electron beam lithography. This conductive layer can be kept on the substrate surface after fabrication. Several studies reported a key role of the substrate’s electric properties for the excitation of SLRs. The suppression of LSPRs and SLRs by a conductive sublayer was discussed in Kravets et al.,¹²⁶ where it was found that in-plane SLRs can be completely suppressed by a 5 nm thick Cr layer as observed under normal incidence illumination. SLRs (albeit of lower quality) reappeared for oblique incidence of p-polarized light while s-polarized light still showed no sign of SLRs.¹²⁷ The reason for the suppression of SLRs in arrays that had been made on a substrate having a conductive layer under light of s-polarization is connected to the strong absorption of the diffracted light of s-polarization propagating along the substrate. This strong absorption comes from the excitation of currents in the conductive layer and it suppresses the diffractive coupling of the localized resonances by reducing the dipole sum S. For light of p-polarization, coupling happens via the diffracted beams with the electric field perpendicular to the substrate (so, connected to out-of-plane resonances). These beams do not excite strong currents in the conductive layer (due to its small thickness), and hence SLRs reappear.

Sadeghi et al.¹²⁸ offered a convenient way to tune SLRs by controlling the coupling of light with plasmon resonances in arrays of metallic nanoantennas with the help of ultrathin layers of conducting silicon. This was accomplished by including a thin film of silicon onto a plasmonic array. The authors demonstrated that some plasmonic arrays on a glass substrate that do not show SLRs at normal incidence could nevertheless acquire SLRs after deposition of an ultrathin silicon layer. The authors studied the behavior of these “induced” SLR resonances as a function both of the angle of incidence and of the arrays’ geometrical parameters.

4.3.3. Composite Nanoparticles

Composite nanoparticles are another way in which SLR quality can be improved in an asymmetric environment.¹²⁷ Normally incident light may couple to out-of-plane resonances of composite nanostructures, e.g., dimers,^127,129 and generate SLRs. Figure 18(a) shows the dependence (angular) of the reflection spectra for p- polarized light for arrays of Au nanodimers, with a particle diameter d = 110 nm, where collective resonances result in the reflection peak (instead of reflection drop). One of the narrowest SLR resonances in visible light was recorded in reflection mode for gold dimer arrays made using electron beam lithography but without using a lift-off process; see Figure 18(b).¹²⁷ A strong decrease of p-polarized reflectivity was recorded at λ ∼ 600–650 nm with fwhm of resonances lower than 3–5 nm. The origin of such a small width of SLRs in this system is still an open question.

Figure 18.

Properties (optical) of the regular arrays of gold dimers on a glass substrate. (a) Reflection spectra of gold dimers for p- polarized light as a function of the angle of incidence. Array period a = 320 nm, particle diameter d = 110 nm and height h = 90 nm. (b) Reflection spectra of embedded gold dimers for p- polarized light as a function of incident angle (a = 320 nm, d = 130 nm, h = 90 nm). Shown in the insets are SEMs. Adapted with permission from ref (127). Copyright 2014 American Physical Society.

4.4. Subwavelength Arrays

It is also interesting to note the importance of out-of-plane dipole moments for profoundly subwavelength arrays of nanoparticles. Such arrays are involved in remarkable effects such as the emergence of collective plasmonic, Dirac-like modes,^130−132 where predictions involve honeycomb arrays with periods that are smaller than the resonance wavelength by an order of magnitude.¹³¹ With such small separations, near-field interactions take on an important role. The collective tunable excitations in graphene-like nanostructures exhibit some of the special features that electrons exhibit in graphene and can be accompanied by a variety of effects such as, e.g., a nontrivial Berry phase behavior.¹³³ For example, particle arrays made from the metal tin (Sn)¹³⁴ showed pronounced resonances for subwavelength periods observed in both homogeneous (matching oil) and asymmetric environment for large size particles, thus confirming the theory.

Finally we note in this section that surface lattice resonances can be observed in nonplasmonic systems. Ghenuche et al. studied arrays of nanoparticles made of the dielectric silicon nitride (SiN_x).¹³⁵ In this case, NPs were placed in a homogeneous (index-matched) environment. Angle resolved transmission data from polarized light revealed both a shifting and splitting of the resonance peaks as angle of incidence was varied, in good agreement with calculations based on the dipole-lattice sum approach described above. These data showed that grating-induced effects and symmetrical/asymmetrical environments could play an important role in the optical response of regular arrays of nonplasmonic nanoparticles. Lattice resonances have also been predicted for arrays of particles that support exciton-polariton modes, thus opening a pathway to the exploitation of lattice effects in organic material systems.¹³⁶

4.5. Section Summary

To summarize, factors that influence SLRs are as follows:

• 1.A homogeneous (symmetric) refractive index environment is necessary for the observation of SLRs at the normal angle of incidence for arrays of relatively short nanoparticles.
• 2.SLRs for tall nanostructures or under oblique incidence can be observed in an inhomogeneous (asymmetric) environment.
• 3.Out-of-plane plasmon modes can facilitate the generation of high quality SLRs.
• 4.Substrate conductivity may suppress SLRs at normal angle of incidence.
• 5.For arrays fabricated on conductive substrates, SLRs reappear for p-polarization under oblique illumination.

5. What Are the Limiting Factors for the Resonance Quality?

Improving the quality of localized surface plasmon resonances is important for many applications, from nanolasers to biosensing. We have already seen that the early reports of plasmonic surface lattice resonances achieved quality factors of Q ∼ 40–60.^78,79 This was nearly a factor of 10 improvement over typical LSP resonances of individual gold nanoparticles.^37,47 The width of an SLR mode depends on the relation between the particle susceptibility and the dipole sum; from Markel’s theory it may even be exponentially small.⁶⁹ At the same time, the width of an SLR depends on the number of particles that interact coherently. This number might in turn be limited by the spatial coherence of the illumination, the physical size of the array area, disorder, substrate curvature, etc. In this section we look at several different approaches that have been explored to further improve the quality factor.

5.1. SLRs at Attenuated Total Reflection

The first method we discuss was that of modifying the excitation geometry by making use of attenuated total reflection (ATR) in prism coupling (Turbadar–Kretschmann–Raether) geometry;¹⁰⁴ a Q of ∼150 was achieved in this way for a deep red resonance; see Figure 19. An asymmetric index arrangement was used, with the two media being water and glass. This high quality SLR was achieved in the ATR geometry using 90° prism of refractive index 1.5 for the array parameters as follows: a = 318 nm, d = 132 nm, and s = 140 nm at the incidence angle of 45°. This is an order of magnitude better compared to that of conventional LSPRs in gold where Q ∼ 10.^18,19

Figure 19.

(a) Surface lattice resonance seen using ellipsometry in reflection in an attenuated total reflection geometry (Q ≈ 150 where water was used as a buffer layer). (b) SEM image of Au nanodots arrays. Figure reproduced with permission from ref (104). Copyright 2010 The Optical Society.

5.2. High Quality SLRs Using Out-of-Plane Resonances

Out-of-plane resonances have been used in an interesting way to realize high quality SLRs—in the form of arrays of monopole oscillators, being achieved by making use of the metallic mirror plane immediately below the metal particles.^137,138 For large angles of incidence Q-factors of over 200 were achieved. These results were achieved in the infrared (λ ∼ 5 μm); the resonators were made of indium tin oxide (a good plasmonic material in the IR,¹³⁹ the metallic ground plane being made of gold). Note that the sharpness of SLRs depends on Im(1/α – S) which can be made smaller for larger particles and for resonances at longer wavelengths (where both Im(1/α) and Im(S) become small). Out-of-plane resonances may be used to increase the height (effective) of the nanostructures fabricated on a metal substrate as explained below and hence to improve the resonance quality even further.

5.3. Narrow SLRs at High Angles of Incidence in Nanostripes on a Metallic Film

The third method moved away from the use of particle arrays and explored a related structure, that of a metallic grating. In this study¹⁴⁰ the authors observed very narrow SLRs in the near IR with a spectral width below 5 nm fwhm and associated Q-factors of ∼300 using a grating structure comprising gold nanostripe arrays fabricated above a thin gold film. Measured quality factors of up to 300 are among the highest reported from arrays of diffractively coupled nanostructures at telecom wavelengths around 1.5 μm.^137,138,140

5.4. High Quality SLRs for High Aspect Ratio Particles

In the fourth and last example discussed here, Zilio et al.¹⁴¹ experimentally investigated the optical properties of high-aspect-ratio out-of-plane metallic slanted silver nanorod dimers standing on a metallic substrate. The proposed architecture mimics a 3D split-ring resonator with a nanometric gap. High-quality-factor resonances with Q ≈ 390 were reported in the mid-IR (10–12 μm) because of the efficient excitation of collective modes in dimer arrays. It was shown that the tiny gap between the nanorods renders possible an effective near-field coupling between the rods that leads to the splitting of the single rod resonance into two hybrid dimer modes (called bonding and antibonding ones). The tilt of the structure on the other hand is demonstrated to be the important feature that enables the excitation of the bonding resonance of the structure using far-field illumination. By optimizing the grating pitch and illumination conditions, the value of Q could be further raised up to 500. It is easy to see the trend that the longer the SLR wavelength observed in the array, the higher the quality of SLR that can be achieved (∼100 for visible light, ∼300 for telecom wavelengths, ∼500 for mid-IR). The reason for this trend is the decrease of the imaginary part of susceptibility of nanoparticles and the dipole sum at larger wavelengths (physically connected with the fact that larger nanoparticles mostly scatter light instead of absorbing it). Note that high resonance quality does not have to mean high field enhancement for SLRs.¹¹⁶

5.5. Section Summary

To summarize, the quality of SLRs follows the following trends:

• 1.The longer the SLR wavelength, the higher the quality of SLR that can be achieved.
• 2.A substrate metal mirror layer can significantly improve SLR quality for large angles of incidence.
• 3.The ATR geometry, monopole emitters, and composite particles can be used to improve SLR quality.
• 4.It is difficult at the present state of knowledge to determine an upper limit on the maximum quality factor of SLRs that might be possible.

6. Phase Singularities under Surface Lattice Resonances: Optical Sensing

An interesting and alternative way to view the nanoparticle arrays that support surface lattice resonances is to see if one can consider them as thin films of an effective medium. In this section we do just this, and in doing so make a connection with another topical area, that of metasurfaces.

6.1. Zero Reflection, Phase Singularities, and Optical Sensing

6.1.1. Zero Reflection and Phase Singularity

The absorption of light under conditions for which plasmons are excited leads to a drop of the reflected (or transmitted) light intensity. A general property of the light intensity falling toward a zero value (something we refer to as darkness) is that the phase of the light experiences a sharp jump with a magnitude of up to π; the phase is undefined for a zero value of intensity.^15,142 In general, the lower the intensity of the minimum, the sharper the associated phase jump. It is worth noting that while it is easy to achieve a theoretical zero reflection in, e.g., the surface plasmon resonance (SPR) configuration, sufficient loss (e.g., scattering due to roughness, or indeed sufficient absorption¹⁴³) could suppress darkness and spoil observation of a phase singularity.

6.1.2. Phase Singularity and Optical Sensing

When employed in optical sensing tasks that rely on refractive-index-based monitoring of binding-recognition events (see Introduction), these sharp characteristics (singularities) of the phase of light enable orders of magnitude better sensitivity when compared with more conventional amplitude-based approaches. In particular, a significant gain in sensitivity may be obtained when phase is used as the sensing parameter in the Turbadar–Kretschmann–Raether SPR biosensing geometry.^{14,15,144,145} In terms of the minimum-detectable bulk refractive index change, the sensitivity of phase-sensitive SPR schemes can reach down to10^–8 refractive index units (RIU), which is at least a factor of 10 lower than with amplitude-based parameters (these include the spectral or angular position of the SPR reflectivity dip, together with its depth).^15,145 The lower detection limit of conventional sensitive SPR devices is typically estimated to be 1 pg/mm² of biomaterial accumulated on the surface of the sensor.¹⁴⁶ Therefore, the employment of phase sensitivity gives access to sub-100 fg/mm² level sensitivity.

6.1.3. Sharp Phase Jumps under SPR and SLRs

As noted above, in practice the phase jump is not perfectly sharp (Heaviside-like) under SPR excitation because of the unavoidable roughness of the Au film surface, which limits the resulting improvement of the detection limit of phase-sensitive SP devices. An example of the behavior of the phase and amplitude parameters under SPR excitation for a high quality gold film having the optimal thickness in the Turbadar–Kretschmann–Raether geometry (∼50 nm) is shown in Figure 20(a). One can see that under nearly optimal width of the resonance (30 nm fwhm), the parameter Ψ exceeds 8° at the resonance minimum corresponding to ∼5% of the optical intensity when compared with off-resonance conditions. As a result, the jump of phase of the light is considerably smoothed out; such a phase smoothing effect limits the sensitivity of this approach. It was recently shown that the intensity at the minimum of the resonance may be reduced by using alternative graphene/copper¹⁴⁷ or graphene/gold¹⁴⁸ structures for plasmon excitation; however these alternative geometries need their own functionalizing protocols to be developed.

Figure 20.

Experimental spectra for the phase and amplitude of reflected light under resonant plasmonic conditions: (a) Excitation of SPPs for a 50 nm gold film in the Turbadar–Kretschmann–Raether prism geometry (classical SPR). Owing to the finite roughness of the gold film surface, the Ψ value is well away from zero, leading to a smooth phase change in the minimum of the resonance curve. (b) Diffractively coupled array of gold nanodots (SLRs). The SLR is seen to be much narrower, and the value of Ψ is close to zero, leading to a very sharp jump in the phase close to the resonance minimum. Reproduced and adapted with permission from (149). Copyright 2016 The International Society for Optical Engineering.

The employment of diffractively coupled nanoparticles, SLRs, enables one to revisit the use of phase properties and their sensing applications. Indeed, in addition to the above-mentioned drastic narrowing of plasmonic resonances, diffractive coupling may also lead to a dramatic fall in intensity at the resonance minimum and an associated sharpening of the phase feature.^39,67,104Figure 20(b) shows the amplitude and phase characteristics of light that is reflected from a 2D array of 100 nm Au nanodots (array period 320 nm, angle of light incidence ∼65°, glass substrate). One can see that the excitation of a SLR can lead to a dramatic falloff of intensity at the minimum of the resonance (i.e., a fraction of 1%, compared with off-resonance conditions) and an associated narrowing of the phase feature. The behavior of the phase becomes singular (Heaviside-like) under zero reflectivity (optical darkness) at the resonance. Such a sharp phase characteristic can lead to a very high phase sensitivity, enabling a sub 10^–9 RIU detection limit.¹⁰⁴

6.2. Topological Darkness

Kravets et al.³⁹ considered in detail the topological properties of phase and the conditions needed to implement the use of these sharp phase features (singularities) in plasmonic metamaterials that support SLRs. To make use of such singularities, zero reflection is required for a thin film on a dielectric substrate, Figure 21(a).

Figure 21.

(a) Reflection (schematic) from a nanostructured gold film. (b) The phase Δ, of p-polarized light for the structure shown in (a) as a function of wave-vector calculated with the effective medium theory for θ = 60°, array period = 320 nm, gold and PMMA height 90 nm, PMMA stripe width 165 nm. The blue line marks the smooth phase behavior away from the zero reflection condition, the yellow line marks the phase jump. (c) The dispersion curves for plane gold and nanostructured gold along with their ellipsometric reflection spectra. For the nanostructured gold, it is seen that the dispersion curve can pass through the zero reflection condition (brown curve) and the reflection attains exactly the value zero, which is topologically protected. Reproduced and adapted with permission from ref (39). Copyright 2013 Nature Publishing Group.

Figure 21(c), brown curve (lower right), shows a set of n, k (here n̂ = n + ik represents the film’s complex refractive index) for which the reflection is exactly zero for a 170 nm film deposited onto a glass substrate, and for an angle of incidence θ = 60°. This line divides the n–k space into two distinct regions with the reflected electric field changing sign on crossing the brown line. The line is thus an important topological feature for reflectivity in n–k space: when a thin film is introduced at the interface, zero reflection is still possible for a dielectric film near the Brewster angle, but this effect cannot be achieved by using a continuous metal film. As an example, the dispersion relation for gold n(λ), k(λ), leads to the curve shown at the top of the figure; it results in nonzero reflection for gold films across the whole of the visible part of the spectrum (the ellipsometric reflection for a 170 nm gold film is indicated in Figure 21(c), top panel).

For a nanostructured material where resonances such as SLRs may be supported, the situation is different. By using a plasmonic metamaterial comprising an array of metallic nanoparticles, one can manipulate the effective n_eff(λ), k_eff(λ) with the aim of having them intersect the line of zero reflection in Figure 21(c). As an example, in Figure 21 such a result is obtained for Au nanostripes that were made by depositing gold (yellow, thickness 85 nm) onto a poly(methyl methacrylate) (PMMA) stripe-array (purple, thickness 85 nm). Similar results may be achieved with other nanostructured materials. A narrow plasmon resonance can be seen that has a quality factor Q ∼ 200 and a half-width of ≈12 nm.

6.2.1. Jordan Theorem

An analysis demonstrates that the intensity of the light may go to zero for a certain combination of angle of incidence and wavelength; this produces a singular character for the phase in Fourier space. As noted above, the line of zero reflection (brown) delineates two different regions of phase in the (n, k) plane because of the nature of the reflection (Fresnel) coefficients. Since the dispersion curve of the nanostructured gold begins in one region and ends in the other, the dispersion curve will always intersect the zero reflection line (due to the Jordan theorem,¹⁵⁰ i.e. the line connecting two different regions that are separated by a boundary will always intersects that boundary), Figure 21(c). By varying the angle of incidence it is possible to match the light wavelengths at the intersection point. Relatively low levels of imperfection or variation of the structure (or relatively low level perturbations of the effective optical constants determined using different methods) will not alter this, the dispersion curve of a nanostructured gold system will connect two different regions of the (n, k) plane. As a result, zero reflection for a somewhat different structure is still expected to be observed, although at a slightly different wavelength. It is for this reason that the point of zero reflection (for a nanostructured material) is described as topologically protected. Such points were referred to in ref (39) as points of “topological darkness”. Topological darkness (in Fourier space) has previously been observed for arrays with different unit cells: single and double dots, dumbbells, arrays of holes and stripes in metal films.³⁹

6.3. SLRs and Phase Detection Techniques

It is possible to radically improve the sensitivity of plasmonic sensors by profiting from the singular phase behavior under excitation conditions appropriate for SLRs.³⁹ By using reversible hydrogenation of graphene, it was demonstrated that the areal mass sensitivity for devices based on SLRs can achieve a level of femtograms per mm². More recently, a recent study¹⁵¹ reported that bulk plasmonic metamaterials can exhibit topological darkness using an inexpensive fabrication technique based upon self-assembly, thereby enhancing the prospects for phase-sensitive plasmonic measurements in device applications.

Note that phase and amplitude sensitivities do not always correlate with each other in different plasmonic geometries. Indeed, the spectral sensitivity of SLRs in nanoperiodic arrays is typically much lower when compared to that of surface plasmons (PSPs), while the phase sensitivity is higher. This situation is illustrated by Figure 22(a), where a change in SLR (red) and PSP (black) features is shown as a function of the refractive index of the medium; these changes were accomplished through the use different concentrations of glycerin.

Figure 22.

Spectral dependence (measured) of the spectral position of the resonance (a) and the phase angle (b) to variations in the refractive index for diffractive coupled SLR (red) and for conventional SPR with a 50 nm gold film (black). Figure adapted with permission from (149). Copyright 2016 The International Society for Optical Engineering.

The increase of RI produces a shift to longer resonance wavelengths for both configurations. The gradient of the linear fit yields a sensitivity of 400 nm/RIU for SLRs, this is similar to the best reported values of sensitivity for localized plasmons³⁷ but about an order of magnitude lower than that obtained using thin film-based PSP sensing in the Turbadar–Kretschmann–Raether prism geometry (∼3,600 nm/RIU). The limitation in using SLRs concerns the diffractively coupled nature of localized plasmons; diffractively based phenomena have sensitivity that is typically of the order of the array lattice constant Δλ/Δn ∼ a(152) (unless the arrays are 3D¹⁵³). However, the same considerations do not hold for phase sensitivities. Indeed, as shown in Figure 22(b), PSPs have a rather moderate phase sensitivity (2.3 × 10⁴ deg of phase per RIU), while the SLR phase sensitivity may easily exceed 10⁵ deg of phase per RIU; see Figure 22(b). This is due to the significantly lower light intensity in the minima associated with diffractively coupled resonances, compare Figure 20(b) with Figure 20(a). Thus, despite a poorer amplitude sensitivity for SLRs, the use of phase sensitivity more than compensates for this.

The best sensitivities to-date of SLRs to refractive index variations in gaseous and aqueous media were reported in ref (104). It was shown that the SLR phase sensitivity may be more than 2 orders of magnitude greater than the best amplitude sensitivity for the same nanodot array and an order of magnitude better than the PSP sensitivity in the Turbadar–Kretschmann–Raether configuration. In experiments involving gaseous media it was found that the best SLR phase sensitivity (5.2 × 10⁵ degrees of phase shift per RIU) is better by more than 2 orders of magnitude than the corresponding SPR amplitude sensitivity.^144,145 It seems realistic to develop a phase sensitive SLR sensor with the threshold at subnanolevel of 10^–10 RIU by appropriate optimization of array parameters (e.g., the lattice period). It is clear that to achieve such a low detection limit requires the development of low-noise phase detection schemes, such as those based on interferometry^14,144 or polarimetry.^15,154

6.4. SLR and Optical Chirality

The previous sections focused on how plasmonic arrays could be effectively used to manipulate the reflected/transmitted light amplitude and phase. When arrays are made of chiral elements, more subtle optical effects are possible with light propagation being different for light of left and right circular polarizations. This asymmetry leads to circular dichroism, characterized by different levels of optical absorption for the two circular light polarizations, and optical activity, where linearly polarized light rotates polarization during its propagation.¹⁵⁵ Chirality can be introduced either through a careful design of the shape of constituent elements or through an arrangement of these elements into chiral superstructures.¹⁵⁶ At the same time, the optical effects associated with chirality can be strongly enhanced with the help of plasmonics.^157−161 The fascinating world of chiral metasurfaces and their optical properties have been extensively reviewed.^{138,156,162−164} Chiral materials are often made in the form of 2D structures (metasurfaces) which are arranged in regular arrays in order to avoid scattering.^157−161 Therefore, one can expect that plasmonic surface lattice resonances could enhance further the optical effects of chirality (e.g., circular dichroism and optical activity). An enhancement has been indeed observed for chiroptical effects—circular dichroism in particular—in plasmonic arrays under oblique light illumination where SLR modes can be excited more easily.¹⁶⁵ The dependence of SLR modes on the angle of incidence was used in ref (166) to realize spectrally tunable and strong chirality in diffractive metasurfaces. In this case, the diffraction-assisted chirality—circular polarization dependent light transmission and circular dichroism—was very large near the main SLR modes of the plasmonic chiral array. Cotrufo et al.¹⁶⁷ showed that lattice resonances play a primary role in controlling the spin-dependent emission of light from planar chiral metallic nanoparticle arrays embedded in a light-emitting dye-doped slab. They found that the photoluminescence observed from these arrays showed a high degree of circular polarization near the position of the SLR, which emphasizes the important role that diffractive coupling may have for optical spin–orbit effects. It is worth noting that investigations of SLR modes in chiral arrays started only recently and could bring new surprises.

6.5. Section Summary

To summarize, SLRs can lead to the following:

• 1.Zero reflection and singular behavior in the phase of the reflected light.
• 2.Topologically protected darkness (zero reflectivity) with improved phase sensitivity toward binding events.
• 3.Optical sensors based on SLRs with surface area sensitivity at the level of <10 fg/mm² (better than conventional SPR by several orders of magnitude).
• 4.Phase sensitive SLRs with 10^–10 RIU detection limit (better than conventional SPR sensors by 4 orders of magnitude).
• 5.Strong enhancement of chiroptical effects in chiral plasmonic arrays.

7. Surface Lattice Resonances and the Emission of Light

Array structures may effectively couple light from nearby emitters (dye molecules, quantum dots, etc.) to light, and as a result their use is a subject of active investigation for applications potential in light-emitting diodes, lasing, and strong coupling; we explore each of these below.

7.1. Surface Lattice Resonances and Spontaneous Emission and Absorption

Interest in using SLRs to control the emission of light is perhaps the most explored of these three areas of potential. Here we look at two classes of emitting source: dye molecules and inorganic semiconductors.

7.1.1. Dye Molecules

Vecchi et al. initiated much of the work concerning the coupling of emitters of light via SLRs with their 2009 article on shaping the fluorescent emission from dye molecules using an array of nanoantennas produced by nanoimprint lithography.¹¹⁰ They showed that the emission direction could be controlled by making use of SLRs. The same group reported a ∼10-fold enhancement of emission from dye molecules as a result of coupling to SLRs, again making use of arrays made by nanoimprint lithography.¹⁶⁸ Interestingly, they exploited the multipolar plasmonic resonances of their antennas, as nicely revealed by simulations of the field profiles associated with the modes involved. The same group explored the sensitivity of the emission via SLRs to the spatial location of the emitting sources¹⁶⁹ and investigated other aspects important to the design of useful structures through combined experimental/numerical work.¹⁷⁰ In a separate study, ring-shaped nanoantennas were used to illustrate the potential to control the line width, shape, and amplitude of the emission.¹⁷¹ The concept of using SLRs as intermediaries to control the emission of light was extended to the UV part of the spectrum by making use of an array of Al nanoantennas produced by focused ion-beam lithography.¹⁷²

Further work with a specific focus on exploiting SLRs in the context of solid-state lighting has also been reported.¹⁷³ In this work, the authors sought to control the directionality of the emission from a phosphor layer pumped by a blue LED. By placing a large-area nanoimprinted hexagonal array of aluminum nanoparticles between the blue LED and the phosphor, they were able to couple phosphor emission to SLRs and thereby control the directionality of the emission from the phosphor. For the phosphor, they used a 700 nm thick layer of polymer doped with the light-emitting molecules Lumogen F Red (BASF); the emission was characterized using Fourier microscopy. The authors noted that this approach might also enable control over the color of solid-state lighting devices. The scope for making use of different nanostructure designs for the antennas was demonstrated through the use of nanopyramid arrays, with the shape of these particles allowing control over the balance between forward and backward emission of emitters of light.¹⁷⁴ The physics underlying this effect was discussed in terms of the enhanced magnetic and magnetoelectric response of the nanopyramids.

7.1.2. Inorganic Semiconducting Emitters

Surface lattice resonances can be used to control the emission of inorganic semiconducting emitters. Diffractive arrays comprising nanocylinders made of silver were used to enhance the efficiency of radiation from InGaN/GaN quantum wells whose visible emission was in the blue/green part of the spectrum (around 495 nm).¹⁷⁵ Significant enhancements in the luminescence output (a factor 5 or more) were found when the period of the array exceeded the wavelength of the emission in the semiconductor material. The results, from both experiment and associated numerical simulations, were indicative of an underlying mechanism based upon a strong resonant coupling between the SLR of the arrays and the light-emitting quantum well excitons. Rodriguez et al. demonstrated that SLRs in an array of silver nanoantennas may be used to modify the emission from a thin layer of CdSe/CdS core/shell quantum rods (QRs)¹⁷⁶ (randomly oriented) yielding a highly directional and enhanced polarized light source. By tailoring the spectral/angular dependence between the emission spectra and the SLR, it has been shown that a Lambertian source can be converted into a directional emitter of polarized light.¹⁷⁶ Strong modifications of the emission characteristics of quantum dots in the presence of plasmonic nanoarrays were also demonstrated in ref (177), where coupling with the plasmonic modes was found to boost the spontaneous emission decay rate of quantum dots. Murai et al.¹⁷⁸ studied the mechanism where photoluminescence from a thin Eu(III)-complex that would otherwise suffer total internal reflection and be trapped in the film could instead be recovered as emission into free space using SLRs. Periodic arrays of Al nanocylinders nanoparticles were used, and it was shown that directional photoluminescence enhancement as large as 5-fold can be achieved by excitation of SLRs.

7.1.3. Light Absorption and SLRs

Surface lattice resonances can also be used to control the absorption of light. Perhaps building on earlier ideas concerning the coherent control of absorption,^179,180 coherent control was used to modify the absorption of light by a layer of dye molecules.¹⁸¹ Of particular interest was the finding that absorption by molecules residing in the regions between the metal particles could be controlled, something that may prove useful for light-harvesting devices.

7.2. Surface Lattice Resonances and Lasing

The idea of trying to harness periodic arrays of plasmonic scatterers for lasing is a natural one, there is a long and successfully history of using periodic dielectric structures to provide lasing feedback.^182,183A priori it is not obvious that plasmonic modes will make good candidates for lasing structures because although they are efficient scatterers they are also absorptive.¹⁸⁴ The combination of gain and plasmonics is a topical one,¹⁸⁵ and a significant amount of recent research has been directed at lasing from individual plasmonic structures. That work is reviewed elsewhere¹⁸⁶ and will not be considered here; instead, we focus on periodic plasmonic structures.

7.2.1. Early Work

An early report of lasing involving feedback derived from gold nanoparticles employed the light-emitting polymer LPPP as the gain medium.¹⁸⁷ However, lasing occurred at ∼490 nm, shorter than the spectral region for which gold supports a plasmonic response, owing to interband absorptions. More recently lasing involving gold nanoparticle arrays was reported.⁴² Here the gain medium, a dye-doped polymer, offered gain in the near IR spectral range, around ∼900 nm, far from the gold interband absorption. Plasmonic lattices were used to provide feedback for lasing based on a dye-doped polymer film.¹⁸⁸ These same authors studied the effect the nature of the arrays had on the lasing characteristics, focusing in particular on a comparison of periodic, aperiodic, and random lattices.^189,190 In their work, it seems probable that the lasing mode was a waveguide mode supported by the dye-doped polymer rather than SLR.

7.2.2. Tunable Lasing Based on SLRs

Two recent reports have significantly extended the area of lasing based upon SLRs. In the first Yang et al.¹⁹¹ employed an interesting strategy. Work on amplification and lasing in plasmonics has frequently employed liquid gain media; such media have fewer problems with bleaching of the gain.¹⁸⁵ Yang et al. made use of liquid media by employing microfluidics to deliver the gain material to the metallic array. Importantly they used this approach to tune the emission of the lasing output. By varying the composition of the liquid, they could control its refractive index. This in turn led to a change in the wavelength of the surface lattice resonance. Figure 23 shows the lasing spectrum for different refractive indices of the fluid used. Also shown is the fluorescence emission profile of the dye, indicating the overall gain profile.

Figure 23.

Lasing emission at different wavelengths. Experimental data of lasing based on surface lattice resonances associated with gold nanoparticle arrays. The different lasing spectra correspond to different refractive indices of the optical environment, from n = 1.42 to n = 1.50, achieved by altering the refractive index of the solution maintaining the gain molecules. The lasing emission intensities have all been normalized to a value of 1. Also shown (gray) is the luminescence spectrum. Figure reproduced with permission from ref (191). Copyright 2015 Nature Publishing Group.

In the second report a liquid gain medium was also used, this time with the emission of light being in the visible part of the spectrum.¹⁹² In this elegant piece of work two lasing modes were observed, associated with band edge surface lattice resonances, as shown in Figure 24. The surface lattice resonance mode that is usually observed in experiments is in fact one of two possible modes. This “common” mode involves electric dipole distributions of charge on the particles and thus easily couples to light, hence its designation as bright. The other mode is associated with a quadrupolar charge distribution and does not usually couple to light, hence its designation as dark. In the work of Hakala et al.¹⁹² both modes were observed to lase. The lasing observations were combined with measurements of the dispersion of the modes involved and spatial emission measurements so as to help identify the underlying physics.

Figure 24.

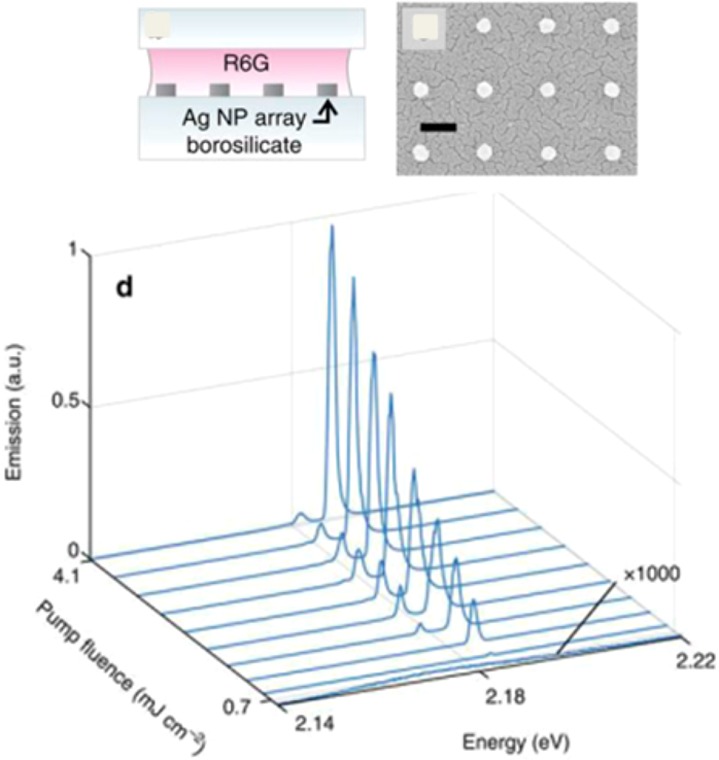
Lasing emission at different pump powers for a square array of silver nanoparticles, diameter 60 nm, and array period of 375 nm; the array was 100 × 100 (μm)². The gain medium employed was standard laser dye molecule R6G, and the lasing structure is shown in the insets. The scale bar in the SEM of the array is 200 nm. Reproduced with permission from ref (192). Copyright 2017 Nature Publishing Group.

Recently Wang et al.¹⁹³ have demonstrated multimodal lasing from plasmonic superlattices covered by liquid dye solution. Plasmonic superlattices were produced by grouping patches of nanoparticles into microscale arrays. It was shown that plasmonic superlattices may support band-edge SLR modes that are capable of multimode nanolasing at predetermined wavelengths of emission. They found that population inversion can be achieved at plasmonic hot spots and that this could be spatially controlled through the order of diffractive coupling of the patches. In addition, superlattices that were symmetry-broken were demonstrated to support switchable operation between single mode lasing and lasing on and multiple modes. The relative intensities of the different modes were controlled by altering the size of nanoparticles and the concentration of the local gain. Wang et al.¹⁹³ proposed a design of light sources (nanoscale) based on SLRs with controlled spacing, mode positions, and output properties which may lead to multiplexing for on-chip photonic devices.

7.2.3. Subwavelength Plasmon Lasers

A new geometry for plasmon lasers at the subdiffraction limit was put forward in ref (194). These authors suggested the possibility of unidirectional lasing using ultrasmooth, two-dimensional (2D) plasmonic crystals made using the template stripping approach. In their device 2D plasmonic (Au or Ag) crystals surrounded by dye molecules exhibited lasing in a single emission direction when optically pumped. Furthermore, the lasing wavelength could be controlled/tuned through modulation of the dielectric environment. In these 2D plasmonic crystal lasers, lasing wavelengths were tuned by altering the gain media (dye and/or solvent combinations).

7.2.4. Hole Arrays and Other Geometries

Interesting alternatives using hole-arrays have also been explored. Hole-arrays in films of Au have been successfully coupled to InGaAs gain layers and used to yield plasmonic hole-array lasers,¹⁹⁵ with good evidence of a correlation between the pump-power dependence of both lasing threshold and line width.^196,197 A number of alternative structures have also been investigated. In one example, a dye-doped polymer layer (PMMA) was situated above a silver film of 20 nm thickness. A square lattice (2D) of gold nanopillars having period 865 nm was then fabricated on top of the doped polymer layer to provide the feedback element. The authors of ref (198) investigated how the fields supported by SLRs are modified by the inclusion realistic optical gain.

Recently, the amplification of out-of-plane SLRs in gain-assisted nanoparticle arrays has been predicted.¹⁹⁹ These out-of-plane SLRs demonstrated lower thresholds for lasing compared with in-plane lattice plasmons, due to enhancement and more efficient localization of the electric field. The results¹⁹⁹ also suggest that gain thresholds for SLRs are much lower than those of individual nanoparticles. A consequence of the low radiative loss of surface lattice modes is to give active nanoparticle arrays a clear advantage of a lower lasing threshold than gain-assisted nanoparticles. Such active nanoarrays may also find application in luminescence and Raman scattering studies, in photocatalysis, and in nonlinear optics.

7.3. Surface Lattice Resonances and Strong Coupling

Strong coupling between cavity modes and quantum emitters is a rapidly emerging field in which an ensemble of light emitters (e.g., dye molecules, quantum dots, etc.) exchanges energy with an electromagnetic resonance, e.g. light confined (and thereby enhanced) in a microcavity.²⁰⁰ Surface plasmon modes are also suitable optical resonances;^201−203 indeed, the extent of the field confinement they offer has recently led to the report of single molecule strong coupling.²⁰⁴

The combination of strong coupling between confined optical fields and molecular resonances is a fascinating one because it offers the prospect of control over chemical processes. As an example, control over photoswitching of spiropyran molecules was demonstrated using a planar optical microcavity.²⁰⁵ Similar switching behavior was also achieved using the localized surface plasmon modes on metal nanoparticles, again with spiropyran molecules as described in ref (206). Strong coupling of excitons with PSPs was also achieved using resonances with excitons of organic semiconductors, specifically J-aggregates of TDBC dye molecules.²⁰⁷

Strong coupling involving surface lattice modes and dye molecules was explored and achieved in 2013 by two groups, both making use of the standard laser dye molecule R6G and silver nanoparticle arrays. In one report the authors used conformal imprint lithography;²⁰⁸ in the other particle arrays were produced by electron beam lithography.²⁰⁹ Taken together these results show that SLRs offer a powerful means by which light–matter interactions may be manipulated.

7.4. SLRs and Nonlinear Effects

Nonlinear optics at the nanoscale is attracting increasing interest, and this applies to arrays of plasmonic particles.²¹⁰ An interesting study concerning the role of SLRs in second-harmonic generation (SHG) was carried out by Czaplicki et al.,²¹¹ where arrays of metal nanoparticles were employed. They demonstrated that by altering the incident angle it was possible to tune the SLR to match the fundamental wavelength for SHG and thereby improve the quality of the resonance for better enhancement of the SHG process. When compared with results obtained at normal incidence, an enhancement by a factor of ∼10 was observed. However, the authors concluded that more studies are needed if the SLR-enhanced nonlinear response is to be fully understood. Michaeli et al.²¹² experimentally demonstrated SHG from rectangular arrays of split-ring resonators at oblique incidence and found the conditions which provide more than 30-fold enhancement of the emitted second harmonics compared with light incident normally. They showed that these conditions agree well with the existence of a SLR at the wavelength of SHG.

It has also been shown^213−216 that enhanced nonlinear interactions in plasmonic/dielectric structures may be associated with the excitation of SLRs, with their origin connected to nonlinearity in the metal and field enhancement in the surrounding material. In the future, the nonlinear susceptibilities of plasmonic nanostructures are expected to become part of the design of nonlinear integrated devices and optical information processing applications.

Kolmychek et al.²¹⁷ demonstrated magnetic modulation of SHG from 100 nm diameter gold NPs arranged in a square array of 400 nm period, covered by an iron-garnet layer (90 nm) doped with Bi. They observed that SHG generation is resonantly enhanced under the excitation of SLRs and studied the magnetization-induced change of SHG in their system.

In another study,²¹⁸ a single bow-tie nanoantenna embedded in an array of scattering nanoparticles was presented. The authors demonstrated the possibility for implementing multifrequency (several mid-IR wavelengths) operation through the use of nested particle arrays having multiple periodicities, possibly paving the way for broadband nanoantennas to be developed that may be used as near-field probes for nanoimaging, biosensing, and spectroscopy.²¹⁸

7.5. Section Summary

To summarize, SLRs can strongly affect the process of light emission:

• 1.SLRs can enhance directional output of light from dye molecules by at least an order of magnitude.
• 2.SLRs can be used to control the following characteristrics of light emitted by LED: direction, wavelength, and polarization.
• 3.Absorption of light by dye molecules can also be modified by SLRs.
• 4.SLRs can reduce lasing thresholds and provide control over lasing wavelength and direction.
• 5.Strong coupling of emitters with light can be achieved through surface lattice modes.
• 6.SLR modification of nonlinear effects is possible, although much more work is required to assess the potential.

8. SLRs and 2D Materials

As we have seen elsewhere in this review (section 6), the confined and enhanced optical fields associated with plasmonic resonances, including surface lattice resonances, make these modes sensitive to their immediate environment. That sensitivity extends to atomically thin 2D materials, including graphene,²¹⁹ and van der Waals materials such as MoS₂ (semiconducting) and NbSe₂ (superconducting).^130,220 Another important reason for using plasmonic surface lattice modes vs propagating “flat” plasmons lies in the field distribution: PSPs often provide enhanced electromagnetic fields which are perpendicular to the plane of 2D materials and hence do not interact strongly with them.²²¹ Here we look at the combination of surface lattice resonances and these 2D materials.

8.1. Graphene and SLRs

The spectral position of surface lattice resonances can be modified by adding a 2D material on top of the plasmonic particle array. A significant spectral shift (∼10 nm) of the SLR arising from the presence of a layer of graphene has been shown,^39,222 where the possibility of using this effect to study graphene’s surface chemistry was also discussed. The results obtained so far have led to suggestions that graphene-functionalized plasmonics may provide a new platform in chemical sensing applications involving polarized light investigations and enhanced Raman scattering.²²²

8.2. SLRs and Optical Modulators Based on Graphene

A promising application of SLRs is associated with the field of active plasmonics; the spectrally sharp plasmonic features might enable the modulation of light, especially at telecom wavelengths. Recent investigations theoretically predicted²²³ and experimentally demonstrated¹⁴⁰ that graphene-plasmonic hybrid devices are capable of controlling the phase and intensity of the light phase at gigahertz frequencies in the near-IR spectral range. Such devices combine two remarkable behaviors: electro-optical properties of graphene and highly tunable ultranarrow SLRs.^130,140,223 It was found¹⁴⁰ that hybrid graphene plasmonic modulators based on the SLR can provide the modulation depth of 20% in reflection operated by gating of a single layer graphene at telecom wavelengths.

Graphene-based optical modulators normally utilize the effect of Pauli blocking where the absorption of light in graphene can be blocked by populating the conduction/valence band by applying a gating voltage.¹³⁰ Such modulators provide high frequency of modulation;²²⁴ however, the modulation strength is modest (several percent) and the modulation wavelength is limited to the mid-IR and near-infrared.²²⁴ Plasmonic nanostructures can provide an enhancement of the modulation strength;^221,225 however, it is difficult to push graphene modulators into the visible.²²⁶ SLRs combined with nanomechanical motion of 2D graphene/hBN heterostructures can allow one to achieve strong light modulation over a large spectral range—from the visible out to the mid-IR. To this end, authors²²⁷ fabricated a gold nanostripe array on a gold substrate, a combination that supports very high quality SLRs (Q up to 300 at telecom range) at large angles of incidence, and suspended graphene/hBN heterostructures over the array. The application of a gating voltage to the graphene resulted in nanomotion of the heterostructure and a strong modulation at the position of SLRs, >10% at visible, near-infrared, and mid-infrared wavelengths.

8.3. Other 2D Materials

The control of light–matter interactions in 2D atomically thin (graphene-like) semiconducting crystals is a promising way to yield new optoelectronic performance. Tran et al.²²⁸ have reported the enhanced PL from coupling Ag or Au NP arrays to single-photon emitters in 2D hBN. Specifically, they have demonstrated an enhancement in the spontaneous emission rate, along with an enhanced count rate and modified ultrafast dynamics. Lee et al.²²⁹ reported substantial changes in the excitation of and emission from excitons in MoS₂, leading to spectrally tunable, large photoluminescence enhancement for chemically grown monolayers of MoS₂. In their work, the plasmonic array was made of silver “bowtie” nanoantennas; see Figure 25. The strong plasmonic field associated with the SLR of the bowtie arrays was found to give rise to enhanced Raman scattering from the MoS₂.²²⁹ The same group also looked at strong coupling involving the plasmonic modes associated with silver nanodisk arrays and excitons in a monolayer of MoS₂, studied via angle-resolved reflectance microscopy.²³⁰ Taken together the results discussed here indicate that strong interactions between plasmonic nanostructures and atomically thin 2D crystals may enable the observation of new/modified optical phenomena. They are also indicative of a new way to make devices with applications ranging from detectors, modulators, sensors, and improved light sources to photovoltaics.

Figure 25.

Monolayer MoS₂-bowtie resonator array and associated optical properties. (a) Schematic of device indicating parameters of bowtie array: metal thickness (h), gap separation (g), triangle size (s), and pitch of unit cell (p = (p_x, p_y)). (b) Photoluminescence spectra of bare MoS₂, bowtie array and bowtie-MoS₂. Reproduced and adapted with permission from ref (229). Copyright 2015 American Chemical Society.

8.4. Section Summary

Despite the fact that the application of SLRs for flat optics is still in its infancy, the interaction of SLRs and 2D materials may be useful to

• 1.Provide a new way to control 2D material chemistry.
• 2.Realize broadband optical modulators.
• 3.Strongly modify emission of light from 2D materials.

9. Miscellaneous: Applications of SLRs in Biosensing/Biorecognition, Photovoltaics, Photocatalysis, etc.

Here we briefly consider other possible applications of SLRs in science and technology.

9.1. Biosensing and Biorecognition

Label-free optical biosensing involves monitoring the effect of changes in refractive index that occur near a surface when biological molecules of interest are bound to that surface. The refractive index (RI) of most biological molecules, n_bio, is usually larger than that of water; n_bio ∼ 1.45–1.55, compared to n_water = 1.33. Consequently, when molecules bind to a surface, the local refractive index rises. Surface optical phenomena, such as surface plasmons (both propagating and localized), are sensitive to this local refractive index, and their properties, e.g. spectral position of resonance, change.²³¹ Central to the success of this approach is the use of a layer of biorecognition molecules on the sensor surface. The idea is that the biorecognition molecules only allow the analyte molecules of interest to bind, thus providing the specificity of the sensor. A successful sensor requires specificity (through appropriate biochemistry) and sensitivity; it is sensitivity that plasmonic techniques offer (we note that there are many other approaches, see e.g. ref (232) for a review). Any biological binding event of target analyte from the solution with its associated receptor (immobilized on the surface) is accompanied by a change of RI of a thin near-surface layer; typically this layer is between a few nm and a few tens of nm. This approach conveniently avoids the use of labels, convenient because labels often reduce the activity of target molecules by occluding the binding site. In addition, in optical transduction one can follow biomolecular interactions in real time and thus obtain information on kinetic constants of reactions, which is hardly possible with labeling methods.²³²

Biological sensing based on the transition from LSPRs to SLRs was studied in arrays of gold nanoantennas covered by an ultrathin silicon layer by Gutha et al.²³³ They showed that SLRs may lead to very high sensitivities to small changes of refractive index; they did this by detecting biomonolayers and streptavidin-conjugated semiconducting quantum dots. Sadeghi et al.²³⁴ investigated the application of SLRs of arrays of large metal nanodisks to chemical and biological sensing. They demonstrated that narrow SLRs could be shifted from the visible (∼650 nm) through to the infrared (∼900 nm) range by altering the environment’s refractive index. Gutha et al.²³⁵ confirmed that 2D arrays of large gold metallic nanodisks may have a greater sensitivity to changes in the superstrate’s refractive index in the near IR region. The authors tuned the SLRs modes, using ultrathin layers of silicon, in the range from 1 to 1.7 μm and achieved a reasonably high refractive index sensitivity of ∼795 nm/RIU. Lee et al.²³⁶ studied the optical properties of a 1D chain of silver capped nanoslits under oblique illumination and compared the sensing performance of these structures for a range of plasmonic modes, including SLRs. They detected the reaction involving bovine serum albumin and anti-bovine serum albumin, and they obtained a lower detectable limit of 1 ng/mL (0.14 pg/mm²), comparable with that of the standard SPR technique.

9.2. Propagating Surface Plasmons

Surface plasmon resonance techniques are at the heart of existing label-free optical sensing technology, offering superior sensitivity due to the enhanced electric field.²³⁷ The rapid and widespread progress of SPR technology over the past few years has been assisted by the development of many affinity models and the establishment of many preparation protocols for gold surfaces. However, SPR biosensors could still benefit from improved sensitivity in the detection of small analytes (typically less than 500 Da). Localized plasmon resonances of metallic nanostructures seem better suited and bring added functionalities, for example spectral tunability; however, these resonances have nearly an order of magnitude lower sensitivity. In addition, LSPR are typically spectral very broad,³⁷ which makes it difficult to achieve sensitive control of their position and thus limits the precision of sensing measurements. It is natural to consider using SLRs to reduce the line width of the resonances and thereby see if they can be used to improve the sensitivity.

9.3. SLR vs SPR

The involvement of SLRs enables one to make significant advances to state-of-the-art biosensing technology using plasmonics, although sensing tasks require the adaptation of SLR excitation geometries for the operation in an essentially asymmetric (w.r.t. refractive index) environment when metal nanoparticles are located at a substrate/water or substrate/air interface. In general, geometries enabling the excitation of SLRs that make use of out-of-plane dipole moments are well suited for these tasks.^78,119 Under these conditions, the characteristics of SLRs are almost independent of the asymmetry of the environment,⁷⁸ while SLRs can be efficiently excited even under the attenuated total reflection geometry in which light does not propagate through the sample liquid/air medium (important if the effect of bulk refractive index on the desired signal is to be avoided).¹⁰⁴ Danilov et al.²³⁸ compared the conditions for excitation of SLRs involving array Au nanoparticles (size ∼100–200 nm, period 320 nm) supported on glass substrates, both in the direct and in the attenuated total reflection (ATR) geometries, and they assessed their performance relevant for biosensing. They showed that the spectral sensitivities to modes located predominantly in liquid medium were dictated by the period of the lattice in both direct and ATR geometries (∼320 nm per RIU change), while the substrate mode demonstrated, as expected, a much lower sensitivity. They also demonstrated that the phase sensitivity does not depend on the periodicity of the structure and may exceed 10⁵ degrees of phase shift per RIU change, thereby outperforming the relevant parameter for all other plasmonic sensing approaches.

The oblique incidence arrangement is rather complicated in terms of experimental setup when compared with the simple transmission geometry.⁷⁹ Therefore, significant efforts have been applied to enable the excitation of SLRs under normal incidence illumination while still employing an asymmetric environment. Partial success in narrowing the resonances for a water/substrate interface was achieved through control of the shape and size of suitable nanostructures.^80,123,124 More recently, Thackray et al.¹¹⁶ demonstrated efficient excitation of very narrow SLRs, down to a width of several nm fwhm under normal incidence, via the employment of a specially designed array of Au nanocubes (area 200 nm x 200 nm, height 200 nm). Compatibility with standard microscope systems is important since it removes the need for specialist optics, making the technique much more accessible for bio- and chemical sensing.

9.4. Figure of Merit and Sensitivity

The reduced spectral width of SLRs helps to improve the precision of biosensing tests using plasmonic nanostructures. To take account of the sharp nature of the resonance and thus examine the effectiveness of a system to sensitively measure small wavelength changes, one normally uses a characteristic “Figure of Merit” (FOM) parameter:²³⁹ FOM = (Δλ/Δn)(1/Δω), where Δω is the full-width of the resonance (e.g., reflectivity) at half-maximum and Δλ is the resonance wavelength shift for a Δn change in refractive-index. The wavelength shift of an LSP peak with the refractive index of the surrounding medium is nearly linear so that the refractive index sensitivity, S, associated with a particular type of nanoparticle is usually stated in nanometers of peak shift per refractive index unit (nm/RIU): S = dλ_R/dn. The spectral sensitivities of LSPR and SLR features are typically of order 100–450 nm/RIU.^37,238

The sensitivity S is usually normalized to give the FOM by dividing by the fwhm of the resonance dip (a sharper peak gives a more precise indication of the resonance minimum position).^240,241 This FOM adequately quantifies the sensing potential of plasmonic modes in configurations similar to those used in commercial instruments, where the angular shift of the resonance angle of incidence is changing quickly with angle and is used to detect changes in the refractive index at the surface. It should be noted that SLRs do not exactly fit the Lorentzian profile, which complicates the measurement of the width of the SLR. Recently an alternative figure of merit was suggested by Becker et al.,²⁴² termed FOM*, as another metric for comparison of the sensing capabilities of different nanostructures. Complex plasmonic nanostructures often do not have a simple, single line shape so that FOM* is defined instead in terms of the relative change in intensity dI/I at a given wavelength λ that results from a small change dn in the local refractive index, thereby avoiding the line-width. This approach allows sensors based on changes in intensity to be compared with those making use of peak shifts. For the latter (peak shift) type, FOM* can be written in terms of the refractive index sensitivity S as FOM* = [S dI/dλ)/I]_max = [(dI/dn)/I]_max. Note that FOM* is based on the wavelength that yields the greatest intensity change with refractive index.

It is known that typical FOMs and FOM*s do not exceed 8 and 23, respectively, for the sensors based on LSP^37,243 and PSP,²⁴⁴ respectively. The employment of SLRs enables one to increase these parameters up to a factor of 100 or more. Offermans et al.²⁴⁰ showed that SLRs in ordered arrays of gold NPs provide a sensing performance more than an order of magnitude better than the LSPRs associated with disordered particle arrays. They found that the FOM scales similarly for Au, Ag, and Cu particles because the losses (Ohmic) in these metals are all small. They used calculations based on arrays of coupled dipoles to reproduce this universal scaling and further explained their results on the basis of a simple coupled oscillator model.²⁴⁰ Later studies^245,246 experimentally demonstrated a high-performance refractive index sensor using a double-layered metal grating (DMG) having FOM and FOM* values reaching 38 and 40, respectively, for normal illumination. These high FOM and FOM* values arise because of the sharp SLRs associated with coherent interference between the LSP of each gold stripe and the diffracted light. It is important for sensing that such a hybrid guided mode confines a large proportion of the optical field between the upper and lower gold structures, leading to remarkably narrow line widths. These authors additionally noted^245,246 that DMGs may be made using a cost-effective and simple approach employing a combination of thin-film metal deposition and two-beam optical interference lithography. In general, the employment of SLRs makes possible a very significant enhancement in both FOM and FOM* for plasmonic biosensing. As an example, Thackray et al.¹¹⁶ reported FOM*s up to 120 under normal incidence of illuminating light together with the analysis of resonant features in the transmitted light.

9.5. Lower Limit of Detection

Surface lattice resonances may lead to substantial improvements in the lower limit of detection (LOD) for plasmonic biosensors. However, to record these LOD one must pass from spectral to phase sensitivity. As noted above in section 6, spectral and phase sensitivities do not correlate with each other as they have different origins. For SLR the spectral sensitivity is conditioned by diffraction phenomena and is typically similar to the period of the array Δλ/Δn ∼ d (200–450 nm/RIU), while the phase sensitivity may reach 5 × 10⁵ deg of phase shift per RIU,¹⁰⁴ due to very low reflectivity on resonance.³⁹ To assess the applicability of phase-sensitive SLRs for biosensing, Kravets et al.³⁹ used a calibrated and established protocol that employs the streptavidin–biotin system.²⁴⁷ Functionalization of the surface of a plasmonic (nanodot) structure with carboxylate groups was carried out, and biotin was then attached to the resulting carboxylate binding sites. Lastly, the biotin-covered nanodots were exposed to 10 pM of streptavidin (SA) solution in 10 mM phosphate-buffered saline for a period of 3 h; this led to SA being bound to all the biotin sites. The binding of SA altered the phase of the reflected light by ∼25° (at 710 nm) and incident at 53°. This phase change corresponds to 20–100 SA molecules being bound to each nanodot, so that the experimental LOD is just 1–4 molecules per nanodot. For a thermally stabilized system the resolution of phase measurements can exceed 5 × 10^–3 deg;¹⁵ thus, in principle one might resolve the attachment of 0.004–0.02 SA molecules per nanodot or resolve <1 molecule being bound to each square micron of device, with the total number of molecules detected in the illuminated area being ∼2000.³⁹ This detection limit was 100–1000× better than achieved before using conventional plasmonic nanosensors where optical intensity rather than phase is monitored³⁷ and nearly 100× lower than for the PSP approach.¹⁷⁻¹⁹

Finally, SLRs open up access for novel and promising nanoarchitectures for biosensing. As an example, Yanik et al.²⁴⁸ proposed an interesting architecture based on combining a very dispersive Fano resonance with dark (subradiant) modes; they employed a hole rather than a particle array (see section 7). The observed resonances were due to incident light coupling to the subradiant multipolar modes. Naked eye detection of just one monolayer of antibodies (mouse IgG antibody) was reported. The lift-off free fabrication approach adopted by Yanik et al.²⁴⁸ allows the frequency regime to be easily tuned by varying the structural parameters of the array. Arrays of rectangular metallic antennas suitable for THz SLRs have also been suggested for a sensor-on-chip approach to liquid sensing,²⁴⁹ Such arrays could perhaps be combined with a microfluidic system for in situ sensing.

9.6. Metallic Photonic Crystals for Biosensing

Arrays of nanoparticles can also be combined with dielectric cavities to form metallic photonic (plasmonic) crystals (MPCs).^{213,250−253} Different optical sensors based on MPC waveguides were reported to offer a sensitive test for biomolecular interactions, potentially providing a practical approach for label-free detection of specific bioreactions. The improvement in sensitivity was due to coupling of the waveguide resonance mode and SLR.^{213,250−253} Giessen et al.²⁵⁰ proposed a design of MPCs and explained its operation by a waveguide-mediated collective interaction process between light and gold NPs. This approach offers a compact design when compared with conventional devices based on arrays of NPs.³⁷ The concept of such sensors is based on the combination of a photonic microcavity and nanostructures supporting SLRs; for example, metal nanorods placed appropriately above a metal mirror form a microcavity. The combination is thus a coupled photonic-plasmonic system.²⁵³ MPCs combined with waveguides have been demonstrated to enable efficient and sensitive detection of the HIV-1 virus.²⁵⁴ A hybrid waveguide–plasmon system consisting of a waveguide layer of ZrO₂ upon which was placed gold nanopillar arrays was also proposed.^214,215 The momentum coupling between the PSPs and the waveguide modes comes from the periodic arrangement of the metallic nanoparticles. On passing from normal incidence to oblique incidence measurements, an increase in the FOM of up to 5 times was achieved. New architectures based on nanocavity perfect absorbers were proposed, which may also be integrated in biosensors to increase their FOM.^255,256 In these works, metal–insulator–metal (MIM) nanocavity arrays demonstrated good performance, with a sensitivity to bulk refractive index changes equal to 300–400 nm/RIU at the near IR wavelengths.

9.7. SLRs and Spectroscopy

Another promising approach for biosensing brings together the combination of SLRs and spectroscopic techniques. In particular, an approach based on the SLRs of metallic nanoantenna arrays was proposed for the direct detection of vibrational signatures using infrared absorption spectroscopy of a single protein monolayer.^248,257 Here the vibrational spectra from proteins were investigated at low concentration (zeptomole) and for sensitivities amounting to <155 molecules per antenna. The plasmonic (near-field) character of the absorption enhancement was shown using a ramped increase in protein film thicknesses,²⁵⁷ and ultrasensitive collectively enhanced IR absorption (CEIRA) spectroscopy was employed to identify the vibrational signature of protein monolayers (silk fibroin). Figure 26(c) shows that the protein absorption bands were resolved in spectra collected from the protein coated arrays (period 1.6 μm). Minima in the reflectivity are associated with the plasmonic response, and absorption due to the presence of amide II and I are indicated in Figure 26(c) at 1,537 and 1,660 cm^–1, respectively; the protein layer also produced a slight red-shift of the plasmonic resonance.

Figure 26.

(a) Atomic force microscope measurement of silk film thickness, for a 4 nm thick film. (b) Protein backbone vibrational modes associated with Amide-I and II. (c) Reflectance spectra from the 1.6 μm periodic array before (dashed line) and after (solid line) coating with a 2 nm film of protein. Vertical lines (dashed) mark the positions of the amide-I and II peak absorptions. (d) Spectral characteristics of the arrays before and after protein coating, recorded as difference reflection spectra. Reproduced and adapted with permission from ref (257). Copyright 2009 National Academy of Sciences.

An ultrahigh FOM refractive index sensor based on a near-infrared narrow-band plasmonic absorber was designed and analyzed in ref (258). The system featured a good signal-to-noise ratio (>250) together with a useful range of refractive indices; it also had a quality factor >110 and a wavelength tunability from 800 nm to 1,500 nm. The design featured arrays of gold bowtie nanoantennas with a metal–insulator–metal (MIM) configuration. Such nanoantennas might be of use in a range of applications, including reflective filtering, label-free biochemical detection, optical trapping, heat-assisted magnetic recording, and hot-electron generation.

Recently it was shown that a chemical analysis of living cells may be undertaken using out-of-plane plasmonic antennas.²⁵⁹ The good adhesion between antennas and biological cells enables sensitive SERS analysis of cell membrane components in a biocompatible system. SERS Raman spectra from living cells were obtained with a near-IR laser source at very low pump intensities. Spectra were obtained showing an enhancement of the amplitude of the incident field of approximately 45 times.

9.8. SLRs and Solar Cells

Plasmonics offers a novel means to improve the efficiency of solar cells,^41,260−266 especially through increased absorption of incident sunlight.²⁵² In particular, enhanced coupling of light from the sun into the active region of a semiconductor solar cell can be achieved via guiding and localization light at the nanoscale using plasmonic nanoparticles covering such structures. Out-of-plane lattice plasmons have been proposed as a way to bring together the advantage of LSPRs in individual nanoparticles (high field-confinement) and the advantage of PSPs on continuous metal films (tunability of dispersion) in 2D metal–insulator (MI) and metal–insulator–metal (MIM) structures;^262−264 such architectures may also offer potential for chemical and biological sensing, photocatalysis, surface enhanced spectroscopies, and photovoltaics. Moreover, plasmonic crystals composed of materials with more than one functionality, e.g. Ag, Au, Pt, Pd, and metal/dielectric stacks, have been demonstrated¹⁹⁹ that may be useful for practical photonic applications.

Zhukovsky et al.²⁶⁵ demonstrated the SLRs could enhance and control photoelectron emission in solar cells and Schottky barrier photodetectors when plasmonic nanoparticle arrays are included. They showed that the interaction between broad-band LSPs and narrow-band SLRs leads to a stronger local field enhancement. A notable increase in the photocurrent when compared with the excitation of individual particles was found. These findings may be used to help design photodetectors having a tunable spectral response and may detect photons whose energy is below the bandgap of the semiconductor and to develop solar cells with improved efficiency.²⁶⁵ Crystalline Si nanopillar arrays on a Si substrate have huge potential in surface enhanced spectroscopy and thin film solar cells.²⁶⁷ These SLR resonances are due to coherent oscillations in the nanopillars and can be tuned spectrally via the nanopillar diameter and lattice period; they strongly suppress reflection from the Si surface. Further, the reduced reflectivity is accompanied by an increased electromagnetic field in the Si. The physical nature of the SLRs suggests that not only does more electromagnetic energy becomes available for harvesting due to the suppressed scattering losses, but it is also efficiently confined in a thin layer of the solar cell. It is worth noting that SLRs in a Si array system rely on localized Mie resonances rather than plasmon modes.²⁶⁷

Using a metal–dielectric composite “black-body” composed of a properly selected mixture of nanostructured plasmonic and dielectric films, one can ensure that impedances are matched and that substantial absorption of light over a wide optical frequency range is achieved.^260,261,266 In this case, the fact that the light interacts with metal only within the skin depth looks promising, since only the electronic surface states of semiconductors contribute to solar cell performance. In such blackbody nanostructures, plasmonic nanoparticles embedded in a dielectric matrix effectively enhance the optical path length for incident light by a factor of ∼50 due to the scattering of light by nanoparticles and subsequent total internal reflection. Recent investigations showed that the optical path enhancement can break the limit for Lambertian surfaces due to the plasmonic trapping in structures inspired by the human eye retina.²⁶⁶

9.9. SLRs and Photocatalysis

The use of plasmonic structures to enable efficient combination of light-harvesting and catalytic functions in one material is another distinctive feature of plasmonic nanostructures, one that renders possible relatively high photocatalytic reaction rates. Detailed descriptions of a wide range of photochemical reactions enhanced by surface plasmons can be found in the review by Ueno and Misawa.²⁶⁸ The review summarized recent results on the application of plasmonic nanostructures for the development of novel photochemical schemes, including photocatalysis, nanolithography, water-splitting systems, and photovoltaic cells. In these systems, the plasmon-enhanced electric field plays a crucial role in both excitation and photochemical reaction (e.g., photoinduced electron transfer reaction) processes.²⁶⁸ In the near future we hope to find out whether a useful reduction of carbon dioxide via photocatalytic reaction using near-infrared light is possible in this way.

The addition of metallic nanoparticles is now a widely adopted approach to boost the phocatalytic performance of semiconducting photoanodes.^{258,268−271} Regular arrays of metallic nanoparticles located on the surface of the semiconductor capture electrons produced by photoexcitation, thereby increasing the electron–hole pair separation. It is hoped that the use of plasmonic nanostructures to confine sunlight in small volumes will be an important element that promotes their use in the design of complex solar fuel photocatalysts.²⁷² By altering the shape and size of plasmonic nanostructures, the absorption band of composite photocatalysts may be extended into regions that are not accessible for standard semiconductors.^269,270 As an example, by adjusting the size of gold nanospheres (30–100 nm) fabricated on arrays of TiO₂ nanowires, the absorption of photocatalysts in the spectral region 300 to 800 nm may be enhanced, leading to increased incident photon-to-electron conversion efficiencies (IPCE).²⁷³ Plasmon-assisted water splitting was also verified by using gold nanorods (220 nm × 110 nm × 40 nm) arrayed on the surface of a single crystal photoanode.²⁷⁴ The geometric arrangement of plasmonic nanostructures exerts a measurable influence on plasmonic photocatalysts. Lin et al.²⁵⁸ designed Au@SiO₂@CuO₂ core–shell nanostructures with the aim of enhancing broadband solar absorption. In such nanostructures, the Au core converts the incident light into LSPRs and then acts to transfer this energy to the semiconducting shell (CuO₂) via a process of resonant energy transfer, thereby inducing charge separation in the semiconductor. The dipole–dipole interaction between the semiconductor CuO₂ charge displacements and the Au plasmons enhances the photovoltaic activity when compared with the semiconductor alone. The Au core also leads to strong near-field enhancement, thus helping to increase the optical absorption efficiency. For the core–shell nanostructure based on the metal–semiconductor combination, the thickness of semiconductor shell should be carefully tuned because it significantly alters the LSPR characteristics of photocatalysts.²⁵⁸ Other studies^271,273 also confirm that hybrid metal–dielectric nanostructures may help to enhance charge separation in a semiconductor and improve the operation of photovoltaic and photocatalytic devices.

The authors of ref (275) demonstrated that a combination of near- and far-field coupling of LSPRs associated with nanoparticles of aluminum deposited on titania (TiO₂) films significantly enhances (by 2 orders of magnitude) the photocatalytic activity under visible light illumination of the semiconductor material. The excitations of SLRs result in enhanced rates of production of hot-electrons and thus lead to higher redox reaction rates. Further, the authors of ref (276) show a correlation between photocatalytic activity and waveguide-plasmon polariton excitation in Al nanowire gratings produced on thin TiO₂ films. It was suggested that this may be due to hot-electron injection from aluminum nanowires into TiO₂, a process that is strengthened because of the increased absorption of visible light and a decreased radiative damping associated with the waveguide-plasmon polaritons.

Recent work from Linic’s group^277,278 demonstrates advances in photochemical catalysis on nanostructures of plasmonic metals. These authors pointed out that when optically excited the plasmonic modes of metallic nanoparticles may promote chemical reactions directly on their surfaces. Furthermore, it was shown²⁷⁷ that the process of charge transfer from plasmonic nanoparticles to photocatalytic materials causes specific and direct excitation of electrons from occupied to unoccupied orbitals of the molecule–nanoparticle complex. These findings indicate that the role of the local electronic structure in plasmonic photocatalysis is to a degree decoupled from the role of LSPRs and that plasmonic nanomaterials may be tuned so that when illuminated, selective enhancement of particular chemical pathways occurs. The work of Linic’s group^277,278 demonstrates ways to engineer plasmonic nanomaterials having resonance wavelengths that correspond to the charge excitation energies of photocatalytic structures. Perhaps plasmonic catalysts that selectively activate targeted chemical bonds could be produced, thereby opening several opportunities in the area of selective chemical synthesis.

9.10. SLRs and Electrochemistry

Frank et al.²⁷⁹ presented a nanostructure based on double-layered NP stacks suitable for spectra-electrochemical applications. Their structure was based on a continuous gold layer upon which periodic arrays of tantalum pentoxide (Ta₂O₅) nanodisks were formed. On top of these dielectric discs, a further disc of gold was added. To demonstrate the applicability of this structure for electrochemical analysis, potassium ferricyanide was used as a standard redox compound and cyclic voltammetry (CV) measurements undertaken. This area is largely unexplored and would benefit from further investigation.

9.11. SLRs and Magneto-Optics

SLRs may also be used to enhance magnetic effects by (i) directly using magnetic materials and (ii) indirectly using nanometamaterials structures that exhibit magnetic dipole moments. Adopting the first of these approaches, Kataja et al. studied arrays of magnetic nanoparticles with a view to enhancing magneto-optical (MO) responses and so use magnetic fields to control plasmonic systems and to tune the MO properties of individual nanostructures.²⁸⁰ In a combined experimental and theoretical investigation, they found that rectangular magnetic nanoparticle arrays exhibit SLR modes and that the two lattice directions were coupled by spin–orbit coupling in nanoparticles that may be controlled via the magnetic field. The authors investigated the interplay between the single-particle optical and magneto-optical response of magnetic nickel (Ni) particles on the one hand and their periodic arrangement on the other. Rectangular arrays of Ni particles displayed SLRs, and this produced a strong and spectrally narrow MO response. The polar Kerr effect and Kerr rotation were enhanced, at a specific wavelength, 4- and 3-fold, respectively, when compared with a system of randomly oriented particles.

To enhance the MO response, Sachan et al.²⁸¹ looked at a novel way to boost the strength of the response of individual nanoparticles by combining two materials, one plasmonic (metallic) and the other ferromagnetic, to make individual nanostructures: they called the resulting resonance a “ferroplasmon”. Hybridized resonances associated with these heterodimers, formed by noble metal nanoparticles and ferromagnetic metal nanoparticles, were also discussed in ref (281 and 282). The authors reported^281,282 the excitation of sharp resonance modes in materials with nonexistent/highly damped surface plasmon modes. Here, the hybridization of the Ag plasmonic mode at 2.89 eV with a strongly damped plasmon mode of Co located at 3.74 eV generated a lower energy LSPR mode at 2.2 eV, as soon as the nanospheres approach each other at close distances and another one at 2.89 eV with almost identical energy to that one of the isolated Ag plasmon mode (Figure 27). The near-field enhancement generated in the gap between the spheres, determined at each of the peak energies, was ∼30 times bigger than the enhancement produced using isolated Ag spheres excited at the lower (2.2 eV) energy modes, and 10 times bigger than the enhancement at the higher (2.89 eV) energy modes (Figure 27).

Figure 27.

(a) Comparison between the extinction spectra of a single 60 nm diameter spherical Ag NP (orange line), a 60 nm spherical Co NP (blue line), and the extinction spectra of a dimer (green line) formed by the interaction of these two NPs separated by a 1 nm gap as illustrated in the schematic below. The dimer exhibits two peaks, one at 2.20 and the other at 2.89 eV; the first is at a much lower energy than the peaks associated with the isolated Co NP and Ag NP, and the second is also lower in energy than the Co NP but at almost the same energy of the isolated Ag NP. (b) Electromagnetic field enhancement (E/E₀) distribution around the nanoparticle dimer at the two peak energies produced by the interaction of a plasmonic NP and a nonoplasmonic ferromagnetic Co NP shown in panel A. The insets in the figure show higher resolution views of the field enhancement around the NP dimer marked by the squares. Figure reproduced with permission from ref (282). Copyright 2014 American Chemical Society.

It would be interesting to see how arrays of these ferroplasmonic heterodimers behave in terms of the SLRs they support. We anticipate that high quality arrays of ordered nanoparticle structures with magnetic and plasmonic composition would allow one to create new composite plasmonic nanomaterials with extremely promising magnetic functionalities. From the technological point of view, one could envision several potential applications employing such magnetic metamaterials, and one of these applications is in the field of magnetic data storage. Current hard disk devices (HDDs) with capacities of several terabits of information have data storage cells with dimensions of around 100 nm × 100 nm. The reduction of grain sizes of magnetic materials to minimize the bit cell size could increase the capacities of current HDDs; a problem, however, is that storage for materials with grains below a certain size becomes unstable, while their magnetization may undergo arbitrary changes due to thermal effects.²⁸³ The combination of plasmon-induced heating by light with ferromagnetic Co nanoislands (heat-assisted magnetic recording) enables one to overcome limitations imposed by the grain size. As an example, Stipe et al.²⁸⁴ developed a recording device having a data density of 1.5 Pb m^–2 by employing an integrated plasmonic antenna. It is expected that the reports of ferroplasmons^281,282 will inspire future work in this direction.

Arrays of elliptical nickel nanoantennas were studied by Maccaferri et al.²⁸⁵ They showed that the diffractive coupling in these arrays is dictated by two orthogonal and spectrally detuned in-plane plasmonic responses of the individual elements, one directly induced by the incident light, the other produced through an external magnetic field being applied. This led to highly tunable and enhanced magneto-optical effects when compared with a continuous Ni film or compared with surfaces made from disordered noninteracting anisotropic magnetoplasmonic antennas. In another very interesting approach, Kataja et al.²⁸⁶ recently investigated the magneto-optical and optical response of Au and Ni nanoparticles organized in a checker board configuration. Analysis of the optical fields indicate that both the Au and Ni nanoparticles contribute to SLRs and thus to the magneto-optical activity of these hybrid arrays, the approach may thus lead to new possibilities for the realization of tunable and sensitive magneto-plasmonic nanostructures. In addition, it was shown that both the magneto-optical and the optical response of the hybrid arrays could be adjusted by altering the size of the gold (nonmagnetic) nanoparticles. The concepts presented in refs (171) and (285) show that novel magnetoplasmonic designs may lead to a variety of attractive effects based on SLRs including magnetic tunability of light polarization and label-free sensing.²⁸⁷

We mentioned at the beginning of this section that there is an alternative approach to achieving magnetic effects, that is employing metamaterials; such an approach was investigated by Tang et al.²⁸⁸ They used pairs of magnetic rods as the elements in their arrays. Such particles are known to exhibit magnetic effects owing to the displacement currents they support.¹²⁹ Tang et al. suggested a way to enhance the magnetic fields at optical frequencies by using diffractive coupling of magnetic surface plasmon resonances in 2D periodic arrays of paired metal rods, a kind of metamaterial. The authors predicted narrow-band hybrid plasmon/magnetic modes that occur because of the strong interaction between magnetic resonances and the collective surface lattice resonances of the array. Magnetic fields in the pairs of metal rods were 5-fold greater than the relevant fields of isolated individual pairs of metal rods. This strong magnetic field enhancement indicates there is much potential for metamaterials; indeed, Tang et al. suggested that it may be possible to enhance the second-harmonic generation using magnetic nonlinearities.²⁸⁸

9.12. SLRs and Liquid Crystals

Another promising external field modulation can be provided using liquid crystals (LCs) in combination with plasmonic nanoarrays. Li et al.²⁸⁹ proposed devices consisting of a 1D periodic Au nanoparticle array immersed in an aligned nematic LC cell. In such a cell, the spectral position of SLR may be controlled through the application of a voltage so as to change the relative orientation between the optical axis of the LC and the incident light. The spectral tunability was proportional to the index difference Δn = n_e – n_o of the LC and the interparticle distance, which was as large as 100 nm. It was shown that the resonance could shift by as high as 100 nm, leading to high sensitivity when the system is used for sensing or switching operations. An electrically tunable if rather complex plasmonic crystal with a nematic LC layer on its surface was reported in ref (290). The associated coupled surface lattice mode has its electric field mostly normal to the surface, making the coupled resonance sensitive to molecular reorientation of the LC. It was shown that the SLRs could be red-shifted by 8 nm with an associated 35% change in the relative transmission light intensity through the application of external voltages to the LC layer, thereby producing an SLR-LC optical modulator.

9.13. Other Applications

Liu et al.²⁷² demonstrated that a pair of orthogonal electric dipolar and optically induced magnetic dipolar resonances can be excited in arrays of various configurations of metal-core/dielectric-shell NPs. These two resonant modes can interfere simultaneously with SLRs of the periodic array via diffractive coupling, opening new opportunities for near-field manipulations, which may find applications in nonlinear switching in plasmonic nanostructures and metamaterials. Collective effects in arrays of meta-molecules based on plasmonic double antennas were also studied.²⁹¹ Collective behavior in this structure was observed through experiment and found to differ substantially from that observed using single-antenna counterparts. These results indicate that plasmonic metamaterials that exhibit collective effects are very sensitive to the topology and design of the meta-molecules they comprise and perhaps offer the prospect new approaches to the design of metamaterials with engineered optical properties. Dense packing of arrays of plasmonic nanodots is a very important factor for building metamaterials not only in the visible but also in the IR and terahertz regions. Singh et al.²⁹² concluded that there is an optimal packaging density in metamaterials to induce the strongest dispersion. Adjusting the period involved enables the design of frequency selective surfaces that have an adjustable Q factor and may lead to the development of terahertz devices and components having a tunable refractive index of the substrate.²⁹²

Yang et al.²⁹³ realized SLRs in the terahertz range using a metamaterial that comprised two particular split-ring resonators that supported extremely sharp trapped-modes. Their unit cell structure dramatically reduced the radiative damping and improved the resonance quality. New designs of metamaterials for the terahertz region based on arrays of split ring resonators were suggested by Manjappa et al.²⁹⁴ where a lattice-induced transparency has been observed and explained through coupling of the first-order lattice mode to a structural resonance. Banon et al.²⁹⁵ developed a method of calculating the angle-resolved spectroscopic Mueller matrix describing SLRs of two-dimensional plasmonic photonic crystals. Their method could be inverted to extract geometrical parameters of a rectangular array (for a known geometrical shape of nanoparticles) from experimentally measured ellipsometry data. Wang et al.²⁹⁶ also made use of Mueller matrix spectra to investigate complex anisotropic optical nanostructures in the presence of SLRs. They suggested that Mueller matrix spectroscopic ellipsometry is ideal for fast, noninvasive, and precise metrology of all plasmonic modes existing in plasmonic metasurfaces. Yang et al.⁴⁵ have demonstrated programmable engineering of ultranarrow resonances across the visible regime. They made arrays of aluminum nanoparticles immersed in an elastomeric slab that showed high-quality SLRs features with line widths down to 3 nm. Such elastomeric slabs allow dynamic modulation of interparticle spacing, allowing selective access to and optimization of either dipolar or quadrupolar lattice modes. This offers a new approach for real-time tunable materials, of interest for biosensing, fluorescence enhancement, photocatalysis, and plasmonic nanolasers.

9.14. Section Summary

SLRs provide a generic platform for research in a number of topical areas of science and technology.

10. General Summary

To summarize, metal nanoparticles arranged in ordered 1D or 2D arrays can produce remarkably narrow plasmon resonances down to 1–2 nm in spectral width due to diffractive coupling of the localized plasmon resonances associated with individual nanoparticles. These coupled resonances can be understood reasonably well within the framework of the coupled dipole approximation (modified if necessary). SLRs manifest themselves in reflection, transmission, extinction, and absorption with as little as 50 particles required to achieve narrowing of the plasmonic resonances. Positional disorder in the array suppresses SLRs while particle size disorder makes them wider. SLRs are an important consequence of the interaction of nanoparticle arrays with light: they were observed for various array geometries and various shapes and forms of the nanoparticles. In general, diffraction edge phenomena accompany the formation of SLRs. An homogeneous (symmetric) refractive index environment is helpful but not necessary for the observation of SLRs; indeed, SLRs have been observed in asymmetric environments for oblique light incidence and/or relatively large nanoparticles (where out-of-plane modes could be important). The longer the SLR wavelength, then the higher the resonance quality that may be achieved, with quality factors reaching 300 in the near-infrared and 500 in the mid-infrared. One of the many useful properties of SLRs is the fact that they can provide topologically protected zero refection of light with improved phase sensitivity to binding events. At the same time, the directional properties of SLRs combined with spectral selectivity could provide a platform to enhance the directional emission of light and to control LEDs and lasers. In addition, SLRs present a natural way to couple light to 2D materials and heterostructures which is an active and exciting area of research.

The success story for surface lattice resonances comes from an intriguing redistribution of the electromagnetic field associated with an incident wave through the use of diffractive coupling from ordered plasmonic arrays in such a way that the field is concentrated near the plane of the array. This leads to a range of characteristic properties for SLRs: stronger field enhancement as compared to LSPR, ultranarrow widths of plasmon resonances, strong light extinction at SLR, and the absence of reflection under some conditions. From the many applications discussed above it is clear that plasmonic arrays supporting SLRs strongly enhance light–matter interaction in 2D. By coupling surface lattice modes with various types of molecules and media, one can achieve ultrasensitive biodetection, improved photovoltaic cells, new optoelectronic and communication devices, more efficient photocatalysis, enhanced magneto-optical signals, advanced liquid crystal devices, and new metamaterials. This list is growing quickly, with new applications of SLRs emerging to tackle various scientific and technological problems.

Biographies

Vasyl G. Kravets received his Ph.D. degree in physics (1990) from Taras Shevchenko University, Kiev, Ukraine. He worked in the Institute for Information Recording, Kiev, as a postdoctoral research scientist and later as a postdoctoral research fellow, University of York, UK, and an invited research scientist, University of Duisburg, Germany. He is currently a research associate in the plasmonic group of Professor A. Grigorenko in School of Physics and Astronomy, the University of Manchester, UK. His current research interest focuses on development of hybrid plasmonic-two-dimensional graphene (semiconductor) nanostructures and their applications in bio- and medical sensing and plasmonically coupled optoelectronic devices and the solar photovoltaics field.

Andrei V. Kabashin is a specialist in optical biosensing/imaging and laser-ablative synthesis of nanomaterials for biomedical applications. He obtained his Ph.D. degree in 1994 from A.M. Prokhorov General Physics Institute, Moscow, Russia. From 1999 to 2008 he worked as a Research Professor in Ecole Polytechnique de Montreal at the University of Montreal, Canada. Since 2009 he has held a Research Director position of the French National Center of Scientific Research (CNRS) in Aix-Marseille Univ, Marseille, France. He is also a scientific supervisor of Institute of Engineering Physics for Biomedicine and of International Laboratory “Bionanophotonics” in MEPHI, Moscow, Russia, as well as holding faculty positions in the Institute of Lasers, Photonics and Biophotonics in State University of New York at Buffalo (USA) and the University of Sherbrooke (Canada).

Bill Barnes is Professor of Photonics at the Department of Physics and Astronomy at the University of Exeter, UK. He leads a research group that is now focused on light–matter interactions, especially those involving molecular materials. He was awarded B.Sc. (1983) and Ph.D. (1987) degrees by the University of Exeter before spending several years as a postdoc at the University of Southampton, UK, working on optical fiber lasers and amplifiers. He is fortunate to currently hold a European Research Council Advanced Investigator Award (AdG-photmat-742222).

Alexander Grigorenko is Professor of Physics at the School of Physics and Astronomy at the University of Manchester, UK. He leads a nano-optics lab which studies light–matter interactions at the nanoscale. He was awarded MPhys (1986) and Ph.D. (1989) degrees by the Moscow Institute of Physics and Technology. Before Manchester, he worked as a senior researcher at the A.M. Prokhorov General Physics Institute, Moscow, Russia, and as PDRA at Bath and Plymouth Universities. His research interests include optics, magnetism, superconductors, plasmonics, hybrid 2D materials, and photochemisty.

The authors declare no competing financial interest.