Estimating the frequency of indolent breast cancer in screening trials

Abstract

Cancer screening can detect cancer that would not have been detected in a patient’s lifetime without screening. Standard methods for analyzing screening data do not explicitly account for the possibility that a fraction of tumors may remain latent indefinitely. We extend these methods by representing cancers as a mixture of those that progress to symptoms (progressive) and those that remain latent (indolent). Given sensitivity of the screening test, we derive likelihood expressions to simultaneously estimate (1) the rate of onset of preclinical cancer, (2) the average preclinical duration of progressive cancers, and (3) the fraction of preclinical cancers that are indolent. Simulations demonstrate satisfactory performance of the estimation approach to identify model parameters subject to precise specifications of input parameters and adequate numbers of interval cancers. In application to four breast cancer screening trials, the estimated indolent fraction among preclinical cancers varies between 2% and 35% when assuming 80% test sensitivity and varying specifications for the earliest time that participants could plausibly have developed cancer. We conclude that standard methods for analyzing screening data can be extended to allow some indolent cancers, but accurate estimation depends on correctly specifying key inputs that may be difficult to determine precisely in practice.

INTRODUCTION

In recent years, overdiagnosis due to cancer screening has become a focus of attention and controversy. Overdiagnosis occurs when screening detects a cancer that would not have produced symptoms or have been diagnosed in the absence of screening. If a cancer is overdiagnosed, then treatment cannot be beneficial; in this case, it is considered overtreatment.

Some studies have suggested that overdiagnosis may account for as many as 31% of breast cancers detected,¹ but there is a great deal of uncertainty about the magnitude of the problem due to different definitions and measures of overdiagnosis and different assumptions imposed across studies.²

Understanding overdiagnosis requires understanding the natural history of cancer and its heterogeneity. Of prime importance are the distributions of the preclinical sojourn time (i.e., the time from onset of a preclinical tumor to clinical diagnosis in the absence of screening) and the associated lead time (i.e., the time by which screening advances the date of diagnosis). The sojourn time distribution is a direct determinant of the likelihood of overdiagnosis since overdiagnosis occurs whenever the sojourn time is longer than the time from screen detection to other-cause death. Thus, overdiagnosis may be thought of as arising from a process of competition between clinical diagnosis and other-cause death.

There is extensive literature on the estimation of sojourn and lead times using data from screening trials. The most common approach is based on maximum likelihood estimation of the sojourn time while accounting for interval censoring of the times to onset and times from onset to clinical diagnosis. Day and Walter³ and Shen and Zelen^{4, 5} used this approach assuming a parametric progressive disease model with an exponential distribution for sojourn time. Louis et al.⁶ and Etzioni and Shen⁷ explored methods for this problem that did not require a parametric specification for the sojourn-time distribution. Shen and Zelen⁸ and Shen and Huang⁸ developed a robust version of this approach.

The aforementioned methods all rely on a progressive disease assumption, which is most often expressed as a single-component distribution (commonly exponential) for the sojourn time. In this case, overdiagnosis arises from competing mortality together with potentially slow-growing but progressive disease. However, it has been suggested that breast and other cancers may consist of a mixture of progressive and indolent cancers.⁹ In this setting, overdiagnosis can arise from indolent cancers in addition to competing mortality for progressive cancers. Etzioni and Gulati¹⁰ recently showed that ignoring the indolent component could lead to underestimation of the fraction of cancers overdiagnosed, particularly under short-term follow-up. Few studies of overdiagnosis in breast cancer explicitly account for an indolent fraction. However, even among those that have done so,^11–14 estimation methods tend to be highly customized.

Most published studies of cancer overdiagnosis do not even attempt to estimate natural history. Rather, they use excess incidence in screened versus non-screened groups as a proxy for overdiagnosis.^{1, 15} However, this method has been shown to be systematically biased^{16, 17} even in randomized trials, and is prone to overestimation except under fairly specific circumstances.¹⁸

In this paper, we extend the probability modeling framework of Shen and Zelen⁴ to estimate natural history comprised of a mixture of progressive and indolent cancers using data from screening trials. This extension estimates the risk of developing preclinical cancer, the mean sojourn time for progressive cancers, and the fraction of preclinical cancers that are indolent. We demonstrate the framework using data from four breast cancer screening trials. Our extension of established methods for estimating cancer natural history is a necessary precursor to estimating the frequency of overdiagnosis under any specified screening protocol.

METHODS

Data and Notation

Consider a cohort of asymptomatic individuals enrolled in a screening program with regular (e.g., annual) screening exams. In Shen and Zelen,⁴ the natural history of the disease is modeled as transitions from a healthy or cancer-free state (S₀) to a preclinical state (S_p) to a clinical state (S_c) (Figure 1A). An underlying assumption is that all individuals would eventually transition out of the preclinical state and into the clinical state given sufficient follow-up. We generalize this assumption by assuming that a fraction of patients develop tumors that will remain in the preclinical state (S_p′) indefinitely (Figure 1B).

Figure 1.

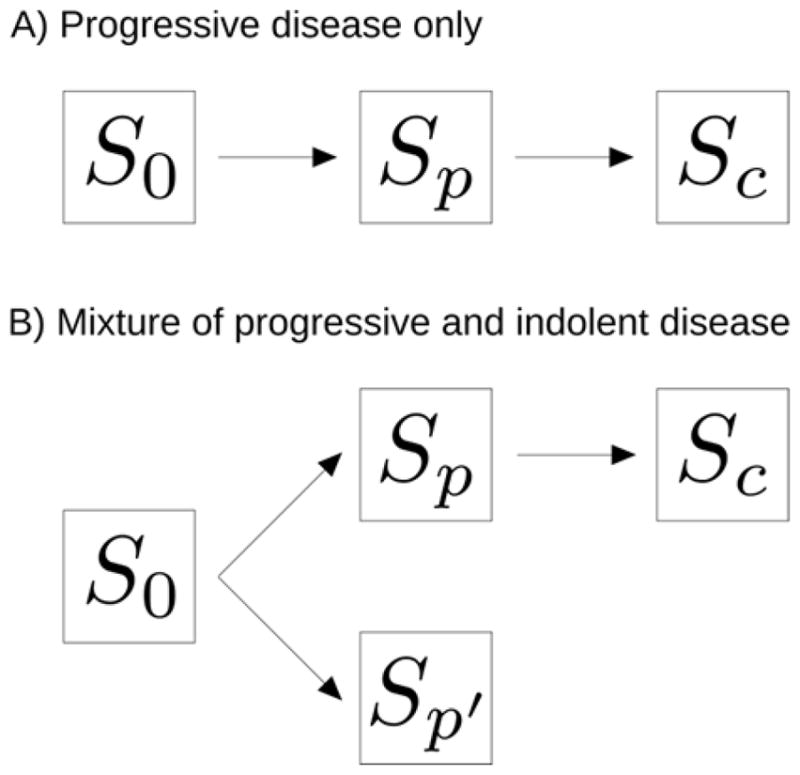
Standard and generalized multi-state models of cancer natural history. In either model, an individual begins in a healthy or cancer-free state (S₀), can enter the preclinical state (S_p), and can progress to the clinical state (S_c). A) All cancers progress to the clinical state. B) Cancers can progress to the clinical state or remain indolent indefinitely (S_p′).

In our motivating breast cancer screening trials, asymptomatic participants in the screening arm were invited to receive regular screening exams. The observed data were grouped by screening rounds as follows. Let t₁ < ⋯ < t_k−1 represent the k − 1 scheduled exams and let t_k denote the follow-up time after the last exam. For i = 1, …, k − 1, let n_i be the number of individuals at the t_i exam, s_i the number of cancers detected at the t_i exam, and r_i the number of so-called “interval cancers” diagnosed in the interval between the t_i and t_i+1 exams. Thus, the data associated with the ith screening round are (n_i, s_i, r_i).

To estimate the underlying cancer development and progression when all cancers are progressive, let w denote the annual probability of latent disease onset. As shown in Figure 1, let U denote the sojourn time measured from onset of preclinical state (S_p) to clinical state (S_c), and let q(t) and Q(t) = Pr(U > t) denote the corresponding probability density and survivor functions, respectively, with parameter λ. Finally, let β be the sensitivity of the screening exam to detect latent cancer; we assume the test sensitivity is the same for progressive and indolent cancers. Then the unknown parameters are θ = (w, λ, β).

To allow a fraction of individuals with indolent cancers, we consider a distribution of sojourn times that is a mixture as follows:

$$Q(t)=(1-\psi )Pr(U>t\mid U<\infty )+\psi =(1-\psi )Q_1(t)+\psi ,,$$

where Q₁(t) is a proper survivor function representing progressive sojourn times and ψ is the fraction of cancers with infinite sojourn times (i.e., indolent cancers). If λ is the parameter associated with Q₁(t) or the associated probability density function q₁(t), the unknown parameters are θ = (w, λ, ψ, β).

Estimation and Inference from the Likelihood

The proposed estimation procedure extends previous work by Shen and Zelen,⁴ who developed a maximum likelihood procedure to fit to the observed screen-detected and clinically diagnosed cancer data in a prospective screening study. Estimating the parameters of a mixture of cancers can be done using an approach that is similar to the one for estimating the parameters when all cancers are progressive.⁴ Briefly, the data available for a given individual consist of a screening history with screening test results and time of diagnosis or last follow-up. In the case of a screen-detected cancer, the final screening test is positive. In the case of an interval cancer, the final screening test is negative and diagnosis occurs at a known date thereafter. In each case, the screening history and diagnosis status provide information about the natural history.

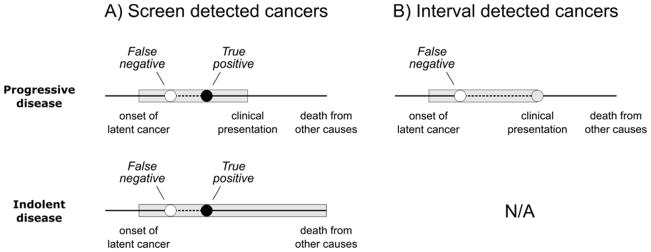
For example, a case where a first screening test is negative and a second screening test is positive with disease diagnosis occurring at the time of this test provides the following information: (a) preclinical onset must have occurred before the time of diagnosis; (b) the sojourn time must be at least as long as the interval from preclinical onset to the second screening test; (c) if preclinical onset occurred before the first screening test, then the individual had one false negative test; and (d) the individual had one true positive test. There are several natural histories that are consistent with this information, and all possible histories could apply to a progressive cancer or to an indolent cancer (Figure 2A). In contrast, an interval cancer must be progressive (Figure 2B). In general, the likelihood comprises probabilities of diagnosis at and after each screening test expressed in terms of parameters θ = (w, λ, ψ, β) and fits these within a multinomial framework given the observed numbers of cancers detected at and after each test.

Figure 2.

Possible clinical histories for cancers detected A) by a screening exam or B) between screening exams. Shaded bands represent preclinical durations. Screening exams can detect (true positive) or miss (false negative) progressive or indolent preclinical cancer. However, only cancers that progress to a clinical state can present in the interval between screening exams.

Let D_i(θ) be the probability that cancer is detected at the ith exam and I_i(θ) be the probability of an interval diagnosis in the ith interval. To derive expressions for these probabilities, first note that prevalence of latent disease at the first exam can be written:

$$P_0(t_1)=w{\int }_{t_0}^{t_1}Q(t_1-u)du,$$

where t₀ is the earliest time before the start of the trial at which any prevalent cancers among trial participants could plausibly have developed. Let Δ₀ = t₁ − t₀. The probability of screen detection at the first exam is D₁(θ) = βP₀(t₁).

Because latent cancer detected at a given exam either only became detectable after the previous exam or was missed during one or more previous exams, the general expression for the probability of a latent cancer being screen detected at exam t_j (j = 2, …, k − 1) is:

$$D_j(\theta )=\beta \sum _{l=1}^{j}w{(1-\beta )}^{j-l}{\int }_{t_{l-1}}^{t_l}Q\left(t_j-u\right)du.$$

Similarly, a cancer diagnosed in an interval between screens either only became detectable after the previous exam or was latent and missed by one or more previous exams. The probability of an interval diagnosis between exams t₁ and t₂ is:

$$I_1(\theta )=w(1-\psi ){\int }_{t_1}^{t_2}\left[(1-\beta ){\int }_{t_0}^{t_1}{q}_1(t-u)du+{\int }_{t_1}^t{q}_1(t-u)du\right]dt.$$

The general expression for an interval diagnosis between t_j and t_j+1 (j = 2, …, k − 1) is:

$$I_j(\theta )=w(1-\psi ){\int }_{t_j}^{t_{j+1}}\left[\sum _{l=0}^{j-1}{(1-\beta )}^{j-l}{\int }_{t_l}^{t_{l+1}}{q}_1(t-u)du+{\int }_{t_j}^t{q}_1(t-u)du\right]dt.$$

It is intuitive that indolent cancers can only be detected by screening and thus only contribute to D_j(θ). In contrast, progressive cancers can be detected by screening and contribute to D_j(θ) or be interval diagnosed and contribute to I_j(θ). The associated trinomial log-likelihood function is:

$$l(\theta )\propto \sum _{j=1}^k\{s_{j}log[D_j(\theta )]+r_{j}log[I_j(\theta )]+(n_j-s_j-r_j)log[1-D_j(\theta )-I_j(\theta )\left]\right\}.$$

Due to concerns about identifiability of all model parameters, we consider the test sensitivity parameter (β) known and estimate the annual probability of preclinical onset (w), the mean sojourn time among progressive cancers (λ), and the fraction of indolent cancers (ψ). We use external data to provide an estimate of β based on prior studies.^{4, 5, 19} Although long-term follow-up after the final screening test helps to identify the parameters,¹⁰ this may not be available in practice²⁰; thus, we focus on the case where we have only short-term follow-up (equal to the inter-screening interval) after the last screening test as in the motivating screening trials.

Under this model, one focus of interest is to test the null hypothesis ψ = 0, i.e., the lower boundary of the parameter space [0,1). Therefore, the asymptotic distribution of the likelihood ratio test has a nonstandard form in a discontinuous way, which should be properly adjusted.²¹

Simulation Study

We conducted a simulation study to assess the performance of the proposed estimation method. The assumptions and parameter settings in the simulation were motivated by published studies of breast cancer natural history.⁴ We specified a constant annual preclinical onset probability and indolent cancer frequency starting Δ₀ = 20 years before entry to the trial. We used an exponential distribution for the sojourn time among progressive cancers and a constant annual latent incidence corresponding to a 1-year net cumulative incidence of 3 per 1 000 women. We set the inter-screening interval to be 1 year, test sensitivity to be 70%, 80%, or 90%, mean sojourn time for progressive cancers to be 1.5 or 2.5 years, and the indolent fraction to be 0%, 5%, and 15%. Under each scenario, we examined the bias of our parameter estimates, standard errors (SEs), and the power of the likelihood ratio test of the hypothesis that ψ = 0. We generated a cohort of 50 000 individuals undergoing 4 exams with follow-up after the last exam equal to the inter-screening interval. We repeated the simulations 2 000 times for each scenario.

Based on the simulation results (Table 2), estimates of the indolent fraction (ψ̂) and the mean sojourn time among progressive cancers (λ̂) were virtually unbiased for the setting with short preclinical sojourn times among progressive cancers (λ = 1.5 years) and a low frequency of indolent cancers (ψ ≤ 0.05). Under a higher frequency of indolent cancers, the estimated indolent fraction was somewhat higher than its true value and the mean sojourn time among progressive cancers was underestimated. When the indolent fraction and the progressive mean sojourn time were at their highest settings, the model was least able to differentiate between indolent tumors and progressive tumors with longer sojourn times.

Table 2.

Simulation Study of the Proposed Estimation Approach When the Risk of Developing Preclinical Cancer Is w = 0.003 Starting Δ₀ = 20 Years before Entry with Screening Interval Δ = 1.

Parameter settings			Parameter estimates*				Type I error or power†
Screen sensitivity	Mean sojourn	Indolent fraction	Mean sojourn		Indolent fraction
β	λ	ψ	λ̂	SE(λ̂)	ψ̂	SE(ψ̂)
0.70	1.5	0.00	1.42	0.13	0.01	0.01	0.05
		0.05	1.30	0.20	0.06	0.02	0.97
		0.15	0.94	0.19	0.20	0.03	1.00
	2.5	0.00	2.36	0.24	0.01	0.02	0.03
		0.05	2.24	0.41	0.07	0.03	0.57
		0.15	1.69	0.43	0.21	0.04	0.97
0.80	1.5	0.00	1.44	0.12	0.01	0.01	0.05
		0.05	1.37	0.18	0.06	0.02	0.95
		0.15	1.15	0.18	0.18	0.02	1.00
	2.5	0.00	2.37	0.22	0.01	0.01	0.04
		0.05	2.35	0.39	0.06	0.03	0.59
		0.15	1.97	0.37	0.20	0.03	0.98
0.90	1.5	0.00	1.45	0.11	0.01	0.01	0.05
		0.05	1.45	0.17	0.06	0.02	0.94
		0.15	1.32	0.18	0.17	0.02	1.00
	2.5	0.00	2.39	0.20	0.01	0.01	0.05
		0.05	2.42	0.35	0.06	0.03	0.62
		0.15	2.21	0.37	0.18	0.03	0.99

^*In all settings, the estimated onset rate is ŵ = 0.003 with SE(ŵ) = 0.0001.

^†This column shows the type I error rate when ψ = 0 and power when ψ > 0.

In an extended simulation study, we varied the first time a latent cancer can develop across Δ₀ = 20, 10, and 5 years before entry to the trial, set the inter-screening interval to Δ = 1 or 2 years, and varied the indolent fraction across 0%, 5%, 10%, and 25% (see Supplementary Materials). With a longer screening interval (Δ = 2), the estimates were less biased, which is likely due to the increased frequency of interval cancers. Indeed, interval cancers are more informative about sojourn times than screen-detected cancers. In all scenarios, the rate of onset of preclinical cancer was estimated accurately. When preclinical cancer can develop Δ₀ = 20 years before entry, estimates of the mean sojourn time were negatively biased, and estimates of the indolent fraction were positively biased, especially for larger values of the indolent fraction. When preclinical cancer can only develop closer to entry into the trial (Δ₀ = 5 or 10 years), the bias in both estimates was larger in magnitude but less sensitive to the value of the indolent fraction.

To assess the robustness of the estimators against misspecification of the test sensitivity, we fixed the true value at β = 0.80 and specified values above or below this value (β̃ = 0.70 and 0.90). When β̃ = 0.70, the estimated fraction of indolent cancers and the mean sojourn time for progressive cancers were overestimated, but the estimates generally differed only modestly from their true values (not shown). In contrast, when β̃ = 0.90, the estimate of the indolent fraction tended to be nearly unbiased but the mean sojourn time for progressive cancers was underestimated. These results are reasonable because, when the true test sensitivity is underestimated, the estimation procedure compensates by identifying parameters that yield increased latent prevalence at screening tests; conversely, when the true test sensitivity is overestimated, the estimation procedure identifies parameters that yield reduced latent prevalence at screening tests.

Analysis of Breast Cancer Screening Clinical Trials

We analyzed data from the Health Insurance Plan (HIP) of New York study^{22, 23}, the Canadian National Breast Screening Study (CNBSS)^{24, 25}, and the Swedish Two-county Trial^{26, 27} to estimate the frequency of indolent cancers among preclinical breast cancers. In these trials, participants in the screening arm were invited to receive an initial screening test and 2–3 additional screening tests.

The HIP study was the first randomized trial designed to determine the efficacy of breast cancer screening with mammography and clinical breast exam (CBE) in reducing mortality from breast cancer.^{22, 23, 28} More than 63 000 women aged 40–64 with at least one year of membership in the insurance plan were eligible. After excluding women who had breast cancer, about 62 000 women were randomized. About 65% (n=20 166) of the women in the screening group appeared for their initial examination; high proportions of these women (75%) participated in the subsequent re-examinations.

The CNBSS was designed to evaluate the efficacy of annual mammography plus CBE relative to CBE alone. CNBSS-I enrolled women aged 40–49 years and CNBSS-II women aged 50–59 years who had no history of breast cancer and no mammograms in the previous 12 months.^{24, 25} In CNBSS-I, 25 214 women were randomized to the screening group underwent the first screening exam. In CNBSS-II, 19 711 women underwent the first screening exam.

The Swedish Two-county Trial examined efficacy of screening mammography relative to no screening.^{26, 27} This trial enrolled 77 080 women aged 40–74 years in the screening arm and invited women aged 40–49 to screening exams every 2 years and women aged 50–74 to screening exams every 33 months, so the average screening interval was 2.6 years for the total screening cohort.¹² Some 68 770 women underwent the first screening exam.

Breast cancers detected by screening exam and interval cancers are summarized in Table 1. Only data from the first 3 exams are shown for the Swedish Two-county Trial because this trial was closed and the control arm was invited to screening at this time. Test sensitivity pertains to screening mammography plus CBE in the HIP and CNBSS studies and to screening mammography alone in the Swedish Two-country study. Given external estimates of test sensitivity, which range from 0.70 to 0.90 from eight randomized breast cancer screening trials,^{4, 5, 19} we estimate the unknown model parameters and test whether the indolent fraction is zero using a likelihood ratio test. We use the bootstrap method to estimate standard deviations of the parameter estimates with 300 re-samplings. For the HIP, CNBSS-II, and the Swedish Two-county trials, we set Δ₀ to be 4 years, and for the CNBSS-I trial, which enrolled younger women (age 40–49 at entry), we set Δ₀ to be 2 years. Since the value of Δ₀ is not known, we also examine results for Δ₀ ranging from 1 to 5 years as well as an extreme value of 10 years while varying values of the test sensitivity from 0.70 to 0.90 in the sensitivity analyses.

Table 1.

Summary Results of Screening Arms in Four Breast Cancer Screening Trials

	Screening exam
	First	Second	Third	Fourth
HIP
Total participants	20 166	15 936	13 679	11 971
No. of screen-detected cancers	55	32	18	27
No. of interval cancers	13	8	10	10
CNBSS-I
Total participants	25 214	22 424	22 066	21 839
No. of screen-detected cancers	98	39	44	52
No. of interval cancers	19	16	8	10
CNBSS-II
Total participants	19 711	17 669	17 347	17 193
No. of screen-detected cancers	142	66	43	54
No. of interval cancers	15	10	8	9
Swedish Two-county
Total participants	68 770	58 601	43 320
No. of screen-detected cancers	384	214	173
No. of interval cancers	123	78	89

Results from the HIP Trial

The estimated parameters and their standard errors are summarized in Table 3. Depending on the assumed sensitivity of screening mammography plus CBE between 0.70 and 0.90, the estimated rate of preclinical onset was 2.1–2.3 women per 1 000 person-years, which is similar to published detection rates of histologically confirmed breast cancer of 2.1 in the screening arm.²³ The estimated mean sojourn time for progressive cancers varied from 1.2 to 1.7 years, which is somewhat lower than previous estimates of 1.7 to 2.5 years when the possibility of indolent cancers was ignored.^{3, 5} The estimated indolent fraction varied from 32% if test sensitivity was 0.70 to 0% if test sensitivity was 0.90.

Table 3.

Estimated Parameters in Four Breast Cancer Screening Trials

Trial*	Screen sensitivity	Parameter estimates						P-value†
		Preclinical onset		Mean sojourn		Indolent fraction
	β	ŵ	SD(ŵ)	λ̂	SD(λ̂)	ψ̂	SE(ψ̂)
HIP
	0.70	0.0021	0.0002	1.20	0.55	0.32	0.14	0.03
	0.80	0.0022	0.0002	1.68	0.40	0.08	0.12	0.10
	0.90	0.0023	0.0002	1.58	0.25	0.00	0.07	0.17
CNBSS-I
	0.70	0.0027	0.0002	3.40	1.78	0.23	0.22	0.50
	0.80	0.0027	0.0002	3.55	1.34	0.02	0.25	0.32
	0.90	0.0027	0.0002	2.73	0.96	0.00	0.26	0.22
CNBSS-II
	0.70	0.0033	0.0002	2.30	2.13	0.48	0.23	0.00
	0.80	0.0033	0.0002	2.44	1.71	0.35	0.26	0.00
	0.90	0.0035	0.0002	3.44	1.01	0.00	0.21	0.10
Swedish Two-county
	0.70	0.0023	0.0008	2.99	0.98	0.42	0.10	0.02
	0.80	0.0022	0.0007	2.94	1.47	0.33	0.19	0.03
	0.90	0.0022	0.0006	1.00	1.29	0.56	0.20	0.02

^*Estimation uses Δ₀ = 2 (CNBSS-I) or Δ₀ = 4 (HIP, CNBSS-II, and Swedish Two-county) years.

^†P-value for likelihood ratio test that ψ = 0.

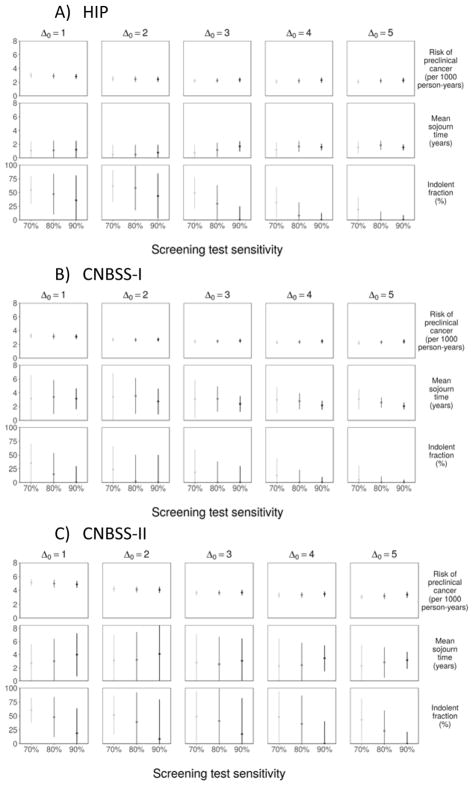
Our sensitivity analysis revealed that convergence to the lower boundary (0%) for the indolent fraction occurred for either higher assumed test sensitivity or for a greater number of years at which onset could occur before the start of the trial (Figure 3); this was particularly the case for Δ₀ = 10 years, where the estimated indolent fraction converged to 0% under all settings for sensitivity. Both of these settings increase the prevalent pool at the first screening test and, in accordance, with the simulation studies, we find that the estimation algorithm yields a correspondingly reduced estimate of the indolent fraction.

Figure 3.

Sensitivity Analyses: Parameter Estimates to Assumed Test Sensitivity and Number of Years of Onset before the First Screening Exam.

Results from the CNBSS Trials

As shown in Table 3, the estimated mean sojourn time for progressive cancers is comparable in CNBSS-I (2.7–3.6 years) and CNBSS-II (2.3–3.5 years) to previous estimates in Shen and Zelen.⁵ Further, the estimated indolent fraction varies from 48% if test sensitivity is 0.70 to 0% if test sensitivity is 0.90.

Figure 3 illustrates sensitivity of the parameter estimates to test sensitivity (β ranging from 0.70 to 0.90) and the latent onset time origin (Δ₀ ranging from 1 to 5 years). The figure shows that estimates of λ and ψ are quite sensitive to these inputs, whereas the estimate of w is more robust. Estimates of ψ are most sensitive to the test sensitivity β and the latent onset time origin Δ₀, with higher β settings leading to generally lower estimates of the indolent fraction and the 10-year setting for Δ₀ leading to an indolent fraction estimate that converged to 0% under all settings for sensitivity in CNBSS-I and under all but β = 0.70 in CNBSS-II. As noted above, a higher setting for β or Δ₀ enables the likelihood to explain the observed screen-detected prevalence without having to account for a high fraction of indolent cancers.

Results from the Swedish Two-county Trial

For test sensitivity 0.70 or 0.80, the estimated mean sojourn time for progressive cancers (2.9–3.0 years) is between corresponding estimates from the CNBSS-I and CNBSS-II (Table 3). For test sensitivity 0.90, the estimated mean sojourn time converged to the lower boundary (1.0) allowed in the estimation procedure. The estimated indolent fraction varies from 48% if test sensitivity is 0.70 to 0% if test sensitivity is 0.90.

Our sensitivity analysis shows similar dependence of estimates of λ and ψ on the test sensitivity β and the latent onset time origin Δ₀ (Figure 3), though all estimates are more precise than those from the other trials due to the larger number of women in this trial.

DISCUSSION

Overdiagnosis is the primary potential harm of cancer screening, but uncertainty about the frequency of overdiagnosis in breast cancer screening persists. To date there is no consensus regarding how best to estimate overdiagnosis, and different approaches yield varying results. In practice, overdiagnosed breast cancer cases may be comprised of a mixture of (a) women with indolent breast cancer whose disease does not progress beyond the preclinical state and (b) women whose disease would progress in the absence of other-cause death but who die before the disease becomes clinically apparent. Our modeling approach yields estimates of first type, expressed as the indolent fraction among women with preclinical onset. This is a necessary precursor to estimating the total frequency of overdiagnosis.

Prior studies that estimate the natural history of breast cancer from screening data have generally not acknowledged the potential mixture nature of breast cancers. This weakness has been cited in critiques of modeling studies and lead time estimation as precursor to estimating overdiagnosis.⁹ This article extends an established statistical modeling approach to accommodate a mixture of sojourn times with an unknown fraction of indolent breast cancers within a stable disease model.⁴ The approach inherits the simplifications of the most commonly used framework in the literature on estimation of natural history for screening trial data. Results provide insights regarding the limits of what can be learned about mixture natural histories from commonly used models for screening trial data and have implications for more complex models involving mixtures, which may be subject to even greater identifiability challenges.

Strictly speaking, the indolent fraction reflects a lower bound on the risk of overdiagnosis among women with preclinical cancer. Estimating the risk of overdiagnosis requires incorporating the risk of mortality from other causes for women with progressive cancers using long-term follow-up data.²⁹ We note that screen-detected women in these trials were young and relatively healthy, and their mortality due to competing risks given a sojourn time for progressive cancers with mean 2–3 years was unlikely. It is technically straightforward to add a post-estimation step to incorporate the competing risk when screened subjects are older or the mean progressive sojourn time is longer.

Our simulation results indicate that the mixture modeling approach is most likely to provide reliable results when the mean sojourn time among progressive cancers is short and the indolent fraction is small to moderate. Further, accuracy is likely to be improved if the inter-screening interval is wide enough to allow for adequate numbers of interval cancers since these are the cancers that are more informative about the sojourn time. However, screening intervals that are too wide may result in a net loss of information in the grouped data setting considered here.

When assuming test sensitivity is 80%, our estimates of the indolent fractions for HIP and CNBSS-I are 8% and 2%, respectively, which are close to the estimated overdiagnosis rates of 1–5% for two Swedish breast screening trials,¹² but our estimates for CNBSS-II and the Swedish Two-county Trial were considerably higher (35% and 33%, respectively). In the absence of age-specific data, the estimators of the mean sojourn time and indolent fraction imply an average over the given age group for each trial. Further work is needed to determine the reasons for this heterogeneity in results, which may be due to differences in the screened populations or to clinical practices affecting the sojourn time distribution.

As shown in our simulation study and in the trial results, the model estimates of the indolent fraction tend to be subject to a high degree of uncertainty. In addition, the assumed sensitivity of the screening exam significantly impacts results. If the test sensitivity is too low, the model compensates with a surplus of indolent cancers. In other words, to fit the observed number of screen-detected preclinical cancers, the model tends to overestimate the indolent fraction. That the reliability of our estimates is conditional on a reasonable assessment of the test sensitivity is a key limitation of the analysis. However, analytic methods that aim to extract information about mixtures of natural histories from prospective screening data must inevitably constrain the estimation procedure to avoid a non-identifiability problem, which occurs when different sets of parameters corresponding to a specified natural history model are equally consistent with an observed dataset. We chose to fix test sensitivity and considered values for this parameter within a range informed by the results of prior studies.^{4, 5, 19} We assumed similar test sensitivities for progressive and indolent cancers since disease-type-specific test sensitivities are not identifiable from grouped screening trial data. The same problem is likely to manifest in more complex models of mixture natural histories, such as models of in-situ and invasive breast cancers with non-progressive potential. If the difference in test sensitivity between indolent and progressive tumors was known, then the model could be adapted in a straightforward manner to allow for differential test sensitivity while still retaining a single sensitivity parameter. However, there are no existing estimates of how test sensitivities might differ for progressive versus indolent breast cancers. Some studies have suggested that test sensitivity might differ for in-situ and invasive breast cancers,^{30, 31} but the definition of sensitivity in those studies (screen-detected cancers divided by screen-detected plus interval cancers) is different from the definition of sensitivity in our study (screen-detected cancers divided by latent cancers). Moreover, even though in-situ tumors are more likely to be indolent than invasive tumors, the categorization of tumors as in-situ versus invasive is not the same as indolent versus progressive.

In conclusion, this work shows that, in principle, the methods originally developed by Zelen³² and Shen and Zelen⁴ may be extended to account for a mixture of indolent and progressive cancers. However, the results will depend critically on specifications for test sensitivity and the interval prior to the start of the trial during which latent cancers among trial participants could plausibly have developed. Consequently, reliability of the extended method will rest on being able to identify defensible values for these inputs. We note that estimation of the indolent fraction via the mixture model is only a precursor to estimating overdiagnosis frequencies, which will depend on the time by which diagnosis is advanced by the screening protocol and on the risk of other-cause mortality. Further research is needed to investigate whether more precise estimation of the indolent fraction may be possible using individual-level data, including age-specific screening histories and diagnoses from a prospective screening program.