Monte Carlo simulation of chemistry following radiolysis with TOPAS-nBio

Abstract

Simulation of water radiolysis and the subsequent chemistry provides important information on the effect of ionizing radiation on biological material. The Geant4 Monte Carlo toolkit has added chemical processes via the Geant4-DNA project. The TOPAS tool simplifies the modeling of complex radiotherapy applications with Geant4 without requiring advanced computational skills, extending the pool of users. Thus, a new extension to TOPAS, TOPAS-nBio, is under development to facilitate the configuration of track-structure simulations as well as water radiolysis simulations with Geant4-DNA for radiobiological studies. In this work, radiolysis simulations were implemented in TOPAS-nBio. Users may now easily add chemical species and their reactions, and set parameters including branching ratios, dissociation schemes, diffusion coefficients, and reaction rates. In addition, parameters for the chemical stage were re-evaluated and updated from those used by default in Geant4-DNA to improve the accuracy of chemical yields. Simulation results of time-dependent and LET-dependent primary yields G_x (chemical species per 100 eV deposited) produced at neutral pH and 25°C by short track-segments of charged particles were compared to published measurements. The LET range was 0.05–230 keV/µm. The calculated G_x values for electrons satisfied the material balance equation within 0.3%, similar for protons albeit with long calculation time. A smaller geometry was used to speed up proton and alpha simulations, with an acceptable difference in the balance equation of 1.3%. Available experimental data of time-dependent G-values for ^•OH agreed with simulated results within 7%±8% over the entire time range; for e⁻_aq over the full time range within 3%±4%; for H₂O₂ from 49%±7% at earliest stages and 3%±12% at saturation. For the LET-dependent G_x, the mean ratios to the experimental data were 1.11±0.98, 1.21±1.11, 1.05±0.52, 1.23±0.59 and 1.49±0.63 (1 standard deviation) for ^•OH, e⁻_aq, H₂, H₂O₂ and H^•, respectively. In conclusion, radiolysis and subsequent chemistry with Geant4-DNA has been successfully incorporated in TOPAS-nBio. Results are in reasonable agreement with published measured and simulated data.

1 Introduction

The simulation of the radiolysis of water and subsequent chemical interactions following initial ionizations by incident particles is motivated by the importance of chemistry on inducing molecular damage in the cell (Nikjoo et al. 2006), (O’Neill and Wardman 2009). Monte Carlo (MC) track structure codes such as PARTRAC (Ballarini et al. 2000), RITRACKS (Plante and A. 2011; Plante and Devroye 2017), (Kreipl, Friedland, and Paretzke 2009) and those based on Geant4-DNA (Incerti et al. 2010; Bernal et al. 2015), provide accurate descriptions of the initial physical process of ionization, along with the pre-chemical production of ion species and subsequent chemistry, in a single application. Other codes provide such capabilities in separate applications, for either the physical or chemical stages, (see, for example, the review articles [1] and [6] for a more complete list). Geant4-DNA provided a set of libraries in the Geant4 toolkit (Agostinelli et al. 2003) has a distinct advantage for developers and users due to its open source architecture. This is likely a key factor in the increased rate of publications using Geant4-DNA since 2010 (Incerti et al. 2016). Geant4-DNA allows a user with both advanced programing skills and an in depth knowledge of Geant4 to develop an application, generally focused on a specific problem.

To help circumvent the need for specialized expertise in programming and Geant4, the TOPAS tool (Perl et al. 2012) wraps and extends Geant4, allowing a much wider group access to the modeling of complex radiotherapy applications without the need for advanced programming skills. The TOPAS-nBio project aims to extend TOPAS to facilitate the configuration of track structure simulations by providing an interface to the Geant4-DNA physics and chemistry processes as well as the use of complex radiobiological geometries (McNamara et al. 2017), variance reduction techniques (Ramos-Méndez et al. 2017) and scorers for radiobiological quantities of interest. These features are compatible with advanced TOPAS capabilities such as 4D simulation (Shin et al. 2012) and advanced Geant4 capabilities such as multithreading (Dong et al. 2012), both critical to full water radiolysis simulation. The ability to perform such simulations in TOPAS-nBio is a key step towards an integrated MC tool for physics and biology.

In this work, we present a TOPAS-nBio extension to configure water radiolysis simulations with Geant4-DNA. We demonstrate the use of this extension to calculate results of water radiolysis quantified in terms of the time-dependent G-value (number of molecular species per 100 eV of energy deposit) for electrons, protons and alpha particles (alphas) for a wide range of linear energy transfer (LET). We compare our simulation results with collected experimental data from the literature and results from other codes for several chemical species for the current state of Geant4-DNA. For that, we reviewed and updated the electron solvated thermalization distance, diffusion coefficients and reaction rates used by default in Geant4-DNA with values from the literature for the simulation of the chemical stage.

2 Materials and methods

2.1 Water radiolysis simulations in Geant4-DNA

The Geant4-DNA project extended the Geant4 toolkit to perform water radiolysis simulations by providing models for the physical processes of the interaction of ionizing radiation at very low energies, reported in (Bernal et al. 2015; Incerti et al. 2010), and the chemical processes for the subsequent pre-chemical and nonhomogeneous chemical interactions (Mathieu Karamitros et al. 2011; M. Karamitros et al. 2014). The radiolysis of liquid water simulations is performed in three stages. In the first stage, called the “physical stage” (< 10⁻¹⁵ s), the so-called G4EmDNAPhysics_option1 constructor is used to simulate the ionization, excitation and vibrational excitation of water molecules resulting from the interaction of the primary ionizing particles and their secondaries. In the second stage, called the “pre-chemical stage” (10⁻¹⁵–10⁻¹² s), initial chemical species resulting from dissociative decay or auto-ionization of excited water molecules (H₂O^*) and ionized water molecules (H₂O⁺) in addition to the thermalization of sub-excitation electrons (e⁻_sub) are simulated. In the third stage, called the “chemical stage” (10⁻¹²–10⁻⁶ s), the initial chemical species diffuse and react with each other under specific rates, producing new chemical species and reducing the number of initial chemical species. Although some reactions can also occur in the pre-chemical stage (Frongillo et al. 1998), for simplicity it is assumed that these occur at the beginning of the chemical stage (Hervé du Penhoat et al. 2000) and up to 10⁻⁶ s, at which time all chemical products are considered homogeneously distributed. In Geant4-DNA, the chemical species diffuse step-by-step by Brownian motion (based on the solution to the Smoluchowsky equation in three dimensions (Risken 1989)) through the medium, which is considered as a continuum. In addition, Geant4-DNA assumes that the reactions are diffusion-controlled (M. Karamitros et al. 2014; Mathieu Karamitros et al. 2011); that is, the reaction time between two bodies is negligible in comparison with the time for the two bodies to diffuse in the same neighborhood (Rubinstein and Torquato 1988). Thus a reaction occurred every time two chemical species reached a distance smaller than their reaction radius (Plante 2011b). Limitations of the approach to the chemical stage adopted by Geant4-DNA are described in (Bernal et al. 2015).

All three stages are performed history-by-history and step-by-step, independent of subsequent histories. The medium is assumed to be water of neutral pH and an ambient temperature of 25°C.

2.2 The chemistry interface of TOPAS-nBio

Water radiolysis simulations with Geant4-DNA require a large set of configuration parameters (reaction rates, diffusion coefficients, etc.). These may be hard coded for ease of use and to help prevent errors. This can be an obstacle for users that require different configurations, including the onerous requirement of rebuilding the application for each configuration. TOPAS-nBio provides the means to easily configure track structure simulations, access to scoring information at different stages along the simulation, variance reduction techniques (Ramos-Méndez et al. 2017) and complex geometries at micrometer and nanometer scales (McNamara et al. 2017), making TOPAS with the TOPAS-nBio extension a powerful yet easy-to-use MC platform for track structure simulations. In this work, TOPAS-nBio has been extended to allow the user to easily configure parameters for water radiolysis simulation in a clear way that mitigates user error and allows the user to perform regression tests when updating to the latest version. An alpha version of TOPAS-nBio built on the top of Geant4 version 10.3.p01 was used in all the calculations.

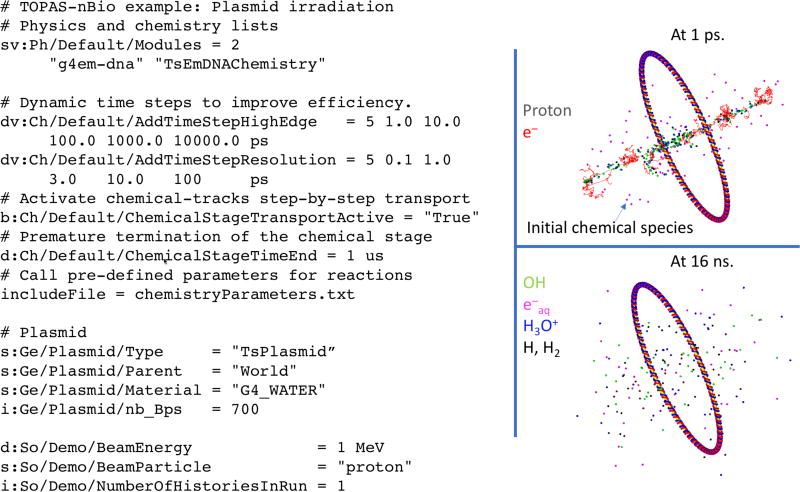
A special nomenclature was adopted in TOPAS-nBio to allow clarity and flexibility in the configuration of parameters for the pre-chemical and chemical stages. For example, the name of the chemical species, shown in Table 1, is used to define reaction rates and diffusion coefficients. All features of the chemistry interface are accessible to the user by using just a few parameters, depicted in Figure 1 and described below:

# Physics list and chemistry list:
sv:Ph/Default/Modules = 2 "g4em-dna" "TsEmDNAChemistry"
s:Ch/ChemistryName = "Default"
# Active step-by-step transport of chemical species
b:Ch/Default/ChemicalStageTransportActive = "True"

Table 1.

Chemical species nomenclature used in TOPAS-nBio, diffusion coefficients of Geant4-DNA (default values) and TOPAS-nBio (used for this work), and reaction radii r_I

Chemical species	Name in TOPAS- nBio	Diffusion coefficients D (10−9m2s−1) at 25°C		Reaction radius (nm)
		Geant4-DNA Default	TOPAS- nBio
e−aq	SolvatedElectron	4.9	4.9	0.5
•OH	Hydroxyl	2.8	2.2	0.22
H•	Hydrogen	7.0	7.0	0.19
H3O+	Hydronium	9.0	9.46	0.25
H2	Dihydrogen	5.0	4.8	0.14
OH−	Hydroxide	5.0	5.3	0.33
H2O2	HydrogenPeroxide	1.4	2.3	0.21
O2	Oxygen	–	2.4	0.17
O2−	SuperoxideAnion	–	1.75	0.22
HO2	HydroPeroxide	–	2.3	0.21
HO2−	Dioxidanide	–	1.4	0.25

Figure 1.

A simplified representation of a DNA plasmid with 700 base pairs (bps) shown in blue and red on the right, with TOPAS-nBio parameters set for the simulation shown on the left. Top: Physical tracks of 1 MeV proton (grey lines) and secondary e− (red lines) and initial chemical species spatial distribution at 1 ps (small points). Bottom: stacked chemical tracks of species at 16 ns after the irradiation: ^•OH (green), e⁻_aq (magenta), H3O⁺ (blue) and H^•, H₂ (black).

2.2.1 Configuration parameters for the pre-chemical stage: branching rations and dissociation schemes

For the pre-chemical stage, the definition of dissociation schemes and branching ratios for excited or ionized water molecules are required to produce the initial chemical species (Uehara and Nikjoo 2006). The number of decay channels and their probabilities depend on the MC platform. These parameters are usually adjusted to match the picosecond yield of chemical species (Ballarini et al. 2000). Geant4-DNA uses the revised branching ratios and dissociative schemes from (Kreipl, Friedland, and Paretzke 2009), as reported in (Mathieu Karamitros et al. 2011; Bernal et al. 2015). These values, listed in Table 2, were set as defaults in TOPAS-nBio, with the possibility to override those values. For example, parameters associated with the electronic states of the water A¹B₁ and B¹A₁ can be defined as follows:

u:Ch/Default/IonizationState/DissociativeDecayProbability = 1.00
u:Ch/Default/A1B1/DissociativeDecayProbability = 0.65
u:Ch/Default/A1B1/RelaxationProbability        = 0.35
u:Ch/Default/B1A1/AutoIonizationProbability    = 0.55
u:Ch/Default/B1A1/DissociativeDecayProbability = 0.15
u:Ch/Default/B1A1/RelaxationProbability        = 0.30
u:Ch/Default/RydbergStatesAndDiffuseBands/AutoIoinisationProbability = 0.5
u:Ch/Default/RydbergStatesAndDiffuseBands/RelaxationProbability      = 0.5

In this work, the thermalization distance of sub-excitation electrons followed the linear approach as a function of the sub-excitation energy with constant equal to 1.8 from (Ballarini et al. 2000). This approach differed from that provided by default in Geant4-DNA, which uses a density distribution adjusted to full Monte Carlo simulations of low energy electrons down to thermalization (Bernal et al. 2015).

Table 2.

Branching ratios and dissociation schemes used in this work and given by default in Geant4-DNA (Kreipl, Friedland, and Paretzke 2009), (Mathieu Karamitros et al. 2011).

Process			Probability (%)
Ionization state	Dissociative decay	H3O+ + •OH	100
A1B1	Dissociative decay	•OH + H•	65
	Relaxation	H2O + ΔE	35
B1A1	Auto-ionization	H3O+ + •OH + e−aq	55
	Auto-ionization	•OH + •OH + H2	15
	Relaxation	H2O + ΔE	30
Rydberg, diffuse bands	Auto-ionization	H3O+ + •OH + e−aq	50
	Relaxation	H2O + ΔE	50

2.2.2 Configuration parameters for the chemical-stage: diffusion coefficients, reaction rates and time steps

In the chemical stage, the chemical species diffuse through a homogeneous water phantom. Diffusion coefficients of various chemical species in water are reported as a function of the temperature in reference (A. . Elliot 1994). As proposed elsewhere (Hervé du Penhoat et al. 2000), diffusion coefficients for e⁻_aq, H₃O⁺ and OH⁻ were obtained via fits to these experimental data, with values at 25°C used in TOPAS-nBio. They agreed with those values from [18], and those values used in [5] and [21]. Diffusion coefficients for the remaining chemical species, shown in Table 1, were obtained from references (Plante and Devroye 2017). In Table 1, default values used in Geant4-DNA (Mathieu Karamitros et al. 2011) are also shown for comparison. The pre-defined diffusion coefficients may be overwritten in a user parameter file, for example:

sv:Ch/Default/DiffusionCoefficient/Molecules = 2 "SolvatedElectron" "Hydroxyl"
dv:Ch/Default/DiffusionCoefficient/Values  = 2    5.5e–9   3.0e–9     m2/s

Following the notation from (Uehara and Nikjoo 2006), the observed reaction rate constants k_obs for the reactions given in Table 3 can be defined in TOPAS-nBio either manually or automatically. If automatically, k_obs is estimated from an Arrehnius function fit to experimental data of the temperature-dependent k_obs or activation rate constant k_act from (A. . Elliot 1994). If k_act is used, then k_obs is obtained using the Noyes equation:

$$\frac{1}{k_{\text{obs}}}=\frac{1}{k_{\text{act}}}+\frac{1}{k_{\text{diff}}},$$ (1)

where, k_diff is the diffusion rate constant given by the Smoluchowsky equation for neutral interactions or the Smoluchowsky-Debye equation for electrostatic interactions (see, for example (M. Karamitros et al. 2014; Hervé du Penhoat et al. 2000; Plante 2011b)). The reaction radii (Table 1) used in k_diff were derived from fits to experimental data of temperature-dependent reaction rates from (A. . Elliot 1994). Nevertheless, k_obs values at 25°C used in this work were set manually to the values obtained from a recent publication (Plante and Devroye 2017). The reactions, listed in Table 3, were those reactions provided by default in Geant4-DNA (Mathieu Karamitros et al. 2011; M. Karamitros et al. 2014; Bernal et al. 2015) with the corresponding k_obs also listed in the table.

Table 3.

List of reactions and observed reaction rate constants k_obs used in this work and given by default in the Geant4-DNA chemistry module.

	Reaction rate constant kobs (1010 M−1s−1)
Reaction	Geant4-DNA Default	TOPAS-nBio
e−aq + e−aq → H2 + 2OH−	0.5	0.636
e−aq + •OH → OH−	2.95	2.95
e−aq + H• → H2 + OH−	2.65	2.5
e−aq + H3O+ → H•	2.11	2.11
e−aq + H2O2 → OH− + •OH	1.41	1.10
•OH + •OH → H2O2	0.44	0.550
•OH + H• → H2O	1.44	1.55
H• + H• → H2	1.2	0.503
H3O+ + OH− → H2O	14.3	11.3

A provision was added to TOPAS-nBio for the user to add reactions by specifying the pair of chemical species involved in the process, the products, and optionally k_obs. Only those reactions explicitly defined are simulated. For example, for the reaction of two chemical species named A and B (as from Table 1) yielding the products named C and D, the corresponding TOPAS parameters are the following:

sv:Ch/Default/BinaryReaction/A/B/Products = 2 "C" "D"
d:Ch/Default/BinaryReaction/A/B/ReactionRate = 2.95e10 /M/s

In Geant4-DNA the time evolution of diffusing chemical species (in a step-by-step approach) is sampled by using a combined approach of fixed and dynamical time steps (M. Karamitros et al. 2014). In this work, the recommended dynamic time steps with limits described in Table 4 of reference (M. Karamitros et al. 2014) were used.

Table 4.

Primary electron initial energy, maximum energy loss E_thr before terminating the primary track, and average LET_100eV over that track segment, errors are statistical.

Initial energy (keV)	Ethr (keV)	Ethr in percent of initial energy (%)	Average LET100eV (keV/µm)
2.0	1.2	60	8.53±0.32
3.5	1.6	45	4.91±0.15
7.5	2.3	30	2.48±0.07
12.5	3.8	30	1.82±0.13
30.0	6.0	20	0.76±0.06
80.0	8.0	10	0.42±0.07
1000.0	10.0	1	0.08±0.01

2.2.3 Verification of the scoring of spatial-temporal information of chemical species

The spatial-temporal information of the chemical stage was accessed by means of the TOPAS scoring manager. This allows retrieval of information from any geometrical component in a step-by-step fashion (see Figure 1), and is compatible with the multithreaded capability of Geant4. For example, the diffusion range distributions of chemical species were obtained by simulating the track of mono-energetic electrons of 200 eV in a homogeneous water phantom, sufficiently large to contain the entire track with all physical and chemical secondaries. The distance from the origin position of chemical species at 1 µs was scored with a tuple scorer ( TsMoleculeTuple), and the diffusion range probability distributions were estimated. This scorer allows retrieval of tuple data (in either binary, ascii or ROOT format) containing the history number, global position, vertex information, name, interacting volume (where a hit occurred) and time-of-flight of molecular species in the chemical stage at user-given time intervals. The diffusion range probability distributions were compared with the solution to the Smoluchowski equation (in the same notation as shown in (M. Karamitros et al. 2014)) evaluated with the diffusion coefficient of each chemical species.

2.2.4 Comparison of simulated and measured chemical yields

The yield of chemical species produced (or consumed) at a specific time per 100 eV of energy deposit is referred to as the G-value (Burton 1947). At times when reactions are complete (~1 µs in this work), the G-value is referred to as the primary (or scape) yield G_X, where X is any of the species described in Table 1, e.g. G_•OH, G_H•, etc. In water radiolysis simulations, the decomposition of water widely assumes material balance of reducing products G_red and oxidizing products G_ox (Allen 1961; I. Draganic and Draganic 1971). That is, the following equalities should be satisfied (I. Draganic and Draganic 1971)

$$G_{\text{ox}}=G_{•\text{OH}}+2G_{{\mathrm{H}}_2{\mathrm{O}}_2}=G_{-{\mathrm{H}}_2\mathrm{O}}$$ (2)

$$G_{\text{red}}=G_{{\mathrm{e}}_{\text{eq}}^{-}}+2G_{{\mathrm{H}}_2}+G_{\mathrm{H}•}=G_{-{\mathrm{H}}_2\mathrm{O}}$$

These criteria were verified in the TOPAS-nBio simulations. In addition, the evolution along the time of G-values from 1 ps to 1 µs and the G_x as a function of the linear energy transfer (LET) for electrons, protons and alphas were calculated and compared with experimental data, and calculations from the literature.

G-value setup for electrons

For electrons, the setup consisted of a cubic water phantom of 1 km width, large enough to stop all secondary particles generated in Geant4-DNA (electromagnetic processes only). A smaller volume would have minimal impact on calculation efficiency. The phantom was irradiated with an isotropic and mono-energetic electron point source located at the center. Based on (Uehara and Nikjoo 2006; Ballarini et al. 2000; Mathieu Karamitros et al. 2011) only a segment of the entire physical track was used. That is, the primary electron track was terminated once its accumulated energy loss along the track exceeded a user defined energy threshold, E_thr. All secondary electrons generated were simulated. The energy loss of each primary was calculated by accumulating the difference between the electron energy at the energy deposition event at step i and the electron energy at the energy deposition event at step i+1. To represent the dependence of G_x as a function of LET, the LET_100eV was averaged over the track segments by dividing the sum of the energy deposited by the primary electron added to the energies of the secondary electrons with energy lower than 100 eV, by the total primary electron track length (ICRU 1970). In Table 4, the primary electron energies, energy thresholds E_thr, and averaged LET over the track segments are shown.

G-value setup for protons and alphas

For protons and alphas E_thr was unnecessary because the geometry considered was thin enough so that the primary particles had sufficient energy to fully traverse the geometry. The setup consisted of a cubic water phantom of 5 µm side where mono-energetic and mono-directional point sources were placed along the whole length of one edge, as used in (M. Karamitros et al. 2014). In that study, G-values calculated with Geant4-DNA were calculated for protons from about 1–38 keV/µm. For protons, the averaged LET was estimated in separate simulations under the same geometry conditions, using condensed-history MC with the TOPAS scorer protonLET. This scorer calculates the LET by weighting the unrestricted electronic stopping power from lookup tables of Geant4 with the energy deposition at the beginning of each proton step (Granville and Sawakuchi 2015). This weighting method was used to calculate the average LET of alphas as well, but in this case the stopping power was calculated in a step-by-step basis by dividing the energy deposition of each particle by it step length, as described in (Romano et al. 2014).

3 Results

3.1 Verification of the scoring of spatial information for chemical species

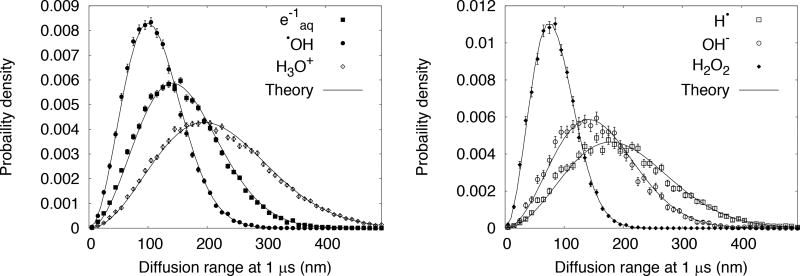
Simulations were done to demonstrate that the TOPAS scoring manager can access the spatial position of species (see section 2.2.3) since the classes that manage the transport of chemical species in Geant4 are different than those that manage the transport of physical particles. The diffusion range distribution obtained from the scored spatial positions of chemical species (Table 1) at 1 µs, using the TsMoleculeTuple, are shown in Figure 2. The probability distributions described by the solution to the Smoluchowski equation were in good agreement with the calculations, as expected, since the implementation is based on this equation. For clarity, the curve for H₂ was not included, because its diffusion coefficient is very close to that of e⁻_aq.

Figure 2.

Diffusion range of chemical species set in motion in homogeneous water at 1 µs from incident electrons with energy 200 eV, calculated from TOPAS-nBio with Geant4 version 10.3.p1. Error bars represent statistical uncertainties at 1 standard deviation. Theory refers to the Smoluchowski equation.

3.2 Comparison of simulated and measured chemical yields

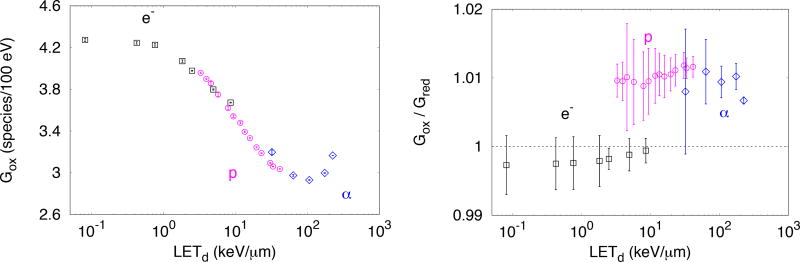
The components of the material balance equation for electrons, protons and alphas as a function of LET are shown in Figure 3. For electrons, the balance equation was satisfied within 0.3% or 1 standard deviation; whereas statistically significant differences of 1% (for some values well outside 3 standard deviations) were found for protons and alphas.

Figure 3.

Oxidizing products G_ox of material balance equation, see Equation 2 (left plot); and the ratio between oxidizing to reducing G_red products (right plot). Results calculated with TOPAS-nBio for electrons (e-, black points), protons (p, magenta points) and alphas (α, blue points) are shown.

3.2.1 Time evolution of chemical yields

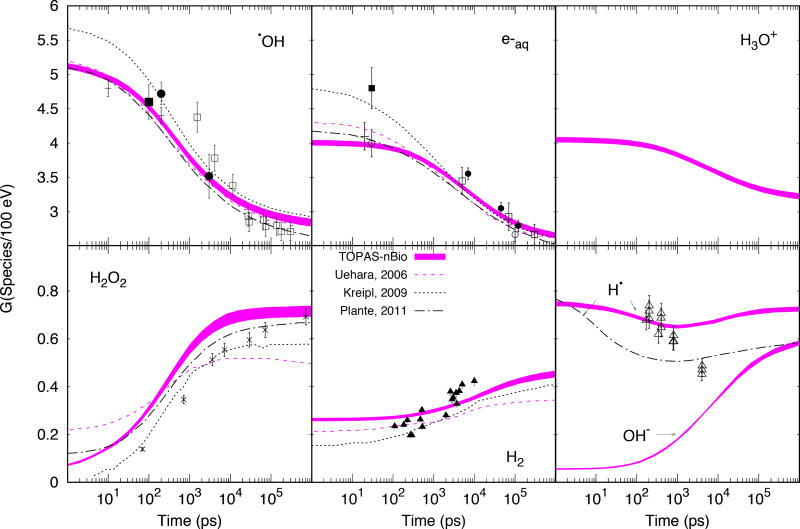
Pimblott and LaVerne (Pimblott and LaVerne 1998) showed that the G-value for electrons is unaffected by increasing the initial energy above 100 keV. As the published experimental data is limited to energies in the MeV region, 1 MeV electrons were used to compare the temporal evolution of the G-values in the chemical stage (1 ps to 1 µs).

TOPAS-nBio results are displayed in figure 4 where the thickness of the line represents the standard deviation of the mean. Also in figure 4, data from other MC codes are shown for comparison purposes: 1 MeV electrons from (Uehara and Nikjoo 2006), 750 keV electrons from (Kreipl, Friedland, and Paretzke 2009) and 300 MeV protons from (Plante 2011a). The available experimental data is also shown. The G-values of chemical species created at the pre-chemical stage (see Table 2) reduced monotonically with increasing time with the exception of H^•, which reached a minimum at about 1 ns. All other molecules created at the chemical stage (H₂O₂, H₂ and OH⁻) increased up to saturation at 1 µs. As shown, overall reasonable agreement of Geant4-DNA results in the range of the experimental data was achieved: For ^•OH, after 3 ns, comparison with data from (Laverne 2000) showed differences within 7%±8%, whereas at 10 ps and 200 ps comparison with data from (El Omar et al. 2011) showed differences within 3%±4% and −1%±5%, respectively; for e⁻_aq after 5 ns and overall averaged difference within 3%±3% was found with all experimental data, whereas differences of −3%±5% (20 ps) and −1%±6% (30 ps) with data from (Muroya et al. 2005) and (Wolff et al. 1973) were found, respectively; for H₂O₂ the calculated data differences by up to 49%±7% at earliest stages were found and reduced down to 3%±12% at saturation. Measured data found for H₂ and H^• consisted of G-values measured at different scavenging concentrations. They are displayed in figure 4 for reference only.

Figure 4.

Time evolution of G-values for mono-energetic electrons of 1 MeV. TOPAS-nBio results as thick colored lines, with the thickness of the lines representing 1 standard deviation of the mean. Calculated data from other MC codes are shown with dashed (Uehara and Nikjoo 2006), dotted (Kreipl, Friedland, and Paretzke 2009) and dot-dashed (Plante 2011a) lines. Experimental data are plotted as points. For ^•OH: □ ⁶⁰Co γ-rays (Laverne 2000), ■ ~2 MeV electrons (Jay-Gerin and Ferradini 2000), ● 20–22 MeV electrons (Jonah and Miller 1977), the latter with data scaled by a factor of 0.8 (see (Kreipl, Friedland, and Paretzke 2009)), + 7 MeV electrons (El Omar et al. 2011). For e⁻_aq: □ ~35 MeV electrons (Shiraishi et al. 1988), ■ ~45 MeV electrons (Sumiyoshi and Katayama 1982), ○ ~40 MeV electrons (Wolff et al. 1973; Hunt et al. 1973), ● ~2.9 MeV electrons (Buxton 1972), + 20 MeV electrons (Muroya et al. 2005). For H₂O₂: × ⁶⁰Co γ-rays (Laverne 2000). For H₂: ∆ ⁶⁰Co γ-rays (Draganić and Draganić 1975). For H^•: ∆⁶⁰Co γ-rays (Z. D. Draganic and Draganic 1972).

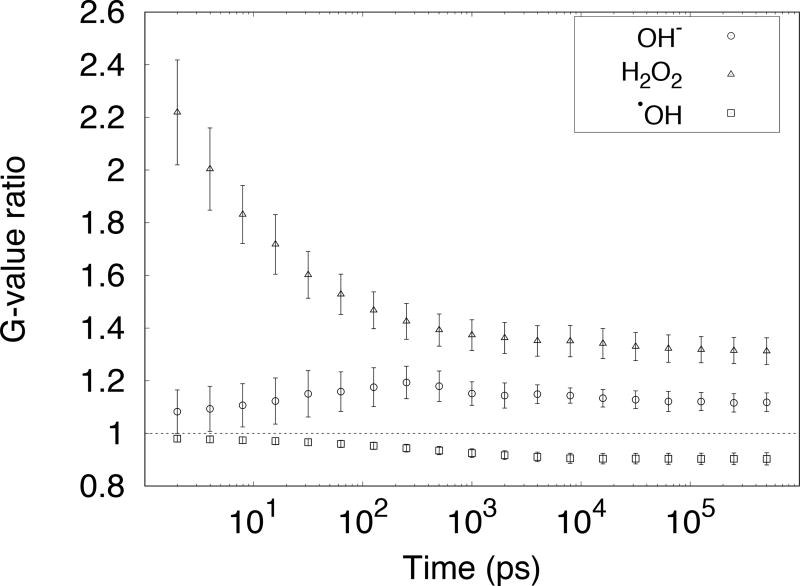
As shown in Tables 1 and 3, some diffusion coefficients and reaction rates used in TOPAS–nBio (see section 2.2.2) differ from those provided by default in Geant4-DNA. This was expected to lead to differences in chemical yields in the chemical stage. The largest differences in G-values were found for ^•OH, OH⁻ and H₂O₂. The ratios of the G-values calculated with TOPAS-nBio with respect to G-values calculated with the default Geant4-DNA parameters for these species are shown in Figure 5.

Figure 5.

Ratio between G-values calculated with diffusion coefficients and reaction rates from this work, to G-values calculated with diffusion coefficients and reaction rates from Geant4-DNA default (see Tables 1 and 3).

3.2.2 LET-dependent primary chemical yields

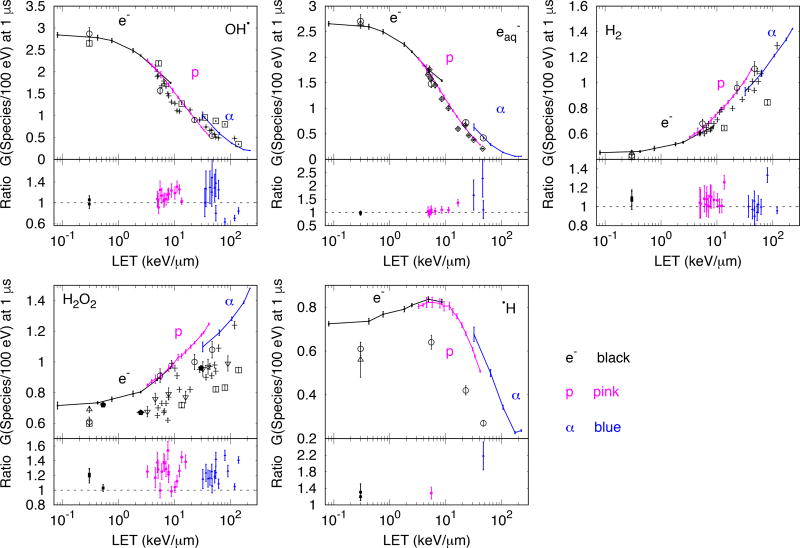
The LET-dependent G_x for six chemical species calculated with TOPAS-nBio for electrons, protons and alphas, are compared to each other and to the available experimental data in Figure 6. Experimental data for ^•OH, H₂O₂ and H₂ obtained from (Burns 1981) correspond to irradiations with ⁶⁰Co, protons, alphas, ¹⁴N and ²⁰Ne. The LET values were obtained from the same reference with the corresponding errors from (Bisby, Cundall, and Burns 1975). Data shown for ^•OH (with material balance equation), e⁻_aq, H₂O₂, H₂ and H^• obtained from (Appleby and Schwarz 1969) correspond to irradiation with ⁶⁰Co, deuteron and alphas. In reference (Appleby and Schwarz 1969), the particle primary energies but no LET values were provided. Thus, the LET values were calculated with the method described in section 2.2.2 for charged particles and a LET of 0.3 keV/µm was used for ⁶⁰Co, as previously used by (Plante 2011b; Hervé du Penhoat et al. 2000). Data shown for e⁻_aq obtained from (Sauer et al. 1977) correspond to irradiation with deuterons and alphas, reported at 10⁻⁵ s. For clarity, some points around 5 keV/µm were omitted. Data shown for e⁻_aq, H₂O₂, H₂ and H^• obtained from (A. . et al. Elliot 1993) correspond to ⁶⁰Co. Data shown for H₂O₂ were obtained from (Pastina and LaVerne 1999) for protons and alphas. In (Pastina and LaVerne 1999) the LET provided was track-length averaged. For comparison, the LET shown in the figure was re-calculated to dose averaged LET with the methods referenced in section 2.2.2. Data shown for H₂O₂ were obtained from (Wasselin-Trupin et al. 2002) for ¹³⁷Cs (LET of 0.53 keV/µm), protons and carbon ions. Data shown for ^•OH, H₂O₂, and H₂ obtained from (Anderson and Hart 1961) correspond to irradiation with protons, deuteron and alphas, with the LET re-calculated to dose averaged LET (from the beam energies provided in the reference) using the methods referenced in section 2.2.2.

Figure 6.

G_x as a function of LET_100eV for mono-energetic electrons (e−), protons (p) and alpha (α) particles. Results calculated with TOPAS-nBio are shown with points connected with solid lines (e− black, p pink, α blue). At the bottom of each panel, the ratio of calculated to experimental G-values are shown. Statistical errors of simulations are 1 standard deviation. Experimental data: □ (Burns 1981), ○ (Appleby and Schwarz 1969), ◇ (Sauer et al. 1977), ∆ (A. . et al. Elliot 1993), ∇ (Pastina and LaVerne 1999) with LET recalculated to dose averaged LET from track-length averaged LET, see text, ⬟ (Wasselin-Trupin et al. 2002) and + (Anderson and Hart 1961) (for details see section 3.2.2)

The ratio of calculated to experimental G_x values are also shown in Figure 6. The mean ratios were 1.11±0.98, 1.21±1.11, 1.05±0.52, 1.23±0.59 and 1.49±0.63 (1 standard deviation, combined experimental and statistical calculation uncertainty) for ^•OH, e⁻_aq, H₂, H₂O₂ and H^•, respectively.

4 Discussion

The simulations done for this work were the result of combining the capabilities of Geant4-DNA for modeling radiolysis of water with the capabilities of TOPAS-nBio to configure parameters and set up geometries. The TOPAS-nBio platform provided a clear way to test different chemical parameters and to combine complex geometries with the new chemistry scoring capabilities, using a reduced number of TOPAS parameters. The resulting simplified procedure for simulating radiolysis was demonstrated in this study in the calculation of G-values and primary yields G_x of electrons, protons and alphas, with comparison to published experimental data.

The material balance equation (equation 2) was used as a quality control on the simulation. The equation was satisfied for electrons within 0.3%. In this case the geometry was large enough to score all chemical species created even if the primary electron was terminated after losing energy E_Thr. This was verified for protons of 300 MeV by running a simulation using a cubic box with a 100 µm side (same geometry as in (Plante 2011a; Hervé du Penhoat et al. 2000)). The G_x obtained was 2.71±0.07 for ^•OH/100 eV, 0.59±0.01 for H₂O₂/100 eV, 2.31±0.07 for e⁻_aq/100 eV, 0.44±0.02 for H₂/100 eV and 0.71±0.01 for H^•/100 eV. These values satisfied equation 2. However, the calculation was very inefficient. The CPU time was reduced by about a factor of 20 by shrinking the cubic box to a 5 µm side. In this case the balance equation showed up to 1.3% difference for protons and alphas. The smaller geometry (5 µm length), used for protons and alphas in this study, resulted in undercounting species as a result of the reaction of species that diffused backwards from the entrance of the water box, where the beam was initially positioned. For the smaller geometry, despite the slight deviations from the balance equation, the agreement with the experimental G_x was satisfactory, well within the observed variation in the measured data. The use of the smaller box for protons and alphas provided a reasonable tradeoff between accuracy and calculation time.

The time evolution of G-values (Figure 4) agreed reasonably well with measured and simulated data from the literature. There are no published experimental data available at the pre-chemical stage (~1 ps), as this requires direct observation of G-values in this very short time frame, although G-values at tens of picosecond had been published (El Omar et al. 2011) (at 10 ps for ^•OH) (Muroya et al. 2005) (at 20 ps for e⁻_aq). Currently, comparisons at this stage rely on other MC codes whose initial yields strongly depend on several factors: the physical models (mainly the elastic scattering model), branching ratios and dissociation schemes (Uehara and Nikjoo 2006). The latter two factors are typically adjusted to match the temporal evolution of G-values (Ballarini et al. 2000). The level of agreement between the published results of different MC codes was comparable to that for Geant4 v10.3p01 with TOPAS-nBio and agreed within uncertainties with published G-values at earliest stages available 10 ps and 20 ps for ^•OH and e⁻_aq, respectively.

When comparing with experimental data (Figure 4), the MC results of this work predicted 7% higher yields after 3 ns for ^•OH and about 50% for H₂O₂. The discrepancy is possibly due to the algorithm used to determine which chemical species are near enough to interact as they diffuse and the reaction probability, as follows. The proximity algorithm may not find all of the chemical pairs that are near enough to react. In addition, the current implementation of the chemistry stage in Geant4-DNA leads to a reaction every time two reactant chemical species are separated by a distance shorter than their effective reaction radius (M. Karamitros et al. 2014). However, different reaction probabilities have been used by others for partially diffusion-controlled reactions where ^•OH and H₂O₂ are mostly involved. The reader is referred to (Plante 2011b; Plante and Devroye 2017) for a comprehensive description of non-homogeneous chemistry of the radiolysis for Monte Carlo simulations.

Regarding G_X, the experimental data for protons and alphas were reported as a function of the track-averaged LET (data from (Pastina and LaVerne 1999) in figure 6) or as a function of the primary particle energy (data from (Appleby and Schwarz 1969) in figure 6). In those cases, the dose-averaged LET was calculated with condensed-history MC as done in (Granville and Sawakuchi 2015) for protons and (Romano et al. 2014) for heavier ions. This caused a slight shift to lower LET values and led to a better agreement of experimental and calculated data.

There was a lack of specificity in the experimental uncertainties reported for LET-dependent G_x values. The observed range in the measurements (Figures 4 and 6) suggests that reported uncertainties were primarily based on repeatability. The approximate 6% uncertainty estimate in Figure 4 for ^•OH and e−_aq for the combined systematic and random uncertainty was inferred from systematic uncertainties reported for the time-dependent G-values. Uncertainties in the results of MC simulations were statistical, with a sufficient number of histories run to achieve at minimum a 2% uncertainty. Experiment and simulation generally agreed within the combined experimental and calculation uncertainty. However, significant differences between the results of our simulation and the experimental data for H₂O₂ and H^• were found. The case of H₂O₂ is of particular importance when simulating cellular radiobiology. Despite the agreement within the experimental uncertainty at low LET (<1 keV/µm, see also figure 4), at much higher LET (figure 6) the increment in concentration of H₂O₂ is considerable, requiring consideration of reactions that lead to the reduction of H₂O₂ yield, such as H₂O₂ + ^•OH → HO₂ + H₂O and H₂O₂ + ^•H → ^•OH + H₂O (Pastina and LaVerne 1999). These reactions were not included in the present study as they are not part of the default reactions in Geant4-DNA. In addition, experimental data to determine the yields of H₂O₂ in most of the cases contain a certain amount of scavenger, that has been shown to reduce the G-value with increasing scavenging capacity (Pastina and LaVerne 1999). However, scavenging is not yet fully developed in Geant4-DNA and the simulation of such systems was out of the scope of the current study. The effect of multiple ionization in single ion water collisions, currently not included in Geant4-DNA physics, had been proposed to cause a progressive reduction in the yield of H₂O₂ as LET increases from about 10 keV/µm, as studied in (Meesungnoen and Jay-Gerin 2005). Finally, as described before, the totally diffusion controlled scheme implemented in Geant4-DNA may be complemented with partially-diffusion controlled reactions. Together these points could improve the accuracy of Geant4-DNA and we anticipate that TOPAS-nBio will facilitate the study of such complex scenarios.

5 Conclusions

We have included water radiolysis in TOPAS-nBio, a new extension to the TOPAS MC toolkit for radiobiological simulations. The extension is easy to use without advanced programming skills, while allowing the user to exploit the tools under development for Geant4-DNA. The diffusion coefficients, reaction rates and branching ratios are easy to configure by means of the TOPAS parameter system. Additional reactions and chemical species may be easily specified. We have further re-evaluated the Geant4-DNA radiochemistry parameters and included updated values in TOPAS-nBio.

The extension was successfully used to simulate G-values, with results compared to published measured data and the results of other codes. In general, agreement between measurement and simulation is within the estimated uncertainty, including an approximate estimate of the systematic uncertainty in the measurement.

The capability to score the spatial-temporal information of chemical species in a step-by-step way allowed the combination of complex simulations involving the physical, pre-chemical and chemical stages with sophisticated geometries, moving TOPAS-nBio further towards the goal of becoming an integrated radiobiological MC tool. Further work is needed to improve calculation efficiency to facilitate high precision benchmarking and improve the reliability of the simulation.