Abstract
Supporting decision making in drug development is a key purpose of pharmacometric models. Pharmacokinetic models predict exposures under alternative posologies or in different populations. Pharmacodynamic models predict drug effects based on exposure to drug, disease, or other patient characteristics. Estimation uncertainty is commonly reported for model parameters; however, prediction uncertainty is the key quantity for clinical decision making. This tutorial reviews confidence and prediction intervals with associated calculation methods, encouraging pharmacometricians to report these routinely.
Pharmacometric models describe drug‐related characteristics, such as pharmacokinetic (PK) or pharmacodynamic (PD) properties. Input parameters include the dose, dosing regimen, treatment duration, and other possible factors.
Frequently, models are used not only to describe the available clinical or nonclinical data but model‐based simulations are used to explore the expected outcomes of treatment options. Typical questions may include “what drug concentration is required to induce the targeted pharmacological effect in x% of treated patients?” or “how many patients are predicted to experience an adverse event on this dose?” Beyond the predictions, the uncertainty surrounding them is of equal importance. With a large uncertainty, decision makers might want to be more conservative in their choice of treatment option or consider further experimental assessments to reduce their level of uncertainty to an acceptable level.
Confidence intervals, which are a measure used to describe the uncertainty in a prediction or point estimate, are common in use, but are often misinterpreted. A frequentist confidence interval is defined as follows: if you could repeat an experiment many, many times and create an interval for some parameter with each experiment, then a 90% confidence interval is such that 90% of those intervals contain the true value. A confidence interval is not the probability that the confidence interval contains the true value (that is a Bayesian credible interval).
Predicting the value of a future observation has inherently more uncertainty because it deals with a future unobserved observation. The corresponding interval around that prediction, which is called a prediction interval, is, therefore, generally wider.
Thus, the two types of intervals must be distinguished: (1) confidence intervals related to a statistic of the observed data, such as the mean (e.g., the 90% confidence interval around the mean), and (2) prediction intervals related to predictions related to future observations (e.g., the 90% prediction interval for a single future patient or the mean of a number of future patients).
For pharmacometric models, the uncertainty around model‐predicted quantities originates from the uncertainty about model parameters. These parameters are typically estimated from data (e.g., from clinical study data), and their estimates will change with a different dataset (e.g., if another clinical study with the same study design is conducted).
Model diagnostics reported from clinical studies typically include parameter estimates, standard errors, and relative standard errors for single model parameters, such as the absorption rate constant or drug clearance. An additional postprocessing step is required for translating parameter estimation errors to uncertainty around the quantity of interest (i.e., confidence intervals for the response), which may be a single value (e.g., the response at the end of treatment) or a curve (e.g., drug concentration over time or the difference to placebo in clinical response over time).
Uncertainty around a parameter estimate allows the derivation of statistical quantities, such as power estimates (e.g., the probability of detecting a given difference between two treatment groups). In particular, it is important when making predictions to answer questions such as “which dose is required to achieve a given trough level concentration in 90% of all patients” or “how many patients are expected to experience a biomarker level outside the normal range?” Of interest is the derivation of confidence or prediction intervals or bands (over time) around the model prediction that assess the reliability of such estimates and may be important for decision making.
Standard linear and nonlinear models commonly assume identical and independent distributions of the observations with variability arising solely from residual variability. Software for regression analysis commonly provides confidence intervals for the fitted curve (e.g., the functions lm, nlm, or nls in R1 or GraphPad2 routines). The underlying algorithm can vary because different methods are available and they often provide different results.
Pharmacometric mixed‐effects models introduce a further level of variability between units, such as human beings or animals. The observed variability originates from interindividual variability and residual variability. Interindividual variability is modeled by random effects describing the deviation from population average parameter values (fixed effects). As additional known or fixed effects, parameters can further depend on covariates, such as body weight. The combination of known and unknown effects in variability is reflected in the term mixed‐effects modeling.
Mixed‐effects models can arise in many forms, including linear mixed‐effect and nonlinear mixed‐effect (NLME) models.3 A further level of complexity arises with time as a model component, for example, in describing drug concentrations over time for a particular patient population. Longitudinal NLME models are the most common type of models in pharmacometrics.4 Model parameters can differ between individuals with differences originating from different sources: known (fixed) effects, such as age on drug clearance or body weight on apparent volume of distribution along with unexplained variability (random effects), such as differences in drug clearance for unknown reasons.
With random effects, interindividual variability (differences between subjects) is the most typical case, but models may include other random effects, such as interoccasional variability, which attributes variability to different occasions, such as visits to the clinic. Simulations and quantification of confidence intervals for these models are complicated by the fact that model simulations themselves are (prediction) intervals because they describe outcomes for the population, including the random parameter variability. This variability can be termed “uncertainty” because the individual parameter of a future subject is unknown, resulting in uncertainty for an individual prediction. However, this uncertainty is quantified by a model parameter (describing the observed variability), not to be confused with uncertainty about the parameter value. Note that the estimated variability parameter also has an uncertainty. To clearly distinguish between variability related to model parameter estimation and variability in the data described by the model, the former is termed “uncertainty” and the latter “variability” for the remainder of this tutorial.
For mixed‐effect models with hierarchical variability structure, the question that is addressed determines at which level, the individual level or the population level, confidence and prediction intervals need to be calculated. For example, it might be important to determine the percentage of patients in which a given dosing is predicted to result in concentration exceeding a safety threshold. In this case, the calculation of a prediction interval needs to take interindividual variability into account. In contrast, taking only parameter uncertainty into account might suffice when assessing the difference in exposure levels of typical subjects of two different populations. The tutorial covers different scenarios for NLME models and typical questions that are addressed in each.
Starting with proper definitions of the terminology related to uncertainty, basic concepts are reviewed before different methods for the calculations of confidence and prediction intervals are discussed. Exact calculations of confidence and prediction intervals for linear models illustrate the general principles before approximation and estimation methods are introduced for nonlinear models. Finally, these methods are discussed for NLME models. Case studies illustrate the different methods and allow for a comparison between them.
All models are abstractions, and confidence in model predictions depends on the extent of knowledge and data that went into their development. Uncertainty is always here to stay, but modelers need to be — and are — able to quantify it. Pharmacometricians are encouraged to routinely provide confidence and prediction intervals when providing input to decision making in drug development. Vice‐versa, collaborators, including physicians, clinical pharmacologists, and managers, are encouraged to ask for them if they are not provided.
Terminology
Before embarking on discussing the concepts and calculus of confidence and prediction intervals, a proper definition of the terminology is vital because common terms are not used consistently across publications. It is appreciated that the terminology is related to scientific viewpoints, such as the frequentist or the Bayesian perspective. The terminology used here is close to the frequentist perspective; the Bayesian framework is discussed later.
This tutorial covers two types of models, standard regression models and NLME models. Both models comprise a structural component (i.e., a function deterministically linking independent variables) such as time to a response (e.g., a concentration) given a set of model parameters. Residual variability is added by the error model, describing random deviations of the prediction from the observed data. For NLME models, an additional layer of random variability is introduced by assuming that the model parameters differ randomly between individuals or occasions.
In the following, the terms related to (i) both kinds of models, (ii) mixed‐effects models, and (iii) error models for describing residual variability are introduced. Error models apply to both, regression and mixed‐effects models.
General terms
Uncertainty is the precision up to which an unknown quantity can be determined given the available observations. Examples of unknown quantities include drug clearance, exposure to drug over a steady‐state dosing interval (given individual PK parameter estimates), or a PD effect, such as blood pressure in a typical subject at the time after the first dose. Note that uncertainty is only related to the precision with which the model parameters can be estimated.
Variability is all unexplained variation, random effect(s), and residual error(s) but not parameter uncertainty.
The estimate/estimator and estimation error is the value calculated according to a certain method as an estimate for an unknown quantity based on the available data and its uncertainty depending on the information content of the data.
A model parameter is an unknown quantity. Model parameters are estimated by statistics, such as the mean, but are more commonly referred to as parameter estimates in the pharmacometrics literature. Examples include drug absorption and elimination rate constants, interindividual model parameter (co‐)variance, or residual error variability.
Variance, covariance, and SD are statistical terminology to denote a parameter of a distribution that defines the spread of the data. Examples include the variances of the normal and the log‐normal distributions.
A residual error is an unexplained variability when all other components (fixed and random effects) are accounted for. Examples include additive and multiplicative residual errors.
Residual variability is the variability parameter that defines all unexplained variability in the data, which may be due to assay error, etc. An example is the SD parameter of the additive residual error.
Mixed effects modeling terms
Fixed effects are the known deviations from the population‐typical parameter. Examples include the effect of body weight on apparent volume of distribution or the effect of age on apparent drug clearance.
Random effects are the unexplained variability between parts of data. Examples for parts include data from individuals in a population or occasions, such as visits to the clinic.
Interindividual variability is an unexplained variability between individual population members (“individuals”). In NONMEM5 terminology, this denotes the η (eta) parameter of random effects assumed to be normally distributed with mean 0 and covariance matrix Ω (Omega).
Interoccasion variability is the variability between occasions, such as different mean measurements at different visits to the clinic.
A study simulation is the simulation of the number of individuals of a population, as defined in the study protocol. Repeated simulations with identical model parameters may result in differences in the results due to expected random differences between studies. Study simulations typically aim at assessing response to treatment (e.g., the primary endpoint of the study) and uncertainty. Such simulations are frequently used for statistical power estimation.
A population simulation is the simulation of a large number of individuals. The number should be selected large enough such that results from repeated simulations with identical model parameters are negligible. The higher the random interindividual and intraindividual variability, the larger the number required. Population simulations aim at assessing the overall response to a treatment and its distribution.
Error models
An appropriate error model that reflects the nature of the observations needs to be chosen. For concentrations that cannot be negative, a normal distribution of residuals independent of the predicted value may be inappropriate because the suggested prediction interval could expand to negative values.
The normal distribution, however, is frequently used for its computational properties. Many non‐normal distributions of observations can be transformed to the normal distribution (and back). Concentrations are typically assumed to be log‐normally distributed and the logarithmically transformed concentrations can be described by a normal distribution. In other cases, residuals are normally distributed but their variability depends on the predicted value, hence, the SD needs to be conditioned on the predicted value f(x, ).
Commonly used error models in pharmacometric modeling are additive (Eq. (1)), proportional (Eq. (2)), a combination of additive and proportional (Eq. (3); denoted as combined in the following), or exponential (Eq. (4)) with ε ∼ N(0, 1).6
| (1) |
| (2) |
| (3) |
| (4) |
Basic concepts of confidence and prediction intervals
Confidence intervals quantify how precisely a variable can be determined based on available information. Being interested in the average body weight of an entire population, the arithmetic mean of a sample can serve as an estimate. The larger the sample, the more precisely average body weight can be determined. The precision of the estimate can be characterized by the 90% confidence interval. Note that with the law of large numbers, confidence intervals generally get smaller with increasing numbers of observations because the standard error of the estimate gets smaller.
Prediction intervals are wider because they take confidence intervals and include the inherent random variability of a future observation. Using the previous weight example, a prediction interval quantifies the expected range of body weight in a future population of subject(s), not just in the dataset used to estimate the average.
Bayesian techniques, which incorporate prior beliefs into the confidence interval calculation, base inference on what is called the highest posterior density (HPD) creating what is called a credible interval. The HPD interval reflects what is known about the parameter (i.e., the distribution after having updated the prior information with data). The HPD is commonly defined as the area that contains a specified percentage of the posterior density (such as 90%) with no value outside the area having higher probability than any value inside the area.7, 8, 9
To some extent, the difference is philosophical: whereas the frequentist would postulate that the 90% confidence interval contains the true value in 90% of the cases if the experiment could be repeated many times (therefore, a frequentist argument), the Bayesian would state that the 90% HPD is the interval that contains the unknown parameter value with 90% probability. If nothing is known about the prior distribution, that prior distribution is said to be noninformative (i.e., flat), and frequentist confidence intervals and Bayesian credible intervals are generally the same.10, 11 The Bayesian definition is frequently attributed to a frequentist interval (i.e., assuming that the frequentist interval contains the true value with x% probability).
A confidence interval is, therefore, a statement about the precision of the estimated value or statistic given the variability in the data, whereas prediction intervals quantify the expected range for one or multiple additional future observations, including uncertainty about the parameter and random variability.
In this tutorial, a simulation is defined as any future prediction and Monte‐Carlo simulation that takes into account random variability.
Focusing on confidence and prediction intervals for model prediction, the confidence intervals for model parameters are not discussed in detail in this tutorial. Nevertheless, their definition is shortly described for the various methods introduced.
CONFIDENCE AND PREDICTION INTERVALS FOR REGRESSION MODELS
Exact calculation for linear models
In the case of linear regression models of the form with independent observations, confidence and prediction intervals can be determined analytically. The method, ordinary least squares, minimizes the sum of the squared errors in the y‐direction (i.e., with , with the hat symbol, , denoting parameter estimates). Therefore, the confidence interval is determined in the direction of the dependent variable only (y).8 It is noted that these models are frequently used for data for which the independent variable is not measured error‐free and the error should be minimized in both directions. Such methods (that are computationally more burdensome) are known as errors‐in‐variables models.12
For a given value of x, the confidence interval is dependent on the SD, , of the residuals, the sample size, , and the distance from the arithmetic mean of x ( ) as follows:
| (5) |
Details are provided in Supplementary Material S2.1.
The confidence interval is smallest at the x‐value with most information (i.e., the mean of x ( ) for the linear regression model), and gets wider the farther away the x‐value is from .
For the prediction interval of a future observation, the interval containing a future observation with a given probability, additional variability from the SD of the residual is added because the observation has not been observed yet. It becomes apparent immediately that prediction intervals are always wider than confidence intervals. Note that , an estimator for the true SD, is considered to be independent of x or y ( is added with a constant in the regression model depicted above). As discussed later, the prediction interval directly depends on the assumption how residuals are distributed (i.e., which error model is assumed). Supplementary Material S2.2 provides the full equations.
In the computing environment R,1 model fits, and confidence and prediction intervals can be calculated in a straightforward manner:
set.seed(38497)
df <‐ data.frame(x=rnorm(10))
df$y <‐ −3 + 0.2 * df$x + rnorm(nrow(df))
fit <‐ lm(y ∼~ x, data = df)
predict(fit, interval="confidence", level=0.9)
predict(fit, interval="prediction", level=0.9)
Estimation approaches for confidence intervals
For nonlinear models, such exact calculation for the confidence intervals of the model prediction as discussed above does not exist in general. Estimators of confidence and prediction intervals are introduced in the following and their calculus illustrated. Note that a comparison of the analytical solution and the estimation approaches for the linear case are provided in the Supplementary Material.
Estimation by the Delta method
The Delta method works by approximating the underlying model with a first‐order Taylor series expansion.8, 13 The uncertainty of the parameter estimates (i.e., the covariance matrix ) is translated to uncertainty in the predictions via the Jacobian matrix, , containing the partial derivatives of the model function f with respect to the model parameters . The Jacobian matrix defines the change in model prediction for changes in model parameters at the estimated value (i.e., at the maximum likelihood).
| (6) |
It is noted that the approximation is generally biased, but becomes more exact if using second‐order or higher derivatives. The error due to the approximation can be quantified.14 Confidence intervals of model parameters are based on the covariance matrix of the estimates, .
Estimation by simulation
In contrast to approximation methods, such as the Delta method, simulation methods generally estimate the unknown quantity accurately on average and for large numbers of simulations: the method is unbiased. For many problems, conducting simulations is substantially easier to implement than computing the Jacobian matrix using the Delta method.
The straightforward simulation approach for calculating confidence intervals for model predictions is to perform simulations based on parameters sampled from the uncertainty distribution of the parameters.15 The parameter estimates are assumed to be multivariate normally distributed, as defined by their covariance matrix, . Thus, the calculation of confidence intervals for the model prediction involves iterating over: (1) sampling of parameters; (2) calculation of model predictions; and (3) determination of the interval boundaries as percentiles of the model prediction distribution.
As for the Delta method, confidence intervals for model parameters are calculated based on the covariance matrix, .
Estimation by simulation/re‐estimation (bootstrap)
If it would be possible to repeat the experiment or study to obtain the data a large number of times, the parameter distribution across all datasets would represent the uncertainty with which they can be determined. As this approach is not feasible in most cases, simulated datasets are used that mimic the many observed datasets. Simulated datasets can be generated using either Monte‐Carlo simulations based on the model or bootstrapping from the data.
Monte‐Carlo simulations
With Monte‐Carlo simulations, model predictions are calculated for the observed data. Simulated datasets are created by sampling residuals according to the residual error model. This method is called parametric bootstrap because it is based on a parametric distribution to sample from.
(Nonparametric) bootstrap
Nonparametric bootstrapping is another alternative to generate simulated datasets. The bootstrap, as proposed by Efron & Tibshirani16 and Efron,17 involves resampling a dataset with replacement. A particular feature of this approach is that the correlation structure between covariates is kept when entire associated observations are drawn. Furthermore, random sampling is cheap with respect to computing time. Inference is, in turn, drawn from the sampled datasets.8, 17, 18 Consider an application randomly sampling patient data by sampling from the set of patients yields a large number of new datasets with the same number of patients but, in each dataset, some patients occur more than once and others not at all (due to sampling with replacements). If there are correlations in the patient characteristics (e.g., between age and body weight), the correlation is preserved because only the entire observations are sampled.
Pharmacometric datasets commonly comprise longitudinal data of individual subjects (i.e., multiple observations per subject). Therefore, resampling should generally be performed at the subject level and not at the observation level (i.e., subject identifiers are sampled, and all data from the sampled subjects enter the dataset). This may generate datasets with a different number of total observations than in the original dataset. Care should be taken that the randomness of the bootstrap procedure reflects the randomness of the study conduct. If bootstrapping is performed on a combined dataset (e.g., with healthy subjects and patients), the bootstrapped dataset should contain the same number of healthy subjects and patients as the original dataset. Covariates, such as sex, should be adjusted for if the adjustment is specified in the study setup (e.g., the protocol). If not, it is part of the randomness.
Once the simulated datasets are generated by Monte‐Carlo simulation or bootstrapping, parameters are estimated for each dataset. The sets of estimated parameters provide empirical distributions of the parameter estimates. Confidence intervals are calculated from the set of parameter estimates (e.g., the 90% confidence interval for a particular parameter is estimated as the range from the 5th to the 95th percentile of the set of parameter estimates). Thus, this approach provides a stochastic approximation (not assuming any distribution) of confidence interval estimation for parameter estimates. This is in contrast to the Delta method and the simulation approach that uses a parametric definition of the distribution of parameter estimates (i.e., a multivariate normal distribution defined by the estimates and their covariance matrix, ).
To finally derive confidence interval for model prediction, these are calculated for each set of re‐estimated parameters. The set of model predictions across all sets of re‐estimated parameters provides a nonparametric distribution that confidence intervals are derived from.
Approximation of prediction intervals
For the simulation and the simulation‐estimation approach, at each iteration, randomly sampled residuals are added to the predicted value to obtain a distribution of simulated values from which the prediction interval is derived. For the simulation approach, the residual variability estimate based on the original dataset is used. For the simulation‐estimation approach, the estimated residual variability of the current iteration based on a simulated dataset is used. The Delta method does not define prediction intervals.
Because prediction intervals include the residual variability, they directly depend on the model that describes the residual distribution (i.e., the error model).
ESTIMATION OF CONFIDENCE AND PREDICTION INTERVALS FOR POPULATION MODELS
Population or NLME models strive to explain only part of the observed variability based on known determinants and residual variability but also acknowledging random interindividual variability. In the example discussed earlier, for body weight, the observed variability is only to a small extent due to measurement errors. There is a contribution of known factors, such as sex, age, or nutritional supply, on the one hand and the natural interindividual variability of body weights on the other. Thus, two levels of random variability are included. To describe interindividual variability, parameters are typically assumed to be normally distributed and, thus, the mean and SD of this distribution are parameter estimates for the population model.
Scenarios
The question to be answered drives how the different layers of variability are considered when calculating confidence and prediction intervals in the context of NLME models. With a population model, inferences can be made for individuals or for the population. Different scenarios are distinguished.
Scenario 1: prediction of the response for a typical subject
We use, for example, a 40‐year‐old white man. For the model prediction of a “typical subject” or “reference subject” (or, in fact, any subject with given characteristics), the confidence interval comprises only the uncertainty of parameter estimates: only the fixed effects of the model are considered and the same methods apply as for the regression model and will not be discussed in the following. Examples of questions that are addressed by this scenario are the difference between exposures for typical subjects of two different populations, or whether two different posologies would lead to different treatment effects in a typical subject.
Scenario 2: prediction of the distribution of (future) individual observations
The idea is to simulate a large number of individuals and determine the prediction interval based on the percentiles of the distribution of simulated observations. Interindividual and residual variability as well as parameter uncertainty are required to characterize the distribution. The simulation approach or the estimation/simulation approach can be used. A typical question for this scenario is, for example, the expected exposure variability across the whole patient population for dosing regimen with and without adjusting the dose with covariates.
Scenario 3: population‐level outcomes
As an example, estimation of the proportion of responders in a population or the exposure is achieved by at least 90% of the population. Hence, for a large number of times, a population is simulated and summarized by the statistic of interest. For example, the 90% prediction interval of the population's 5th percentile ranges from the 5th to the 95th percentile of the distribution of 5th percentiles across all iterations. As for scenario 2, uncertainty of model parameter estimates, interindividual variability, and residual variability are taken into account. The Delta method is not defined but the simulation and the estimation/simulation approaches can be used. The key difference is that confidence and prediction intervals are defined for statistics (e.g., mean, median, or quantiles) of the distribution in a simulated population. As an example, confidence and prediction intervals quantify responder fractions to a treatment.
For both scenarios 2 and 3, two types of simulations are distinguished depending on their purpose. For assessment of (future) clinical studies or for model diagnostics, the number of individuals is a design parameter defined in the study protocol. Study simulations include simulation of a population of individuals of this size. Prediction intervals for clinical studies are often addressing questions related to study design (e.g., whether responses for different treatment arms can be distinguished sufficiently). For projecting the results to a general (target) population and making general population statements, population simulations of an infinite number of individuals should be used. A question addressed here could be the expectation of how many adverse events have to be expected for the marketed drug.
To further illustrate the difference and purposes of study vs. population simulation, assume that body weights were assessed in a set of K individuals of a population. Study simulation relates to the question of what (mean) body weight can be expected if another set of K individuals would be assessed. The smaller K the more the mean body weight differs between sets of K individuals purely by chance. Even if true mean body weight and interindividual variability are known, the prediction interval would not be of 0 width. In contrast, population simulations are used to quantify the expectation for the mean or spread of body weights in the overall population. Here, prediction and confidence intervals only depend on the interindividual variability and parameter estimation uncertainty.
In practice, a large number is sufficient. Following our terminology, these intervals are prediction intervals because random variability is taken into account. However, if they are used as model diagnostics, they are often referred to as confidence intervals (i.e., in the context of visual predictive checks).
In the following, calculation of confidence and prediction intervals for scenarios 2 and 3 using the simulation and the estimation/simulation approach are explained in detail.
Estimation by simulation
When calculating the prediction interval for individual observations (scenario 2), for each individual, a set of parameter means (also referred to as structural or population typical parameters), parameter SDs (i.e., interindividual variability), and error model parameters are drawn from their uncertainty distribution. From the mean and parameter SD, an individual parameter set is sampled and the individual prediction calculated and a residual added. Finally, summary statistics, such as quantiles or means, are calculated pooling all individual predictions.
For the simulation on the population level (scenario 3), at each iteration, as for scenario 2, a set of parameter means (also referred to as structural or population typical parameters), parameter SDs (i.e., interindividual variability), and error model parameters are drawn from their uncertainty distribution. Many sets of individual parameters are sampled and model predictions calculated for all individuals in the population. A residual sample error is added to the prediction that is sampled from the error distribution. As the last step of iteration, a summary statistic of interest is calculated (e.g., the population mean, the 90th percentile, or a percentage of individuals for which the prediction or simulation is above a certain value). Thus, at each iteration, a prediction for a population is calculated that is finally again summarized across all iterations. A typical result would be the prediction interval for the 95th percentile of the model prediction distribution.
Estimation by simulation/re‐estimation (bootstrap)
As in the case of a regression model, compared to the simulation approach, the parameters used for the prediction/simulation at each iteration are re‐estimated using a simulated (Monte‐Carlo simulation) or resampled (bootstrapping) dataset and not sampled from the uncertainty distribution. The same procedure is applied otherwise.
For scenario 2, each individual simulation is used to estimate model parameters based on a bootstrapped or Monte‐Carlo simulated dataset. In scenario 3, the new set of estimated parameters is used for population simulation. Because parameter estimation is computationally expensive, this approach is typically not applied in scenario 3. The calculation steps for the simulation approach and the repeated estimation/simulation with either bootstrapped or simulated datasets are summarized in Figure 1 and Figure 2, respectively.
Figure 1.
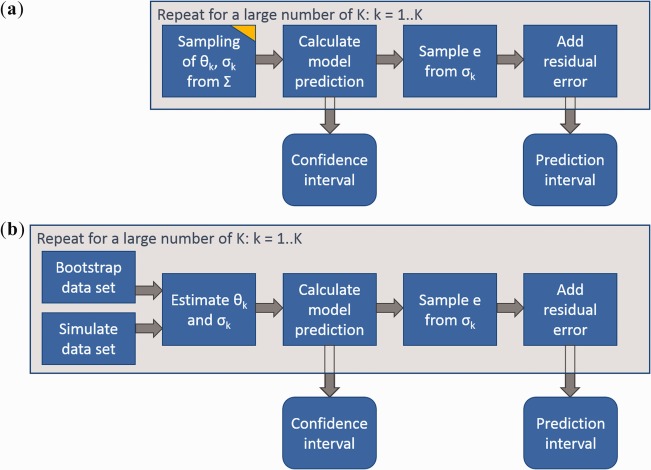
Calculation of confidence and prediction intervals for regression models. (a) Simulation approach. (b) Repeated estimation/simulation. The yellow edge indicates sampling from uncertainty in contrast to sampling from random variability. Confidence and prediction intervals are determined as quantiles of the simulated values (e.g., 5th and 95th percentile). Notation: Θ, model parameters; σ, residual variability; Σ, parameter covariance matrix; e, residual error; K, number of sampled parameter sets.
Figure 2.
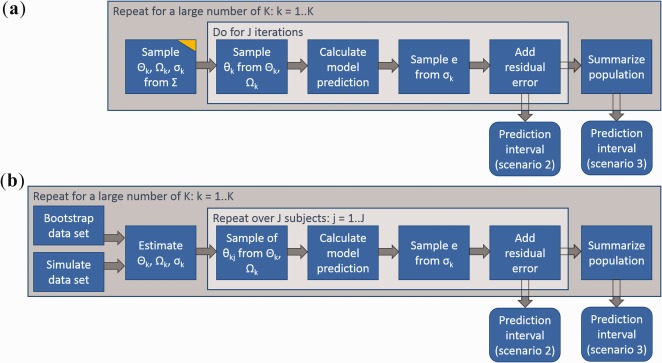
Calculation of prediction intervals for nonlinear mixed effect models. (a) Simulation approach. (b) Repeated estimation/simulation. The yellow edge indicates sampling from uncertainty in contrast to sampling from random variability. Prediction intervals are determined as quantiles of the simulated values (e.g., 5th and 95th percentile). Notation: Θ, population parameters; σ, residual variability; Σ, parameter covariance matrix; Ω, random‐effects covariance matrix; θ, individual parameter set; e, residual error; K, number of sampled parameter sets; J, number of sampled individuals from a population.
CASE STUDIES
Datasets
Data from a phase I study of ponesimod were used to demonstrate the confidence interval calculation methods. Ponesimod is an S1P1 receptor modulator that reduces total lymphocyte counts in the systemic circulation by preventing them from leaving lymph nodes. In this study, ponesimod was administered once daily with an increasing dose every fourth day. Drug plasma concentrations and total lymphocyte count in blood as the PD readouts were assessed.19
Two datasets were obtained from the study: a PK/PD dataset containing time‐matched ponesimod plasma concentrations and total lymphocyte count in blood and a PK dataset containing only ponesimod concentrations over time. Because censoring was not applied, concentrations below the limit of quantification were discarded in the PK data. However, to avoid discarding data informing on total lymphocyte count reduction at very low or zero concentrations, concentrations below the limit of quantification were set to 0 in the PK/PD dataset.
Data from all subjects (i.e., actively treated and placebo‐treated), were included in the PK/PD data, whereas only subjects treated according to the protocol with ponesimod were considered in the PK data.
The PK/PD data comprised 517 observations from 16 subjects, whereas for the PK analysis 463 concentration records from 10 subjects were included. The datasets are shown in Figure 3.
Figure 3.
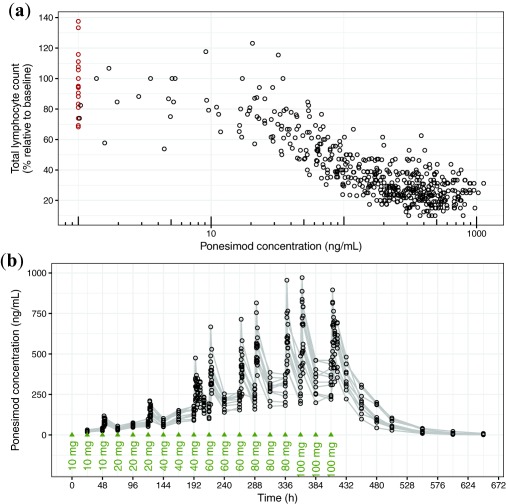
Case study datasets. (a) Pharmacokinetic/pharmacodynamic dataset. Observed data with concentrations above and below the limit of quantification are indicated as black and red circles. (b) Pharmacokinetic dataset. Observed are indicated as black circles. Gray lines connect data from individuals. Dosing times are indicated with green triangles.
Case study 1: PK/PD regression analysis
The relationship between plasma concentration, c, and total lymphocyte count reduction relative to baseline levels was described by an maximum effect (Emax) model with baseline E0, maximum effect Emax, the concentration achieving 50% of the effect, half‐maximal effective concentration, and nonlinearity parameter (Hill coefficient) γ.
| (7) |
Parameters and their covariance matrix were estimated using nonlinear least squares (NLS) and maximum likelihood estimate (MLE). Because with standard implementations of NLS the residual error cannot be conditioned on the predicted value f(c, ), an additive error was applied.
Parameter estimates for NLS and MLE and their SEs and confidence intervals determined by different confidence interval calculation methods are very similar, leading to very similar model predictions (Supplementary Figure S1). In this case, the methods only differ with respect to the computing time that is considerably shorter for NLS than for MLE (Table 1). In particular, simulation‐estimation methods require considerably longer computation times than the Delta method or the simulation approach. Using the Delta method for confidence interval calculation is fastest because it is an analytical solution. In the following, the confidence intervals are discussed for MLE only.
Table 1.
Computation times in seconds for PK/PD regression case study.
| CI calculation method | NLS | MLE |
|---|---|---|
| Delta method | 0.64 | 0.73 |
| Simulation approach | 1.11 | 1.30 |
| Simulation/estimation using bootstrap | 8.62 | 128.57 |
| Simulation/estimation using Monte‐Carlo simulation | 7.11 | 132.79 |
CI, confidence interval; MLE, maximum likelihood estimation; NLS, nonlinear least squares; PD, pharmacodynamic; PK, pharmacokinetic.
Computation times include parameter estimation as well as confidence and prediction interval calculation using the R framework pecan that is described in the Supplementary Material. Calculation was performed using R version 3.0.2 on a Lenovo ThinkPad T440s with a 2.1 GHz quad core Intel i7‐4600U processor and 8 GB RAM. The 1,000 simulations were performed for the simulation approach and 1,000 parameter re‐estimations for the simulation/estimation approaches.
The Delta method, the simulation approach, and the Monte‐Carlo simulation‐estimation give comparable results for the confidence intervals, whereas the intervals are wider for nonparametric bootstrap (Figure 4 a). These results are not generalizable and can be different in different situations of data and model. The smallest confidence interval width is around a concentration of 300 ng/mL, in which many data points are available. Larger confidence intervals are in the concentration range around 30 ng/mL (at which the effect is changing with concentration) and at concentrations for which fewer data points are available.
Figure 4.
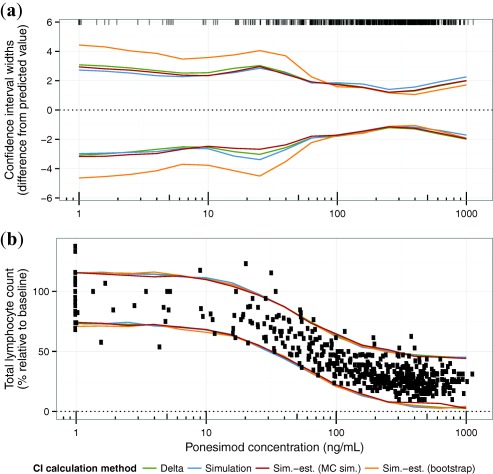
Comparison of confidence and prediction intervals calculated by different methods. (a) The 95% confidence interval width of total lymphocyte counts (i.e., the difference of the 2.5th and the 97.5th percentile from the predicted value) f (c, ). Concentration values are indicated by ticks at the top of the panel. (b) The 95% prediction intervals. Observed data are indicated as circles. The 1,000 simulations (simulation approach) and 1,000 parameter re‐estimations (simulation‐estimation approaches) were performed.
Because the residual variability is considerably larger than the prediction variability attributed to the parameter estimation error, the differences in confidence intervals for different calculation methods have no consequence for the prediction interval. However, the overlay of prediction intervals and data indicate that the residual variability might be larger for larger lymphocyte counts. Hence, an additive error model might not be the best choice (Figure 4 b).
The error models in Eqs. (3), (4), (5), (6) were fitted using MLE to illustrate the impact of the error model on the results. Supplementary Table S1 compares parameter estimates and their estimation errors for different error models. Figure 5 visualizes the confidence intervals and prediction intervals for different error models using the simulation approach for confidence interval calculation. For the additive error model, the confidence interval width does not change considerably for different concentrations. In contrast, for the combined, proportional, and exponential error models, confidence intervals are larger at low concentrations and large lymphocyte count values. As indicated before, using the additive error model, the prediction interval tends to underestimate the variability in the lower concentration range. Using an exponential or a proportional error, it is overestimated. The combined error seems to be most appropriately describing the variability of the data. In line with this observation, it has the lowest Bayesian information criterion even though the penalization term of the Bayesian information criterion is larger compared to the other models due to an additional parameter.
Figure 5.
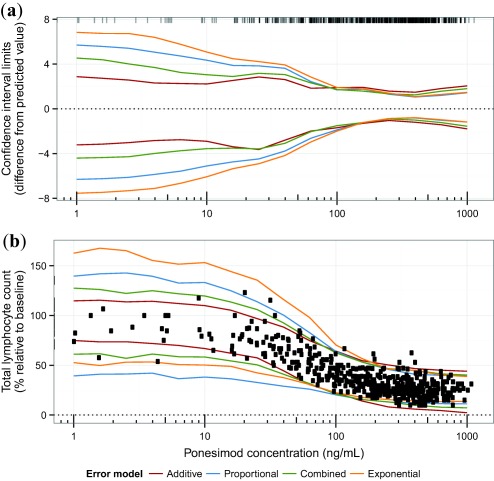
Comparison of confidence and prediction intervals for different error models. (a) 95% confidence interval width (i.e., the difference of the 2.5th and 97.5th percentile from the predicted value), f (c, ). Concentration values of the data are indicated by ticks at the top of the panel. (b) 95% prediction intervals. Observed data are indicated as circles. 1,000 simulations (simulation approach) and 1,000 parameter re‐estimations (simulation‐estimation approaches) were performed.
In summary, the confidence intervals for the concentration‐response relationship calculated by the different methods were very similar. In this case study, the data basis was solid and allowed for small parameter estimation errors. Note that the error model had an impact on the confidence intervals and not only on the prediction interval to which it is directly linked. Assuming that the combined error best describes the data, using the additive error would lead to a too narrow prediction interval at low concentrations while using a proportional or exponential error model it would be too wide.
Case study 2: Nonlinear mixed effects modeling for a PK dataset
A two‐compartment model with first‐order absorption was chosen to describe the PK of ponesimod after oral administration20 parameterized in terms of absorption rate constant ka, central and peripheral volumes V1 and V2, intercompartmental clearance Q, and clearance CL with interindividual variability on all parameters using Monolix.
Prediction intervals according to scenarios 2 and 3 for the median as well as the 5th and 95th percentiles were calculated according to the simulation and the simulation‐estimation approaches introduced. For the simulation approach, parameters were sampled from a multivariate Normal distribution defined by the estimated parameters and covariance matrix. Parameters were re‐estimated 1,000 times either based on a bootstrapped dataset or a simulated dataset using the parameter estimates based on the original observed data (Monte‐Carlo simulation). For each set of sampled or estimated parameters, a population of 1,000 individuals was simulated. To derive prediction intervals for individuals (scenario 2), median, 5th, and 95th percentiles were determined. For prediction intervals for population summaries (scenario 3), first, the simulated concentration distribution was summarized by the median, 5th, and 95th percentile across the sets of 1,000 individuals of a simulated population. Then, the prediction intervals were calculated as the ranges from the 5th to the 95th percentile of the summaries.
For the prediction intervals of individuals, the approaches suggest similar prediction intervals.
In contrast, regarding the prediction intervals for population summaries, differences between the approaches exist. The bootstrapping approach has very narrow prediction intervals for all the summaries of the concentration distribution in the population over time (Figure 6). The Monte‐Carlo simulations, as well as the simulation approach, suggest wider confidence intervals because these approaches rely on the estimated covariance matrix and lead to a more pessimistic assessment of the reliability of the predictions.
Figure 6.
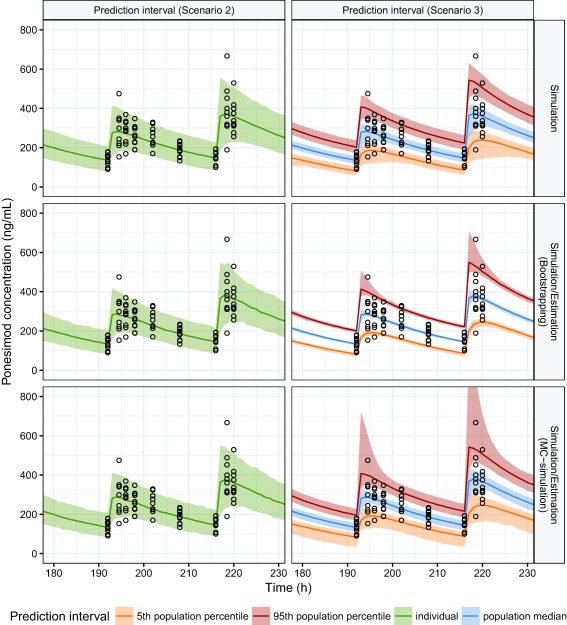
Confidence and prediction intervals for the nonlinear mixed effect pharmacokinetic model. For the estimation/simulation approaches, parameters were re‐estimated 1,000 times using bootstrapped or simulated datasets. A population of 1,000 subjects was simulated for each set of re‐estimated parameters. For the simulation approach, parameters were sampled 1,000 times from the estimate covariance matrix. A population of 1,000 subjects was simulated for each set of sampled parameters. Observed data are indicated as circles.
For both the bootstrapping approach and the Monte‐Carlo simulation approach, the main difference between the confidence and the prediction interval is that the 5th and 95th percentiles are more spread from the median of the population.
DISCUSSION
Confidence interval calculation methods for nonlinear models were introduced and illustrated using datasets from clinical studies (i.e., concentration‐response (PK/PD) data and concentration‐time (PK) data). Advantages and disadvantages of the implemented confidence interval calculation methods, the Delta method, the simulation approach, and simulation‐estimation approaches using either nonparametric bootstrap or Monte‐Carlo simulation were highlighted.
All methods reviewed estimate confidence intervals and prediction intervals in a point‐wise manner: For a fixed independent variable value x, the confidence interval and prediction interval are calculated. To derive a confidence interval or prediction interval band around the model predictions for a range of independent values x, the confidence interval or prediction interval is evaluated at each x (or a sufficiently fine x‐grid). Uncertainty with respect to the independent variable is not considered. Modeling approaches accounting for variability in both independent (x) and dependent variable (y; errors‐in‐variables models) were not covered here, as they are not commonly used in pharmacometrics.
Assumptions of confidence interval calculation methods, the Delta method, and the simulation approach rely on the estimated covariance matrix, assuming a multivariate normal distribution of the parameters to describe the parameter estimate uncertainty. An appropriate parameter transformation (e.g., a logarithmic transformation), can be applied to approximately fulfill this condition if needed.
In addition, the Delta method involves a linearization of the model with respect to the estimated parameters leading to symmetric confidence intervals around the predicted value. These symmetric confidence intervals may only be a good approximation depending on how good the linear approximation is. For very nonlinear models, the Delta method may not be a good choice. Consider an application to drug concentration data: whereas the data cannot be negative, the confidence interval based on the Delta method may extend to negative values.
Simulation‐estimation approaches, using either Monte‐Carlo simulations or nonparametric bootstrap, do not assume a multivariate normal distribution for the estimated parameters. As with the simulation approach, the confidence intervals for the prediction will also not include inappropriate values (e.g., negative concentrations) if the model itself excludes them. Using a simulated instead of a bootstrapped dataset for parameter re‐estimation implies that the model is an accurate representation of the data, including the error model, and has the advantage that the datasets generated by Monte‐Carlo simulation have exactly the same independent variables as the observed dataset, which is not the case for the bootstrapped dataset. In the bootstrapped datasets, some observations do not occur and others will be duplicated. Obviously, the dataset needs to be reasonably large to allow for a resampling approach.
One additional issue that was not observed in the case studies reported here but may occur is the handling of nonconverging re‐estimations. Often, these are ignored when summarizing the results. This can result in biased estimates for confidence intervals and prediction intervals because nonconverging estimations occur systematically (e.g., depending on the inclusion of extreme values in bootstrapped datasets).4, 21, 22, 23
Noteworthy, sometimes predictions must be made not based on the original model function but based on other functions of the model parameters. For example, it may be of interest to form a point estimate for the half‐life of a drug that is calculated as Ln(2)*V/CL with CL and V denoting clearance and central volume, respectively. The introduced methods can be applied in this case as well by substituting the model function by the function of interest in the calculation.
Current uses in pharmacometrics
The multiple comparison and modeling method24 for analysis of dose‐response relationships in clinical trials implements the Delta method to derive confidence and prediction models. This method is not used in population‐based models, as it is not developed for NLME models. Comparing the estimated variability of population‐based models to the variability in the observed data was introduced years ago: visual predictive checks allow for comparison of observed and model‐predicted (simulated) variability corresponding to calculation of prediction intervals for study simulations.25 The next step, provision of intervals describing variability of simulation scenarios, is not routine yet. This is partially owed to the lack of standardized methods and software for derivation and visualization of the corresponding intervals.
Computational effort
The Delta method is the computationally fastest among the compared confidence interval calculation methods. The simulation approach is also fast compared to the methods that involve repeated parameter estimation for which the computational effort increased 100‐fold for the PK/PD case study. Re‐estimation based on bootstrapped datasets is faster compared to re‐estimation based on Monte‐Carlo simulated datasets.
Impact of the error model
The error model has a direct impact on the prediction interval because it includes the residual variability defined by the error model. The confidence interval of the prediction that is a result of parameter estimation uncertainty is influenced indirectly. The error model impacts the parameter estimates and their estimation error. As could be seen for the PK dataset example, high estimation errors led to unreasonable confidence intervals when simulating by sampling from the parameter covariance matrix. The other methods were more robust to determine the prediction confidence interval. In particular, nonparametric bootstrap and Monte‐Carlo simulation‐estimation may be more robust because they do not rely on model linearization or a normal distribution of model parameters.
Implementation in current software
In R, functions from the basic statistics package (i.e., lm and glm) and functions for fitting (generalized) linear models provide confidence intervals for the predictions. For lm, confidence intervals of the prediction are calculated using the analytical solution, whereas likelihood profiling26 (an approximation) is used for glm. For the nonlinear parameter estimation routines (e.g., nls), calculation of confidence intervals for model prediction is not implemented. The nlsTools package27 provides some additional functionality for nls objects, including nonparametric methods (i.e., jackknife and bootstrap), for confidence interval estimation for parameters but not for model predictions. Additional packages exist that include confidence intervals for predictions. The DoseFinding package24 that implements the multiple comparison and modeling approach fits linear as well as nonlinear models to dose‐response data using least‐squares and provides confidence intervals based on the Delta method.
Typical software used for population PK and PK/PD modeling (e.g., Monolix28 and NONMEM), primarily focus on the parameter estimation step. Within the graphical user interface of Monolix, simulations or nonstandard analyses are possible. Recently, the software has been extended with several tools for data visualization and simulation. The mlxR29 package provides a link between Monolix modeling results and R. In NONMEM, simulations can be run and statistics for parameter estimates are provided. For estimation postprocessing, several tools were developed and implemented in Perl (PsN) and R (Xpose).30 Using these postprocessing tools, confidence interval calculation can be implemented by the modeler.
All confidence interval calculation methods discussed in this tutorial were implemented in an R library (see the Supplementary Material for details). Using this implementation based on standard R packages, parameter estimations as well as confidence interval and prediction interval calculations can be performed by a single function call for naive‐pooled regression. Next to the numerical output, the main results (i.e., parameter estimates and an overlay of confidence intervals, prediction intervals, and observed data), are displayed graphically (Figure 7). The R library can be used directly for confidence interval calculations for any other model and dataset. The code also gives an example of how to implement the discussed methods in R. In addition, an R Shiny31 application (available at https://carumcarvi.shinyapps.io/pecan/) provides access to the same functionality for a broader audience for a set of standard models used in pharmacometric analyses.
Figure 7.
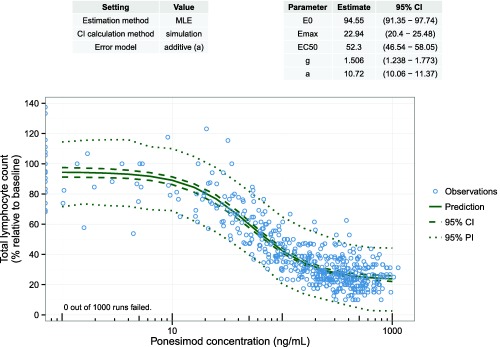
Result visualization with the R library pecan to calculate confidence intervals and prediction intervals for nonlinear regression models. Settings for parameter estimation and confidence interval calculation are given in the left table. The right table displays the parameter estimation results (i.e., parameter estimates with confidence intervals). Observed data (blue circles) and prediction with confidence interval and prediction interval (solid, dashed, and dotted green line). CI, confidence interval; EC50, half‐maximal effective concentration; Emax, maximum effect; MLE, maximum likelihood estimate; PI, prediction interval.
CONCLUSIONS
The simulation/re‐estimation methods are preferable over the Delta method and the simulation approach given that the computational effort allows their implementation. Using bootstrapped datasets is favorable if the data are not too sparse. Approximation of the model by linearization and the assumption that the uncertainty of the estimates can be described by the normal distribution are often not appropriate. The pure simulation approach can be an acceptable compromise if the parameter covariance matrix is well‐defined and parameter estimation errors are limited.
Pharmacometricians are encouraged to routinely include the quantification of prediction uncertainty in modeling projects. Confidence and prediction intervals should be a standard element of visualizations by which model predictions are communicated. Because model predictions are often the key result and the basis for decision making, the confidence in these predictions needs to be assessed and shared with the stakeholders for informed decision making.
Conflict of Interest
The authors declared no conflict of interest.
Source of Funding
No funding was received for this work.
Supporting information
Supplementary Material
Table S1
Acknowledgments
The authors thank Ahmad Y. Abuhelwa and Richard N. Upton (University of South Australia, Adelaide) for providing the NONMEM ADVAN‐style R implementation of typical PK models32 that is used in the software provided online.
References
- 1. R Development Core Team . R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2012).
- 2. Software G. GraphPad Prism Version 7.00 for Windows (GraphPad Software, La Jolla, California, 2017).
- 3. Davidian, M. & Giltinan, D.M. Nonlinear Models for Repeated Measurement Data. Vol. 62 (CRC Press, Boca Raton, FL, 1995). [Google Scholar]
- 4. Mould, D.R. & Upton, R.N. Basic concepts in population modeling, simulation, and model‐based drug development‐part 2: introduction to pharmacokinetic modeling methods. CPT Pharmacometrics Syst. Pharmacol. 2, e38 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Beal, S.L. , Sheiner, L.B. , Boeckmann, A.J. & Bauer, R.J. NONMEM Users Guides (Icon Development Solutions, Ellicott City, MD, 1989–2009).
- 6. Lavielle, M. Mixed Effects Models for the Population Approach: Models, Tasks, Methods and Tools (CRC Press, Boca Raton, FL, 2014). [Google Scholar]
- 7. Gelman, A. , Carlin, J.B. , Stern, H.S. , Dunson, D.B. , Vehtari, A. & Rubin, D.B. Bayesian Data Analysis. Vol. 2 (CRC Press, Boca Raton, Florida, 2014). [Google Scholar]
- 8. Bonate, P.L. Pharmacokinetic‐Pharmacodynamic Modeling and Simulation, 2nd edn (Springer, New York, NY, 2011). [Google Scholar]
- 9. Bolstad, W.M. & Curran, J.M. Introduction to Bayesian Statistics (John Wiley & Sons, Hoboken, NJ, 2016). [Google Scholar]
- 10. Berger, J.O. Statistical Decision Theory and Bayesian Analysis (Springer Science & Business Media, New York, NY, 2013). [Google Scholar]
- 11. Box, G.E.P. & Tiao, G.C. Bayesian Inference in Statistical Analysis (Addison‐Wesley, New York, NY, 1973). [Google Scholar]
- 12. Seber, G. & Wild, C. Nonlinear Regression (John Wiley & Sons, Hoboken, NJ, 2005). [Google Scholar]
- 13. Ver Hoef, J.M. Who invented the delta method? Am. Stat. 66, 124–127 (2012). [Google Scholar]
- 14. Zegarelli, M. Calculus II for Dummies (John Wiley & Sons, Hoboken, NJ, 2008). [Google Scholar]
- 15. Mandel, M. Simulation‐based confidence intervals for functions with complicated derivatives. Am. Stat. 67, 76–81 (2013). [Google Scholar]
- 16. Efron, B. & Tibshirani, R.J. An Introduction to the Bootstrap (CRC Press, Boca Raton, Florida, 1994). [Google Scholar]
- 17. Efron, B. Bootstrap methods: another look at the jackknife. Ann. Statist. 7, 1–26 (1979). [Google Scholar]
- 18. Hall, P. The Bootstrap and Edgeworth Expansion (Springer Science & Business Media, New York, New York, 2013). [Google Scholar]
- 19. Hoch, M. , D'Ambrosio, D. , Wilbraham, D. , Brossard, P. & Dingemanse, J. Clinical pharmacology of ponesimod, a selective S1P1 receptor modulator, after uptitration to supratherapeutic doses in healthy subjects. Eur. J. Pharm. Sci. 63, 147–153 (2014). [DOI] [PubMed] [Google Scholar]
- 20. Krause, A. , Brossard, P. , D'Ambrosio, D. & Dingemanse, J. Population pharmacokinetics and pharmacodynamics of ponesimod, a selective S1P1 receptor modulator. J. Pharmacokinet. Pharmacodyn. 41, 261–278 (2014). [DOI] [PubMed] [Google Scholar]
- 21. Thai, H.T. , Mentré, F. , Holford, N.H. , Veyrat‐Follet, C. & Comets, E. A comparison of bootstrap approaches for estimating uncertainty of parameters in linear mixed‐effects models. Pharm. Stat. 12, 129–140 (2013). [DOI] [PubMed] [Google Scholar]
- 22. Thai, H.T. , Mentré, F. , Holford, N.H. , Veyrat‐Follet, C. & Comets, E. Evaluation of bootstrap methods for estimating uncertainty of parameters in nonlinear mixed‐effects models: a simulation study in population pharmacokinetics. J. Pharmacokinet. Pharmacodyn. 41, 15–33 (2014). [DOI] [PubMed] [Google Scholar]
- 23. Dartois, C. , Lemenuel‐Diot, A. , Laveille, C. , Tranchand, B. , Tod, M. & Girard, P. Evaluation of uncertainty parameters estimated by different population PK software and methods. J. Pharmacokinet. Pharmacodyn. 34, 289–311 (2007). [DOI] [PubMed] [Google Scholar]
- 24. Pinheiro, J. , Bornkamp, B. , Glimm, E. & Bretz, F. Model‐based dose finding under model uncertainty using general parametric models. Stat. Med. 33, 1646–1661 (2014). [DOI] [PubMed] [Google Scholar]
- 25. Bergstrand, M. , Hooker, A.C. , Wallin, J.E. & Karlsson, M.O. Prediction‐corrected visual predictive checks for diagnosing nonlinear mixed‐effects models. AAPS J. 13, 143–151 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Cole, S.R. , Chu, H. & Greenland, S. Maximum likelihood, profile likelihood, and penalized likelihood: a primer. Am. J. Epidemiol. 179, 252–260 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Baty, F. , Ritz, C. , Charles, S. , Brutsche, M. , Flandrois, J.‐P. & Delignette‐Muller, M.‐L. A toolbox for nonlinear regression in R: the package nlstools. J. Stat. Softw. 66, 1–21 (2015). [Google Scholar]
- 28.Lixoft‐Incuballiance. Monolix User Guide 4.2.0 ed. Orsay, France; 2012.
- 29. Lavielle, M. simulx (mlxR) version 3.1. <http://simulx.webpopix.org/simulx/bookdown/mlxR-bookdown.pdf> (2016). Accessed 2017.
- 30. Keizer, R.J. , Karlsson, M.O. & Hooker, A. Modeling and simulation workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst. Pharmacol. 2, e50 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Chang, W. , Cheng, J. , Allaire, J. , Xie, Y. & McPherson, J. Shiny: web application framework for R. version 0.14.2. https://cran.r-project.org/web/packages/shiny> (2016). Accessed 2017.
- 32. Abuhelwa, A.Y. , Foster, D.J. & Upton, R.N. ADVAN‐style analytical solutions for common pharmacokinetic models. J. Pharmacol. Toxicol. Methods 73, 42–48 (2015). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material
Table S1


