4D CONTINUOUS MEDIAL REPRESENTATION BY GEODESIC SHAPE REGRESSION

Abstract

Longitudinal shape analysis has shown great potential to model anatomical processes from baseline to follow-up observations. Shape regression estimates a continuous trajectory of time-discrete anatomical shapes to quantify temporal changes. The need for shape alignment and point-to-point correspondences represent limitations of current shape analysis methodologies, and present significant challenges in shape evaluation. We propose a method that estimates a continuous trajectory of continuous medial representations (CM-Rep) from a set of time-discrete observed shapes. To avoid the traditional step of aligning individual objects, shape changes are modeled via diffeomorphic ambient space deformations. Using a medial shape representation, we separately capture object pose changes and intrinsic geometry changes. Tests and validation with synthetic and real anatomical shapes demonstrate that the new method captures extrinsic shape changes as well as intrinsic shape changes encoded with CM-Reps, a highly relevant property for studying growth and disease processes.

1. INTRODUCTION

Increased availability of repeated longitudinal scans of individual subjects enable studies of spatiotemporal shape changes. Preliminary results show great potential to improve our understanding of anatomical changes related to growth, disease progression, or degeneration [1]. Challenges for longitudinal studies of anatomical objects are variability in the number of observations as well as time intervals of observations which encode spatiotemporal changes. Shape regression estimates continuous evolution of shapes from a sparse set of shapes distributed over time [2]. To address the importance of including multiple sources of geometry as a multi-object complex, ambient space regression methods have been proposed. These methods are based on the large deformation setting (LDDMM), where several sources and types of geometry contribute to the estimation of a single time-varying deformation of the ambient space [3, 4]. This concept overcomes limitations of traditional shape analysis often performed on single shapes independently, where analysis is inherently biased towards shape alignment. While ambient space methods account for interactions between neighboring structures, the momenta vectors which parametrize shape changes do not readily differentiate between extrinsic changes of pose and intrinsic changes of shape geometry. Extrinsic and intrinsic changes are coupled and prohibit straightforward interpretation.

Representation of intrinsic shape properties has been widely studied by skeletonization methods in image processing and graphics [5]. Medial surface geometry and associated radii capture intrinsic shape properties, but statistical analysis is challenging depending on the definition of correspondence between medial surface and shape boundary [5]. In [6], the authors propose a fixed graph to aid statistical analysis on intrinsic shape properties. Continuous medial representation (CM-Rep) [7] deforms a template CM-Rep and updates its attached radius scalar field to match a target shape. Analysis of longitudinal data requires an extension of skeletonization to a 4D continuous skeleton, a concept which to our knowledge has not yet been presented.

In this paper, we propose geodesic shape regression of time-discrete CM-Reps to estimate a continuous medial surface trajectory as well as a reconstructed volumetric shape trajectory with an explicit radius scalar field model. The novel method estimates a model of continuous change of CM-Reps over time in the LDDMM setting by matching a continuous trajectory of CM-Rep surfaces to those from observed shapes. We demonstrate on synthetic and real medical data that our method captures ambient space deformations in the same manner as previous methods, while additionally capturing continuous intrinsic changes. This allows for the straight-forward interpretation and statistical analysis of the evolution of multi-object complexes in their natural anatomical space, a result not yet available to the research community.

2. METHODS

Continuous Medial Representations

For a 3D volumetric shape, X, a CM-Rep m is a parametrized continuous medial surface model with radius scalar field R attached on the surface [8]. X is reconstructed by a maximum inscribed ball (MIB) with radius R on each point of m. X can be parametrized as X^±(u) which X⁺ and X⁻ are on opposite sides of a parametrized surface m(u), where u is a surface parameter of m. Because m is a continuous surface, the surface of X^± can be considered as the set of points of tangency between X(u) and MIB of m(u) and R(u),

$${\mathbf{X}}^{\pm }(u)=\mathbf{m}(u)+\mathbf{R}(u){\mathbf{U}}^{\pm }(u).$$ (1)

U^± is the unit outward normal vectors on both directions of X,

$${\mathbf{U}}^{\pm }=-{\nabla }_{\mathbf{m}}\mathbf{R}\pm \sqrt{1-{\Vert {\nabla }_{\mathbf{m}}\mathbf{R}\Vert }^2}{\mathbf{N}}_{\mathbf{m}},$$ (2)

where N_m and ∇_m are a surface normal of m and gradient with respect to m, respectively. U is a function of m and R. X can be, therefore, defined as a function of m and R.

At each time point t_i, a CM-Rep surface ${\mathbf{m}}_{t_i}^O$ and a radius scalar field ${\mathbf{R}}_{t_i}^O$ are estimated by the method suggested in [8] to match an observation shape ${\mathbf{O}}_{t_i}$. In other words, the observation shape ${\mathbf{O}}_{t_i}$ are now decomposed to CM-Rep surfaces ${\mathbf{m}}_{t_i}^O$ and radius scalar fields ${\mathbf{R}}_{t_i}^O$, which represent pose changes and radius changes independent from pose changes, respectively. A CM-Rep surface ${\mathbf{m}}_{t_i}^O$ estimated to match the first observation shape ${\mathbf{O}}_{t_0}$ is used as an initial baseline CM-Rep as a template m₀ for CM-Rep shape trajectory estimation which will be explained in the following section. CM-Rep surface trajectory estimation also makes use of a set of radius scalar fields ${\mathbf{R}}_{t_i}^O$ to create reconstructed volumetric shapes with CM-Rep surface trajectory to show a continuous trajectory of reconstructed shapes to match with observations.

For implementation purposes, a CM-Rep m is represented as a surface triangular mesh with a fixed number of vertices. The edge information of the reconstructed shape X is copied from m on both sides of X^± to create a surface mesh. This guarantees the surface mesh of X is well-defined from the medial surface mesh. Since the deformation flow of m over time is a flow of diffeomorphisms, the reconstructed surface mesh stays well-defined.

Geodesic CM-Rep Surface Regression

The proposed method estimates a diffeomorphic shape trajectory of CM-Rep m over time t from a set of observed shapes ${\mathbf{O}}_{t_i}$ with a CM-Rep surface ${\mathbf{m}}_{t_i}^O$ and a fixed radius scalar field ${\mathbf{R}}_{t_i}^O$ estimated individually for each ${\mathbf{O}}_{t_i}$. The geodesic flow of diffeomorphisms ϕ_t is estimated at control points c on an ambient space of all ${\mathbf{m}}_{t_i}\mathrm{s}$. The control points c carry momenta vectors α which define the entire flow [4].

The energy function of a CM-Rep trajectory estimation measures the sum of distances between the modeled CM-Rep surface ${\varphi }_{t_i}({\mathbf{m}}_0)$ from the trajectory and ${\mathbf{m}}_{t_i}^O$ at each observation time point t_i with a regularity term Reg(ϕ_t) of deformation:

$$E({\mathbf{m}}_0,{\varphi }_t)={\displaystyle \sum _{i=1}^{N_{\mathit{obs}}}{\Vert {\varphi }_{t_i}({\mathbf{m}}_0)-{\mathbf{m}}_{t_i}^O\Vert }_{W\ast }^2}+\mathit{Reg}({\varphi }_t),$$ (3)

where ${\Vert ·\Vert }_{W\ast }^2$ is varifold shape distance metric [9]. The varifold metric has desired properties which it does not require correspondence between ${\mathbf{m}}_{t_i}^O$ and ${\mathbf{m}}_{t_i}$ since it can be defined on the ambient space of shapes [3]. The metric is also robust to flipped normals on meshes which might be present on ${\mathbf{m}}_{t_i}$.

By optimizing Eq. 3, the geodesic flow of diffeomorphisms ϕ_t and also the initial baseline CM-Rep surface m₀ are updated to match the set of observation shapes. The entire flow of diffeomorphisms is defined by the control points and momenta vectors on the ambient space of CM-Rep surfaces.

The diffeomorphic regularity term Reg(ϕ_t) and the formulation of the geodesic flow of diffeomorphisms defined by control points and momenta vectors ensure CM-Rep surfaces of the shape trajectory to have same topology to each other, see [4] for more details. This also guarantees that the reconstructed volumetric shapes of the CM-Reps have the same topology to each other since they are homologous to the CM-Rep surfaces.

To reconstruct a volumetric shape trajectory of the CM-Rep surface trajectory, radius scalar fields of the CM-Rep shape trajectory over time R_t are estimated by a linear regression model of the radius scalar fields of all observations ${\mathbf{R}}_{t_i}$. X_t is reconstructed by combining a CM-Rep surface trajectory ϕ_t(m₀) and the estimated radius scalar field R_t.

It is worthwhile to note that if given only two data points, a baseline and a follow-up shape, the proposed method works as a geodesic shape matching method based on CM-Reps with shape interpolation. CM-Rep surfaces and radius scalar fields are estimated on both shapes. The CM-Rep surface trajectory and linearly interpolated radius fields create continuous interpolation in time, and the end point of the volumetric shape trajectory matches the follow-up shape.

3. EXPERIMENTAL RESULTS

Results of the proposed method with synthetic shapes and real anatomical data from a control group in the PREDICT-HD database [10] are presented to demonstrate the ability of the proposed method in comparison to shape regression that works directly on shape boundaries.

Synthetic Data

We create two synthetic examples to show the ability and feasibility of the proposed method. We first consider an ellipsoid as the source, and deform it to match a target putamen shape, which allows the synthetic example to contain significant nonlinear deformations and radius changes. A second example (Set 2) is created by inducing only pose changes to the synthetic set (Set 1) whereas the intrinsic shape properties of the two sets is identical (Fig. 1 top).

Fig. 1.

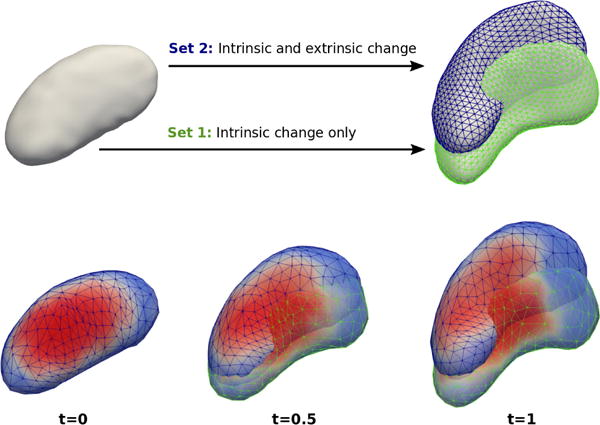
(Top) Two experiments (Set 1: green and Set 2: blue) of synthetic shapes which start from the same source shape and match target shapes which differ only in pose. (Bottom) Estimated shape trajectories using the proposed method, colored by radius. Radius fields of both pairs are nearly identical since pose changes are encoded on CM-Reps, which show that our method captures intrinsic changes even in the presence of additional extrinsic changes.

Fig. 1 shows the results using the proposed method. While the shapes change and deform over time, the estimated radius scalar fields are almost identical between Set 1 and Set 2, which were imposed in creating the synthetic example. Fig. 2 plots mean radius changes estimated by the proposed method and the mean magnitude of displacements between shape boundaries of each Set 1 (green) and Set 2 (blue). Even when volume changes are not significant, the magnitude of deformation can be large due to pose changes. The deformation caused by pose changes is encoded on the CM-Rep surfaces as shown in the mean magnitude of displacements of CM-Rep surfaces. Local radius change is also traceable with the radius scalar fields colored on the shape surfaces.

Fig. 2.

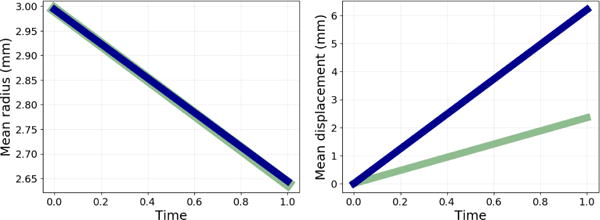
(Left) Mean radius measured from estimated CM-Rep trajectories of the two synthetic sets (Set 1: green and Set 2: blue). Intrinsic properties of the shape are captured nearly identically despite significant pose changes. (Right) Mean point displacement between the two estimated CM-Rep trajectories show large differences, with pose changes encoded on the CM-Rep surface. Our method is able to model both intrinsic and extrinsic properties of shape changes.

Compared to standard geodesic shape regression methods [4] working on shape boundaries, the proposed method may lose accuracy regarding shape matching since it models shapes as reconstructed boundaries of CM-Reps with fixed topology. However, we claim that the loss may not be significant if we choose a proper CM-Rep template for given shapes, also experimentally shown by the mean and the standard deviation of shape surface distances of the proposed method for the synthetic example is 0.2744 ± 0.0571(mm) in the range from 0.2176mm to 0.3403mm while the results of [4] is 0.2136 ± 0.0043(mm) from 0.2072mm to 0.2176mm.

Regression for Normative Model of Aging

We apply our method to analyze the shape changes of caudate and putamen of the basal ganglia complex of subjects of a control group in PREDICT-HD Huntington’s disease (HD) database [10]. A CM-Rep surface trajectory is estimated for 107 baseline scans with an age range from 24 to 70 years old. A CM-Rep surface trajectory colored by radius scalar fields and a reconstructed volumetric shape trajectory are shown in the top row of Fig. 3. Pose change of the shape complex can be observed as the structures are pushed outward by the expansion of lateral ventricles with age. Such pose changes and intrinsic shape changes are coupled together in the deformation estimated by a shape regression method working directly on shape surfaces.

Fig. 3.

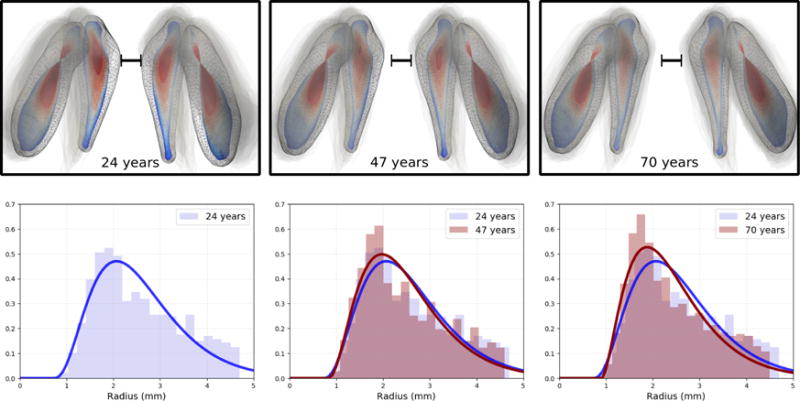
Normative model of aging. (Top) CM-Rep surfaces colored with radius scalar fields. Reconstructed shape complexes (mesh) are sampled from the reconstructed shape trajectory at age 24, 47, and 70 from left to right. The oldest 20 observations are overlaid as transparent gray to show the final location of the shape-complex. (Bottom) Normalized radius histograms of each left caudate shape from the top row. We observe that radius distributions tend to have a larger portion of smaller radii (thinning) with increased age. Gamma functions are fitted to show the change of radii distribution with age.

The proposed method decouples the pose changes and radius changes over time and captures intrinsic shape properties as shown in the bottom row of Fig. 3. In addition to the large pose change from ventricle expansion with normal aging, we also clearly capture the thinning of the caudate and putamen. The thinning is not readily differentiated from pose changes by momenta vectors only. Our model estimates such momenta vectors and shape boundaries at essentially the same level of accuracy of previous methods, but with the added benefit of trajectories of intrinsic changes (histograms such as in Fig. 3 can be viewed as an animation in a supplemental video). Also, point correspondences are established between the reconstructed shape surfaces and CM-Rep surfaces along the trajectory. Thus tracking and statistical analysis of local shape properties are also possible with the proposed method which have not been available before.

We calculated the sum of surface distances of all 107 observations to the estimated reconstructed volumetric shape trajectory. Observed shapes are compared to the shapes of the estimated trajectory at the corresponding time points. The mean of surface distances of the proposed method is 5.1mm and the results of [4] was 4.7mm for all observations with a set of four shapes. Therefore, the proposed method maintains accuracy if compared to the shape regression method working directly on shape surfaces while it reveals extra information on intrinsic shape properties of a set of shapes over time, e.g. quantifying locality and magnitude of intrinsic shape changes.

4. CONCLUSIONS

This work presents a novel 4D continuous medial representation by geodesic shape regression for characterization of spatiotemporal shape changes. Extending the CM-Rep method to 4D, the medial shape model decouples temporal shape deformations into changes of pose and intrinsic property changes, thus overcoming limitations of current schemes where surface changes could not be attributed to changes of shapes themselves or mere motion. The strength of the proposed scheme is demonstrated by the driving clinical application of modeling changes of the set of subcortical structures of the human brain over time. Ambient space deformations of the multi-object set of shapes clearly show that these are affected by adjacent objects, which may lead to wrong clinical conclusions. To our knowledge, this is the first presentation of a continuous 4D skeleton representation for spatiotemporal shape analysis. Future work focuses on the development of a statistical framework for 4D medial analysis, and on applying the methodology to anatomical shapes from large-scale clinical neuroimaging studies including the PREDICT-HD Huntington’s disease database [10].