Genomic Selection for Late Blight and Common Scab Resistance in Tetraploid Potato (Solanum tuberosum)

Abstract

Potato (Solanum tuberosum) is a staple food crop and is considered one of the main sources of carbohydrates worldwide. Late blight (Phytophthora infestans) and common scab (Streptomyces scabies) are two of the primary production constraints faced by potato farming. Previous studies have identified a few resistance genes for both late blight and common scab; however, these genes explain only a limited fraction of the heritability of these diseases. Genomic selection has been demonstrated to be an effective methodology for breeding value prediction in many major crops (e.g., maize and wheat). However, the technology has received little attention in potato breeding. We present the first genomic selection study involving late blight and common scab in tetraploid potato. Our data involves 4,110 (Single Nucleotide Polymorphisms, SNPs) and phenotypic field evaluations for late blight (n=1,763) and common scab (n=3,885) collected in seven and nine years, respectively. We report moderately high genomic heritability estimates (0.46 ± 0.04 and 0.45 ± 0.017, for late blight and common scab, respectively). The extent of genotype-by-year interaction was high for late blight and low for common scab. Our assessment of prediction accuracy demonstrates the applicability of genomic prediction for tetraploid potato breeding. For both traits, we found that more than 90% of the genetic variance could be captured with an additive model. For common scab, the highest prediction accuracy was achieved using an additive model. For late blight, small but statistically significant gains in prediction accuracy were achieved using a model that accounted for both additive and dominance effects. Using whole-genome regression models we identified SNPs located in previously reported hotspots regions for late blight, on genes associated with systemic disease resistance responses, and a new locus located in a WRKY transcription factor for common scab.

The potato (Solanum tuberosum L.) is considered the sixth most important agricultural commodity worldwide after sugar cane, maize, rice, wheat and milk. In 2014, the global production of potatoes exceeded 385 million tons, positioning China as the largest producer with more than 66 million tons, followed by Russia, India and the United States (FAOSTAT 2016). As a staple food, this crop represents one of the main sources of carbohydrates, fiber, minerals and vitamins, providing essential nutrients and energy needed for healthy body development and function (Kolasa 1993; Drewnowski and Rehm 2013).

Despite its great economic and food security importance, potatoes face high production losses caused mainly by biotic factors. Among them, pathogens such as late blight (Phytophthora infestans (Mont.) de Bary), represent the most devastating disease for potato worldwide. Late blight infects vegetative tissues, typically killing the entire plant, within 7 to 10 days. This pathogen accounts for annual losses of 16% of the global potato production (Haverkort et al., 2009). Under increasingly variable weather conditions, late blight incidence is expected to escalate worldwide, affecting mainly highlands in developing countries (Sparks et al. 2014).

Soil-borne pathogens such as common scab (Streptomyces scabies Thaxter), reduces the potato quality and marketability by causing superficial lesions on the tuber surface (Dees and Wanner 2012). Susceptibility to common scab is dependent upon genotype, time and environmental conditions (Wanner 2006; Wanner and Kirk 2015), having a negative impact mainly in underground tissues in development, such as stolons and tubers. This pathogen has spread worldwide and due to its saprophyte nature, (common scab can survive in winter), thus becoming a permanent source of inoculum for the next planting seasons, causing losses up to $100/Ha (Wanner and Kirk 2015).

Pathogen infection can be controlled by using protectants or systematic fungicides; however, there methods can be ineffective if the environmental conditions favor pathogen dispersion (Nowicki et al. 2011) or the emergence of fungicide-resistant genotypes (Pomerantz et al. 2014). The most effective way to control the incidence of late blight and common scab in potatoes is through the generation of resistant varieties (Ahn and Park 2013). However, breeding for resistant varieties via phenotypic selection can take up to 15 years, making traditional breeding time-consuming and sometimes ineffective against fast-evolving pathogens (The Potato Genome Sequencing Consortium 2011; Lozano et al. 2012).

Marker-assisted (Barone 2004) and genomic selection (GS) strategies (Meuwissen et al. 2001) can accelerate the process of breeding disease resistance. Several studies on late blight and common scab resistance have reported variants conferring resistance to these pathogens; however, most of the genomic research has focused on late blight (Gebhardt et al. 2004; Malosetti et al. 2007; Muktar et al. 2015; Mosquera et al. 2016; Braun et al. 2017a) and are largely based on phenotype-single marker association analyses. To the best of our knowledge, no study so far has considered the use of GS for breeding resistance to late blight and common scab in potato. Therefore, in this article, we use Whole-Genome Regression methods commonly used in GS to: (i) study important features of the genetic architecture of resistance to late blight and common scab (including trait heritability, extent of genetic-by-environment interactions (G×E) and the importance of non-additive effects), (ii) identify large-effect variants contributing to resistance to late blight and scab, and (iii) assess the prediction accuracy of GS for resistance to those two pathogens.

Our data involves (up to) nine years of field evaluations for late blight and common scab at two Michigan State University’s (MSU) research centers. We considered models that accounted for additive effects and various forms of dominance and evaluated two different statistical methods. Our results suggest that sizable fraction of the inter-individual differences in disease resistance (∼46% for late blight and 45% for common scab) can be captured by the SNP set used in the study. The extent of G×E was low for common scab and high for late blight. We found that additive models can capture more than 90% of the genetic variance. We report large-effect SNPs contributing to late blight resistance in chromosomes V and IX, that have been previously reported to harbor resistance genes to this pathogen. We also report the first SNP associated with common scab resistance, located on chromosome IX, and positioned in a transcription factor known for its role in systemic defense and resistance responses. Our results demonstrate that genomic selection can yield moderately accurate prediction of disease resistance for genotypes that have been not evaluated in field trials. Thus, GS could be used for rapid cycling selection for resistance to both late blight and common scab in tetraploid potato.

Materials and Methods

Data

Data were collected from early generation and advanced tetraploid potato genotypes derived from bi-parental crosses at the MSU potato breeding program. Additional advanced breeding genotypes from other United States breeding programs and reference varieties were also included. The available genotypes (n = 381) represent different market classes for fresh market, chip-processing, and russet-type fresh market and processing varieties. These genotypes were evaluated in field trials that included annual selections from MSU’s potato breeding program, where each year poorly performing genotypes were replaced with new genotypes, while maintaining control genotypes during consecutive years.

Late blight field resistance trials (273 genotypes and a total of 1,763 disease records) were conducted in inoculated foliar field trials during seven years (2010-2015 and 2017) at the MSU’s Clarksville Research Center (Clarksville, MI). Potato seed tubers were hand planted early- to mid-June as four-plant hills in 1.5 m plots in a randomized complete block design with one to three replicates. Late blight-susceptible rows and plots were planted around the perimeter and between blocks to promote an even late blight distribution in the field. After approximately 60 days, all plots were inoculated with a zoospore suspension of late blight at 3x10⁶ spores/mL at the end of July or beginning of August of each year. Over the 7-year period, different isolates were used to infect the trial depending on the prominent isolate in the region. The P. infestans strain (clonal lineage) detected in each year in the trial can be found in Table S1 in File S4. Following inoculation, plots were rated visually for the percentage of foliar area affected by late blight. Ratings were taken at 3 to 7-day intervals, based on the rate of disease progression during 35-50 days post inoculation (DPI). Finally, the percent defoliation data were used to calculate the relative area under the disease progress curve - RAUDPC (Fry 1978).

Common scabfield resistance trials (370 genotypes and a total of 3,885 disease records) were conducted under field conditions during nine years (2009-2017) in a disease nursery at the MSU’s Montcalm Research Center (Lakeview, MI). The field was inoculated with common scab from aggressive Michigan isolates, and has been cultivated for high disease pressure for the past nine years. The trials were planted in a randomized complete block design consisting of one to four replications of five-hill plots. After harvesting, mature tubers in plots were assessed for their overall plot disease rating scale of 0-5. The rating was based on a combined score for common scab coverage and lesion severity in which a rating of 0 indicates zero infection and 3.0 or greater scores represent highly susceptible genotypes with >50% infection and severe pitted lesions (Driscoll et al. 2009).

SNP genotypes were obtained using the Infinium 8303 Potato Array. Plant DNA was isolated from young potato leaves or tubers using the Qiagen DNeasy Plant Mini Kit (Qiagen, Germany), following manufacturer’s instructions. DNA was quantified using the Quant-iT PicoGreen dsDNA Assay kit (Invitrogen, San Diego, CA). Genotype scoring was performed using the GenomeStudio software (Illumina, San Diego, CA). The tetraploid SNP calling was performed as per Hirsch et al. (2013), using a custom tetraploid genotype calling based on theta values from the Illumina GenomeStudio (Illumina, San Diego, CA) and subsequently filtered, removing poor quality markers. SNPs were coded by counting the number of copies of a reference allele (e.g., B) where 0 denotes fully homozygous allele (AAAA), 1-3 represent heterozygous genotypes (AAAB, AABB, ABBB, respectively) and 4 the other homozygous genotype (BBBB). The genotype file was filtered by retaining SNPs with minor allele frequency (MAF) >0.05 and missing rate <0.15. The remaining missing SNP-based genotypes were imputed with the SNP means. The final number of SNPs that passed the quality filtering were 4,110.

We compared the observed and expected rates of heterozygous loci, the later derived under the assumption of Hardy-Weinberg (HW) equilibrium. Averaged across loci, the observed rates of heterozygosity (0.663) was only slightly higher than the one predicted from estimated allele frequencies (0.647). The regression of the observed and expected frequency of heterozygous loci had an estimated slope of 0.98 (SE = 0.0025) and a R² of 0.974. Moreover, we did not identify any clear outlier SNP that may have indicated a significant deviation of the observed frequency of heterozygous relative to the one predicted from the estimated allele frequency of the locus.

Genomic relationships were computed from centered and scaled SNP-based genotypes according to VanRaden (2008): $\mathit{GRM}=\frac{\stackrel{\sim }{\mathit{X}}\stackrel{\sim }{\mathit{X}}\prime }{ncol(\stackrel{\sim }{\mathit{X}})}$. Here, $\mathit{GRM}$ is a matrix describing genomic relationships between genotypes, $\stackrel{\sim }{\mathit{X}}=\left\{[X_{im}-mean\left(X_{im}\right)]/sd(X_{im})\right\}$ is a matrix of centered and scaled SNP-based genotypes ($X_{im}\in \left\{0,1,2,3,4\right\}$ counts the number of copies of the reference allele at the m^th loci. Subtracting the $mean\left(X_{im}\right),$ centers the SNP-based genotypes to a null mean and dividing by the SNP standard deviation, $sd(X_{im})$, scale SNP-based genotypes to unit variance). Finally, division by the number of SNP-based genotypes, $ncol(\stackrel{\sim }{\mathit{X}})$, makes the average diagonal value of $\mathit{GRM}$ equal to one. We use this matrix to quantify genomic relationships and to derive principal components, the later were computed by applying the eigen() R-function to GRM.

Statistical analyses

We use whole-genome regression models (Meuwissen et al. 2001; de los Campos et al. 2013) for estimation of marker effects and variance component analyses and for assessment of prediction accuracy. The general form of the statistical model used was as follows:

$$y_{ijk}=\mu +{\displaystyle \sum }_{h=1}^{5}P{C}_{hi}{\gamma }_h+b_j+g_i+g{e}_{ij}+{\epsilon }_{ijk}$$ [1]

where $y_{ijk}$ is a phenotypic score (for either late blight or common scab) of the k^th replicate of the i^th genotype collected in year j, $\mu$ is an intercept, ${\displaystyle \sum }_{h=1}^{5}P{C}_{hi}{\gamma }_h$ is a regression on the first five SNP-derived principal components, $b_j$ are year effects, $g_i$ is the main effect of the i^th genotype (alternative specifications of this effect are discussed below), $g{e}_{ij}$ represents a genotype-by-year interaction and ${\epsilon }_{ijk}$ are error terms, which were treated as normal, independently and identically distributed (iid) with year-specific variances, that is ${\epsilon }_{ijk}\begin{array}{c}iid\\ \sim \end{array}N\left(0,{\sigma }_j^2\right)$.

Year had seven levels for late blight and nine levels for common scab (2009, 2010,.., 2017) and was treated as a random effect. Genetic and genetic-by-year interactions were also modeled as random effects. We considered four specifications for modeling the main effect of genotypes:

• Genotype effect. In this specification we assumed that the main effects of the genotypes where iid draws from normal distributions $g_i\begin{array}{c}iid\\ \sim \end{array}N\left(0,{\sigma }_g^2\right)$. In this specification, no genetic information (SNPs) was used and no assumptions about gene action (additive, dominance, epistasis) were made. This specification was used as a baseline for a model that could be fitted without having genomic information. The other three specifications included genotypes as inputs.

• Additive model (A)$.$ Here, the main effect of the genotype was represented using a linear combination of the marker genotypes, that is $g_i={\displaystyle \sum }_{m=1}^{4110}{\stackrel{\sim }{X}}_{im}{\alpha }_m$ where ${\stackrel{\sim }{X}}_{im}=[X_{im}-mean\left(X_{im}\right)]/sd(X_{im})$ were centered and scaled genotypes code at the m^th SNP in the i^th genotype and ${\alpha }_m$ is the additive effect of the markers.

• Additive + Dominance (A+D). In this case, the main effects of genotypes have an additive component plus one that accounted for dominance; therefore in this model $g_i={\displaystyle \sum }_{m=1}^{4110}{\stackrel{\sim }{X}}_{im}{\alpha }_m+{\displaystyle \sum }_{m=1}^{4110}{\stackrel{\sim }{D}}_{im}{d}_m$ where ${\stackrel{\sim }{D}}_{im}=\left[D_{im}-mean\left(D_{im}\right)\right]/sd\left(D_{im}\right)$ are (centered and standardized) dummy variables for heterozygous loci, here $D_{im}$=1 (=0) indicates that the m^th SNP of the i^th genotype was in heterozygous (homozygous) state and $d_m$ is the dominant effect of the markers.

• General model (G)$.$ Here, $g_i={\displaystyle \sum }_{m=1}^{4110}{\displaystyle \sum }_{n=0}^4{\stackrel{\sim }{W}}_{imn}{\gamma }_{mn}$, where ${\stackrel{\sim }{W}}_{imn}$ are (centered and standardized) dummy variables for genotypes carrying n copies of the reference allele and ${\gamma }_{mn}$ is the general effect of the markers. Since there are up to five distinct genotypes (0,1,…,4) this model includes up to four degree of freedom per locus. This parameterization allows for any form of interactions of alleles within locus; thus, it can be considered the most general specification for a model accounting for additive and dominance effects.

Prior distributions for effects

Marker effects (including both additive, dominance and those of the G model) were treated as random. We considered two prior distributions of effects: (i) treating SNP effects as draws from normal distributions with null mean and model-specific variances (i.e., there were separate variances for additive and dominance), this approach was implemented using the Bayesian Ridge Regression (BRR) specification in the Bayesian Generalized Linear Regression (BGLR) R-package (Pérez and de los Campos 2014), and (ii) a Bayesian shrinkage-variable selection method (BayesB, Meuwissen et al. 2001). As with BRR, in BayesB different regularization parameters (probabilities of non-null effects and scale parameters) were assigned to effects in additive and dominance. BayesB was implemented in BGLR using the “BayesB” keyword for the model argument of the linear predictor.

Genotype-by-year effects ($g{e}_{ij}$) were treated as IID normal with mean zero and variance common to all the interactions, that is, $g{e}_{ij}\begin{array}{c}iid\\ \sim \end{array}N\left(0,{\sigma }_{ge}^2\right).$

Sequence of models:

Using the specifications described above, we produced a sequence of models designed to quantify the amount of variance explained (and the contribution to prediction accuracy) of each of the terms entering in the model of expression [1]. The sequence of models considered is summarized in Table 1.

Table 1. Sequence of models.

Model # (label)a	Effects Included
	Year	Genotypeb	PCc	Additived	Dominancee	Generalf	Genotype-by -Yearg	Error
M1	×							×
M2	×	×						×
M3	×	×					×	×
M4	×	×	×				×	×
M5 (A)	×		×	×			×	×
M6 (A+D)	×		×	×	×		×	×
M7 (G)	×		×			×	×	×

^aM1-M7 are model numbers. ^bRandom effect of the genotype (no SNPs used, no assumption about gene action are made).

^cPrincipal components, ^dlinear regression on allele content (0/1/2/3/4), ^eSimple dominance (1 degree of freedom per locus representing heterozygous) and ^fGeneral model for additive + dominance (with up to 4 degrees of freedom per locus). ^gGenotype-by-year interaction. An ‘×’ indicates that the effects was included in the model.

We used the whole-genome regression models described above for three purposes: (1) estimation of variance components, (2) identification of variants with high contribution to additive variance and (3) assessment of prediction accuracy in cross-validation.

Variance components:

The amount of variance accounted for by each of the terms included in the model was estimated using the methods described in de los Campos et al. (2015) and Lehermeier et al. (2017) (see Supplementary File S1 for further details). We use these methods to decompose the total phenotypic variance into components due to year, genetics factors, genotype-by-year interactions (G×E) and within-year error variance. We also use this approach to assess the relative contribution of SNP-additive and dominance effects.

Identification of SNPs With a sizable contribution to additive variance:

Response to selection is directly proportional to additive variance (Falconer and Mackay 1996). Thus, in GS, the single-loci additive variance represents a natural metric to assess the relative importance of individual loci from a breeding perspective. Under linkage equilibrium, the contribution of each locus to additive variance is given by $Var\left(X_{im}{\alpha }_m\right)=Var\left(X_{im}\right){\alpha }_m^2$. In our case, genotypes were standardized to unit variance; therefore, $Var\left(X_{im}{\alpha }_m\right)={\alpha }_m^2$. We used samples from the posterior distribution of SNP effects from the A model to assess the contribution of individual loci to additive variance. (Further details about how these quantities were computed can be found in the script provided with the Supplementary File S1). It is important to note that this measure does not account for linkage disequilibrium; thus it can only be taken as a proxy of the contribution of a locus to additive variance.

Prediction accuracy evaluation:

We implemented two cross-validation schemes. First, we used a fivefold cross-validation, assigning genotypes to folds. When using this approach all the phenotypic records of a genotype are assigned to either training or testing populations. Thus, this approach yields an estimate of the prediction accuracy that can be achieved predicting the performance of genotypes that have not been evaluated in field trials (i.e., prediction based on genotype data only) and is equivalent to the method labeled as Cross-Validation one (CV1) in Burgueño et al. (2012). For this scheme, genotypes were assigned to folds completely at random and the fivefold Cross Validation (CV) was repeated 100 times to obtain accurate estimates of the average prediction correlation and its standard deviation.

In a second prediction scheme (CV2), we assigned years to folds (i.e., there as many folds as years). Thus, when analyzing the j^th fold, data from the j^th year was assigned to testing and data from all the other years was used for training. This CV approach yields an estimate of the prediction accuracy that can be achieved when attempting to predict future year performance based on past data. Note that in this case, unlike CV1, when predicting data for the i^th genotype on the j^th year all the data from the i^th genotype collected in other years was part of the training dataset.

In both CV schemes prediction accuracy was evaluated by computing the within-year correlation between phenotypes and CV predictions.

Software:

All the analyses were conducted using R (The R Development Core Team 2010). Models were fit using the BGLR-R package. For each model, we ran the Gibbs sampler algorithm for a total of 33,000 cycles, discarding the first 3,000 samples for burn-in; one of every five of the remaining samples was saved and used to estimate posterior means and standard deviations.

Data availability

Scripts demonstrating how each of the models were implemented in BGLR are given in File S1. The genotype and phenotype data are provided in Files S2 and S3 for late blight and common scab, respectively. File S4 contains Tables S1-S5. Supplemental material is available at Figshare: https://doi.org/10.6084/m9.figshare.6336911 and https://doi.org/10.25387/g3.6262214.

Results

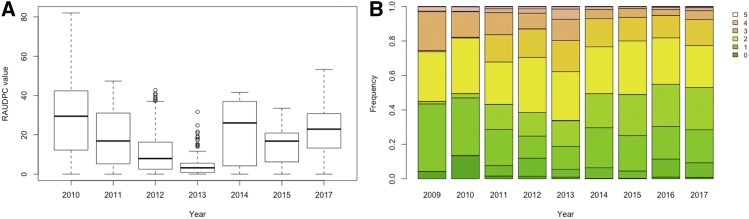
The distribution of late blight and common scab infection varied substantially between years (Figure 1). In general, RAUDPC median values decreased from 2010 to 2012, with US-22 as the prevalent late blight strain on infected plants. In subsequent years, a differential response for late blight resistance was observed when US-23 was the prevalent strain. Disease pressure changes, together with the environment fluctuations between years contribute to explain the phenotypic variation observed for the late blight resistance response. Similarly, for common scab, a reduced frequency of resistant genotypes (0-1 score) was observed from 2009 until 2013, having at the same time an increasing number of intermediate susceptible genotypes (2-3 scores). Since 2013 and until 2017, an increased frequency of common scab resistant genotypes was observed (Figure 1).

Figure 1.

Boxplot of late blight scores (A, relative area under the disease progress curve- RAUDPC) and bar plot for common scab scores (B, 0-5 rating scale).

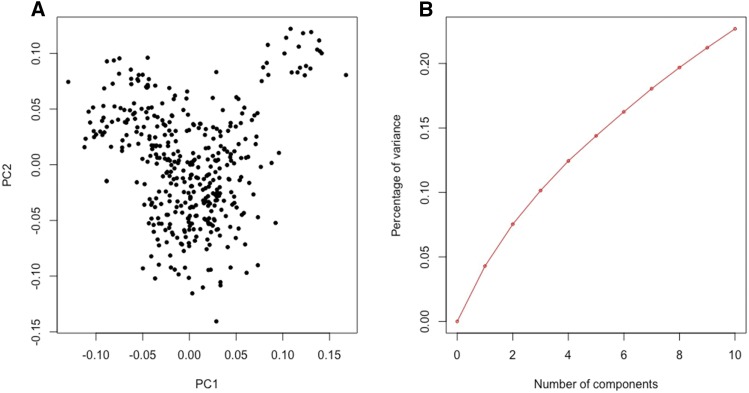
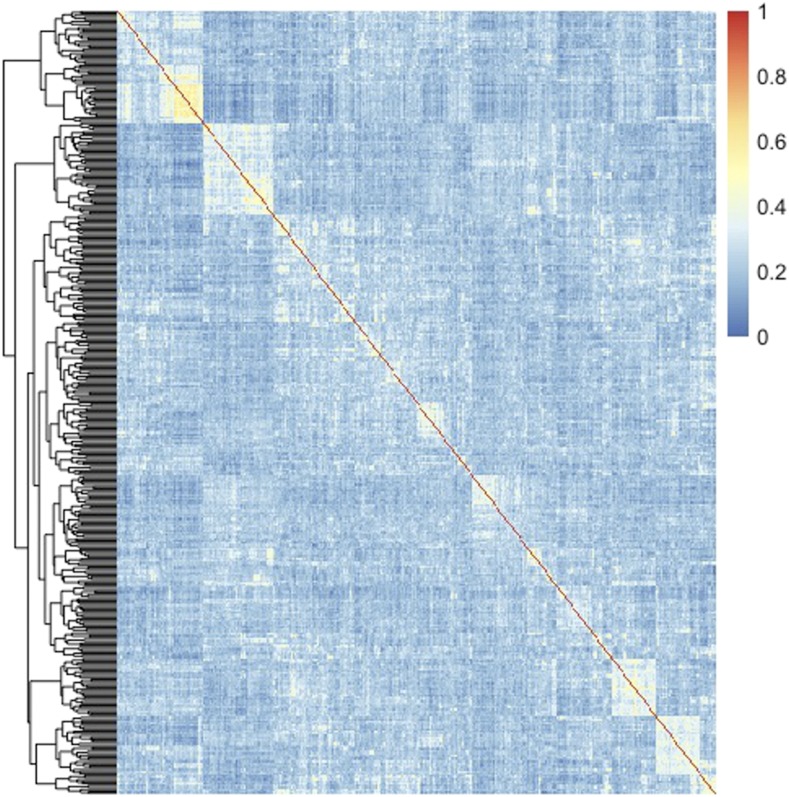
A principal component (PC) analysis showed that potato genotypes clustered in two groups, one involving 391 genotypes, and a small one including 22 genotypes (Figure 2). The eigenvalues associated to the first two PCs explained about 8% of the total genotypes variance (Figure 2). A cluster analysis using a correlation matrix derived from SNP markers supports the PC-analysis results (Figure 3). The heatmap also reveals that the strength of genomic relationships among the different materials is relatively small (the clear majority of the genotypes have genomic relationships with other genotypes smaller than 0.1, with only a few genotypes showing relationships comparable to parent-offspring or full-sib relations, i.e., 0.5, Figure 3).

Figure 2.

Principal component analysis of the Michigan State University’s potato breeding genotypes derived from 4,110 SNPs: loadings on the first two marker-derived principal components (A) and proportion of variance explained by the top 10 principal components (B).

Figure 3.

Heatmap of the genomic relationship matrix (GRM) from the Michigan State University’s potato breeding genotypes.

Variance Components Estimates

The variance components analyses for late blight resistance (Table 2 and Table S2 in File S4) revealed that year explained roughly 25% of the variance in disease scores. For this trait, and taking as a reference the model M3, the main effect of genotype explained about 34% of the variance, genotype-by-year interactions explained 25% of the variance and the error term explained roughly 14% of the variance in late blight scores. These results suggest that a substantial proportion of within-year variance in late blight scores (roughly 70%, computed as 0.34/[0.34+0.144]) can be explained by main effects of genotypes. For late blight, the amount of genetic variance captured by the A model was roughly 94% of the variance captured by the G model (computed as 0.330/0.352).

Table 2. Variance components estimates (posterior standard deviation) derived from BayesB model for late blight and common scab resistance by model. Phenotypic scores were standardized to unit variance; hence estimates can be interpreted as the proportion of variance explained by each component. Results obtained with the fully Gaussian model (BRR) are presented in Table S2.

Model # (label)a	Year	Genetic						Genotype-by-yearg	Error
		Genotype	Marker-derived				Total geneticf
			PCb	Additivec	Dominanced	Generale
Late blight
M1	0.266 (0.021)								0.735 (0.025)
M2	0.256 (0.014)	0.434 (0.018)					0.434 (0.018)		0.303 (0.011)
M3	0.250 (0.027)	0.340 (0.031)					0.340 (0.031)	0.253 (0.019)	0.144 (0.006)
M4	0.244 (0.026)	0.265 (0.028)	0.096 (0.024)				0.351 (0.032)	0.251 (0.018)	0.144 (0.006)
M5 (A)	0.240 (0.027)		0.135 (0.069)	0.292 (0.051)			0.330 (0.035)	0.275 (0.020)	0.144 (0.006)
M6 (A+D)	0.240 (0.027)		0.135 (0.062)	0.166 (0.063)	0.141 (0.049)		0.340 (0.034)	0.267 (0.020)	0.144 (0.006)
M7 (G)	0.249 (0.028)		0.107 (0.043)			0.280 (0.034)	0.352 (0.033)	0.251 (0.019)	0.144 (0.006)
Common Scab
M1	0.033 (0.006)								0.971 (0.022)
M2	0.030 (0.004)	0.456 (0.016)					0.456 (0.016)		0.523 (0.012)
M3	0.029 (0.005)	0.440 (0.021)					0.440 (0.021)	0.059 (0.009)	0.483 (0.013)
M4	0.029 (0.006)	0.419 (0.021)	0.030 (0.012)				0.447 (0.023)	0.056 (0.009)	0.485 (0.013)
M5 (A)	0.031 (0.006)		0.132 (0.087)	0.507 (0.076)			0.443 (0.025)	0.061 (0.009)	0.485 (0.013)
M6 (A+D)	0.031 (0.006)		0.107 (0.073)	0.356 (0.087)	0.151 (0.060)		0.448 (0.024)	0.057 (0.009)	0.485 (0.013)
M7 (G)	0.031 (0.006)		0.051 (0.030)			0.442 (0.031)	0.451 (0.023)	0.056 (0.009)	0.484 (0.013)

^aM1-M7 are model numbers (label). The effects included in each of them are described in the columns.

^bPrincipal components, ^clinear regression on allele content (0/1/2/3/4), ^dSimple dominance (1 degree of freedom per locus representing heterozygous) and ^eGeneral model for additive + dominance (with up to 4 degrees of freedom per locus). ^fTotal genetic variance, ^gGenotype-by-year interaction.

For common scab (Table 2 and Table S2 in File S4) the main effect of genotype explained about 44% of the total variance, year and genotype-by-year effects explained only 3% and 6% of the total variance, respectively, and the error term accounted for almost one half (48%) of the variance in disease scores. For common scab we also observed that the amount of genetic variance captured by the A model was very similar to the one captured with the G model.

The proportion of the total genetic variance that could be attributed to the first-5 PCs was substantial for late blight (∼30%, computed as 0.107/0.352) and low for common scab (∼10%, 0.051/0.451).

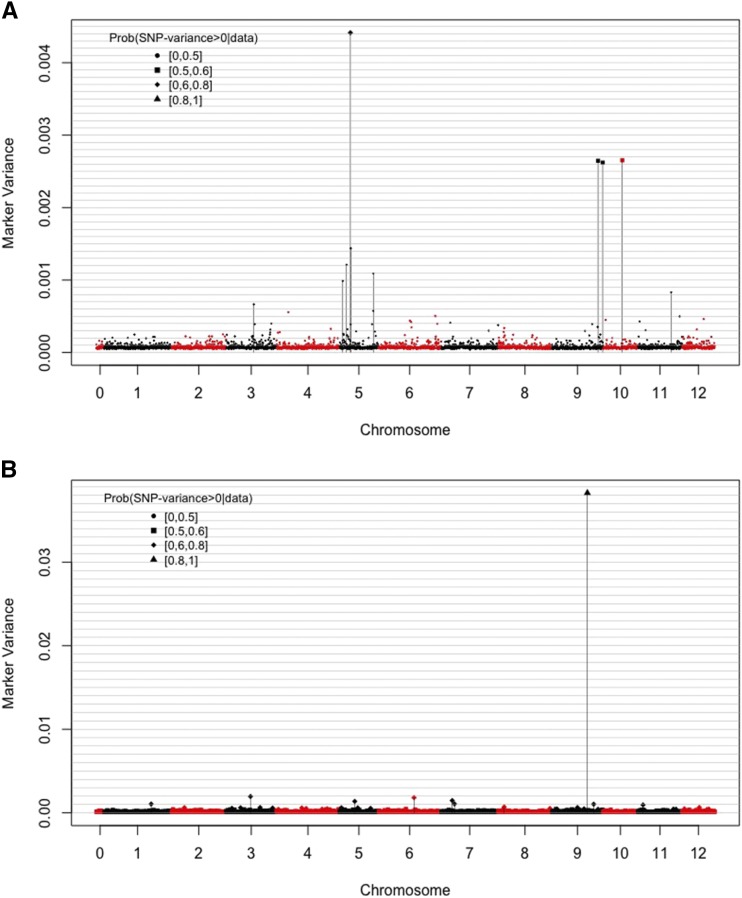
For the A model (fitted using BayesB), we computed single-locus variances and used these estimates as proxies for the SNP relevance (Figures 4a and 4b). Additionally, we report in Figures S1 and S2, linkage disequilibrium (LD) plots for the 10 leading SNPs (i.e., those with the larger single-SNP variance) for each trait. For both pathogens, there were a few regions with large single-SNP-variance. Specifically, for late blight, there were multiple SNPs distributed across the potato chromosomes (Figure 4a and Table S3 in File S4) with a sizable contribution to variance, suggesting that multiple genes contribute to the resistant phenotype. Conversely, for common scab, there was one SNP, located in chromosome IX (Figure 4b and Table S4 in File S4), that stands out for its contribution to variance and a few SNPs with a moderate contribution to phenotypic variance.

Figure 4.

Estimated SNP-variances derived from BayesB model using the additive model for late blight (A) and common scab (B). (In both cases, phenotypes were disease scores standardized to a variance equal to one. Vertical lines indicate the positions of the top-10, according to estimated SNP-variance markers).

The results from the first cross-validation analysis (CV1) yielded an estimated prediction correlation of about 0.31 for late blight resistance using the G model. For this trait, there was a relatively small, albeit significant, increase in prediction correlation for the G model relative to the A model. Likewise, there was a slight superiority of BayesB over BRR (Table 3). In the case of common scab, the A model (with a prediction correlation of ∼0.27) outperformed the A+D (correlation ∼0.26) and G (correlation ∼0.22) models. These results agree with the variance component analyses results, where we also found evidence of a slightly higher relevance of non-additive effects in the case of late blight, compared to common scab.

Table 3. Cross-validation correlations obtained with BRR and BayesB models by trait and model.

				Proportion of times that the model in row gave a higher correlation than the model in columns
		CV-Correlation		BRRa			BayesBa
Priora	Model # (label)b	Averagec	SDd	M5 (A)	M6 (A+D)	M7 (G)	M5 (A)	M6 (A+D)	M7 (G)
Late Blight
BRR	M5 (A)	0.258	0.023		0.96	0.00	0.33	0.91	0.00
	M6 (A+D)	0.241	0.023	0.04		0.00	0.04	0.57	0.00
	M7 (G)	0.312	0.017	1.00	1.00		1.00	1.00	0.5
BayesB	M5 (A)	0.260	0.024	0.67	0.96	0.00		0.94	0.00
	M6 (A+D)	0.240	0.024	0.09	0.43	0.00	0.06		0.00
	M7 (G)	0.313	0.017	1.00	1.00	0.50	1.00	1.00
Common Scab
BRR	M5 (A)	0.268	0.025		0.81	0.99	0.1	0.55	1.00
	M6 (A+D)	0.259	0.023	0.19		0.99	0.07	0.20	0.99
	M7 (G)	0.218	0.022	0.01	0.01		0.00	0.02	0.63
BayesB	M5 (A)	0.278	0.026	0.9	0.93	1.00		0.91	1.00
	M6 (A+D)	0.265	0.025	0.45	0.8	0.98	0.09		0.98
	M7 (G)	0.216	0.022	0	0.01	0.37	0.00	0.02

^aBRR uses a Gaussian prior for effects, BayesB uses a prior that has a point of mass at zero and a scaled-t slab.

^bA: Additive model, A+D: additive+dominance; G: general model (with up to 4 degrees of freedom per locus).

^cAverage from 100 cross-validations.

^dStandard deviation.

Note that in Table 3 we only included results from models using genotypes. Results from other models (e.g., M2 and M3) are not presented because in CV1 they render zero within-year correlation. This happens because in CV1 predictions are entirely depending on borrowing of information between genotypes, a feature that is not possible in models that do not use genotype or pedigree information.

The results from the second cross-validation (i.e., where years were assigned to folds, CV2) yielded higher estimates of prediction accuracy than those obtained in CV1 (Table 4 and Table S5 in File S4). This happens because in CV2 there is within-genotype borrowing of information across years. For late blight, prediction correlations ranged from 0.41 to 0.74, depending on the model and year. Likewise, for common scab, we obtained correlations ranging from 0.46 to 0.76. For both traits, the across-year average correlations showed small differences between models (with a slight superiority in favor of the G model).

Table 4. Year cross-validation correlations obtained with BayesB model by trait and model.

Year	Model # (label)a
	M2	M3	M5 (A)	M6 (A+D)	M7 (G)
Late blight
2010	0.551	0.537	0.463	0.465	0.517
2011	0.652	0.658	0.608	0.611	0.642
2012	0.583	0.604	0.586	0.586	0.624
2013	0.422	0.415	0.484	0.485	0.492
2014	0.621	0.596	0.633	0.640	0.655
2015	0.719	0.730	0.678	0.696	0.745
2017	0.508	0.504	0.471	0.491	0.506
Average	0.579	0.578	0.560	0.568	0.597
SD	0.098	0.104	0.087	0.089	0.095
Common scab
2009	0.459	0.460	0.472	0.471	0.466
2010	0.520	0.522	0.535	0.533	0.517
2011	0.610	0.611	0.622	0.625	0.618
2012	0.625	0.628	0.628	0.626	0.634
2013	0.750	0.759	0.731	0.737	0.750
2014	0.615	0.611	0.634	0.636	0.635
2015	0.649	0.653	0.666	0.671	0.659
2016	0.639	0.639	0.652	0.647	0.647
2017	0.508	0.510	0.519	0.520	0.515
Average	0.597	0.599	0.606	0.607	0.605
SD	0.088	0.090	0.082	0.083	0.089

^aM2 includes year and genotype (no SNP information); M3: extends M2 with the addition of genotype-by-year interaction; M5 includes year, first 5 marker-derived PCs, additive effect of SNPs and genotype-by-year interaction; M6 expands M5 by adding the effects of dominance; M7 includes year, 5-PCs, genotype-by-year interactions and SNPs with up to 4 degrees of freedom per locus (‘General’ model).

Discussion

Genomic selection has been quickly adopted for breeding in diploid species (Heffner et al. 2009; Daetwyler et al. 2013; de los Campos et al. 2013). However, the volume of research and the adoption of the GS technology for breeding of polypoid species has been much more limited (e.g., Habyarimana et al. 2017; Sverrisdóttir et al. 2017). In this study, we demonstrate how genomic models commonly used in GS of diploid organisms can be applied for the analysis and prediction of disease susceptibility in autotetraploid potato.

Our results indicate that a sizable fraction of the within-year inter-individual differences in disease resistance (about 0.46 ± 0.04 for late blight and 0.45 ± 0.02 for common scab) can be explained using 4,110 codominant SNPs from the Infinium 8303 Potato Array used in this study. These moderately high genomic heritability estimates for complex disease phenotypes indicates that, in principle, genomic prediction could be used successfully to select for resistance to late blight and common scab.

Previous studies have reported heritability estimates for these traits; however, differences in the nature of the genetic materials (diploid vs. tetraploid, hybrids vs. genotypes) and of the environmental conditions (natural vs. induced infection) makes the comparisons across studies difficult (Nelson 1978; Braun et al. 2017b). For instance, Haynes and Christ (1999) reported much higher heritability estimates for late blight resistance (0.8), but this study was based on diploid hybrids. For the same trait, estimates of heritability obtained using tetraploid genotypes are closer to the ones reported here (ranging from 0.31 to 0.69, Pajerowska-Mukhtar et al. 2009; Solano et al. 2014).

For common scab, previous heritability estimates are also highly variable, depending on the genetic material and the environmental conditions. For instance, using diploid potatoes derived from a cross between wild relatives (S. phureja × S. stenotonum) and cultivated potatoes (di-haploid S. tuberosum × S. chacoense), Haynes et al. (2009) and Braun et al. (2017b) reported broad sense heritability estimates ranging from 0.18 to 0.72 for different environments. However, studies involving tetraploid potatoes have reported higher heritability estimates with values ranging from 0.32 to 0.93 (Haynes et al. 1997; Bradshaw et al. 2008; Tai et al. 2009). More recently, 18 dedicated common scab and standard breeding program trials were conducted in fields with high disease pressure. The broad sense heritability estimates reported from these studies ranged from 0.75 to 0.90 for dedicated common scab trials and from 0.06 to 0.82 for standard breeding programs trials involving advanced breeding materials (Navarro et al. 2015).

The amount of variance in disease resistance that could be attributed to genotype-by-year interactions was high for late blight and very small for common scab. These differences are likely to be due to the different nature and characteristics of infection on the fields used to evaluate late blight and common scab. Specifically, for late blight, the mean scores varied substantially between years (e.g., it was clearly low in 2013) reflecting changes on the late blight aggressiveness and late blight genotypes present in different years, resulting in a large extent of genotype-by-year interactions for this pathogen. On the other hand, our common scab data were generated in a nursery that has been used to evaluate common scab resistance in potato breeding genotypes for several years. Consequently, there was less variability in the mean scores across years and therefore we observed substantially less extent of G×E. A similar result was reported under comparable conditions by Murphy et al. (1995). Results based on fields trials performed in different locations for this pathogen have shown much higher variability over the years (Haynes et al. 2009).

The comparison of the genomic variance estimates obtained with the A model and those obtained with the G model suggest that, for both pathogens, a sizable fraction of the total genetic variance (0.94 and 0.98, for late blight and common scab, respectively) can be captured by an additive model (Table 2 and Table S2 in File S4). The amount of genetic variance captured by the A model reflects an estimate of the variance that can be captured by regression on allele content (i.e., by allele substitution effects). However, when dominance is included in the model (A+D), the estimated ‘additive variance’ no longer represents the variance explained by allele substitution effects; therefore, the additive component in the A+D model is smaller than the additive component estimated with the A model.

While our variance component estimates indicate that most of the genetic variance can be captured by an A model, our cross-validation analysis suggests that accounting for non-additive effects could improve prediction accuracy by a small but statistically significant margin in the case of late blight. These results agree with the theory that suggests that dominance and epistasis are expected to contribute to the expression of traits subjected to directional selection or those affecting the plant fitness such as late blight resistance (Killick and Malcolmson 1973). This may explain why the G model captured slightly more variance and predicted slightly more accurately late blight scores than the A model.

The presence of linkage disequilibrium (LD) between loci makes the partition of the total genetic variance into (orthogonal) locus-specific components not possible (de los Campos et al. 2015). However, it is worth looking at the relative size of estimated effects to explore features of the genetic architecture of the trait. We did this by inspecting the estimated SNPs variances (Figure 4). Overall, the proportion of variance explained by individual SNPs was low, reinforcing the idea that resistance to both common scab and late blight is polygenic. However, there were some SNPs with relatively large SNP-variances for both late blight (located mainly in chromosomes V and IX) and common scab (located in chromosome IX). (Figure 4, Table S3 and S4 in File S4). For late blight resistance, multiple quantitative trait loci (QTL) have been reported across the 12 potato chromosomes in tetraploid and diploid potato populations (Tiwari et al. 2013). Most of these major QTL are located in chromosomes III, IV, V, VII, XI and XII, characterized for harboring hotspot regions for resistance to late blight and other pathogens, not only for genes involved in quantitative resistance such as R genes, but also for genes involved in qualitative resistance (Malosetti et al. 2007; Pajerowska-Mukhtar et al. 2009; Álvarez et al. 2017). For instance, genes involved in carbohydrate metabolism such as sucrose synthase (Table S3 in File S4) play an active role in the defense response elicitation. Sucrose synthesis down-regulation has been described in the Capsicum annuum - Phytophthora nicotianae pathosystem, showing a decreasing concentration after challenging with beta-aminobutyric acid (BABA) and priming the synthesis of metabolites associated with the production of defense-related compounds (Stamler et al. 2015). Additionally, these results validate earlier QTL reports obtained from MSU-derived populations using potato varieties carrying different late blight resistance genes coming from species previously used in resistance breeding such as S. demissum and S. berthaultii (Massa et al. 2015; N. Manrique-Carpintero, personal communication).

For common scab resistance, our results suggest an additive resistance effect with a clear major-effect SNP located on chromosome IX. This SNP is associated with a WRKY transcription factor known for their role in the modulation of the resistance responses in systemic and acquired plant resistance, activating or repressing the transcription of genes involved in the synthesis of defense related-proteins such as R proteins (Pandey and Somssich 2009; Buscaill and Rivas 2014). In addition to the loci discussed above, we were also able to identify additional SNPs with a sizable contribution to variance across the potato chromosomes (Figure 4). Interestingly, the SNP in the WRKY gene that appeared to have a sizable contribution to inter-individual differences in common scab resistance is located in a region where LD is relatively weak (see Figure S2).

For instance, we found one SNP located in chromosome III (Table S4 in File S4) associated with the primary metabolism-related protein fructokinase, whose concentration increases under pathogen attack as a mechanism to reduce the costs attributed to the defense response in soil-borne pathogens (Zimaro et al. 2011). Likewise, in chromosome V, we found one SNP related to the RNA synthesis-related protein DEAD-box ATP-dependent RNA helicase, reported for its role in plant resistance by enhancing the defense response in both necrotrophic and biotrophic pathogens (Li et al. 2008). Overall, the evidence we found support the hypothesis that resistance to common scab involves multiples mechanisms of defense including the activation of genes related to systemic and R gene-mediated resistance.

There are few studies reporting QTL for common scab resistance. For instance, two QTL located in chromosome XI were detected in a diploid parental-derived population for the percentage of surface area infected and lesion type caused by common scab, explaining 21% and 18.2% of the total phenotypic variance, respectively (Braun et al. 2017a). For tetraploid populations, Amplified Fragment Length Polymorphisms (AFLPs) and Simple Sequence repeats (SSRs) markers have been used to establish an association between potato genotypes and the common scab resistance phenotype in a tetraploid bi-parental derived-population. Two copies of a dominant allele were detected in a QTL localized in chromosome II, explaining 8.1 and 7.1% of the phenotypic variance, respectively. A second QTL was localized in chromosome VI explaining 6.9% of the total phenotypic variance (Bradshaw et al. 2008). Therefore, the large-variance SNP detected in this study represents a new genomic region associated with common scab resistance, providing a framework for the development of molecular markers for marker-assisted selection and understand the genetics behind common scab resistance.

Our variance component estimates suggest that for both, late blight and common scab, a sizable amount of inter-individual differences in disease resistance can be captured using whole-genome regressions. However, the successful implementation of GS requires being able to predict future outcomes from past data. We assessed this using two CV analyses. Our results are based on genotypes derived from potato breeding programs. Some of these genotypes are related through pedigrees and there is some level of population stratification. Therefore, the prediction accuracies reported in our study should be considered representative of the prediction accuracy that one may be able to achieve when applying GS to breeding populations.

We considered two different prediction problems and implemented different CV schemes to represent each prediction problem. Our first CV focused on the prediction of future scores from genotypes that were not evaluated in field trials (i.e., prediction based on information from other genotypes). These analyses rendered moderately low CV-correlations (∼0.22-0.31 with some small differences between traits and models).

It is important to highlight that in CV1 the correlations reflect the prediction accuracy that can be achieved when predicting future phenotypes for genotypes that have not been evaluated in field trials. These predictions, although imperfect, could enable several rounds of rapid selection based on genotype data alone. The predictive correlation obtained in CV1 was about half of the correlation between phenotypes across years (compare results in Table 3 with those for M2 in Table 4). Thus, we conclude that with the array and sample size used in this study, the predictive accuracy for late blight and common scab scores obtained from a newly developed genotype that has been genotyped but not tested in the field is about half of the predictive power of a single phenotype record. If more than two selection cycles can be carried out per year, the reduction on generation interval that can be achieved with genomic prediction would overcome the lower accuracy and, eventually lead to faster yearly genetic gains.

Our second CV used years as folds; therefore, in this case, disease scores predictions for one-year data were obtained from the same genotypes over years. The results of the model based on year and genotype (M2), give a baseline estimates of the prediction accuracy that can be achieved with phenotypic prediction. In CV2, we obtained higher prediction correlations (0.56-0.61, Table 4) than with CV1. However, the performance of the genomic models was only slightly superior to predictions based on past phenotypes-only (i.e., those that could be obtained with the M2 model). This result agrees with previous studies (e.g., Crossa et al. 2010) that show that the benefits of genomic prediction are more important when predicting phenotypes of materials that have no (or very limited) data from previous field trials.

Conclusions

We confirmed that a sizable fraction of inter-individual differences in late blight and common scab scores can be attributed to genetic factors and can be captured using whole-genome regressions. We found large genotype-by-year interactions for late blight and limited genotype-by-year interactions for common scab. For both late blight and common scab, we found that an additive model could account for a sizable (>90%) of the total genetic variance. However, for late blight, we found small (but statistically significant) gains in prediction accuracy when accounting for dominance. Our analyses confirm strong associations with disease resistance to SNPs in previously reported resistance hotspot regions for late blight and reported a novel locus that has a sizable contribution to common scab resistance. We demonstrated that prediction of disease resistance, using genomic prediction applied to autotetraploid potato, is feasible and can be implemented for SNP-based selection in potato breeding. Further research is needed to explore ways (larger sample size, more controlled environments, higher marker density) in which genomic prediction accuracy can be further improved.