Environmental coupling of heritability and selection is rare and of minor evolutionary significance in wild populations

Abstract

Predicting the rate of adaptation to environmental change in wild populations is important for understanding evolutionary change. However, predictions may be unreliable if the two key variables affecting the rate of evolutionary change, heritability and selection, are both affected by the same environmental variable. To determine how general such an environmentally induced coupling of heritability and selection is, and how this may influence the rate of adaptation, we made use of freely accessible, open data on pedigreed wild populations to answer this question at the broadest possible scale. Using 16 populations from 10 vertebrate species, which provided data on 50 traits (body mass, morphology, physiology, behaviour and life history), we found evidence for an environmentally induced relationship between heritability and selection in only 6 cases, with weak evidence that this resulted in an increase or decrease in expected selection response. We conclude that such a coupling of heritability and selection is unlikely to strongly affect evolutionary change even though both heritability and selection are commonly postulated to be environment dependent.

Introduction

In the face of global environmental change, it is imperative to understand whether and how fast populations can adapt to novel conditions to be ‘rescued’ by evolution¹. Despite evidence of genetic variance and selection in many wild populations, genetic response to selection (adaptive micro-evolution or rate of adaptation) in natural populations is rarely observed^{2, 3}. An apparent lack of a response to selection may have a variety of biological and/or methodological causes^{4, 5}. One potential reason is an environmentally induced coupling between selection and additive genetic variation, which can mask the true evolutionary potential of a population if not recognised. By its definition, selection is mediated by the environment^{6, 7} and has been shown to vary from season to season and between geographical regions, depending on resource availability (including mating opportunity) and predation pressure, for example8, 9, 10, 11, 12 (but see ref. 13). Genetic variation is, however, also known to vary with the environment (known as genotype-by-environment interaction), being sometimes increased and sometimes reduced under benign conditions (e.g. when mean fitness in the population is high)^{14, 15, 16}, although the ecological drivers of changes in the genetic variance–covariance matrix remain largely unknown¹⁷.

Although the environmental dependency of both selection and genetic variation has been thoroughly documented, our knowledge on how they may interact to result in evolutionary change in natural populations is very limited. In their recent review, Wood and Brodie¹⁶ identified 23 studies that measured environmental effects on selection and 28 studies that measured environmental effects on additive genetic variation. Overall, reviewing a great variety of taxa, environments and traits, they found that environmental effects on selection and genetic variance were broad and inconsistent. Importantly, most studies on environment-dependent genetic variation were done in laboratory settings (and those on selection mostly in wild populations) and extrapolating laboratory findings to natural conditions is not necessarily straightforward. To date, only two studies of natural populations have measured how both genetic variation and selection within the same trait covaried across environments. A study on Soay sheep (Ovis aries) demonstrated increased selection for a higher birth weight in harsh environments, whereas total genetic variance was highest in benign environments¹⁸. The opposite was found in the great tit (Parus major), where warmer springs, which are associated with increased mismatch between offspring energetic demands and food availability, were associated with stronger selection for early egg-laying as well as high additive genetic variance for that trait¹⁹. Thus, in the former example, selection and genetic variance covaried with the environment in opposite directions, whereas in the latter example they did so in the same direction. The negative covariance between selection and genetic variation in Soay sheep led to an 21% decrease in expected response to selection as opposed to a situation where genetic variance was assumed to not vary with the environment¹⁸. In the great tit, the positive association between additive genetic variance and selection gradients resulted in a 20% increase in predicted response to selection as compared to a situation where heterogeneity in both selection and genetic variance was ignored¹⁹. A more recent study investigated the environmental dependency of genetic variance and selection in several morphological traits in the Soay sheep population, but did not explicitly address the relationship between them, presumably since environment-dependent genetic variance was found to be absent²⁰. The environmental coupling of selection and genetic variance (or heritability) may therefore provide an important explanation for the discrepancy between observed and expected responses to selection in some natural populations, but the prevalence of this mechanism—and how it may alter the expected response to selection—in wild populations remains largely unknown.

We investigated the prevalence and strength of an environmentally induced correlation between heritability and selection—and its expected evolutionary consequence—in a variety of wild populations. We searched for multiannual, pedigreed datasets on wild populations freely accessible from online data repositories and used these data to quantify environment-dependent additive genetic variation (using random regression animal models) and standardised selection gradients for a suite of life-history, morphological, behavioural, physiological and body mass traits. We then regressed heritability against selection for 50 traits from 16 populations and compared expected selection responses with and without considering environmental heterogeneity in heritability. We had no specific expectation as to the prevalence of a correlation between heritability and selection but, if anything, expected it to be more common in life-history and morphological traits, since selection in these traits tends to be strong and variable²¹. Our approach using open data²² speaks to recent recommendations to use available data to address novel, outstanding questions in ecology and evolution that transcend a single study system^{23, 24}.

Results

Data acquisition and author response

We performed a search in online data repositories (see Methods) for multiannual (≥ 6 years) datasets containing pedigrees of wild populations accompanied by phenotypic measures on individually marked animals. From 106 acquired pedigreed datasets (Supplementary Table 1), we used 14 that were suitable for our analysis (see Methods). We added one unpublished dataset from our own database (pied flycatcher, Ficedula hypoleuca). These 15 datasets comprised 16 different populations, spanning ten species, eight of which were avian species, one a lizard, and one a mammal (Table 1).

Table 1. Overview of studies used in the gene-by-environment and selection analyses.

The studies and traits listed are the ones that met inclusion criteria (see Supplementary Table S1 for an untrimmed overview of datasets) and could be successfully analysed.

Species	Data source (refs.)	Locality	Study aim of the original paper	Trait	Nobs	Nind	Nyear	h2 (s.e.)	Selection used in analysis
Cinclus cinclus	91, 95	ZU	Estimate biases in inbreeding depression	Wing length (mm)	1132	672	18	0.464 (0.066)	F
Chyonomis nivalis	90	CW	Predict genetic changes in body mass	Body mass (g)	3382	931	9	a: 0.188 (0.064)	F
								j: 0.069 (0.056)	V
				Body length (mm)*	2761	791	8	a: 0.139 (0.062)	–
								j: 0.093 (0.070)	V
				Tail length (mm)*	3382	931	9	a: 0.281 (0.079)	–
								j: 0.101 (0.054)	V
Cyanistes caeruleus	41, 94	TA	Estimate the developmental stability of behavioural syndromes	Nestling handling aggression	6149	6149	8	0.235 (0.043)	V
				Adult handling aggression	1633	1103	8	0.283 (0.057)	V
				Nestling breath rate (breaths/s)	5863	5863	7	0.266 (0.037)	V
				Adult breath rate (breaths/s)	1526	1031	7	0.194 (0.063)	V
	83, 96	DR	Investigate spatial variation in G-matrix in populations with contrasting population history and selective environment	Incubation duration (d)	1104	740	24	0.195 (0.074)	V
				Laying date	1104	740	24	0.214 (0.094)	V
				Clutch size	1104	740	24	0.345 (0.104)	V
				Wing length (mm)	2916	1597	24	0.374 (0.040)	V
				Body mass (g)	2916	1597	24	0.347 (0.038)	V
		EP	As above	Incubation duration (d)	997	637	35	0.011 (0.102)	V
				Laying date	997	637	35	0.043 (0.148)	V
				Clutch size	997	637	35	0.108 (0.145)	V
				Wing length (mm)	2260	1187	26	0.287 (0.065)	V
				Body mass (g)	2260	1187	26	0.332 (0.065)	V
	85, 97	EB	Quantify selection on parental care to explain stasis in evolution of offspring body size	Wing length (mm)	1677	847	8	0.448 (0.151)	V
				Body mass (g)	1677	847	8	0.262 (0.117)	V
Falco tinnunculus	93, 98	SP	Quantify multivariate heredity of colouration, mass and immunity	Tail-band width (mm)	688	444	17	0.699 (0.086)	F
Ficedula hypoleuca	60	HV	None (published for the purpose of this paper)	Laying date	3044	2211	39	0.149 (0.072)	F
Hirundo rustica	84, 99	SP	Estimate genetic correlation between arrival date and life-history traits	Spring arrival date	2337	1407	17	0.131 (0.076)	F
Lacerta agilis	82, 100	AS	Test for trade-off between offspring size and number	Clutch size	472	288	10	0.294 (0.066)	F
				Laying date	370	236	9	0	F
				Mean offspring mass (g)†	452	279	10	0.384 (0.064)	F
Parus major	92, 101	WW	Estimate genetic variance in colour expression across the visual spectrum	Plumage reflectance at 349 nm‡	2904	1618	6	0.015 (0.035)	V
				Plumage reflectance at 449 nm‡	2901	1616	6	0.194 (0.051)	V
				Plumage reflectance at 549 nm‡	2901	1616	6	0.098 (0.043)	V
				SWS ratio (plumage reflectance)	2901	1616	6	0.336 (0.051)	V
				Double cone (plumage reflectance)	2901	1616	6	0.092 (0.044)	V
				Wing length (mm)	2892	1614	6	0.478 (0.054)	V
				Body mass (g)	2878	1613	6	0.357 (0.052)	V
	89, 102	WW	Investigate the genetic architect of a suite of parameters in two populations	Adult body mass	2919	1358	12	0.004 (0.034)	V
				Offspring fledgling weight (g)†	3162	328	13	0.022 (0.107)	V
				Wing length	3206	1408	12	0.055 (0.042)	V
		HV/WH	As above	Adult body mass (g)	1543	477	16	0.472 (0.027)	F§
				Clutch size	1585	943	17	0.058 (0.181)	F§
				Offspring fledgling weight (g)†	8569	744	17	0	F§
				Wing length	1908	1275	17	0.158 (0.140)	F§
	50, 81	HV	Test for bias in selection on life-history traits	Clutch size	4054	2861	57	0.318 (0.055)	F
				Laying date	4054	2861	57	0.157 (0.052)	F
		VL	As above	Clutch size	3700	2368	52	0.306 (0.044)	F
				Laying date	3700	2368	52	0.277 (0.048)	F
	88, 103	HV	Estimate heritability of within-family variance in fledgling weight	Fledgling weight (g)	17535	17535	36	0.235 (0.027)	V
				Clutch size	2175	1598	36	0.282 (0.082)	F
Perisoreus infaustus	87, 104	OB	Disentangle plastic and genetic changes in body mass	Body mass (g)	1619	1025	30	0.408 (0.058)	F
				Wing length (mm)	1453	1016	28	0.516 (0.056)	F
Passerculus sandwichensis	86, 105	KI	Investigate the relationship between heritability/evolvability and selection	Day-8 to Yr-1 wing length (mm)	2839	2469	20	a: 0.353 (0.072)	F
								j: 0.430 (0.063)	F
				Day-8 to Yr-1 tarsus length (mm)*	1913	1615	20	a: 0.398 (0.070)	–
								j: 0.292 (0.080)	V
				Day-8 to Yr-1 body mass (g)	2469	2362	20	a: 0.064 (0.018)	F
								j: 0.330 (0.059)	V

Note. Locality: AS = Asketunnan, Sweden; CW = Churwalden, Switzerland; DR = D-Rouvière, France; EB = Edinburgh, UK; EP = E-Pirio, France; HV = Hoge Veluwe, NL; KI = Kent Island, Canada; OB = Ostrobothnia, Finland; SP = Spain; TA = Tammisaari, Finland; VL = Vlieland, the Netherlands; WH = Westerheide, NL; WW = Wytham Woods / Bagley Woods, UK; ZU = Zürich, Switzerland.

Selection: F = fecundity; V = viability; ‘–’ = disregarded due to fixed nature of trait in adults.

N_obs/N_ind/N_year: number of observations/individuals/years (environments); h²: narrow-sense trait heritability (a: adult; j: juvenile; significant values in boldface).

^*’Fixed’ trait: may change from juvenile to adult stage but are assumed to be relatively constant within adult lifespan.

^†Trait considered maternal.

^‡Trait consitutes one out of a range of 198 2-nm bands; three bands equally spaced apart and spanning most of the gradient were chosen for analysis.

^§Fecundity based on number of fledglings, not recruits.

Authors were generally supportive of the use of their data. We contacted 14 authors (of 18 datasets) about our use of their data and found that 4 datasets were not usable. This was mainly related to a bias in our approximation of the environment, i.e. the population-mean trait value (see Methods) and selection in a given year when a non-random portion of the population was not represented in the dataset. Only in two cases authors were initially reluctant to cooperate, but all authors eventually informed us about the appropriateness of our analyses of their data (see Culina et al.²⁵ for a full account on author correspondence associated with this article).

Estimating environment, heritability and selection

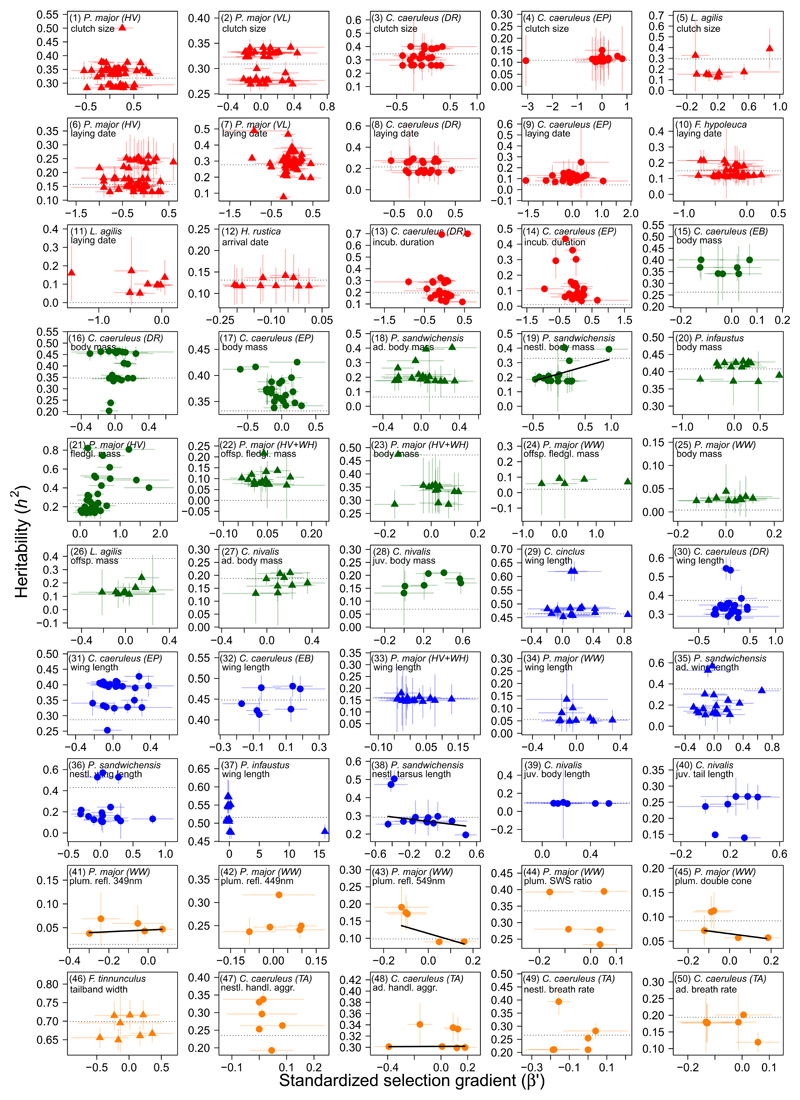
From the included datasets, we extracted a total of 50 morphological, behavioural, physiological, life-history and body mass traits. We used these traits first to estimate a standardised measure of the environment, the standardised annual population-mean trait value^{26, 27, 28, 29}. We estimated the heritability (h², the relative additive genetic variation) of the traits and found that the majority showed significant heritable variation within the population (Table 1). We then fitted random regression animal models (RRAMs) with an interaction between the additive genetic effect and the standardised measure of the environment. We extracted environment-dependent heritability estimates resulting from these RRAMs (as heritability determines the short-term evolutionary change) and regressed them against annual standardised selection gradients^{30, 31, 32} (β′; Supplementary Figure 2), while accounting for uncertainty in both predictor and response. In 6 out of 50 cases (all in bird species), this led to a statistically significant relationship between selection and heritability (Figure 1; Supplementary Table 2). None of the 14 life-history traits exhibited such a relationship, despite considerable variation in both selection and heritability. We found a positive, significant relationship in nestling body mass in Passerculus sandwichensis, based on viability selection on nestlings (slope [95% bootstrapped confidence interval] = 0.102 [0.045, 0.191], r² = 0.369 [0.089, 0.596]). As the only morphological example, nestling tarsus length in P. sandwichensis showed a significantly negative correlation based on viability selection (slope = –0.057 [–0.118, –0.023], r² = 0.148 [0.038, 0.340]). Finally, four avian physiological and behavioural traits exhibited a significant association between heritability and selection, all based on viability selection: P. major plumage reflectance at 349 nm (slope = 0.018 [0.009, 0.037], r² = 0.284 [0.052, 0.507]), 549 nm (slope = –0.190 [–0.440, –0.040], r² = 0.467 [0.054, 0.949]) and spectral sensitivity (double cone; slope = –0.055 [–0.173, –0.010], r² = 0.248 [0.027, 0.751]), and Cyanistes caeruleus adult handling aggression (slope = 0.001 [0.0004, 0.003], r² = 0.009 [0.002, 0.021]).

Figure 1. Heritability as a function of the standardized selection gradient.

Standard errors (SEs) are omitted when SE_h² > 0.5 and SE_β^′ > 1 for visual aid. Regression lines result from weighted least-squares regression models (weights: 1/[(SE_h²)²]), with bootstrapping to account for uncertainty in β′, shown only when the 95% CI did not include zero. Colours denote different trait classes (red: life history; green: body mass; blue: morphology; orange: miscellaneous), whereas shapes indicate selection based on survival (circles) or based on number of fledglings or recruits (triangles). Dotted horizontal lines denote the constant heritability as estimated from a standard animal model. Duplicate traits (from same population but different dataset) are not shown. Data sources by panel: (1,2,6,7) ref. 81; (5,11,26) ref. 82; (3,4,8,9,13,14,16,17,30,31) ref. 83; (10) unpubl. data; (12) ref. 84; (15,32) ref. 85; (18,19,35,36,38) ref. 86; (20,37) ref. 87; (21) ref. 88; (22–25,33,34) ref. 89; (27,28,39,40) ref. 90; (29) ref. 91; (41–45) ref. 92; (46) ref. 93; (47–50) ref. 94.

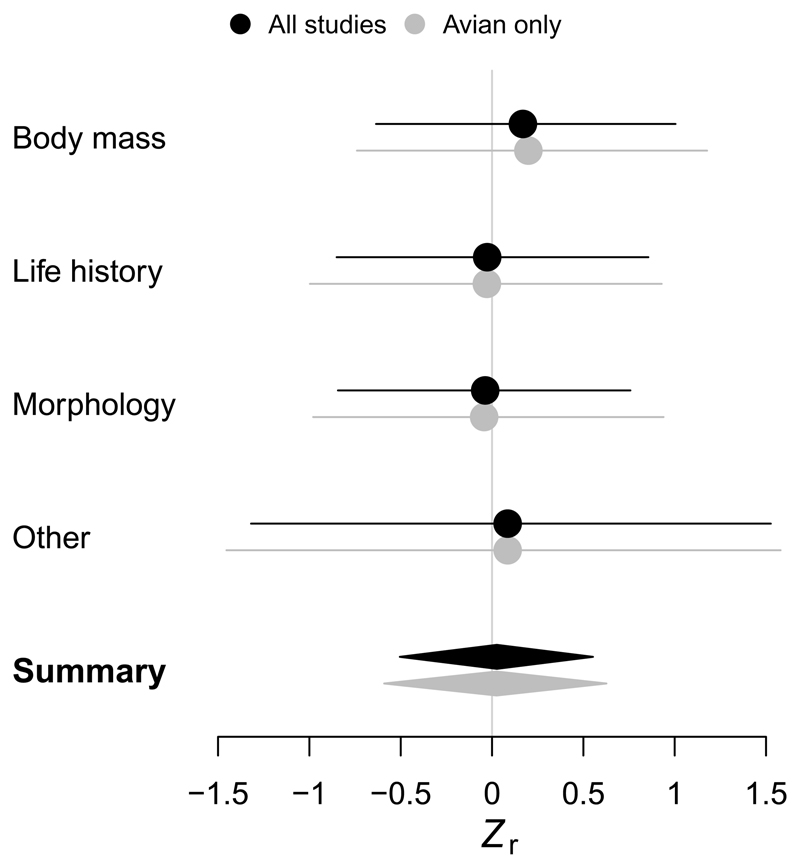
A formal meta-analysis on the correlation coefficient r from each heritability–selection regression, correcting for independence of traits within studies (weighted linear mixed-effects model with random effect ‘study’), reaffirmed that the overall correlation was weak and not dependent on the class of trait (Figure 2). We found similar results when we disregarded non-avian traits.

Figure 2. Meta-analysis on the heritability–selection correlation coefficients.

Coefficients r were standardised using Fisher’s Z transformation prior to analysis. Estimates and bootstrapped 95% CIs are shown, predicted from a linear mixed-effects model and unconditioned on the random term ‘study area’. The summary statistic results from a model that included only the intercept as a fixed term. Estimates from an analysis excluding non-avian traits are shown for comparison.

Comparing expected responses to selection

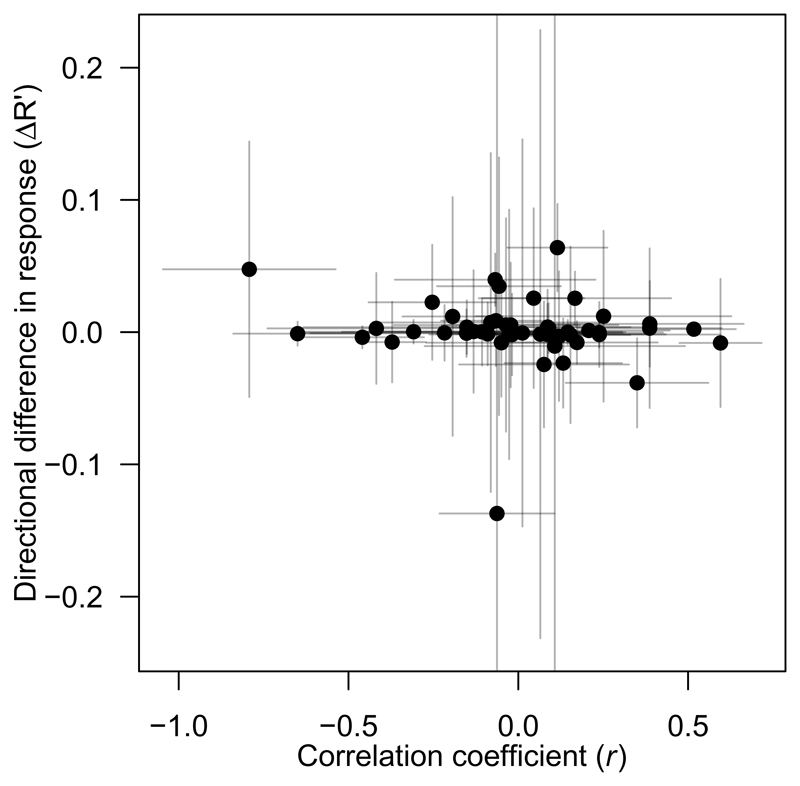
Environmental coupling of (additive) genetic variance and selection can affect the predicted response to selection^{18, 19}. We therefore predicted for the six datasets identified above the standardised selection response for each environment j $(R_j^{\prime }),$ assuming either constant or environment-dependent heritability $(R_j^{\prime }=h^2{\beta }_j^{\prime }\text{or}{h}_j^2{\beta }_j^{\prime }).$ When we calculated the mean difference in response across environments between the two approaches (accounting for uncertainty in estimates), we found that environmental variation in heritability significantly affected the mean expected response in all six cases, but this effect was not in a consistent direction (i.e. either reduced in case of a negative association or increased in case of a positive association; Table 2). Finally, we modelled the directional difference in expected response as a function of the correlation coefficient between h² and β′ for all datasets (cf. ref. 16), and found that the difference in expected response was not affected by this correlation coefficient (slope = 0.002 [–0.001, 0.004]; Figure 3).

Table 2. Predicted selection response assuming constant vs. environment-dependent heritability.

Predicted response (R′) differed in absolute terms from year to year under the two approaches for all six cases where a correlation between heritability and selection was found; in none of these cases the difference was in a consistent direction.

Species	Trait	ΔR′absolute [95% CI]	ΔR′directional [95% CI]
Cyanistes caeruleus	Adult handling aggression	0.031 [0.015, 0.049]	0.005 [–0.026, 0.031]
Parus major	Plumage refl. (at 349 nm)	0.007 [0.003, 0.012]	0.005 [–0.001, 0.011]
	Plumage refl. (at 549 nm)	0.012 [0.005, 0.021]	0.005 [–0.007, 0.016]
	Double cone plumage refl.	0.008 [0.003, 0.014]	–0.001 [–0.010, 0.007]
Passerculus sandwichensis	Nestling tarsus length	0.059 [0.038, 0.085]	0.005 [–0.034, 0.046]
	Nestling body mass	0.072 [0.046, 0.101]	–0.019 [–0.062, 0.024]

Note. R′ is measured in phenotypic standard deviations. Estimates of differences were calculated using bootstrapping procedures

Figure 3. No effect of a correlation between heritability and selection on differences in selection response.

Correlation coefficients (r ± standard errors) result from WLS regressions of heritability against standardised selection gradients; ΔR′ (± standard errors) is the mean, directional difference between expected responses to selection assuming varying vs. constant heritability. Each data point represents a single trait–species–population combination.

Discussion

Little evidence for environmental coupling of heritability and selection

We investigated the prevalence of an environmentally induced relationship between heritability and selection across traits and study systems by using open data available in data repositories. Our study extends the limited evidence for this phenomenon^{18, 19} to 50 traits from 10 species in 16 populations. Relying on robust statistical methods to (i) quantify the relationship between heritability and selection, (ii) synthesise results of different studies using meta-analysis, and (iii) infer expected evolutionary response, we conclude that, despite being a current topic in ecology and evolution^{14, 15, 16, 33, 34}, its evolutionary importance in natural populations is small—at least for the range of species for which we have data.

So far, only two studies have investigated this relationship within the same trait and population^{18, 19}. Reanalysis of egg-laying date in the Hoge Veluwe great tit population¹⁹ yielded different results, potentially linked to the different approximation of the environment (see below), although the environment in that population, i.e. mean spring temperature, explains much of the variation in the trait (r² = 0.66)³⁵. The correlations between selection and heritability or additive genetic variance found by Husby et al.¹⁹, however, were marginally or non-significant, respectively, and were not subjected to rigorous correction for uncertainty like our bootstrapping methods. Thus, even in a population with (i) a strong link between the environment (temperature) and a life-history trait (laying date) and (ii) demonstrated increases in selection and additive genetic variance under increased temperatures, evidence for an environmental link between heritability and selection was modest at best. Heritability of life-history traits is generally found to be low^{26, 36, 37}, potentially due to high environmental variance³⁸ or genetic canalisation³⁹, but life-history traits are inherently likely to exhibit gene-by-environment interactions whenever selection pressures vary with the environment, because of their close association with fitness³⁸. It is, then, remarkable that heritability was not related to selection in any of the life-history traits investigated here (Figure 1), even though substantial variation existed in the strength of selection (Supplementary Figure 2).

Finding a significant relationship between heritability and selection requires sufficient statistical power. Although the number of years and individuals varied considerably between study systems (Table 1), significant relationships were not exclusively found in the largest datasets (Figure 1). A visual inspection of the components that make up this relationship, as well as the relationship between selection and the environment, suggested that statistical significance was neither influenced by the variance in the predictor and response variables nor by the number of years or the total number of observations available (Supplementary Figure 3). Given the larger statistical power associated with larger datasets, the lack of the sought correlation in our largest datasets suggests that the effect size is likely too small to be biologically meaningful.

Using an analytical model informed by data from a literature review, Wood and Brodie¹⁶ predicted that the strength of the relationship between selection and genetic variance would impact the mean and, to a greater degree, variance in responses to selection across hypothetical populations. Yet even in the few cases in which we demonstrated a reasonably strong relationship between heritability and selection (Figure 1; cf. ref. 18), this was not sufficient to fuel a change in the rate of expected response to selection (Table 2). This is partly because both components of the relationship came with prediction error that needed to be accommodated in the estimation of the response. From the studies investigated here, we therefore conclude that even when we find environmental coupling between heritability and selection, its net effect on the predicted evolutionary change is small and is hence an unlikely explanation for potential discrepancies between observed and expected responses to selection in natural populations⁴.

Methodological considerations

An important aspect in analysis of genotype-by-environment interactions, i.e. testing whether genetic variance and heritability differ among environments, is the choice of the environmental variable. However, in most of the analysed datasets no such environmental variable was included. Instead of obtaining such data from other sources and testing whether the chosen variable was predictive for the trait in question, we used environment-specific, population-mean trait values as the environmental variable (covariate) in our analyses, an accepted practice in animal and plant breeding^{26, 28}. This approach has three major advantages. First, the daunting task of searching environmental data relevant to each trait becomes unnecessary. Second, it enables the inclusion of traits for which it is difficult to conceive and collect environmental data (compare, for example, breeding time in great tits, which is strongly temperature dependent⁴⁰, with a physiological trait like handling aggression in blue tits C. caeruleus, for which no clear environmental component has been identified, despite substantial year-to-year and residual variation⁴¹). Third, because the population-mean phenotype encompasses all unmeasured or unobserved components of the environment, it will generally be an accurate representation of the environment for the trait of interest²⁶, circumventing the problem of misidentifying the relevant environmental component and, consequently, erroneously inferring the presence or absence of variation in reaction norm slopes. For example, in a population of collared flycatchers (Ficedula albicollis), Brommer et al.⁴² found significant between-individual variation in breeding-time reaction norms in response to average temperatures in spring, but not to rainfall or North Atlantic Oscillation, even though these variables correlated well with breeding time. Similarly, Husby et al.⁴³ could show between-individual variation in reaction norms for breeding time in great tits while Charmantier et al.⁴⁴ did not find this in the same population when using a different environmental variable. Indeed, simulations have shown that random regression models with ‘mean trait’ as the environment yielded similar variation in reaction norm slopes to models with a ‘real’ environmental driver of the trait⁴⁵. In contrast, using other environmental measures that did not drive the trait but correlated with the ‘real’ environment to a decreasing degree (r = 0.9 to 0.1) yielded increasingly downwardly biased estimates of both the slope and the variance in the reaction norm. This is an important finding because it shows that environment-specific mean phenotypes can serve as a ‘yardstick’ when testing for gene-by-environment interactions⁴⁵.

Ideally, heritability should be estimated at the same level as where selection operates, because the correlation at this level is what ultimately matters. Since selection is generally estimated at an annual level (where each year captures all components of the environment), heritability should be estimated at this level too. This would, however, require an enormous number of individuals in each year to estimate the annual genetic variances reliably—and hence generally not be feasible. Using (continuous) environmental covariates instead to estimate genetic variance along an environmental gradient^{46, 47} is the next best option, and the best way to do this is to choose a metric that captures most features of the environment in a given year (which annual mean phenotypes do). This alleviates the need to establish a link between an environmental covariate and selection, which will not necessarily be informative when investigating the correlation between heritability and selection—in particular when statistical power is limited.

A concern when estimating selection in natural populations is to identify the real target of selection^{30, 32, 48}. The use of the Breeders’ Equation to predict evolutionary change in natural populations has therefore been advised against, and the Robertson-Price identity has been suggested as an appropriate alternative^{48, 49}. However, estimating the genetic covariance between a trait and fitness at an annual basis to estimate variation in selection is rarely, if ever, possible, due to the large datasets required to reliably estimate genetic covariances. Furthermore, Reed et al.⁵⁰ showed that in a wild population of great tits, environmental bias in phenotypic selection estimates for egg-laying date and clutch size is small at best. A similar conclusion was reached by Morrissey and Ferguson⁵¹, who showed for brook charr (Salvelinus fontinalis) that estimates of phenotypic selection on body size are highly congruent with estimates of genetic selection.

Benefits and limitations of open data

One important development in ecology and evolution in recent years has been the requirement to make the data used to produce the results of studies (usually published studies) publicly available^{23, 52}, leading to a surge in data output onto online data repositories. The potential advantages of open data archiving in revolutionising the natural sciences are now increasingly recognised^{22, 24}. Yet Evans⁵³ showed that data from long-term population studies archived in Dryad Digital Repository are never used by third parties. Our multi-study approach makes extensive use of such long-term data to address an outstanding question in evolutionary ecology. Indeed, the use of open data comes with important logistical and ethical issues^{52, 54, 55} that need to be addressed before biological conclusions can be safely drawn. Our study, however, shows that it can be done successfully (see also ref. 25).

From the 106 initially considered datasets in our example, we could eventually use only 14 (plus the previously unpublished pied flycatcher dataset), due to various reasons such as small and/or biased sample sizes, a lack of appropriate fitness data, unusable pedigrees (e.g. relatedness matrices, which we were unable to use after data manipulation because they required a specific ordering of the individuals in the phenotype file), and a low number of years. Moreover, the data were heavily biased towards birds and mammals (50 and 31 datasets, respectively). We therefore need to make the cautionary note that we cannot necessarily extrapolate the evolutionary importance of an environmental correlation between selection and genetic variance across a wider range of taxa. The general taxon bias in quantitative genetic studies of wild populations toward birds and mammals can be explained by the fact that linking individual offspring to their parents, necessary to construct a pedigree, is comparably straightforward⁵⁶. Relatedness matrices based on genomic markers may make pairwise relatedness estimates a less stringent requirement in evolutionary studies in the future and in that way greatly augment the taxonomic scale at which important evolutionary questions can be addressed⁵⁷. Time will resolve issues like samples sizes and number of years, but whether or not a dataset is suitable will ultimately depend on the type of analysis and the type of data required. In the era of Open Science that encourages publication of datasets while increasing their quality, it is but a matter of time before taxon biases in multi-annual meta-studies similar to ours may dissipate. Such long-term datasets of individually marked animals are invaluable tools in ecology and evolution and will inevitably serve to elucidate the ecological and evolutionary consequences of environmental change^{56, 58}.

Methods

Data acquisition

In May and July 2016 we conducted a search for datasets that contained pedigree information on a wild species through twelve different aggregators of research data repositories (Europe PMC, DataCite, BASE, OpenAIRE, Science Research, DataOne Mercury search, Web of Science Data Citation Index, Scielo, Research Data Australia, DLI Service, Dryad Digital Repository, DataMED). These aggregators collect information on datasets (e.g. title, keywords, abstract and description) that have been deposited in different data repositories, and allow for search through multiple data sources in one search interface. Datasets were tracked using fixed search terms (see Supplementary Methods 1); search results were screened based on title, abstract, dataset description, and/or keywords, if available. Remaining datasets were further checked for relevance by opening the data files and/or reading the related publication if necessary, leaving only datasets containing pedigree information for a wild or captive animal population. Recording of datasets was done according to PRISMA guidelines^{25, 59}.

Next, we screened and filtered this data subset (103 datasets) to keep those where: (i) the pedigree file could potentially be used (i.e. when the file was not embargoed, corrupted or otherwise unsuitable for our particular analysis, e.g. relatedness matrices lacking the specific links between parents and offspring); (ii) the pedigree contained a sufficient number of individuals (final datasets had, on average, >40 observations/individuals per year); (iii) individuals in the pedigree also had information on a phenotype on which selection could act; (iv) there was natural environmental variation in the phenotype (this excluded all laboratory populations); (v) the associated phenotype file contained at least six years of data; and (vi) there were no additional issues (e.g. non-matching IDs of animals in pedigree and phenotype file). In addition to these 103 datasets, we did an additional search in Web of Science (on 9 September 2017; see Supplementary Methods 1) and from the resulting 396 studies, we discovered three additional suitable datasets overlooked by the initial search, using the inclusion criteria above. Lastly, we added our own, previously unpublished data from the long-term study of pied flycatchers (Ficedula hypoleuca, ref. 60; see ref. 61 for more information on that population), totalling 107 retrieved datasets (Supplementary Table 1).

The total number of datasets included in the analysis amounted to 15, covering 10 species from 16 populations and a variety of life-history, morphological, physiological, behavioural and body mass traits (Table 1). This excludes datasets that initially appeared suitable to us but whose suitability for our analysis was refuted by the original authors (see ‘Enquiring with original authors’; Supplementary Table 1).

Quantifying the environment

None but two of the final datasets provided information about the environment. Therefore, we used a standardised protocol to quantify the environment. For each year, we calculated the population-mean trait value (x̄) as a measure of the general environment and mean- and variance-standardized it across seasons/sites:

$$E{\prime }_j=\frac{{\overline{x}}_j-{\mu }_{\overline{x}}}{{\sigma }_{\overline{x}}},$$

where j denotes the j^th season, and μ and σ the grand mean and standard deviation, respectively. Note that this measure does not identify any specific environmental parameter but captures the environment as a whole in a specific season. The method is commonly used in animal and plant breeding studies in a process called ‘joint-regression analysis’, where genotype-specific interactions are partitioned into a component explained by mean population performance and a residual component (ref. ²⁶, pp. 672–678). It was first proposed by Yates and Cochran²⁹ and later brought into prominence in a barley yield experiment by Finlay and Wilkinson²⁷, and has now become widely accepted in the plant- and animal-breeding literature^{26, 28}. It has the advantage that all of the complex (and potentially unobserved) features of the environment are integrated into a single measure, allowing for the ranking of seasons in terms of overall environmental quality. Note that this method disqualifies traits that do not vary at the annual level (i.e. fixed adult traits were not used in our analyses).

One complication with our measure of the environment is that such a measure is potentially biased when a non-random portion of the population in a given season is removed from the dataset (e.g. because certain individuals are never sampled), or when changes in the demographic structure of the population strongly affect the mean trait value. When this was the case (see ‘Enquiring with original authors’; Supplementary Table 1), the dataset was dropped from further analysis.

Standard trait heritability

For each of the traits in our full data (Table 1), we tested for evidence of additive genetic variance following a standardized protocol. First, we constructed ‘minimum adequate’ mixed-effects models (MAMs) with the trait of interest as response variable (all with Gaussian errors) using restricted maximum likelihood (REML) estimation in ASReml-R^{62, 63}. This method provides a fast and efficient away of estimating variance components and allows for the inclusion of additive genetic effects. Note, however, that we used a Bayesian approach to estimate environment-dependent heritability estimates, as this allows for estimation of posterior confidence regions, which we needed to reliably account for uncertainty in our environment-dependent heritability estimates in subsequent analysis (see ‘Genotype-by-environment analysis’). Fixed effects were the environment (E′), as continuous variable, and additional effects provided in the dataset, based on mixed-effects models in the associated original paper. Significance of these effects, as well as that of interactions between effects, was tested with conditional Wald F tests, removing non-significant (p > 0.05) terms in a backward stepwise manner (but always keeping E′). Random effects were those identified in the original papers (always containing a ‘permanent environment’ effect, i.e. individual ID, when there were multiple observations of the same individual), but sometimes we constructed our own additional effects when deemed biologically appropriate (e.g. in nestling traits, ‘nest-box ID’ and ‘year’ were combined to identify common-environment effects within a single brood). Significance of random effects was tested using likelihood-ratio tests (D = 2[log(L_m1) − log(L_m0)], where D is asymptotically χ² distributed with one degree of freedom). The MAM was extended to an ‘animal model’^{64, 65} (AM) by adding a random additive genetic effect based on the pedigree with maternal and paternal links (see references in Table 1 for how pedigrees were constructed). Thus, the AMs took the form

$$\mathit{\text{y}}=\mu +{\mathit{\text{X}}}_{\mathbf{1}}{\mathit{\text{β}}}_{E\prime }+\cdots +{\mathit{\text{X}}}_{\mathit{\text{n}}}\mathit{\text{β}}+{\mathit{\text{Z}}}_{\mathbf{1}}\mathit{\text{p}}\mathit{e}+{\mathit{\text{Z}}}_{\mathbf{2}}\mathit{\text{a}}+\cdots +{\mathit{\text{Z}}}_{\mathit{\text{n}}}u+\epsilon ,$$

where y is a vector of phenotypes, X_1…n and Z_1…n are the design matrices relating the fixed (β) and random effects (pe, permanent environment; a, additive genetic; u, other) to y, μ is the mean and ε is the error term. The narrow-sense heritability was calculated as $h^2={\sigma }_{\mathit{\text{a}}}^2/{\sigma }_P^2,$ where ${\sigma }_P^2$ represents the total phenotypic variance comprising all variance components, conditioned on the fixed effects (Table 1).

Genotype-by-environment analysis

To model the interaction between additive genetic variance and the environment (G×E), we extended the AM to a random regression animal model (RRAM) using the ‘MCMCglmm’ package^{66, 67} (ignoring years with <8 observations). In the RRAMs, we allowed the environment to interact with both the permanent environment (if present) and the additive genetic effect:

$$\mathit{\text{y}}=\mu +{\mathit{\text{X}}}_{\mathbf{1}}{\mathit{\text{β}}}_{E\prime }+\cdots +{\mathit{\text{X}}}_{\mathit{\text{n}}}\mathit{\text{β}}+{\mathit{\text{Z}}}_{\mathbf{1}}\left(\mathit{\text{p}}\mathit{e},E\prime ,n_1\right)+{\mathit{\text{Z}}}_{\mathbf{2}}\left(\mathit{\text{a}},E\prime ,n_1\right)+\cdots +{\mathit{\text{Z}}}_{\mathit{\text{n}}}u+\epsilon ,$$

where n₁ is the first-order polynomial of the regression function. Fixed and random terms were those identified from the (M)AMs; note that because E′ explains most of the variation related to seasonal effects, it replaced the random effect of year in most analyses. We constructed two 2×2 unstructured variance–covariance matrices for the intercept and the slope of the permanent environment and the additive genetic effect:

$$\mathbf{\text{P}}=\left[\begin{array}{cc}{\sigma }_{\mathit{\text{p}}{\mathit{e}}_{\mathit{\text{int}}}}^2& {\sigma }_{\mathit{\text{p}}{\mathit{e}}_{\mathit{\text{int}}},\mathit{\text{p}}{\mathit{e}}_{sl}}\\ {\sigma }_{\mathit{\text{p}}{\mathit{e}}_{sl},\mathit{\text{p}}{\mathit{e}}_{\mathit{\text{int}}}}& {\sigma }_{\mathit{\text{p}}{\mathit{e}}_{sl}}^2\end{array}\right]\text{and}\mathbf{\text{G}}=\left[\begin{array}{cc}{\sigma }_{{\mathit{\text{a}}}_{\mathit{\text{int}}}}^2& {\sigma }_{{\mathit{\text{a}}}_{\mathit{\text{int}}},{\mathit{\text{a}}}_{sl}}\\ {\sigma }_{{\mathit{\text{a}}}_{sl},{\mathit{\text{a}}}_{\mathit{\text{int}}}}& {\sigma }_{{\mathit{\text{a}}}_{sl}}^2\end{array}\right].$$

In cases where there was no permanent-environment effect but only a maternal or common-environment effect (in juvenile-only traits), only the G matrix was fitted. To avoid artificial inflation of slope variance estimates in the P and G matrices due to heterogeneity in residual variance across the environmental gradient, we partitioned the residual component ε into ‘environmental blocks’⁶⁸, following categorisation of environments into n equal-interval groups. Thus, we fitted the residual matrix as an n×n identity matrix,

$$\mathbf{\text{R}}=\left[\begin{array}{ccc}{\sigma }_{{\epsilon }_1}^2& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_{{\epsilon }_n}^2\end{array}\right],$$

where n was the number of environments divided by 5, but was always ≥3 (e.g. in a dataset with 20 environments n = 4, but with 10 environments n = 3).

To illustrate that our environmental metric (E′) was valid in this context, Gienapp⁴⁵ ran random regression models on simulated data using several different quantifications of the environment related to a ‘true’ environmental driver of the phenotype, as well as the annual trait mean. He found no evidence that variance estimates of reaction norm intercepts and slopes were biased by the annual trait mean (relative to the ‘true’ environmental driver) and showed that this metric outperformed environmental correlates. Although we concur that additive genetic variance may not only be affected by current environmental conditions but also be the outcome of past selection processes, it is evident from many quantitative genetic studies of wild populations that year-to-year variation in phenotypes is mostly attributable to phenotypic plasticity and that the share of genetic change from year to year is generally very small and undetectable^{2, 3}. Consequently, we believe that using environment-specific mean trait values will lead to more reliable results than an environmental variable that correlates too weakly with the real driver of plasticity, thereby underestimating variation in (genetic) reaction norm slopes.

To obtain independent samples in the MCMC sampling process, we used a thinning interval of 20,000 in all models, with a burn-in period of 200,000 samples and a total effective sample size of 250 (i.e. 5,200,000 samples). In exploratory stages of the analysis, we found that a larger effective sample size (1000) did not affect the posterior estimates, but these models take substantially longer to complete. Effective sample size in all models included never fell substantially below 250 and autocorrelation between samples was almost always <0.1 but never exceeded 0.2 for any variance component; models that did not meet these criteria were discarded (not listed in Table 1). For the residual term, we specified Inverse-Wishart (IW) priors (V = diag(x) and nu = 1.002, where x is the dimension of the matrix). For the random terms we explored two alternative priors: the IW prior (specifications as above) and parameter-expanded (PE) priors (V = diag(x), nu = x, alpha.mu = 0, alpha.V = diag(x)*500). Although both priors yielded similar results in most cases, the posterior variances tended to be smaller when real variance was close to zero under the PE compared to the IW prior. This is in agreement with previously voiced concerns that the IW prior may behave poorly when true variance is close to zero^{66, 69, 70}. We therefore only present posterior estimates from the models based on PE priors. We refrained from ‘significance’ testing of the G×E interaction, because—issues concerning model-selection criteria such as DIC aside^{66, 71, 72}—of potentially limited power in the smaller datasets and our main interest in testing the covariance between h² and selection. We instead opted for a pragmatic approach and used the highest posterior density intervals (HPDIs) to account for uncertainty in all subsequent analyses. The rationale behind this was that if we had excluded all ‘non-significant’ G×E interactions, of which some may have been false negatives, we may have overlooked a potentially strong covariance between h² and selection (see below). By accounting for the uncertainties in environment-specific h² estimates, the true negatives in G×E will not lead to a spurious covariance between h² and selection.

The posterior mean variance for each variance component in environment j was derived from the estimated G and P matrix as⁷³

$${\sigma }_j^2={\sigma }_{\mathit{\text{int}}}^2+2{\sigma }_{\mathit{\text{int}},sl}{\mathit{\text{β}}}_{E{\prime }_j}+{\sigma }_{sl}^2{\mathit{\text{β}}}_{E{\prime }_j}^2.$$

The 95% HPDIs were likewise derived from the upper and lower HPDI matrices. Environment-dependent heritability was defined as the mean of posterior variance estimates, $h_j^2={\sigma }_{{\mathit{\text{a}}}_j}^2/({\sigma }_{{\mathit{\text{a}}}_j}^2+{\sigma }_{\mathit{\text{p}}{\mathit{\text{e}}}_j}^2+\cdot \cdot \cdot +{\sigma }_{{\epsilon }_j}^2),$ with 95% HPDIs estimated from the lower and upper HPD limits of each variance component. Standard errors of $h_j^2$ were then calculated as half the 95% HPDI divided by 1.96.

Selection

To quantify selection on the trait in a given environment, we made use of provided reproductive fitness data (number of offspring or recruits) or survival data (Table 1). When such data were not provided, we inferred (annual) reproductive success by linking animals to sires and dams in the pedigree using their birth year (when available). If we could not infer annual recruits from the pedigree, we determined survival from one year to the next by identifying reappearance of individuals in the dataset in subsequent years, assuming the last year of appearance was the last year the individual was alive. As with quantifying the environment (see above), inferring fitness is problematic if a non-random portion of the population appears in the dataset (aside from the non-random disappearance due to selection; see also ref. 48). When this was likely to be problematic (see ‘Enquiring with original authors’; Supplementary Table 1) the dataset in question forewent inclusion in the analysis.

To estimate annual, standardised selection gradients (β′), we constructed general(ised) additive models (GAMs, package ‘mgcv’⁷⁴), where the fitness component was the response variable following either a Gaussian, Poisson or negative binomial distribution for fecundity measures (number of offspring produced or recruits), depending on the distribution of the data, or a binomial distribution for survival (1/0 response). As fixed effects, we initially included an interaction between year and the trait of interest and used it as a null model to identify additional significant fixed effects (using F or χ² tests) that influenced the fitness measure (e.g. age or sex and additional quantitative traits). Based on these findings, we ran annual GAMs (without ‘year’) and calculated annual β′ using the ‘gam.gradients’ function from the ‘gsg’ package⁷⁵. This procedure estimates β′s as

$$\beta \prime =\frac{Cov\left(w,z\right)}{{\sigma }_z},$$

where the numerator is the covariance between the trait and relative fitness, i.e. the partial regression coefficient after taking into account the effect of traits potentially simultaneously under selection, and the denominator is the standard deviation of the trait, following Lande and Arnold^{30, 31}. Standard errors of β′ were estimated through parametric bootstrapping (1000 iterations).

Covariance between selection and heritability: a meta-analysis

As we were interested in studying the effect of environmental variation in selection and genetic variance on selection response, we examined the (linear) relationship between heritability and selection. We refrained from making this analysis conditional on the presence of an underlying correlation between β′ and E', because in cases where statistical power may be an issue, such a two-step approach would decrease the likelihood of detecting a real relationship between h² and β′ if datasets were omitted based on this criterion. A similar reasoning applied to testing for an underlying relationship between h² and E' (see above). For each dataset, we regressed h² against β′ in linear weighted least-squares (WLS) regressions, weighting data points by 1/[(standard error of h²)²]. To account for uncertainty in the predictor, β′, we substituted each of its values (j) with a randomly drawn value from a random normal distribution (n = 1000, $\mu ={\beta }_j^{\prime }$ and σ = standard error of ${\beta }_j^{\prime }$) and iterated the entire process 1000 times. We obtained the mean and the 0.025 and 0.975 quantiles (i.e. the 95% bootstrapped confidence interval CI) of the model estimates (intercepts and slopes) resulting from these iterations; estimates were considered statistically significant if the 95% CI did not include 0. Note that in reality, estimates of β′ are not entirely independent because some individuals are included in multiple estimates, potentially affecting the estimates from (W)LS regression models. We believe, however, that this issue was sufficiently accounted for by our pragmatic bootstrapping approach.

When estimating the covariance between selection and heritability we took the sign of the estimated selection gradients into account, i.e. we did not correlate heritability with the absolute strength of selection (cf. ref. 16). The rationale was that (1) it is biologically relevant whether there is selection for larger or smaller trait values and (2) using absolute or signed selection gradients has different implications for evolutionary change. If a correlation between absolute strength of selection and heritability exists, the overall selection response will not be altered because episodes of strong selection in either direction are always coupled with either high or low heritability. This is, however, not the case when signed selection estimates are used, because in this case strong selection in one direction is coupled with low heritability, whereas strong selection in the other direction is coupled with high heritability.

To examine the overall correlation coefficient across studies and trait types, we performed a meta-analysis using the mean correlation coefficients (r) and their standard errors (SE_r, i.e. half the 95% CI divided by 1.96) resulting from each bootstrapped regression model. Following Nakagawa and Cuthill⁷⁶, we transformed coefficients prior to meta-analysis to Fisher’s Z,

$$Z_r=0.5\times \text{ln}\left(\frac{1+r}{1-r}\right).$$

Variance in Z_r was calculated as⁷⁷

$${\sigma }_{Z_r}^2={{SE}_r}^2\times {\left(\frac{1}{\left[1+r\right]\times \left[1-r\right]}\right)}^2.$$

We estimated the (weighted) mean correlation coefficient (n = 50) in a linear mixed-effects model (REML, package ‘lme4’⁷⁸) with trait type (life history, body mass, morphology, or other) as a fixed effect, study area (i.e. by species; n = 16) as a random effect, and $1/{\sigma }_{Z_r}^2$ as weights. We initially included a random effect of species, which explained 0 variance and was therefore removed from the model (note that the bias toward passerine birds in the acquired datasets precluded phylogenetic analysis). Mean Z_r and 95% CI, predictions unconditioned on the random term, were calculated for each trait type and from a null model excluding the fixed term (i.e. intercept only) through bootstrapping with 1000 iterations. The procedure was repeated on a subset of the data that excluded non-avian traits (n = 43 coefficients, 14 studies). To quantify the consistency among studies, we estimated for both sets of analysis (all data or avian-only) the heterogeneity (I², the proportion of variance that cannot be explained by chance) in the random-effects components for the random-only models (see ref. 79 for details). Residual variance in Z_r was estimated at 1.55 and 1.76, respectively, whereas ‘study’ variance was 0.002 in both cases. Error variance (${\sigma }_m^2$ in ref. 79) was small (0.016 and 0.014, respectively) and I² was estimated at 0.99 in both cases.

Expected response to selection

To quantify the consequence of a covariance between h² and β′ on the response to selection, we predicted the absolute response to selection under the assumption of constant vs varying heritability following the Breeder’s Equation^{30, 80}, i.e. $R_j^{\prime }=R_j{{{\displaystyle \sigma }}_z}^{-1}=h^2{\beta }_j^{\prime }vs.h_j^2{\beta }_j^{\prime }.$ Note that the expected response is in units standard deviation^{30, 32} (hence σ_z), indicated by the apostrophe. The standard error for $R_j^{\prime }$ was derived by adding up the relative standard errors of h² (or $h_j^2$) and ${\beta }_j^{\prime }.$ We then calculated the mean absolute (1) and directional (2) difference in response between the two approximations (ΔR′), with the assumption that non-constant heritability does affect the response from any one year to the next (1) and that this difference is directional (2), i.e. positive when the correlation between h² and β′ is positive and vice versa^{18, 19}. We estimated mean ΔR′ across seasons in a linear model without an intercept and with a fixed effect of ‘study’. As a response variable, ΔR′ in each environment (j) was determined as the difference between two randomly drawn (absolute) values for $R_j^{\prime }$ from two random normal distributions (n = 1000, $\mu =R_j^{\prime }$ and σ = standard error of $R_j^{\prime }$). Mean ΔR′ was derived as the mean, study-specific intercept from 1000 iterations, along with the 0.025 and 0.975 quantiles (i.e. 95% CI).

Loosely based on Wood and Brodie III¹⁶, we estimated whether the strength of the relationship between heritability and selection affected expected (difference in) selection response. We repeated the procedure above for all the datasets (except those for which h² = 0) and calculated the expected, mean directional difference (± standard error) in expected response to selection assuming varying vs. constant heritability (ΔR′). We also extracted the correlation coefficients, r, along with their 95% CIs, from each WLS regression model described in the previous section and calculated standard errors of r as half the 95% CI divided by 1.96. We ran a WLS regression model with ΔR′ as a response variable and 1/[(standard error of ΔR′)²] as weights. The correlation coefficient r was the predictor, randomly drawn from a random normal distribution (n = 1000, μ = r and σ = standard error of r); the procedure was iterated 1000 times and mean estimates and the 0.025 and 0.975 quantiles (95% CI) were extracted. We also tested this relationship with ‘study area’ as a random effect in a linear mixed-effects model, but found that this factor explained 0 variance.

Enquiring with original authors

A potential danger of using open data is that the investigator may not be familiar with the study system and therefore make false assumptions about the data^{52, 54, 55}. Hence, for every dataset potentially suitable for analysis, we wrote a letter to the leading author and/or principal investigator of the associated paper, informing them about the general project aim, as well as a description with specifics regarding the use of their dataset (see Supplementary Methods 2). The description contained information about which data files we used, what our study aim was using their datasets, how we went about preparing the data for analysis (e.g. combining multiple files, (re)construction of the pedigree, calculation of the environment based on the population-mean trait value, identification of reproductive performance or survival), how we analysed the data (including which variables we included in the (M)AMs and RRAMs) and a brief overview of tentative findings. We were specifically interested in the authors’ verdict on our quantification of the environment and fitness. All analyses presented here are based on datasets that were deemed ‘appropriately used’ by the original authors. A common concern with discarded datasets was that reproductive success or survival could not be reliably inferred, for example because a non-random portion of recruits disperse away from the study area, or because surviving individuals were not included in the dataset because they had no phenotype. Similarly, non-random dropping of individuals was likely to affect the estimation of the environment (E′), in which case the dataset forewent inclusion in the analysis. We refer the reader to Supplementary Table 1 for a full list of considered datasets and the reason for their exclusion. We report on the author correspondence in more detail in Culina et al.²⁵.