Dynamic field‐of‐view imaging to increase temporal resolution in the early phase of contrast media uptake in breast DCE‐MRI: A feasibility study

Abstract

Purpose

To increase diagnostic accuracy of breast MRI by increasing temporal resolution and more accurately sampling the early kinetics of contrast media uptake. We tested the feasibility of accelerating bilateral breast DCE‐MRI by reducing the FOV, allowing aliasing, and unfolding the resulting images.

Methods

Previous experience with an “ultrafast” protocol for bilateral breast DCE‐MRI (6–10 s temporal resolution) showed that the number of significantly enhancing voxels is very low in the first 30–45 s after contrast media injection. This suggests that overlap of enhancing voxels in aliased images will be very infrequent. Therefore, aliased images can be acquired during the first 30–45 s after contrast media injection and unfolded to produce full‐FOV images with few errors. In a proof‐of‐principle test, aliased images were simulated from the first 30 s of full‐FOV acquisitions. Cases with relatively dense early enhancement were selected to test this method in a worst‐case scenario. In an initial test, an FOV of 60% the size of the full FOV was simulated. To reduce the probability of errors due to overlapping voxels in aliased images, we then tested a dynamic FOV approach. The FOV was progressively increased so that enhancing voxels could not overlap at multiple time‐points, and areas where enhancing voxels overlapped at a given time‐point could be unfolded by interpolating between the preceding and subsequent time‐points (acquired with different FOVs). The simulated FOV sizes for each of the time‐points were 31%, 44%, and 77% of the full FOV. Subtraction images (post‐ minus precontrast) were generated for aliased images and filtered to select significantly enhancing voxels. Comparison of early, highly aliased images, with later, less aliased images then helped to identify the true locations of enhancing voxels.

Results

In the initial aliasing simulations, an average of 2.9% of the enhancing voxels above the chest wall overlapped in the aliased images (range 0.1%–6.7%). The similarity between simulated unfolded images and the correct full‐FOV images, evaluated using CW‐SSIM (complex wavelet similarity index), was 0.50 ± 0.26, 0.76 ± 0.09, and 0.80 ± 0.10 for the first, second, and third time‐point, respectively (numbers closer to 1 indicate more similar images). For the dynamic FOV tests, an average of 11% of the enhancing voxels above the chest wall overlapped (range 0%–40%) due to greater aliasing at early time‐points. Despite more voxels overlapping, the CW‐SSIM values for the data acquired with dynamic FOVs were 0.64 ± 0.25, 0.93 ± 0.04, and 0.97 ± 0.02 for the first, second, and third time‐points, respectively.

Conclusions

Dynamic FOV imaging allows accelerated bilateral breast DCE‐MRI during the early contrast media uptake phase. This method relies on the sparsity of enhancement at the early phases of DCE‐MRI of the breast. The results of simulations suggest that dynamic FOV imaging and unfolding produces images that are very close to fully sampled images, and allows temporal resolution as high as 2 s per image.

1. Introduction

Dynamic contrast‐enhanced MRI (DCE‐MRI) is a highly sensitive tool for the detection of breast cancer. A recent meta‐analysis by Zhang et al.¹ reported DCE‐MRI's sensitivity to breast cancer detection as 93.2% and specificity as 71.1%. However, its reported specificity in individual studies is variable and sometimes low (e.g., an analysis by Turnbull et al. reported it in the range of 37% to 89%²), suggesting that improvements in diagnostic accuracy are needed. Typically, routine clinical breast DCE‐MRI protocols have high spatial resolution, and since relatively large fields‐of‐view (FOV) are required for bilateral scans, temporal resolution is usually low (roughly 60–90 s per scan). ³ The excellent anatomic detail in these scans allows morphological evaluation of lesions by radiologists, but contrast media kinetics in lesions cannot be accurately characterized at this temporal resolution, especially during the time immediately following the contrast agent injection, when signal intensity is rapidly changing. The kinetics of contrast media uptake may yield important markers for malignancy. In recent years, interest in high temporal resolution bilateral breast scans has increased, as studies have shown that lesion conspicuity is highest shortly after the injection of contrast media and that parameters that describe the initial uptake kinetics may aid in lesion classification.^{4, 5, 6, 7, 8, 9, 10, 11} As a result, high temporal resolution imaging during the initial uptake phase could yield valuable information and increase diagnostic accuracy, especially when combined with high spatial resolution images after the initial postcontrast phase (e.g., after one minute postcontrast media administration).

High temporal resolution is also important for accurate quantitative analysis. Knowledge of the arterial input function (AIF) is necessary to perform pharmacokinetic analysis of lesions, and high temporal resolution is necessary to measure individual AIFs. For example, Parker et al. calculated an AIF with 5 s temporal resolution,¹² while Henderson et al. reported that a temporal resolution of 1 s is necessary to measure the AIF.¹³ In preclinical models Yankeelov et al. imaged with 0.9 s temporal resolution to obtain the AIF in rats,¹⁴ while Kershaw et al. used 0.44 s temporal resolution in rabbits.¹⁵ Even if a population AIF were to be used for pharmacokinetic analysis, Kershaw et al. showed that a temporal resolution of 1.5 s or higher should be used with the adiabatic approximation of tissue homogeneity (AATH) model.¹⁶ While Henderson et al. recommended using 4 s temporal resolution or faster to accurately recover uptake parameters,¹³ and an anthropomorphic phantom study by Knight et al. recommended using an 8.1 s temporal resolution for quantitative analysis.¹⁷ These previous studies show that high temporal resolution could be useful for both clinical interpretation and quantitative analysis of breast DCE images.

There are several approaches to increasing temporal resolution in breast DCE‐MRI. Many groups have focused on view‐sharing or sliding window reconstruction techniques, which sample the center of k‐space more frequently than the periphery, and combine k‐space data from a few different acquisitions (e.g., DISCO, TWIST, TRICKS, TRAK). ^{10, 18, 19, 20} These approaches capture the initial rate of signal enhancement in lesions, sometimes without significant sacrifices in spatial resolution or coverage. However, the strategy of sampling the outer portions of k‐space less frequently than the center makes it difficult to interpret the kinetics of enhancement, especially for small features with high spatial frequency components. In addition, methods that sample different spatial frequencies with different temporal resolutions may produce errors in quantitative analysis.²¹ Compressed sensing approaches have also been developed for breast DCE‐MRI, employing nonuniform k‐space sampling (e.g., RICS, GRASP). ^{22, 23, 24, 25} However, these approaches are susceptible to artifacts, particularly when enhancement patterns are changing very rapidly. To avoid problems with nonuniform k‐space sampling, some laboratories, including this group, have used conventional Fourier sampling methods to image contrast media uptake with high temporal resolution.^{4, 5} Improvements in temporal resolution in these studies came at the expense of either greatly reduced coverage or significantly lower spatial resolution than standard clinical scans. Nevertheless, these studies showed advantages in conspicuity of preinvasive lesions and estimation of pharmacokinetic parameters compared to standard, low‐temporal resolution, clinical scans.

Prior experience with high temporal resolution standard Fourier sampling showed that significant image enhancement in the breast is very sparse during the first 30–45 s after contrast media injection.⁴ Less than 6% of pixels in the breast enhance significantly during this early phase. Here we propose to take advantage of this sparse early enhancement to increase temporal and/or spatial resolution while maintaining uniform k‐space sampling. To do this we propose to image with a reduced field‐of‐view (rFOV) and allow aliasing at early times after injection. Due to the sparse enhancement, there is a low probability that two enhancing areas will overlap, and the few overlaps that do occur can be addressed as demonstrated below. Because we are not limited by signal‐to‐noise ratio, enhancement can be detected at a higher temporal resolution. Aliased images can be “unfolded” to estimate images acquired with a full FOV, using images acquired with a full FOV after the initial phase of contrast media uptake as a reference. In the research reported here, reduced field‐of‐view images are simulated from real breast MRI data acquired with high temporal resolution, and the effectiveness of unfolding is evaluated in two scenarios: one where a single reduced FOV is used for the first 30 s postcontrast administration and another where the FOV is progressively enlarged (dynamic FOV).

2. Methods

Five cases were selected from an Institutional Review Board approved study testing an ultrafast DCE‐MRI protocol, where the first minute postcontrast media administration was imaged with a temporal resolution of 6–10 s. Images were acquired on a 3.0 T scanner (Philips Achieva‐TX, Philips, The Netherlands) with a 16‐channel bilateral breast coil. The ultrafast DCE protocol consisted of a series of axial, fat‐suppressed 3D spoiled gradient echo sequences, before and after administration of gadobenate dimeglumine (0.1 mM/kg, MultiHance, Bracco, Princeton, NJ, USA) with the following acquisition parameters: TR/TE = 3.2/1.6 ms, acquisition voxel size 1.5 × 1.5 × 3.0 mm³, flip angle 10⁰. The five cases selected for this proof‐of‐principle study were read by radiologists as having moderate or marked background parenchymal enhancement and enhancing lesions. We selected cases with relatively dense enhancement to test how this method would work in a worst‐case scenario.

Because few voxels enhanced significantly in the first 30–45 s, two rapidly enhancing areas were relatively unlikely to overlap when the FOV was reduced in the phase‐encode direction and the image aliased. Fully sampled images were approximated from the rFOV images based on the known position of enhancing areas in the full‐FOV images acquired at longer times after injection. Images acquired for the first 30 s after contrast media administration were simulated with an rFOV, and following this period the simulated FOV was expanded to provide full coverage with no aliasing. The unaliased full‐FOV images were then used as a reference to inform the “unfolding” of the rFOV images. While the acquired DCE images were not sparse, subtraction images (postcontrast minus precontrast) were sparse during the early postinjection period when enhancement was sparse.

In an initial test of this method, we simulated DCE‐MRI images acquired with an rFOV equivalent to 60% of the full FOV from the precontrast images and the first three time‐points of the original series. Subtraction images were created for the three rFOV time‐points by subtracting the precontrast aliased images from the postcontrast images. We also created subtraction images for the 4^th time‐point, leaving the FOV intact (fully sampled). These images were used as a reference to guide the following unfolding process (Fig. 1):

• Significantly enhancing voxels in the rFOV subtraction images and full FOV reference images were identified. As defined in this study, these were voxels with greater than 25% relative enhancement, and a post‐ minus precontrast signal value greater than 3.5 times the standard deviation in the precontrast signal (measured over five precontrast acquisitions).

• The possible locations of each significantly enhancing rFOV voxel in the full FOV were determined. In this case there were two possible locations for voxels in the area where aliasing could occur (toward the edges of the FOV), or only one possible location if the enhancing voxel was near the center of the rFOV.

• Enhancing rFOV voxels that were not in an area where aliasing could occur were copied to the corresponding location in the unfolded (full‐FOV) image.

• Enhancing voxels that could have been aliased in the rFOV image were copied to the unfolded image using the reference image as a guide (e.g., the image acquired at 30 s postinjection). If only one possible location enhanced in the reference image, the voxel was copied to that location. If both locations were enhanced in the reference image (i.e., if two significantly enhancing voxels could have overlapped in the rFOV), the voxel was copied to both locations.

Figure 1.

Diagram of “unfolding” method. A first approximation is created by replicating the aliased portions of the image. Each enhancing voxel (P) is copied to the possible locations it could have originated from (P1 and P2). The unfolded image is compared to later reference images acquired with a larger or fully sampled FOV. If only one of the potential locations is enhanced (“on”) in the later images, the voxel is copied to that location and its alias is zeroed out; if both locations are “on”, the voxel is copied to both locations. [Color figure can be viewed at wileyonlinelibrary.com]

This process led to unfolded images that approximated fully sampled subtraction images. However, if enhancing voxels aliased onto one another in a particular rFOV, then the signal measured in each of these “overlapping” voxels was the sum of the “true” signal in each voxel and its aliases. These voxels were artificially brighter in the reconstructed images. We recorded the number of overlapping voxels in the full‐FOV reconstruction.

While the method described above led to approximate full‐FOV images, it did not provide enough information to accurately distribute the signal of voxels that overlapped in aliased images. To provide a more robust method of unfolding rFOV images, we simulated a “dynamic FOV” method (Fig. 2). We began with an rFOV that was 31% of the full FOV at the first time‐point, and enlarged this to 44% at the second time‐point, and 77% at the third. Under these conditions, enhancing voxels aliased to different locations at different times. As a result, no pair of voxels overlapped at more than one time‐point. Overlapping voxels within a single rFOV were approximated by interpolating the signal between the immediately preceding and following time‐points. In this dynamic FOV method, full‐FOV images were reconstructed using the following procedure:

• Significantly enhancing voxels were identified (as described above in the static case).

• Initial full‐FOV estimates were created by copying significantly enhancing voxels from the aliased rFOV images to all of their possible locations. These first estimates were more densely populated than a fully sampled image.

• Voxels that enhanced in one of the full‐FOV estimates without enhancing at all subsequent time‐points (including the reference image) were determined to be aliasing ghosts and were eliminated. After this step, the only enhanced voxels remaining in the full‐FOV reconstruction were those that did not overlap with any other enhancing voxels (in their correct position, with the ghost eliminated) and enhancing voxels that overlapped in the rFOV image (copied to both locations in the full FOV). As in the “static” aliasing case, at this stage the latter set of voxels appeared brighter in the reconstructed image.

• To estimate the correct distribution of signal between overlapping voxels, we interpolated between the time‐point immediately before and immediately after the time‐point where overlap occurred. The interpolated values were constrained so that the sum of the estimated signals was equal to the signal in the voxel in the original rFOV image. The last step ensured that no signal was erroneously augmented or reduced.

Figure 2.

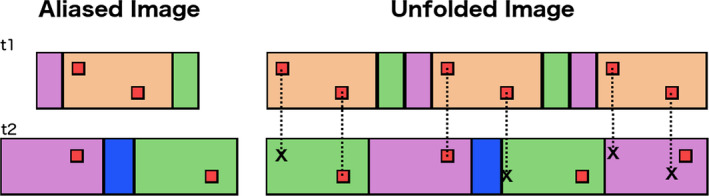
Diagram of “unfolding” with a dynamic FOV. An unfolded image is compared to later reference images acquired with a larger or fully sampled FOV. Because FOVs differ in subsequent time‐points, each enhancing voxel will be copied to sets of points that agree only on a single location at all subsequent times. [Color figure can be viewed at wileyonlinelibrary.com]

The unfolded images from the simulated rFOV acquisitions were compared to subtraction images (noise filtered as in step “a” above) from the original, fully sampled data using the complex wavelet structural similarity index (CW‐SSIM).²⁶ CW‐SSIM and SSIM²⁷ are commonly used metrics in computer vision, designed to approximate the subjective similarity of images to a human observer. We used CW‐SSIM over the more commonly used SSIM metric because SSIM does a poor job differentiating between images with sparse structure. CW‐SSIM sharply punishes small deviations between images when little structure is present and is therefore better‐suited to evaluate sparsely enhancing images than SSIM. Though it is difficult to reliably interpret objective image quality metrics in subjective terms, SSIM values above 0.5 roughly correspond to a “fair” mean opinion score, values above 0.75 to “good”, and values above 0.9 to “excellent”.²⁸ This metric was used to analyze the effectiveness of the methods presented here in preserving information in the reconstructed images.

In order to determine the accuracy of lesions in the reconstructed images, signal enhancement curves and lesion texture parameters were compared with those from the fully sampled images. Regions‐of‐interest (ROIs) encompassing the entire lesion volume were drawn on the original fully sampled images and propagated to the unfolded images. The mean signal intensity in the whole ROI was calculated at each time‐point. Lesion texture was evaluated via the gray‐level co‐occurrence matrix (GLCM).²⁹ In each case, the lesion was isolated and its GLCM was calculated for each slice and time‐point. A homogeneity parameter (“h”) was calculated for each GLCM by measuring the closeness of the GLCM to a diagonal matrix. A chi‐squared (χ ²) statistic was calculated between each set of h values in between the unfolded and original images.

3. Results

Figure 3 shows images of representative slices throughout the process of unfolding with the “static” aliasing method (with a 40% reduction in FOV size). The figure shows fully sampled and aliased images, along with the unfolded images. Areas of hyperintensity (relative to the original images) correspond to significantly enhancing voxels that overlapped in the rFOV images — some examples are marked with arrows. Figure 4 shows maximum intensity projections (MIPs) from some of the simulations, including a color‐coded image where the number of overlaps in each position across all slices is shown. The average number of overlapping enhancing voxels in the unfolded images above the chest wall, across all slices, in the rFOV images (expressed as a percentage of all enhancing voxels above the chest wall at the same time‐point) were 2.6% (range: 0.1%–6.5%), 2.8% (0.1%–6.7%), and 3.4% (0.5%–6%), for the first, second, and third time‐points, respectively. These numbers show that even when using an rFOV equivalent to 60% of the fully sampled FOV only a relatively small number of enhancing voxels alias onto each other in the rFOV images. However, enhancing voxels were copied to both of the possible locations in the reconstructed full‐FOV image if both enhanced in the reference image, artificially increasing the signal intensity at locations where significantly enhancing voxels overlapped. The CW‐SSIM numbers for each time‐point were 0.50 ± 0.26, 0.76 ± 0.09, and 0.80 ± 0.10, respectively.

Figure 3.

Example slices from two static aliasing tests, showing enhancing lesions from cases with a simulated FOV of 60% of the original size: (a) original dynamic image; (b) aliased dynamic image; (c) aliased post‐ minus precontrast subtraction image; (d) unfolded subtraction at full FOV; (e) original subtraction image. Arrows indicate areas that appeared brighter in the reconstructed images compared to the original subtractions. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 4.

Examples from two test cases, 2nd time‐point is shown (14–20 s postcontrast): (a) Original maximum intensity projections (MIPs) of difference images; (b) MIPs reconstructed from static aliasing at 60% of the FOV; (c) MIPs reconstructed from dynamic aliasing at 44% of the FOV; (d) & (e) Color maps showing the number of overlaps (in all slices and time‐points) per MIP pixel location in static (d) and progressive (e) aliasing simulations. [Color figure can be viewed at wileyonlinelibrary.com]

Examples from the progressive aliasing and unfolding (dynamic FOV) simulations can be seen in Fig. 5, and MIPs with overlap color maps are shown in Fig. 4. There are more overlapping voxels in these images compared to the static cases because the first and second time‐points were simulated to have rFOVs smaller than those used in the static cases. The average number of overlapping enhancing voxels above the chest wall (and for the entire acquired slab) in the rFOV images, again expressed as a percentage of all enhancing voxels above the chest wall at the same time‐point, were 14.3% (range: 7.6%–23.7%), 18.6% (2.9%–39.7%), and 0.2% (0%–0.4%). While some differences remain between the full‐FOV images and the unfolded images, these differences are less prominent with dynamic FOV imaging than in the static case, due to the fact that the signal at each overlapping location was interpolated. This is reflected in the CW‐SSIM numbers: 0.64 ± 0.25, 0.93 ± 0.04, and 0.97 ± 0.02, for rFOVs equivalent to 31%, 44%, and 77% of the full FOV, respectively. CW‐SSIM numbers were significantly greater for the dynamic FOV simulations than for the static cases (P < 0.001). This is to be expected for the third time‐point where the rFOV was larger than the rFOV used for the static case, but significant improvement was also seen for the first two time‐points where the rFOVs were markedly smaller.

Figure 5.

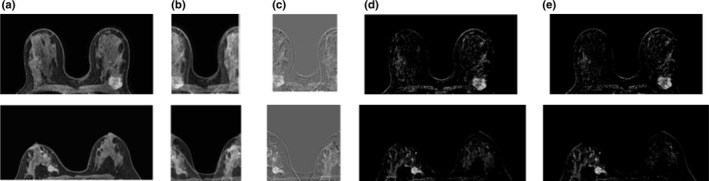
Example slices from two dynamic FOV tests, showing enhancing lesions from cases with a simulated FOV of 44% of the original size: (a) original dynamic image; (b) aliased dynamic image; (c) aliased post‐ minus precontrast subtraction image; (d) unfolded subtraction at full FOV; (e) original subtraction image.

All lesions present in the cases used in these simulations were recovered in the reconstructed unfolded images (Fig. 6). This figure shows noticeable areas of difference between the static case and the original data; however, the lesions in the dynamic FOV images closely resemble the fully sampled data. This is reflected in the plots of mean signal enhancement versus time (Fig. 7), where mean signal across the reconstructed lesion closely tracks that of the fully sampled data. The only lesion for which there was a slight overestimation of signal in the dynamic FOV unfolded images was the one represented in Fig. (7b); this case was not pictured in Fig. 6 due to its low enhancement during the first three time‐points. The overestimation of signal in this case is likely due to the overlap of the lesion with enhancing areas in the contralateral breast. The results also showed that the dynamic FOV method preserved the texture of signal enhancement in the lesions. Homogeneity numbers calculated via the GLCM were consistent between the original data and the images unfolded with the dynamic FOV method (P < 0.002).

Figure 6.

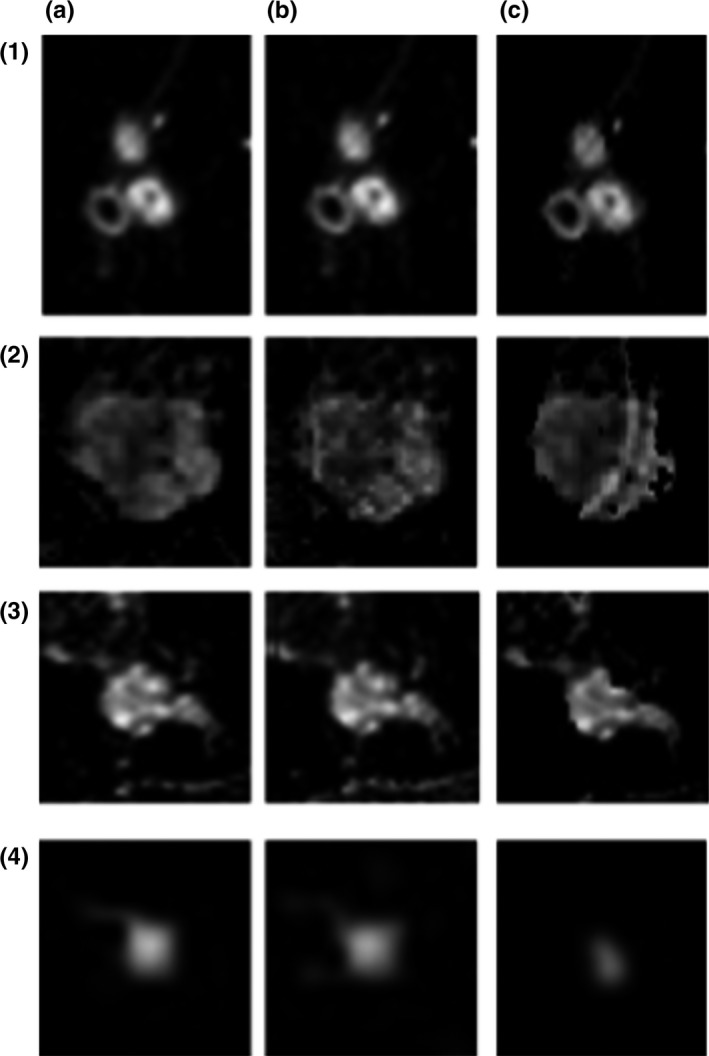
Example slices containing lesions. (a) Original subtraction images, (b) progressive unfolding reconstruction, and (c) static unfolding reconstruction. (1–3) Invasive ductal carcinoma; (4) fibroadenoma.

Figure 7.

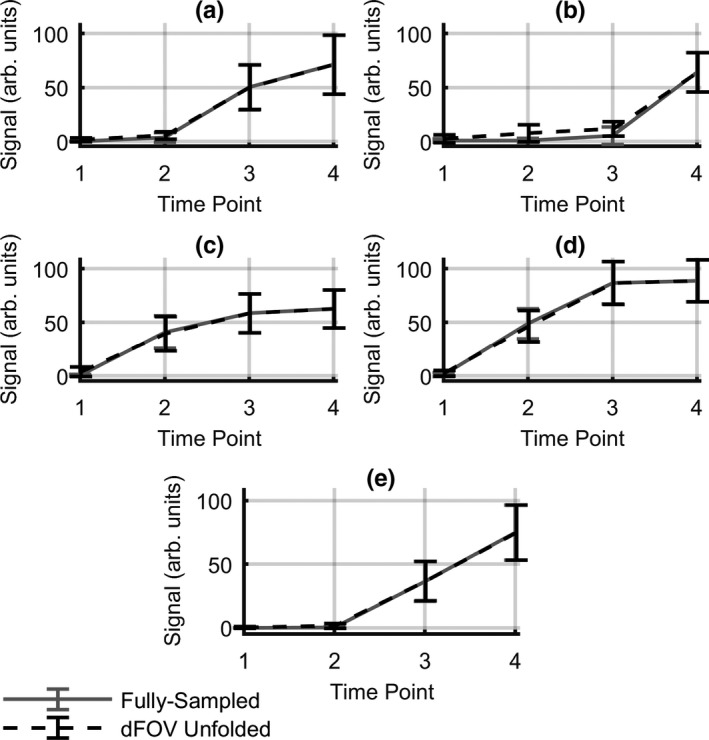
Mean lesion signal enhancement versus time curves for all lesions present in the cases used in the simulation. Plots for fully sampled and dynamic FOV unfolded images are shown. This figure does not depict the entire kinetic curve, only the time‐points used in this analysis. Error bars indicate median absolute deviation in each ROI. Solid lines show mean lesion signal from full‐FOV images; dotted lines show mean lesion signal from dFOV unfolded images. Plots (a,c,d) invasive ductal carcinoma; (b) usual ductal hyperplasia; (e) fibroadenoma.

4. Discussion

The simulations described here show that it is possible to recover difference images that closely approximate fully sampled images from rFOV acquisitions during the first 30 s postcontrast administration. The dynamic FOV imaging and unfolding approach estimates the signal value of overlapping enhancing voxels. The methods presented here are practical because difference images (i.e., post‐ minus precontrast) are very sparse during the first 30–45 s after contrast media injection. These methods require a fully sampled set of images following the period of rFOV acquisitions, which are used as reference images to inform the “unfolding” process. In addition, this method is parameterized by FOV size choices only and is simple to implement, as it does not require complex parameter tuning. The simulations presented here demonstrate up to a 69% reduction of acquisition time or an increase in spatial resolution without sacrificing temporal resolution. Ideally, a balance can be achieved between temporal and spatial resolution in order to estimate accurate perfusion parameters while resolving the heterogeneity of enhancement within lesions and avoiding partial volume effects.

Several methods exist for accelerating image acquisition with reduced FOVs and unfolding aliased acquisitions. Sensitivity encoding (e.g., SENSE³⁰ or GRAPPA³¹), relies on the spatially varying sensitivities of coil elements to inform the unfolding of rFOV images into approximate fully sampled images. The method presented here could be combined with SENSE acceleration by accounting for the shift in the position of the ghosts that would result from combining SENSE with an rFOV acquisition.³² Dynamic FOV imaging could also be incorporated into the SENSE reconstruction to reduce the ghosting artifacts that arise from SENSE. Ghosts in initial unfolded reconstructions from the aliased images acquired with each coil element could be sparsified with the method proposed here (by comparison with later fully sampled images). Coil sensitivity data would then be used to reconstruct the full‐FOV images, as with the standard SENSE algorithm. Unfolding progressive rFOVs before applying SENSE has potential to reduce the appearance of SENSE artifacts and will be studied further in future simulations.

The UNFOLD method corrects for aliasing by Fourier‐encoding the overlapping regions of the images in the temporal dimension.^{33, 34} In this method, the phase of aliased voxels changes in subsequent acquisitions, providing additional information that can be used in creating full‐FOV images. The UNFOLD method is very effective when the dynamic process that is being sampled has limited bandwidth (e.g., changes in the time domain are gradual or periodic) and thus is well represented within a limited temporal bandwidth. In the present work, we are trying to detect very sharp changes in the time domain because these changes may be diagnostically important. These changes occur rapidly on the time scale of the MRI acquisitions. This means that we want to keep the bandwidth of our temporal sampling as broad as possible and avoid using some of the bandwidth to encode spatial information. Furthermore, not all imaging sequences can support UNFOLD. The dynamic FOV imaging method and the UNFOLD method have different goals and different approaches to sampling. CAIPIRNHA (controlled aliasing in parallel imaging results in higher acceleration) is another alternative method for removing aliasing artifacts and increasing temporal resolution, where multiband RF pulses are used to produce phase shifts in overlapping slices that can be used to reconstruct images without aliasing artifacts.³⁵ In contrast, the method presented here is, to our knowledge, the only method that unaliases rFOV acquisitions based on temporal enhancement patterns, requiring consistency in image space rather than k‐space, and modifying the sampling density as the density of enhancement increases. Its applicability outside of the breast may be limited, as it is the geometry of axial breast acquisitions and the properties of early enhancement that allow recovery of fully sampled images.

Use of novel k‐space sampling schemes and reconstruction methods (such as view‐sharing, sliding windows, or compressed sensing) have definite advantages: in particular, they produce visually appealing images acquired at high temporal resolution. Recently, Chen et al.²⁴ proposed a method for the acceleration of breast DCE‐MRI based on constraining the temporal total variation (TV) in the dynamic series. In this work they demonstrate the ability to obtain 6‐ to 10‐fold acceleration factors, while maintaining high image quality. However, due to penalties enforced on the temporal TV, the reconstruction process may result in temporal smoothing and the potential loss of sharp, diagnostically important temporal features (e.g., the arrival of the contrast media bolus in the lesion). Adluru et al.²³ proposed a method using nonlocal means to enforce similarity constraints in neighborhoods of pixels and relax the sampling requirements for high resolution images in a dynamic series. They showed improvements over sliding window and TV‐constrained reconstructions while achieving a 5‐fold acceleration factor in breast DCE‐MRI. However, by enforcing similarity in neighborhoods of pixels, a degree of spatial smoothing may occur. This smoothing may result in a loss of heterogeneity in lesions. In contrast to the other methods discussed here, dynamic field‐of‐view imaging does not enforce smoothness in the spatial or temporal domains. Furthermore, the effects of nonuniform k‐space sampling and, particularly, undersampling the periphery of k‐space, in cases with rapid enhancement have not been adequately characterized (as is the case in the early phases of breast DCE‐MRI). Data acquired in this laboratory⁴ suggest that new k‐space sampling methods may not be necessary, given the very sparse enhancement detected in the breast at early times after contrast media injection. Alternatively, dynamic field‐of‐view imaging could be used in combination with other methods to reduce errors and artifacts. The method used here undersamples k‐space, leading to aliased acquisitions, but uses uniform Cartesian sampling and may better characterize changes that occur at the periphery of k‐space.

Similarity indices were significantly higher for the dynamic FOV simulations than for those using the same rFOV for all acquisitions. However, the earliest set of images had modest CW‐SSIM values. This is likely due to the fact that very few voxels enhanced at very early times and even small deviations in sparse images are severely penalized by CW‐SSIM. While most of the differences in the images come from the overlap of significantly enhancing voxels, differences between the fully sampled images and the unaliased reconstructions may also come from voxels with minimal enhancement overlapping with enhancing voxels and adding a small amount of signal to the enhancing voxel in the reconstructed image. There were some artifacts present in the reconstructed images, and in some cases in the enhancing lesions themselves, but we do not believe that the presence of these artifacts would affect the detection of these lesions. If this method were to be implemented in a clinical setting, the early high temporal resolution images could be used to detect areas of abnormal enhancement, while later images, acquired without aliasing and/or with higher spatial resolution could be used to obtain a diagnosis.

The dynamic FOV imaging method proposed here has some limitations. The optimal FOV reduction factors will be somewhat case dependent. In this study, the undersampling factors were chosen to be co‐prime (to minimize repeated overlaps) and give sufficiently high temporal resolution at early time‐points to capture the rise of the arterial input function (AIF). The optimal factors to obtain high temporal resolution with a limited number of artifacts may not be the same for all cases. In this work the smallest FOV used was 31% of the full FOV, corresponding to roughly a 3‐fold acceleration factor; this factor is lower than the acceleration factor obtained by other advanced methods (e.g., compressed sensing). While previous experience with high temporal resolution imaging has shown that early enhancement in the breast is sparse, cases in which the enhancement is dense could limit the accuracy of the unfolded images, as the likelihood of voxels overlapping would be greater, and the accuracy of the reconstruction would depend on the performance of the interpolation scheme. Patient motion could also lead to inaccurate reconstructions, given that later images are used to guide the unfolding process and the locations of significantly enhancing voxels may shift in cases with motion in between acquisitions. Image registration could be used to limit the effect of motion, though the application of image registration algorithms to rFOV images could prove challenging due to fold‐over artifacts. Though the analysis presented here has focused on the breast (above the chest wall), this method could lead to inaccurate reconstructions of axillary lymph nodes, given that they may overlap with the heart in rFOV images, thus obscuring axillary lymph nodes at early time‐points.

The research described here faced some obstacles not inherent to the method. The data used to simulate rFOV acquisitions were acquired at a lower temporal resolution than if actual rFOV images had been acquired. Since less time would have elapsed between the points being used for the interpolation, the temporal interpolation used in estimating the signal at each of the locations for overlapping voxels would perform better with real high temporal resolution data than in these simulations. Additionally, more detailed analysis of the noise properties of the aliased images is needed. In the simulations described here, the standard deviation of several precontrast images was used to determine a threshold above which signal enhancement was deemed significant. More work is required to determine whether different noise thresholds should be used for different areas of the image depending on the degree of fold‐over, or if a measure other than standard deviation more adequately determines a noise threshold. The simulations presented here were based on modulus images, which amplify the effect of noise when simulating the intensity in aliased voxels. It is possible that in practice (when dealing with complex data) fewer low‐signal voxels will be misclassified as enhancing, and as a result, reconstructions will be more similar to fully sampled images.

We plan a number of improvements to “dynamic FOV imaging”. These include use of information from neighboring voxels to identify artifacts resulting from the unfolding process. For example, if a voxel is many times brighter than most of its neighboring structures, this could be an indication that its signal was artificially increased in the unfolding process. We also plan to use additional information from fully sampled precontrast images to improve the accuracy of the unfolding process. It is possible that structural information in these images could be used to identify aliased areas in the rFOV acquisitions and reduce artifacts in the final unfolded images. In this study, we did not use image registration to remove artifacts in the subtraction images resulting from motion in between pre‐ and postcontrast acquisitions. While there were not significant motion artifacts in the cases selected, it is possible that a small shift in position could lead to errors in the subtraction images. Image registration would help eliminate these artifacts and increase the similarity of the unfolded images to the original full‐FOV acquisitions.

5. Conclusions

This paper reports that the temporal resolution of breast DCE‐MRI can be increased by reducing the field‐of‐view resulting in aliased images acquired during the 30–45 s after contrast media injection, producing very sparse subtraction images, and then approximating fully sampled images by “unfolding” the aliased subtraction images using enhancement patterns to inform the unaliasing process. A novel dynamic field‐of‐view approach was developed and shown to closely approximate full‐FOV images. As temporal resolution increases with dynamic FOV imaging, postcontrast enhancement in early images becomes even sparser than in the images used in these simulations, increasing reconstruction accuracy. This method could be used to increase the temporal resolution of early uptake phase breast DCE‐MRI, and there are potential applications to other areas of the body. Future studies will further refine this method by including more information in the unfolding process.

Conflicts of interest

The authors certify that they have no financial interests in the subject matter or materials discussed in this manuscript.