The Best of Times, the Worst of Times: Understanding Pro-cyclical Mortality

Abstract

It is well known that mortality rates are pro-cyclical. In this paper, we attempt to understand why. We find little evidence that cyclical changes in individuals’ own employment-related behavior drives the relationship; own-group employment rates are not systematically related to own-group mortality. Further, most additional deaths that occur when the economy is strong are among the elderly, particularly elderly women and those residing in nursing homes. We also demonstrate that staffing in nursing homes moves counter-cyclically. These findings suggest that cyclical fluctuations in the quality of health care may be a critical contributor to cyclical movements in mortality.

Why do death rates rise when the unemployment rate falls? Pro-cyclical mortality rates in the United States (and elsewhere) are well-documented, but the causes of this association remain poorly understood. The most frequently cited explanation is that the business cycle affects individuals’ time use, stress levels, and related health investments through its effects on hours of work. In this paper, we show that pro-cyclical mortality in the United States is not driven by changes in individuals’ own time use associated with their own employment changes. Instead, we find evidence that alternative mechanisms are at work, including cyclical variation in the quality of health care.

The negative relationship between the unemployment rate and the mortality rate has been documented in a series of influential papers by Christopher Ruhm (2000, 2003, 2005a, 2005b, 2007). A typical estimate suggests that a one-percentage point increase in a state’s unemployment rate leads to a 0.54 percent reduction in that state’s mortality rate (Ruhm, 2000). When applied to U.S. mortality counts from 2006, this implies that a one percentage point increase in unemployment would lead to about 13,000 fewer annual deaths. Ruhm’s findings are widely cited in the health economics literature and have been echoed in work by Dehejia and Lleras-Muney (2004) who find that infant health outcomes and economic downturns are positively linked. The most common interpretation throughout this literature has been that good economic times have a negative impact on individuals’ health because of an increase in work hours, the opportunity cost of time, and resulting changes in individuals’ decisions about how to allocate their time. Related studies find that obesity and smoking both exhibit a pro-cyclical pattern, and that diet and exercise also improve when the unemployment rate rises – patterns that are consistent with changes in the value of time associated with work (Ruhm, 2005b).¹ Business cycle induced variation in mortality rates may also be driven by other factors, however, that have not been fully explored.

This paper delves into the mechanisms behind pro-cyclical mortality in the United States. We are particularly interested in separating the effects of changes in individual behavior that result from changes in one’s own employment status from the effects of other factors that fluctuate with the unemployment rate. This distinction is important because of differences in the associated policy prescriptions. In addition, understanding the underlying mechanisms will shed light on a well-known empirical puzzle–while mortality rates are pro-cyclical, job loss is known to have negative effects on individuals’ health. Sullivan and von Wachter (2009), for example, find that individuals who experience a job loss via a mass-layoff experience a substantial increase in their mortality hazard that lasts over the next 20 years.² As Ruhm (2008) notes, the estimated impact of individuals’ own job loss can be reconciled with the aggregate patterns only if the aggregate fluctuations in mortality are concentrated among those who do not change employment status. This suggests that the mechanisms driving pro-cyclical mortality are more complex than a simple connection between own-employment and health.

We find strong evidence that this is the case. Using state-year panel data models similar to Ruhm’s, we find that own-group labor market indicators are not positively related to that group’s mortality, and that cyclical variation in nursing home deaths among those over age 65 – a group with very low labor force attachment—can more than account for the total cyclical variation in mortality. We also find that states in which a higher fraction of the elderly population reside in nursing facilities exhibit more cyclical variation in mortality. Our analyses suggest that nursing home deaths’ pivotal contribution may be driven by cyclically induced impediments to staffing in health-care occupations.

In the next section, we describe our data and econometric approach. In section II, we present our results on the cyclicality of mortality, focusing on analyses that are disaggregated by age, gender, and place of death. Our estimates show that any explanation of cyclical mortality must look beyond the working age population and beyond motor vehicle deaths. The next section focuses on deaths among the elderly and identifies the important role played by deaths that occur in nursing homes. We conclude in section III.

I. Data and Methodology

We begin by estimating a specification that has become standard in the literature. Specifically, our main regression takes the following form:

$$H_{jt}={\alpha }_t+X_{jt}\beta +E_{jt}\gamma +S_j+S_{j}t+{\epsilon }_{jt}$$ (1)

where H is the natural log of the mortality rate in state j and year t, E is a measure of the state’s economic health (usually the state unemployment rate), X is a vector of demographic controls including the fraction of the population who are: less than five years old, 5 to 17 years old, 18 to 30 years old, greater than 65 years old, high school dropouts, with some college, college graduates, black and Hispanic. The vector of year specific fixed effects, ${\alpha }_t$, captures year effects, and the vector of state specific indicator variables, $S_j$, controls for time-invariant state characteristics. State-specific time trends are also included $(S_{j}t)$. This specification is identical to Ruhm’s, and when we use his data we are able to produce nearly identical estimates, which suggest that a one percentage point increase in the unemployment rate is associated with a 0.5 percent decrease in the predicted death rate (see Appendix Table A.1).

To conduct the most thorough analysis possible, our study exploits both new data sources and additional years of data. We pool monthly CPS files (January-December) to construct state unemployment and employment rates. This means we begin our analysis in 1978, the first year all individual states are identified in the CPS files, but are able to extend it beyond 1998 (the last year in Ruhm’s (2007) data set). We also use the CPS to create state-year unemployment measures for specific demographic groups and to create the demographic controls described above. Our main results are based on data from 1978 through 2006. Most of our analyses are population weighted regressions using population counts collected by the National Cancer Institute’s Surveillance Epidemiology and End Results (Cancer-SEER) program. Appendix Table A.1 provides unweighted estimates.

Our state-year mortality rates are based on death counts from Vital Statistics’ micro-record “multiple cause of death” files (numerator), and state by age population counts from Cancer-SEER (denominator). We age adjust these data to create a measure of the mortality rate that holds the age distribution constant over time. We describe our age adjustment in Appendix A where we also document how these and other changes affect Ruhm’s (2000) results. The age adjustment is important given the longer time period we study, and tends to increase the size of the estimated coefficient on the unemployment rate when mortality across all age groups is the focus. When we focus on narrower age groups, as expected, the age adjustment is less important, and does not drive our main findings. Adding years after the early 1990s tends to diminish the estimated degree of cyclicality. Taken as a whole, however, the modifications that we make have limited impact on the estimated association between macroeconomic fluctuations and health. Our baseline estimate of $\gamma$ is −0.0033, which suggests that a one percentage point increase in the unemployment rate is associated with a 0.3 percent decrease in the predicted death rate.

II. Why are Recessions Good for your Health?

II.A. Mortality Patterns by Age, Gender and Cause

Having confirmed that mortality is pro-cyclical through the mid 2000s, the major question we explore is why the probability of dying increases when economic times are good. As a starting point, Ruhm (2000) proposes four possible mechanisms. First, leisure time declines when the economy improves, making it more costly to undertake health-producing activities that are time-intensive. Second, health may be an input into the production of goods and services. Hazardous working conditions, job related stress and the physical exertion of employment, for example, may all have negative effects on health, and are expected to increase when the economy is expanding. Both of these mechanisms work through changes in individuals’ own work hours or opportunity cost of time. A third explanation is that the relationship reflects the impact of external factors that fluctuate with the economy. In particular, when more people are working, roadways are more congested, and this leads to an increase in the probability of being involved in a fatal auto accident. There is a fair amount of direct evidence in support of this mechanism. For example, Evans and Graham (1988) and Ruhm (1996) show that drinking and driving exhibit a pro-cyclical pattern, and Ruhm (2000) shows that motor vehicle fatalities are more sensitive to the business cycle than any other cause of death. Similarly, pollution may vary over the business cycle and contribute to mortality fluctuations.³ Ruhm’s fourth hypothesis is that business cycles affect geographic mobility, which may increase crowding or otherwise bring transition costs that impact mortality.

These hypotheses do not find immediate support from broad patterns in the data, however. For example, Table 1 shows the estimated relationship between the state mortality rate and unemployment, after dividing our sample into four age by cause-of-death cells. We divide deaths into those due to motor vehicle accidents and those arising from all other causes, and we focus on two age groups: those under age 65 and those age 65 and over. In this and all future tables, the estimated coefficients and standard errors associated with the unemployment rate are multiplied by 100. Thus, a one percentage point increase in the unemployment rate reduces motor vehicle deaths among the non-elderly by 2.6 percent. We see that for both age groups, deaths related to motor vehicle accidents are strongly cyclical: coefficient estimates are on the order of 10 times the estimated coefficients in the “all other causes” category. In contrast, non-motor vehicle deaths among the non-elderly—the group most likely to be attached to the labor force—do not exhibit statistically significant cyclical fluctuations. This is one piece of evidence that own-work behavior is unlikely to provide the key explanation.

Table 1.

Unemployment Rate Coefficients by Broad Age and Cause of Death

1978-2006	Cause/Place of Death		Percent of overall cyclicality due to cause/age cell
Age group	MVA	All Other Causes	MVA	All Other Causes
<65	−2.641***	−0.136	14.99 percent	11.64 percent
	(0.544)	(0.207)
Mean Deaths per Year	38,649	581,475
65+	−2.197***	−0.301***	2.28 percent	71.09 percent
	(0.610)	(0.082)
Mean Deaths per Year	7,077	1,606,329
			Average deaths per year–total	2,233,530

Notes: Dependent variable is age-adjusted log death rate for motor vehicle accidents (MVA) or all other causes, by age group. Parameters are the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. Each cell is a separate regression. Controls include State and Year Fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Given that the distribution of deaths across age (and cause) groups is not uniform, the estimated coefficients do not provide sufficient information to determine which cells drive the overall effect.⁴ We investigate this further by noting that the overall coefficient can be decomposed into the weighted sum of the group-specific coefficients, where the weights are the number of deaths occurring in each cell. For each cell in Table 1 we show the annual average number of deaths, and, using the number of deaths as weights, we compute the fraction of the overall cyclicality that can be attributed to each of the four cells.⁵ Motor vehicle accidents comprise only about two percent of all deaths in a typical year, and thus variation in motor vehicle accidents explains only about 17 percent of the total cyclical movement in mortality. Further, the vast majority (71 out of the remaining 83 percent) is driven by cyclical variation among those over 65. This broadly disaggregated analysis does not tell the full story, and obscures important cyclical responses among more narrowly defined subgroups, which we will explore more fully below. The key point, however, is that any story with the potential to explain a substantial portion of the overall effect must go beyond motor vehicle deaths and must not apply primarily to the working age population.

Table 2, which presents the contribution of more narrowly defined age and gender groups to the overall coefficient estimate, lends further support to this argument. The first row of Table 2 presents estimates for the population as a whole, and separately for men and women.⁶ We find that while a one percentage point increase in the unemployment rate decreases the female mortality rate by 0.40 percent, it decreases the male mortality rate by only 0.24 percent.⁷ The remaining rows of Table 2 show comparable estimates for five year age groups by gender,⁸ and Figure 1 summarizes the coefficient estimates for each year of age. Like Ruhm, we find that mortality among young adults is more sensitive to the business cycle than mortality among other working age adults. For example, we estimate that a one percentage point increase in the unemployment rate reduces the mortality rate among 20 to 24 year olds by about 2 percent. Since young adults’ employment fluctuates more than other workers’, this finding at first appears to be consistent with the hypothesis that pro-cyclical declines in health are driven by changes in individuals’ own behavior. Closer inspection of Table 2, however, reveals several patterns that are not consistent with such a story. First, while we estimate a large semi-elasticity among 20 to 24 year olds, estimates for individuals between the ages of 25 and 59 are substantially smaller and for many prime-age workers, the point estimates are near zero. It is also the case, however, that there are wide confidence intervals around the estimates for these age groups, in which deaths are relatively rare. Second, some of our biggest coefficient estimates are associated with age groups that are certain not to be working, such as 0-4 year olds. Third, the coefficient estimates among those who are over 65 tend to be more negative than the estimates among those 35 to 64.

Table 2.

Effects of Unemployment on Mortality by Age Coefficients and Additional Deaths

	Coefficients			Additional Deaths from 1 percent Increase in Unemployment Rate (based on 2006 #s of deaths)
Age Group	All	Men	Women	All	Men	Women
All ages	−0.332***	−0.245**	−0.402***	−8057	−2940	−4920
	(0.099)	(0.105)	(0.111)
0 to 4	−1.36***	−1.475***	−1.195***	−451	−273	−175
	(0.266)	(0.282)	(0.304)
5 to 9	−0.905*	−1.026**	−0.775	−25	−16	−9
	(0.477)	(0.499)	(0.866)
10 to 14	−0.458	0.275	−1.827*	−16	6	−24
	(0.496)	(0.432)	(0.930)
15 to 19	−1.395***	−1.467***	−1.076**	−192	−145	−41
	(0.433)	(0.506)	(0.509)
20 to 24	−1.796***	−1.822***	−1.461***	−380	−294	−73
	(0.386)	(0.433)	(0.443)
25 to 29	−0.777*	−1.068**	0.184	−162	−162	11
	(0.411)	(0.475)	(0.382)
30 to 34	−0.449	−0.78	0.401	−99	−117	28
	(0.633)	(0.709)	(0.597)
35 to 39	0.12	0.013	0.414	38	3	47
	(0.550)	(0.711)	(0.418)
40 to 44	0.183	0.124	0.254	94	40	50
	(0.379)	(0.475)	(0.335)
45 to 49	−0.025	0.068	−0.161	−20	33	−49
	(0.244)	(0.293)	(0.252)
50 to 54	−0.155	−0.053	−0.307*	−164	−35	−122
	(0.179)	(0.233)	(0.163)
55 to 59	−0.051	0.091	−0.225	−67	74	−117
	(0.160)	(0.162)	(0.200)
60 to 64	−0.119	−0.122	−0.084	−177	−107	−51
	(0.121)	(0.138)	(0.126)
65 to 69	−0.224**	−0.219	−0.218*	−386	−216	−160
	(0.093)	(0.141)	(0.112)
70 to 74	−0.377***	−0.261**	−0.494***	−823	−311	−488
	(0.070)	(0.101)	(0.113)
75 to 79	−0.202**	−0.088	−0.305*	−603	−135	−438
	(0.094)	(0.071)	(0.165)
80 to 84	−0.334***	−0.252*	−0.355**	−1236	−437	−697
	(0.119)	(0.130)	(0.136)
85+	−0.27	0.048	−0.432**	−1893	115	−1988
	(0.190)	(0.204)	(0.198)
Sum of deaths (wgtd avg)	−0.2881
		−0.2152	−0.3463	−6562	−1977	−4296

Notes: Dependent variable is age-adjusted log death rate for the age group and gender indicated. Parameters are the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. Each cell is a separate regression. Controls include State and Year Fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Figure 1.

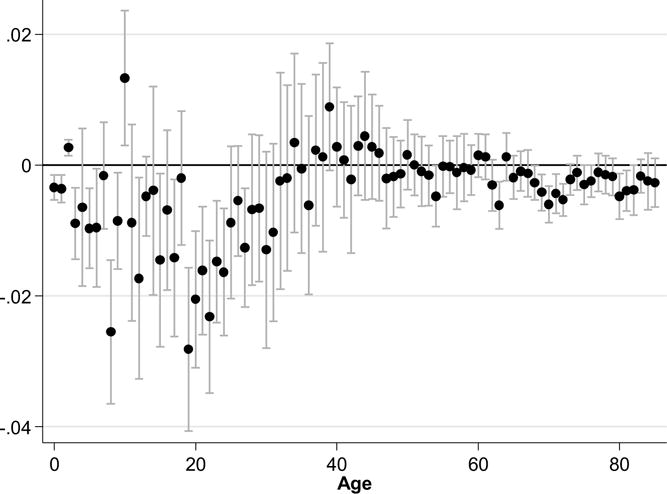
By-Age Semi-Elasticity of Mortality with Respect to Unemployment

Notes: Log-linear models estimated separately for each age. Controls include state and year fixed effects, state trends, and demographic and education variables. Bars give 95 percent confidence intervals. Standard Errors clustered on state.

The last three columns in Table 2 show the additional number of deaths generated by a 1 percent decrease in the unemployment rate, using as a base the number of deaths that occurred within each age and gender group in 2006.⁹ Echoing the results in Table 1, we see that, even though the coefficient estimates are largest among young people, young people are unlikely to have much impact on the cyclical behavior of fatalities overall because deaths among children and adolescents are rare. As in Table 1, we weight the age-specific coefficients by the number of deaths in each age group and see immediately that most business cycle induced deaths occur among those with relatively weak labor force attachment: fewer than 10 percent of the additional deaths occur among those between the ages of 25 and 64.¹⁰ In fact, we predict that improvements in the unemployment rate lead to more additional deaths among 0-4 year olds than among 30-50 year olds. In contrast, 70 percent of the additional deaths from a decline in the unemployment rate are among those over age 70. These results strongly suggest that the mechanisms at play must go beyond changes in individuals’ own work behavior.¹¹

Using the “additional deaths” metric makes clear that cyclical mortality is particularly strong among elderly women. The coefficient estimates are notably larger for elderly women than they are for men in the same age range: women age 65+ account for 57 percent of the roughly 6600 additional deaths (across all ages and genders) that are predicted to result from a 1 percentage point drop in unemployment. In contrast, only 14 percent of the additional deaths are among working age men and women. This result further emphasizes the likelihood that something other than changes in individuals’ own work behavior is generating pro-cyclical fluctuations in mortality.

The overall effect can also be decomposed by cause of death. Miller et al. (2009) have done this using an empirical strategy similar to ours and their analyses provide further evidence against the own-work-behavior hypothesis. Specifically, they document that cyclical deaths are concentrated among the elderly and are driven by cardiovascular deaths, respiratory deaths, degenerative brain diseases, and deaths due to infections. We have expanded on these results and improved the categorization of causes, reducing the number of deaths previously assigned to the “other” category. The new categorization is documented in Appendix B and Appendix Table A.2, and new by-age-and-cause estimates are presented in Appendix Table A.3. Our by cause estimates are similar to those reported in Miller et al. (2009).¹² As in that paper, none of the largest “by cause” contributors to cyclicality is obviously related to work or time use, which reinforces the need to look for alternative mechanisms.

One alternative explanation that is consistent with these patterns is that business cycle changes lead to changes in the quantity or quality of purchased health inputs, which in turn affect mortality rates. This process would be external to both individual work-related decisions and outcomes, and should be most salient among the elderly, who are relatively intensive users of health care. The remainder of this paper explores the viability of this potential mechanism, which we conclude may be critical.

II.B Relative Importance of “Own-Group” vs. “Other-Group” Employment Opportunities

In this section we estimate the importance of own versus other responses to the business cycle by looking at how mortality rates for different subgroups respond to variation in that subgroup’s unemployment rate relative to variation in other groups’ unemployment rates. If most of the mortality effect is driven by changes in “own” behaviors then a group’s own unemployment rate should have the strongest impact on that group’s mortality.¹³ To investigate this possibility we use the Current Population Survey (CPS) to calculate unemployment and employment rates for broad age/gender groups. We then re-estimate equation (1) separately for men and women who are 25-44 years old, 45-61 years old, and older than 62. By creating broadly defined age groups that correspond to different parts of individuals’ working lives, we are able to maintain sample sizes that are large enough to produce precisely estimated state-level labor market measures, while retaining the ability to distinguish whether it is one’s own group employment status that matters or that of other groups.¹⁴

The unemployment rate may not fully capture differences in employment status among the elderly, so for this part of the analysis, we replace the unemployment rate with the age-group-specific employment-to-population ratio. Thus, our expectation is that the estimated coefficient on the regressor of interest will be positive. To facilitate comparison with earlier results, the first row in each section of Table 3 shows estimated coefficients on the aggregate unemployment rate. The second row in each section substitutes the aggregate employment-to-population ratio, and the third set of rows for each group includes results from including the three age-specific employment-to-population ratios together in each regression.

Table 3.

Response of Mortality by Age and Gender to Group-Specific Employment-Population Rates

	Ages 25 to 44	Ages 45 to 61	Ages 62 and Over
Panel A: All Sexes
BLS Unemployment	−0.153	−0.0440	−0.309***
	(0.422)	(0.143)	(0.0807)
CPS Overall Emp/Pop	0.120	−0.0524	0.122**
	(0.258)	(0.0876)	(0.0580)
Emp/Pop Ages 25-44	−0.531**	−0.121	0.0746
	(0.242)	(0.0837)	(0.0452)
Emp/Pop Ages 45-61	0.464**	0.0639	0.0859**
	(0.174)	(0.0596)	(0.0379)
Emp/Pop Ages 62+	0.194	0.0807	0.00878
	(0.140)	(0.0556)	(0.0273)
Panel B: Men
BLS Unemployment	−0.346	0.0788	−0.190***
	(0.507)	(0.169)	(0.0634)
CPS Overall Emp/Pop	0.245	−0.192*	0.0705
	(0.314)	(0.111)	(0.0446)
Emp/Pop Ages 25-44	−0.0408	−0.112	0.0993**
	(0.226)	(0.0983)	(0.0379)
Emp/Pop Ages 45-61	0.170	−0.00708	0.0205
	(0.238)	(0.0569)	(0.0278)
Emp/Pop Ages 62+	0.0604	0.0334	−0.0123
	(0.129)	(0.0470)	(0.0193)
Panel C: Women
BLS Unemployment	0.320	−0.207*	−0.402***
	(0.324)	(0.122)	(0.118)
CPS Overall Emp/Pop	−0.179	0.152**	0.157*
	(0.219)	(0.0730)	(0.0845)
Emp/Pop Ages 25-44	−0.299	0.00792	0.00602
	(0.159)	(0.0665)	(0.0439)
Emp/Pop Ages 45-61	0.123	0.104**	0.0853*
	(0.113)	(0.0499)	(0.0437)
Emp/Pop Ages 62+	−0.00842	0.0395	0.0317
	(0.131)	(0.0668)	(0.0383)

Notes: Dependent variable is age-adjusted log death rate for the age group and gender indicated. Parameters are the estimated mortality semi-elasticity with respect to the state-year unemployment rate or employment-to-population ratio, with coefficients multiplied by 100. Each cell is a separate regression, except for the employment-to-population ratio divided by age group, in which all three are included in the same regression. The sample size is 1479. Controls include State and Year Fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Table 3 produces little support for the notion that an individual’s own group employment rate is driving cyclical fluctuations in mortality. Few of the own group employment coefficients are statistically significant, and most of the estimates on own group employment that are statistically significant are in the opposite direction of our population estimate.¹⁵ Only for women between the ages of 45 and 61 is the own group employment-to-population ratio significantly positively associated with mortality, and the coefficient is smaller than when we use the overall employment to population ratio. This may reflect the fact that, as we focus on narrower age and gender groups, we increase the likelihood of picking up reverse causality (poor individual health causing lower employment). Since the main purpose of this exercise is to refute the hypothesis that individual employment losses are leading to improvements in the same individuals’ health, the lack of systematically positive and statistically significant own-group results in Table 3 remains relevant. This could be either because the effect of the business cycle is operating through mechanisms external to the individuals directly experiencing employment changes, because of individual health affecting employment in the opposite direction, or both.

Note also that the employment rate among women 45 to 61 years old (a group likely to supply labor as paid caregivers) has a positive, statistically significant effect on older women’s death rates. We will return to this point when we discuss the potential role of the supply of health care providers. We also see that mortality fluctuations among the oldest group (over age 62 in this table) are primarily driven by employment changes among younger individuals. While the relationship between mortality among the older groups and employment measures of younger groups are not always statistically significant, they are always positive, and are statistically significant in three out of the six cases. This provides an important insight into our earlier finding that pro-cyclical mortality is mainly driven by the top end of the age distribution. It is not this critical group’s own employment status that drives the relationship, but rather the employment status of the younger groups.

We have conducted a similar analysis in which we further disaggregate by race (black or white), and then include age- and gender-specific employment rates both for one’s own racial group and the other racial group.¹⁶ Once again, we find that own group mortality is, if anything, negatively correlated with one’s own group employment rate (defined now by age, gender, and race). In only one case out of 18 is the estimated coefficient on own group employment positive and statistically significant.

II.C. Place of Death and Health Care Inputs

Given the evidence thus far that 1) mortality fluctuations over the business cycle are concentrated among the elderly, and 2) mortality fluctuations are not driven by “own” labor market opportunities, we devote the rest of our paper to exploring possible mechanisms that do not involve changes in individuals’ own employment status or time use. An obvious possibility is that variation in mortality rates is driven by cyclical changes in the quality, quantity or nature of health care inputs that are relatively heavily utilized by those over age 65. Previous studies have found evidence that employment in the health care sector is lower during expansions than during recessions. Goodman (2006), for example, estimates a strong negative correlation between changes in hospital employment and changes in aggregate employment and concludes that “… at times of peak U.S. hiring, when the labor shortage in hospitals may be particularly intense, hospitals with staffing shortages may face restrictions on the volume of business that can be performed at a particular time.”

Some of the most severe documented staffing constraints during good economic times involve relatively low-skilled staff. Low-skilled, direct care workers are distinct from the more skilled, professionalized health care workers that are often the focus of quality of care discussions. The Direct Care Alliance (Paulson 2011) reports (based on CPS tabulations) that direct care workers are nearly 90 percent female, and more than half have a high school education or less. The median hourly wage for these workers in 2009 was $10.58. Yamada (2002) notes that during the late 1990’s very low unemployment rates exacerbated already severe labor shortages for such direct care workers—nursing aides, home health workers, and other paraprofessional caregivers, and cites a study from the state of New York that suggests that between 70 to 90 percent of home health care agencies and nursing homes indicated shortages of direct care workers. If such shortages become particularly acute during good economic times, then we might expect higher mortality among the elderly to follow.¹⁷ Because nursing homes use large numbers of these relatively low-skilled, “direct-care” workers, such facilities may be particularly susceptible to this form of cyclicality.

The possibility of a role for direct care workers is particularly relevant given that cyclical mortality among older women appears to be greater than among older men (Table 2). Women tend to marry older men, and men have a shorter life expectancy than women, so older women are relatively more likely to have a market-based caregiver than are older men, and they are more likely to reside in nursing homes at the end of their lives (Murtaugh, Kimber, and Spillman 1990). Older men and older women may therefore be differentially affected by fluctuations in the quality of health care.

All of this suggests that changes in health care inputs over the business cycle might be part of the story. We explore this possibility by comparing mortality patterns in nursing homes to mortality patterns elsewhere, and by comparing estimated business cycle effects across states whose elderly have different types of living arrangements. We also look at how occupations that are typically associated with nursing home care vary with fluctuations in the economy.

Direct Evidence from Vital Statistics Place of Death Data

We begin by examining mortality patterns among individuals living in nursing homes using the place of death information that is provided by the Vital Statistics mortality files. We know that those residing in nursing homes are in direct contact with paid health care providers, and so this is a natural starting point for investigating this quality of care mechanism. Death certificates indicate whether the death occurred in a hospital, nursing home, residence, or other location. While this is only a weak proxy for where an individual was living prior to death (many nursing home residents will die in a hospital after being transferred there for an illness, for example), information on place of death is readily available in the Vital Statistics files and death in a nursing home is likely a strong indicator of substantial contact with paid caregivers.

The Vital Statistics place of death codes are available only starting in 1979 and, over the period we analyze, they have experienced two substantial changes. First, in 1989 death certificates were changed such that physicians no longer filled out an open-ended question regarding the deceased individual’s place of death. Instead, they began to fill out boxes indicating whether the death occurred in a hospital, residence or nursing home. For years prior to 1989, the categories listed in the Vital Statistics codebook include hospitals (and several subsets), “other institutions providing patient care”, and all other reported places. We assume that “other institutions providing care” are primarily nursing homes. Second, in 2003 the categories associated with the boxes were changed slightly. “Nursing home” was replaced by “nursing home/long-term care” and a separate category was added for deaths in a hospice. We have recoded the categories across years into: nursing homes, hospitals, and “other.” Appendix Figure A.2 shows the fraction of deaths occurring in each category by year and shows that these changes do not appear to have had an impact in the mortality-by- place-of-death time series. The timing of the coding changes does not appear to be associated with any breaks in any of the series.

Table 4 presents results based on data from 1979-2006 and 1979-2002. Our dependent variable is the age-adjusted mortality rate among those age 65 and over.¹⁸ When we use data covering the longer time period, the estimated impact of the unemployment rate on elderly mortality (−0.24) is similar to our main results. The cyclicality of deaths that occur in nursing homes is very large, negative, and statistically significant, with a coefficient of −4.69, which suggests that nursing home deaths may play an important role. When we drop deaths in nursing homes and focus on all other deaths (which comprise nearly 80 percent of deaths) the estimated coefficient on the unemployment rate is positive and statistically significant. Understanding the mechanisms that lead to counter-cyclical mortality among non-nursing home residents may be a promising area for future work, but it appears that nursing home deaths are more critical to understanding the pro-cyclical relationship that is the focus of this (and many other) studies. This fact suggests that the key mechanisms have little to do with work, time use, or health behaviors.

Table 4.

Effect of Unemployment Rate on Log Mortality by Place of Death: Nursing Homes vs. All Other

	1979-2006			1979-2002
	All	Men	Women	All	Men	Women
All places	−0.237***	−0.1433**	−0.3142**	−0.385***	−0.199***	−0.512***
	(0.082)	(0.071)	(0.122)	(0.062)	(0.071)	(0.098)
Nursing Homes	−4.688**	−4.644**	−4.725**	−5.820**	−5.892**	−5.756**
	(2.278)	(2.267)	(2.286)	(2.439)	(2.446)	(2.437)
Not Nursing Homes	0.615**	0.437*	0.801**	0.619*	0.518**	0.762*
	(0.303)	(0.261)	(0.365)	(0.316)	(0.256)	(0.390)
N=	1428	1428	1428	1224	1224	1224

Notes: Dependent variable is age-adjusted log death rate for the location and gender indicated. Parameters are the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. Each cell is a separate regression. The first three columns include the years 1979-2006, and the second three columns include only the years 1979-2002. Controls include state and year fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

In the next panel, as a robustness check, we drop the years after 2002, when the second change in the place of death code took place. Similar to earlier results, dropping the last four years of observations substantially increases the magnitude of the estimated coefficient for the full sample, to −.39. The estimate continues to be driven by deaths in nursing homes, where we observe a statistically significant coefficient estimate of −5.82. In contrast, among deaths taking place elsewhere, the estimated impact of the unemployment rate is positive, at 0.62 and statistically significant. This pattern holds for both men and women. Focusing on this shortened period gives relatively more weight to the late 1990s, when unemployment rates were particularly low and labor shortages within low-skilled health care occupations may have been particularly acute. Nevertheless, in both sample periods, nursing home deaths are associated with an estimated coefficient that is an order of magnitude larger than the coefficient that is estimated among deaths taking place elsewhere.

This finding motivates us to break down the estimates in Table 1, where we initially stratified by age and cause of death, even further. Limiting the sample to the years when we can observe place of death (dropping 1978) we repeat the analyses in Table 1, stratifying further by whether or not the death occurred in a nursing home. This yields coefficients almost identical to those in Table 4 (since very few motor vehicle deaths occur in nursing homes) Given the positive effect of the unemployment rate on non-elderly mortality outside of nursing homes, and small numbers of deaths in the non-elderly categories, this suggests that all of the aggregate coefficient can be explained by the cyclicality of elderly nursing home deaths.¹⁹

Finally, the potentially important role of nursing homes in driving pro-cyclical mortality raises the question of whether Medicaid funding changes over the business cycle could be a factor.²⁰ Our investigations find little to suggest that this is an important part of the puzzle. First, existing work suggests that Medicaid spending does not vary substantially over the business cycle (Kane, Orszag, and Gunter 2003).²¹ We have also explored the connection between the business cycle and several measures of Medicaid spending with data through the most recent recession, and similarly find little systematic variation in spending over the business cycle. In particular, we use data from 1999 through 2011 on both total Medicaid spending and Medicaid payments to skilled-nursing facilities and find no significant effect of the unemployment rate on either measure. A longer time series using total spending from 1981 through 2011 yields a similar result.

Interactions with Institutionalized Fraction of the Elderly

Because place of death is not a perfect indicator of where a person was living prior to death, we supplement our Vital Statistics analyses with a different approach that makes use of information on residence in institutional group quarters that is available in the Census. The Census does not report residence in nursing homes specifically, but it does indicate whether individuals are living in group quarters, which typically include military barracks, nursing homes, college dormitories and prisons. For individuals over age 65, it is likely that the vast majority of residents in group quarters are living in nursing homes.²² The fraction of older individuals who live in group quarters thus provides a reasonable approximation of the fraction of the elderly in each state who reside in nursing homes. If nursing home staffing or quality of care is an important component of cyclical mortality we should expect to see greater cyclicality in states with larger nursing home populations.

To investigate this possibility, we begin by using data from the 1980 Census to calculate the fraction of individuals over age 65 living in group quarters in each state.^23,24 In 1980, 2-4 percent of men, and 5-7 percent of women over age 65, lived in group quarters. This fraction rises sharply with age, with just 1 percent of those aged 65 to 74 living in group quarters, but more than 17 percent of those 85 and above in group quarters. The lower panel of Table 5 shows the extent to which these fractions vary across states. Going from the 25^th to the 75^th percentile of the distribution of (state-level) nursing home residence moves the fraction by one to two percentage points for both men and women.

Table 5.

Cyclicality of Mortality by Fraction Living in Nursing Homes

	Deaths Ages 65+ (age-adjusted)
	Women	Men
Unemployment Rate	−0.070	−0.079
	(0.176)	(0.097)
UER X percent Over 65 Living in Group Quarters	−5.306**	−2.737
	(1.833)	(2.539)
1980 Census measures of percent over 65 in group quarters
25th percentile state	0.053	0.032
median state	0.065	0.037
75th percentile state	0.076	0.046

Notes: Dependent variable is age-adjusted log death rate for persons aged 65 and older, for women (column 1) and men (column 2). Each parameter is the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100, which is allowed to vary by the share of individuals over 65 living in group quarters. The sample includes the years 1979-2006. Additional controls include state and year fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

In the top half of Table 5 we show what happens when we add to our main specification an interaction between the unemployment rate and the state’s fraction of women (or men) over age 65 living in group quarters. The dependent variable in these regressions is the log of the age-adjusted mortality rate for women (or men) over age 65.

Among women, the interaction between the unemployment rate and the fraction in group quarters is negative and statistically significant, suggesting that mortality’s pro-cyclical nature is stronger in states where larger fractions of the elderly reside in nursing homes. The estimate suggests that increasing the unemployment rate by 1 percentage point decreases mortality rates by 0.28 percent in a state whose nursing home population is at the 25^th percentile of the distribution and by 0.40 percent in a state at the 75^th percentile. For men, the estimated coefficient on the interaction term is smaller and not statistically significant, though the point estimate is consistent with a much stronger cyclical response in states with more nursing home residents. The estimated magnitudes for women are consistent with the estimates produced by our analyses using place of death from the mortality files. If we calculate an out-of-sample prediction (using the results from Table 5) of the implied coefficient on the unemployment rate for an area in which all elderly residents live in nursing homes, we predict that the effect of a one percentage point increase in the unemployment rate is comparable to the estimates in Table 4; between −3 and −5. We obtain very similar results when we use the fraction in group quarters in each state averaged over 1980, 1990, and 2000 for the interaction.

Finally, the interaction between the unemployment rate and the fraction in nursing homes also helps to explain the difference between elderly men and women shown in the lower rows of Table 2. Using the estimated coefficients on the unemployment rate and its interaction with the fraction in nursing homes in Table 5, evaluated at the gender-specific median fraction in nursing homes (also shown in Table 5), implies a total effect of the unemployment rate of −.42 for women, and −0.18 for men.

We have also repeated this exercise, using age-adjusted deaths among those ages 0 to 45 as the dependent variable. This specification relates mortality at younger ages to the fraction of elderly in nursing homes. We expect that the interaction terms will be be zero. Unfortunately, the placebo test is uninformative, with wide confidence intervals that contain both zero and meaningfully large effects.²⁵

In sum, both our Vital Statistics and Census analyses indicate that mortality fluctuations over the business cycle cannot be explained without focusing on the elderly, particularly elderly persons who reside in nursing homes. This raises further questions about why nursing home status influences cyclical variation. One explanation for this pattern could still center around the behavior of those directly experiencing employment changes over the cycle. Suppose that family members are on the margin between caring for an ailing parent themselves and moving that parent to a nursing home. In good economic times, these family members may be more likely to move a parent into a nursing home as a result of the high demands on, or market value of, their own time. If this is an important mechanism then low unemployment rates should be associated with greater flows into nursing homes, which might in turn increase the number of deaths through crowding, or through changes in the composition of nursing home residents. In other words, the business cycle may simply relocate elderly patients—and potential deaths—into nursing homes, possibly as the result of changes in the value of time of their family caregivers. If marginal nursing home entrants are sicker than the average nursing home resident, then the average health of nursing home residents will fall during good economic times, contributing to pro-cyclical movement in death rates.

We explore these possibilities using restricted-use data with state identifiers from the Health and Retirement Study (HRS), which allow us to examine how individual transitions into nursing homes are related to the state unemployment rate. Specifically, we use waves 1 through 8 of the HRS data, covering years 1992 through 2006, linked to state identifiers and state unemployment rates, and use a linear probability model to estimate the probability that an individual moves into a nursing home (logit hazard models yield similar results). The model controls for state, year, and single-year of age fixed-effects, state-level trends, and the same state-level demographic averages as our main regression models.²⁶ If caregivers’ own-employment and time use are behind the higher degree of cyclicality observed in nursing homes, we would expect to see a negative coefficient on the unemployment rate, particularly for less healthy subsets of the elderly population.

Table 6 summarizes these results, which do not support the idea that cyclicality in transitions into nursing homes (with high unemployment associated with fewer transitions into nursing homes) is a key part of the story. The first column shows a statistically significant increase in transitions into nursing homes when the unemployment rate is high. The estimated coefficient is positive and significantly different from zero, and suggests that a one percentage point increase in the unemployment rate raises the probability that an individual transitions to a nursing home by 0.3 percentage points, or roughly 20 percent of the baseline annual transition rate. In the remaining columns of the table we repeat this exercise for groups that may be considered less healthy: those with more than 2 diagnosed chronic conditions; those who could be considered either “frail elderly” due to a low BMI, or obese, and those reporting their health as fair or poor. None of these groups are more likely to enter nursing homes when economic times are good. If anything, transitions among less healthy groups exhibit even more counter-cyclicality than the overall population. We find no differences in the extent of cyclicality in these transitions by the amount of time or care the individual is receiving from family members.

Table 6.

Effects of Unemployment Rate on Probability of Transitioning to a Nursing Home

Prob (Transition to Nursing Home)	Full Sample	> 2 Chronic Conditions	BMI < 23	BMI > 30	Health Fair or Poor
Unemployment Rate Coefficient	0.327**	0.258**	0.654**	0.043	0.581**
	(0.141)	(0.127)	(0.301)	(0.154)	(0.251)
N	90768	53006	37657	32340	28335

Notes: Dependent variable is annual probability of transitioning into a nursing home. Regressions are estimated as linear probability models, using waves 1-8 of the Health and Retirement Survey, and restricted to respondents ages 65 and over. Coefficients are multiplied by 100. Additional controls include single year of age dummies, sex, state and year fixed-effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighted by HRS sample weights.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Two additional data sources similarly show little evidence that high unemployment is associated with less reallocation of the elderly into nursing homes. First, we use the fraction of those over age 65 living in group quarters in each state (as calculated for the analysis in Table 5) from the 1980, 1990, 2000 and 2010 Census files and regress those shares on unemployment rates, state and year fixed effects, and the set of controls used throughout in our mortality regressions. The coefficient on the unemployment rate on the share of the state’s elderly population in group quarters is always small and positive (consistent with the HRS results above), though it is never statistically significant. For men and women combined, the coefficient on the unemployment rate (times 100) is 0.045 (standard error 0.039), suggesting that a one percentage point increase in the unemployment rate would increase the share in nursing homes by roughly one percent. Evaluated at the mean this would imply an increase of roughly .048 to 0.0485. A primary concern here is whether a higher unemployment rate is associated with a reduction in the share living in nursing homes; even at the lower end of the confidence interval around the unemployment rate coefficient the implied reduction would be very small.

Finally, we have used data from 1995 to 2011(from http://www.cdc.gov/nchs/hus/contents2011.htm#trendtables) that provides state-level counts of the stock of current nursing home residents to examine whether the stock of patient counts change significantly over the business cycle. Here, we do find negative point estimates for the unemployment rate on occupancy rates and total patient counts, but they are not close to statistical significance (a t-statistic of 1.1). Because the time period after 1995 is one for which our main finding of pro-cyclical mortality is itself quite weak, we do not interpret this as evidence that reallocation of patients into nursing homes is driving our main results.

Since the number or type of nursing home residents are not changing in a way that could explain pro-cyclical nursing home mortality, we next turn to issues of staffing and quality of care within nursing homes. In the final section, we present evidence pointing to changes in nursing home staffing levels over the business cycle, which are consistent with counter-cyclical variation in the quality of care.

Evidence From Institution-level Measures of Health Care Labor Inputs

The patterns in our data could be generated by difficulties that nursing homes face with respect to hiring and retaining paid caregivers when the economy is strong. We are unable to look directly at how the quality of nursing home staff changes with the business cycle, but data from the Online Survey Certification and Reporting Database (OSCAR) allow us to estimate how the number of hospital and nursing home workers changes with the unemployment rate. OSCAR includes data on any institutional healthcare provider that is certified to provide services under Medicaid or Medicare. The dataset covers 97 percent of all hospital and skilled nursing facilities in the US, and contains detailed information on staffing levels.

We use these data to examine changes in skilled nursing facility staffing levels over the business cycle. Table 7 shows estimates of the relationship between the log of employment (or occupation-specific employment, including physicians, registered nurses and licensed practical nurses, certified aides, and “other”) in skilled nursing facilities and the unemployment rate. The estimates are produced by regressions that include either state-level fixed effects or provider-level fixed effects, along with state-specific trends. The regressions are weighted by the provider size, or by the total number of beds.²⁷

Table 7.

Cyclicality of Employment by Occupation: Skilled Nursing Facilities

	Total	Physicians	Nurses	Certified Aides	Other
With Facility FEs	3.8854*	1.6530	2.4686*	3.2187**	3.6527**
	(1.9464)	(2.7267)	(1.4333)	(1.3295)	(1.5501)
With State FEs	4.3484**	1.2928	2.8005**	3.7723**	4.3494**
	(1.9416)	(2.5562)	(1.3497)	(1.4110	(1.6594)
N	186945	56854	186651	183706	185974
Mean Employees per Facility	121	0.2	27	45	48

Notes: Dependent variable is log number of employees in category, as indicated at column heading. Each cell is a separate regression, with the first row including facility fixed effects, and the second row including state fixed effects. Each parameter is the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. The sample includes survey years from 1991-2008, and the data are taken from the Online Survey Certification and Reporting (OSCAR) Database from 1990 to 2006. Additional controls include state and year fixed effects, state-specific trends, demographic and education controls, as well as total number of beds in facility. Standard errors clustered at the state level. Estimates weighted by facility-level average of bed available over time period.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

We find that staffing levels in nursing homes rise during periods of high unemployment.²⁸ A one percentage point increase in the unemployment rate raises total full-time employment at skilled nursing facilities by approximately three percent. There is no statistically significant increase in the number of physicians, but there are significant increases in nurses, certified aides, and other occupations.²⁹ Because physicians are an extremely small part of total employment in nursing homes, the non-MD categories all rise by approximately the same amount as total employment; around 3 percent for a one percentage point increase in the unemployment rate. This is consistent with previous studies’ findings of chronic shortages of aides in nursing homes, particularly when the economy is strong. More specifically, and recently, Baughman (2013) shows that direct care workers in nursing homes have longer employment spells when the unemployment rate is high.

While these estimated effects are statistically significant, their substantive importance for health care quality and, potentially, mortality, is less clear. In order to gauge this, we combine our findings with estimates from the literature on the relationship between nursing home staffing and residential outcomes produced by two quasi-experimental studies. Tong (2011) uses a regulatory change in California to examine the relationship between nursing staff and nursing home mortality, and finds that the increase in certified nurse assistants (CNAs) that resulted from the new staffing regulation was 0.26 hours per resident-day (compared to a baseline level of 1.987 hours per resident-day), and that this was accompanied by a decrease in patient mortality of 4.6 percent. If we interpret this reduction in mortality as coming solely through the CNA channel, this implies an elasticity of −0.35.³⁰ When this mortality-staffing elasticity is combined with the estimated staffing-business cycle elasticity from Table 7 (approximately equal to 3), we predict that a 1 percentage point increase in the unemployment rate will lead to a 1 percent reduction in mortality. This elasticity would suggest that approximately 2/9^th of the total mortality effect shown in Table 4 could be due to the counter-cyclical nature of nursing home staffing.

Extrapolating from a study by Konetzka, Stearns, and Park (2008), who use a facility fixed effects model to estimate the impact of nurse and nurse assistant staffing on the incidence of bed sores and urinary tract infections, produces even higher estimates. Their elasticity estimates are −1.3 (bed sores) and −0.9 (urinary tract infections), and these estimates become larger when they instrument for staffing levels with a variable that captures the introduction of a prospective payment system. If we take Konetzka, Stearns and Park’s elasticity estimates as rough proxies for the impact of staffing on mortality rates (a strong assumption), and combine them with our estimates of the relationship between staffing and unemployment rates, the resulting estimate suggests that the entire correlation between mortality and unemployment could be driven by cyclical fluctuations in the number of nursing staff. It is also possible, of course, that the elasticity of mortality in this setting could be quite different than Konetzka, Stearns, and Park’s estimates for bedsores and infections. Nevertheless, existing evidence suggests that the magnitude of cyclical changes in nursing home staffing that we find could play a substantively important role in explaining cyclical movements in mortality.

To supplement our OSCAR analysis we have also used the CPS to construct measures of employment, and employee characteristics, for several health care occupations. Specifically, we construct measures of the fraction of the population in each state-year cell who are MDs, Nurses (which can be further divided into registered nurses (RNs) and licensed practical nurses (LPNs), and Aides (also divided into Health Aides and Nursing Aides).³¹ For occupations other than MD, where there may be some flexibility in the level of education required, we also calculate the fraction of each occupation with particular levels of education. Unfortunately, in 2003 there are changes in the occupational coding of some of the key health care occupation categories. As a result, this analysis only includes years 1983 through 2002.

We use these measures to examine how the employment in these occupations fluctuates with the business cycle. Specifically, we regress the fraction of employment in each of these occupations on a set of state and year fixed effects, state-specific trends, and the same set of state-year demographic controls that are included in our main analyses. The results of this exercise, summarized in Table 8, confirm that employment in low-skilled health occupations moves counter-cyclically. Each row of Table 8 shows results from a separate regression in which the dependent variable is the fraction of a state’s employment in a given occupation. This dependent variable is different from that used in our OSCAR analyses because it captures employment in the given occupation across all types of employers (not only nursing homes). Also unlike our OSCAR analyses, occupational categorization in the CPS is determined by workers rather than employers. The CPS regressions are also based on a different set of years (1983-2002 instead of 1990-2006).

Table 8.

Effects of the Unemployment Rate of Employed in Health Occupations

Occupation	Mean	Coefficient on
	Fraction of State	Unemployment
	in Occupation	Rate (×100)
MDs	0.0032	−0.015***
		(0.005)
LPNs	0.0022	−0.007**
		(0.003)
RNs	0.0094	−0.002
		(0.010)
Nursing Aides	0.0093	0.018**
		(0.007)
Health Aides	0.0020	−0.003
		(0.004)

Notes: Dependent variable is share of individuals in a state employed in an occupation, indicated in the left column. Each row is a separate regression. Parameters are effect of state-year unemployment rate on fraction of state-year employment in the given occupation. Controls include state and year fixed effects, state-specific trends, demographic and education controls. Standard errors clustered at the state level. Estimates weighed by population. Data for fraction in occupations from monthly Current Population Survey, 1983-2002.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

The first rows of Table 8 show results for the fraction employed as doctors and nurses. The estimates provide evidence that employment in these more skilled occupations is pro-cyclical. In the lower rows of the table we show results for health and nursing aides. We find evidence that nursing aides exhibit counter-cyclical patterns; for all aides combined (not shown) and nursing aides, a higher unemployment rate is associated with a statistically significant increase in employment. A one percentage point increase in the unemployment rate raises the fraction of employment in the nursing aide occupation by more than 1 percent. This is consistent with work by Baughman and Smith (2012) who show that direct care workers are likely to exit direct care employment jobs by leaving the health care sector, and by Baughman (2013) who documents the increased likelihood of exit from direct care employment in nursing homes during booms. Our finding that aides exhibit countercyclical employment is consistent with our earlier evidence on nursing home deaths, since nursing aides are heavily concentrated in skilled nursing facilities (GAO, 2001).³²

It is important to acknowledge there could be mechanisms other than changes in the level of staffing that explain why nursing home deaths are particularly sensitive to the business cycle. One possibility that is related to, but distinct from, changes in the number of staff is that during booms there are increases in staff turnover. There is a substantial literature suggesting an association between rates of turnover among nurses and nursing aides and quality of care, patient-care errors, and appropriate transfer to hospitals.³³ While these studies typically do not convincingly establish causality running from turnover to outcomes, it does suggest that stability of staffing may also be important.

Finally, mechanisms which involve interactions between nursing home residency and cyclical changes in time use of family caregivers have not been definitively ruled out. We note, however, that recent evidence suggests a relatively small response in time spent caring for other adults—which could include elderly parents or other relatives—when work hours fall over the course of a recession. Aguiar, Hurst, and Karabarbounis (2013) show that approximately four percent of the reduction in market work during a recession is replaced with increases in time spent caring for other adults. A related possibility is that reductions in visits by friends and family members when the economy is strong could affect the well-being of nursing home residents. This could occur either because fewer visits mean that problems with care are less likely to be corrected (which would likely interact with reduced staffing), or because nursing home residents are more depressed or anxious in the absence of regular visits from family.

III. Conclusion

This study provides strong evidence that mortality’s pro-cyclical nature is not driven by changes in health related behaviors that are related to individuals’ own labor market opportunities. We motivate our approach by showing that variation over the business cycle is mainly driven by non-motor vehicle related deaths among the elderly. Motor vehicle accidents account for just 18 percent of all cyclically induced deaths, and cyclical variation in non-elderly mortality due to other causes explains a very small fraction of the overall variation. We also estimate effects separately by demographic group and find that own-group labor market indicators are not systematically related to that group’s mortality.

These findings motivate us to investigate explanations that are likely to be most salient for the elderly population. We find three pieces of evidence in support of the hypothesis that cyclical changes in the quality of health care contribute to pro-cyclical variation in the elderly mortality rate. First, we show that, relative to other places of death, deaths occurring in nursing homes are particularly responsive to the state unemployment rate. Second, we show that mortality is more pro-cyclical in states with a higher fraction of nursing home residents. We also show that these findings are not explained by additional flows into nursing homes when the economy is strong–a possibility that would be consistent with cyclically induced increases in family caregivers’ opportunity cost of time. In fact, transitions into nursing homes appear to be negatively related to the state of the economy. Finally, we show that employment levels in skilled nursing facilities show statistically significant declines when the unemployment rate falls, findings that are corroborated when we look at occupation data in the CPS.

Taken together, our analyses suggest that the mechanisms driving pro-cyclical mortality have little to do with individual level behavioral changes in time use over the business cycle. Instead, we provide new evidence that staffing difficulties among relatively low-skilled nursing occupations may be an important focus for efforts to improve the quality of health care. In addition, our findings help to resolve the tension in the literature between studies based on aggregate data (generally at the state level), which document a negative relationship between mortality and unemployment, and studies based on individual data, which find that job loss reduces individuals’ health.

As was noted in the introduction, the simplest explanation for the apparent conflict between individual level and aggregate studies is that studies based on aggregate data are picking up deaths among individuals who do not themselves change hours or employment status as the result of the recession. Consistent with this explanation, we find that deaths among the elderly –who are unlikely to be attached to the labor force–play a central role. We also find that many of these cyclically induced deaths take place in nursing homes. The fact that overall mortality falls during recessions may not, therefore, be driven primarily by improvements in the health behaviors of working age adults, but rather by the sensitivity of elderly mortality to purchased health care inputs that become relatively more abundant when labor markets for low-skilled workers are weak.

Pro-cyclical mortality remains a well-established but puzzling pattern in the U.S. (and elsewhere). In this paper we shed light on this pattern by proposing and testing hypotheses that relate to groups with very low labor force attachment, and we find that the proposed mechanisms are very important. Our findings go a long way toward clarifying why the overall mortality rate varies contemporaneously with the business cycle. As Coile, Levine, and McKnight (2014) have shown recently, broader patterns of mortality in response to bad economic times may vary across age groups, across different lag periods, and across interactions of these two factors. Future work should explore these interactions, keeping in mind a potentially important role for changes in health care inputs and quality.

Appendix A – Details on the Differences between Ruhm’s Analysis and Ours

We began by replicating Ruhm’s analysis with his own data which he generously shared with us. The basic regression equation takes the following form:

$$H_{jt}={\alpha }_t+X_{jt}\beta +E_{jt}\gamma +S_j+S_{j}T+{\epsilon }_{jt}$$ (1)

where H is the natural log of the mortality rate in state j and year t, E is a measure of the state’s economic health (usually the state unemployment rate), X is a vector of demographic controls including the fraction of the population who are: less than five years old, greater than 65 years old, high school dropouts, with some college, college graduates, black and Hispanic. Most of Ruhm’s control variables come from the Census decadal counts and are interpolated in between Census years. The vector of year specific fixed effects, ${\alpha }_t$, captures national time effects, and the vector of state specific indicator variables, $S_j$, controls for time-invariant state characteristics. State-specific time trends are also included. State unemployment rates are taken from unpublished statistics put together by the Bureau of Labor Statistics, and mortality rates come from Vital Statistics publications. Ruhm’s analysis is based on data from 1972-1991.

Our replication results are presented in the first column of Table A.1. We present estimates produced by both unweighted regressions and regressions weighted by state-year population,³⁴ although we find that weighting makes little difference in the magnitude of the estimated coefficient on the state unemployment rate, which is between −0.0054 and −0.0056. The estimates, which are nearly identical to Ruhm’s, suggest that a one percentage point increase in the unemployment rate is associated with a 0.5 percent decrease in the predicted death rate.

In order to investigate the potential mechanisms behind pro-cyclical mortality, we exploit both new data sources and additional years of data. The remaining columns of Table A.1 show what happens to the estimated relationship between mortality and unemployment as we systematically make these changes. Column 2 shows what happens when we continue to use Ruhm’s data but eliminate years between 1972 and 1977. Ultimately, we want to extend our analysis through 2006 so that we can include more recent business cycles in our analysis, but we do not have a consistent measure of the unemployment rate between 1972 and years beyond 2000. Instead, we pool monthly CPS files (January-December) to construct employment and unemployment rates by state and demographic group between 1978 and 2006 (estimates for all states prior to 1978 are not available in the CPS). Here, we show that eliminating the first six years of Ruhm’s data has little impact on the estimated coefficient; the estimated effect of a one percentage point rise in the unemployment rate continues to be approximately −0.005.

Column 3 shows how the estimates change when we replace Ruhm’s mortality rate variable with a “new and improved” measure of the mortality rate whose numerator is based on death counts from Vital Statistics’ micro-record “multiple cause of death” files and whose denominator comes from population counts collected by the National Cancer Institute’s Surveillance Epidemiology and End Results (Cancer-SEER) program. The “multiple cause of death” data are less aggregated than the Vital Statistics data Ruhm uses, and this will later allow us to construct state-level death counts by narrowly defined age groups. We replace Ruhm’s population estimates with the Cancer-SEER population counts because the Cancer-SEER estimates are based on an algorithm that incorporates information from Vital statistics, IRS migration files and the Social Security database. As such, they are likely to be more accurate than population estimates that are interpolated between Census years. Changing the dependent variable reduces the estimated unemployment effect by about 20 percent (from −0.005 to −0.004), but it continues to be strongly statistically significant. Most of this change is driven by the change in the population denominator.

In the fourth column of Table A.1, we replace Ruhm’s unemployment variable with the CPS unemployment rate. We also replace some of Ruhm’s control variables, which are interpolated between census years, with state-year measures of the same variables calculated from the CPS data. We add in a richer set of covariates to control of the state’s age distribution. These changes have little effect on the estimated unemployment effect when the regressions are weighted, although they do increase the magnitude of the estimate in the unweighted regressions from −.004 to −.005.

Next, we extend the data through 2006 (column 5). We find that adding fifteen years of data cuts the estimated coefficient on the unemployment rate in half: the new coefficient estimate is between −0.002 (weighted) and −0.003 (unweighted), which suggests that the overall effect of the business cycle on mortality may not be as large as previously thought. On the other hand, the smaller coefficient estimates may also result from other important changes that have occurred over the past fifteen years. In particular, there have been remarkable increases in longevity —between 1978 and 2006, for example, the fraction of Americans over age 65 grew from 11 to 12.5 percent. If this shift in the age distribution occurred unevenly across states, then, given the tight correlation between mortality and age, controlling for these shifts could prove to be very important. Indeed, the age structure in different parts of the country has evolved quite differently over this time period. In California, the fraction of individuals over age 65 increased by less than a percentage point, from 10.0 to 10.8 percent, but in Michigan the fraction of residents over age 65 increased by 3 percentage points, from 9.5 to 12.5 percent.

Age adjustment of mortality rates in this setting is likely to be very important since both mortality and the unemployment rate can vary systematically with age. Consider a hypothetical example in which there are just two age groups—young and old. Mortality is high for the old and low for the young; unemployment is high for the young and low for the old. Over time, an increase in the fraction of a state’s population that is old will, all else constant, raise the mortality rate and lower the unemployment rate. Because the core of this study relates state-specific changes in unemployment and mortality, it is crucial to control as fully as possible for changes in the age distribution.

We control for this phenomenon by replacing the dependent variable with the log of an age-adjusted mortality rate. Consider the mortality rate for state j in a given year t, and note that it can be written as the sum of each age-specific mortality rate weighted by the fraction of individuals in each age interval

$$M{R}_{jt}={\displaystyle \sum }_{a=0}^{85+}M{R}_{\mathit{ajt}}{f}_{\mathit{ajt}}$$

In order to abstract from within state-year changes in f_ajt, we replace the variable with the 1990 nationwide fraction of individuals in each age category, f_a-US-1990. This creates a measure of the state-year mortality rate that holds the age distribution constant and is defined only by the state-year cell’s relative number of deaths. Returning to the hypothetical examples above, this procedure, by removing the movement in mortality over time driven by changes in the fraction old in a state, will avoid the possibility of a spurious correlation between mortality and unemployment.

Figure A.1, which plots our age-adjusted and unadjusted mortality rates over time, suggests the potential importance of this adjustment; because the U.S. population is aging, the unadjusted series appears to be relatively flat, while the age-adjusted series shows a fairly dramatic decline over time.

Replacing the unadjusted mortality variable with an age adjusted mortality rate turns out to have important effects on our estimates in the top row. In column 6, the estimated coefficient on the unemployment rate moves back up to −0.0033. State-specific shifts in the age distribution are clearly correlated with state-level unemployment movements over this period. Note that the need to age-adjust our dependent variable is directly related to our inclusion of additional years of data, which creates a longer period over which states’ age distributions can evolve differentially. If we age adjust the mortality rate and repeat the analysis only for the years 1978 through 1991, the estimated unemployment coefficient only moves from −0.0038 to −0.0043 (not shown).³⁵ Finally, we note that an alternative to age adjustment is to include even more detailed controls for the age distribution in the state. We have re-estimated the results in Column 5 using the unadjusted mortality, but adding controls for the fraction of the state population in every single year of age category. This produces an estimated effect of the unemployment rate of −.030 (standard error of .009), very close to the coefficient using age adjusted mortality of −0.033.

Taken as a whole, our changes have a limited impact on the estimated association between macroeconomic fluctuations and health. Consistent with Ruhm’s earlier studies, every entry in Table A.1 is negative, statistically significant, and of substantive magnitude. In the main body of the paper we focus on weighted regressions in which the dependent variable is the age adjusted mortality rate.

Figure A.1.

Crude and Age-Adjusted Death Rates, 1970-2006

Notes: Shaded areas are recessions

Appendix Figure A.2.

Deaths by Type of Place as a Fraction of all deaths

Notes: The two vertical lines denote when place of death codes were changed.

Appendix Table A.1.

Replication of Ruhm (2000) estimates, Different Specifications and years

Mortality Measure	Ruhm	Ruhm	Ours	Ours	Ours	Age-adjusted mortality	Unadjusted mortality
Controls	Ruhm	Ruhm	Ruhm	Ours	Ours	Ours	Ours, Detailed Age Controls
Years	1972-1991	78-91	78-91	78-91	78-06	78-06	78-06
Weight by Population
URate	−0.54***	−0.4827***	−0.3766***	−0.3994*	−0.1908*	−0.329**	−0.3019***
	(0.0975)	(0.1036)	(0.0713)	(0.0808)	(0.0957)	(0.0997)	(0.0851)
Unweighted
URate	−0.5609***	−0.5334***	−0.404***	−0.5195***	−0.2839***	−0.373***	−0.3088***
	(0.0899)	(0.0998)	(0.0774)	(0.0995)	(0.0796)	(0.0741)	(0.0834)
Year-Varying Population Weights
URate	−0.535***	−0.4725***	−0.3707***	−0.3981***	−0.2087**	−0.352***	−0.3213***
	(0.0971)	(0.1035)	(0.0711)	(0.0815)	(0.0934)	(0.0975)	(0.0829)
Weight by Population: Subgroups
Women
URate				−0.3447***	−0.2274*	−0.4019***	−0.3141***
				(0.0820)	(0.0912)	(0.1113)	(0.0826)
Men
URate				−0.4395***	−0.1283	−0.2446**	−0.2415**
				(0.0913)	(0.1127)	(0.1054)	(0.0995)
Women 65+
URate				−0.4321***	−0.2295**	−0.4093***	−0.3236***
				(0.0924)	(0.0987)	(0.1204)	(0.0780)
Men 65+
URate				−0.354***	−0.028	−0.1809***	−0.1565**
				(0.0927)	(0.0828)	(0.0637)	(0.0682)

Notes: Dependent variable is log death rate. In columns 1 and 2, the log death rate is calculated using Ruhm’s estimates; in columns 3-5 and 7, it is our own calculations. In column 6, the death rate is age-adjusted (described in text). Each cell is a separate regression, with specifications or outcome variable varying according to the panel heading. Each parameter is the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. The time period of each sample is listed at the head of the column. Our RHS variables include the fraction of the state population who are: less than five years old, greater than 65 years old, high school dropouts, with some college, college graduates, black and Hispanic, taken from annual CPS files. Ruhm’s control variables are similar, but based on interpolations between Census years. Column 7 includes detailed age controls, which are share of _____. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Appendix Table A.2.

Classification of ICD Recodes into Cause of Death Categories

	Cause of Death	Recodes	Raw codes reclassified from “other
1	Cardiovascular	ICD8: 310,320,330,350,360,370,380,390,400,410,430,440,450,460,470,480 ICD9: 320,330,340,360,370,380,390,400,410,420,440,450,460,470,480,490 ICD10: 55,56,57,59,60,62,63,65,66,67,68,69,70,71,73,74,75	ICD8: 7824
2	Cancer	ICD8:150,160,170,180,190,200,210, 220,230,240 ICD9: 160,170,180,190,200, 210,220,230,240,250 ICD10: 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 38, 39, 40, 41, 42, 43, 44
3	Respiratory	ICD8:490,510,520,540,550,560 ICD9: 500,520,530,550,560,570,580 ICD10: 77,78,80,81,83,84,85,86, 87,88,89	ICD8: 450, 510, 5112, 512, 513, 514, 5150, 5151, 5159, 517, 518, 5190, 5191, 5192, 5193, 5199 ICD9: 500, 501, 5070, 5109, 5119, 512, 5130, 514, 515, 5168, 5183, 5184, 5185, 5188, 5191, 5198, 7991 ICD10: R092
4	Infections and immune deficiency	ICD8:10,20,40,50,60,70,80,90,100, 110,120,130,280 ICD9: 10,20,40,50,60,70,80,90,100, 110,120,130,140,290 ICD10: 1,2,3,5,6,7,8,9,10,11,13, 14,15, 16,17,18,50	ICD8:5990 ICD9: 2791,2793,5990 ICD10: D849,N390
5	Degenerative brain diseases	ICD10: 51,52	ICD8: 2900, 2901, 299, 3049, 3099, 323, 3304, 340, 341, 342, 3439, 3441, 3449, 3451, 3452, 3459, 3471, 3479, 794, 7330 ICD9: 2900, 2901, 2902, 2904, 2949, 2989, 3109, 311, 319, 3239, 3310, 3314, 3319, 3320, 3352, 340, 3419, 7855, 797, 3440, 3451, 3453, 3459, 3481, 3483, 3485, 3489, 3568, 3580 ICD10: F019, F03, F069, F109, F179, F329, F79, G122, G319, G35, G409, G419, G459, G700, G809, G825, G919, R54, R628, G934, M349
6	Kidney and urethra	ICD8:630,640,650 ICD9: 650,660,670,680 ICD10: 98,99,100,101,102	ICD8:465,592,5931,5932,595,5999,792 ICD9: 5920,5939,5996 N289
7	Nutrition-Related	ICD8:250,260,270 ICD9: 260,270,280 ICD10: 45,46,48,49	ICD8:277 ICD9: 2720,2724,2780 ICD10: E668,E669,E780,E785
8	Motor Vehicle Accidents	ICD8:770 ICD9: 800 ICD10: 114
9	Other Accidents	ICD8:780 ICD9: 810 ICD10: 115,116,118,119,120, 121, 122, 123
10	Suicides	ICD8:790 ICD9: 820 ICD10: 125,126
11	Homicides	ICD8:800 ICD9: 830 ICD10: 128,129,130
12	Other, Unspecified and ill-defined	ICD8:Remainder of 740,750 ICD9: Remainder of 770,780 ICD10: Remainder of 110,111
13	Misc: Birth defects; diseases of blood/bone/gastrointestinal/metabolic/Sautoimmune; drug abuse; and other external	ICD8:570,580,590,600,610,660,680,690,700,720,730,810 ICD9: 590,600,610,620,630,690,710,720,730,750,760,840 ICD10: 90,91,92,94,95,96,103,104,106,107,108,109,132,133,134,135	ICD8: 251, 2730, 274, 276, 279, 2869, 2871, 288, 2910, 3032, 3039, 3310, 4510, 4519, 453, 4549, 4560, 4589, 5301, 5304, 5309, 5340, 535, 5379, 5621, 5630, 5631, 5670, 5679, 5693, 5694, 5699, 570, 5730, 5739, 5760, 5769, 5770, 7123, 7130, 715 ICD9: 2733, 2762, 2765, 2769, 2770, 2773, 2779, 2866, 2869, 2873, 2875, 2880, 2898, 303, 3049, 3050, 3059, 3334, 3591, 4512, 4519, 4560, 4589, 4590, 4599, 5301, 5303, 5305, 5559, 556, 5570, 5571, 5579, 558, 5621, 5672, 5679, 5698, 570, 5722, 5724, 5728, 5733, 5739, 5761, 5770, 5771, 5789, 7140, 7330, 7373 ICD10: D65, D689, D696, D70, D869, E854, E859, E86, E870, E872, E875, E878, E889, F101, F102, F141, F191, F192, G10, K222, K224, K509, K529, K550, K559, K562, K566, K572, K578, K579, K631, K639, K650, K659, K729, K759, K760, K767, K830, K85, K860, K861, K922, M069, M321, M819, M869

Appendix Table A.3.

Effects of Unemployment on Mortality by Age and Cause and Additional Deaths

	Coefficients on Unemployment Rate				Additional deaths from 1 percent Increase in Unemployment Rate
	Age Group				Age Group
Cause of Death	All	0 to 24	25-64	65+	All	0-24	25-64	65+
Cardiovascular	−0.0035**	−0.0023	−0.0007	−0.0037**	−2905	−6	−110	−2504
	(0.0011)	(0.0042)	(0.0014)	(0.0012)
Cancer	0.0026***	0.0017	0.0020*	0.0027***	1488	5	351	1096
	(0.0006)	(0.0042)	(0.0011)	(0.0007)
Respiratory	−0.0085***	−0.0228**	−0.0104***	−0.0064**	−1939	−40	−318	−1248
	(0.0028)	(0.0096)	(0.0036)	(0.0031)
Infections & Immune Deficiencies	−0.0058	−0.0181**	−0.0190	−0.0091***	−478	−27	−543	−477
	(0.0061)	(0.0079)	(0.0154)	(0.0029)
Degenerative Brain Diseases	−0.0090***	−0.0005	−0.0058*	−0.0073*	−1793	−1	−69	−1353
	(0.0032)	(0.0122)	(0.0034)	(0.0041)
Kidney	−0.0092**	−0.0101	−0.0080	−0.0088*	−430	−3	−65	−335
	(0.0045)	(0.0128)	(0.0060)	(0.0044)
Nutrition Related	−0.0012	−0.0074	−0.0012	−0.0011	−112	−3	−32	−68
	(0.0043)	(0.0122)	(0.0050)	(0.0048)
MVA	−0.0254***	−0.0275***	−0.0254***	−0.0220***	−1149	−360	−640	−155
	(0.0055)	(0.0052)	(0.0062)	(0.0061)
Other Accidents	−0.0083**	−0.0163***	−0.0033	−0.0091	−634	−133	−128	−270
	(0.0038)	(0.0043)	(0.0067)	(0.0056)
Suicide	0.0137**	−0.0005	0.0188***	0.0097	455	−2	444	51
	(0.0055)	(0.0074)	(0.0061)	(0.0058)
Homocide	−0.0088	−0.0155*	−0.0073	0.0110	−167	−107	−82	9
	(0.0079)	(0.0076)	(0.0090)	(0.0089)
VS “Other”	−0.0176**	−0.0484***	−0.0297**	−0.0049	−1194	−320	−606	−199
	(0.0083)	(0.0064)	(0.0130)	(0.0083)
Residual	−0.0054*	−0.0052	−0.0090	−0.0016	−725	−126	−430	−100
	(0.0031)	(0.0033)	(0.0065)	(0.0021)

Notes: Dependent variable is log age-adjusted death rate for a given cause listed in each row. Each column is a different age group, indicated at column head. Each cell is a separate regression, and each parameter is the estimated mortality semi-elasticity with respect to the state-year unemployment rate, with coefficients multiplied by 100. Controls include state and year fixed effects, state-specific trends, demographic and education controls. The columns to the right of the table estimate the number of deaths averted (or caused) by a 1 percent increase in the unemployment rate, based on the number of deaths in each age-group and category in 2006. The sample includes the years 1978-2006. Standard errors clustered at the state level. Estimates weighted by state-year population of relevant age group.

^***Significant at the 1 percent level.

^**Significant at the 5 percent level.

^*Significant at the 10 percent level

Appendix B – Mortality classifications

We grouped causes of death into 13 categories according to codes and recodes published by the Center for Disease Control for each version of the International Classification of Diseases (ICD). More about the ICD can be found at http://en.wikipedia.org/wiki/International Statistical Classification of Diseases and Related Health Problems. We used the ICD-8, ICD-9 and ICD-10, which correspond to the years 1968-1978, 1979-1998 and 1999-2004. The ICD groups reported causes of death into categories called “recodes.” Within a given year, there are several different sets of re-codes. For example, the 1990 data include a 272 cause recode, a 72 cause recode and a 61-cause recode. For deaths occurring in 1968-1978 we use the ICD-8 69-cause recode. We use the ICD-9 72-cause recode for deaths occurring in 1979-1998, and the ICD-10 113-cause recode for deaths occurring in 1999-2004. Column 2 of Appendix Table A.2 shows how we assigned each re-code category into our 13 causes of death groups.

There are some causes of death which the CDC recodes as "other and unspecified" but which seemed to fit our categories. For example, in the ICD8 years, code 782.4 was classified as “other” by the 69-cause recode. Further investigation of this recode, however, made clear that this “other” category was related to cardiovascular deaths, so we reclassified all deaths that had been assigned the 782.4 code as cardiovascular deaths. The third column of Appendix Table A.2 shows which “other” recodes in the ICD were reclassified into each of our 13 causes of death groups.