A model for postzygotic mosaicisms quantifies the allele fraction drift, mutation rate, and contribution to de novo mutations

Abstract

The allele fraction (AF) distribution, occurrence rate, and evolutionary contribution of postzygotic single-nucleotide mosaicisms (pSNMs) remain largely unknown. In this study, we developed a mathematical model to describe the accumulation and AF drift of pSNMs during the development of multicellular organisms. By applying the model, we quantitatively analyzed two large-scale data sets of pSNMs identified from human genomes. We found that the postzygotic mutation rate per cell division during early embryogenesis, especially during the first cell division, was higher than the average mutation rate in either male or female gametes. We estimated that the stochastic cell death rate per cell cleavage during human embryogenesis was ∼5%, and parental pSNMs occurring during the first three cell divisions contributed to ∼10% of the de novo mutations observed in children. We further demonstrated that the genomic profiles of pSNMs could be used to measure the divergence distance between tissues. Our results highlight the importance of pSNMs in estimating recurrence risk and clarified the quantitative relationship between postzygotic and de novo mutations.

Postzygotic mosaicism describes individuals who developed from a single zygote but consist of multiple cell populations with different genotypes (Strachan and Read 1999). The mosaicism arises due to postzygotic errors in DNA replication (De 2011; Lupski 2013) and can lead to disease states in the mosaic carriers (Poduri et al. 2013; Priest et al. 2016; Terracciano et al. 2016), or in the heterozygous offspring inheriting the mutant allele (Dal et al. 2014; Huang et al. 2014; Acuna-Hidalgo et al. 2015; Dou et al. 2017), and contribute to the recurrent risk of genetic disorders in children (Depienne et al. 2010; Xu et al. 2015; Takahashi et al. 2017). With the recent development of deep sequencing technology, a small number of studies reported the genomic pattern of postzygotic single-nucleotide mosaicisms (pSNMs) in noncancerous human samples (Huang et al. 2014, 2018; Dou et al. 2017; Ju et al. 2017), and this has enabled the quantitative analysis of pSNMs during the normal developmental process.

Compared to germline mutations, the minor allele fraction (AF) of postzygotic mosaicisms should deviate from 50%. Since mosaicisms with varied AFs have different impacts on transmission probability and disease penetrance (Bernkopf et al. 2017; Kono et al. 2017), it is important to quantify the AF distribution of mosaicisms. Campbell et al. (2014) developed a Galton-Watson process model to predict the recurrence risk of de novo mutation with potential parental mosaicism, by considering both the cell division rate and mutation rate. However, with the limited data at that time, they assumed a constant mutation rate and only quantified the mean and variance of the AF distribution. More recently, Ju et al. (2017) reported the AF distribution of postzygotic mosaicisms in blood samples from patients with breast cancer and estimated an approximately 2:1 asymmetric contribution of daughter cells during early embryogenesis. However, they assumed the same deterministic bifurcating lineage tree for every embryo, which might be unrealistic due to the occurrence of cell death and variations in cell number in human preimplantation embryos (Hardy et al. 1989, 2001; Mottla et al. 1995). As such, the shape of the AF distribution has not been properly investigated with consideration of the cell death rate during stochastic embryogenesis nor the quantification of the mutation rate of pSNMs and the contribution to de novo mutations.

To address these questions, we developed a new mathematical model to describe the AF distribution. We modeled the dynamics of AF for mosaicisms by introducing the mutant status of each cell into a previous Galton-Watson branching process accounting for the possibility of cell death. We then generated the theoretical AF distribution by considering the accumulation of mosaicisms. We fitted our model with two large-scale pSNM data sets from noncancerous individuals (Dou et al. 2017; Huang et al. 2018) to quantitatively characterize the accumulation and AF distribution of pSNMs during normal human development, especially in regard to those arising during early embryogenesis.

Results

Modeling the AF distribution of postzygotic mosaicisms

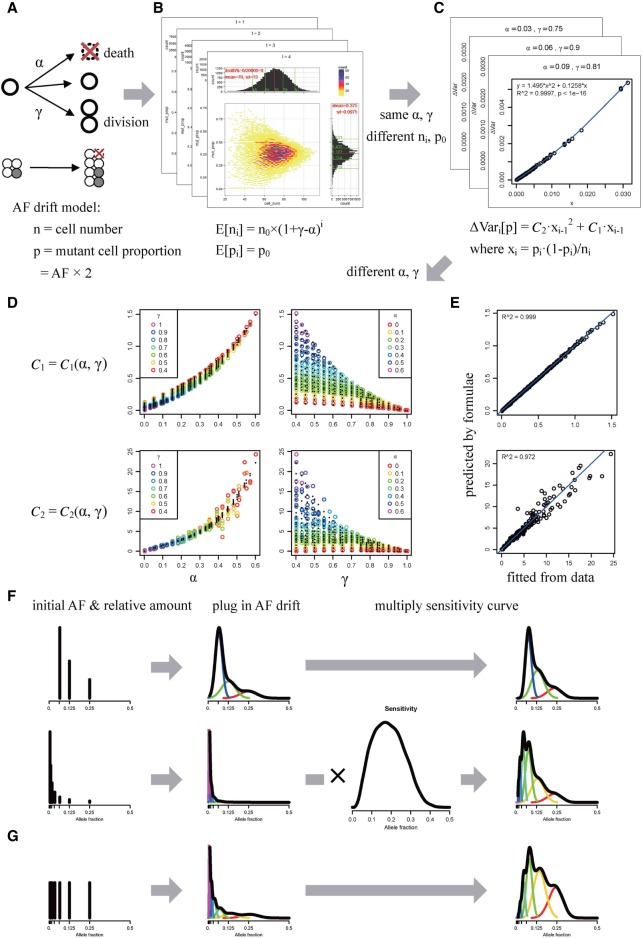
During the development of the human body, mosaicisms arise due to postzygotic mutations that have escaped from DNA repair machinery. Mutations that occurred in different time stages will lead to different initial AF of mosaicisms. The AF could further drift and deviate from its initial value due to the stochastic process of cell division and death in the development. To quantitatively describe the dynamics of AF drift, we extended the classical Galton-Watson branching process (Hardy et al. 2001) by introducing the initial mutant status of each cell in the initial cell population (Fig. 1A; Supplemental Methods). The branching process assumed cells to have synchronous cleavage, and each cell could either divide with a probability γ, die with a probability α, or do neither at each cleavage step (Fig. 1A). The behavior of the extended process was determined by the initial cell number (n₀) and initial mutant cell proportion (p₀), as well as the parameters α and γ. For a postzygotic mutation, the mutant allele is often present in a fraction of cells as heterozygous genotype and absent in the remaining cells. Therefore, the mutant cell proportion is theoretically equal to AF × 2. We simulated the cleavage branching process and analyzed the distribution of the cell number (n_i) and mutant cell proportion (p_i) after each cleavage step (Fig. 1B; Supplemental Methods). We found that the mean of cell number after i steps followed the exponential growth E[n_i] = n₀ × (1 + γ − α)ⁱ, and the mean of the mutant cell proportion remained the same at the initial mutant cell proportion E[p_i] = p₀. The variance of the mutant cell proportion introduced in each step ΔVar_i[p] = Var[p_i] − Var[p_i−1] could be well fitted by the quadratic regression, C₂ · x_i−1² + C₁ · x_i−1, where x_i = p_i · (1−p_i)/n_i (Fig. 1C; Supplemental Fig. S1). In addition, the estimated coefficients C₂ and C₁ could be further fitted as functions of α and γ (Fig. 1D,E), as shown in the following equations:

$$\begin{array}{rl}{C}_1(\alpha ,\gamma )& =0.2169687-0.3578442\cdot {\gamma }^3+3.6104356\cdot {\alpha }^3\\ & +0.5658542\cdot {\gamma }^2-0.7517724\cdot {\alpha }^2-0.4307415\cdot \gamma \\ & +1.9079553\cdot \alpha -1.1744103\cdot \gamma \cdot \alpha (R^2=0.999),\\ C_2(\alpha ,\gamma )& =141.17428\cdot {\alpha }^3-29.15594\cdot {\alpha }^2+16.76288\cdot \alpha \\ & -91.07249\cdot {\alpha }^3\cdot \gamma (R^2=0.972).\end{array}$$

Figure 1.

Model describing the accumulation and allele fraction (AF) of postzygotic mosaicisms. (A) The extended Galton-Watson branching process for cell cleavage and AF drift. In each synchronized cleavage step, a cell could die with a probability α or divide with a probability γ. Mutant status (gray) is introduced for mosaicisms, summarized as mutation cell proportion (p) with cell number (n) as parameters. (B) The simulated joint distribution of cell number (n_i, x-axis) and mutant cell proportion (p_i, y-axis) after the i cleavage steps for each combination of initial parameters (α, γ, n₀, and p₀). (C) The quadratic regression of the increment of variance of mutant cell proportion ΔVar_i[p] = Var[p_i] − Var[p_i−1] = C₂ · x_i−1² + C₁ · x_i−1, where x_i = p_i · (1−p_i)/n_i, for each combination of α and γ. The blue curve shows the fitted quadratic regression. (D) The regression of the fitted coefficients C₁ and C₂ on the combination of α and γ. The colored circles are the sample points, and the black dots show the fitted values. Different colors indicate different γ in the plot with α as the x-axis and different α in the plot with γ as the x-axis. (E) The formulas C₁(α, γ) and C₂(α, γ) predict C₁ and C₂ well. The blue line is the diagonal line. (F,G) The expected positions of the initial AF and the relative amount for mosaicisms generated in each cleavage step, assuming a constant mutation rate for simple demonstration. (F) Theoretically, the relative ratio for naturally occurring mosaicisms should be proportional to the number of haploid genomes (similar to “exponential growth”). (G) If we consider parental mosaicisms present in one child as de novo mutations, the relative ratio for each cleavage step should stay as 1. The inner bell-shape curves with different colors show the components for different cleavage steps. Parameters were set as α = 0.05 and γ = 0.95, assuming no bottleneck and a constant mutation rate, for demonstration.

With the preceding formulas, we could explicitly calculate the variance of AF drift introduced by each cleavage step for any specific p, n, α, and γ and then sum the variances of all the steps to acquire the final cumulative variance. When α and γ were constant and n_i was in exponential growth, the first 10 steps contributed to ∼90% of the variance (Supplemental Fig. S2; Supplemental Methods), suggesting that most of the variance of the AF drift would come from early cell divisions.

In theory, for the accumulation of mosaicisms when postzygotic mutations were arising, say at the i-th cleavage step, the initial AF should be the inverse of the number of haploid genomes [1/(2 · n_i)], whereas the number of mosaicisms should be proportional to the number of haploid genomes (2 · n_i) and the mutation rate [μ_c(i)] (Fig. 1F). After taking the AF drift into consideration, the AF distribution of mosaicisms generated from each cleavage step would expand from the spikes to Gaussian distributions (Fig. 1F). Therefore, we could model the theoretical AF distribution as a Gaussian mixture. Further taking into account the varied detection sensitivities for mosaicisms with different AFs, the observed AF distribution from real sequencing data would be the product of the theoretical distribution and the sensitivity curve (Fig. 1F). As shown in Supplemental Figure S3, the shape of the AF distribution depended on the relative mutation rate and death rate, suggesting that the AF distribution observed in data might be used to infer these parameters during the cell cleavage process.

We also modeled the amount of de novo mutations transmitted from postzygotic mosaicisms in the parents (transmitted parental mosaicisms). Assuming no proliferative advantage between mutant and wild-type cells, the transmission probability of a mosaicism should be equal to its AF, and the expected number of parental mosaicisms generated in the i-th cell division and present in one child was deduced to be equal to the mutation rate μ_c(i) (per haploid base pair per division) (Supplemental Methods). Compared to the AF distribution of all occurrent mosaicisms, the AF distribution of the transmitted parental mosaicisms would weigh more on mosaicisms with higher AFs, since they would be more likely to transmit the mutant alleles to offspring (Fig. 1G).

Elevated postzygotic mutation rate in early cell divisions, especially in the first division

To estimate the rate of postzygotic mosaicisms in the human genome, we analyzed two large-scale data sets generated by our laboratory. The WGS data set contained whole-genome sequencing of 25 postmortem tissues with no evidence of clonal expansion from five healthy donors, in which 159 nonclonal autosomal pSNMs were identified and validated (Huang et al. 2018). The WES data set contained whole-exome sequencing of 730 families in the Simons Simplex Collection (Fischbach and Lord 2010), in which 187 autosomal pSNMs were identified and validated from 1301 children (Dou et al. 2017). For both data sets, the identified pSNMs were thoroughly validated by targeted ultradepth resequencing (Xu et al. 2015) with an average depth-of-coverage of ∼4000–10,000× (Dou et al. 2017; Huang et al. 2018).

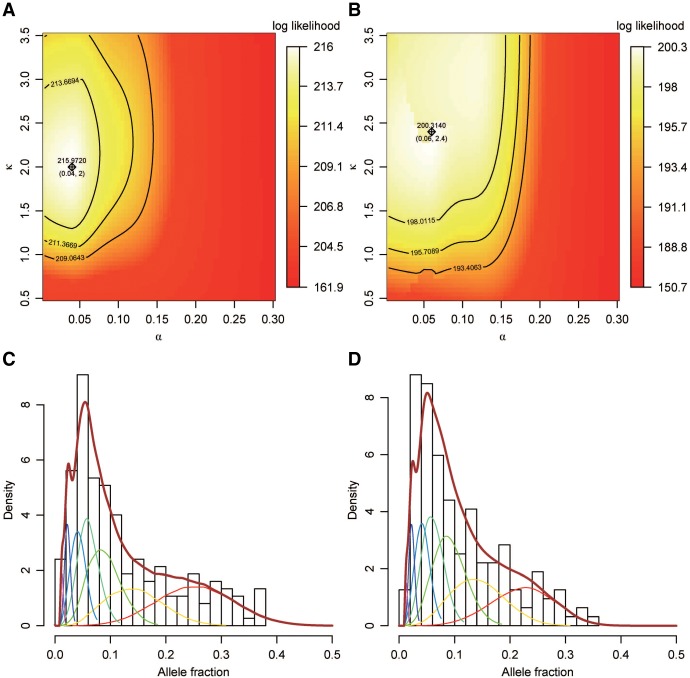
We applied a maximum likelihood approach to fit our model using these two data sets (Supplemental Methods). Because evidence shows that characteristic cell death would not appear before the third cell division in human embryos (Hardy et al. 2001), we introduced cell death from the third division and set the death rate α to zero for the first two divisions. We also introduced a “bottleneck” with 50% death rate at the sixth division (about 16 cells randomly selected from 32 cells, and then dividing to 32 cells if in complete bifurcation), according to the differentiation of inner cell mass during the blastocyst stage (Hardy et al. 1989). In addition, because it was reported that the mutation rate might be higher during the first cell division in Drosophila (Gao et al. 2011), we allowed the mutation rate of the first cell division to be different from the mutation rate of the latter divisions and set κ as the relative ratio between the first and latter divisions. As shown in Figure 2A and B, the maximum likelihood estimate (MLE) of death rate α was ∼0.04–0.06 in both data sets, and κ was estimated to be ∼2–2.4, with the 10% likelihood interval not overlapping κ = 1. Consistent with the observation in Drosophila (Gao et al. 2011), our analysis suggested a significantly elevated mutation rate of the first cell division relative to the latter divisions in human embryos. We then merged both data sets and found the MLE of α and κ was 0.05 and 2.15, respectively, which fitted both data sets well; these were used in further analyses (Fig. 2C,D). With the estimated parameters (Supplemental Table S1) and correction for the pSNM detection sensitivity (Supplemental Fig. S4), we estimated the mutation rate to be ∼8 × 10⁻¹⁰ per haploid base pair per division for the first cell division and ∼3.7 × 10⁻¹⁰ for latter divisions (Supplemental Table S2). Since the majority of postzygotic mosaicisms we studied should occur during early embryogenesis, which is much earlier than the timing of sexual differentiation, we expected a similar occurrence rate of postzygotic mosaicisms between males and females. Indeed, we observed 132 and 55 validated autosomal pSNMs in 897 male and 404 female children of the WES data set (Supplemental Table S3), suggesting no sex difference in the occurrence of mosaicisms (P-value = 0.6, Poisson regression).

Figure 2.

Maximum likelihood estimation (MLE) of cell death rate (α) and relative mutation rate ratio (κ) with the observed AF distribution. (A,B) Contour plots of the likelihood of our model fitted on the (A) WES and (B) WGS data sets. The x-axis denotes the death rate (α), and the y-axis denotes the relative ratio of the mutation rate between first division and latter divisions (κ). The MLEs of α and κ and the corresponding log likelihood are labeled with a cross. The curves from inside to outside show 10%, 1%, and 0.1% likelihood intervals, respectively. Aside from α and κ, the division rate (γ) is free to change, whereas the other parameters “mut steps,” “death from,” “bottleneck at,” bottleneck α, and bottleneck γ are set to 7, 3, 6, 0.5, and 0.5, respectively (Supplemental Table S1; Supplemental Methods). (C,D) Histogram of the AF distributions observed in the (C) WES and (D) WGS data sets. The thick brown curves denote the MLE-fitted, observed AF distribution with α = 0.05, γ = 0.95, and κ = 2.15. The thin inner bell-shape curves with different colors denote the components for different cleavage steps.

We then estimated the average mutation rate per cell division from de novo heterozygous mutations and compared it with the mutation rate we estimated from pSNMs. Based on the trio sequencing data from the WES data set of 1301 children, a list of 1571 single-nucleotide de novo mutations in 1295 children with known parental ages at children's birth was obtained, after excluding sites that were validated as pSNMs but misidentified as de novo mutations in previous studies (Iossifov et al. 2014; Dou et al. 2017). Considering the effective base pair number for detecting de novo mutations (Supplemental Methods), the single-nucleotide de novo mutation rate was 2μ_d ≈ 2.5 × 10⁻⁸ per diploid base pair per generation. As 75%–90% of de novo mutations were reported to be of paternal origin (Venn et al. 2014; Yuen et al. 2016), the average per-division mutation rate was about 4.2–5.1 × 10⁻¹¹ and 0.8–2.4 × 10⁻¹⁰ per haploid base pair in the father and mother, respectively (Supplemental Table S4). The different average mutation rates of germline cells from males and females might be explained by a reduced mutation rate during post-pubertal spermatogenesis (Rahbari et al. 2016). As a result, the mutation rate during early embryogenesis is significantly higher than the average mutation rate per cell division in either male or female gametes. The male and female gamete mutation rate is only 14% and 67% as high as the early embryonic mutation rate, respectively. This conclusion also remained consistent if we only considered the pSNMs identified from the WES data set (Supplemental Table S2).

Parental mosaicisms occurring during the first three cell divisions contribute to ∼10% of the de novo mutations in children

In clinical applications, a heterozygous mutation is defined as “de novo” if the mutant allele is undetectable in both parents. Previous studies have demonstrated that some mutations thought to be “de novo” were actually inherited from parental mosaicisms that were missed by conventional Sanger sequencing (Jones et al. 2001; Depienne et al. 2006; Chen et al. 2014). Based on our model, assuming that most mutations are neutral and the mutation rate is constant for each division, the contribution of parental mosaicisms to de novo mutations would be linearly proportional to the number of cell divisions in which the detectable mosaicisms occurred, and parental mosaicisms occurring in the first 10 cell divisions would contribute to ∼5%–10% of de novo mutations. (Supplemental Fig. S5). With the elevated mutation rate for early cell divisions estimated from the pSNM data sets, the contribution of early parental mosaicisms would be increased, which would reach to ∼10% for parental mosaicisms that had occurred in just the first three cell divisions (with AF greater than ∼4%) (Supplemental Fig. S5).

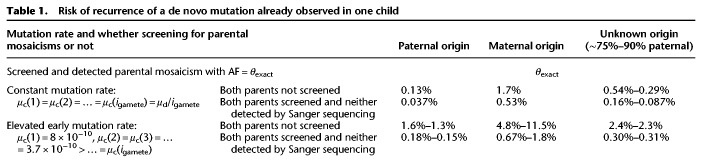
Theoretically, parents with detectable mosaicism should have a much higher possibility to have children with recurrent de novo mutations. Using a Bayesian framework based on our model, we estimated the risk of recurrence for de novo mutations that were already observed in one child. Similar to previous estimates (Campbell et al. 2014), when assuming a constant mutation rate for each division, the risk of recurrence for de novo mutations already observed in one child would be 1.7% for maternal origin and 0.13% for paternal origin (Table 1). However, when we considered the elevated mutation rate in early cell divisions, the risk of recurrence would be as high as 4.8%–11.5% for maternal origin and 1.3%–1.6% for paternal origin (Table 1), which is an approximately threefold to 10-fold elevation compared to that of a constant mutation rate. Our model also demonstrated the value of screening for parental mosaicisms during genetic counseling (1) if a corresponding parental mosaicism was detected with confirmed AF (θ_exact), the recurrence risk would equal to θ_exact; otherwise, (2) if a corresponding parental mosaicism was not detected by a detection method with a lower AF threshold θ_L, the recurrence risk would be reduced to approximately θ_L/40 to θ_L/2.5, and this would be higher for mosaicisms of maternal origin compared to that of paternal origin (Supplemental Fig. S6). For instance, considering that conventional Sanger sequencing can only detect mosaicisms with an AF of 5% or more (Depienne et al. 2006; Chen et al. 2014; Xu et al. 2015), screening parental mosaicism by Sanger sequencing might reduce the risk of recurrence to ∼0.67%–1.8% for maternal origin or ∼0.15%–0.18% for paternal origin.

Table 1.

Risk of recurrence of a de novo mutation already observed in one child

Distance measure between tissues based on the AF of shared mosaicisms

After a postzygotic mutation has occurred, all daughter cells would carry the mutant allele. Therefore, the similarity of profiles for postzygotic mosaicisms could theoretically reflect the cell lineage tree across different tissues from the same individual. Our model predicted that mosaicisms with different AFs should have different variances for AF drift; thus, the Euclidean distance between vectors of AFs for shared mosaicisms is theoretically improper due to the different variance between elements. To stabilize the variance of AFs, we proposed $\mathrm{Var}\left[(p_2-p_1)/\sqrt{p_0\cdot (1-p_0)}\right]$ as the measure of inter-tissue distance, where p₀, p₁, and p₂ are the mutant cell proportion (AF × 2) in the ancestor cell population, one tissue sample, and the other tissue sample, respectively (Methods; Fig. 3A). This distance was solely based on the AF of shared pSNMs between tissues, assuming that each tissue had undergone an independent developmental process from the most recently common ancestral cell population (Fig. 3A).

Figure 3.

Measuring inter-tissue distance based on the AF similarity of shared mosaicism. (A) The AF difference of shared mosaicisms in two tissues could be traced back to their most recent common ancestral cell population, but not to an earlier stage when the mosaicisms were generated. (B,C) Clustering trees based on the pairwise distance matrix estimated from the WGS data set for (B) males and (C) females. The bootstrapping values labeled on the internal branches show the bootstrap supporting percentage on the partition of that branch.

To assess the performance of this pSNM-based measure, we applied it against the pSNM profiles of five individuals from the WGS data set. Considering that the developmental process was generally identical across individuals, our method enabled us to combine the pSNM lists identified from the specific tissues of multiple individuals. We clustered the tissues from males and females separately based on the pairwise distance matrix between tissues. As shown in Figure 3, B and C, colon and liver were closely clustered, whereas skin shared more similarity with prostate or breast than brain, colon, or liver. These results were in accordance with the knowledge that colon and liver are endodermal, brain is ectodermal, whereas skin, breast, and prostate are mixtures of ectodermal and mesodermal origins (Pansky 1982; Argani et al. 1998; Gilbert 2003).

Discussion

The drift of newly arisen mutations among cells of one individual shares many similarities to the drift of variants among individuals in a growing population. Previous studies in population genetics had developed the Wright-Fisher model (Fisher 1922; Wright 1931, 1939) or Moran model (Moran 1958) to describe the genetic drift, and diffusion approximation can be applied in a large population (Kimura 1954, 1955). However, a human embryo develops from a zygote and contains only a few cells in the first several divisions of embryogenesis, and the approximate linear formula might be unsuitable for such a small population size (Supplemental Fig. S1). Here, we proposed a quantitative model for describing postzygotic mosaicisms, which was derived from the Galton-Watson branching process that had been commonly used to model the dynamics of rare alleles and exponential population growth. Since our model focused on neutral postzygotic mosaicisms, we applied our model to analyze the AF distribution of pSNMs from two data sets after excluding those sites with evidence of clonal expansion (Dou et al. 2017; Huang et al. 2018), because they might be driven by selective advantage between mutant and wild-type cells (Abyzov et al. 2017).

Recently, Ju et al. (2017) reported a decrease of 25% AF on the AF distribution and thus explained the phenomenon by the asymmetric contribution of daughter cells resulting from a bottleneck during early embryogenesis. However, we did not observe a decrease of 25% AF in the two data sets we used (Fig. 2C,D). Based on our simulation, a decrease at expected initial AF could only be led by asymmetric contribution restricted to a small range deviated from 0.5, or a nonrandom bottleneck in complete bifurcating cleavage (Supplemental Fig. S7). When introducing deterministic asymmetric contribution into our model, the estimated contribution of the two daughter cells at the two-cell stage was about 0.6:0.4. However, the fitting was usually not significantly better than the symmetric setting (likelihood ratio test), except for the most flexible model (Supplemental Table S5; Supplemental Methods). In addition, the sensitivity for detecting mosaicism in Ju et al. (2017) was lower (peak value <5%) than our method (Huang et al. 2017). Further studies with a larger sample size and better detection methods might be required to resolve these conflicting observations.

We estimated the embryonic postzygotic mutation rate as being 8 × 10⁻¹⁰ per haploid base pair per division for the first cell division and 3.7 × 10⁻¹⁰ for latter divisions, whereas the average mutation rate estimated from de novo mutations was 4.2–5.1 × 10⁻¹¹ per haploid base pair per division in germline cells from males versus 0.8–2.4 × 10⁻¹⁰ in germline cells from females. The observed elevated mutation rate during the early cell divisions and the first cell division was robust when assuming complete bifurcating cleavage and allocation of pSNMs into different AF groups (Supplemental Table S6). In addition, we examined and found that adding noise to observed AF, relaxing some parameter constraints in maximum likelihood estimation, allowing changeable death rate and division rate, or taking asymmetric contribution into consideration did not affect the two main findings: (1) Postzygotic mutation rate during early cell divisions was higher than the average mutation rate per cell division estimated from de novo mutations; and (2) the mutation rate of the first division was even higher than the mutation rate of the latter divisions (Supplemental Table S5; Supplemental Fig. S8; Supplemental Methods). Furthermore, we found that introducing changeable death rate and division rate did not fit the AF distribution significantly better (P-value > 0.6, likelihood ratio test).

Our model demonstrated that postzygotic mosaicisms could be regarded as a partition along the mutation process in the germline lineage, and the amount of mosaicisms that can be detected should exponentially increase with a lower detection threshold of AF. We reported that early parental mosaicisms in the first three cell divisions contributed to ∼10% of de novo mutations in the offspring, which was close to a previous estimation of 8.6% observed for Dravet syndrome (Xu et al. 2015). We further highlighted an elevated risk of recurrence for de novo mutations in the offspring when early divisions had elevated mutation rates. Since mutations with different AFs showed varied impacts on the disease phenotype (Meng et al. 2015), the AF distribution of mosaicism could be different between healthy and disease-associated genomes. Theoretically, we could extend our model by introducing more parameters, including prebirth lethality 1−v(θ), post-birth penetrance p(θ), and fertility r(θ) (Supplemental Table S7; Supplemental Methods), but the accurate estimation of such parameters requires more data from different disease states.

For screening parental mosaicism, it was ideal to use gametes, such as sperm samples, rather than blood samples. As shown in previous findings, mosaicisms with high AF were probably shared in multiple tissues, indicating their early arising during embryogenesis and the usage of blood sample for screening parental mosaicisms (Huang et al. 2014; Yang et al. 2017). Since blood stem cells and germline stem cells are known to segregate at roughly the 15th division (Campbell et al. 2014), germline mosaicisms with low AF that have occurred after blood–germline segregation (AF lower than ∼3 × 10⁻⁵) could be only detectable in gametes but not blood samples. In addition, mosaicisms may occur later and rise to high AF as a result of clonal expansion (Goriely et al. 2013; Xie et al. 2014; Huang et al. 2018), which has not been modeled in this work. Screening parental mosaicisms from blood samples may miss the germline mosaicisms under selfish selection, which may cause serious diseases such as Costello syndrome (Goriely et al. 2013). Therefore, the AF of mosaicisms in germline and blood samples may be different, and the results of clinical application of blood test for parental mosaicisms should be interpreted with caution.

We noticed that our distance measure based on AF of shared mosaicisms was similar to F_ST and the F-statistics applied in population genetics (Reich et al. 2010; Patterson et al. 2012). All of these metrics used p · (1−p) as the denominator to normalize the metric, which was required when attempting to combine information from different sites with different frequencies p. The distance measure could also be calculated by the procedure proposed for normalized F-statistic (Reich et al. 2010; Patterson et al. 2012), which gave different weight for each site and produced results similar to our procedure (Supplemental Table S9; Supplemental Methods). We inferred the lineage tree of multiple types of tissue obtained from five donors, assuming the developmental process of tissues is generally identical across individuals. Our result suggested that skin was clustered with prostate or breast rather than brain. Considering that our skin samples consisted of more dermis than epidermis, this clustering pattern could be explained by the shared mesodermal origin between dermis, prostate, and breast. F-statistics have been demonstrated to infer mixture in population genetics, which could be potentially applied to study mosaicisms.

In this study, we modeled the accumulation and AF distribution of postzygotic mosaicisms by formulating the AF drift and generating a theoretical AF distribution as a Gaussian mixture, with consideration of cell death during zygote cleavage. Our model provided an estimation regarding the occurrence rate of postzygotic mutations and highlighted their roles in the origination of de novo mutations. With the development of next-generation sequencing techniques and growing data sets regarding postzygotic mosaicisms, we should be better able to test our model and describe the dynamics of postzygotic mosaicisms in the future. Our work sheds new light on the quantitative characterization of postzygotic mosaicisms in human development and provides guidance for screening mosaicism for use in clinical applications.

Methods

Estimation of mosaicism occurrence rate

To estimate the mutation rate, we calibrated the pSNM detection sensitivity for the WGS and WES data sets (Supplemental Fig. S4) by mixing, in silico, the sequencing reads of two well-genotyped individuals, NA12878 and NA12891 (Supplemental Table S8), following published protocols (Huang et al. 2014, 2017). We quantified the number of effective base pairs after filtering out repeat regions. Considering the relatively low sensitivity for detecting pSNMs from low-coverage regions (Huang et al. 2014, 2017), we only focused on the sites with depth ≥40× (baseQ ≥ 20 and mapQ ≥ 20). This filter was also applied to the validated mosaicisms in the WGS data set (Huang et al. 2018) and the WES data set (Dou et al. 2017).

To compare the mosaicism occurrence rate and the de novo mutation rate, we unified the unit to the mutation rate per haploid base pair per cell division. The average mutation rate per haploid base pair per division was calculated by dividing the de novo mutation rate per (paternal or maternal) haploid base pair per generation μ_d by the cell division number from zygote to sperm in the father or from zygote to egg in the mother (Supplemental Table S4) as follows:

$${\overline{\mu }}_{\mathrm{c}}={\mu }_{\mathrm{d}}/i_{\mathrm{gamete}}=\{\begin{array}{c}{\mu }_{\mathrm{d},\mathrm{paternal}}/i_{\mathrm{sperm}},\mathrm{for}\mathrm{father}\\ {\mu }_{\mathrm{d},\mathrm{maternal}}/i_{\mathrm{egg}},\mathrm{for}\mathrm{mother}\end{array}$$

The data set we used for estimating average mutation rate is the same WES data set from Simons Simplex Collection (Fischbach and Lord 2010), with detailed information of parental ages at children's birth (Iossifov et al. 2014, Supplementary Table 1). For the cell division number in the father, we took the paternal age into consideration and estimated the cell division number for each father with the formula 34+23 × (father_age_at_child_birth−38 × 7/365−15) + 4 (Rahbari et al. 2016, Supplementary Figure 1).

For pSNMs, the detection sensitivity varied across the different AF (Huang et al. 2014, 2017), which should be taken into consideration. We introduced constant death rate (α) and division rate (γ) from the third division, leaving the first two divisions completely bifurcating (set α = 0 and γ = 1). We introduced the relative ratio of the mutation rate for the first cell division to the mutation rate of latter divisions (κ). We estimated α, γ, and κ from the two data sets using a maximum likelihood approach (Supplemental Methods). We then estimated the mutation rate by dividing the amount of pSNMs allocated for each cell division by the effective base pair number and expected number of haploid genomes, after calculating the theoretical proportion of pSNMs for each cell division adjusted for the sensitivity and the probability reaching fixed or lost (AF reaching 0.5 or 0) (Supplemental Table S2). For details, see Supplemental Methods.

Contribution of parental mosaicisms to de novo mutations in children

Assuming no selection between mutant and wild-type cells, our model showed that the expected amount of parental mosaicisms occurred at the i-th cleavage step and transmitted to one child was equal to μ_c(i), the mutation rate per haploid base pair for the i-th cell division. Denote μ_d as the de novo mutation rate per haploid base pair per generation, then ${\mu }_{\mathrm{d}}\approx {\sum }_{i=1}^{i_{\mathrm{gamete}}}{\mu }_{\mathrm{c}}(i)$, where i_gamete is the number of cell divisions along the germline lineage from zygote to gamete. Therefore, the contribution of parental mosaicisms occurring in the $i_{{\theta }_{\mathrm{U}}}\sim i_{{\theta }_{\mathrm{L}}}$-th cell division to de novo mutations in children could be written as ${\sum }_{{i=i}_{{\theta }_{\mathrm{U}}}}^{i_{{\theta }_{\mathrm{L}}}}{\mu }_{\mathrm{c}}(i)/{\sum }_{i=1}^{i_{\mathrm{gamete}}}{\mu }_{\mathrm{c}}(i)$, which could be regarded as a partition along the mutation process in the germline lineage. With the estimated elevated mutation rate for pSNMs (μ_c(1) ≈ 8 × 10⁻¹⁰ for the first cell division, and μ_c(2) ≈ μ_c(3) ≈ μ_c(4) ≈ 3.7 × 10⁻¹⁰ for later divisions), after calculating ${\mu }_{\mathrm{c}}^{\mathrm{\prime }}(i)$ adjusted for fixation or lost (Supplemental Table S2), the proportion of two times (for both parents) the cumulative mutation rate in the diploid de novo mutation rate $2[{\mu }_{\mathrm{c}}^{\mathrm{\prime }}(1)+{\mu }_{\mathrm{c}}^{\mathrm{\prime }}(2)+\cdots ]/2{\mu }_{\mathrm{d}}$ was calculated, as shown in Supplemental Figure S5. For details, see Supplemental Methods.

Recurrence risk

The risk of recurrence for de novo mutations could be calculated in a Bayesian framework derived from the mosaicism accumulating process. The recurrence risk of a mosaicism already known to have been transmitted to one child can be deduced as

$$R{R}^{(1)}=\int {\mu }_{\mathrm{m}}^{(1)}(\theta )\theta \text{d}\theta \approx \sum _{i=1}^{i_{\mathrm{gamete}}}\frac{{\mu }_{\mathrm{c}}(i)}{{\sum }_{j=1}^{i_{\mathrm{gamete}}}{\mu }_{\mathrm{c}}(j)}\cdot \frac{1}{2n(i)}=\sum _{i=1}^{i_{\mathrm{gamete}}}\frac{{\mu }_{\mathrm{c}}(i)}{{\mu }_{\mathrm{d}}}\cdot \frac{1}{2n(i)}$$ (1)

When the mutation has been screened to confirm the mosaic AF status in both parents:

1. If we detect the mosaicism with AF = θ_exact in the gametes of either parent, then the recurrence risk will become θ_exact.

2. If we could not detect the mosaicism with AF ≥ θ_L in either parent, then the recurrence risk will become

   $$R{R}^{(1^{\mathrm{\prime }})}\approx \sum _{i=i_{{\theta }_{\mathrm{L}}}}^{i_{\mathrm{gamete}}}\frac{{\mu }_{\mathrm{c}}(i)}{{\sum }_{j=i_{{\theta }_{\mathrm{L}}}}^{i_{\mathrm{gamete}}}{\mu }_{\mathrm{c}}(j)}\cdot \frac{1}{2n(i)}=\sum _{i=i_{{\theta }_{\mathrm{L}}}}^{i_{\mathrm{gamete}}}\frac{{\mu }_{\mathrm{c}}(i)}{{\mu }_{\mathrm{d}}-{\sum }_{j=1}^{i_{{\theta }_{\mathrm{L}}}-1}{\mu }_{\mathrm{c}}(j)}\cdot \frac{1}{2n\left(i\right)}$$ (2)

The paternal contribution to the origin of a de novo mutation was set to ∼75%–90% (Venn et al. 2014; Yuen et al. 2016), which influenced the estimate of the de novo mutation rate μ_d per paternal or maternal haploid. For numerical estimation of recurrence risk, here we set the number of cell divisions i_gamete as 30 for maternal egg or 400 for paternal sperm, which was estimated assuming 30-year-old parents (Rahbari et al. 2016). For a constant mutation rate, the mutation rate μ_c(i) was set to the average mutation rate μ_d/i_gamete, assuming no bottleneck. For an elevated early mutation rate, the risk of recurrence was conservatively estimated assuming that the mutation rate of all early divisions was 3.7 × 10⁻¹⁰ (per haploid base pair per division), with the exception of 8 × 10⁻¹⁰ for the first division, which might coerce the later mutation rate close to 0. For Sanger screening, the lower detection limit θ_L is set to ∼5%; therefore, we set the corresponding $i_{{\theta }_{\mathrm{L}}}\approx 3$. The numerical results are shown in Table 1. For details, see Supplemental Methods.

Measuring the distance between tissues by the variance of the AF difference between shared mosaicisms

When the initial cell number of a tissue differentiated from the common ancestor cell population was large (n₀ ≥ 40), the quadratic term of AF drift C₂ · x² could be omitted, and the final AF of a neutral mosaicism in a tissue (p₁/2) would approximately follow the normal distribution (Fig. 3A)

$$p_1\sim N\left(p_0,\frac{p_0(1-p_0)}{n_{0,1}}\cdot \sum _i\frac{C_1({\alpha }_1,{\gamma }_1)}{{(1+{\gamma }_1-{\alpha }_1)}^i}\right).$$

The expectation stays at p₀ and the variance can be decomposed into two parts: p₀ · (1−p₀), which is dependent on the AF itself, and

$$d_1:=\frac{1}{n_{0,1}}\cdot \sum _i\frac{C_1({\alpha }_1,{\gamma }_1)}{{(1+{\gamma }_1-{\alpha }_1)}^i},$$

which represents the developmental process from the ancestor cell population to the mature tissue. Assuming the two tissues developed independently after differentiation from their most recent common ancestral cell population, we would have

$$\begin{array}{rl}& (p_2-p_1)\sim N(0,p_0(1-p_0)\cdot (d_1+d_2))\\ & \Rightarrow \text{Var}[p_2-p_1]=E\left[{(p_2-p_1)}^2\right]=p_0(1-p_0)\cdot (d_1+d_2)\end{array}$$

Since the distance (d₁ + d₂) is dependent only on the developing processes of the two tissues and should be stable for a specific pair of tissues, we proposed a distance measure

$$\text{Var}\left[\frac{p_2-p_1}{\sqrt{p_0(1-p_0)}}\right]=E\left[{(\frac{p_2-p_1}{\sqrt{p_0(1-p_0)}})}^2\right]$$

to estimate (d₁ + d₂) between tissues, which could normalize and summarize the AF difference of each neutral mosaicism shared in two specific tissues to estimate the relative distance between tissues.

In the real WGS data, we used ${\hat{p}}_0=(p_1+p_2)/2$ as a simple guess of p₀, and $\mathrm{Var}[(p_2-p_1)/\sqrt{{\hat{p}}_0(1-{\hat{p}}_0)}]$ was calculated using

$${\left(\text{MAD}\left[\frac{p_2-p_1}{\sqrt{{\hat{p}}_0(1-{\hat{p}}_0)}}\right]\right)}^2$$

where median absolute deviation MAD[x] = 1.4826 × median(abs(x)), to make the estimate less sensitive to outliers.

Based on the pairwise distance matrix between multiple tissues, hierarchical clustering was carried out using the Ward agglomeration method. To evaluate the confidence of the clustering results, we performed bootstrapping by resampling the mosaicisms shared between two tissues and obtained a bootstrap distribution of the distance. We reported the clustering trees in which all the bootstrapping values were 65 or greater. For details, see Supplemental Methods.